Communications and Network
Vol.2 No.2(2010), Article ID:1867,4 pages DOI:10.4236/cn.2010.22021
Multiobjective Duality in Variational Problems with Higher Order Derivatives
1Department of Mathematics, Jaypee Institute of Engineering and Technology, Guna, India
2Department of Statistics, University of Kashmir, Srinagar, India
E-mail: {ihusain11, rumana_research}@yahoo.com
Received December 16, 2009; revised April 25, 2010; accepted April 30, 2010
Keywords: Multiobjective Variational Problem; Efficiency, Duality, Pseudoinvexity, Quasinvexity, Nonlinear Programming
Abstract
A multiobjective variational problem involving higher order derivatives is considered and optimality conditions for this problem are derived. A Mond-Weir type dual to this problem is constructed and various duality results are validated under generalized invexity. Some special cases are mentioned and it is also pointed out that our results can be considered as a dynamic generalization of the already existing results in nonlinear programming.
1. Introduction
Calculus of variation is a powerful technique for the solution of various problems appearing in dynamics of rigid bodies, optimization of orbits, theory of variations and many other fields. The subjects whose importance is fast growing in science and engineering primarily concern with finding optimal of a definite integral involving a certain function subject to fixed point boundary conditions. In [1] Courant and Hilbert, quoting an earlier work of Friedrichs [2], gave a dual relationship for a simple type of unconstrained variational problem. Subsequently, Hanson [3] pointed out that some of the duality results of mathematical programming have analogous in variational calculus. Exploring this relationship between mathematical programming and the classical calculus of variations, Mond and Hanson [4] formulated a constrained variational problem as a mathematical programming problem and using Valentine’s [5] optimality conditions for the same, presented its Wolfe type dual variational problem for validating various duality results under convexity. Later Bector, Chandra and Husain [6] studied Mond-Weir type duality for the problem of [4] for weakening its convexity requirement. In [7] Chandra, Craven and Husain studied optimality and duality for a class of non-differentiable variational problem with non-differentiable term in the integrand of the objective functional while in [8] they derived optimality conditions and duality results for a constrained variational problem having terms with arbitrary norms in the objective as well as constrained functions.
Recently Husain and Jabeen [9] studied a wider class of variational problem in which the arc function is twice differentiable by extending the notion of invexity given in [10]. They obtained Fritz John as well as KarushKuhn-Tucker necessary optimality conditions as an application of Karush-Kuhn-Tucker optimality conditions studied various duality results for Wolfe and Mond and Weir type models.
In single objective programming we must settle on a single objective such as minimizing cost or maximizing profit. However, generally any real world problems can be identified with multiple conflicting criteria e.g., the problems of oil refinery scheduling, production planning, portfolio selection and many others can be modelled as multiobjective programming problems.
Duality results are very useful in the development of numerical algorithms for solving certain classes of optimization problems. Duality for multiobjective variational problem has been studied by a number of authors, notably Bector and Husain [11], Chen [12] and many others cited in these references. Applications of duality theory are prominent in physics, economics, management sciences, etc.
Since mathematical programming and classical calculus of variations have undergone independent development, it is felt that mutual adaptation of ideas and techniques may prove useful. Motivated with this idea in this exposition, we propose to study optimality criteria and duality for a wider class of multiobjective variational problems involving higher order derivative. These results not only generalize the results of Husain and Jabeen [9] and Bector and Husain [11] but also present a dynamic generalization of some of the results in multiobjective nonlinear programming already existing.
2. Invexity and Generalized Invexity
Invexity was introduced for functions in variational problems by Mond, Chandra and Husain [10] while Mond and Smart [13] defined invexity for functionals instead of functions. Here we introduce extended forms of definitions of invexity and various generalized invexity for functional in variational problems involving higher order derivatives.
Consider the real interval 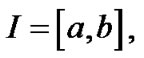 and the continuously differentiable function
and the continuously differentiable function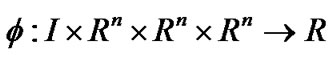 , where x is twice differentiable with its first and second order derivatives
, where x is twice differentiable with its first and second order derivatives 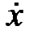 and
and 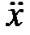 respectively. If
respectively. If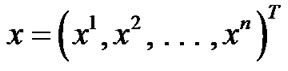 , the gradient vectors of f with respect to
, the gradient vectors of f with respect to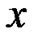 ,
, 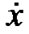 and
and 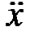 respectively denoted by
respectively denoted by
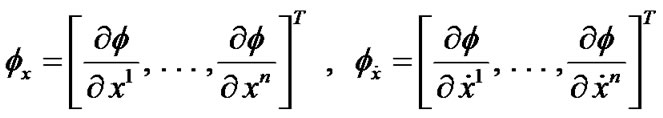
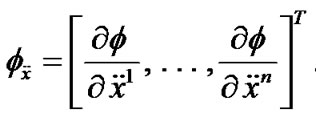
DEFINITION 1. (Invexity): If there exists vector function 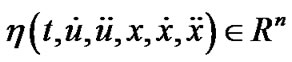 with
with 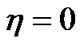 and
and 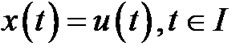 and
and 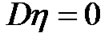 for
for 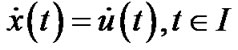 such that for a scalar function
such that for a scalar function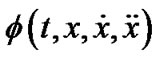 , the functional
, the functional 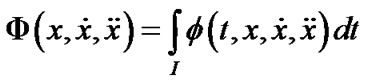 satisfies
satisfies
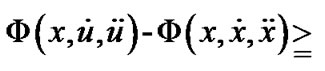
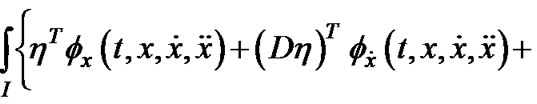
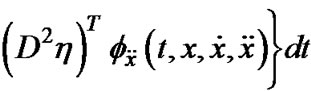
Φ is said to be invex in 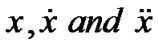 on I with respect to η.
on I with respect to η.
Here D is a differentiation operator defined later.
DEFINITION 2. (Pseudoinvexity): Φ is said to be pseudoinvex in 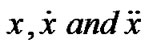 with respect to
with respect to 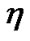 if
if
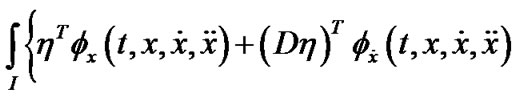

implies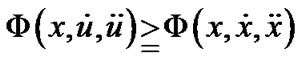 .
.
DEFINITION 3. (Quasi-invex): The functional Φ is said to quasi-invex in 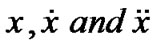 with respect to η if
with respect to η if
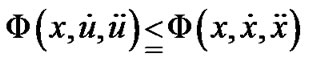 implies
implies
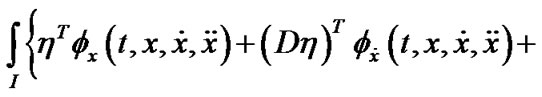
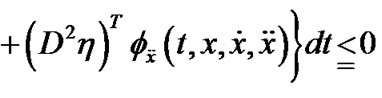
3. Variational Problem and Optimality Conditions
Before stating our variational problem and deriving its necessary optimality condition, we mention the following conventions for vectors x and y in n-dimensional Euclidian space Rn will be used throughout the analysis of this research.
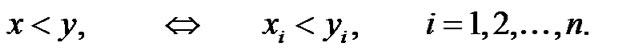 x
x
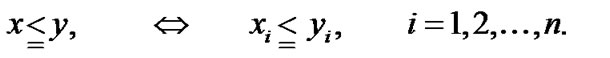
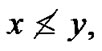
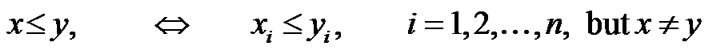 is the negation of
is the negation of 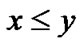
For 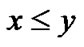
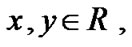 and
and 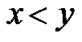 have the usual meaning.
have the usual meaning.
In this section, we present the following variational problem whose optimality conditions will be derived and duality will be investigated in the subsequent sections:
(VPE) Minimize
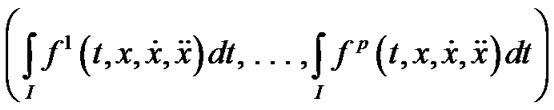
Subject to
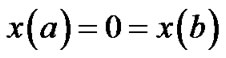 (1)
(1)
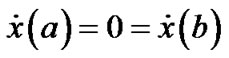 (2)
(2)
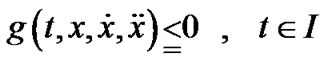 (3)
(3)
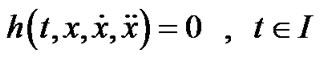 (4)
(4)
where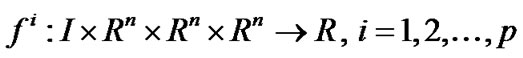 ,
,
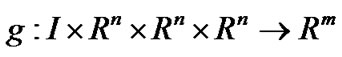 and
and 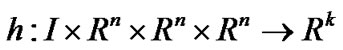 are continuously differentiable functions, and X designates the space of piecewise functions
are continuously differentiable functions, and X designates the space of piecewise functions 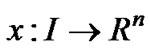 possessing derivatives
possessing derivatives 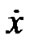 and
and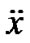 with the norm
with the norm 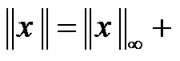
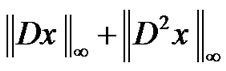 , where the differentiation operator D is given by
, where the differentiation operator D is given by
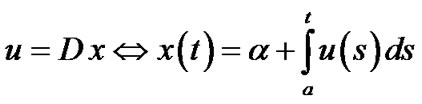
where α is given boundary value; thus 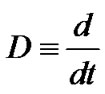 except at discontinuities.
except at discontinuities.
In the results to follow, we use 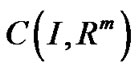 to denote the space of continuous functions
to denote the space of continuous functions 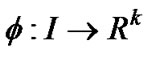 with the uniform norm
with the uniform norm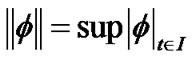 ; the partial derivatives of g and h are
; the partial derivatives of g and h are 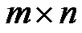 and
and 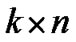 matrices respectively; superscript T denotes matrix transpose.
matrices respectively; superscript T denotes matrix transpose.
We require the following definition of efficient solution for our further analysis.
DEFINITION 4. (Efficient Solution): A feasible solution 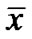 is efficient for (VPE) if there exist no other feasible
is efficient for (VPE) if there exist no other feasible 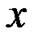 for (VPE) such that for some
for (VPE) such that for some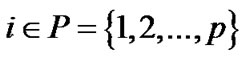 ,
,
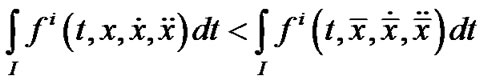
and 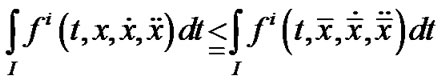 for all
for all ,
, .
.
In relation to (VPE), we introduce the following set of problems 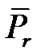 for each
for each 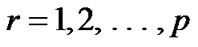 in the spirit of [14], with a single objective,
in the spirit of [14], with a single objective,
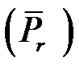 Minimize
Minimize 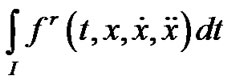
Subject to
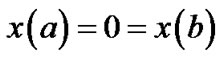 ,
,
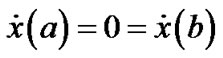 ,
,
 ,
,
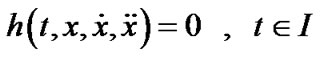 ,
,
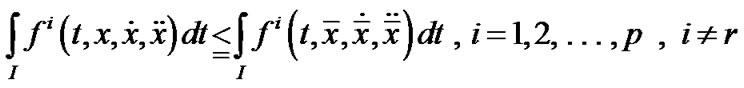
The following lemma can be proved on the lines of Chankong and Haimes [14].
LEMMA 1: 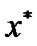 is an efficient solution of (VPE) if and only if
is an efficient solution of (VPE) if and only if 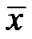 is an optimal solution of
is an optimal solution of 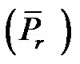 for each
for each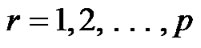 .
.
(P0) Minimize 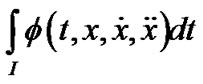
Subject to
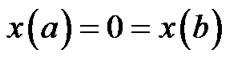 ,
,
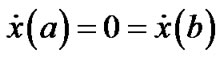 ,
,
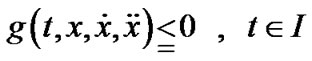 ,
,
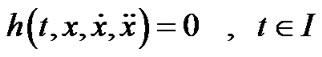 where
where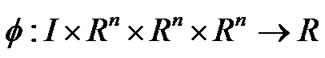 .
.
PROPOSITION 1. [9]: (Fritz John Optimality Conditions) If  is an optimal solution of (P0) and
is an optimal solution of (P0) and 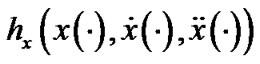 maps X into the subspace of
maps X into the subspace of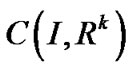 , then there exists Lagrange multiplier
, then there exists Lagrange multiplier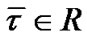 , the piecewise smooth
, the piecewise smooth 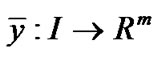 and
and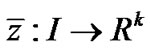 , such that
, such that
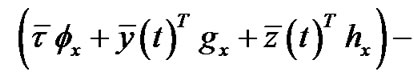
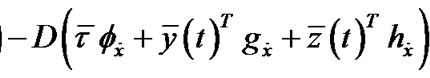
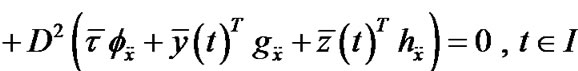
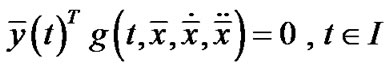 ,
,
 ,
,
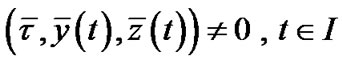 .
.
If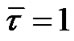 , then the above optimality conditions will reduce to the Karush-Kuhn-Tucker type optimality conditions and the solution
, then the above optimality conditions will reduce to the Karush-Kuhn-Tucker type optimality conditions and the solution 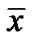 is referred to as a normal solution.
is referred to as a normal solution.
We now establish the following theorem that gives the necessary optimality conditions for (VPE).
THEOREM 1: (Fritz-John Conditions): Let 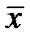 be an efficient solution of (VPE) and
be an efficient solution of (VPE) and 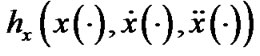 maps X into the subspace of
maps X into the subspace of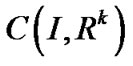 , then there exist
, then there exist 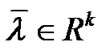 and the piecewise smooth
and the piecewise smooth 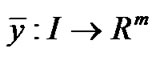 and
and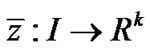 , such that
, such that
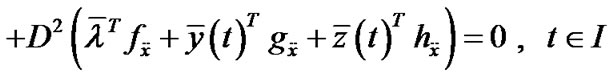
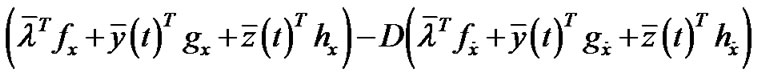 , (5)
, (5)
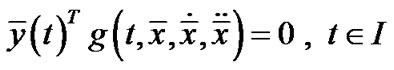 , (6)
, (6)
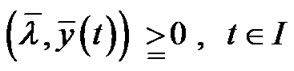 . (7)
. (7)
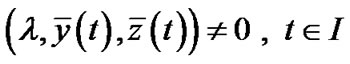 . (8)
. (8)
PROOF: Since 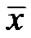 is an efficient solution of (VPE) by Lemma 1,
is an efficient solution of (VPE) by Lemma 1, 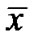 is an optimal solution of (
is an optimal solution of (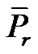 ), for each
), for each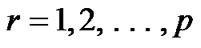 . From Proposition1, it follows that, there exist scalars
. From Proposition1, it follows that, there exist scalars 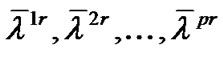 and piecewise smooth function
and piecewise smooth function 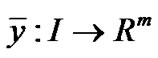 and
and 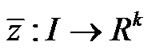 , such that
, such that
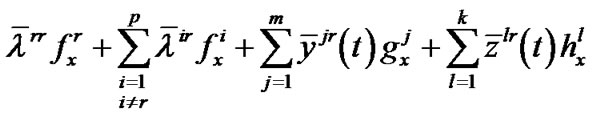
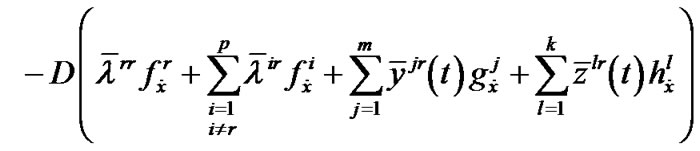
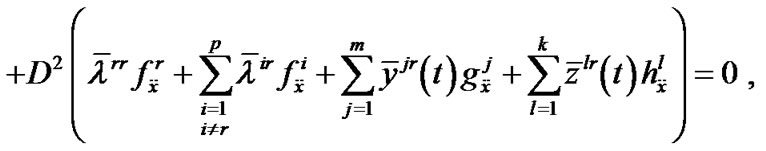
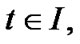
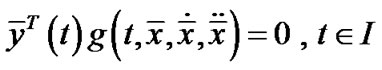 ,
,
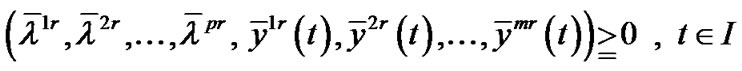
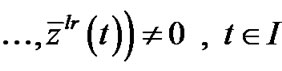
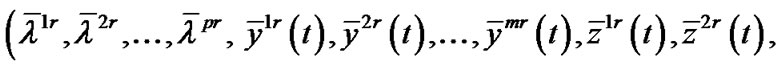 .
.
Summing over r, we have
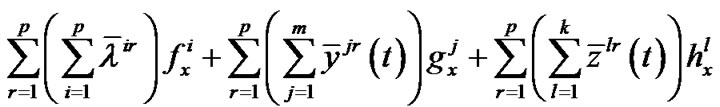
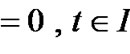
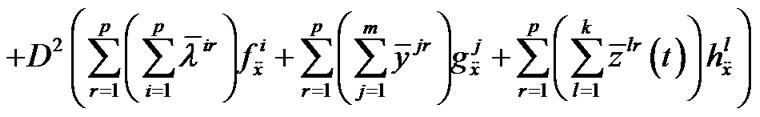
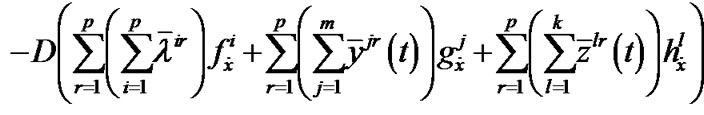
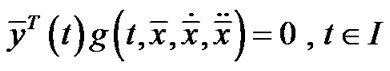 ,
,
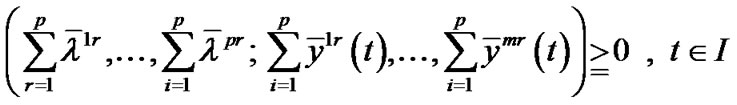
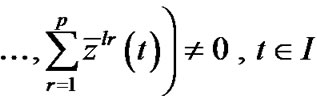
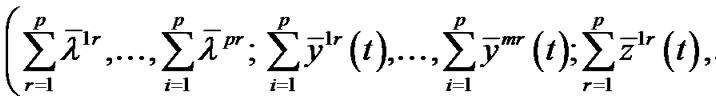 .
.
Setting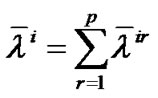 ,
,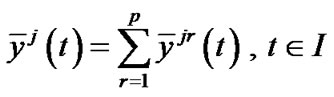 and
and
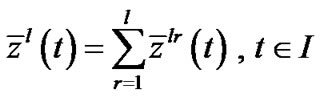 , we have
, we have
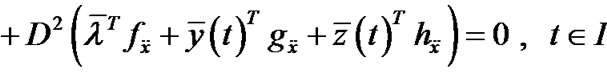
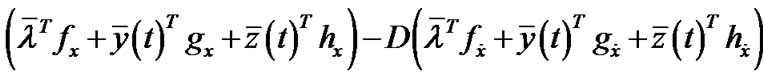
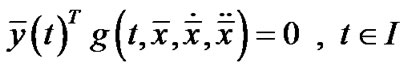 ,
,
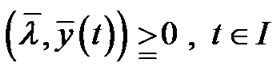 ,
,
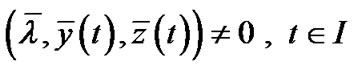 .
.
4. Mond-Weir Type Duality
In this section, we consider the following variational problem involving higher order derivatives, by suppressing the equality constraint in (VPE).
(VP) Minimize
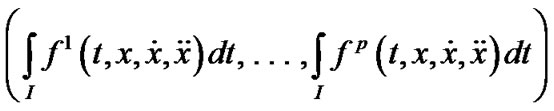
Subject to
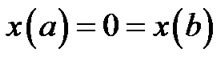
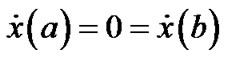

We formulate the following Mond-Weir type dual to the problem (VP) and establish various duality results under invexity defined in the preceding section.
(M-WD) Maximize
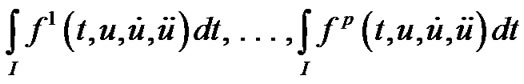
Subject to
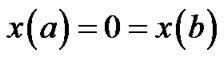 (9)
(9)
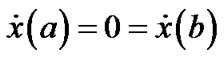 (10)
(10)
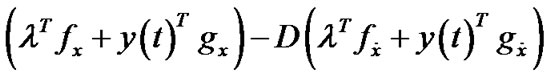
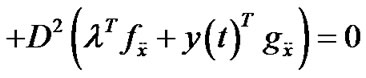 (11)
(11)
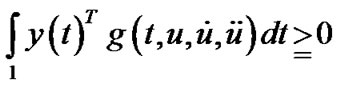 (12)
(12)
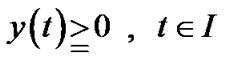 (13)
(13)
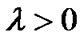 . (14)
. (14)
THEOREM 2. (Weak Duality): Let 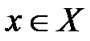 be feasible for (VP) and
be feasible for (VP) and 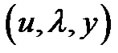 be feasible for (M-WD) if for allfeasible
be feasible for (M-WD) if for allfeasible 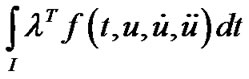
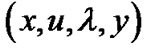 is pseudoinvex and
is pseudoinvex and 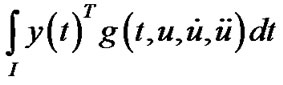 is quasi-invex with respect to the same η.
is quasi-invex with respect to the same η.
Then,
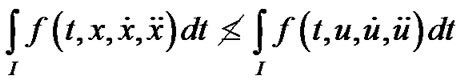 .
.
PROOF: The relations 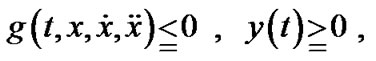
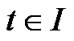 imply
imply
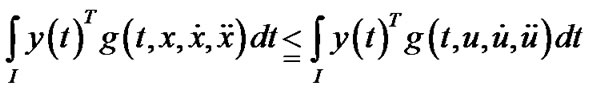
This, because of the quasi-invexity of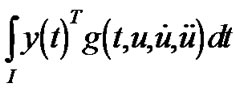 , implies that
, implies that
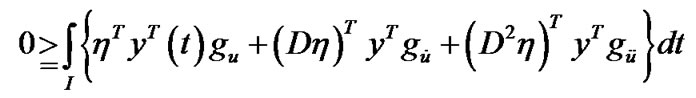
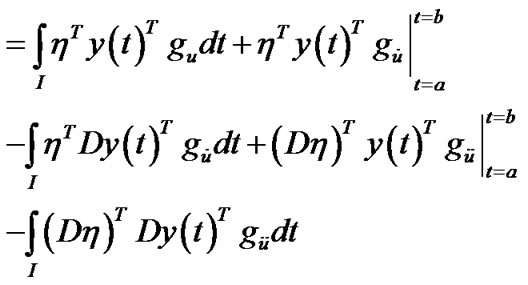
(By integration by parts)
Using the boundary conditions which gives
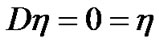 at
at 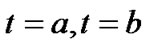
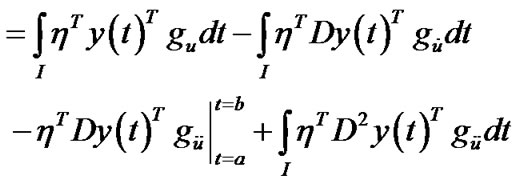
(By integration by parts)
Using the boundary conditions which give 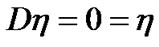 at
at 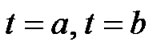
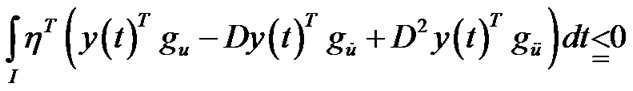

From Equation (11) this yields,
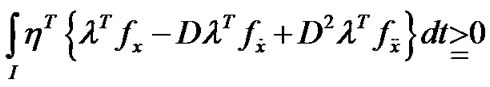
This by integration by parts and then using boundary conditions gives,
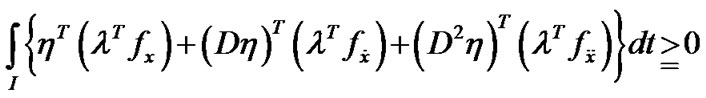 This, in view of psedoinvexity of
This, in view of psedoinvexity of 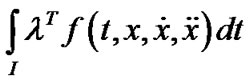 implies that
implies that
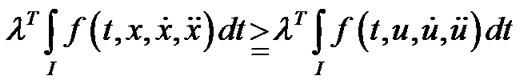 .
.
For this, it follows
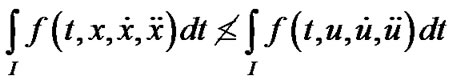 .
.
THEOREM 3. (Strong Duality): If  is a feasible solution for (VP) and assume that
is a feasible solution for (VP) and assume that  is an efficient solution and for at least one
is an efficient solution and for at least one 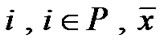 satisfies a regularity condition for [7] for
satisfies a regularity condition for [7] for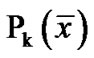 .
.
Then there exists one 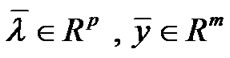 such that
such that 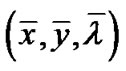 is efficient for (VD). Further if the assumptions of Theorem 2 are satisfied, then
is efficient for (VD). Further if the assumptions of Theorem 2 are satisfied, then 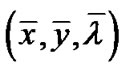 is an efficient solution of (VD).
is an efficient solution of (VD).
PROOF: Since 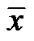 is efficient solution by Lemma 1, it is an optimal solution of
is efficient solution by Lemma 1, it is an optimal solution of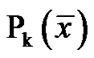 . By Proposition 1, this implies that there exists
. By Proposition 1, this implies that there exists 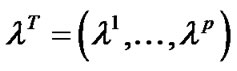 and piecewise smooth
and piecewise smooth 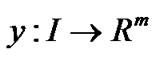 such that,
such that,
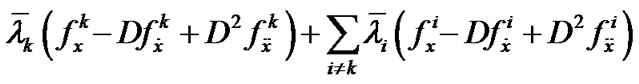
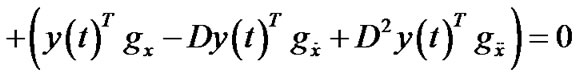 (15)
(15)
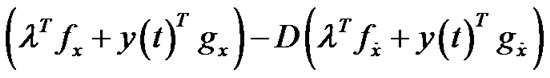
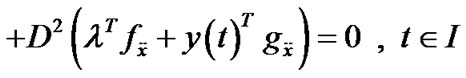 (16)
(16)
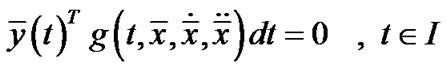 (17)
(17)
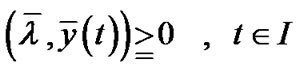 (18)
(18)
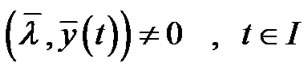 (19)
(19)
From (17), we have
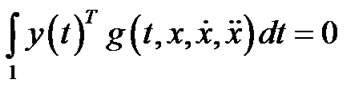 (20)
(20)
Equations (16), (17) and (18) imply that 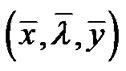 is feasible for (M-WD). The equality of objective functional of primal and dual problems is obvious from their formulations. Efficiency of
is feasible for (M-WD). The equality of objective functional of primal and dual problems is obvious from their formulations. Efficiency of 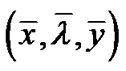 is immediate from the application of Theorem 2.
is immediate from the application of Theorem 2.
As in [4], by employing chain rule in calculus, it can be easily seen that the expression 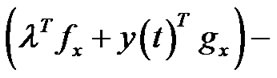
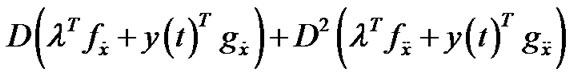 ,may be regarded as a function
,may be regarded as a function 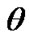 of variables
of variables 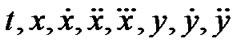 and
and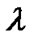 , where
, where 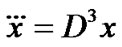 and
and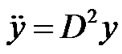 . That is, we can write
. That is, we can write
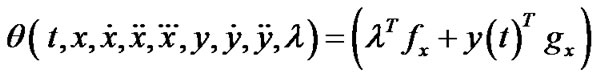
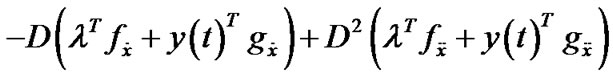
In order to prove converse duality between (VP) and (M-WD), the space X is now replaced by a smaller space 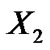 of piecewise smooth thrice differentiable function
of piecewise smooth thrice differentiable function 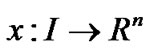 with the norm
with the norm 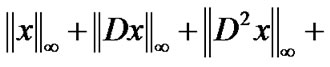
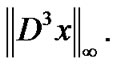 The problem (M-WD) may now be briefly written as, Minimize
The problem (M-WD) may now be briefly written as, Minimize
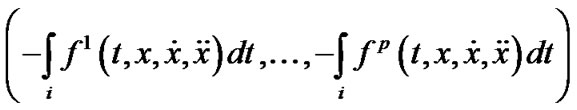
Subject to
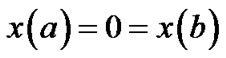
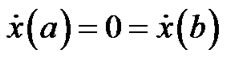
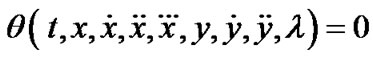
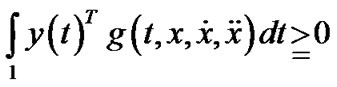
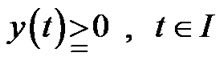
Consider 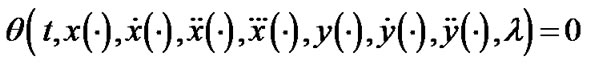 as defining a mapping
as defining a mapping 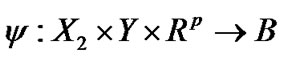 where Y is a space of piecewise twice differentiable function and B is the Banach Space. In order to apply Theorem 1 to the problem (M-WD), the infinite dimensional inequality must be restricted. In the following theorem, we use
where Y is a space of piecewise twice differentiable function and B is the Banach Space. In order to apply Theorem 1 to the problem (M-WD), the infinite dimensional inequality must be restricted. In the following theorem, we use 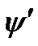 to represent the Frèchèt derivative
to represent the Frèchèt derivative
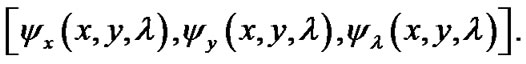
THEOREM 4. (Converse Duality): Let D be an efficient solution with 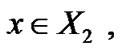
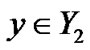 and
and 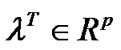 and
and 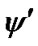 have a (weak*) closed range hypothesis. Let f and g be twice continuously differentiable. Assume that
have a (weak*) closed range hypothesis. Let f and g be twice continuously differentiable. Assume that
(H1) 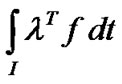 be pseudoinvex and
be pseudoinvex and 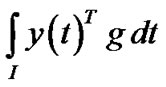 be quasi-invex with respect to same
be quasi-invex with respect to same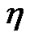 .
.
(H2)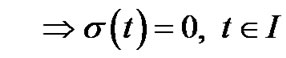
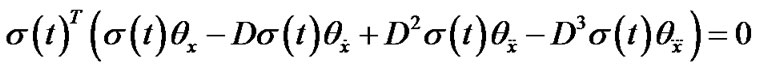 .
.
(H3) 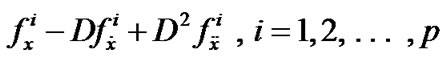 are linearly independent.
are linearly independent.
Then  is an efficient solution of (VP).
is an efficient solution of (VP).
Proof: Since 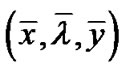 where
where 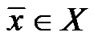 and
and 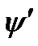 having a closed range, is an efficient solution of (M-WD), by Theorem 2, it implies that there exist
having a closed range, is an efficient solution of (M-WD), by Theorem 2, it implies that there exist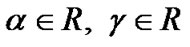 ,
, 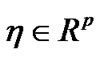 and piecewise smooth
and piecewise smooth 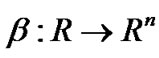 and
and 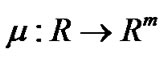 satisfying the following conditions .
satisfying the following conditions .
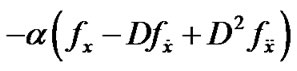
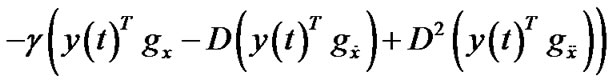
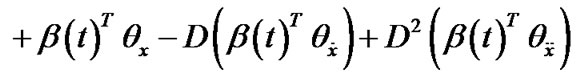
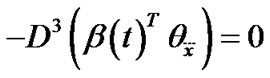 (21)
(21)
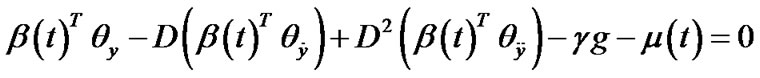 (22)
(22)
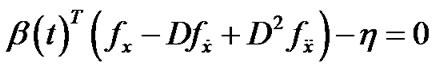 (23)
(23)
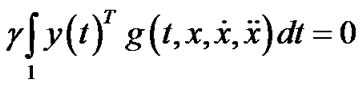 (24)
(24)
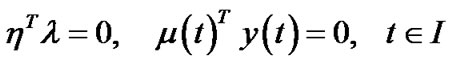 (25)
(25)
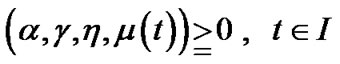 and
and
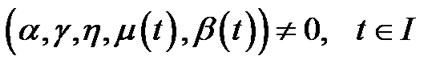 (26)
(26)
Since 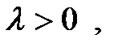
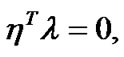 which implies
which implies 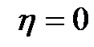
This yields from (23)
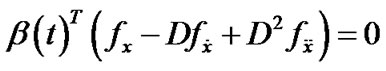 (27)
(27)
Using the equality constraint (11) in (21), we have
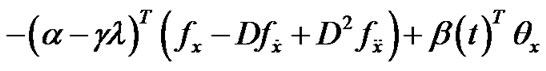
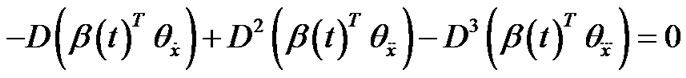 (28)
(28)
Postmultiplying Equation (21) by 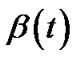 and using (27) in (28) we get,
and using (27) in (28) we get,
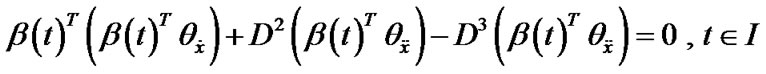
This by hypothesis (H2) implies 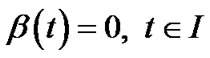
Also from (28) we have
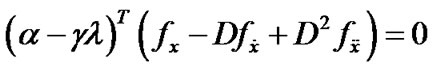
This, because of linear independence of 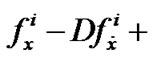
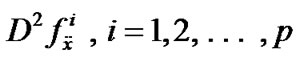 , gives
, gives
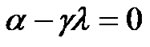 (29)
(29)
Now suppose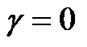 , then, from (22) and (29) we have
, then, from (22) and (29) we have 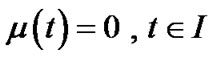 and
and 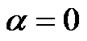 respectively.
respectively.
This implies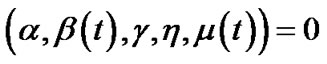 , which is the contradiction to
, which is the contradiction to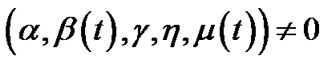 ,
,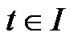 .
.
Hence 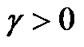 and by (29) we have,
and by (29) we have,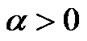 .
.
The relation (22) in conjunction with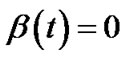 , and
, and 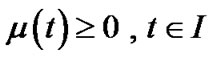 gives
gives
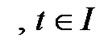
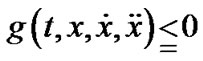
This implies the feasibility of 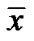 for (VP) and its efficiency is evident from and application of Theorem 2.
for (VP) and its efficiency is evident from and application of Theorem 2.
5. Natural Boundary Values
The duality results obtained in the preceding sections can easily be extended to the multiobjective variational problems with natural boundary values rather than fixed end points.
Primal (P1) Minimize
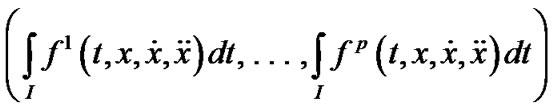
Subject to
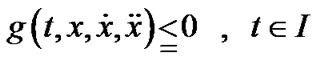
Dual (D1) Maximize
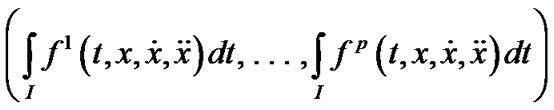
Subject to
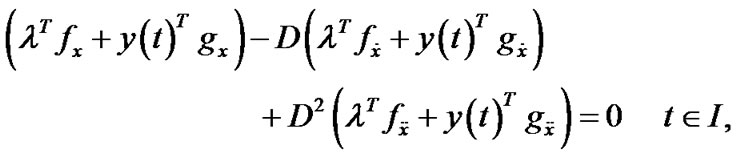
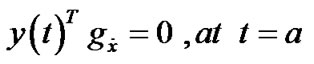 and
and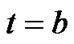 ,
,
 and
and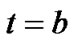 ,
,
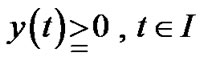 .
.
6. Nonlinear Programming
If the problems (P1) and (D1) are independent of t, then they will reduce to the following multiobjective nonlinear programming problems studied in [15]
(NP): Minimize 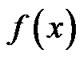
Subject to
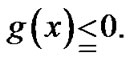
(ND): Maximize 
Subject to
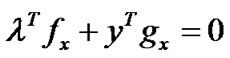
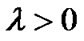 ,
,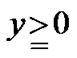 .
.
7. References
[1] R. Courant and D. Hilbert, “Methods of Mathematical Physics,” Wiley, New York, Vol. 1, 1943.
[2] K. O. Friedrichs, “Ein Verfrahren der Variations-Rechung das Minimum eines Integrals Maximum eines Anderen Ausdruckes Dazustellan,” Göttingen Nachrichten, 1929.
[3] M. A. Hanson, “Bonds for Functionally Convex Optimal Control Problems,” Journal of Mathematical Analysis and Applications, Vol. 8, No. 1, February 1964, pp. 84-89.
[4] B. Mond and M. A. Hanson, “Duality for Variational Problems,” Journal of Mathematical Analysis and Applications, Vol. 18, No. 2, May 1967, pp. 355-364.
[5] F. A. Valentine, “The Problem of Lagrange with Differential Inequalities as Added Side Conditions,” Contributions to the Calculus of Variations, 1933-1937, University of Chicago Press, 1937, pp. 407-448.
[6] C. R. Bector, S. Chandra and I. Husain, “Generalized Concavity and Duality in Continuous Programming,” Utilitas Mathematica, Vol. 25, 1984, pp. 171-190.
[7] S. Chandra, B. D. Craven and I. Husain, “A Class of Nondifferentiable Continuous Programming Problems,” Journal of Mathematical Analysis Applications, Vol. 107, No. 1, April 1985, pp. 122-131.
[8] S. Chandra, B. D. Craven and I. Husain, “Continuous Programming Containing Arbitrary Norms,” Journal of Australian Mathematical Society (Series A), Vol. 39, No. 1, 1985, pp. 28-38.
[9] I. Husain and Z. Jabeen, “On Variational Problems Involving Higher Order Derivatives,” Journal of Applied Mathematics and Computing, Vol. 27, No. 1-2, March 2005, pp. 433-455.
[10] B. Mond and S. Chandra and I. Husain, “Duality of Variational Problems with Invexity,” Journal of Mathematical Analysis and Applications, Vol. 134, No. 2, September 1988, pp. 322-328.
[11] C. R. Bector and I. H. Husain, “Duality for Multiobjective Variational Problems,” Journal of Mathematical Analysis and Applications, Vol. 166, No. 1, 1 May 1992, pp. 214-224.
[12] X. H. Chen, “Duality for Multiobjective Variational Problems with Invexity” Journal of Mathematical Analysis and Appliactions, Vol. 203, No. 1, October 1996, pp. 236-253.
[13] B. Mond and I. Smart, “Duality with Invexity for a Class of Nondifferentiable Static and Continuous Programming Problems,” Journal of Mathematical Analysis and Applications, Vol. 136, 1988, pp. 325-333.
[14] V. Chankong and Y. Y. Haimes, “Multiobjective Decision Making: Theory and Methodology,” North Holland, New York, 1983.
[15] R. R. Egudo and M. A. Hanson, “Multiobjective Duality with Invexity,” Journal of Mathematical Analysis and Appliactions, Vol. 126, No. 2, September 1987, pp. 469- 477.

