Advances in Pure Mathematics
Vol.06 No.05(2016), Article ID:65885,15 pages
10.4236/apm.2016.65027
Global Stability in Dynamical Systems with Multiple Feedback Mechanisms
Morten Andersen, Frank Vinther, Johnny T. Ottesen
Department of Science and Environment, Roskilde University, Roskilde, Denmark

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 February 2016; accepted 23 April 2016; published 26 April 2016
ABSTRACT
A class of n-dimensional ODEs with up to n feedbacks from the n’th variable is analysed. The feedbacks are represented by non-specific, bounded, non-negative C1 functions. The main result is the formulation and proof of an easily applicable criterion for existence of a globally stable fixed point of the system. The proof relies on the contraction mapping theorem. Applications of this type of systems are numerous in biology, e.g., models of the hypothalamic-pituitary-adrenal axis and testosterone secretion. Some results important for modelling are: 1) Existence of an attractive trapping region. This is a bounded set with non-negative elements where solutions cannot escape. All solutions are shown to converge to a “minimal” trapping region. 2) At least one fixed point exists. 3) Sufficient criteria for a unique fixed point are formulated. One case where this is fulfilled is when the feedbacks are negative.
Keywords:
Odes, Multiple Feedbacks, Stability, Global Stability, Attracting Trapping Region, Nonlinear Dynamics

1. Outline
First, an n dimensional system with feedbacks from the n’th variable is introduced and some applications from bio-medicine and biochemistry are described. Then, analysis of a scaled version of the system is made including fixed point investigation. Finally, an easy applicable sufficient criterion for a unique, globally stable fixed point is formulated and proved.
Mathematically, the results in this paper follow from the dimensionless form of the equations stated in (6) of Section 2. But before turning to this form we motivate and discuss the dimensional form of the equations in Section 1 as we relate the system to applications and earlier results.
2. Introduction
Many applications of ODEs to physics, chemistry, biology, medicine, and life sciences give rise to non-linear non-negative compartment systems. These include metabolic pathways, membrane transports, pharmacodynamics, epidemiology, ecology, cellular control processes, enzyme synthesis, and control circuits in biochemical pathways [1] - [9] .
This paper concerns the stability of the solutions of such models. More specifically, the paper presents criteria for both local and global stability of all systems of ODEs that can be presented as a compartment model with n compartments, on the form shown in Figure 1. Here the n’th variable may have a non-linear feedback on any of the variables. The main results of this paper are:
・ Existence of a “trapping region”―a compact set with non negative elements in which any solution will be trapped after finite time.
・ At least one fixed point exists and a real valued function of one variable and the system parameters determines the fixed point.
・ A unique, globally stable fixed point exists if the norm of a real valued function of one variable and the system parameters is less than 1.
2.1. Motivating Background
Figure 1 reflects typical hormone regulation. Since a hormone has to bind to a receptor to cause a feedback, a bounded number of receptors justify that the feedback functions 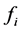 are bounded. Examples of systems corresponding to Figure 1 with
are bounded. Examples of systems corresponding to Figure 1 with 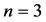 are models of the hypothalamic-pituitary-adrenal axis (HPA axis) concerning the interplay of three hormones in the human body [1] - [5] [10] [11] . Here cortisol exerts a feedback on two other hormones that are involved in the production of cortisol. The system is related to stress and depression. Also testosterone secretion has been modelled by a three dimensional compartment ODE-model including a single feedback [12] which is included in the system investigated here. Similar models exist of gonadotropin hormone secretion [13] , for describing female fertility [14] - [16] and for cellular metabolism [17] .
are models of the hypothalamic-pituitary-adrenal axis (HPA axis) concerning the interplay of three hormones in the human body [1] - [5] [10] [11] . Here cortisol exerts a feedback on two other hormones that are involved in the production of cortisol. The system is related to stress and depression. Also testosterone secretion has been modelled by a three dimensional compartment ODE-model including a single feedback [12] which is included in the system investigated here. Similar models exist of gonadotropin hormone secretion [13] , for describing female fertility [14] - [16] and for cellular metabolism [17] .
A two dimensional model of the HPA axis corresponding to Figure 1 is found in [18] . Here the focus is on a sufficient criterion for a locally stable fixed point. However it is made clear that a global investigation is preferable. Criteria for global stability of solutions are rare. An example is through use of a Liapunov function [6] [12] that can be employed to some problems. Existence and construction of a Liapunov function are unfortunately not easily addressed in general, and Liapunov functions are not used in this article.
Some general and analytical considerations partly similar to our has been considered in previous papers [8] [19] . However, [8] investigate only a feedback from compartment n to compartment 1. The approach of [20] proves the existence of periodic solutions but does not touch upon global stability.
The mathematical results derived in this article relate to the robustness of hormonal systems, cellular metabolism, etc. The existence of a trapping region ensures that non negative initial (hormone) values lead to (hormone) levels that stay non negative and bounded which is reasonable. Existence of locally stable fixed points may be interpreted as states where (hormone) levels may settle. Perturbing parameters such that a solution enters the basin of attraction to another fixed point may then be interpreted as a new (physiological) state (for a person). Or distinct stable fixed points may be interpreted as states for distinct groups (of people). In case of a unique, globally stable fixed point the long term behaviour is very robust to perturbations.
2.2. Mathematical Formulation
We consider an n dimensional system of differential equations with n non negative variables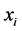 ,
,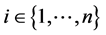 .
. 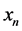 may exert a feedback on all the variables thus making the system non-linear.
may exert a feedback on all the variables thus making the system non-linear.
Figure 1. Compartment model of the system.
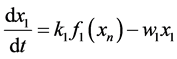 (1a)
(1a)
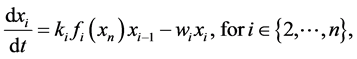 (1b)
(1b)
with production rates 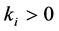 and consumption rates
and consumption rates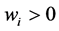 . The feedback from
. The feedback from 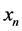 on
on 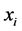 occurs through the function
occurs through the function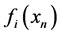 . The following demands are posed for the feedback functions:
. The following demands are posed for the feedback functions: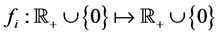 ,
, 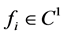 ,
, 








back function is the sigmoidal Hill-function



integer. Such Hill-functions are often the result of underlying inter cellular enzymatic reactions regulating feedbacks in the quasi-steady-state approximation [21] . In neural networks applications a utilized feedback function is the hyperbolic tangent [22] .
3. Analysis
First a scaling is performed to facilitate the analysis. Defining dimensionless variables 


where 


Choosing 



and

A scaling of Equation (1) thus leads to the dimensionless system


with constants










3.1. Existence and Uniqueness of Solutions
Since 





at least one global solution exists. Here we have made exclusive use of the fact that the
3.2. Positivity of Solutions
Avoiding negative modelling hormone levels is necessary for a sound model and is proved in the following lemma.
Lemma 1. The non negative hypercube is an invariant solution set to Equation (6)
Proof. Given a solution initially in the non negative hypercube we consider the behaviour at a boundary of the hypercube―a hyperplane defined by


which is non negative for all non negative

which is a product of non negative factors for all non-negative
3.3. Existence of a Fixed Point
The fixed point condition of Equation (6) can be expressed

This means that for each fixed point value 

may not be explicitly solvable for
Define the functions

and

Thus, finding fixed points of Equation (6) is equivalent to finding 



Now choose 


Furthermore,

Define the function

Since L and R are continuous so is 






3.4. Sufficient Criteria for a Unique Fixed Point
We now discuss a sufficient criterion for existence of a unique fixed point of the system. Let 










If the feedback functions correspond to negative feedbacks or are independent of




3.5. Trapping Region
A trapping region is a set, 
Lemma 2. Let 


and define

Then 

Proof. 





region’ for 



This ensures that 
Notice that if 





For 


3.6. All Solutions Get Arbitrarily Close to U in Finite Time and Stay Close to U
For any 








Lemma 3. Let







Proof. Follows by the comparison theorem for integrals. W
Lemma 4. Let











Proof. If 






Lemma 5. Consider Equation (6). For any 

Proof. Fix





Since 

















Since 










Since 




U is the ‘minimal’ trapping region. However, if 

4. Sufficient Criteria for a Globally Stable Fixed Point
Fix any



This means H is the restriction of R to
To continue we assume H is positive and a contraction on 






For 


Thus, two linear systems of differential equations can be constructed with initial condition 



and


Then 












Since




This means especially

Choosing 

since


then

Define

From above there exists a finite time 


Now a sequence of sets, 

where

and

Lemma 6. 

Proof. The proof is done by induction. 


Since 







are well defined and finite. Then 

Since by assumption



and ensures
Due to the squeezing of the solutions using linear systems we have shown that if 







We now want to prove that 






Lemma 7. Let p be the contraction constant for H. Then

Proof. Follows from the contraction property and the triangle inequality. W
Similarly it follows.
Lemma 8. Let p be the contraction constant for H. Then

Lemma 7 and 8 means we can bound the maximum and minimum of H applied on a compact interval by the maximal distance between any two points in the interval and H evaluated at an end point of the interval.
As mentioned a specific choice of 


where 



For simplicity we put

Then,

To simplify notation further we introduce

Since 

Thus,

For later use we emphasize that

Define















Lemma 9. If H is a contraction and positive on 

Proof. The proof is by induction. Since 



and

We will show

By inequality (51)

Because 





By equality (34)

Using Equation (56)

Then,

Since H is continuous on the compact sets,

Using the contraction property as shown in lemma 7 and lemma 8

and

From the definitions of

and

Thus, we have upper and lower bounds for each of the sets




By definition

and applying Equation (68)

Using Equation (52)

which completes the proof. W
Lemma 10. Let H be defined as in Equation (23). If H is a contraction and positive on 

Proof. Fix





Since H is a contraction on a complete metric space the Banach Fixed Point Theorem applies, i.e. a uniquefixed point of 


Choose

By Equation (72) there exists 




and similarly

There exists a 




Inserting from Equations (73)-(76).

Therefore 




When 








Since 



This means that all solutions with initial conditions in 
Since all solutions outside 



Sufficient Criteria for a Contraction
A sufficient, easily applicable criteria for H being a contraction can be formulated [24] .
Lemma 11. Let 




If H is positive on 





With the results of Section 3 we now have established the main result of global stability of system (6).
Theorem 1. If



5. Discussion
The general formulation and results in this paper guarantee that the hormone levels in the models [1] - [7] [10] [20] stay in a trapping region where non-negative concentrations are impossible which is a physiological necessity. A repeating pattern is often visible in hormone levels. However, for Equation (1) periodic solutions are impossible outside the “minimal” trapping region. This narrows the domain for interesting initial conditions. The one dimensional function 
A model of mRNA and Hes1 protein production fits Figure 1 [25] [26] . However, a time delay in the feedback has to be included in order to obtain experimentally observed oscillations. A model of testorone dynamics including delay in the feedback is investigated in [27] . Including time delays in models corresponding to Figure 1 has proved useful in the search for oscillatory behaviour [28] - [30] . One may wonder whether the feedback itself can cause oscillations or if a time delay needs to be included. The contribution of this paper may help in quickly ruling out oscillatory behaviour in the case of no time delay.
Including time delay in the feedbacks, global stability criteria have been formulated for a subset of possible feedback functions in systems resembling 1 [31] . This requires that all feedbacks are monotone functions. The approach is different from ours and relies on control theory.
Summary
A general formulation of an n-dimensional system of differential equations with up to n feedbacks from the n’th variable is formulated. The feedbacks may be non-linear but must be represented by bounded functions which are considered to be the case for some biological systems. Some relevant general results are shown.
・ Existence and uniqueness of solutions are guaranteed.
・ Non-negative initial conditions cause non-negative solutions for all future time.
・ A trapping region, 


・ All solutions of the system enter 

・ At least one fixed point exists and all fixed points are contained in U. Using 

If the feedback functions correspond to negative feedbacks or are independent of 
・ If



Cite this paper
Morten Andersen,Frank Vinther,Johnny T. Ottesen, (2016) Global Stability in Dynamical Systems with Multiple Feedback Mechanisms. Advances in Pure Mathematics,06,393-407. doi: 10.4236/apm.2016.65027
References
- 1. Savic, D. and Jelic, S. (2005) A Mathematical Model of the Hypothalamo-Pituitary-Adrenocortical System and Its Stability Analysis. Chaos, Solitons & Fractals, 26, 427-436.
- 2. Savic, D., Jelic, S. and Buric, N. (2006) Stability of a General Delay Differential Model of the Hypothalamo-Pituitary-Adrenocortical System. International Journal of Bifurcation and Chaos, 16, 3079-3085.
http://dx.doi.org/10.1142/S0218127406016665 - 3. Vinther, F., Andersen, M. and Ottesen, J.T. (2010) The Minimal Model of the Hypothalamic-Pituitary-Adrenal Axis. Journal of Mathematical Biology, 63, 663-690.
http://dx.doi.org/10.1007/s00285-010-0384-2 - 4. Andersen, M. and Vinther, F. (2010) Mathematical Modeling of the Hypothalamic-Pituitary-Adrenal Axis. IMFUFA tekst 469, Roskilde University, NSM.
- 5. Andersen, M., Vinther, F. and Ottesen, J.T. (2013) Mathematical Modeling of the Hypothalamic-Pituitary-Adrenal gland (Hpa) Axis, Including Hippocampal Mechanisms. Mathematical Biosciences, 246, 122-138.
http://dx.doi.org/10.1016/j.mbs.2013.08.010 - 6. Haddad, W.M., Chellaboina, V. and Hui, Q. (2010) Nonnegative and Compartmental Dynamical Systems. Princeton University Press, Princeton.
http://dx.doi.org/10.1515/9781400832248 - 7. Griffith, J.S. (1968) Mathematics of Cellular Control Processes I. Negative Feedback to One Gene. Journal of Theoretical Biology, 20, 202-208.
http://dx.doi.org/10.1016/0022-5193(68)90189-6 - 8. Tyson, J.J. and Othmer, H.G. (1978) The Dynamics of Feedback Control Circuits in Biochemical Pathways. Progress in Theoretical Biology, 5, 1-62.
http://dx.doi.org/10.1016/B978-0-12-543105-7.50008-7 - 9. Tyson, J.J. (1983) Periodic Enzyme Synthesis and Oscillatory Repression: Why Is the Period of Oscillation Close to the Cell Cycle Time. Journal of Theoretical Biology, 103, 313-328.
http://dx.doi.org/10.1016/0022-5193(83)90031-0 - 10. Bingzhenga, L., Zhenye, Z. and Liansong, C. (1990) A Mathematical Model of the Regulation System of the Secretion of Glucocorticoids. Journal of Biological Physics, 17, 221-233.
http://dx.doi.org/10.1007/BF00386598 - 11. Hosseinichimeh, N., Rahmandad, H. and Wittenborn, A. (2015) Modeling the Hypothalamus-Pituitary-Adrenal Axis: A Review and Extension. Mathematical Biosciences, 268, 52-65.
http://dx.doi.org/10.1016/j.mbs.2015.08.004 - 12. Murray, J. (2002) Mathematical Biology: I. An Introduction. Third Edition, Springer, New York.
- 13. Smith, W.R. (1980) Hypothalamic Regulation of Pituitary Secretion of Luteinizing Hormone II. Feedback Control of Gonadotropin Secretion. Bulletin of Mathematical Biology, 42, 57-78.
- 14. Clarke, I. and Cummings, J. (1984) Direct Pituitary Effects of Estrogen and Progesterone on Gonadotropin Secretion in the Ovariectomized Ewe. Neuroendocrinology, 39, 267-274.
http://dx.doi.org/10.1159/000123990 - 15. Harris-Clark, P., Schlosser, P. and Selgrade, J. (2003) Multiple Stable Solutions in a Model for Hormonal Control of Menstrual Cycle. Bulletin of Mathematical Biology, 65, 157-173.
http://dx.doi.org/10.1006/bulm.2002.0326 - 16. Karsch, F., Dierschke, D., Weick, R., Yamaji, T., Hotchkiss, J. and Knobil, E. (1973) Positive and Negative Feedback Control by Estrogen of Luteinizing Hormone Secretion in the Rhesus Monkey. Endocrinology, 92, 799-804.
http://dx.doi.org/10.1210/endo-92-3-799 - 17. Chitour, Y., Grognard, F. and Bastin, G. (2003) Lecture Notes in Control and Information Sciences: Stability Analysis of a Metabolic Model with Sequential Feedback Inhibition. Springer Berlin/Heidelberg.
- 18. Conrad, M., Hubold, C., Fischer, B. and Peters, A. (2009) Modeling the Hypothalamus-Pituitary-Adrenal System: Homeostasis by Interacting Positive and Negative Feedback. Journal of Biological Physics, 35, 149-162.
http://dx.doi.org/10.1007/s10867-009-9134-3 - 19. Strogatz, S.H. (1994) Nonlinear Dynamics and Chaos. Perseus Books Publishing, LLC, New York.
- 20. Hastings, S., Tyson, J. and Webster, D. (1977) Existence of Periodic Solutions for Negative Feedback Cellular Control Systems. Journal of Differential Equations, 25, 39-64.
http://dx.doi.org/10.1016/0022-0396(77)90179-6 - 21. Fall, C., Marland, E., Wagner, J. and Tyson, J. (2002) Computational Cell Biology. Springer-Verlag, New York.
- 22. Enciso, G.A. (2007) A Dichotomy for a Class of Cyclic Delay Systems. Mathematical Biosciences, 208, 63-75.
http://dx.doi.org/10.1016/j.mbs.2006.09.022 - 23. Sastry, S. (1999) Nonlinear Systems; Analysis, Stability and Control; Interdisciplinary Applied Mathematics. Springer-Verlag, New York.
- 24. Istratescu, V.I. (1981) Fixed Point Theory. Second Edition, D. Reidel Publishing Company, Dordrecht.
http://dx.doi.org/10.1007/978-94-009-8177-5 - 25. Monk, N.A. (2003) Oscillatory Expression of Hes1, p53, and NF-κB Driven by Transcriptional Time Delays. Current Biology, 13, 1409-1413.
http://dx.doi.org/10.1016/S0960-9822(03)00494-9 - 26. Jensen, M.H., Sneppen, K. and Tiana, G. (2003) Correspondence Sustained Oscillations and Time Delays in Gene Expression of Protein Hes1. FEBS Letters, 541, 176-177.
http://dx.doi.org/10.1016/S0014-5793(03)00279-5 - 27. Enciso, G. and Sontag, E.D. (2004) On the Stability of a Model of Testosterone Dynamics. Journal of Mathematical Biology, 49, 627-634.
http://dx.doi.org/10.1007/s00285-004-0291-5 - 28. Momiji, H. and Monk, N.A.M. (2008) Dissecting the Dynamics of the Hes1 Genetic Oscillator. Journal of Theoretical Biology, 254, 784-798.
http://dx.doi.org/10.1016/j.jtbi.2008.07.013 - 29. Lewis, J. (2003) Autoinhibition with Transcriptional Delay. Current Biology, 13, 1398-1408.
http://dx.doi.org/10.1016/S0960-9822(03)00534-7 - 30. Ruan, S. and Wei, J. (2001) On the Zeros of a Third Degree Exponential Polynomial with Applications to a Delayed Model for the Control of Testosterone Secretion. IMA Journal of Mathematics Applied in Medicine and Biology, 18, 41-52.
http://dx.doi.org/10.1093/imammb/18.1.41 - 31. Enciso, G.A. and Sontag, E.D. (2006) Global Attractivity, I/O Monotone Small-Gain Theorems, and Biological Delay Systems. Discrete and Continuous Dynamical Systems, 14, 549-578.
1Then the fixed point can be found by choosing any 










