Open Journal of Civil Engineering
Vol.05 No.03(2015), Article ID:60051,12 pages
10.4236/ojce.2015.53034
The Behavior of Recycled Concrete through the Application of an Isotropic Damage Model
Marcelo Pedreira da Silva, Magno Teixeira Mota, Anderson de Souza Matos Gadéa, Mônica Batista Leite, Koji de Jesus Nagahama
Civil and Environmental Engineering Post-Graduate Program, State University of Feira de Santana, Feira de Santana, Brazil
Email: koji@uefs.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 26 September 2015; published 29 September 2015
ABSTRACT
The main goal of this paper is to describe the mechanical behavior of the CDW recycled concrete in compression, using an isotropic damage model adapted to the variation of the replacement rate of natural aggregates by recycled ones. The isotropic model by Mazars was used as a constitutive equation for the CDW concrete and its adjustment parameters, A and B, were written as quadratic polynomials according to the aggregates replacement rate. The model was evaluated for conventional and recycled concretes. For the latter ones, the aggregates replacement ratios evaluated were 50% and 100%. The results show good approximation between the analytical and numerical values obtained with the adapted isotropic damage model and experimental concrete results for both compressive and flexural strength.
Keywords:
Recycled Concrete, Construction and Demolition Waste, Isotropic Damage, Mazars Isotropic Model

1. Introduction
The description of the mechanical behavior of conventional concrete already has consistent analytical models in science. Models based on the theory of elasticity, plasticity, in the mechanics of fracture and damage and in their combinations, are able to describe the real phenomena in a broad sense. However, special concretes, such as recycled concretes, still need specific constitutive equations so to be analytically represented.
Recycled concrete, for example, shows a specific mechanical behavior as a consequence of the use of aggregates that show differentiated characteristics when compared to natural aggregates. The construction and demolition waste (CDW) composition and the aggregate production procedures result in the variability of the physical, chemical and mechanical characteristics of the aggregates that will considerably interfere in the mechanical behavior of the recycled concrete achieved.
Experimental studies of recycled concrete behavior have been carried out by number of researchers, evaluating concrete compressive and flexural strength [1] -[3] , impact load on beams [4] [5] , bond behavior [6] [7] , among other properties. Etxeberria et al. [1] found that the use of 100% of recycled coarse aggregate has reduced the compressive strength by 20% to 25% compared to conventional concrete. Leite [2] identified a great influence of the porosity of the recycled aggregate and the transition zone in the compressive strength of concrete containing CDW.
Maruyama et al. [3] investigated the flexural properties of recycled concrete beams reinforced with steel bars. Considering the same value of stress in the beam, the authors observed that recycled concrete presented bigger crack width than conventional concrete and furthermore, smaller spacing between the cracks.
The recycled concrete beam behavior under impact load was evaluated by Rao et al. [5] . For a given impact energy major deformations were found for the concrete with substitution ratios of 50% and 100% when compared to the values obtained for conventional and recycled concretes with 25% of recycled aggregate.
It can thus be observed that the use of recycled aggregates from CDW for concrete production impairs the concrete properties in the hardened state due to specific characteristics, such as high heterogeneity of the recycled aggregates and their higher porosity [1] [2] .
1.1. Considerations about Constitutive Models for Recycled Concrete
In general the researches focusing on obtaining mathematical models that describe the recycled concrete behavior, are based on consistent models established for conventional concrete. The use of these models to design reinforced concrete members, despite being allowed by international standards, show some restrictions related to the type of the recycled aggregate and to the maximum replacement rate of the natural aggregate [8] -[11] .
Xiao et al. [12] investigated experimentally the mechanical properties of recycled concrete submitted to uniaxial loading in view of the analytical description of its behavior. Through the expression proposed by Guo and Zhang [13] for conventional concrete and adopted by the Chinese Standard GB50010/2002, the authors adapted the variables shown achieving good approximation for the experimental stress-strain curves of the CDW concrete.
Bhikshma and Kishore [14] applied the expression proposed by Saenz [15] that describes the conventional concrete behavior in the study of recycled concrete submitted to axial compression. The authors concluded that this model describes in a satisfactory way the mixtures of concrete used in the experimental program.
Du et al. [16] also investigated the mechanical performance of recycled concrete under axial compression load. The description of the ascending branch of the analytical stress-strain curve was based upon a polynomial equation proposed by Guo [17] . An exponential model using three adjustable parameters was proposed for the descending branch. So, the authors could describe theoretical curves very close to the experimental curves.
The generalization of the conventional concrete constitutive models for recycled concretes is a big challenge for the researchers in this field. The variability in the gravimetric composition of recycled aggregates and the lack of experimental results are factors that hamper the broad validation of the existing analytical models.
Thus, the main goal of this study is to propose an analytical model that will incorporate the changes in the behavior of concrete resulting from the variation of the recycled aggregate contents and that will provide the adaptation and generalization needed due to the characteristics of the recycled aggregates. This study is also based on the hypothesis that an analytical model with parameters of explicit adjustment can be used. Furthermore, it can make possible such parameters sensitive to the variability of the recycled aggregate and be able to express the changes in the mechanical behavior of the recycled concrete depending on the aggregates replacement rate. Thereby this approach intends to describe the mechanical behavior of CDW recycled concrete in compression using the isotropic damage model by Mazars [18] .
1.2. The Isotropic Damage Model in Compression Proposed by Mazars
Seen from a mathematical point of view, the isotropic damage model proposed by Mazars [18] named in this paper as Mazars model, is a function that combines in a non-linear form two parameters of adjustment, A and B, that express implicitly inherent characteristics to the modeled material.
Such a function for the uniaxial cases of load, can be written as follows
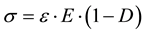 (1)
(1)
if 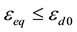 then
then  (2)
(2)
if 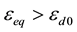 then
then 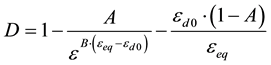 (3)
(3)
where,
σ = uniaxial strength
ε = deformation in the direction of load application
εeq = equivalent deformation
εd0 = peak deformation in tensile strength
E = initial longitudinal modulus of elasticity
D = damage
A and B = adjustment parameters that incorporate material characteristics
The contribution of each parameter in the mechanical behavior of the material can be obtained through an analysis of parametric influence, similar to the one carried out by Álvares [19] .
1.3. Model Parameters
The values of parameters A, B and εd0 were suggested by Mazars [18] for conventional concrete. The intervals of the parameters are expressed as follows
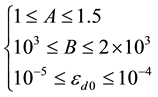
Using these intervals, Álvares [19] studied the influence of the parameters of the model in the development of stress-strain curves for uniaxial loads.
Observing Figure 1, the following conclusions were drawn
・ the variation of εd0 (Figure 1(a)) influences the beginning and initial slope of the non linear branch of the curve, as well as the asymptotic value of σ.
・ the variation of B (Figure 1(b)) alters both the initial slope of the non-linear branch and the peak value of the stress-strain curve.
・ the variation of parameter A (Figure 1(c)) has an influence in the initial slope of the non-linear branch of the curve and in the value of the horizontal asymptote.
It can be observed that each parameter has its own specific influence to build the analytical stress-strain curve.

Figure 1. Analysis of the parametric influence of (a) εd0, (b) B and (c) A [19] .
From the understanding of the parametric influence on, it is necessary to establish values for the parameters considering an experimental curve to be adjusted. For Álvares [19] this is one of the most delicate phases in the use of a model, mainly when it has only few parameters available for adjustment.
According to the second fundamental hypothesis of the Mazars model, the damage is caused only by the existence of stretching in at least one of the main directions of deformation [18] . This way, deformation εd0, corresponding to the peak stress, determines the beginning of the cracking of the analytical model and must be obtained through direct tensile strength or split tensile strength tests in cylindrical samples. Thus, it is necessary to get a definition of an equivalent deformation (εeq) to apply the model in compression loading situations.
The equivalent deformation that refers to the positive part of the main deformation in direction is defined by Equation (4) as follows
 (4)
(4)
In the case of the split tension test (Equation (5)) and compression test (Equation (6)) we have
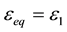 (5)
(5)
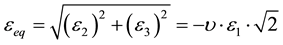 (6)
(6)
 is the only positive deformation in Equation (5) (deformation in the direction of load application). The remainder being eliminated.
is the only positive deformation in Equation (5) (deformation in the direction of load application). The remainder being eliminated.
In Equation (6), 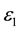 is negative
is negative  and the components in directions 2 and 3 are positive and proportional to the Poisson ratio
and the components in directions 2 and 3 are positive and proportional to the Poisson ratio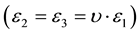 .
.
The values of parameters A and B can be found using a least square regression.
2. Methodology
The damage parameters adjustment using the Mazars model allows a greater reliability of the prediction of the concrete mechanical properties. As seen before, important modifications occur in the behavior of the recycled concrete with the increase of the aggregate substitution rate, which indicates that this variable is of great importance to the adapting of the original model.
In this paper, the aggregate substitution rate (ASR) was added to the Mazars model as an independent variable directly associated to the parameters A and B. The adapted model will thus be the function of two independent variables ASR and ε, related respectively to the aggregate substitution rate and to the development of the deformation.
The relationship between the damage parameters (A and B) and the ASR was established based on the observation of experimental stress-strain curves. The variable ASR was evaluated in the interval of 0% to 100% in three points of its domain, the extreme limits 0% and 100% and the central point. The aimed relationship arises, therefore, from the curve that best adjusts the points that were evaluated and can be expressed by a polynomial function.
The proceeding that follows shows the stages of this evaluation
・ obtainment of the experimental curves
・ parametric identification of the experimental curves
・ obtainment of the functions for the curves “A versus ASR” and “B versus ASR”.
2.1. The Experimental Curves
In this paper the experimental data that were used for the adapting of the Mazars model were obtained by Leite [20] who studied the mechanical behavior of recycled concretes submitted to axial compression and direct tensile strengths to be applied in elements of pre-cast concrete. The CDW used by Leite [20] showed around 54.5% of mortar, 26% of brick and 16.4% of concrete as a gravimetric composition.
Leite [20] assessed six concrete mixtures varying the replacement rate of the natural aggregate by recycled ones. The author also casted three samples for each mixture. These mixtures were produced with two water/ce- ment ratios (0.45 and 0.80) and are listed below.
・ Reference-0% of substitution rate, named here as REF
・ one mixture using 50% of recycled fine aggregate, named here as H-RFA
・ one mixture using 50% of recycled coarse aggregate, named here as H-RCA
・ one mixture using 100% of recycled fine aggregate, named here as F-RFA
・ one mixture using 100% of recycled coarse aggregate, named here as F-RCA
・ one mixture using 50% of recycled fine aggregate and 50% of recycled coarse aggregate, named here as H-RFCA.
The experimental curves were achieved from axial compression tests with displacement control at 28 days of age. Leite [20] used a hydraulic servo-controlled machine, model UH-F 1000kN- and a system of data acquisition composed of an ADS2000 conditioner of 16 bits and an AQDados® software.
2.2. Parametric Identification of the Experimental Curves
Applying a regression method to obtain the values of A and B parameters ensures the best adjustment of the model of the experimental data as well as it allows the evaluation of the quality of the adjustment achieved through R2. According to Álvares [19] , the parametric evaluation must begin by the choice of the error function (Equation (7)) making possible the evaluation of the numeric answer with relation to the experimental one. Using the least squares regression, the error is estimated by Equation (7).

where,
Err = global error;


The adjustment of the Mazars model resulted in a system of coupled equations, not linear, in order to fulfill the conditions established by Equation (7). The solution of systems like these needs iterative methods. So, the Levenberg-Marquardt method was chosen in this study. The initial values of the parameters A and B were the same that were used in conventional concrete as suggested by Mazars [18] . The parametric identification pro- cess was done for each experimental curve obtained by Leite [20] in order to increase the accuracy of the results in a total of 36 compression curves.
2.3. Obtaining the Functions for the Curves “A versus ASR” and “B versus ASR”
The behavior of the parameters of the analytical model in relation to the substitution of aggregates is observed by designing curves that adjust the three points previously chosen in the domain (0%, 50% and 100%). The choice of the adjustment function obeys the following criteria
・ the curve must necessarily pass through the 3 points that were obtained experimentally
・ the curve in the intervals between the points (0% to 50% and 50% to 100%) must have a linear or quadratic shape.
3. Presentation and Analysis of Results
Using the average curves of axial and lateral stress-strain of the evaluated mixtures, Leite [20] observed that, in general, the recycled concretes present lower rupture stresses and, comparing a same stress, larger deformations than conventional concretes (reference). Figure 2 shows graphically the behavior of the mixtures for the water/cement ratio of 0.45.
3.1. Identification of the Parameters A and B of the Studied Mixtures
Using the previously presented methodology (Section 2.3), it was possible to obtain values for the parameters of the damage model from the experimental stress-strain curves. As follows, Figure 3 shows the main aspects that were observed in the parametric identification of the model. Then, Table 1 shows the values of the mixture parameters with the water/cement ratio equal to 0.45.
Figure 3 shows graphically the quality of the obtained adjustment through the least square regression. It can be observed that the determination coefficient that was found, 0.988, certifies that the chosen analytical model, even having few adjustment parameters, represents satisfactorily the recycled concrete.
Figure 2. Stress-strain curves for the water/cement ratio equal to 0.45 [20] .
Figure 3. Linear adjustment H-RCA with w/c = 0.45, sample 1.
Table 1 shows the results of the parametric identification for the mixtures of the water/cement ratio equal to 0.45. It can be observed that the smallest coefficient of determination is 0.910 corresponding to the mixture H-RCA (sample 3). The values achieved for the parameter A are close to the inferior limit of the interval suggested by Mazars [18] for this parameter, the variation found ranges from 0.64 to 1. Regarding the parameter B its values lie between 1045.60 and 2251.62, coherent with the expectations for the applied analytical model.
For the mixtures with the water/cement ratio equal to 0.80 the values of the parameter A lie between 0.55 and 0.88 and of the parameter B between 1185.50 and 2057.15.
3.2. Behavior of the Parameters Referring to ASR
Using the average of the values that were obtained for the parameters A and B as shown, the curves “A versus ASR” and “B versus ASR” were drawn. Eight representative curves as follow that represent the behavior of each parameter regarding to the aggregates types-RFA and RCA- and the water/cement ratios −0.45 and 0.80 were found. Figure 4 and Figure 5 show the curves that arose and their respective polynomial functions.
Thus, the model of isotropic damage proposed by Mazars [18] presented in item 1.2 by the Equations (1)-(3), can be adapted to the description of recycled concrete substituting its parameters A and B (originally arbitrated) by polynomial functions that show the degradation of the mechanical properties of the concrete with the substitution of natural aggregates by recycled ones, Equations (8) to (15). Thus, the recycled concrete studied in this paper can be described by the Mazars model using the following functions that result from the behavior shown in Figure 4 and Figure 5.
Table 1. Parametric identification for mixtures.
・ Mixtures with the w/c = 0.45 and substitution of RFA


・ Mixtures with the w/c = 0.45 and substitution of RCA


・ Mixtures with the w/c = 0.80 and substitution of RFA
Figure 4. Behavior of the parameters A and B for the w/c = 0.45.
Figure 5. Behavior of the parameters A and B for the w/c = 0.80.


・ Mixtures with the w/c = 0.80 and substitution of RCA


3.3. Validation of the Adapted Mazars Model
The evaluation of the efficiency of the model created for the recycled concrete was done through the description of the experimental axial compression curves. The suggested model was implemented in the MATLAB® software. The original equation by Mazars [18] had its parameters A and B substituted by the functions presented in item 3.2 according to the characteristics of the mixtures of the experimental program. As follows, Figures 7-11 show graphically the comparisons for some mixtures.
It is possible to note that the model proposed by the authors (adapted Mazars) does not exactly describe individually any of the experimental curves for the mixtures with the water/cement of 0.45 as well as for the water/cement ratio of 0.80. However, the curves allow to observe that the adapted Mazars model is able to draw the approximate behavior of recycled concrete for the different substitution contents. This results in a generalized model with analytical curves that are very close to the experimental curves for all the mixtures.
4. Numerical Application
The analytical model validated in the item 3.3 (Figures 6-10) was used in numerical simulations so to represent the behavior under compression of the recycled concrete. Through the finite element method studies of flexural tensile strength were simulated using the mixtures defined in item 2.1 referring to the water/cement ratio equal to 0.80.
The conditions of geometry and loading for the building of the model followed the guidelines of the Brazilian Standard NBR12142 [21] . Figure 11 shows schematically the configuration of the test.
The considerations assumed to build the numerical model using the DIANA® software are shown in Table 2.
The adapted Mazars model was included in the analyses through stress-strain curves under compression obtained by the substitution of the equations of item 3.2 chosen according to the type of the mixture, in Equation (3), the original Mazars model. The behavior of flexural tensile strength after cracking was represented by a distributed cracking model using the function developed by Hordijk et al. (1986) apud [22] . The band width of

Figure 6. Validation of the model for (a) REF and (b) H-RFA both with the w/c = 0.45.

Figure 7. Validation of the model for (a) F-RFA and (b) H-RCA both with the w/c = 0.45.

Figure 8. Validation of the model for (a) F-RCA with the w/c = 0.45 and (b) REF with the w/c = 0.80.

Figure 9. Validation of the model for (a) H-RFA and (b) F-RFA both with the w/c = 0.80.

Figure 10. Validation of the model for (a) H-RCA and (b) F-RCA both with the w/c = 0.80.
Figure 11. Geometry of the flexural tensile strength test (dimensions in centimeters).
Table 2. Parameters used in the numerical model.
cracking (h) was calculated based on the dimensions of the finite element according to Equation (16) suggested by the DIANA® software user guide.

where,
S = finite element surface
The fracture energies (Gf) that were considered, Table 3, were calculated for each mixture based on Equation (17) [23] .

where,
Gf = fracture energy
b = parameter with value equal to 85.93;
b1 = parameter with value equal to 0.125;
b2 = parameter with value equal to 0.211;
d = maximum size of aggregate;
d20 = parameter with value equal to 20 mm;
t = cure time in days;
t30 = parameter with value equal to 30 days;
λ = parameter with value equal to 1.
Table 3 shows the results that were found from the numerical model and their comparison with the experimental values obtained by Leite [20] . The flexural tensile strength was estimated based on the values obtained in direct tensile strength tests following the Equation (18) proposed by the CEB-FIP 90 [24] .

Table 3. Values used for the fracture energies Gf and results of numerical modeling.
1Flexural tensile strength.
where,
ft = direct tensile strength;
ft,fl = flexural tensile strength;
hb = beam height (mm);
h0 = 100 mm.
5. Conclusions
In this article an isotropic damage model was applied for the description of the mechanical behavior of recycled concrete by means of adapting the parameters A and B described by Mazars [18] for conventional concrete. The results presented allow to conclude that
・ The adapted Mazars model of isotropic damage is able to represent the mechanical behavior of recycled concrete under compression with good approximations. In this paper the determination coefficients found are higher than 0.90;
・ The hypothesis that the generalization of a constitutive analytical model for recycled concrete is possible through the manipulation of its parameters was confirmed. Using the studies of the influence of the parameters A and B to draw the stress-strain curves under compression it was possible to express through polynomial functions the variation of the values of these parameters with the increase of the replacement rate of the aggregates;
・ The methodology used allowed that the applying of the Mazars model could be done through the attribution of values of a single variable, replacement rate of the aggregates (ASR). The validation of the model that was created allowed to observe the proximity of the analytical curves, generated by the model in relation to the experimental curves.
Acknowledgements
The authors thank CAPES and CNPq for their financial support to this research.
Cite this paper
Marcelo Pedreirada Silva,Magno TeixeiraMota,Anderson de Souza MatosGadéa,Mônica BatistaLeite,Koji de JesusNagahama, (2015) The Behavior of Recycled Concrete through the Application of an Isotropic Damage Model. Open Journal of Civil Engineering,05,339-351. doi: 10.4236/ojce.2015.53034
References
- 1. Etxeberria, M., Vásquez, E., Marí, A. and Barra, M. (2007) Influence of Amount of Recycled Coarse Aggregates and Production Processor Properties of Recycled Aggregate Concrete. Cement and Concrete Research, 37, 735-742.
http://dx.doi.org/10.1016/j.cemconres.2007.02.002 - 2. Leite, M.B. (2001) Evaluation of Mechanical Properties of Concrete Produced with Recycled Aggregates from Construction and Demolition Waste. Ph.D. Thesis, University of Rio Grande do Sul. (In Portuguese)
- 3. Maruyama, I., Sogo, M., Sogabe, T., Sato, R. and Kawai, K. (2004) Flexural Properties of Reinforced Concrete Beams. International Rilem Conference on the Use of Recycled Materials in Buildings and Structures, Barcelona, 8-11 November 2004, 526-535.
- 4. Disfani, M.M., Arulrajah, A., Haghighi, H., Mohammadinia, A. and Horpibulsuk, S. (2014) Flexural Beam Fatigue Strength Evaluation of Crushed Brick as a Supplementary Material in Cement Stabilized Recycled Concrete Aggregates. Construction and Building Materials, 68, 667-676.
http://dx.doi.org/10.1016/j.conbuildmat.2014.07.007 - 5. Rao, M.C., Bhattacharyya, S.K. and Barai, S.V. (2011) Behaviour of Recycled Aggregate Concrete under Drop Weight Impact Load. Construction and Building Materials, 25, 69-80.
http://dx.doi.org/10.1016/j.conbuildmat.2010.06.055 - 6. Reis, C.N.S., Leite, M.B. and Lima, P.R.L. (2011) Influence of the Diameter of the Bar and CDW Content on the Bond Behavior of Recycled Reinforced Concrete. 2nd International RILEM Conference on Progress on Recycling in the Built Environment, São Paulo, 2-4 December 2009, 207-214.
- 7. Seara-Paz, S., González-Fonteboa, B., Eiras-López, J. and Herrador, M.F. (2014) Bond Behavior between Steel Reinforcement and Recycled Concrete. Materials and Structures, 47, 323-334.
http://dx.doi.org/10.1617/s11527-013-0063-z - 8. LNEC E 471 (2006) Guideline of Utilization of Coarse Recycled Aggregates in Hydraulic Cementing Based Concrete. National Laboratory of Civil Engineering, Portugal. (In Portuguese)
- 9. Ministry of Fomento (2011) Code on Structural Concrete. Ministry of Fomento, Spain. (In Spanish)
- 10. RILEM TC 121-DRG (1994) Specifications for Concrete with Recycled Aggregates. Materials and Structures, 27, 557-559.
- 11. Grübl, P. and Rühl, M. (1998) German Committee for Reinforced Concrete (DafStb) Code: Concrete with Recycled Aggregate. In: Dhir, R.K., Henderson, N.A. and Limbachiya, M.C., Eds., Sustainable Construction: Use of Recycled Concrete Aggregate, Thomas Telford Publishing, London, 409-418.
- 12. Xiao, J.Z., Li, J.B. and Zhang, C. (2005) Mechanical Properties of Recycled Aggregate Concrete under Uniaxial Loading. Cement and Concrete Research, 35, 1187-1194.
http://dx.doi.org/10.1016/j.cemconres.2004.09.020 - 13. Guo, Z.H. and Zhang, X.Q. (1982) Experimental Investigation of Stress-Strain Curves for Concrete. Journal of Building and Structure, 3, 1-12.
- 14. Bhikshma, V. and Kishore, R. (2010) Development of Stress-Strain Curves for Recycled Aggregate Concrete. Asian Journal of Civil Engineering (Building and Housing), 11, 253-261.
- 15. Saenz, L.P. (1964) Discussion of Paper “Equation for Stress-Strain Curve of Concrete” by Desai, P. and Krishnan, S. Journal of American Concrete Institute, 61, 1229-1235.
- 16. Du, T., Wang, W.H., Liu, Z.X., Lin, H.L. and Guo, T.P. (2010) The Complete Stress-Strain Curve of Recycled Aggregate Concrete under Uniaxial Compression Loading. Journal of Wuhan University of Technology-Mater, 25, 862-865.
http://dx.doi.org/10.1007/s11595-010-0109-9 - 17. Guo, Z.H. (1997) The Strength and Deformation of Concrete (Experimental Basis and Constitutive Relationship). Tsinghua University Press, Beijing.
- 18. Mazars, J. (1984) Application of Continuous Damage Mechanic to Non-Linear Behavior of Concrete Structures. PhD Thesis, Paris 6 University, Paris. (in French)
- 19. Álvares, M.S. (1993) Study of Concrete Damage Model: Formulation, Parametric Identification and Numerical Application Using Finite Element Method. Dissertation (M.Sc.), São Paulo University, São Carlos. (in Portuguese)
- 20. Leite, M.B. (2009) Stress-Strain Behavior Evaluation of Recycled Concrete under Compressive and Direct Tensile Strength. Monograph of Progression of Professor from State University of Feira de Santana. (in Portuguese)
- 21. Brazilian Standard (ABNT) (1994) NBR 12142: Concrete-Determination of Tensile Strength in Flexion in Test. Rio de Janeiro. (in Portuguese)
- 22. DIANA (2005) User’s Manual—Release 9.
- 23. Xiao, J.Z., Li, W.G. and Poon, C.S. (2012) Recent Studies on Mechanical Properties of Recycled Aggregate Concrete in China—A Review. Science China Technological Sciences, 55, 1463-1480.
http://dx.doi.org/10.1007/s11431-012-4786-9 - 24. CEB-FIP Model Code (1990) Design Code. Committee Euro-International du Beton, Lausanne, Thomas Telford Services Ltd., London.
















