Open Journal of Civil Engineering
Vol.04 No.03(2014), Article ID:49800,10 pages
10.4236/ojce.2014.43023
A Review and Update of Analytical and Numerical Solutions of the Terzaghi One-Dimensional Consolidation Equation
Cheikhou Ndiaye1, Meissa Fall1, Mapathe Ndiaye1, Daouda Sangare2, Abib Tall1
1Laboratoire de Mécanique et Modélisation, UFR Sciences de l’Ingénieur, Université de Thiès, Thiès, Sénégal
2Laboratoire d’Analyse Numérique et d’Informatique, UFR Sciences Appliquées et Technologie, Université Gaston Berger, Saint-Louis, Sénégal
Email: cheikhou.ndiaye@univ-thies.sn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2014; revised 8 August 2014; accepted 28 August 2014
ABSTRACT
Practical resolution of consolidation problems that we often face requires an extensive and solid knowledge of the different parameters highlighted by the Terzaghi one-dimensional consolidation theory. This theory, with its assumptions, leads to a partial differential equation of second order in space and first order in time of pore water pressure. Analytical and numerical resolutions of this equation allow determining the water pressure variation before and after the application of a charge. Numerical modeling has enabled the simulation of the whole results obtained by the two methods of resolution (pressure, degree of consolidation, time factor, among others) to have a physical analysis and a lawful observation that lead to a suitable understanding of the phenomenon of Terzaghi one-dimensional consolidation.
Keywords:
Pore Pressure, Numerical Solution, Analytical Solution, Modeling, Consolidation, Time Factor

1. Introduction
The unidimensional consolidation of soils has been described by Terzaghi using partial differential equations [1] . The resolution of these equations can be performed analytically and/or numerically [2] [3] . In this work, we resolved Terzaghi partial differential equations using Fourier method and finite difference respectively for analytical and numerical solutions. At a further step we used numerical modeling to represent graphically the two solutions in order to validate the obtained results.
We consider an example of a clay layer drained on the faces and submitted instantly to the initial conditions to constant stress (load) [4] (Figure 1). It is assumed that the clay layer thickness is 2H with H = 8 m subject to its surface to a total stress Δσv = 30 kPa and with a consolidation coefficient estimated to 2 m2/year.
Solving the Terzaghi one-dimensional consolidation equation, from the hydro mechanical modeling of the solid [2] [3] , and adapted to the parameters of the problem allows for the following simulations:
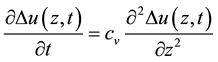 (1)
(1)
where  is the pore water pressure,
is the pore water pressure, 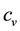 is the coefficient of consolidation,
is the coefficient of consolidation, 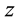 is the depth and
is the depth and 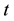 corresponds to the time.
corresponds to the time.
2. Analytical Method
To solve this kind of first-order partial differential equation with respect to time and second-order with respect to space, we must combine two boundary conditions and initial condition for the interstitial pressure.
Boundary conditions (for all time t)
-At the bottom of the layer, z = 0, we have:
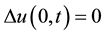
-On the surface of the layer, z = 2H, then:
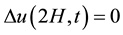
Initial condition (for t = 0)

If we apply the Fourier sine transform  on the left and right members of this equation:
on the left and right members of this equation:
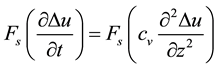 (2)
(2)
where
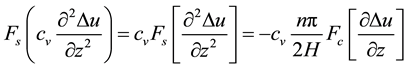 (3)
(3)
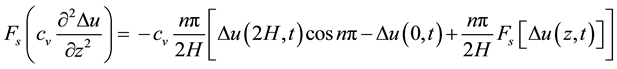 (4)
(4)
The relation (2) is as follows:
Figure 1. Example of a clay layer drained on the two faces (Modified from [4] ).
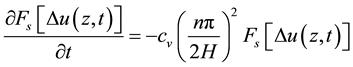 (5)
(5)
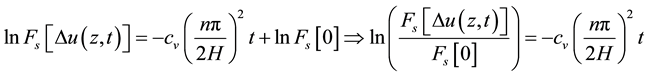 (6)
(6)
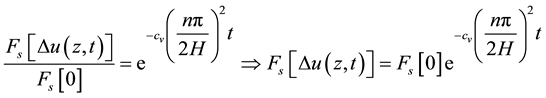 (7)
(7)
Since the method used is the sine Fourier transform based on the odd frequency (sinusoidal) of the interstitial pressure, the development into Fourier series will not affect the coefficients an.

where
By substituting, the equation can be rewritten into this form:


By simplifying and separating constants we obtain the analytical solution of the Terzaghi’s equation from the Fourier method:

Assuming that the ∞ = 100, which is acceptable in numerical analysis [5] , we can evaluate the numerical value of ∆u (which is the exact solution) [6] [7] . For this, we make a loop for each point (zi, ti) and calculate

For a longer time of consolidation (e.g. 20 years), we obtain the following results (Figure 3(a) and Figure 3(b)):
For an infinite time, the phenomenon of pressure dissipation becomes more and more clear and the effective stresses are more important (Figure 4(a) and Figure 4(b)); this means that the load is transmitted to solid grains.
The degree of consolidation and the time factor are derived from the exact solution of the consolidation equation.

Hence the representation of the function 

The dimensionless term which is the ratio between the value of ∆u(z, t) at (t) and its initial value ∆u0 = ∆σv are simulated based on the reduced depth Z = z/H and for different values of Tv.

Figure 2. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 1 year).

Figure 3. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 20 years).

Figure 4. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 100 years).
Figure 5. Respective changes of Uv and Tv, one according to others.

Thus, we can see that the ratio 
linear evolution for Z comprise between 0 and 0.1 (Figure 6). Then for other values of Tv with time steps ranging from 0.05 to 0.2, we obtain the other isochronous which respectively follow the first one, then with a time step of 0.1, the last isochronous; like the first isochronoous they show all ratio values that deviate more and more to 1 (which is the maximum value) when the time factor Tv tends to 1.
3. Numerical Method
The principle of this method consists in substituting the function ∆u(z, t) of the interstitial pressure at the point M at time t in a discrete function 


This form leads to address the resolution by an explicit scheme which uses a discretisation at zi node and at iteration n. By analogy to the consolidation equation the equality between the first order scheme in time and the second order centered scheme in space has been set
Hence it may be evaluated to obtain:

Given
Figure 6. Isochrones of pore pressure for different values of Tv as a function of Z.
iteration k +1:

So the matrix of excess water pore pressure from the resolution is given by the following finite differential method:

Computed results in matrix form obtained by the numerical solution give also performances that converge towards an analytical solution.
For greater stability, θ must be less than 1/2 [8] ; however, we assume that θ = 1/4 and apply the other parameters of the problem for obtaining the following figures (Figure 7(a) and Figure 7(b)):
For a longer time of consolidation (e.g. 20 years), we obtain the following results (Figure 8(a) and Figure 8(b)). With these results, we can notice the phenomenon of dissipation that appears in a clear way:
For an infinite time, the phenomenon of pressure dissipation becomes more clear and the effective stress more important (Figure 9(a) and Figure 9(b)). In fact, the load is transmitted to solid grains.
These results show without any ambiguity that the water interstitial pressure is canceled through the soil layer thickness in the same way as noticed in the analytical resolution:
The pore water pressure obviously vanishes over time with perfect coherence with Terzaghi’s relation (∆σv = ∆σ' + ∆u). The load is more and more transferred towards the solid grains. Then the effective stress tends to the value of the initial stress which is applied at the soil surface.

Figure 7. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 1 year).

Figure 8. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 20 years).

Figure 9. Evolution of the pore water pressure (a) and the effective stress (b) as a function of depth and time (we consider here tmax = 100 years).
4. Conclusions
We found for the different parameters used in our simulations that we almost have the same changes in the numerical and analytical resolutions [6] [7] . However, we notice more accuracy on the analytical resolution due to the fact that the numerical resolution gives an approximate solution while the finite differential method imposes
some specific conditions that lead to a stable resolution; for the example 

the explicit scheme rule [8] .
The problem of Terzaghi one-dimensional consolidation can be easily solved by analytical and numerical methods; and the solutions resulting from this resolution may also be an interesting subject for numerical simulation [9] in order to highlight more clearly the physical interpretation necessary to better understand soil consolidation.
Acknowledgements
I deeply thank the Engineering Group of the UFR Sciences de l’Ingénieur of the University of Thies and researchers from the Laboratory of Mechanics and Modeling for their guidance.
References
- Qin, A.F., Sun, D.A. and Tan, Y.W. (2010) Analytical Solution to One-Dimensional Consolidation in Unsaturated Soils under Loading Varying Exponentially with Time. Computers and Geotechnics, 37, 233-238.
- Hicher, P.Y. (1985) Comportement mécanique des argiles saturées sur divers chemins de sollicitations monotones et cycliques. Application à une modélisation élastoplastique et viscoplastique. Ph.D. Thesis, Université Pierre et Marie-Curie, x p.
- Li, X.-L. (1999) Comportement Hydromécanique des Sols Fins: De l’état saturé à l’état non saturé. Ph.D. Thesis, Sciences appliquées de l’Université de Liège, x p.
- Magnan, J.P. and Soyez, B. (1988) Déformabilité des Sols. Consolidation. Tassement. C 214 Traité Construction, volume C 21.
- Butcher, J.C. (1987) The Numerical Analysis of Ordinary Differential Equations: Runge-Kutta and General Linear Methods. Wiley, Wiley-Interscience.
- The Math Works, Inc., Matlab, Reference Guide, 1984-92.
- Torrésani, B. (2009) Introduction à Matlab et octave, Université de Province Aix Marseille I.
- Goncalvès, E. (2005) Résolution Numérique, Discrétisation des EDP et EDO, Institut National Polytechnique de Grenoble.
- Salazar, G.E.C. (2006) Modélisation du séchage d’un milieu poreux saturé déformable: Prise en compte de la pression du liquide. PhD thesis, Ecole Nationale Supérieure d’Arts et Métiers Centre de Bordeaux.
Annexes
(1) Analytical solution
-Pore water pressure:
function simulation(N,Cv,H,Tmax)
lamda=4*30/pi; %hpa
[z,t]=meshgrid(linspace(0,2*H,50),linspace(0,Tmax,50));
V=0; % V represente la surpression
for m=0:N
V=V+lamda*(1/(2*m+1)*exp((2*m+1)^2*(pi^2)*(Cv*t/(4*H^2))).*sin((2*m+1)*pi*z/(2*H)));
end
mesh(z,t,V)
xlabel depth(m); ylabel time(years); zlabel \DeltaU(z,t)
for i=1:15
view(-100+24*(i-1),30)
m(:,i)=getframe;
end
-effective stress:
function simulation_efective_stress(N,Cv,H,Tmax)
lamda=4*30/pi; %hpa
[z,t]=meshgrid(linspace(0,2*H,50),linspace(0,Tmax,50));
V=0;
for m=0:N
V=V+lamda*(1/(2*m+1)*exp((2*m+1)^2*(pi^2)*(Cv*t/(4*H^2))).*sin((2*m+1)*pi*z/(2*H)));
end
q=30-V; % q=delta_sigma_prime_v : effective stress
mesh(z,t,q)
xlabel depth(m); ylabel time(years); zlabel \Delta\sigma\prime(z,t)
axis([0 20 0 20 0 30])
(2) Numerical solution
-Pore water pressure:
clc; clear;
k=4; %k=cv=
dx=0.25;
r=1/4; dt=dx*dx*r/k;
Tmax=100;
a=0;b=16;
cla=0;clb=0;
nx=(b-a)/dx;
nt=Tmax/dt;
x=0:dx:b; t=0:dt:Tmax;
%[x,t]=meshgrid(linspace(0,2*b,50),linspace(0,Tmax,50));
for i=1:nx-1
N(i)=0;
end
N(1)=r*cla;
N(nx-1)=r*clb;
for i=1:nx-2
M(i,i)=1-2*r;
M(i,i+1)=r;
M(i+1,i)=r;
end
M(nx-1,nx-1)=1-2*r;
for i=1:nx+1
Ci(i)=30;
end
for i=1:nx-1
h(i)=Ci(i+1);
end
j=1;
h=h';
while(j < nt + 2)
for i=1:nx-1
w(i,j)=h(i);
end
h=M*h+N';
j=j+1;
end
for i=nx:-1:2
for j=nt+1:-1:1
w(i,j)=w(i-1,j);
end
end
for j=1:nt+1
w(1,j)=0;
w(nx+1,j)=0;
end
mesh(t,x,w);
xlabel time(t); ylabel depth(m); zlabel \DeltaU(z,t)
for i=1:15
view(-150+24(i-1),30)
m(:,i)=getframe;
end
-effective stress:
clc; clear;
k=4; %k=cv=
dx=0.25;
r=1/4; dt=dx*dx*r/k;
Tmax=100;
a=0;b=16;
cla=0;clb=0;
nx=(b-a)/dx;
nt=Tmax/dt;
x=0:dx:b; t=0:dt:Tmax;
%[x,t]=meshgrid(linspace(0,2*b,50),linspace(0,Tmax,50));
for i=1:nx-1
N(i)=0;
end
N(1)=r*cla;
N(nx-1)=r*clb;
for i=1:nx-2
M(i,i)=1-2*r;
M(i,i+1)=r;
M(i+1,i)=r;
end
M(nx-1,nx-1)=1-2*r;
for i=1:nx+1
Ci(i)=30;
end
for i=1:nx-1
h(i)=Ci(i+1);
end
j=1;
h=h';
while(j < nt + 2)
for i=1:nx-1
w(i,j)=h(i);
end
h=M*h+N';
j=j+1;
end
for i=nx:-1:2
for j=nt+1:-1:1
w(i,j)=w(i-1,j);
end
end
for j=1:nt+1
w(1,j)=0;
w(nx+1,j)=0;
end
q=30-w; % q=deltasigmaprime ( i.e effective stress)
mesh(t,x,q)
xlabel time(t); ylabel depth(m); zlabel \Delta\sigma\prime_v(z,t)
for i=1:5
view(-80+24(i-1),30)
m(:,i)=getframe;
end















