Theoretical Economics Letters
Vol.06 No.02(2016), Article ID:65476,9 pages
10.4236/tel.2016.62021
Fairness in an Ultimatum Game
Mohamed I. Gomaa1, Stuart Mestelman2, S. M. Khalid Nainar3, Mohamed Shehata3
1Accounting, Taxation and Legal Studies in Business, Hofstra University, Hempstead, USA
2Department of Economics, McMaster University, Hamilton, Canada
3Accounting and Financial Management Services, McMaster University, Hamilton, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 February 2016; accepted 10 April 2016; published 13 April 2016
ABSTRACT
We present a controlled laboratory environment in which we use an ultimatum game to generate two endogenous fairness indices. We use these as alternatives to the more conventional exogenous measure, the offer index, in a model of offer-acceptance which includes measures of social value orientations and risk attitudes as variables for explaining the acceptance or rejections of offers in an ultimatum game. In particular we are interested in providing an explanatory model which can support situations in which the likelihood to accept unfair offers (as measured by the offer index) will exceed the likelihood of rejecting a fair offer (again, as measured by the offer index). The offer index in the ultimatum game setting is the amount offered by a sender divided by the total endowment of the sender. Our endogenous fairness indices meet our condition of the likelihood of acceptance of an unfair offer exceeding the likelihood of rejecting a fair offer even though the explanatory power of the offer-acceptance models with the endogenous fairness indices is not significantly different from that with the exogenous fairness index.
Keywords:
Fairness, Social Value Orientation, Risk Attitudes, Ultimatum Game, Endogeneity

1. Introduction
The objective of this paper is to use the ultimatum game setting in a controlled laboratory environment to provide additional empirical evidence on the puzzling phenomenon of why some economic agents may reject non-trivial offers for distributing the surplus of an economic transaction, while others may accept very trivial amounts.1 Typically these phenomena are observed in ultimatum games or in environments in which principals are able to punish agents who do not act in a manner the principal judges to be “fair”. Fairness in these environments is conventionally viewed as a transfer of half of the amount that the “sender” in these game has available to share.2 The greater is the size of the offer, the more likely that the receiver will accept the offer.3 This measure of fairness alone is unable to provide an explanation for the existence of instances when, ceteris paribus, an “unfair” offer may be more likely to be accepted than a “fair” offer.
When fairness is introduced as an explanatory variable in an offer-acceptance model for a one-shot ultimatum game, the fairness measure is typically the amount received by the individual who is asked to accept the offer.4 This fairness measure is exogenous to the individual who must make the acceptance decision. Other attempts to introduce fairness into the offer-acceptance model include the introduction of the receiver’s beliefs about what the sender may offer. Negative deviations from beliefs are likely to result in rejections of offers. The greater the deviations the more likely it is that the offer will be rejected [3] . We use the ultimatum game to derive a measure of fairness that is revealed through the playing of the game. We then replace the above exogenous measure of fairness by an endogenous measure of fairness that is capable of providing an explanation for why, ceteris paribus, some unfair offers are more likely to be accepted than some fair offers without having to ask the participants in these environment to reveal their beliefs about the likely behavior of others.
2. The Controlled Laboratory Experiment and the Endogenous Fairness Index
In a one-shot ultimatum game the predicted outcome is that the sender, recognizing that the receiver has no incentive to reject any positive distribution (something is better than nothing) will choose to send the smallest amount possible. The receiver will accept this. We would not anticipate that the sender or receiver would behave strategically by using their “send” or “accept” decisions to establish a reputation. If decisions different from these are realized, these decisions are based on the attitudes (including social norms) that the participants bring with them to the session in which they will participate. Among these social norms are their social value orientations, their notions of fairness and their attitudes towards risk. Our conjecture is that if we had information about both what an individual receives as an offer from another person as well as what the individual sends as an offer to a third person in a one-shot ultimatum game, we can use the latter value as a measure of what the receiver thinks is a fair offer within the context of this game when responding to what the person has received from another sender. The amount sent could also be interpreted as the sender’s belief in what will be an acceptable offer. We are equating this belief with the person’s attitude of what constitutes a fair offer.
We conceive of an empirical explanatory model to capture the probability that an offer will be accepted (Y) that takes the form
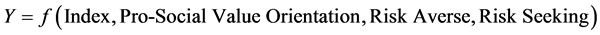 (1)
(1)
where Index is either the exogenous Offer Index (the amount sent divided by the initial amount to be divided) or an endogenous Fairness Index (the amount received by an individual as a responder divided by the amount the individual sent as a sender). The social value orientation and risk attitude variables capture other characteristics that the participants bring to the session and are included as 0 - 1 variables. The individual is either pro-social (value 1) or pro-self (value 0), risk averse (value 1), risk seeking (value 1) or risk neutral (the risk aversion and risk seeking values are 0).5
Suppose the typical individual is risk neutral and pro-self so that the values for value orientation and risk attitudes variables are 0 and that the amount to be divided by a sender is 500. The resulting linear estimating equations are of the form
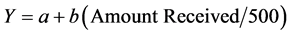 (2)
(2)
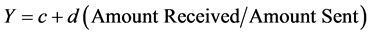 (3)
(3)
and the expectation is that the parameters b and c will be positive. With Equation (2) the likelihood that an offer of 250 is accepted is equal to a + 0.5b. If an offer less than 250 is made, the likelihood that it is accepted will be less than the likelihood that the fair offer is accepted. With Equation (3) the likelihood that an offer of 250 is accepted is equal to c + d (250/Amount Sent). If the amount sent by the responder was 300 the likelihood that the “fair” offer of 250 is accepted is c + 0.833d. However, if the responder received an offer of 150 and also sent 150 in the role of a sender, the likelihood that the responder would accept the 150 is c + d. In these two situations our prediction is that the offer of 250 would be less likely to be accepted than the offer of 150. This result cannot occur with the index used in Equation (2) that has the exogenous fairness index rather than the endogenous fairness index. The endogenous index uses the information provided by the participant to predict the participant’s behavior. In this sense it is similar to the introduction of beliefs as explanatory variables. [3] run rejection regressions which use “offer” and “responder expectation” or “belief about others”.
Either the ratio of what is received to what is sent or the difference between what is received and what is sent may be effective endogenous fairness indices. In particular, we can conceive of a situation in which an exogenously fair offer may be rejected if the individual who must make an acceptance decision has made an offer that is more than fair. This would result in a fairness ratio that is less than unity or a fairness difference that is negative. Both of these could result in the likelihood of accepting a fair offer (as measured by the endogenous fairness index) being less than the likelihood of accepting an unfair offer (as measured by the endogenous fairness index).
To generate the necessary data to obtain an endogenous fairness index we conduct a one-shot ultimatum game in which participants are separated into two groups, each of which is in a different room. Each person (in the role of the sender) makes an offer to another person who is in a different room (and who is randomly selected by the experimenter). The person described previously as the sender, also plays the role of a receiver, and in this role receives an offer from someone in a different room.6 We could obtain the fairness measure we seek by using the strategy vector method to obtain the senders’ decisions about what they would accept if they were in the role of the receiver (see [7] - [9] ). If as participants go from a low value to a high value for what they might receive and there is a single switch-point at which they would change their decision from “reject the offer” to “accept the offer” we could select the lowest acceptable offer as the boundary between fair and unfair offers and use this value as the denominator in our fairness index. While the results on whether using the strategy vector or the direct response have different effects are mixed, the conclusion of [9] is that the evidence does not suggest that the results obtained using the strategy vector are significantly different from those using the direct response. We chose the direct response method.
3. Experimental Design and Summary of Conjectures to Be Tested
A total of 48 participants were recruited from undergraduate classes in the DeGroote School of Business at McMaster University in Hamilton, Canada. During the recruitment phase, students were told that the experiment involved simple decision-making, and that the details would be given to them during the session. In addition, they were told that they were required to participate in two separate sessions. Each session would be conducted on a different day and each session would last no more than two hours. They were also informed that during the course of the sessions they would earn money that would be paid to them in cash at the conclusion of each session. The results we are reporting here are based on the results of the first session and the first round of the second session.
3.1. The First Session (Eliciting Risk Attitudes and Social Value Orientations)7
In the first session, we elicited subjects’ risk preferences and social value orientations. This allows us to isolate intrinsic individual characteristics rather than assume that our subjects are individualistic and risk-neutral profit maximizers when we analyze the offer and offer-acceptance decisions made by people participating in the ultimatum game.
To elicit subjects’ risk preferences, we used the two-stage lottery mechanism developed by [11] and further developed by [12] - [15] . Risk neutrality characterizes a majority of the 48 participants in this experiment. 23 individuals are risk neutral, 8 are risk averse and 17 are risk seeking. Note that the median risk attitude is in the risk-neutral category. Risk attitudes are slightly skewed towards the risk-seeking end of the risk attitude range.
We used the Decomposed (Ring) Game mechanism developed by [16] and [17] to measure subjects’ value orientations.8 This measure permits us to sort individuals into the pro-social categories altruist and cooperator and the pro-self categories individualist, competitor and aggressor. There are no altruists and no aggressors among the 48 participants in this experiment. Approximately 40 percent of the participants (19) are cooperators (pro-social) while only one participant is a competitor. The remaining 28 individuals are individualists. Overall, the distribution of value orientations is skewed towards orientations that we categorize as pro-self. The mean consistency measure for our participants exceeded 0.89. This is considered to be very consistent behavior [22] . The average payoff for this session was $22.
3.2. The Second Session (the Ultimatum Game)
At the beginning of the session, instructions are distributed and read aloud by the experimenter. The first set of instructions describes the ultimatum game and indicates that the game will be played as a one-shot game for the first round of the session. At this point, subjects do not know what will occur in the session subsequently.
Each participant is endowed with 500 lab dollars (L$) at the beginning of the first period. Participants simultaneously play two roles in the ultimatum game as described in Section 2 above. Following the first round, a second set of instructions is distributed and, again, read aloud by the experimenter. Subjects are informed of the new game that will be played. Participants are paid privately at the end of the session. The session lasted for about 60 minutes. The average payoff per participant was $15.40 for the session and $4.06 for the first round.9
3.3. Predictions with Respect to Attitudinal Variables to Be Tested with the Offer Model
Pro-social individuals tend to favor cooperative behavior, which would be consistent with higher offers than lower offers. We are likely to find
Prediction 1. Pro-social individuals make greater offers than pro-self individuals.
Risk-averse individuals may be more concerned that their offers will be rejected and they will receive payoffs of zero than risk-neutral or risk-loving individuals. This suggests.
Prediction 2. Risk-averse individuals will contribute more than risk-neutral individuals and risk-averse individuals.
There is no reason to expect risk-neutral or risk-seeking individuals will provide offers different from one another. Based on risk attitude, neither type has an incentive to deviate from the predicted very small offer.
Prediction 3. There will be no difference between the behavior of risk-neutral and risk-seeking individuals.
3.4. Predictions with Respect to Attitudinal Variables to Be Tested with the Offer-Acceptance Model
In one-shot games receivers cannot send signals to the individuals initiating offers. Risk attitudes should not affect the acceptance decision. Therefore,
Prediction 4. The risk attitudes of individuals playing one-shot games should not affect their decisions to accept an offer.
Social value orientations may be important. Pro-social individuals tend to make decisions regarding distributions of income that maximize group payoffs. Pro-self individuals who are individualists are trying to maximize their own payoffs while those who are competitive try to maximize the amount by which their payoffs exceed the payoffs of others. Aggressors try to minimize the payoffs of others. Therefore,
Prediction 5. Pro-social individuals are more likely to accept offers than individuals who have pro-self social value orientations.
Within the context of an ultimatum game, offers that are less than half of the maximum amount a sender can offer may be viewed as unfair. If the Offer Index is equal to the amount offered divided by the maximum potential offer, an Offer Index less than 0.5 suggests that the offer will be more likely to be rejected than if the Offer Index equals or exceeds 0.5.10 Therefore,
Prediction 6. The greater the Offer Index the more likely an offer will be accepted.
The Offer Index is an exogenous measure of fairness. An endogenous measure of fairness such as one described in Section 2 permits the realization of an outcome in which an exogenously determined fairness offer (such as a 50-50 or 40-60 split) may be rejected while an unfair offer (such as a 30-70 split) may be accepted. An explanatory model that includes an endogenous measure of fairness such as either of those introduced in Section 2 can accommodate this sort of “unexpected” outcome. The “ratio” fairness measure and the “difference” fairness measure described in Section 2 will be evaluated individually and tested against the Offer Index. As with the Offer Index, our expectation is that,
Prediction 7. The greater is the (endogenous) Fairness Index (ratio or difference), the greater is the likelihood that an offer will be accepted.
Whether the Fairness Indices perform better than the Offer Index in accounting for the variation in the offer- acceptance data and whether the resulting parameters for the Fairness Indices in an explanatory model permit us to provide an “explanation” for the rejection of “fair” offers or the acceptance of “unfair” offers are empirical questions about which we have no predictions.
4. Data Analyses and Results
4.1. Offer Decisions
Offer decisions are evaluated with an OLS regression of the variables identifying pro-social value orientations, risk aversion and risk seeking attitudes on the offers sent. The coefficients for the independent variables in the Offer Model are presented in column 1 of Table 1. The regression results permit us to reject the null hypotheses that pro-social value orientations and risk aversion are not statistically significant in favor of the alternatives that pro-social value orientations and risk aversion lead to increased offers (p < 0.02 for each). The null hypothesis that the effect of risk-seeking attitudes are not significantly different from those of risk neutral attitudes cannot be rejected in favor of the alternative that they are different (p = 0.388). These results provide support for Predictions 1, 2 and 3.
4.2. Offer-Acceptance Decisions
A summary of the acceptances by amount offered and by the Fairness Index (measured as the ratio) is presented in Table 2. Amounts offered never exceed L$250. Offers of L$225 or L$250 are always accepted. Offers that are identified as fair according to this Fairness Index are always accepted. Generally, the lower the offer or the Fairness Index the less likely it is that the offer will be accepted.
Offer-acceptance decisions are evaluated with a Probit regression of the variables identifying fairness, pro- social value orientations, risk aversion and risk seeking attitudes on the offer-acceptance decision to accept (variable = 1) or reject (variable = 0) an offer. The coefficients for the independent variables in the Offer-Accep- tance Models are presented in column 2, 3 and 4 of Table 1.
Prediction 4 is that risk attitudes should not be significant in the Offer-Acceptance Model. Tests of the joint significance of the risk attitude variables in each Offer-Acceptance Model permit us to maintain the null hypotheses that risk attitudes do not account for a significant amount of the variation in the offer-acceptance decisions (p = 0.113, p = 0.2075 and p = 0.2225 for the Models I, II and III respectively. The data support Prediction 4.
Pro-social value orientations are predicted to increase the likelihood of accepting an offer relative to pro-self
Table 1. Regression coefficients for the offer and offer-acceptance models.
Note: Robust standard errors are in parentheses, p-values for two-sided t-tests (for the offer model) and p-values for two-sided z-tests (for the offer- acceptance models) are in brackets.
Table 2. Summary of acceptances by amount offered and by fairness index (ratio).
orientations. In Model I, which uses the exogenous Offer Index as the measure of a fair offer, we maintain the null hypothesis that pro-social value orientations do not account for a statistically significant amount of the variation in the offer-acceptance decisions against the alternative that the effect is positive (p = 0.197). However, for both Models II and III the data support Prediction 5. Pro-social value orientations have a positive impact on the likelihood that an offer will be accepted (p = 0.039 and p = 0.029 for Models II and III respectively).
Increases in the fairness measures in each of the three Offer-Acceptance models lead to increases in the likelihood that an offer will be accepted (p = 0.001, p = 0.001 and p = 0.000 for the Offer Index, the Fairness Index (ratio) and Fairness Index (difference) respectively). The data support Predictions 6 and 7.
Three regressions were run that are not presented in Table 1. Two of the regressions add the Offer Index into Offer-Acceptance Models II and III. This was done to evaluate the conjecture that inequity aversion may reduce the likelihood of accepting an offer even if it is a “fair” offer within the context of the Fairness Indices.11 Because none of the amounts offered exceed L$250, any deviation from L$250 will result in an unequal distribution of payoffs. For the amended Models II and III the added variable had the anticipated sign (increased equality increased the likelihood of accepting an offer) but in neither case was the new variable statistically significant (p = 0.940 and p = 0.530 for the augmented Models II and III). The third regression replaced the Fairness Index in Model III with the individual components of the Fairness Index. This was done to capture the result comparable to that in [1] . Both the variables for the amount received and the amount sent by the responder are statistically significant and consistent with the expected signs (positive for the former and negative for the latter). A test of the difference between the magnitudes of the two variables supports the null hypotheses that they are not different (p = 0.5303). Based on this we can conclude that the amended Model III does reflect the results in [3] with our variable “sent” as a measure of the belief of the responder as to what is an acceptable offer. However, this amendment to Model II does not improve on Model III.
The data maintain the null hypotheses that there are no differences between the mean squared residuals for Model I versus Model II (p = 0.4094), for Model II versus Model III (p = 0.3316) and for Model I versus Model III (p = 0.4135). Even though the pseudo-R2 values for each of Models II and III are at least twenty percent larger than that for Model I, these results do not support Prediction 8 and cannot be used to support one fairness measure over any other based on this measure of goodness-of-fit.
An important factor in the selection of a preferred fairness measure is its ability to address the anomalous observation that offers that exceed fifty percent of the sender’s endowment may be rejected while offers falling short of fifty percent of the sender’s endowment may be accepted, given the values for the social value orientation and risk attitude of the receiver. This is not the case for Model I. Offers of L$250 or more will be more likely to be accepted than will offers falling short of L$250 given the values of the other independent variables. For example, if the individual is pro-self and risk neutral and confronted with an offer of L$250, a “fair” offer, the likelihood that this offer is accepted exceeds 99 percent. If the offer is an “unfair” offer of L$150, the likelihood that the offer is accepted falls to 37 percent. However, conditioning the fairness measure with the amount the receiver sends affects the outcome for both Models II and III. For example, using the ratio version of the fairness measure, if the individual is pro-self and risk neutral and confronted with a “fair” offer of L$250 but has sent L$300 to another individual when in the role of the sender, the likelihood that the L$250 offer is accepted is 54 percent. If the individual receives an “unfair” offer of L$150 but has sent L$175 to another individual when in the role of the sender, the likelihood that the L$150 offer is accepted is 61 percent. Models II and III permit anomalous likelihoods while Model I does not. This supports Prediction 9. It should be noted, however, that as long as we are dealing with likelihoods of rejecting offers, it is still possible that we will observe rejections of fair offers and acceptances of unfair offers even though the likelihood of the former is greater than the likelihood of the latter. In the example for Model I above, there is a small chance that the “fair” offer will be rejected and a substantially larger chance that the “unfair” offer will be accepted.
5. Conclusion
We have conducted a controlled laboratory experiment that permitted us to derive an endogenous measure of fairness to use in replace of the more conventional exogenous fairness measure embodied in the amount offered in an ultimatum game. To do this we expand the ultimatum game environment to one in which participants make decisions as both senders and receivers. The receiving decisions are unique in the sense that participants are confronted with an actual offer and must accept or reject this offer (as compared to the strategy vector mechanism). We then tested the Offer Model and Offer-Acceptance Models with the data derived from the experiment. The data supported the predictions anticipated from our Offer Model. The data did not unequivocally support the endogenous fairness measures over the exogenous measure unless we stipulate that the desirable explanatory model should allow for a prediction that some offers less than 50 percent of the sender’s endowment can be more likely to be accepted than some offers of at least 50 percent of the sender’s endowment. If the amount sent by the receiver as well as the offer received can provide a basis for the fairness measure, this condition may be satisfied. There exist examples of these anomalous results for the estimated models using the Fairness Indices but not using the exogenous fairness measure represented by the Offer Index. Therefore, an endogenous fairness index based on the actual behavior of individuals participating in ultimatum bargaining provides insight into understanding why anomalous results may be made and this does not require that we specifically ask people what they believe other people will do. The actual behavior of people can provide sufficient information.
Acknowledgements
S.M. Khalid Nainar and Mohamed Shehata thank the Social Sciences and Research Council of Canada (SSHRC) for financial support. The usual disclaimer applies.
Cite this paper
Mohamed I. Gomaa,Stuart Mestelman,S. M. Khalid Nainar,Mohamed Shehata, (2016) Fairness in an Ultimatum Game. Theoretical Economics Letters,06,186-194. doi: 10.4236/tel.2016.62021
References
- 1. Güth, W. and Kocher, M.G. (2014) Thirty Years of Ultimatum Bargaining Experiments: Motives, Variations, and a Survey of the Recent Literature. Journal of Economic Behavior and Organization, 108, 396-409.
http://dx.doi.org/10.1016/j.jebo.2014.06.006 - 2. Güth, W., Schmittberbger, R. and Schwarze (1982) An Experimental Analysis of Ultimatum Bargaining. Journal of Economic Behavior and Organization, 3, 367-388.
http://dx.doi.org/10.1016/0167-2681(82)90011-7 - 3. Azar, O.H., Lahav, Y. and Voslinsky, A. (2015) Beliefs and Social Behavior in a Multi-Period Ultimatum Game. Frontiers in Behavioral Neuroscience, 9, 1-11.
http://dx.doi.org/10.3389/fnbeh.2015.00029 - 4. Fehr, E. and Schmidt, K.M. (2003) Theories of Fairness and Reciprocity—Evidence and Economic Applications, Advances in Economics and Econometrics. In: Dewatripont, M., Hansen, L.P. and Turnovsky, S.J., Eds., Econometric Society Monographs, Eighth World Congress, Vol. 1, 208-257.
- 5. Carpenter, J.P. (2003) Is Fairness Used Instrumentally? Evidence from Sequential Bargaining. Journal of Economic Psychology, 24, 467-489.
http://dx.doi.org/10.1016/S0167-4870(02)00194-0 - 6. Kanagaretnam, K., Mestelman, S., Nainar, S.M.K. and Shehata, M. (2009) The Impact of Social Value Orientation and Risk Attitudes on Trust and Reciprocity. Journal of Economic Psychology, 30, 368-380.
http://dx.doi.org/10.1016/j.joep.2008.12.003 - 7. Brosig, J., Weimann, J. and Yang, C.-L. (2003) The Hot versus Cold Effect in a Simple Bargaining Experiment. Experimental Economics, 6, 75-90.
http://dx.doi.org/10.1023/A:1024204826499 - 8. Güth, W., Schmidt, C. and Sutter, M. (2003) Fairness in the Mail and Opportunism in the Internet: A Newspaper Experiment on Ultimatum Bargaining. German Economic Review, 42, 243-265.
http://dx.doi.org/10.1111/1468-0475.00081 - 9. Brandts, J. and Charness, G. (2011) The Strategy versus the Direct-Response Method: A First Survey of Experimental Comparisons. Experimental Economics, 14, 375-398.
http://dx.doi.org/10.1007/s10683-011-9272-x - 10. Kanagaretnam, K., Mestelman, S., Nainar, S.M.K. and Shehata, M. (2006) Trust, Reciprocity and the Roles of Sex, Value Orientation and Risk Attitudes in an Investment Game. Department of Economics Working Paper 2006-04, Manuscript, 42 p.
http://www.economics.mcmaster.ca/documents/department-working-papers/2006-04 - 11. Becker, G.M., DeGroot, M.H. and Marschak, J. (1964) Measuring Utility by a Single-Response Sequential Method. Behavioral Science, 9, 226-232.
http://dx.doi.org/10.1002/bs.3830090304 - 12. Harrison, G.W. (1986) An Experimental Test for Risk Aversion. Economics Letters, 21, 7-11.
http://dx.doi.org/10.1016/0165-1765(86)90111-4 - 13. Beck, P.J., Davis, J.S. and Jung, W.-O. (1991) Experimental Evidence on Taxpayer Reporting under Uncertainty. The Accounting Review, 66, 535-558.
- 14. Kachelmeier, S.J. (1990) Experimental Assessment of Monetary Risk Preferences. Working Paper, University of Texas at Austin.
- 15. Kachelmeier, S. and Shehata, M. (1992) Examining Risk Preferences under High Monetary Incentives: Experimental Evidence from the People’s Republic of China. American Economic Review, 82, 1120-1141.
- 16. Griesinger, D.W. and Livingston Jr., J.W. (1973) Toward a Model of Interpersonal Motivation in Experimental Games. Behavioral Science, 18, 173-188.
http://dx.doi.org/10.1002/bs.3830180305 - 17. Liebrand, W.B.G. (1984) The Effect of Social Motives, Communication and Group Size on Behaviour in an n-Person Multi-Stage Mixed-Motive Game. European Journal of Social Psychology, 14, 239-264.
http://dx.doi.org/10.1002/ejsp.2420140302 - 18. Offerman, T., Sonnemans, J. and Schram, A. (1996) Value Orientations, Expectations and Voluntary Contributions in Public Goods. Economic Journal, 106, 817-845.
http://dx.doi.org/10.2307/2235360 - 19. Buckley, N., Mestelman, S. and Shehata, M. (2003) Subsidizing Public Inputs. Journal of Public Economics, 87, 819-846.
http://dx.doi.org/10.1016/S0047-2727(01)00109-8 - 20. Burlando, R.M. and Guala, F. (2005) Heterogeneous Agents in Public Goods Experiments. Experimental Economics, 8, 35-54.
http://dx.doi.org/10.1007/s10683-005-0436-4 - 21. Sonnemans, J., van Dijk, F. and van Winden, F. (2006) On the Dynamics of Social Ties Structures in Groups. Journal of Economic Psychology, 27, 187-204.
http://dx.doi.org/10.1016/j.joep.2005.08.004 - 22. Buckley, N., Chan, K.S., Chowhan, J., Mestelman, S. and Shehata, M. (2001) Value Orientations, Income and Displacement Effects, and Voluntary Contributions. Experimental Economics, 2, 183-195.
http://dx.doi.org/10.1023/A:1011484722011 - 23. Fehr, E. and Schmidt, K.M. (1999) A Theory of Fairness, Competition and Cooperation. Quarterly Journal of Economics, 114, 817-868.
http://dx.doi.org/10.1162/003355399556151
NOTES
1 [1] write “If one searches for “ultimatum bargaining” on http://scholar.google.com/, there are more than 26,500 results. The first result is the original article by [2] that is cited around 3000 times… Thousands of ultimatum game experiments and extensions have been published in the meantime.”
2 [3] identify the typical definition of a fair offer as an offer that is one-half of the maximum amount the sender can offer.
3“… proposals offering the Responder less than 20 percent of the available surplus are rejected with probability 0.4 to 0.6… the probability of rejection is decreasing in the size of the offer… Responders do not behave in a self-interest maximizing manner… the motive indicated for the rejection of positive, yet “low”, offers is that subject view them as unfair [4] .
4See [5] for an example of an offer-acceptance model that includes the offer as an explanatory variable. [5] also describes “fair” offers as 50-50 splits.
5 [6] has shown that when the participant’s sex, social value orientation and risk attitude are incorporated into an explanatory model for trusting or reciprocal behavior, sex is not a significant variable. We do not have data on the sex of the participants in our ultimatum game sessions, but we do have their social value orientations and risk attitudes.
6Suppose there are 6 people participating in a session. The even numbered people are in one room and the odd numbered people are in another room. Participants 1, 3 and 5 are in one room. Participants 2, 4 and 6 are in a different room. Participant 1 sends to participant 2. Participant 2 sends to participant 3. Participant 3 sends to participant 4. Participant 4 sends to participant 5. Participant 5 sends to participant 6. Participant 6 sends to participant 1.
7The descriptions of the derivations of the risk attitudes and the social value orientation measures are included in [10] .
8The ring game has been used extensively by social psychologists, and we believe was first introduced to economists by [18] who were studying voluntary contributions towards the provision of public goods. The sensitivity of results from this mechanism to the stakes in the game and the location of the origin of the ring are presented in [18] . The results of the ring game are used to understand fairness in bargaining games, investment in research and development, voluntary contributions toward public good provision and trust and trustworthiness ( [5] [6] [19] - [21] ).
9Lab dollars were converted into Canadian dollars at the rate L$100 = 1 Canadian dollar.
10 [1] write “evidence from the ultimatum game implies that… responders do not only care about their own monetary payoff but compare their payoff with that of the proposer and become frustrated when their share is much lower.” In situations in which the Offer Index never exceeds 0.5, this variable may also capture an attitude of inequality aversion that the receiver may have. If the Offer Index exceeds 0.5 a better index for capturing inequality aversion can be constructed that will result in offers of 200 and 300 being equally undesirable because both result in distributions that are not equal. In this situation there may be conflict between a “supra fair” offer that provides a larger than fair payoff and a participant’s aversion to inequality.
11See [23] for a development of a model of inequity aversion.








