Received 22 July 2014; revised 12 August 2014; accepted 20 August 2014

ABSTRACT

We propose a procedure to obtain accurate confidence intervals for the stress-strength reliability R = P (X > Y) when (X, Y) is a bivariate normal distribution with unknown means and covariance matrix. Our method is more accurate than standard methods as it possesses a third-order distributional accuracy. Simulations studies are provided to show the performance of the proposed method relative to existing ones in terms of coverage probability and average length. An empirical example is given to illustrate its usefulness in practice.

Keywords:

Bivariate Normal Distribution, Interval Estimation, Likelihood Analysis, Reliability

1. Introduction

Let, be a sample from a bivariate normal distribution with mean 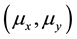and covariance matrix

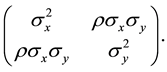
where, and. The stress-strength reliability of a system where X is the strength and Y is the stress is defined by

(1)

with

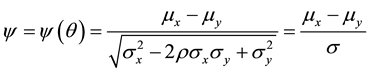(2)

where 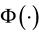is the cumulative distribution function of the standard normal distribution; 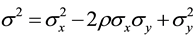is the variance of the difference of the two variables; and 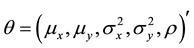denotes the parameter vector of the model.

Nguimkeu et al. [1] recently proposed a third-order method for inference about R for the case where the normal variables X and Y are independents; that is,. However, in many empirical applications, the variables of interest are correlated, either directly or through their dependence over a common auxiliary variable. For example, in financial risk-management one may want to compare the stock returns from two companies. If these companies operate in the same industry the prices of these stocks are likely to be correlated. In welfare economics, comparing households’ income to households’ expenditures can be useful to test households saving capacity or their financial vulnerability. Applying the Nguimkeu et al. [1] test in such context could be misleading.

In this paper, we modify the procedure proposed by Nguimkeu et al. [1] to account for possible correlation between the stress and the strength variables when they are sampled from normal populations. Simulations are used to compute coverage properties of the statistic and compare its performance with existing alternative methods. An empirical example is provided to illustrate the usefulness of the method in practice.

2. The Procedure

From a sample of observations the log-likelihood function of 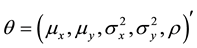is given by

The maximum likelihood estimate (MLE) of R can then be obtained by

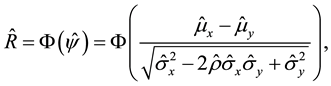(3)

where the MLE of the parameter vector, 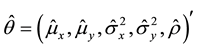is given by

(4)

(5)

From the above log-likelihood function and MLEs, two standard methods for confidence interval estimation of the parameter (and hence R) can be derived: the standardized maximum likelihood estimate method (also known as the Wald method) and the signed log-likelihood ratio method. The Wald method is based on the statistic (q) defined by

(6)

where the delta method can be applied to estimate the variance of by

(7)

An estimated variance of the maximum likelihood estimator is

where

(8)

is the observed information matrix evaluated at.

With the regularity condition stated in Cox and Hinkley [2] (Chapter 9), q is asymptotically distributed as standard normal, and a confidence interval for can be approximated by

(9)

where is the percentile of the standard normal. Although the Wald method is simple, it is not invariant to parameterization.

The signed log-likelihood ratio method is based on the statistic (r) defined by

(10)

where is the constrained MLE of under the constraint that. In contrast to the Wald method, the signed log-likelihood ratio method is invariant to parametrization.

To obtain, we maximize subject to the constraint. The Lagrange multiplier method is applied for this purpose. Let denotes the Lagrange multiplier. The Lagrangian function can be written as

(11)

The constrained MLE and the estimated Lagrange multiplier can then be obtained by numerically solving the first-order conditions:

(12)

The tilted log-likelihood function is defined by and is the same as the log-like-

lihood function when evaluated at the constrained MLE of, i.e.. The observed information

matrix of the tilted log-likelihood function evaluated at, denoted is then defined by

(13)

where and

(14)

Again, with the regularity conditions stated in Cox and Hinkley [2] (Chapter 9), is asymptotically distributed as standard normal. Hence, a confidence interval for based on is given by

(15)

It is well known that both the Wald method and the signed log-likelihood ratio method are first-order methods; that is, both and converge in distribution to the standard normal distribution with rate of convergence. Note that, computationally, confidence intervals for can easily be obtained from (9) but the methodology is not invariant to reparameterization. While confidence intervals for obtained from (15) generally require the use of numerical methods, the method is parameterization invariant. Doganaksoy and Schmee [3] showed that confidence intervals obtained from (15) have better coverage properties than those obtained from (9).

To improve the accuracy of the first-order methods, Barndorff-Nielsen [4] [5] introduced the modified signed log-likelihood ratio statistic

(16)

where is the signed log-likelihood ratio statistic defined in (10), and is a statistic that is based on the log-likelihood function and an ancillary statistic. Barndorff-Nielsen [4] [5] showed that is asymptotically distributed as standard normal with third-order accuracy. Fraser and Reid [6] showed that for the exponential family model, is the standardized maximum likelihood estimate calculated in the canonical parameter scale. Reid [7] and Severeni [8] provide a detailed overview of this development.

The stress-strength reliability with dependent normal random variables correspond to an exponential family model with canonical parameter given by

(17)

To re-express our parameter of interest on this canonical parameter scale, we require and which denote the derivatives of and with respect to. The matrix of derivatives for is

(18)

For the parameter of interest we have

(19)

By change-of-basis then, calculated in the scale of the canonical parameter, , is

where

(20)

Now, notice that and, so that the determinant of the observed information matrix based on the log-likelihood function and the titled log-likelihood function calculated in scale can be obtained by using chain-rule in differentiation. We thus have:

The asymptotic variance of calculated in scale is then

(21)

The standardized MLE of calculated in the scale is therefore

(22)

The modified signed log-likelihood ratio statistic can then be obtained from (16). It is asymptotically distributed as standard normal with a distributional accuracy. The confidence interval for is given by

(23)

Practically, this confidence interval is obtained by numerically solving for in the inequality using a sufficient number of grid points of chosen in an appropriate range. It follows that the confidence interval for R is then given by, where is the cumulative density function of the standard normal distribution.

3. Numerical Studies

An empirical example and Monte Carlo simulation studies are considered in this section. The aim of the empirical example is to illustrate how the various methods considered in this paper can produce quite different confidence intervals for. Simulation studies are then performed to examine the statistical properties of the proposed method in terms of central coverage and average confidence interval length at the nominal size of 95%. To illustrate the accuracy of our proposed method (Proposed), we compare it with the commonly used asymptotic methods, i.e., the signed log-likelihood ratio test (r) and the Wald test (Q). We also compare it with approximations that were recently discussed in Barbiero [9] . Specifically, Barbiero [9] proposed results based on approximate confidence intervals from the asymptotic variance of (denoted AN2), approximate confidence intervals based on a logit transformation of R (denoted LOGIT) and a bootstrap bias-corrected and accelerated percentile confidence interval for R (denoted BCAPB). Since AN2 and LOGIT yield very similar results, only the AN2 and BCAPB procedures of Barbiero [9] are reported here.

3.1. An Example

Table 1 is a data set from Azen and Reed [10] which shows absorbance values of substances analyzed in 19 runs of a laboratory test for serum concentration level of an enzyme, leucine amino peptidase. Controls 1 and 2 are two control samples from the same pool analyzed in the same run. We estimate the confidence interval of the probability that Control 1 (X) is more than Control 2 (Y), assuming a bivariate normal distribution for the data.

For these data, , , , , and. Using the

methods developed in the previous sections, the 90%, 95% and 99% CIs for R are computed and reported in Table 2. The confidence intervals obtained from the five methods are quite different. Hence, simulation studies are performed to examine the accuracy of the five methods.

3.2. Design of the Monte Carlo Simulation Studies

The simulation set up is similar to Barbiero [9] [11] . An array of eight different scenarios has been considered, each corresponding to a different combination of distribution parameters (and thus different reliabilities). These scenarios have been coded with a progressive number which is reported in Table 3. Without any loss in generality, the mean and standard deviation for Y has been set to and while the parameters, and vary. The correlation coefficient takes two values, 0.5 and 0.8. The five parameters have been jointly set in order to assure values higher than 0.5 for the reliability in effort to reflect real practice where there is concern for high reliability for the study component. The analyzed scenarios however cover a large range of

reliability, since R goes from 0.614 to 0.943. Different sample sizes (n = 10, 20, 30, 50) are used in order to examine the reliance of the procedure on small samples. The number of Monte Carlo replications has been fixed at N = 10,000. The simulation study for the comparison of interval estimators proceeds as follows:

1) Set the parameters for the bivariate random variable and compute the corresponding R from Equation (1) (see Table 3);

2) Draw a random sample of size n from;

3) Estimate R and a CI for R, using each of the listed procedures;

4) Check if this CI contains R; compute its length;

5) Repeat the two precedent steps N = 10,000 times and compute the overall CI coverage (proportion of the CIs containing R) and average length (computed over the 10,000 replications) for each interval estimator.

3.3. Results of the Monte Carlo Simulation Studies

The results of the simulation studies are reported in Table 4 and Table 5. Table 4 records the coverage probability produced by each method and Table 5 records the average CI length produced by each method. The accuracy of the proposed method is striking. Inspecting Table 4 reveals how accurate the coverage probability of the proposed method is across all sample sizes and scenarios. Figure 1 presents a graphical illustration of the coverage probabilities of each method graphed against the various scenarios. This figure provides visual confirmation of the accuracy of the proposed method. These findings are consistent with the fact that the proposed method has theoretically a third-order distributional accuracy. Close to our method in terms of accuracy is the bias-corrected and accelerated percentile bootstrap (BCAPB). The approximate estimator (AN2) also performs

reasonably well. The traditional asymptotic methods, r and q, however, perform the worst, especially when the values of the reliability are closer to unity (see scenarios 4 and 8). The Table 4 reveals that our proposed method generally produces the shortest average confidence interval length. From these presented simulation results, the proposed method gives the best coverage probability and it also has the shortest average CI length.

4. Conclusion

In this paper, the modified signed log-likelihood ratio statistic method is proposed to obtain confidence intervals for the stress-strength reliability when stress and strength are distributed as a bivariate normal distribution. An empirical example illustrates that the proposed method gives quite different results from those obtained by the existing methods. Simulation studies illustrate that the proposed method has the best coverage probability and also produces the shortest average length of confidence intervals. The calculations are done in Matlab and the programs are available upon request from the authors.

References

NOTES

^*Corresponding author.