Open Journal of Statistics
Vol.3 No.6(2013), Article ID:41541,3 pages DOI:10.4236/ojs.2013.36052
Characterization of Power-Function Distribution through Expectation*
Department of Statistics, Sardar Patel University, Anand, India
Email: bhattmilind_b@yahoo.com
Copyright © 2013 Milind Bhanuprasad Bhatt. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Milind Bhanuprasad Bhatt. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 12, 2013; revised November 12, 2013; accepted November 19, 2013
Keywords: Characterization; Power Function Distribution
ABSTRACT
For the characterization of the power function distribution, one needs any arbitrary non constant function only in place of independence of suitable function of order statistics, linear relation of conditional expectation, recurrence relations between expectations of function of order statistics, distributional properties of exponential distribution, record valves, lower record statistics, product of order statistics and Lorenz curve, etc. available in the literature. The goal of this research is not to give a different path-breaking approach for the characterization of power function distribution through the expectation of non constant function of random variable and provide a method to characterize the power function distribution as remark. Examples are given for the illustrative purpose.
1. Introduction
Several characterizations of power function distribution have been made notably by Fisz [1], Basu [2], Govindarajulu [3] and Dallas [4] using independence of suitable function of order statistics and distributional properties of transformation of exponential variable.
Other attempts were made for the characterization of exponential and related distributions assuming linear relation of conditional expectation by Beg [5], characterization based on record valves by Nagraja [6], characterization of some types of distributions using recurrence relations between expectations of function of order statistics by Alli [7], characterization results on exponential and related distributions by Tavangar [8], and characterization continuous distributions through lower record statistics by Faizan [9] included the characterization of power function distribution.
Direct characterization for power function distribution has been given in Arslan [10] who used the product of order statistics [contraction is a particular case of product of order statistics which has interesting applications such as in economic modeling and reliability see Alamatsaz [11], Kotz [12] and Alzaid [13]] where as Moothathu [14] used Lorenz curve. [Graph of fraction of total income owned by lowest pth fraction of the population is Lorenz curve of distribution of income [15].
This research note provides the characterization based on identity of distribution and equality of expectation of function of random variable for power-function distribution with the probability density function (p.d.f.)
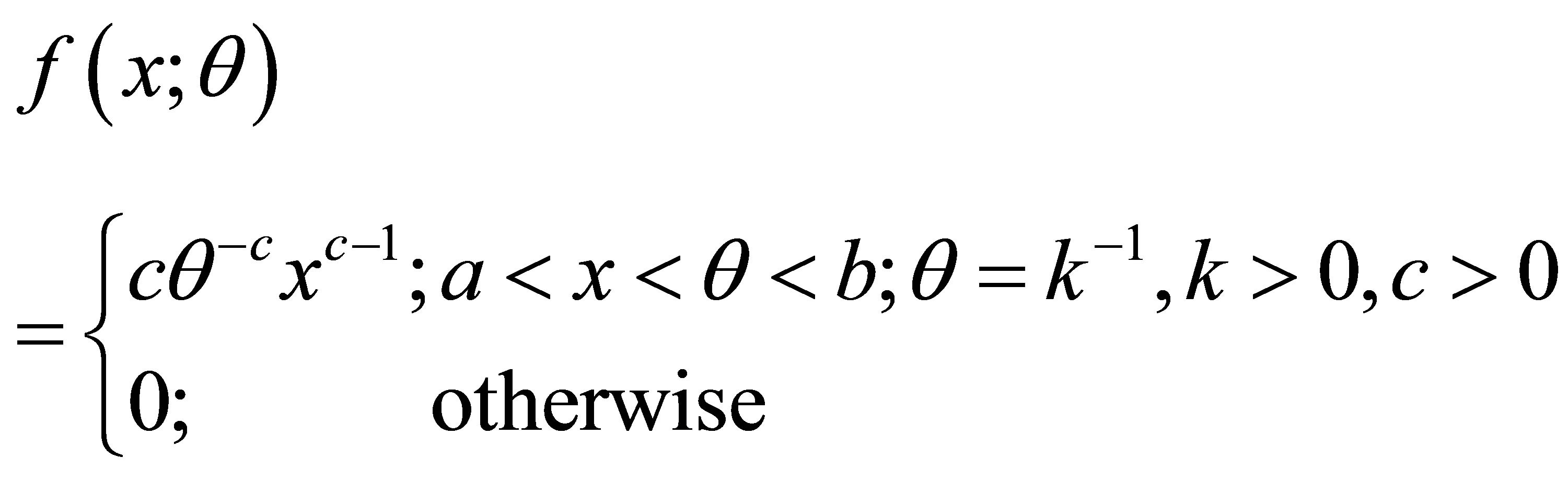 (1.1)
(1.1)
where  are known constants,
are known constants, 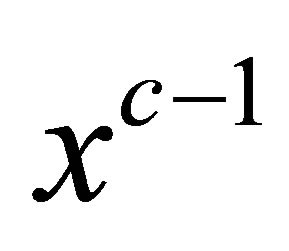 is positive absolutely continuous function and
is positive absolutely continuous function and 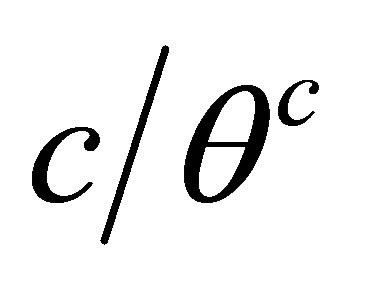 is everywhere differentiable function. Since derivative of
is everywhere differentiable function. Since derivative of  being positive and since range is truncated by
being positive and since range is truncated by 
from right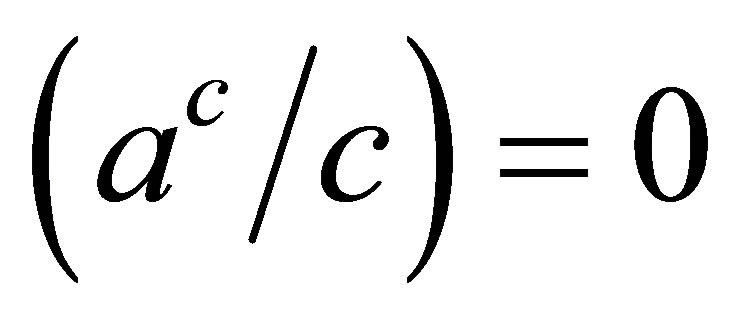 .
.
The aim of the present research note is to give the new characterization through the expectation of function  for the power function distribution. Examples are given for the illustrative purpose.
for the power function distribution. Examples are given for the illustrative purpose.
2. Characterization
Theorem 2.1 Let X be a random variable with distribution function F. Assume that F is continuous on the interval,  where
where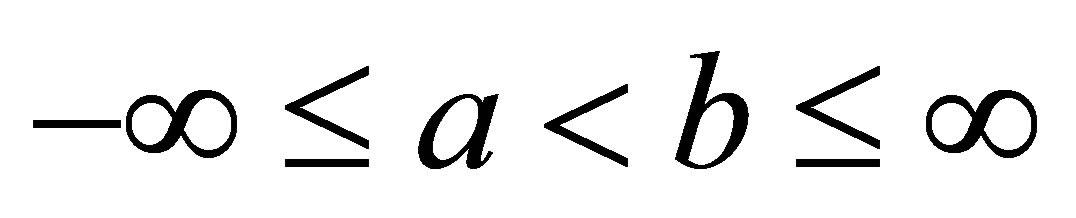 . Let
. Let 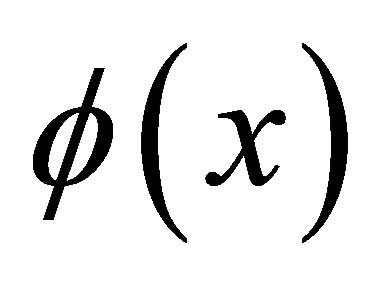 and
and 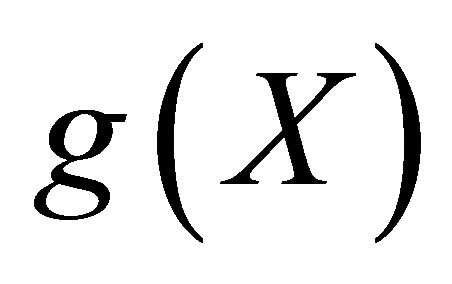 be two distinct differentiable and integrable functions of
be two distinct differentiable and integrable functions of  on the interval
on the interval 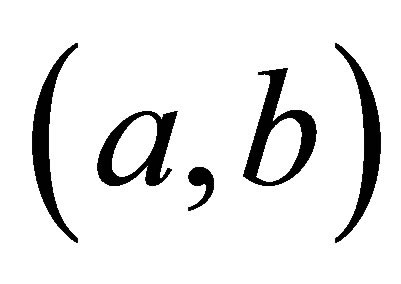 where
where 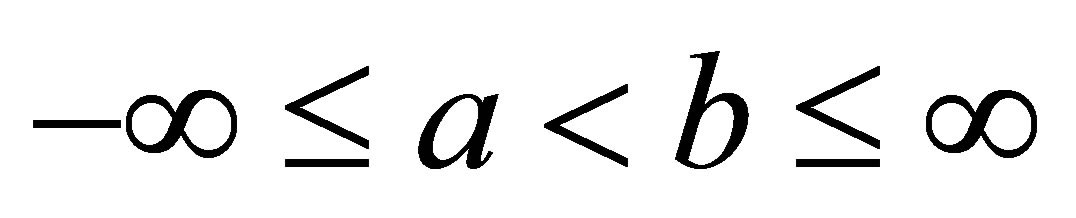 and moreover
and moreover 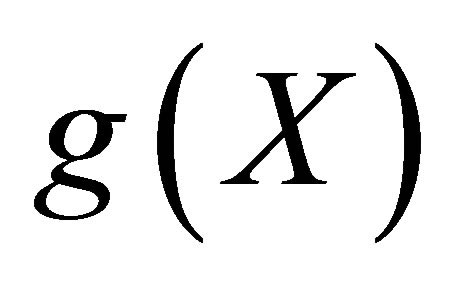 be non constant. Then
be non constant. Then 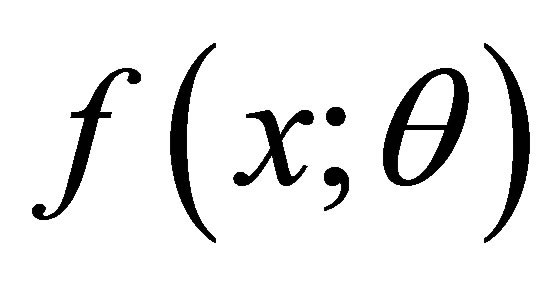 is the p.d.f. of power function distribution defined in (1.1) if and only if
is the p.d.f. of power function distribution defined in (1.1) if and only if
 (2.1)
(2.1)
Proof Given  defined in (1.1), if
defined in (1.1), if 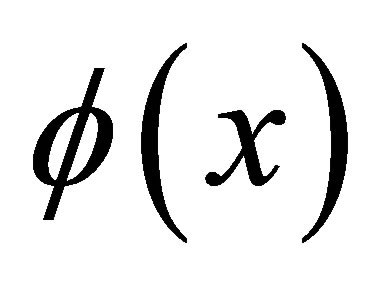 is such that
is such that 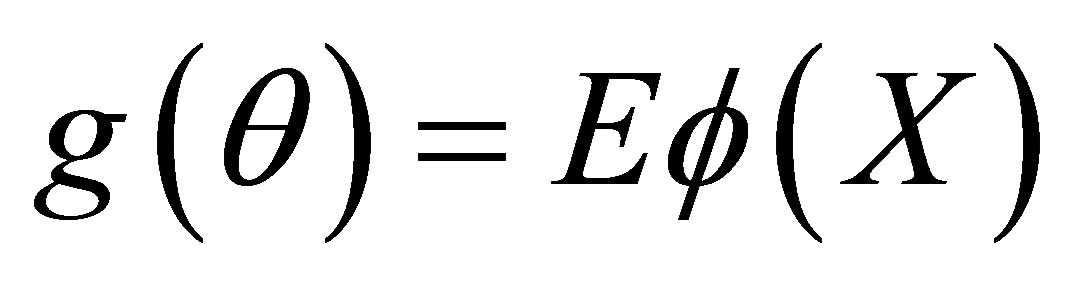 where
where 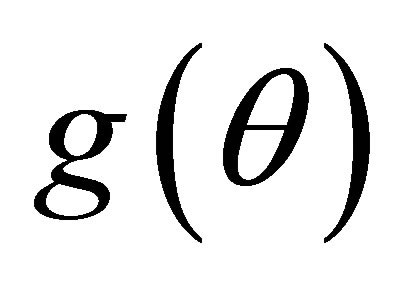 is differentiable function then
is differentiable function then
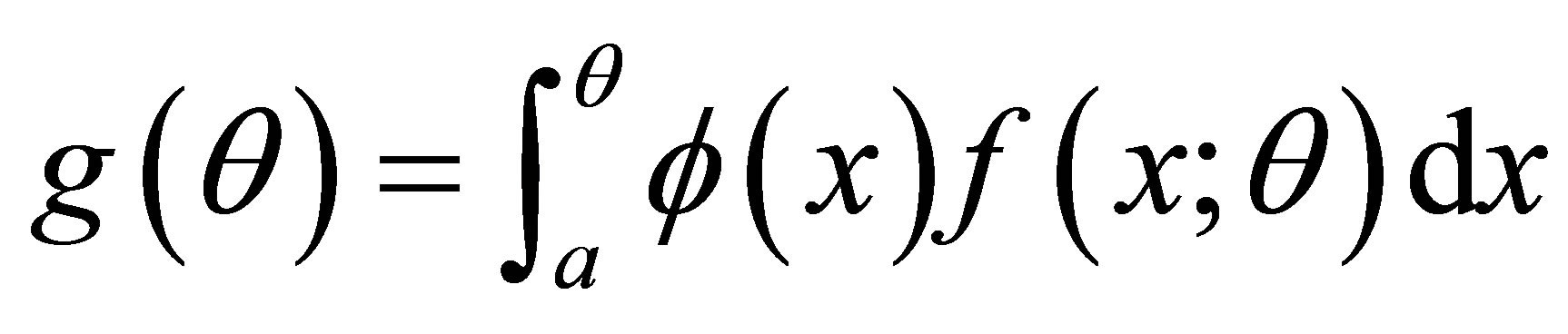 (2.2)
(2.2)
Differentiating (2.2) with respect to  on both sides and replacing
on both sides and replacing 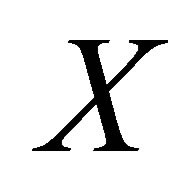 for
for  and simplifying one gets
and simplifying one gets
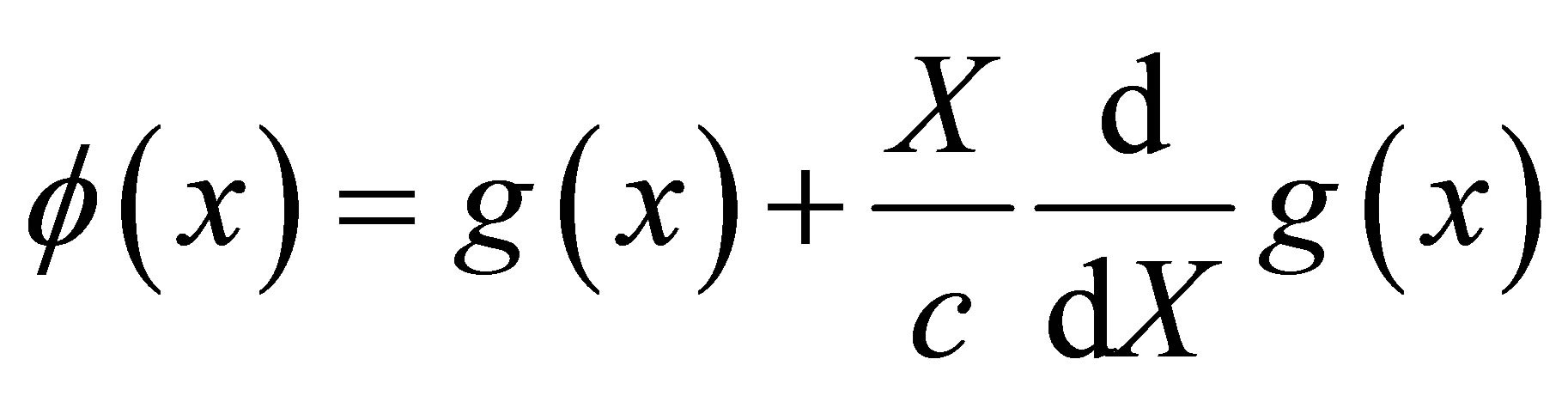 (2.3)
(2.3)
which establishes necessity of (2.1). Conversely given (2.1), let 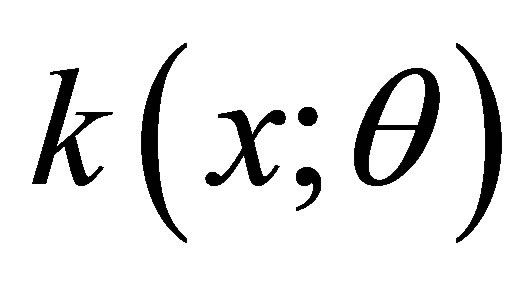 be such that
be such that
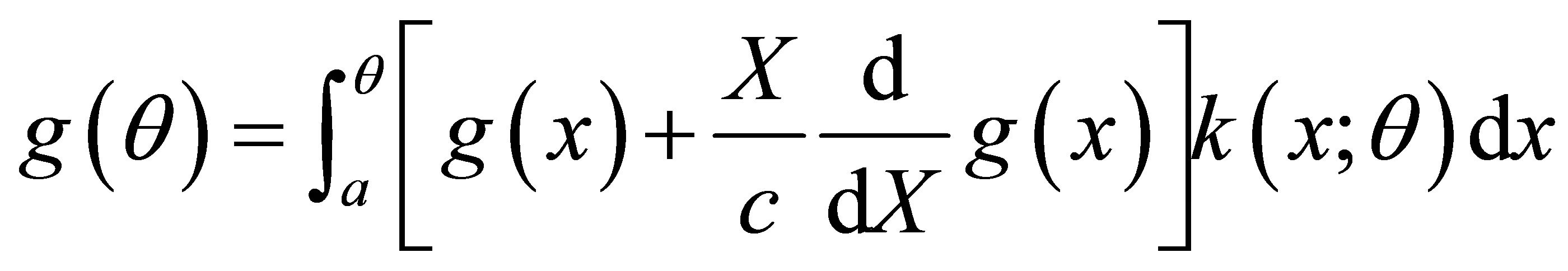 (2.4)
(2.4)
Since  the following identity holds:
the following identity holds:
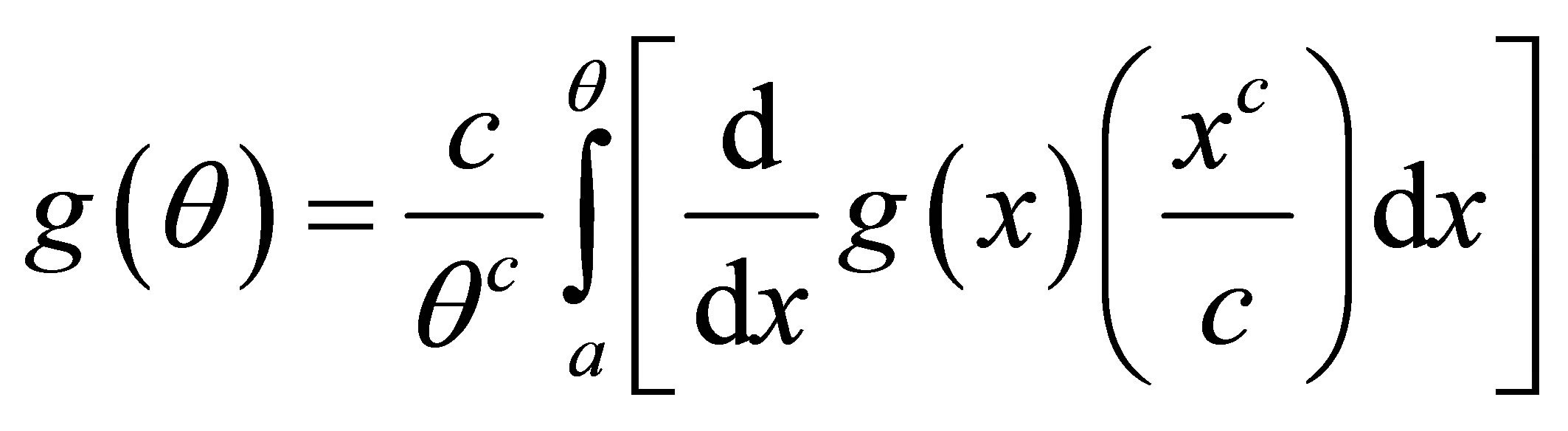 (2.5)
(2.5)
Differentiating integrand of (2.5) and tacking 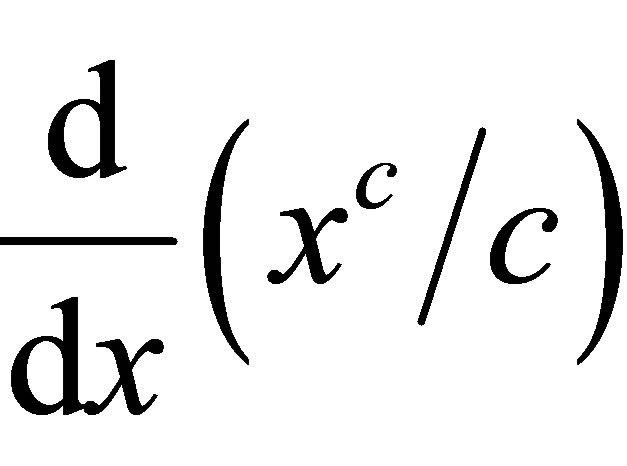
as one factor one gets (2.5) as
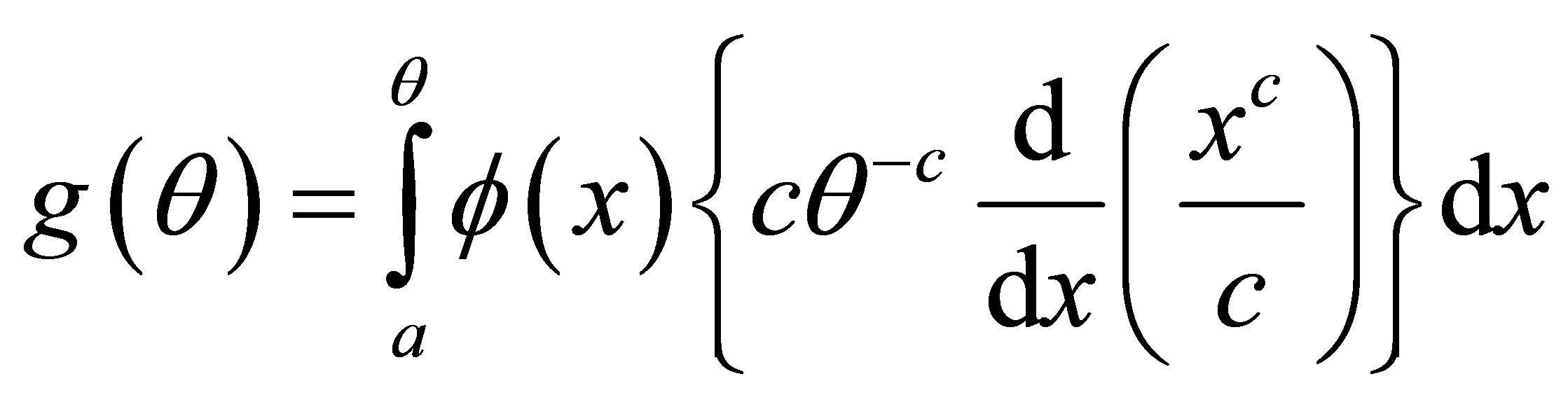 (2.6)
(2.6)
where 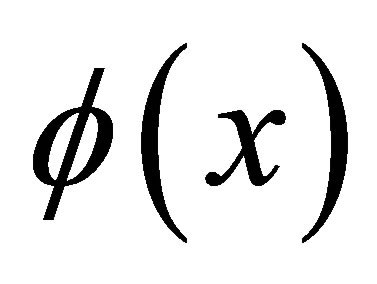 is function of
is function of  derived in (2.3). From (2.4) and (2.6) by uniqueness theorem
derived in (2.3). From (2.4) and (2.6) by uniqueness theorem
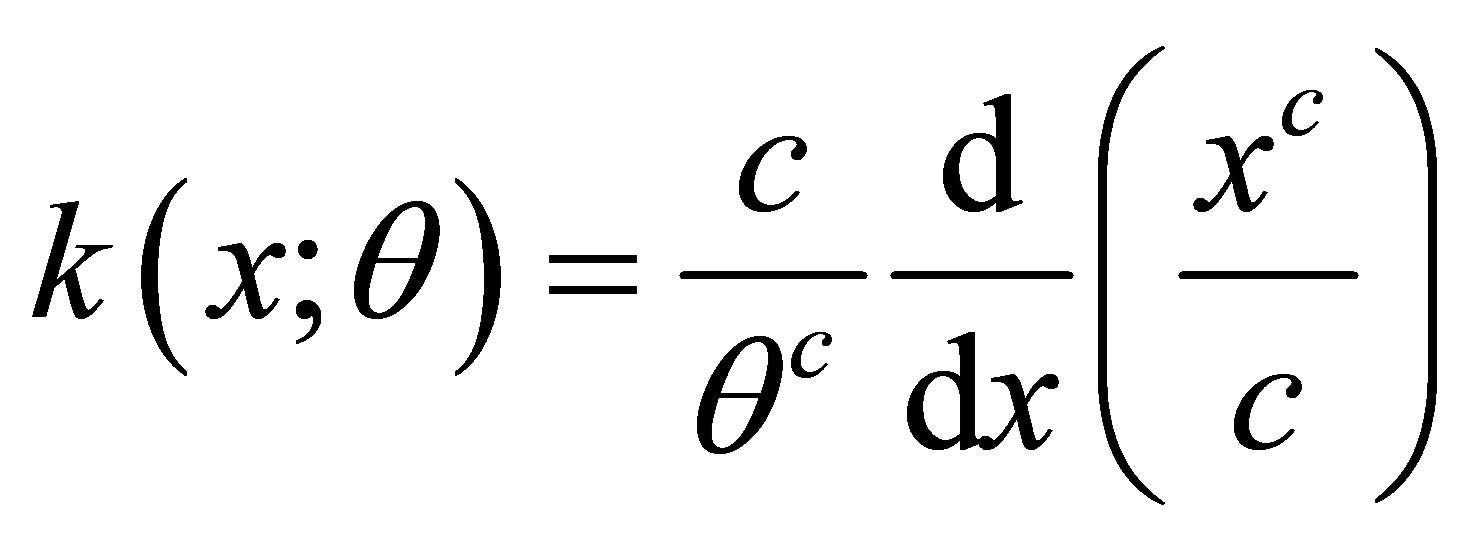 (2.7)
(2.7)
Since 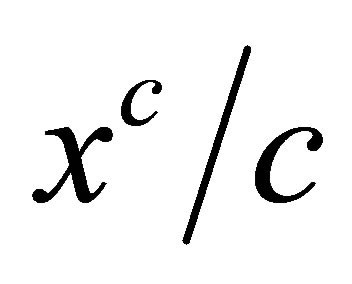 is decreasing function with
is decreasing function with 
and since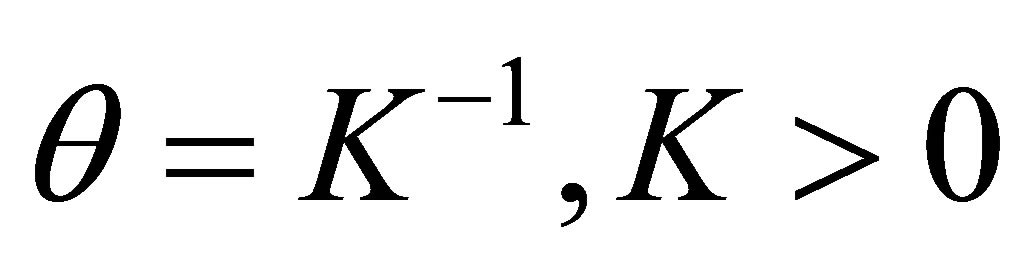 , integrating (2.7) on both sides one gets
, integrating (2.7) on both sides one gets
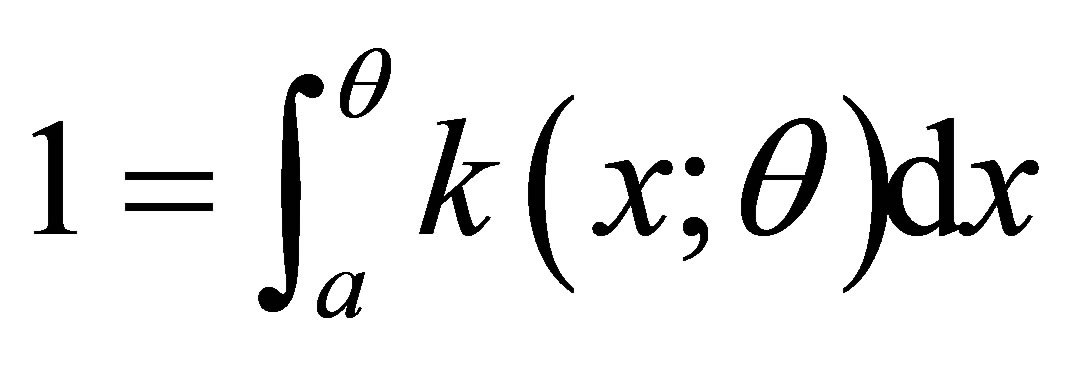 (2.8)
(2.8)
Substituting 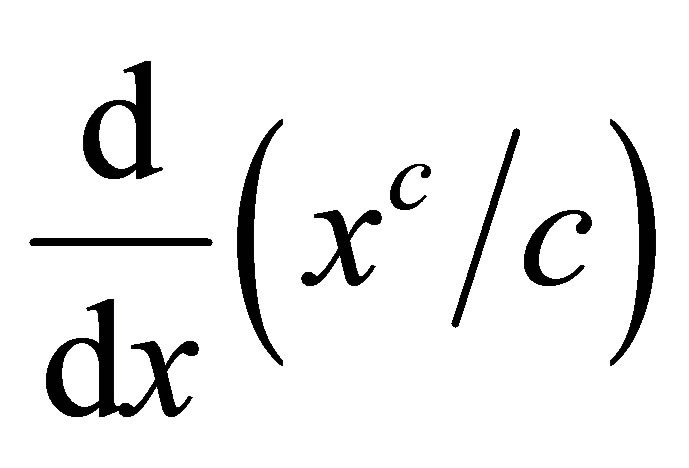 in (2.7),
in (2.7), 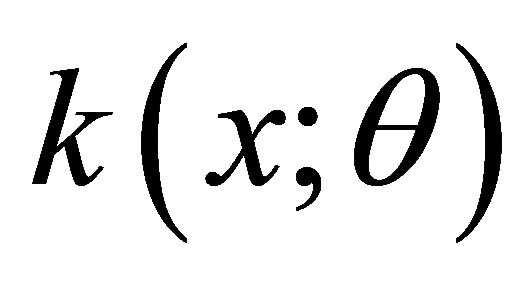 reduces to
reduces to
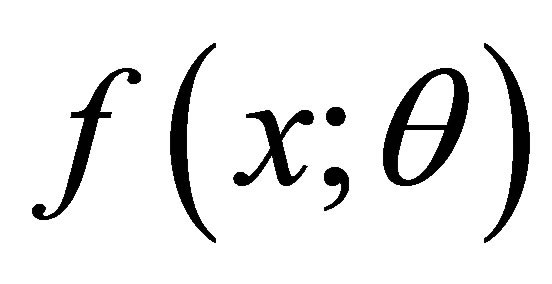 defined in (1.1), which establishes sufficiency of (2.1).
defined in (1.1), which establishes sufficiency of (2.1).
Note: Author does not claim the relations between f and g in the preceding analysis.
Remark 2.1 Using 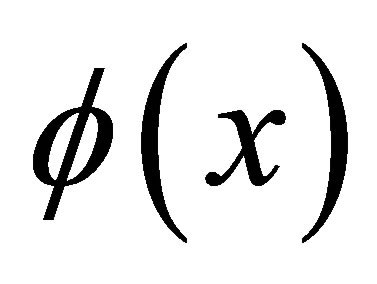 derived in (2.3),
derived in (2.3), 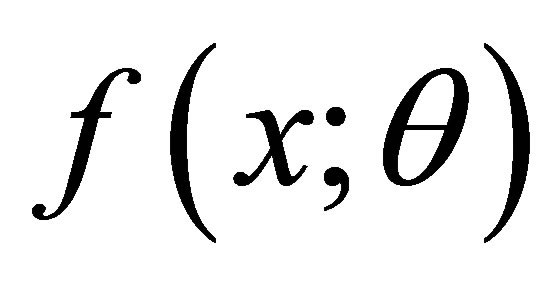 given in (1.1) can be determined by
given in (1.1) can be determined by
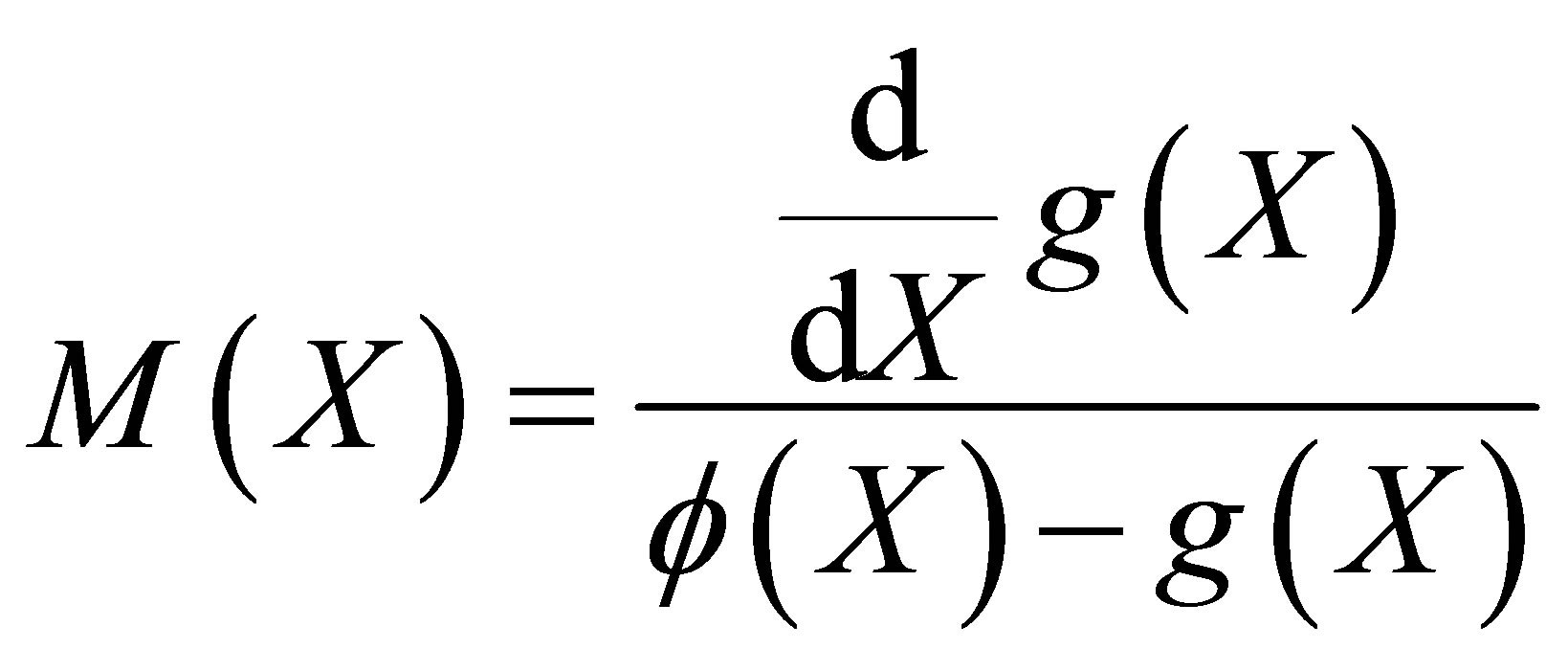 (2.9)
(2.9)
and p.d.f. is given by
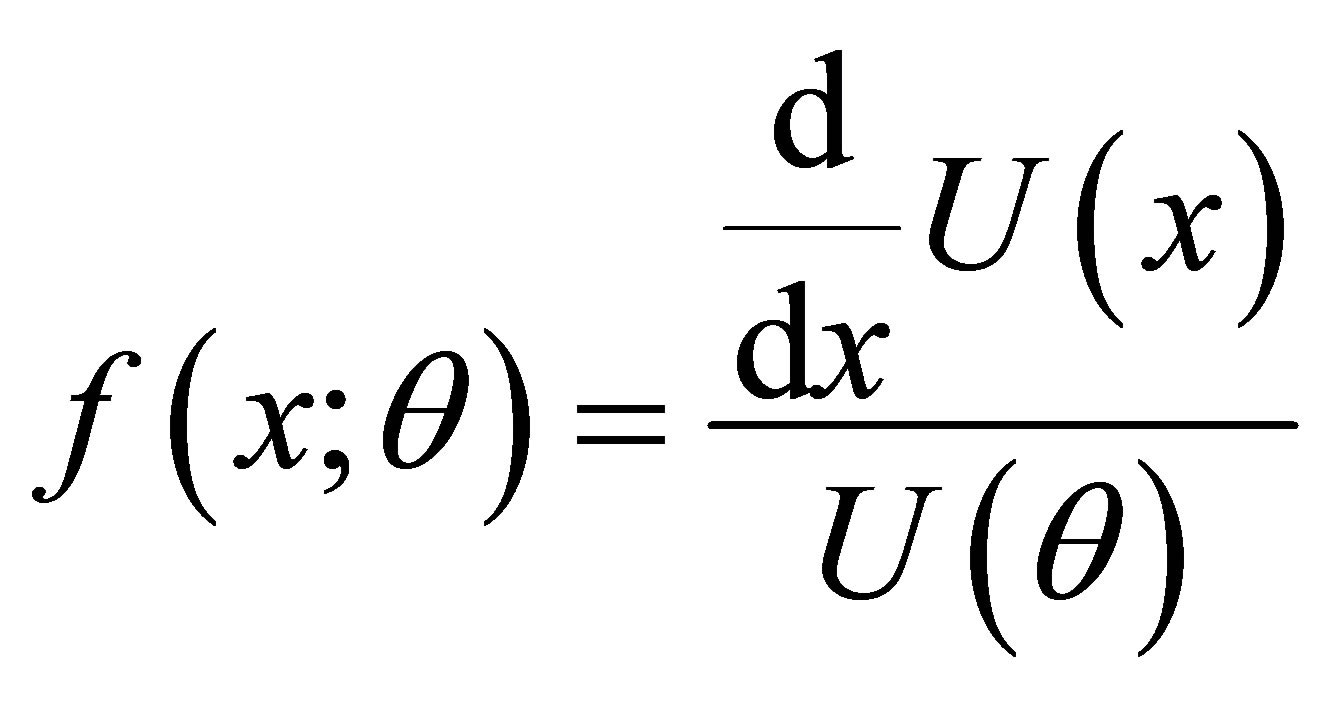 (2.10)
(2.10)
where 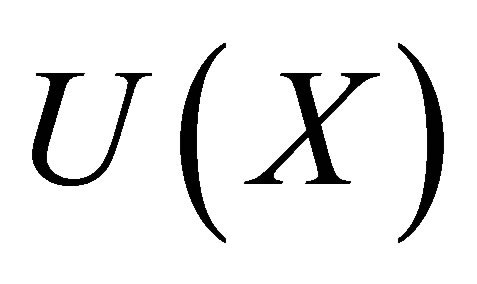 is increasing function in the interval
is increasing function in the interval 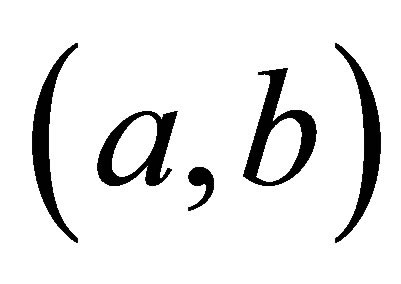 for
for 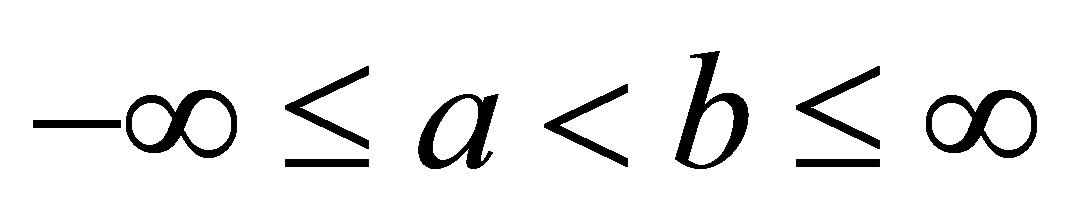 with
with  such that it satisfies
such that it satisfies
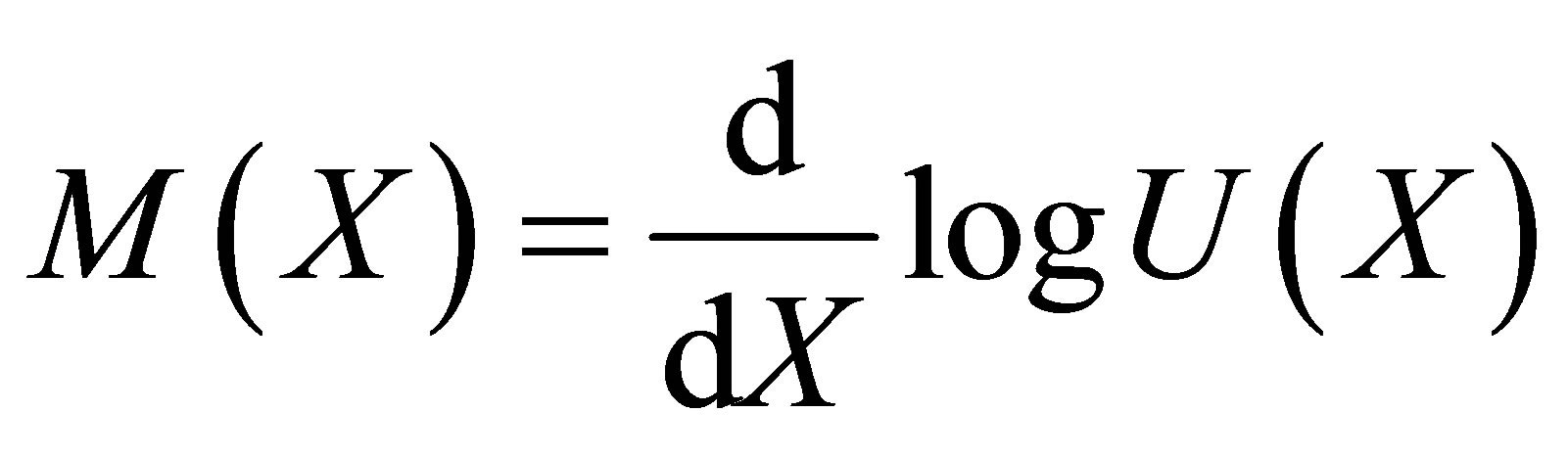
3. Illustrative Examples
Example 1 Using method described in the remark characterization of power function distribution through survival function quantile; 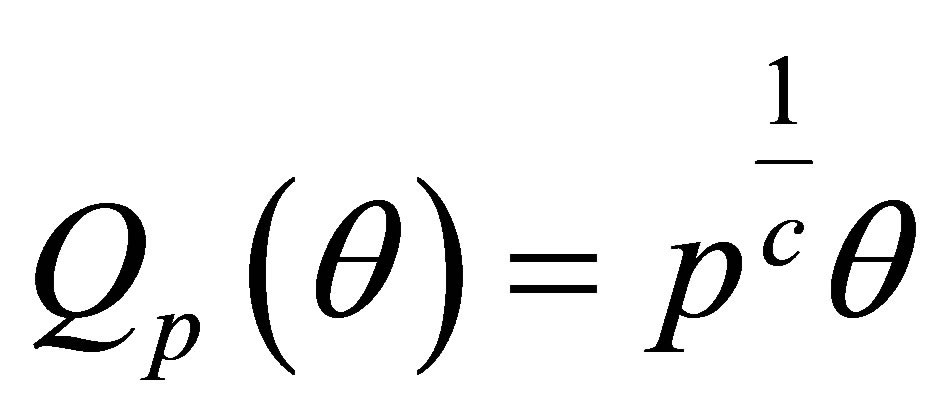 is illustrated.
is illustrated.

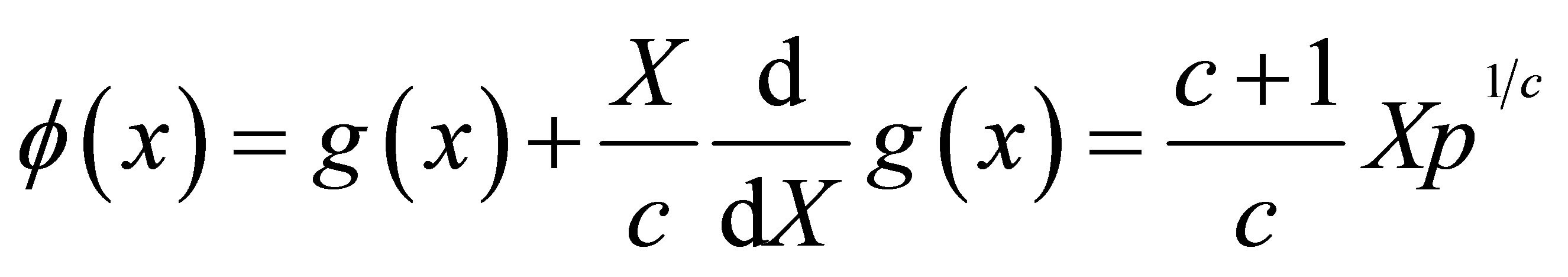



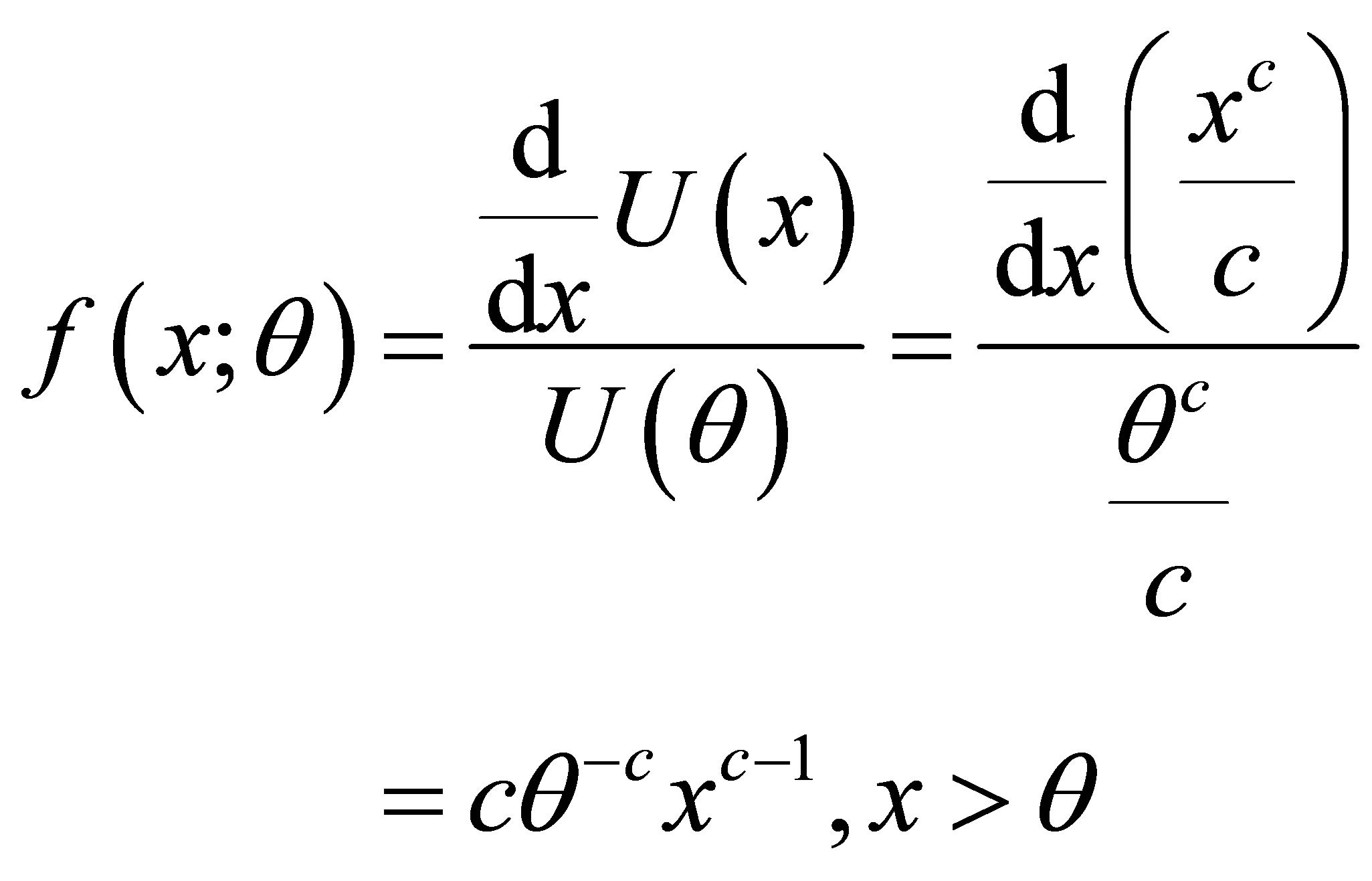
Example 2 The p.d.f. 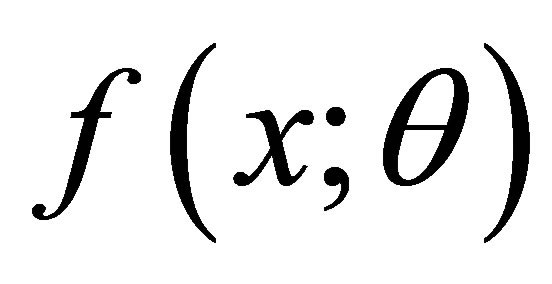 defined in (1.1) can be characterized through non constant functions of
defined in (1.1) can be characterized through non constant functions of 
 such as
such as

by using

and defining  given in (2.9) and using
given in (2.9) and using  as appeared in (2.11) for (2.10).
as appeared in (2.11) for (2.10).
4. Conclusion
To characterize the p.d.f. defined in (1.1), one needs any arbitrary non constant function of  which should be differentiable and integrable only.
which should be differentiable and integrable only.
REFERENCES
- M. Fisz, “Characterization of Some Probability Distribution,” Skand. Aktuarietidskr, Vol. 41, No. 1-2, 1958, pp. 65-67.
- A. P. Basu, “On Characterizing the Exponential Distribution by Order Statistics,” Annals of the Institute of Statistical Mathematics, Vol. 17, No. 1, 1965, pp. 93-96. http://dx.doi.org/10.1007/BF02868158
- Z. Govindarajulu, “Characterization of Exponential and Power Distribution,” Skand. Aktuarietidskr, Vol. 41, 1966, pp. 132-136.
- A. C. Dallas, “Characterization Pareto and Power Distribution,” The Annals of Mathematical Statistics, Part A, Vol. 28, No. 1, 1976, pp. 491-497.
- M. L. Beg and S. N. U. A. Kirmani, “On a Characterization of Exponential and Related Distributions,” The Australian Journal of Statistics, Vol. 16, No. 3, 1974, pp. 163-166. http://dx.doi.org/10.1111/j.1467-842X.1974.tb00933.x
- H. N. Nagaraja, “On a Characterization Based on Record Valves,” The Australian Journal of Statistics, Vol. 19, No. 1, pp. 70-73. http://dx.doi.org/10.1111/j.1467-842X.1977.tb01078.x
- M. A. Ali and A. H. Khan, “Characterization of Some Types of Distributions,” Information and Management Sciences, Vol. 9, No. 2, 1998, pp. 1-9.
- M. Tavangar and M. Asadi, “Some New Characterization Results on Exponential and Related Distributions,” Bulletin of the Iranian Mathematical Society, Vol. 36, No. 1, 2010, pp. 257-272.
- M. Faizan and M. I. Khan, “A Characterization of Continuous Distributions through Lower Record Statistics,” Forum, Vol. 4, 2011, pp. 39-43.
- G. Arslan, “Characterization Based on Product of Order Statistics,” math.ST., 2011. arXiv 1110.2879v
- M. H. Alamatsaz, “An Integer-Valued PTH-Order Autoregressive Structure,” (INAR(p)) Process,” Journal of Applied Probability, Vol. 27, No. 2, 1990, pp. 314-324.
- S. Kotz and F.W. Steutel, “Note on a Characterization of Exponential Distributions,” Statistics & Probability Letters, Vol. 6, No. 3, 1988, pp. 201-203. http://dx.doi.org/10.1016/0167-7152(88)90120-4
- A. A. Alzaid and M. A. Al-Osh, “An Integer-Valued PTH-Order Autoregressive Structure,” (INAR(p)) Process,” Journal of Applied Probability, Vol. 27, No. 2, 1990, pp. 314-324. http://dx.doi.org/10.2307/3214650
- T. S. K. Moothathu, “Characterization of Power Function Distribution through Property of Lorenz Curve,” Sankhy, Journal of Statistics, Series B, Vol. 48, Pt. 2, 1986, pp. 262-265.
- M. G. Kendall and A. Stuart, “The Advanced Theory of Statistics,” C. Griffin, London, 1958.
NOTES
*This work is supported by UGC Major Research Project No: F.No. 42-39/2013(SR), dated 12-3-2013.

