 Optics and Photonics Journal, 2011, 1, 142-149 doi:10.4236/opj.2011.13024 Published Online September 2011 (http://www.SciRP.org/journal/opj) Copyright © 2011 SciRes. OPJ PCRR Based Bandpass Filter for C and L+U Bands of ITU-T G.694.2 CWDM Systems S. Robinson, R. Nakkeeran Department of Electronics and Communication Engineering Pondicherry Engineering College, Puducherry, India E-mail: mail2robinson@pec.edu, rnakeeran@pec.edu Received May 20, 2011; revised June 20, 2011; accepted June 28, 2011 Abstract A two Dimensional (2D) Photonic Crystal Ring Resonator (PCRR) based Bandpass Filter (BPF) is designed to cover C and L+U bands of Coarse Wavelength Division Multiplexing (CWDM) systems. It is devised with two quasi waveguides and a circular PCRR. The simulation results are obtained using 2D Finite Differ- ence Time Domain (FDTD) method. The Photonic Band Gap (PBG) is calculated by Plane Wave Expansion (PWE) method. The BPFs allow the entire C-band (BPF1) and L+U bands (BPF2), which are extended from 1530 to 1565 nm (C band) and 1565 to 1675 nm (L+U bands). The computed bandwidth of BPF1 and BPF2 is 32 nm and 97 nm respectively. The size of the device is minimized from a scale of few tens of millimeters to the order of micrometers. The overall size of the BPF1 is around 12.8 µm × 11.4 µm and 11.4 µm × 11.4 µm for BPF2. Keywords: Photonic Crystal Ring Resonator, Photonic Bandgap, CWDM, Bandpass Filter, FDTD Method, PWE Method 1. Introduction Two Dimensional Photonic Crystals (2DPCs) have ac- quired worldwide fascinating interest in the past two decades due to the existence of band gap and the capabil- ity to control the electromagnetic waves [1,2]. The band gap in PCs is more convenient for the design of required optical devices. The devices based on PC structures usu- ally have the benefit of significant size reduction (10 - 100 times) compared with their conventional devices. The other functional features of devices such as operat- ing speed, life time and output efficiency are not affected due to miniaturization, which are inevitable for the de- sign of integrated optics [3]. Typically, PCs are composed of periodic dielectric or metallo-dielectric nanostructures that have alternate low and high dielectric constant materials (Refractive Index) in one, two and three dimensions, which affect the pro- pagation of electromagnetic waves inside the structure. As a result of this periodicity, PCs exhibit a unique pecu- liar behavior, namely Photonic Band Gap (PBG) where the electromagnetic modes propagation is absolutely zero due to reflection. Hence, the density of states becomes negligible [3]. The periodicity of the structure and thus the completeness of the band gap are revealed by intro- ducing a defects (point or line or both), which allows the propagation of light in the PBG region. This can lead to design PC based optical devices in the PBG region [4]. Recent years, many PC based optical devices are de- signed both theoretically and experimentally. To name a few, add-drop filters [5,6], power splitters/divider [7,8], channel drop filters [9,10], multiplexers and demulti- plexers [11-13], polarization beam splitters [14,15], tri- plexers [16,17], switches [18], directional couplers [19], bandstop filters [20,21], bandpass filters [22-27] etc. Figure 1 shows the schematic layout of optical net work for telecommunication which consists of MUX/ Figure 1. Schematic layout of optical network for telecom- munication.  S. ROBINSON ET AL.143 DEMUX, Bandpass Filter (BPF), Erbium Doped Fiber Amplifier (EDFA) and optical fiber. The entire band of signal arrives from MUX and reaches into DEMUX through fiber and EDFA. Finally, the DEMUX separates the individual band of signal using appropriate BPF for particular application. The Coarse Wavelength Division Multiplexing (CWDM) system is now well-positioned to maximize its network capacity in the access, metro and enterprise networks. ITU-T G.694.2 defines the wavelengths for CWDM sys- tems ranging from 1260 nm to 1675 nm. The standard- ized and currently defined CWDM bands with their wavelength range are listed in the Table 1. Optical filters are the essential elements in the large capacity optical telecommunication network that em- ploys the technique of CWDM systems. Bandpass Filter (BPF) transmits a pre-determined band of wavelengths while rejecting all other wavelengths, by absorption, radiation or scattering. In CWDM network, a large num- ber of information signals are multiplexed on a single optical fiber by changing the frequency and hence the wavelength of the optical carrier for each optical channel. The Multiplexer and/or Demultiplexer may be designed using a series of BPFs which transmits only a specific wavelength. In the literature, it has been done by intro- ducing point defects and/or line defects, for L-Band, bi- periodic structures [22-24] and using liquid crystal pho- tonic band gap fibers [25]. Further, the circular Photonic Crystal Ring Resonator (PCRR) with quasi waveguides [26] and inline quasi waveguides [27] are theoretically studied. Since the Ring Resonator based BPF provides better selectivity, scalability and flexibility in mode de- sign, here, PCRR is considered to design BPFs. In this paper, a circular PCRR based BPF is designed to cover the entire C, L and U bands of CWDM systems for short haul and long haul applications. The output efficiency and bandwidth of the filters are observed through simulation. The Plane Wave Expansion (PWE) method is the most popular method to calculate the band gap of the structure that has been used for calculating the PBG and propagation modes. A 2D Finite Difference Table 1. CWDM bands and their w a velength ranges. Band Description Wavelength Range (nm) O Original 1260 - 1360 E Extended 1360 - 1460 S Short Wavelength 1460 - 1530 C Conventional 1530 - 1565 L Long Wavelength 1565 - 1625 U Ultra long Wavelength 1625 - 1675 Time Domain (FDTD) method has been employed to obtain the wavelength response of the BPF. The paper is arranged as follows: In Section 2, the numerical analysis of PC is presented. The structure de- sign of BPFs and simulated results are discussed in Sec- tion 3 and Section 4 concludes the paper. 2. Numerical Analysis There are many methods such as Transfer Matrix Me- thod (TMM) [28], Plane Wave Expansion (PWE) me- thod [29], Finite Element Method (FEM) [30], Finite Difference Time Domain (FDTD) method [31] and etc., available to analyze the dispersion behavior and trans- mission spectra of PCs. Each method has its own pros and cons. Among these, PWE and FDTD methods are dominating with respect to their performance and also meeting the demand required to analyze the PC based devices. The PWE method is initially used for theoretical analysis of PC structures, which makes use of the fact that eigen modes in periodic structures can be expressed as a superposition of a set of plane waves. Although this method can obtain an accurate solution for the dispersion properties (propagation modes and band gap) of a PC structure, however, it has still some limitations. i.e. transmission spectra, field distribution and back reflec- tions cannot be extracted as it considers only propagating modes. An alternative approach which has been widely adopted to calculate both transmission spectra and field distribution is based on numerical solutions of Maxwell’s equations by using FDTD method. In this analysis, the PWE is used to calculate the band gap and propagation modes of the PC structure whereas 2DFDTD is used to calculate the spectrum of the power transmission. The propagation of electromagnetic waves in a pho- tonic crystal is characterized using Maxwell’s Equations. It is assumed that the material is linear, isotropic, peri- odic with lattice vector and lossless; therefore, the Max- well’s equations have the following form [31] 1HE t (1) 1E t (2) where “E” and “H” are the electric and magnetic fields, and “ε” and “µ” are the dielectric constant and perme- ability. 2.1. PWE Method The band diagram is the most common representation of the band structure of PCs which gives the propagation modes and PBG. The PBG is the main characteristics of Copyright © 2011 SciRes. OPJ  S. ROBINSON ET AL. 144 photonic devices and can be observed using the band diagrams obtained through the PWE method. It is em- ployed both for electric and magnetic fields and the pe- riodic dielectric structure is expanded in Fourier series. This output can be represented as the region within the boundary of irreducible Brillouin zone. In this, X-axis is divided into regions representing the line segments connecting the Γ-Χ-Μ-Γ points in wave vector space and Z-axis is the normalized frequency (ωa/2Пc = a/λ) of electromagnetic waves that propagate in the photonic crystal. The band diagram calculations of electric field are carried out by solving Maxwell’s equation (master equa- tion) [32-34] which is 2 2 1Er Er rc (3) where “c” is the speed of light, “ω” is the angular fre- quency, ε(r) is the dielectric constant (relative permittiv- ity) and E(r) is the electric field of the periodic function. The above equation describes the propagation of light in PCs and it is a consequence of the Bloch-Floquet theorem which signifies that the electromagnetic waves in the periodic media can propagate without scattering and their behavior governed by a periodic function mod- ulated by a plane wave (the product of plane wave and periodic function with lattice period). Because of the periodic 2DPC, the dielectric constant, ε can be described as rr R k (4) where R is the vector of the 2D lattice. Bolch-Floquet theorem provides the solutions for pe- riodic eigen problem that can take the form e ikr k rur (5) where uk(r) is the periodic function of lattice that is 2 2 1 kk k ikiku ru r rc (6) For a given choice of Bloch vector k, the eigen value Equation (5) is discretized into a plane wave basis to yield an algebraic eigen value problem. It is solved for the permissible frequencies ω of the modes, which, in turn, are characterized by the eigenvectors. By scanning k over the Brillouin zone, the band diagram is generated. 2.2. FDTD Method The most common method to solve these Maxwell’s eq- uation is based on Yee’s mesh [35]. It computes E and H field components at points on a grid with grid points spaced ∆x, ∆z apart. The time is broken up into discrete steps of ∆t. The electric field components are computed at times t = n∆t and magnetic field at times t= (n + 1/2)∆t, where “n” is the integer representing computing step. The propagation of electromagnetic signals inside these PBG structures and the penetration depth of the field modes can be conveniently and efficiently studied using the FDTD method. The FDTD method is a rigor- ous solution to Maxwell’s equation and does not have any approximations and restrictions. It is widely used as a propagation solution technique in integrated optics and is a direct solution of Maxwell’s curl equation. In the 2D case, the fields can be decoupled into two transversely polarized modes, the E and H polarizations. The Max- well’s equations can be discretized in space and time by so call Yee-cell techniques [35]. The following FDTD time stepping formulae are spatial and time discretiza- tions of Equations (1) and (2) on a discrete 2D mesh within the XY co-ordinate system for the E-Polarization. 1/21/2 , 1/2, 1/2 1 ,, 0 nn zij zij nn xij xij HH ct EE y (7) 1/21/2 1/2, 1/2, 1 ,, 0 nn ij zij nn yij yij HH ct EE x (8) 1/21/2 ,, , 1/2, 1/21/2,1/2, 0 nn zij zij nn nn xijxijyi jyi j HE EE EE ct yx (9) where the index “n” denotes the discrete time step, indi- ces “I” and “j” denote the discretized grid point in the X-Y plane. These equations are iteratively solved in a leap frog manner, alternating between computing the E and H fields at subsequent ∆t/2 intervals. In order to produce an accurate simulation, the spatial grid must be small enough to resolve the smallest feature of the field to be simulated. To obtain a stable simulation, one must satisfies the following condition which relates the spatial and temporal step size. 22 1 11 t c y (10) where “c” is the speed of the light A broadband Gaussian pulse is launched into input port. Then we placed a time monitor (detector) inside each waveguide channel to measure the time varying electric field. The time monitor is used to record the Copyright © 2011 SciRes. OPJ 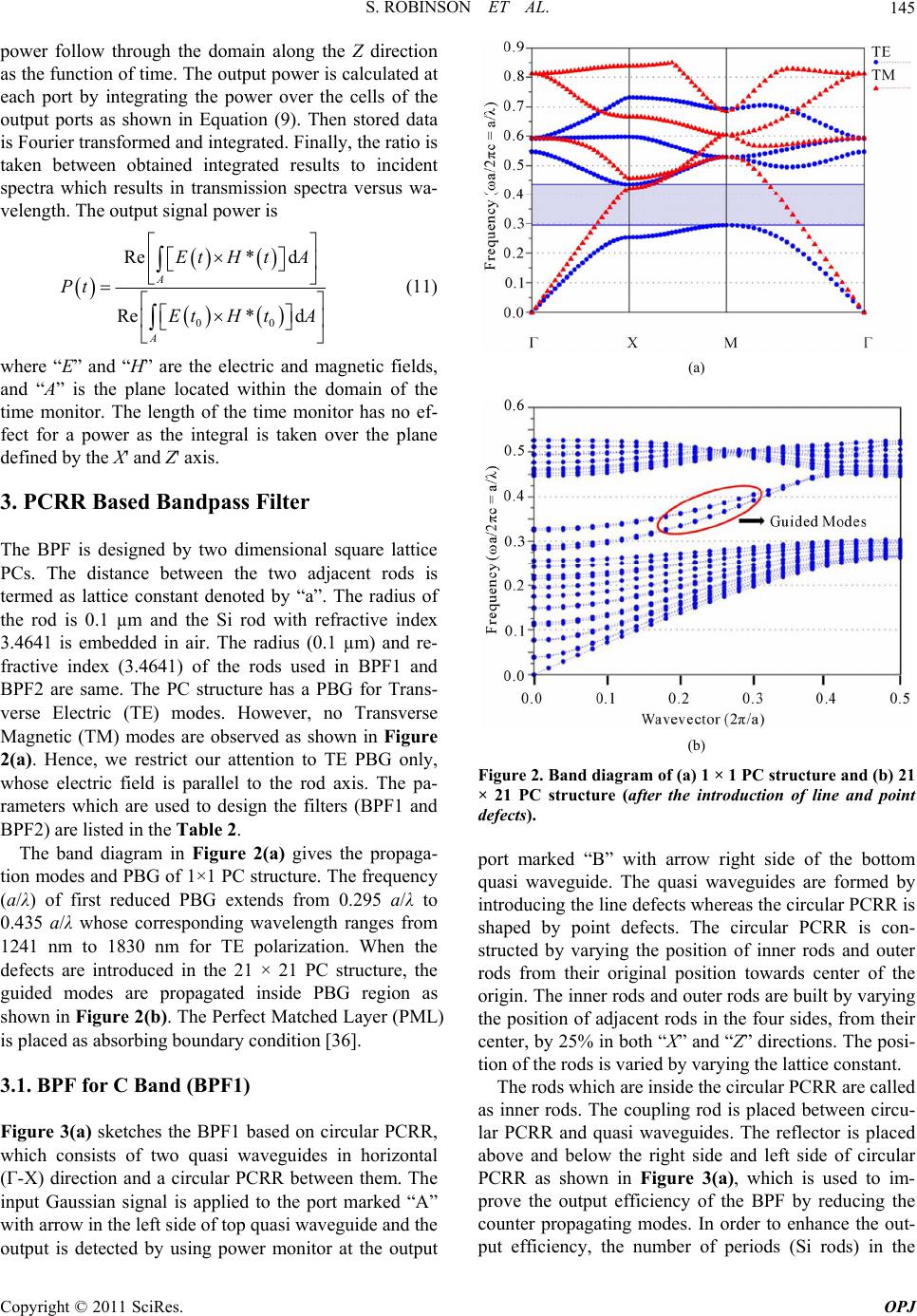 S. ROBINSON ET AL.145 power follow through the domain along the Z direction as the function of time. The output power is calculated at each port by integrating the power over the cells of the output ports as shown in Equation (9). Then stored data is Fourier transformed and integrated. Finally, the ratio is taken between obtained integrated results to incident spectra which results in transmission spectra versus wa- velength. The output signal power is 00 Re* d Re* d A A EtH tA Pt EtH tA (11) where “E” and “H” are the electric and magnetic fields, and “A” is the plane located within the domain of the time monitor. The length of the time monitor has no ef- fect for a power as the integral is taken over the plane defined by the X' and Z' axis. 3. PCRR Based Bandpass Filter The BPF is designed by two dimensional square lattice PCs. The distance between the two adjacent rods is termed as lattice constant denoted by “a”. The radius of the rod is 0.1 µm and the Si rod with refractive index 3.4641 is embedded in air. The radius (0.1 µm) and re- fractive index (3.4641) of the rods used in BPF1 and BPF2 are same. The PC structure has a PBG for Trans- verse Electric (TE) modes. However, no Transverse Magnetic (TM) modes are observed as shown in Figure 2(a). Hence, we restrict our attention to TE PBG only, whose electric field is parallel to the rod axis. The pa- rameters which are used to design the filters (BPF1 and BPF2) are listed in the Table 2. The band diagram in Figure 2(a) gives the propaga- tion modes and PBG of 1×1 PC structure. The frequency (a/λ) of first reduced PBG extends from 0.295 a/λ to 0.435 a/λ whose corresponding wavelength ranges from 1241 nm to 1830 nm for TE polarization. When the defects are introduced in the 21 × 21 PC structure, the guided modes are propagated inside PBG region as shown in Figure 2(b). The Perfect Matched Layer (PML) is placed as absorbing boundary condition [36]. 3.1. BPF for C Band (BPF1) Figure 3(a) sketches the BPF1 based on circular PCRR, which consists of two quasi waveguides in horizontal (Γ-Χ) direction and a circular PCRR between them. The input Gaussian signal is applied to the port marked “A” with arrow in the left side of top quasi waveguide and the output is detected by using power monitor at the output (a) (b) Figure 2. Band diagram of (a) 1 × 1 PC structure and (b) 21 × 21 PC structure (after the introduction of line and point defects). port marked “B” with arrow right side of the bottom quasi waveguide. The quasi waveguides are formed by introducing the line defects whereas the circular PCRR is shaped by point defects. The circular PCRR is con- structed by varying the position of inner rods and outer rods from their original position towards center of the origin. The inner rods and outer rods are built by varying the position of adjacent rods in the four sides, from their center, by 25% in both “X” and “Z” directions. The posi- tion of the rods is varied by varying the lattice constant. The rods which are inside the circular PCRR are called as inner rods. The coupling rod is placed between circu- lar PCRR and quasi waveguides. The reflector is placed above and below the right side and left side of circular PCRR as shown in Figure 3(a), which is used to im- prove the output efficiency of the BPF by reducing the counter propagating modes. In order to enhance the out- put efficiency, the number of periods (Si rods) in the Copyright © 2011 SciRes. OPJ 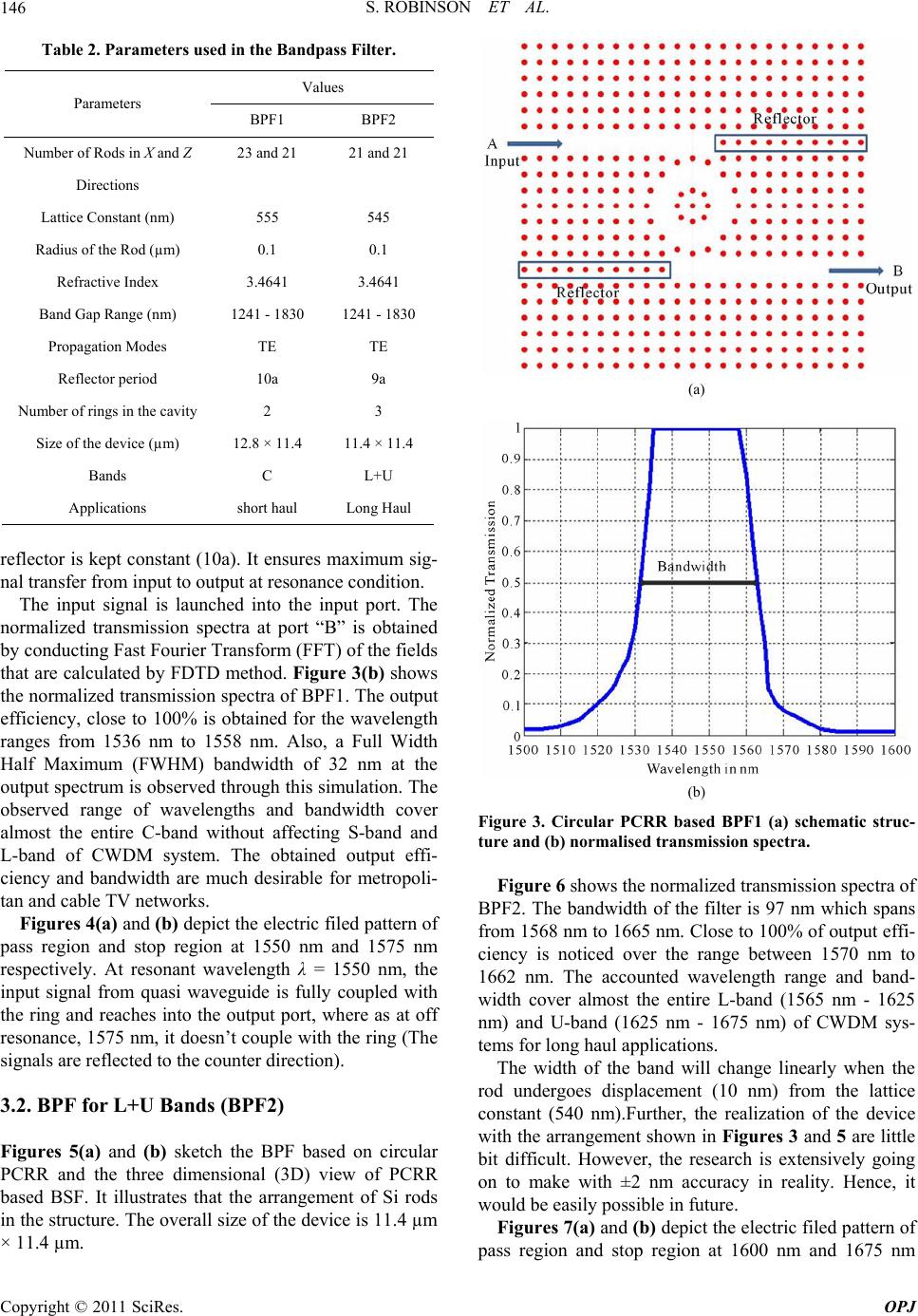 S. ROBINSON ET AL. 146 Table 2. Parameters used in the Bandpass Filter . Values Parameters BPF1 BPF2 Number of Rods in X and Z 23 and 21 21 and 21 Directions Lattice Constant (nm) 555 545 Radius of the Rod (µm) 0.1 0.1 Refractive Index 3.4641 3.4641 Band Gap Range (nm) 1241 - 1830 1241 - 1830 Propagation Modes TE TE Reflector period 10a 9a Number of rings in the cavity 2 3 Size of the device (µm) 12.8 × 11.4 11.4 × 11.4 Bands C L+U Applications short haul Long Haul reflector is kept constant (10a). It ensures maximum sig- nal transfer from input to output at resonance condition. The input signal is launched into the input port. The normalized transmission spectra at port “B” is obtained by conducting Fast Fourier Transform (FFT) of the fields that are calculated by FDTD method. Figure 3(b) shows the normalized transmission spectra of BPF1. The output efficiency, close to 100% is obtained for the wavelength ranges from 1536 nm to 1558 nm. Also, a Full Width Half Maximum (FWHM) bandwidth of 32 nm at the output spectrum is observed through this simulation. The observed range of wavelengths and bandwidth cover almost the entire C-band without affecting S-band and L-band of CWDM system. The obtained output effi- ciency and bandwidth are much desirable for metropoli- tan and cable TV networks. Figures 4(a) and (b) depict the electric filed pattern of pass region and stop region at 1550 nm and 1575 nm respectively. At resonant wavelength λ = 1550 nm, the input signal from quasi waveguide is fully coupled with the ring and reaches into the output port, where as at off resonance, 1575 nm, it doesn’t couple with the ring (The signals are reflected to the counter direction). 3.2. BPF for L+U Bands (BPF2) Figures 5(a) and (b) sketch the BPF based on circular PCRR and the three dimensional (3D) view of PCRR based BSF. It illustrates that the arrangement of Si rods in the structure. The overall size of the device is 11.4 µm × 11.4 µm. (a) (b) Figure 3. Circular PCRR based BPF1 (a) schematic struc- ture and (b) normalised transmission spectra. Figure 6 shows the normalized transmission spectra of BPF2. The bandwidth of the filter is 97 nm which spans from 1568 nm to 1665 nm. Close to 100% of output effi- ciency is noticed over the range between 1570 nm to 1662 nm. The accounted wavelength range and band- width cover almost the entire L-band (1565 nm - 1625 nm) and U-band (1625 nm - 1675 nm) of CWDM sys- tems for long haul applications. The width of the band will change linearly when the rod undergoes displacement (10 nm) from the lattice constant (540 nm).Further, the realization of the device with the arrangement shown in Figures 3 and 5 are little bit difficult. However, the research is extensively going on to make with ±2 nm accuracy in reality. Hence, it would be easily possible in future. Figures 7(a) and (b) depict the electric filed pattern of pass region and stop region at 1600 nm and 1675 nm Copyright © 2011 SciRes. OPJ  S. ROBINSON ET AL. Copyright © 2011 SciRes. OPJ 147 (a) (b) Figure 4. Electric field pattern of the cirular PCRR based BPF at: (a) 1550 nm and (b) 1575 nm. (a) (b) Figure 5. (a) Schematic structure of the circular PCRR based BPF and (b) three diemensional view of BPF. respectively. The bandwidth, wavelength ranges and out- put efficiency of the proposed BPFs are listed in the Ta- ble 3. 4. Conclusions A Photonic Crystal Ring Resonator based Band Pass Filter is designed for Coarse Wavelength Division Mul- tiplexing Systems to cover the entire C, L and U bands. Table 3. Output efficiency and bandwidth of the BP F s. Filters Output Efficiency (Wavelength Range) Bandwidth (Wavelength Range) BPF1 100% (1536 - 1558 nm) 32 nm (1532 - 1563 nm) BPF2 100% (1570 - 1662 nm) 97 nm (1568 - 1665 nm) Figure 6. Normalised transmission spectra of circular PCRR based BPF.  S. ROBINSON ET AL. Copyright © 2011 SciRes. OPJ 148 (a) (b) Figure 7. Electric field pattern of the cirular PCRR based BPF at: (a) 1600 nm and (b) 1675 nm. The output efficiency and bandwidth of the BPFs are investigated through simulation. The output efficiency is approximately, 100% over the wavelengths ranging from 1536 nm to 1558 nm (BPF1) and 1570 nm to 1662 nm (BPF2). Also, the observed Full Width Half Maximum bandwidth of BPF1 and BPF2 is 32 nm and 97 nm re- spectively. The devised circular PCRR based BPF would be the foremost BPF for CWDM applications. The sug- gested BPF1and BPF2 are compact and overall size of the chip is about 12.8 µm × 11.4 µm and 11.4 µm × 11.4 µm respectively. They would be more suitable for inte- grated optics and optical networks. 5. References [1] E. Yablonovitch., “Inhibited Spontaneous Emission on Solid-State Physics and Electronics,” Physical Review Letters, Vol. 58, No. 20, 1987, pp. 2059-2062. doi: 10.1103/PhysRevLett.58.2059 [2] S. John, “Strong Localization of Photons in Certain Dis- ordered Dielectric Superlattices,” Physical Review Letters, Vol. 58, No. 23, 1987, pp. 2486-2489. doi: 10.1103/PhysRevLett.58.2486 [3] J. D. Joannopoulos, R. D. Meade and J. N. Winn, “Photonic Crystal: Modeling of Flow of Light,” Princeton University Press, Princeton, 2005. [4] J. D. Joannopoulos, P. R. Villeneuve and S. Fan, “Photonic Crystals: Putting a New Twist of Light,” Na- ture, Vol. 386, 1997, pp. 143-149. doi: 10.1364/JOSAB.17.001027 [5] Z. Qiang, W. Zhou and Richard A. Soref, “Optical Add-Drop Filters Based on Photonic Crystal Ring Reso- nators,” Optics Express, Vol. 15, No. 4, 2007, pp. 1823- 1831. doi: 10.1364/OE.15.001823 [6] S. Robinson and R. Nakkeeran, “Photonic Crystal Ring Resonator Based Add-Drop Filter Using Hexagonal Rods for CWDM Systems,” Springer Optoelectronics Letters, Vol. 7, No. 3, 2011, pp. 164-166. doi: 10.1007/s11801-011-0172-2 [7] A. Ghaffari, F. Monifi, M. Djavid and M. S. Abrishamian, “Analysis of Photonic Crystal Power Splitters with Dif- ferent Configurations,” Journal of Applied Science, Vol. 8, No. 8, 2008, pp. 1416-1425. doi:10.3923/jas.2008.1416.1425 [8] N. Nozhat and N. Granpayeh, “Analysis and Simulation of a Photonic Crystal Power Divider”, Journal of Applied Science, Vol. 7, No. 22, 2007, pp. 3576-3579. doi:10.3923/jas.2007.3576.3579 [9] M. David, A. Ghaffari, F. Monifi and M. S. Abrishamian, “T-Shaped Channel Drop Filters Using Photonic Crystal Ring Resonators,” Physica E, Vol. 40, No. 10, 2008, pp. 3151- 3154. doi:10.1016/j.physe.2008.05.002 [10] C.-C. Wang and L.-W. Chen, “Channel Drop Filters with Folded Directional Couplers in Two-Dimensional Photonic Crystals,” Physica B, Vol. 405, No. 4, 2010, pp. 1210- 1215. doi:10.1016/j.physb.2009.11.044 [11] K. H. Hwang and G. H. Song, “Design of a High-Q Channel-Drop Multiplexer Based on the Two-Dimen- sional Photonic-Crystal Membrane Structure”, Optics Express, Vol. 13, 2005, pp. 1948-1957. doi:10.1364/OPEX.13.001948 [12] G. Manzacca, D. Paciotti, A. Marchese, M. S. Moreolo and G. Cincotti, “2D Photonic Crystal Cavity-Based WDM Multiplexer,” Photonics and Nanostructures-Funda- mentals and Applications, Vol. 5, No. 4, 2007, pp. 164- 170. doi:10.1016/j.photonics.2007.03.003 [13] A. Ghaffari, F. Monifi, M. Djavid and M. S. Abrishamian, “Heterostructure Wavelength Division Demultiplexers Using Photonic Crystal Ring Resonators,” Optics Com- munications, Vol. 281, No. 15-16, 2008, pp. 4028-4032. doi:10.1016/j.optcom.2008.04.045 [14] T. Liu, A. R. Zakharian, M. Fallahi, J. V. Moloney and M. Mansuripur, “Design of a Compact Photonic-Crystal Based Polarizing Beam Splitter,” IEEE Photonics Tech- nology Letters, Vol. 17, No. 7, 2005, pp. 1435-1437. doi: 10.1109/LPT.2005.848278  S. ROBINSON ET AL.149 [15] V. Zabelin, L. A. Dunbar, N. Le Thomas, R. Houdre, M. V. Kotlyar, L. O’Faolain and T.F. Krauss, “Self-Colli- Mating Photonic Crystal Polarization Beam Splitter,” Optics Letters, Vol. 32, No. 5, 2007, pp. 530-532. doi:10.1364/OL.32.000530 [16] D. S. Park, O. Beom-Hoan, S. G. Park, E. H. Lee, and S. G. Lee, “Photonic Crystal-Based GE-PON Triplexer Us- ing Point Defects,” Proceedings of SPIE, Vol. 6897, 2008, pp. 689711-12. doi: 10.1117/12.762186 [17] T.-T. shih, Y.-D. Wu and J.-J. Lee, “Proposal for Com- pact Optical Triplexer Filter Using 2-D Photonic Crys- tals,” IEEE Photonics Technology Letters, Vol. 21, No. 1, 2009, pp. 18-21. doi: 10.1109/LPT.2008.2008101 [18] Q. Wang, Y. P. Cui, H. Y. Zhang, C. C. Yan and L. L. Zhang, “The Position Independence of Heterostructure Coupled Waveguides in Photonic-Crystal Switch,” Optik Optics, Vol. 121, No. 8, 2010, pp. 684-688. doi:10.1016/j.ijleo.2008.10.010 [19] M. K. Moghaddam, A. R. Attari and M. M. Mirsalehi, “Improved Photonic Crystal Directional Coupler with Short Length,” Photonics and Nanostructures-Funda- mentals and Applications, Vol. 8, No. 1, 2010, pp. 47-53. doi:10.1016/j.photonics.2010.01.004 [20] F. Monifi, M. Djavid, A. Ghaffari and M. S. Abrishamian, “A New Bandstop Filter Based on Photonic Crystals,” Proceedings of PIER, Cambridge, 2008, pp. 1-4. ISSN: 1559- 9450 [21] S. Robinson and R. Nakkeeran, “Photonic Crystal Based Bandstop Filter for Photonic Integrated Circuits,” Inter- national Journal on Information and Communication Technologies (IJICT), Vol. 4, No. 1-2, 2011, pp. 49-54. [22] C. Chao, X. Li, H. Li, K. Xu, J. Wu and J. Lin, “Band- pass Filters Based on Phase-Shifted Photonic Crystal Waveguide Gratings,” Optics Express, Vol. 15, No. 18, 2007, pp. 11278-11284. doi:10.1364/OE.15.011278 [23] R. Costa, A. Melloni and M. Martinelli, “Band-Pass Resonant Filters in Photonic Crystal Waveguides,” IEEE Photonics Technology Letters, Vol. 15, No. 3, 2003, pp. 401-403. doi: 10.1109/LPT.2002.807953 [24] M. Djavid, A. Ghaffari, F. Monifi and M. S. Abrishamian, “Photonic Crystal Narrow Band Filters Using Biperiodic Structures,” Journal of Applied Science, Vol. 8, No. 10, 2008, pp. 1891-1897. doi: 10.3923/jas.2008.1891.1897 [25] L. Wei, T. T. Alkeskjold and A. Bjarklev, “Electrically Tunable Bandpass Filter on Liquid Crystal Photonic bandgap fibers,” Conference on OFC/NFOEC, Alaska, 21-26 March 2010, pp. 1-3. doi:10.1364/OL.35.001608 [26] S. Robinson and R. Nakkeeran, “A Bandpass Filter Based on 2D Circular Photonic Crystal Ring Resonator,” Pro- ceedings of the 7th IEEE International Conference on WOCN’10, Colombo, 6-8 September 2010, pp. 1-4. doi: 10.1109/WOCN.2010.5587343 [27] S. Robinson and R. Nakkeeran, “Photonic Crystal Ring Resonator Based Bandpass Filter,” Proceedings of IEEE ICCCCT-10, Pondicherry, 7-9 October 2010, pp. 83-85. doi: 10.1109/ICCCCT.2010.5670531 [28] J. B. Pendry and A. MacKinnon, “Calculation of Photon Dispersion Relation,” Physical Review Letters, Vol. 69, 1992, pp. 2772-2775. doi:10.1103/PhysRevLett.69.2772 [29] J. B. Pendry, “Calculating Photonic Band Structure,” Journal of Physics: Condensed Matter, Vol. 8, No. 9, 1996, pp. 1085-1108. doi: 10.1088/0953-8984/8/9/003 [30] G. Pelosi, R. Coccioli and S. Selleri, “Quick Finite Ele- ments for Electromagnetic waves,” Artech House, Boston, London, 1997. ISBN: 1596933453 [31] A. Taflove, “Computational Electrodynamics:The Finite- Difference Time-Domain Method,” Artech House, Bos- ton, London, 2005. ISBN: 978-1-58053-832-9 [32] S. G. Johnson and Joannopoulos, “Block-Iterative Fre- quency Domain Methods for Maxwell’s Equation in a Plane Wave Basis,” Optics Express, Vol. 8, No. 3, 2000, pp. 173-190. doi:10.1364/OE.8.000173 [33] S. Guo and S. Alloin, “Simple Plane Wave Implementa- tion for Photonic Crystal Calculation,” Optics Express, Vol. 11, No. 2, 2003, pp. 167-175. doi:10.1364/OE.11.000167 [34] K. Sakoda, “Optical Properties of Photonic Crystals,” Springer-Verlag, Berlin Heidelberg, New York, 2004. ISBN: 3-540-20682-5 [35] K. S. Yee, “Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equation in Isotropic Me- dia,” IEEE Transactions on Antenna Propagation, Vol. 14, No. 3, 1996, pp. 302-307. doi: 10.1109/TAP.1966.1138693 [36] A. Lavrinenko, P. I. Borel, L. H. Frandsen, M. Thorhauge, A. Harpoth, M. Kristensen, T. Niemi and H. M. H. Chong, “Comprehensive FDTD Modeling of Photonic Crystal Waveguide Components,” Optics Express, Vol. 12, No. 2, 2004, pp. 234-248. doi:10.1364/OPEX.12.000234 Copyright © 2011 SciRes. OPJ
|