Journal of Applied Mathematics and Physics
Vol.05 No.02(2017), Article ID:74154,5 pages
10.4236/jamp.2017.52031
Equivalence between Modulus of Smoothness and K-Functional on Rotation Group SO(3)*
Zhuyuan Yang1, Zongwen Yang2
1School of Mathematics and computer Science, Yunnan Minzu University, Kunming, China
2Department of Mathematics, Yunnan University, Kunming, China




Received: January 18, 2017; Accepted: February 12, 2017; Published: February 15, 2017
ABSTRACT
In this paper we obtain the equivalence between modulus of smoothness and K-functional on rotation group SO(3).
Keywords:
Rotation Group, Modulus of Smoothness, K-Functional, Equivalence

1. Introduction
Many results of approximation are based on Euclid spaces or their compact subsets. Periodic approximation is based on compact group {exp(ix)}, whereas matrix group U(n) is the generalization of {exp(ix)}. We know homomorphism between SU(2) and rotation group SO(3), which has many applications in Physics and Chemistry. Some approximation problems on compact groups have been studied since in 1920s F. Peter and H. Weyl proved the approximation theorem on compact group, that is, the irreducible character generate a dense subspace of the space of continuous classes function. For instance, Gongsheng (see [1]) studied the basic problems of Fourier analysis on unitary and rotation groups, including the degree of convergence of Abel sum based on Poisson kernel. Xue-an Zheng (see [2] [3]) studied the polynomial approximation on compact Lie groups. D. I. Cartwright et al. studied Jackson’s theorem for compact connected Lie groups (see [4]), and so on. In this paper, we study the modulus of smoothness and K-functional on rotation group SO(3) and as classical casein Euclid space we will obtain the equivalence between them.
Let  be the rotation group, where
be the rotation group, where 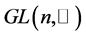 is the group of invertible real (n × n) matrices. For 1 ≤ p < +∞,
is the group of invertible real (n × n) matrices. For 1 ≤ p < +∞,  , where μ is the normalized Harr measure on G. For
, where μ is the normalized Harr measure on G. For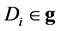 , the Lie algebra of G = SO(3), i = 1, 2, 3, Let
, the Lie algebra of G = SO(3), i = 1, 2, 3, Let 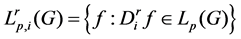 , i = 1, 2, 3, where
, i = 1, 2, 3, where 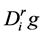 denote the r-order derivative of g in direction
denote the r-order derivative of g in direction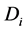 .
.
We also write the difference of function f and modulus of smoothness in the direction Di as follows
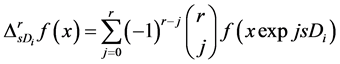 ,
,
and

where 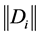 is the norm induced by Killing inner product on g.
is the norm induced by Killing inner product on g.
We denote
 .
.
Accordingly, we denote K-functional as follows
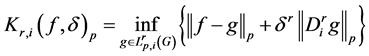
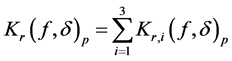
Further, for the isotropic case.
Let multi-indice , and
, and ,
, 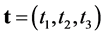 ,
, 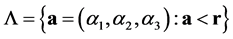 ,
,  , here
, here 

and

and

The corresponding K-functional is defined by

where


In the next paragraph we denote by C or Ci the positive constants but are not the same in the different formula. And 
2. Theorems and Their Proofs
We will use the next lemma 1.
Lemma 1 [5] [6]. If

Theorem 1. If




Proof. For i = 1, 2, 3, we first construct the approximation operators as follows
By Lemma 1,

where
Obviously, 

If we differentiate r times, then

So,

Clearly,

We get

and

Conversely, for

we have
Thus

Theorem 2. For


Proof. Noting that for

we get

Writing 

Moreover, we construct the approximation operator as follows
where

It easy to see that by using the boundedness of
It is similarly to (1), we have


Thus
Remark: Theorem 1 and theorem 2 can be easily generalized to SO(n) (n > 3).
Cite this paper
Yang, Z.Y. and Yang, Z.W. (2017) Equivalence between Modulus of Smoothness and K-Functional on Rotation Group SO(3). Journal of Applied Mathematics and Physics, 5, 341-345. https://doi.org/10.4236/jamp.2017.52031
References
- 1. Gong, S. (1983) Harmonic Analysis on Classical Groups. Science Press, Beijing. (In Chinese).
- 2. Zheng, X.-A., Xu, Z.F. and Zhao, H.S. (987) Approximation by Polynomial on Compact Lie Groups(I). Advance in Mathematics, 16, 61-66. (In Chi-nese)
- 3. Zheng, X.-A., Zhao, H.S. and Xu, Z.F. (1990) Polynomial Approximation on Compact Lie Groups in the Lp Norm(II). Advance in Mathematics, 19, 199-203. (In Chinese).
- 4. Cartwright, D.I. and Kucharski, K. (1988) Jackson’s Theorem for Compact Connected Lie Groups. Journal of Approximation Theory, 55, 352-359. https://doi.org/10.1016/0021-9045(88)90102-5
- 5. Schumarker, L.L. (1981) Spline Functions: Basic Theory. A Wi-ley-Interscience Publication, John Wiley and Sons Inc., New York, Chichester, Brisbane, Toronto.
- 6. Dahmen, W., De Vore, R. and Scherer, K. (1980) Multi-Dimensional Spline Approximation. SIAM Journal on Numerical Analysis, 17, 380-402. https://doi.org/10.1137/0717033
- 7. Gaudry, G.I. and Pini, R. (1986) Bernstein Theorem for Compact, Connected Lie Groups. Mathematical Proceedings of the Cambridge Philosophical Society, 99, 297- 305. https://doi.org/10.1017/S0305004100064215
NOTES
*This research was supported by the national natural science foundation of China (11361076).






