Applied Mathematics, 2011, 2, 1159-1169
doi:10.4236/am.2011.29161 Published Online September 2011 (http://www.SciRP.org/journal/am)
Analysis of DAR(1)/D/s Queue with Quasi-Negative
Binomial-II as Marginal Distribution
Kanichukattu Korakutty Jose1, Bindu Abraham2
1Department of Statistics, St. Thomas College Palai Mahatma Gandhi University, Kottayam, India
2Department of Statistics, Baselios Poulose II Catholicose College,
Mahatma Gandhi University, Kottayam, India
Received March 5, 2011; revised June 13, 2011; accepted June 20, 2011
Abstract
In this paper we consider the arrival process of a multiserver queue governed by a discrete autoregressive
process of order 1 [DAR(1)] with Quasi-Negative Binomial Distribution-II as the marginal distribution. This
discrete time multiserver queueing system with autoregressive arrivals is more suitable for modeling the
Asynchronous Transfer Mode(ATM) multiplexer queue with Variable Bit Rate (VBR) coded teleconference
traffic. DAR(1) is described by a few parameters and it is easy to match the probability distribution and the
decay rate of the autocorrelation function with those of measured real traffic. For this queueing system we
obtained the stationary distribution of the system size and the waiting time distribution of an arbitrary packet
with the help of matrix analytic methods and the theory of Markov regenerative processes. Also we consider
negative binomial distribution, generalized Poisson distribution, Borel-Tanner distribution defined by Frank
and Melvin(1960) and zero truncated generalized Poisson distribution as the special cases of Quasi-Negative
Binomial Distribution-II. Finally, we developed computer programmes for the simulation and empirical
study of the effect of autocorrelation function of input traffic on the stationary distribution of the system size
as well as waiting time of an arbitrary packet. The model is applied to a real data of number of customers
waiting for checkout in an airport and it is established that the model well suits this data.
Keywords: Discrete Autoregressive Process of Order [DAR(1)], Multiserver ATM Multiplexer, Matrix
Analytic Methods, Markov Renewal Process, Markov Regenerative Theory, Teleconference
Traffic, Quasi-Negative Binomial Distribution-II, Generalized Poisson Distribution, Borel-Tanner
Distribution
1. Introduction
In B-ISDN/ATM network, IP packets or cells of voice,
video, data are sent over a common transmission channel
on statistical multiplexing basis. The performance analysis
of statistical multiplexer whose input consists of a super-
position of several packetized sources is not a straight-
forward one. The difficulty in modeling this type of tra-
ffic is due to the correlated structure of arrivals. A com-
mon approach is to approximate this complex non re-
newal input process by analytically tractable arrival pro-
cess, namely discrete autoregressive process (DAR). The
impact of autocorrelation in traffic processes on queueing
performance measures such as mean queue length, mean
waiting times and loss probabilities in finite buffers, can
be very dramatic.
The DAR process, constructed and analyzed by Jacobs
and Lewis [1] has developed into one of several standard
tools for modelling input traffic in telecommunication
networks. The discrete autoregressive process of order 1
[DAR(1)] is known to be a good model for VBR coded
teleconference traffic as in Elwalid et al. [2]. Kamoun
and Ali [3] modeled an ATM multiplexer as a discrete
time multiserver queueing system with on-off sources
and studied the transient and stationary distribution of
the number of packets in the system.
Hwang and Sohraby [4] obtained the closed form ex-
pression for the stationary probability generating fun-
ction of the system size of the discrete time single server
queue with DAR(1) input. Hwang et al. [5] obtained the
waiting time distribution of the discrete time single server
queue with DAR(1) input. Choi and Kim [6] analyzed a

K. K. JOSE ET AL. 1160
multiserver queue fed by DAR(1) input. Kim et.al [7]
derived mean queue size in a queue with discrete
autoregressive arrival of order p.
In this paper we analyzed a discrete-time multi-server
queue with s servers (s > 0) having deterministic service
times (specifically, service time is 1) and the following
arrival process: Let Am be the number of arrivals at time
. Then Am = Am–1 with probability β; other-
wise, Am is sampled independently from a quasi-negative
binomial distribution-II. The stationary distribution of
the waiting time in that queue is calculated numerically
with a matrix analytic method. Specifically, the arrival
process is first analyzed at embedded times when Am is
sampled independently of Am–1 or when Am is less than
the number of servers. This analysis reduces to an analy-
sis of a Markov chain of M/G/1 type as presented in
Neuts [8]. Then the stationary distribution of Am at gen-
eral m is derived, which in turn gives the stationary dis-
tribution of the waiting time.
0,1, 2,m
The rest of the paper is arranged as follows. Quasi-
Negative Binomial Distribution-II is described in Section
2. Queues with input traffic as DAR(1) with marginal
Quasi-Negative Binomial-II is explained in Section 3.
Analysis of DAR(1) /D/s queue with marginal Quasi-
Negative Binomial Distribution-II is given in Section 4.
The stationary distribution of the Markov renewal pro-
cess is given in Section 5. Deriving the stationary distri-
bution of system size and waiting time of an arbitrary pa-
cket is explained in Sections 6 and 7. The quantitative
effect of the stationary distribution of system size and
waiting time on the autocorrelation function as well as
the parameters of the input traffic is illustrated numeri-
cally in Section 8. The application to real data set is
given in Section 9.
2. Quasi Negative Binomial Distribution-II
The quasi-negative binomial distribution (QNBD) obtained
by Janardan [9], Sen and Jain [10] has the probability
mass function as


 


1
11 2
12
12
121 2
12 2
1!
;, ,=
1!!1
for0;> 0,> 0,> 0
and0;< 0;=0,1,2
x
x
n
nxpp xp
Pxnp p
nx pxp
pxpn pifp
pxpifp x


 


 
(1)
where x be the number of occurrences. When p2 = 0 the
QNBD reduces to negative binomial distribution (NBD)
and when n = 1, QNBD reduces to quasi geometric dist-
ribution (QGSD) for n = 1. QNBD tends to the Consul
and Jain’s [11] generalized Poisson distribution. But un-
fortunately the moments of this distribution appear in an
infinite series which is not suitable for summation. The
method of moments fails to provide quick estimates of its
parameters. Hence Ahmad et al. [12] introduced a new
model of quasi negative binomial distribution-II (QNBD-
II). This new model has the probability mass function
 



1
2111 2
1
212
21
11
11
for0 <<1 and0<<1;= 0,1,2
x
xn
nppp pxp
pxn x
np pxp
x
npp x



 






(2)
When 20p

this new model reduces to negative
binomial distribution. The probabilities of QNBD-II de-
creases with the successive occurrences. This tendency
of probabilities suggests its possible applications in
reliability, biometry, and survival analysis. The QNBD-II
is uni-model and only its first moment (mean) appears in
compact form. The lower and upper bound of Mode M is

1
1
1
11
1
1<< ,<1
11
pn
np Mp
pp



.

1
2
2
=,
1
np
Mean p
np<1
2.1. Remarks
1) Let X be a quasi-negative binomial variate with
parameters (n,) and pmf given by (2). If
such that 1
12
,pp
=np
n

and 2=np

then the random
variable X tends to generalized Poisson distribution with
parameters


,


.
2) Let X be a quasi-negative binomial variate with
parameters (n,12
) and probability mass function is
(pmf) is given by (2). If such that
,pp
n 1=n



where then the random variable X tends to
Borel-Tanner distribution defined by Frank and Melvin
[13]
1=


2
p
3) Let X be a quasi-negative binomial variate with
parameters (n, 12
) and pmf given by (2), then zero-
truncated quasi-negative-binomial distribution-II tends to
zero-truncated generalized Poisson distribution as
.
,pp
n
3. Queues with DAR(1) Arrivals with Quasi
Negative Binomial Distribution-II as
Marginal
The input ATM multiplexer with VBR coded telecon-
ference traffic is assumed to be DAR(1) with quasi-
negative binomial distribution-II as marginal. Let




:=0,1,2Yt t be a sequence of i.i.d random vari-
ables. Y(t) assumes positive values only and


==
x
bPYtx

,=0,1,2x,
. When the input process
has quasi-negative binomial distribution-II as marginal
we have bx as the pmf of the form (2).

K. K. JOSE ET AL.1161


Discrete Autoregressive Process of order 1 (DAR(1)
is defined by the regression equa-
tion as


:0,1,2,Xt t
 
    
0=0
=11, =1,2,
XY
XtZtXtZtYt t
where are i.i.d Bernoulli random
variables with and


:1,2,3,Zt t

=0PZt 


=1 =1t
 
= 0<1  
PZ



and


:1,2,3,Zt t

Ytt

is
assumed to be independent of

.
DAR(1) is determined by the parameter
:0,1,2,

and the
distribution of Y(t), so that

:=0,1, 2,
x
bx


 
0= 0XY
 

1with prob.
=with prob.1
Xt
Xt Yt







The properties of DAR(1) are as follows
1) is stationary


:0,1,2Xt t
2) The probability distribution of X(t) is the same as
the distribution of Y(t)

==,=0,1, 2
x
PXtxbx 

3) The autocorrelation function for X(t) at lag t is
obtained as
 



 
0; )
==,
0

t
Cov XXt
t
Var X
 =0,1,2t
the parameter

is the decay rate of the autocorrelation
function.
4. Analysis of DAR(1)/D/s Queue with
Quasi-Negative Binomial-II as Marginal
We assume that the input process is DAR(1) with
quasi-negative binomial distribution-II distribution as the
marginal distribution and there are s servers (s > 0)
whose service occurs at constant rate. In this integer
valued time queue, the time is divided into slots of equal
size and one slot is needed to serve a packet by a server.
We assume that packet arrivals occur at the beginning of
slots and departures occur at the end of the slots. Here
represents packet arrivals so that
X(t) is the number of packets arriving at the beginning of
the t slot.


:0,1,2Xt t
th



Let N(t) be the number of packets in the system say
system size, immediately before arrivals at the beginning
of the tth slot. Then
is a two dimensional Mar-
kov process of M/G/1 queue type. The state space is
 


,:0,1,2Nt Xtt
   
0,0
=, =0,1,2,0,1,2

nni
lnni E
 
The number of phases is infinity. So the computation
of stationary distribution of
is not easy to work out.
 
 
,:0,1,2Nt Xtt
In practice by matrix analytical method and using the
theory Markov regenerative processes, we compute the
stationary distribution of the new process at the em-
bedded epochs


,=0,1, 2t


23
<tt as follows, we have
01
0<<<tt
  
-1
0,=0
= inf t > t :Z = 1 or 01,=1,2





 
t
tXts
Let


=,=0,1,2NNt


0=
J
s





if=0= 1, 2,3
=if= 1= 1, 2,3












Xt Zt
JsZt
The packet arrivals at and after t

are independent of
the information prior to t

given
J

. From this, it is
observed that




=NJ

,:  0,1,2, is the new
Markov renewal process with state space

 
0,1, 20,1Es
The probability transition matrix of the Markov
renewal process is computed as follows.
1) For 0,1, 2n

and 0,1, ,1is
 


 
max,0,withprob.
,
max,0,withprob. 1
nsi i
ni
nsi s









2) For 0,1, 2n











min,1
00
=0
max,0,with prob.
01,
,with prob.
,(1 )11,
0,with prob.1
,withprob. 0,>0
i
i
sns
in
i
l
nsii
bis
nsis
ns bsnis
sb
nlsglnl


g


















where
0
1if=0
=0if 1
n
n
n




0=
s
g
b

1
|
=1,= 1, 2,
l
i
lis
il
gb l 



The transition probability matrix P

K. K. JOSE ET AL. 1162
1





1212
1222
12 1
011
021
32
0
00
000 0


 




 

ssss
sss s
cs
ss
ss
ss
BAA A
BA AA
BA AA
AAAA
AAA
AA























00 0
=,
0

 

i
is
A
is
sg







=0
=,1
i
ij
j
BAi
s
<
We assume that the stability condition

=1
==
m
m
EXtmb s 



 is satisfied.
5. The Stationary Distribution of the
Markov Renewal Process
is obtained as above.
Where the elementary matrices are
0is

00 0 0
01 =
01

 




i
ii
Ai
bb
s






















Consider




,,=0,1,2NJ

 , and


π=lim 0,0
ni = ,=,
P
NnJin

=0
N
A
i
>n
s
18
  We apply
matrix analytic method as described below. The
transition probability matrix P has infinite order, so that
it would have to be truncated before we implement
matrix analytic method. We assume that there exists
some index N such that for all . That is
we assume that the Markov chain does not jump more
than N steps at a time so that the matrix is of finite order,
see Latouche and Ramaswamy [14]. For a numerical
illustration , consider the case when s = 5 and N = 14.
Then the transition probability matrix P can be obtained
as
N
01is
0
s
5678910 11 12 13 1415 16 17 18 19
467891011121314151617
3 4 5 6 78 91011121314151617
2 3 4 5 67 8 910111213141516
12345678910 1112131415
||
5| |
||
||
||
BAAAAAAAAAAAAAA
BAAAA AAAAA AAAAA
BAAAA AAAAA AAAAA
BAAAAAAAAAAAAAA
BAAAA AAAAAAAAAA
0123456789 1011121314
0 1 2 34 56 7 8910111213
012 3456789101112
01 23456 7891011
0 12345 678910
||
0| |
00 ||
000 ||
0000 ||
A
AAAAAAAAA AAAAA
A
AAA AAAAA AAAAA
A
AA AAAAA AAAAA
A
AAAAAAAAAAA
A
AAAAA AAAAA
               

01234 56789
0123 45678
012 34567
01 23456
0 12345
00000 ||
00000 | 0|
00000 |00|
00000 |000|
00000 |0000|
00000 |00
A
AAAA AAAAA
A
AAA AAAAA
A
AA AAAAA
A
AAAAAA
A
AAAAA

               
01234
0123
012
01
0
000 |
00000 |00000 |0
00000 |00000 |00
00000 |00000 |000
00000 | 00000 | 0000
A
AAAA
A
AAA
A
AA
A
A
A
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

K. K. JOSE ET AL. 1163
By arranging the transition probability matrix into (sxs)
matrices we get
012
012
01
0
ˆˆˆ
ˆˆˆ
=ˆˆ
0
ˆ
00
BBB
A
AA
P
A
A
A







or equivalently
023
012
01
0
ˆˆ
ˆ
ˆˆˆ
=ˆˆ
0
ˆ
00
BAA
A
AA
P
A
A
A







In general we can symbolize the transition matrix P as
012 1
012 1
01 2
0
ˆˆˆ ˆ
ˆˆˆ ˆ
=ˆˆ ˆ
0
ˆ
000
n
n
n
BBB B
AAA A
PAA A
A



















 





*1
=1
Ns
ns

or equivalently
023
012 1
01 2
0
ˆˆˆ
ˆ
ˆˆˆ ˆ
=ˆˆ ˆ
0
ˆ
000
n
n
n
BAAA
AAA A
PAA A
A


















 



1
2




3,
The elements of P can be written as
12
12
0
12
ˆ=




ss s
ss s
s
BA A
BA A
B
BA A








,



111
112
11 12
ˆ=




sn snsn
sn snsn
n
sn
sn sn
AAA
AA A
A
AA A


 







=0,1,2,nn


1
ˆ
ˆ=,=1,2,
nn
BAn n


A matrix P of the above structure is said to be of
M/G/1 type, which underlines the similarity to the
embedded Markov chain of the M/G/1 queue. With
respect to the levels , the Markov chain is called skip free
to the left, since in one transition the level can be
reduced only by one.
By the matrix analytic method we proceed as follows.
Step 1: Find the minimal nonnegative solution G of
the matrix equation
=0
ˆ
=n
n
n
GAG


G can be given by the following iteration See Breuer
[15]
0
10
1
1
=1
=1
=0
ˆ
=
ˆ
=,=2,
=

kn
knk
n
k
k
G
GA
GAGk
GG





G is a stochastic matrix ,and hence we can stop the
iteration procedure when 1.1<G

 reaches where
=0.0001

. From this iteration we obtained the upper
limit of k &=let nk
1

. From this we come to
know the truncated index N at which G becomes
stochastic
n
Step 2: Find
=0
ˆ
=nn
n
n
H
BG


and a positive row vector h satisfying =hHh
Step 3:
0
1
01
=0=1 =0
1
1
=0
=
ˆ ˆ
=
ˆ,=1,2
nnn
ii
nnilnli
ili
ni
i
i
xh
x
xBGxAG
I
AG nn




















Step 4: Finally


 




,0 ,11,0 11,
π,πππ =,
=0,1,2,,
nsns sn nsnss Cx
nn


 

where
1
=0
=
n
n
n
Cx

e







and e is the s (s + 1) dimensional
column vector whose components are all ones.
6. Stationary Distribution of






,,=0,1,2NtXt t
Observe that





,,,=0,1, 2NJ t

 is a Markov

K. K. JOSE ET AL. 1164
renewal process and




,:=0,1,Nt tXttt



2
.

given
  



,,0<,,=,NXtNJ ni

   is
stochastically equivalent to
  
,:=0,1,2Nt Xtt
given Hence


00
,=,NJni
 

,:=0,1,2Nt Xtt

is a discrete time Markov
regenerative process with the Markov renewal sequence



,,:=0,1,2

 NJt

.From the theorm See Kul-
karni [16]
   

=lim,=,, =0,1,2
nj t
pPNtXtnjnj
 of
 


,:=0,1,2Nt Xtt are determined by
   
 
 
1
1
t
s 


,=,
=0 =0=
1
=0 =0
π1,=,
π,=,
li Nt Xt nj
li tt
nj s
li
li
ENJli
p
EttN Jli


 










 

(3)
We have
   

 
1
1
=,=,
1,=
1if=,01and
if=,01 and=
if= ,=and=
1
=
if= ,> ,
and divides
0otherwise.
t
tt Nt Xtnj
j
s
nl
js
j
ENJ
ij isnl
bisjs
bisjs nl
bisjsnl
js nl

























,
=
li
nl



The numerator of Equation (3) is

,
=0
ππ,0
π,=
1
π,1
njns j
ns s
n
js
i
j nijss
i
bj
bjs
bjs
















1s
We have
 
1
1
=0 =
,=,
1if0
1if =
1
s
rr
rrs
EttN Jli
is
bb is













1,
The denominator of Equation (3) is
11
=0 =0=0=0=
1
ππ
1
ss
lils rr
lil r rs
bb

 





  (4)
where is the stationary probability

0
=0 =0
πn
l
ll



vector of the Markov process

whose
transition probability matrix is
:=0,1,2J






10,
1
011
=0
==
001
001
00 1
1


 


ijs
s
s
r
r
PJjJ i
bb bb




 
















(5)
The infinitesimal transition matrix of (5) is
Q =


 

1
01
=0
10 1
01 1
00 1


 


s
r
r
bb

b



 

  

 











The balance equations are
=0 & e=1Q


By solving the balance equations we obtain the sta-
tionary distribution of the Markov process


:=0,1, 2J

as
=
=0
=
,0 1
1
π=1,=
1
i
r
rs
li
l
r
rs
bjs
b
is
b



















(6)
By substituting (6) into (4) we obtain the denominator
of the right hand side of (3) as

1
=
1r
rs
b 



Theorem 6.1
The stationary distribution or the limiting pro-
babilities
 





= lim,=,,,=0,1,2
nj t
pPNtXtnjnj
 
are given by



1
1
1
,
=0
ππ ,0
π,=
1
π,1
njnsj
ns s
nj
n
js
i
j
nijss
i
bj
bjs
p
bjs








1s












where
1
=
1=
r
rs
b









π
l s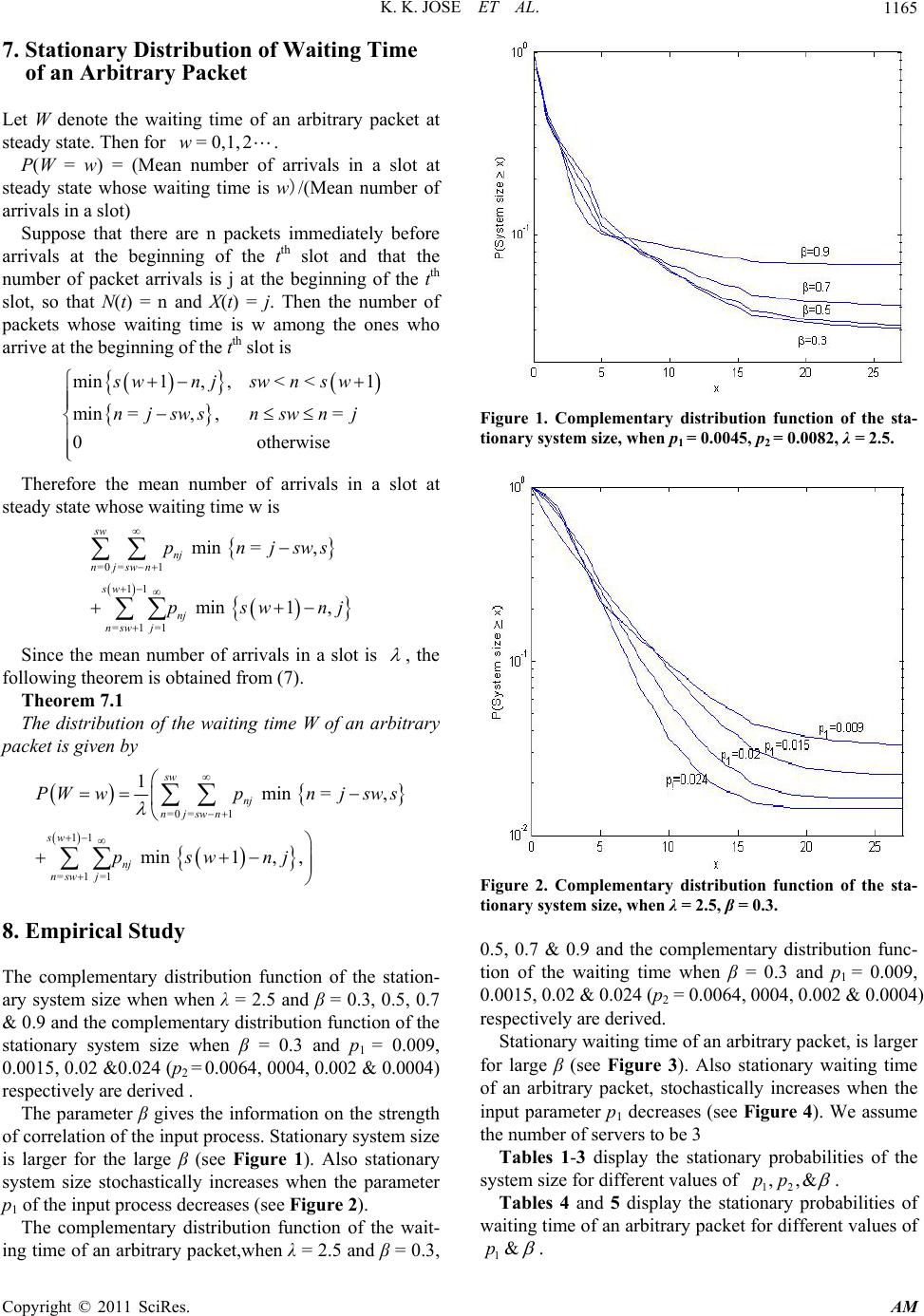

K. K. JOSE ET AL.1165
wise
j
7. Stationary Distribution of Waiting Time
of an Arbitrary Packet
Let W denote the waiting time of an arbitrary packet at
steady state. Then for =0,1,2 .w
P(W = w) = (Mean number of arrivals in a slot at
steady state whose waiting time is w)/(Mean number of
arrivals in a slot)
Suppose that there are n packets immediately before
arrivals at the beginning of the tth slot and that the
number of packet arrivals is j at the beginning of the tth
slot, so that N(t) = n and X(t) = j. Then the number of
packets whose waiting time is w among the ones who
arrive at the beginning of the tth slot is




min1,,< <1
min=, ,=
0other
swnjsw n sw
n jswsnswn j
 






Therefore the mean number of arrivals in a slot at
steady state whose waiting time w is




=0 =1
11
=1=1
min =,
min1 ,
sw
nj
njswn
sw
nj
nswj
pnjsws
pswn








Since the mean number of arrivals in a slot is

, the
following theorem is obtained from (7).
Theorem 7.1
The distribution of the waiting time W of an arbitrary
packet is given by
 



=0 =1
11
=1=1
1min =,
min1, ,
sw
nj
njswn
sw
nj
nsw j
PWwpnj sws
pswnj






 









8. Empirical Study
The complementary distribution function of the station-
ary system size when when λ = 2.5 and β = 0.3, 0.5, 0.7
& 0.9 and the complementary distribution function of the
stationary system size when β = 0.3 and p1 = 0.009,
0.0015, 0.02 &0.024 (p2 = 0.0064, 0004, 0.002 & 0.0004)
respectively are derived .
The parameter β gives the information on the strength
of correlation of the input process. Stationary system size
is larger for the large β (see Figure 1). Also stationary
system size stochastically increases when the parameter
p1 of the input process decreases (see Figure 2).
The complementary distribution function of the wait-
ing time of an arbitrary packet,when λ = 2.5 and β = 0.3,
Figure 1. Complementary distribution function of the sta-
tionary system size, when p1 = 0.0045, p2 = 0.0082, λ = 2.5.
Figure 2. Complementary distribution function of the sta-
tionary system size, when λ = 2.5, β = 0.3.
0.5, 0.7 & 0.9 and the complementary distribution func-
tion of the waiting time when β = 0.3 and p
1 = 0.009,
0.0015, 0.02 & 0.024 (p2 = 0.0064, 0004, 0.002 & 0.0004)
respectively are derived.
Stationary waiting time of an arbitrary packet, is larger
for large β (see Figure 3). Also stationary waiting time
of an arbitrary packet, stochastically increases when the
input parameter p1 decreases (see Figure 4). We assume
the number of servers to be 3
Tables 1-3 display the stationary probabilities of the
system size for different values of 12
,,&pp

.
Tables 4 and 5 display the stationary probabilities of
waiting time of an arbitrary packet for different values of
1&p

.

K. K. JOSE ET AL. 1166
Figure 4. Complementary distribution function of the wait-
ing time of an arbitrary packet, when β = 0.3.
Figure 3. Complementary distribution function of the wait-
ing time of an arbitrary packet,when p1 = 0.009, p2 = 0.0064.
Table 1. Showing the values of distribution of stationary system size P(n, j) for λ = 2.5, β = 0.1, p1 = 0.0045, p2 = 0.0082 and s = 3.
j
n 0 1 2 3 4 5 6 7 8

0 0.5148 0.1005 0.0460 0.0264 0.0158 0.0114 0.0086 0.0067 0.0054

1 0.0460 0.0090 0.0090 0.0026 0.0031 0.0011 0.0008 0.0006 0.0005

2 0.0135 0.0026 0.0495 0.0007 0.0007 0.0014 0.0002 0.0001 0.0001

3 0.0104 0.0021 0.0009 0.0005 0.0004 0.0003 0.0010 0.0001 0.0001

4 0.0081 0.0016 0.0007 0.0004 0.0003 0.0003 0.0002 0.0007 9.E - 04

5 0.0005 0.0012 0.0005 0.0003 0.0002 0.0001 0.0001 0.0001 0.0006

6 0.0043 0.0009 0.0004 0.0002 0.0001 0.0001 0.0001 8.E-04 0.0001

7 0.0034 0.0006 0.0003 0.0001 0.0001 0.0001 8.E - 04 6.E-04 5.E - 04
8 0.0028 0.0005 0.0002 0.0001 0.0001 8.E-04 6.E - 04 0.0001 4.E - 04 
9 0.0028 0.0005 0.0002 0.0001 0.0001 8.E-04 7.E - 04 5.E - 04 4.E - 04 
10 0.0023 0.0004 0.0002 0.0001 9.E - 04 6.E-04 5.E - 04 4.E - 04 8.E - 04
11 0.0019 0.0003 .00017 00011 7.E - 04 5.E-04 4.E - 04 3.E - 04 3.E - 04
         
Table 2. Showing the values of distribution of stationary system size P(n, j) for λ = 2.5, β = 0.3, p1 = 0.009, p2 = 0.0094 and s = 3.
j
n 0 1 2 3 4 5 6 7 8

0 0.5875 0.1148 0.1413 0.0300 0.0020 0.0014 0.0010 0.0008 0.0006 
1 0.0009 0.0001 0.0100 0.0004 0.0018 2.E - 04 1.E - 04 1.E - 04 1.E - 04 
2 0.0097 0.0046 0.0682 00206 0.0040 0.0054 0.0005 0.0003 0.0003 
3 0.0001 3.E - 05 2.E - 05 4.E - 05 0.0014 2.E - 05 0.0009 1.E - 05 9.E - 05 
4 8.E - 05 1.E - 05 1.E - 05 3.E - 05 0.0013 0.0011 1.E - 05 0.0007 7.E - 05 
5 2.E - 05 1.E - 05 7.E - 05 2.E - 05 0.0012 2.E - 05 2.E - 05 1.E - 05 0.0006 
6 3.E - 05 1.E - 05 8.E - 05 2.E - 05 0.0010 0.0010 0.0008 1.E - 05 9.E - 05 
7 3.E - 05 6.E - 06 5.E - 06 1.E - 05 0.0009 1.E - 05 1.E - 05 1.E - 06 1.E - 06 
8 3.E - 05 6.E - 06 5.E - 06 1.E - 05 0.0009 1.E - 05 1.E - 05 1.E - 06 1.E - 06 
9 0.0016 0.0007 0.0005 0.0003 0.0002 0.0002 0.0002 0.0001 0.0007 
10 2.E - 05 4.E - 06 3.E - 06 1.E - 05 0.0007 0.0008 1.E - 05 2.E - 06 0.0005 
11 1.E - 05 3.E - 06 1.E - 06 9.E - 06 0.0006 1.E - 05 2.E - 06 1.E - 06 8.E - 06 
          

K. K. JOSE ET AL.1167
Table 3. Showing the values of distribution of stationary system size P(n, j) for λ = 2.5, β = 0.3, p1 = 0.024, p2 = 0.0004 and s = 3.
j
n 0 1 2 3 4 5 6 7 8

0 0.0922 0.1530 0.1759 0.1358 0.0605 0.0320 0.0147 0.0060 0.0022 
1 0.0064 0.0150 0.0208 0.0190 0.0266 0.0040 0.0020 0.0008 0.0003 
2 0.0603 0.0089 0.0111 0.0115 0.0131 0.0120 0.0012 0.0005 0.0001 
3 0.0024 0.0060 0.0077 0.0073 0.0072 0.0030 0.0052 0.0003 0.0001 
4 0.0013 0.0032 0.0044 0.0041 0.0040 0.004 0 0.0010 0.0019 6.E - 05 
5 0.0001 0.0017 0.0021 0.0022 0.0021 0.0010 0.0006 0.0003 0.0007 
6 0.0004 0.0010 0.0013 0.0013 0.0012 0.0010 0.0017 0.0002 0.0001 
7 0.0002 0.0005 0.0007 0.0007 0.0006 0.0001 0.0004 0.0001 6.E - 05 
8 0.0001 0.0002 0.0003 0.0003 0.0003 0.0004 0.0002 0.0006 4.E - 05 
9 7.E - 05 0.0001 0.0002 0.0002 0.0002 0.0002 0.0005 0.0001 4.E - 05 
10 4.E - 05 9.E - 05 0.0001 0.0001 0.0001 0.0002 0.0001 6.E - 05 0.0002 
11 2.E - 05 4.E - 05 6.E - 05 6.E - 05 6.E - 05 8.E - 05 7.E - 05 4.E - 05 3.E - 05 
          
Table 4. Showing the values of the distribution of waiting time of an arbitrary packet P(W = ω) for different values of β and λ
= 2.5, p1 = 0.009, p2 = 0.0064 and s = 3.
β
ω 0.1 0.3 0.5 0.7 0.9
0 0.2332 0.2326 0.2306 0.2270 0.2211
1 0.1096 0.0991 0.0832 0.0598 0.0245
2 0.0499 0.0473 0.0432 0.0359 0.0187
3 0.0280 0.0289 0.0285 0.0257 0.0158
     
Table 5. Showing the values of the distr ibution of waiting time of an arbitrary packet P(W = ω) for different values of p1, β =
0.3, a nd s = 3.
p2
0.0082 0.0064 0.004 0.002 0.0004
p1
ω 0.0045 0.009 0.015 0.02 0.024
0 0.2326 0.3748 0.4847 0.5303 0.5944
1 0.0991 0.1790 0.2407 0.2267 0.2229
2 0.0473 0.0898 0.1102 0.0890 0.0636
3 0.0289 0.0543 0.0569 0.0341 0.0179
     
9. Analysis and Modeling of a Data Set
In this section we apply the model to a data on the
number of initially waiting customers for checking in an
airport for a time period of 30 minutes each
. The data was collected from morning
8.00 A.M to 11.30 P.M for one week. This includes all
the busy periods as well as idle periods. The data is taken
from the file customer checkout.xlsx available in [17].
Table 6 gives the frequency distribution of the corre-
sponding data, where x is the number of customers
initially waiting for the service.

=0,1, ,30t
In the present paper we assumed the number of arrivals
as DAR(1) with marginal Quasi Negative Binomial II
distribution. Thus the data set can be fitted to the the
Quasi Negative Binomial II distribution as follows.

To test whether there is a significant difference be-
tween an observed distribution and the Quasi Negative
Binomial II distribution, we use Kolmogorov-Smirnov
[K.S.] test for 0
H
: Quasi Negative Binomial II distri-

K. K. JOSE ET AL. 1168
Table 6. Table showing the frequency distribution of the
number of customers waiting for checkout.
x frequency x frequency
0 43 12 8
1 49 13 2
2 47 14 5
3 44 15 3
4 29 16 3
5 22 17 2
6 30 18 0
7 14 19 1
8 15 20 0
9 5 21 1
10 8 22 1
11 4 Total 336
bution with parameter p1 = 0.021 and p2 = 0.00513 is a good
fit for the given data. Here the calculated value of the
K.S. test statistic is 0.017857 and the critical value
corresponding to the significance level 0.01 is 0.088924,
showing that the assumption for number of arrivals
follow Quasi Negative Binomial II distribution is valid
(see Figure 5).
By applying matrix analytic method we obtain the
stationary distribution of system size and waiting time of
an arbitrary customer for the Quasi Negative Binomial
II/D/s queue. Here the mean = λ =4.3125. To satisfy the
stability condition we assume the number of servers as
. Also we assume the value of autocorrelation func-
tion
=5s
=0.1

, 1 and 2. Tables 7
and 8 display the stationary distribution of waiting time
of an arbitrary customer and system size.
=0.021p= 0.00513p
Figure 5. The Probability histogram of real data and the
Quasi Negative Binomial II distribution with p1 = 0.021 and
p2 = 0.00513.
Table 7. Table showing the stationary distribution of wait-
ing time of an arbitrary customer P(W =ω)when β = 0.1, λ =
4.3125, s = 5.
w p(w)
0 0.2832
1 0.1195
2 0.0589
3 0.0380
 
Table 8. Table showing the stationary distribution of system size P(n, j) when β = 0.1, λ = 4.3125, s = 5.
j
n 0 1 2 3 4 5 6 7 8 9

0 0.102 0.123 0.114 0.094 0.075 0.058 0.041 0.031 0.024 0.019 
1 0.007 0.009 0.008 0.008 0.008 0.004 0.003 0.002 0.001 0.001 
2 0.005 0.006 0.007 0.006 0.007 0.003 0.002 0.001 0.001 0.001 
3 0.004 0.005 0.005 0.005 0.005 0.003 0.002 0.001 0.001 0.001 
4 0.004 0.005 0.005 0.005 0.005 0.003 0.002 0.001 0.001 0.001 
5 0.003 0.003 0.003 0.003 0.003 0.002 0.001 0.031 0.000 0.000 
6 0.002 0.003 0.003 0.003 0.003 0.001 0.001 0.000 0.000 0.000 
7 0.002 0.002 0.002 0.002 0.002 0.0033 0.000 0.000 0.000 0.000 
8 0.001 0.001 0.001 0.001 0.001 0.001 0.000 0.000 0.000 0.000 
9 0.001 0.001 0.001 0.001 0.001 0.001 0.007 0.000 0.000 0.000 
           

K. K. JOSE ET AL. 1169
1
0. Conclusions
In this paper we analyze DAR(1)/D/s queue with Quasi-
Negative Binomial Distribution-II as the marginal distri-
bution. Based on the matrix analytic methods and by
using the theory of Markov regenerative processes, we
obtained the stationary distributions of the system size
and the waiting time of an arbitrary packet. From the
definition of autocorrelation function we can say that the
larger the parameter β, the slower the decay of the
autocorrelation of the input process. So it is expected that
stationary system size and waiting time for the case of
large β are stochastically larger than those for the case of
small β. Also the stationary system size and waiting time
increases when the input parameter decreases.
1
p
11. References
[1] P. A. Jacobs and P. A.W. Lewis, “Discrete Time Series
generated by Mixtures III: Autoregressive Processes
(DAR(p)),” Naval Postgraduate School, Monterey, 1978.
[2] A. Elwalid, D. Heyman, T. V. Laksman, D. Mitra and A.
Weiss, “Fundamental Bounds and Approximations for
ATM Multiplexers with Applications to Video Telecon-
ferencing,” IEEE Journal of Selected Areas in Commu-
nications, Vol. 13, No. 6, 1995, pp. 1004-1016.
doi:10.1109/49.400656
[3] F. Kamoun and M. M. Ali, “A New Theortical Approach
for the Transient and Steady—State Analysis of Multis-
erver ATM Multiplexers with Correlated Arrivals,” 1995
IEEE International Conference on Communications, Vol.
2, 1995, pp. 1127-1131. doi:10.1109/ICC.1995.524276
[4] G. U. Hwang and K. Sohraby, “On the Exact Analysis of
a Discrete Time Queueing System with Autoregressive
Inputs,” Queueing Systems, Vol. 43, No. 1-2, 2003, pp.
29-41. doi:10.1023/A:1021848330183
[5] G. U. Hwang, B. D. Choi and J. K. Kim, “The Waiting
Time Analysis of a Discrete Time Queue with Arrivals as
an Autoregressive Process of Order 1,” Journal of Ap-
plied Probability, Vol. 39, No. 3, 2003, pp. 619-629.
[6] B. D. Choi, B. Kim, G. U. Hwang and J. K. Kim, “The
Analysis of a Multiserver Queue Fed by a Discrete Auto-
regressissive Process of Order 1,” Operations Research
Letters, Vol. 32, No. 1, 2004, pp. 85-93.
doi:10.1016/S0167-6377(03)00068-3
[7] J. Kim, B. Kim and K. Sohraby, “Mean Queue Size in a
Queue with Discrete Autoregressive Arrivals of Order p,”
Annals of Operations Research, Vol. 162, No. 1, 2008, pp.
69-68. doi:10.1007/s10479-008-0318-1
[8] M. F. Neuts, “Structured Stochastic Matrices of the
M/G/1 Type and Their Applications,” Dekker, New York.
1989.
[9] K. G. Janardhan, “Markov-Polya urn Model with Pre-
Determined Strategies,” Gujarat Statistical Review, Vol.
2, No. 1, 1975, pp. 17-32.
[10] K. Sen and R. Jain “Generalized Markov-Polya urn
Model Withpre-Determined Strategies,” Journal of Sta-
tistical Planning and Inference, Vol. 54, 1996, pp. 119-
133. doi:10.1016/0378-3758(95)00161-1
[11] G. C. Jain and P. C. Consul, “A Generalized Negative Bi-
nomial Distribution,” Society for Industrial Mathematics,
Vol. 21, No. 4, 1971, pp. 501-513. doi:10.1137/0121056
[12] S. B. Ahmad, A. Hassan and M. J. Iqbal, “On a Quasi
Negative Binomial Distribution–II and Its Applications,”
Preprint, 2010.
[13] A. H. Frank and A. B. Melvin, “The Borel-Tannerdistri-
bution,” Biometrica, Vol. 47, No. 1-2, 1960, pp. 143-150.
[14] G. Latouche and V. Ramaswamy, “Introduction to Matrix
Analytical Method in Stochastic Modelling,” Society for
Industrial Mathematics, Pennsylvania, 1991.
[15] L. Breuer and D. Baum “An Introduction to Queueing
Theory and Matrix Analytic Method,” Springer, Berlin,
2004.
[16] V. G. Kulkarni “Modelling and Analysis of Stochastic
Systems,” Chapman & Hall, London, 1995.
[17] Customer Check Out. xlsx
http://www.westminstercollege.edu