Journal of Geographic Information System
Vol.6 No.4(2014), Article
ID:48681,13
pages
DOI:10.4236/jgis.2014.64031
Mapping Potential Infiltration Patterns Using Digital Elevation Model
Haris Hasan Khan1, Arina Khan2, P. D. Sreedevi3, Shakeel Ahmed3
1Department of Earth Sciences, Pondicherry University, Pondicherry, India
2Hydrogeology Lab, Department of Geology, Aligarh Muslim University, Aligarh, India
3Indo-French Centre for Groundwater Research (IFCGR), Groundwater Division, National Geophysical Research Institute (NGRI), Hyderabad, India
Email: hhkhan2005@gmail.com, arinakhan10@gmail.com, sreedevipagadaladamodaram@gmail.com, shakeel.ngri@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

![]()

Received 3 June 2014; revised 30 June 2014; accepted 25 July 2014
ABSTRACT
This study attempts to simulate the spatial heterogeneity of infiltration in a drainage basin using digital elevation models. Infiltration capacity is one of the controlling factors in the formation of stream channels. Channel formation is also a function of the slope and the contributing area. Natural stream channels, if properly graded and adjusted to the present climate, reflect the interactions of local slope, contributing area, and permeability of surface materials. Channel networks can be delineated from a Digital Elevation Model (DEM) using a variety of algorithms using different thresholds for channel initiation. These algorithms delineate a channel network on the basis of local slope, curvature, and contributing area, without considering the permeability of surface cover. Hence, the difference in the structure of the two drainage networks, i.e. the surveyed drainage network obtained from field observation and the simulated network generated from the DEM, is indicative of the spatial heterogeneities in the permeability of the surface cover as shown in this paper. Spatially variable drainage density maps corresponding to the two networks have been used here to obtain normalized difference maps that characterize the potential infiltration anomalies within the catchment. The simulated spatial pattern is compared with the actual infiltration measurements in the field using infiltration tests. Strong positive correlation between the observed and modeled infiltration confirms the effectiveness of this technique in the rapid assessment of potential infiltration variability.
Keywords:DEM, Permeability, Infiltration Capacity, Drainage Density, Autocorrelation

1. Introduction
Infiltration is defined as the passage of water through the soil surface into the ground. Once the water is in the soil, its further downward movement is defined as percolation. The role of infiltration in the hydrologic cycle was first recognized by [1] . The spatial variability of infiltration in catchments is highly complex and is a result of the interplay of a host of factors. Infiltration rates are affected by soil type, soil textures, soil hydraulic properties, antecedent soil moisture, vegetation, animal activity, climate, etc.
As compared to humid areas, arid and semi-arid areas have more complex infiltration and runoff formation characteristics. Spatial distribution of soil moisture is the key factor determining infiltration patterns in humid areas. In arid and semi-arid areas factors such as extent of bedrock outcrops versus extent of soil cover, slope areas, and differences in the compaction of the constituent material between channel and interfluve areas appear to control the spatial patterns of infiltration and runoff generation [2] .
In semi arid regions, the spatial patterns of infiltration are governed by geomorphology and vegetation pattern [3] . Field studies in arid regions have also shown that the spatial variability of infiltration is related to the geomorphic setting as distinguished by interdrainage area, topographic depression, and drainage area [4] . Infiltration cannot be characterized by soil texture alone and the role of animal activity, vegetation and climate in characterizing the spatial variability of infiltration must be considered [5] . The primary influence on infiltration rates is the land-use, specifically, the ability of the vegetation to produce a deep litter layer [6] . The angle of slope is of less, although significant, importance.
Spatial patterns of the infiltration capacity are crucial for the determination of runoff generating areas especially in semi-arid regions where infiltration excess runoff development (Hortonian flow) is a dominant process [1] . These patterns are also indicative of the potential groundwater recharge zones if several other factors such as lateral redistributions through interflow, evapotranspiration etc. are included. Assessment of a lumped infiltration value for the whole catchment as a unit is generally made by rainfall-runoff differences, but this does not quantify the spatial variability within the catchment. Assessment of spatial variability of infiltration is usually made by in-situ point measurements at selected locations in a catchment. This is a time consuming task since a dense network of observations points is needed to reproduce patterns close to the true variability, especially if the catchment is large.
This paper attempts to assess the infiltration pattern within a catchment using a novel approach. The idea is to use the differences in the drainage density patterns obtained from surveyed and simulated drainage networks. These differences can quantify the potential infiltration variability as shown here. In fact, the proposed approach to assess the infiltration variability is a reverse method, i.e. instead of investigating and integrating the effects of individual factors affecting infiltration capacity and simulating the final infiltration pattern, e.g. [7] , we begin with the end product of infiltration variability—the drainage network, an entity that reflects the interaction between infiltration and runoff process acting over long periods of time.
2. DEM Based Terrain Modeling
Digital Elevation Model is a representation of the terrain elevation as a function of geographic location. The elevation in a DEM is generally sampled on either regular or irregular basis. Elevation data stored in the form of a matrix (gridded DEMs) is the most popular format of elevation data, due to easy storage and processing in the digital form. The elevation data sampled irregularly represents the other DEM type known as TIN-DEM (Triangular Irregular network). The choice of DEM format is dependent on the application and on the availability of data. Most of the widely available DEMs are of the gridded type. The simplicity of the regular grid DEM leads to convenient programming; the topology is implicit, with no need to store the x, y coordinates; and the spatial symmetry allows minimal search time for any application. However, gridded DEMs suffer from data redundancy in flat terrain. Terrain is usually under sampled in highly dissected regions and over sampled in flat regions, and a balance must be found between the sampling intervals [8] . This problem can be effectively addressed by TINs, where data point density is higher in regions of rough terrain and lower in regions of flat topography, thereby optimizing the data storage. However, there exist far more algorithms for the gridded DEMs than the TINs. The grid cell size or the DEM resolution is an important factor that controls the results of the hydrological processing. A finer grid size will be accompanied by longer processing time requirements while a coarser grid size will lead to poor accuracy.
DEMs contain sinks or depressions that are pixels or groups of pixels that have no surrounding pixels at a lower elevation. Sinks may represent a genuine terrain feature, but most of the time, sinks are artifacts of DEM generation or resampling. Sinks generally appear in flatter areas where the mean elevation error exceeds the elevation difference between neighboring points, while on steeper slopes a higher variation would be required. The removal of depressions is a prerequisite for the successful delineation of channel network and watershed boundary. Several methods have been developed for removing depressions from DEMs. These methods vary greatly in terms of their sophistication and impact on the DEM. The two most common depression-removal methods are sink filling and sink breaching. Sink filling raises cells within a depression to the elevation of the outlet cell (i.e. the lowest cell on the depression’s catchment). Sink breaching digs a trench from a depression’s bottom to some point downslope.
Several primary terrain attributes derived from a DEM are an essential prerequisite for the construction of channel networks. These include the slope, curvature, and flow net determination. Slope is generally computed from the drop in elevation between a pixel and the lowest among its eight nearest neighbors. This maximum drop, identified from the steepest descent direction, is divided by either the grid size, dx (if the orientation occurs along the grid coordinate directions), or by (dx)1/2 if the orientation is diagonal).
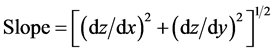 (1)
(1)
There are many different ways in which slope can be calculated from gridded DEMs. Generally, the determination is based on neighborhood operations where calculations are made for a cell based on the values of the cells that are spatially adjacent in the grid. Some methods are better than others in representing the actual slope and aspect of the terrain, while others are more suited to hydrological analysis [8] .
Flow net determination is the process of routing flow through the DEM pixels. Each pixel needs to be assigned a direction where it can divert its flow. Broadly, the flow routing algorithms are classified as single flow direction (SFD) and multiple flow direction (MFD). SFD algorithms work best for zones of convergent flow and along well-defined valleys, while the use of MFD algorithms seems more appropriate for overland flow analysis on hillslopes. Five most commonly used flow routing algorithms are: D8 [9] , Rho8 [10] , FD8 [11] , DEMON [12] [13] , and D∞ [14] .
3. Study Area
The work was carried out in the Maheshwaram catchment (figure 1), situated about 35 km south of Hyderabad metropolis in India. The catchment is the pilot area for extensive research by the Indo-French Centre for Groundwater Research at NGRI, Hyderabad. The catchment, with an outlet in the North-East, has an area of 53 km2 and extends from longitude 78˚24'30''E to 78˚29'00''E and latitude 17˚06'20''N to 17˚11'00''N.
The catchment dips gently from south to north with a topographic relief of 90 meters ranging from 590 m in the North-East to 680 meters above mean sea level in the South-West. The average slope is about 1.79 degrees. The topography is undulating with sub-dendritic type of drainage, marked by a number of gullies draining into local streamlets with eroded banks. Flat areas are seen to occur in the lower reaches that are irrigated by tanks and wells. All the streams drain into the Mankal tank which ultimately drains into the river Musi. The area is characterized by hot and dry summers and cool and dry winters with a distinct rainy season from June to September. The temperature ranges from 22˚C to 44˚C. The region receives more than 80% of its rainfall from the South West Monsoon.
Geologically, the catchment forms a part of the Hyderabad Granite Region, having a relatively homogeneous geology composed of Achaean granites (figure 2). The primary units are biotite-granite with porphyritic K-feldspar and intrusive leucocratic granite characterized by a lower biotitic content, fine grain size, with occasional porphyritic K-feldspar, characteristically weathered to form little hills with outcrops of boulders [15] . The granites are intruded by quartz veins (Archean age) and meter-wide dolerite dykes of several generations. Some basic enclaves, aplite, pegmatite, and epidote dikes are also present. These granites are also characterized by profuse jointing with abundant horizontal and sub-horizontal fractures [16] .
4. Theory
The phenomenon of infiltration shows spatial variations at different scales [17] . Infiltration varies at the hillslope or plot scale and the catchment or regional scale. The variations at hillslope scale are extremely com-

Figure 1. Study area.
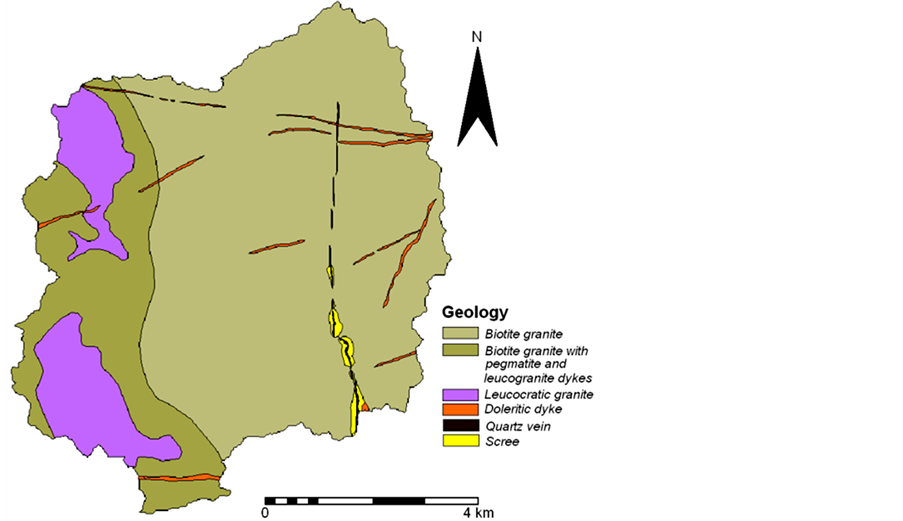
Figure 2. Geology of the study area.
plex and require extensive data and modeling for any generalization to be made. At the hillslope scale, the variations may be attributed mainly to the presence of macropores—hollow tubes formed by the decomposition of plant roots, and the burrowing activity of soil fauna [18] . To some extent, these variations also reflect the patterns of hillslope orientation with respect to the sun [19] . At the catchment scale, however, the spatial variations are usually a response of the underlying lithological and structural patterns, geomorphology, slope, vegetation patterns etc. It is the latter of the two scales that is aimed to be modeled here using elevation data. Conventionally, the spatial patterns of infiltration and potential groundwater recharge zonation at catchment or regional scales are based on the assimilation of various controlling factors in the form of thematic maps. For a review of the work done in this direction, refer to the detailed review by [20] . Such approaches employing the multi-criteria GIS overlay analysis techniques are very effective tools, but the acquisition of accurate lithological, structural, and soil data makes the process a relatively time consuming affair, especially if the final pattern is intended to be employed as a component of a bigger scheme of surface or groundwater modeling study.
An alternative approach is to track the problem in a reverse manner. Instead of acquiring datasets for geomorphology, lithology, structure, soil texture & structure, and vegetation patterns to model the surface permeability, digital elevation model is used to generate a spatial pattern that reflects the integrated effect of the above mentioned factors, to some extent.
Natural stream patterns evolve in response to the cumulative effects of the upslope catchment area, topographic slope [21] , and the permeability of the surface materials [22] . Sites on a landscape draining large upslope or runoff contributing area are prone to high flux of water during rainfall events. If such sites have steep slopes, the mass of flowing water tends to gain additional momentum for eroding the surface. Moreover, if the surface material at that site is less permeable (to soak the water down) the surface runoff may further increase and the chance of surface erosion increases consequently. Stream channel patterns can be mapped in the field or extracted from digital elevation models. Both the sources are ubiquitous. The permeability of surface materials is governed by the geomorphological, lithological, structural, soil, and vegetation patterns in a catchment. However, these factors are also influenced by (e.g. geomorphology, soil, vegetation) or dictate (e.g. lithology, structure) the topography of a region. This implies that the permeability of the surface materials can be exclusively modeled using detailed topographic information as shown in this paper. DEMs provide reasonably good information on the upslope catchment area and local slope within a catchment. The stream channel pattern extracted from a digital elevation model is exclusively controlled by topography and its derivatives (slope, contributing area, curvature etc.). Thus, the drainage network generated form a digital elevation model ignores the variability in the network that would be introduced by spatially varying parameters like surface permeability within a catchment. In reality, however, the channel pattern of the catchment in question is often considerably different. This difference is introduced by the spatial variations of surface permeability. This disparity can be readily utilized to simulate the spatial variability of permeability of the surface. The differences between the two networks can be explained by the spatial variations in geomorphology, lithology, structure, soils, and vegetation patterns. A somewhat similar investigation was made by [23] , where comparison of simulated and surveyed drainage networks was done by applying a simple test of significance for deviation from randomness, using the standard error of the expected difference.
This technique is especially aimed at the rapid assessment of potential infiltration patterns at catchment scales for use as input to various rainfall-runoff and groundwater recharge models.
5. Methodology
5.1. DEM Generation
Survey of India (SOI) topographic map number 56 K/8 at a scale of 1:50,000 was used for the preparation of drainage network maps. The topographic map was geo-referenced to generate a spatial database of drainage lines, contour lines, & spot heights. Field checks using a Trimble differential GPS unit were undertaken to verify the lateral and vertical accuracy of the spatial database. The database was then used for the generation of an elevation model using the open source GIS-SAGA (System for Automated Geo-scientific Analysis) [24] . Kriging technique [25] was employed for the interpolation of elevation points that were derived from contour lines and spot heights. Although Kriging is a time consuming process if the number of data points is more, yet it is employed here because of the ease of superimposing spatial patterns from additional data sources. Stream burning was performed for making the DEM hydraulically connected. The use of a contour interpolated DEM poses the problem of low information content in flat areas. This was overcome by using SRTM (Shuttle Radar Topography Mission) DEM of the study area as an external drift [26] to generate the final digital elevation model for the region. SRTM is a near-global elevation dataset available free of cost at 90 meters spatial resolution [27] . Although the free SRTM DEM contains more information as compared to the DEM interpolated from the 1:50,000 topographic map [28] , it was not directly used for the extraction of channel network rather it was used as an external drift. This was done to overcome the problems arising out of the mismatch between drainage lines derived from the SRTM DEM and the channel network on the topographic map. The advantage of this approach over simply interpolating the data without auxiliary information is that it extracts the small-scale patterns from the auxiliary data in addition to using the large-scale, smoothly varying component from the original data, while a simple interpolation will neglect the small-scale variability.
5.2. Drainage Extraction
In order to extract the channel network from the DEM, the channelization status of each pixel has to be assessed first. This, in turn, is dependant upon the issue of channel initiation. Several criteria have been proposed for the extraction of channel network, employing threshold support area values e.g. [29] [30] , threshold slope-area values e.g. [21] [31] -[37] or critical curvature values [38] . In the present work, a slope area product has been used as threshold criteria. This approach involves identifying channelized sites using a threshold index “i” generated by the product of upslope catchment area and the local slope. The form of the index is as follows:
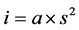 (2)
(2)
where, “i” is the threshold index; “a” is the upslope catchment area; and “s” is the local slope.
The value of threshold for the channel initiation has been chosen objectively using the constant drop property of channel networks [39] . The constant drop property is an empirical geomorphological attribute of properly graded drainage networks that has a physical basis in terms of geomorphological laws governing drainage network evolution [40] . By using the smallest weighted support area that produces networks consistent with this property we are extracting the highest resolution drainage network statistically consistent with geomorphological laws.
Although the simulated drainage extracted from DEM is in complete agreement with geomorphological laws, the drainage network map is a dataset designed for visual inspection, and, as such, it is not well suited for analyzing the spatial variability of surface permeability. In order to perform such an analysis we transformed the drainage network map into a continuous raster map of drainage density.
5.3. Drainage Density Mapping
Drainage density is a fundamental property of natural terrain and is defined as the degree to which a landscape is dissected by stream channels. [1] [22] originally defined drainage density “D” for a catchment as the total length of streams LT in the catchment divided by the total area of the catchment “A”.
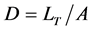 (3)
(3)
According to this definition, drainage density of a catchment is a parameter with a single value and it does not quantify the fluvial dissection pattern of a landscape. However, we are interested in mapping the spatial variability of drainage density within our area of interest. Hence we used the concept of [41] where a drainage density value is defined for every point on a landscape. This concept is based on the close relationship of drainage density to the mean distance one has to walk from a random location before encountering a channel, that is, 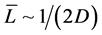 [1] . Thus every point (x, y) on the catchment is assigned a drainage density value D(x, y) based on its downslope or overland flow distance to the nearest stream channel as follows:
[1] . Thus every point (x, y) on the catchment is assigned a drainage density value D(x, y) based on its downslope or overland flow distance to the nearest stream channel as follows:
 (4)
(4)
where L(x, y) is the overland flow distance of the point (x, y) to the nearest channel Using the above criteria, overland flow distance maps were created using the surveyed and the simulated drainage network maps. The overland flow distance (L) for each site was then computed by tracing the downslope path from each unchanneled site/pixel to the first occurrence of a channelized site, and recording the total path length at each site.
6. Field Infiltration Tests@NolistTemp# Infiltration measurements using double ring infiltrometer were carried out in the Maheshwaram catchment at 34 sites (figure 1). Most of the measurements were made over undisturbed parts of the landscape in order to obtain the natural infiltration variability that would have affected the development of channel pattern in the catchment. These mostly undisturbed patches of the landscape are represented by the scrubland within the catchment. A double ring infiltrometer with a diameter of 0.6 m for the outer ring and 0.3 m for the inner ring placed one inside the other was pierced into the soil down to the depth of 5 cm. The rings were driven without tilt or undue disturbance of the soil column and with constant annular space between the rings in all directions. The water column height in inner and outer ring was maintained at 5 cm throughout the duration of the experiment. Infiltration in the inner ring was recorded using a stop watch at 1 minute interval for the first 5 minutes; every 2 minute from 5 to 12 minutes; every 5 minute from 15 to 30 minutes, every 10 minute from 30 to 60 minutes, then every 20 minute from 60 to 80 minutes. All infiltration tests were conducted for duration of at least 60 minutes except those sites where there was no infiltration at all. The infiltration test was conducted till stabilized infiltration rate was achieved.7. Interpolation of Point Infiltration Data
The point infiltration data obtained by the field infiltration tests was regionalized over the extent of the entire catchment (figure 6(a)) by ordinary kriging approach using variogram fitting. The infiltration data was first used for the generation of an experimental variogram to assess the length scale required for estimation at unknown points. The variogram models the spatial dependence of the point observations with each other, providing a range (distance) that is used to interpolate the data in accordance with the observed natural variability of the data.
8. Results & Discussions
The infiltration rates (table 1) calculated at the 34 sites show a large range of values ranging from almost no infiltration to around 348 mm/h. The infiltration values can be clustered into four distinct ranges, i.e. high, medium, low, and very low. The high and medium rates of infiltration are predominantly occurring in the eastern and northern part of the catchment probably reflecting the higher permeability of surface due to the presence of lineaments like quartz veins and dolerite dykes and subsequently induced jointing in the granites. The lowest infiltration values appear to be concentrated in the south western part of the catchment where the absence of veins and dykes and subsequently low density of jointing is quite distinct.
The overland flow distance map for the two channel networks, i.e., surveyed and simulated, along with the respective channel network, is shown in figure 3. The brown tones represent higher overland flow distance values to the nearest channel since they are farthest from any channel segment. Green tones represent low overland flow distance values and these sites are in proximity to the channel segments. It is evident from the maps that the surveyed drainage network and the corresponding overland flow distance map possess a big zone of high overland flow distance in the eastern part of the catchment. However, the pattern of simulated channel network and the corresponding overland flow distance map reveals no such pattern. The runoff contributing area and local slope conditions are favorable for channelization in the eastern part of the catchment, as depicted by the presence of a number of channel segments in the DEM derived channel network. But, in reality, channels are absent in this zone. This is clearly indicative of a permeability anomaly in this zone of the catchment. This anomaly can be partly explained in terms of the geological features and weathering profile in this zone. A number of dolerite dikes and quartz veins traverse this zone (figure 2). The quartz veins and dolerite dykes are positive topographic features in this catchment, and due to their permeable influence in the headwater zones, they tend to retard the process of channel initiation. During the emplacement of dikes and veins, the ambient granitic rocks are fractured at the contacts due to thermal expansion and subsequent contraction as the dikes and veins undergo gradual cooling. Therefore, the contact zones are more jointed and deeply weathered as compared to the surrounding area. Thus, the presence of profuse dykes and veins has increased the degree of jointing and fracturing in the granites of this part of the catchment. Moreover, the quartz veins undergo weathering to produce a very coarse grained soil in this region. The scree deposits that develop on and around the quartz veins are highly permeable types of surface cover, which facilitate the infiltration of major part of the runoff leading to the local absence of surface drainage.
The two overland flow distance maps exhibit a sharp crested pattern due to the fact that two points on either side of a ridge can have a large difference in the overland flow distance to the nearest channel. However, infiltration or surface permeability patterns do not show such abrupt transitions. Hence, there is a need to filter the

Figure 3. Map of overland flow distance derived from surveyed (a) & simulated drainage networks (b).
hillslope scale variability in the overland flow distance maps, before their normalized difference is calculated. Filtering the hillslope scale variability demands the smoothening of overland flow distance grids using a circular moving window of a radius of specified distance. The determination of the specific radius is dependent on the natural length scale associated with the autocorrelation of terrain under study [41] .
At the scale of an individual hillslope, L, the overland flow distance to channel network, is strongly autocorrelated. At larger scales, this correlation breaks down. L becomes essentially independent (uncorrelated) beyond a certain length scale [41] . This natural length scale is chosen as the radius of the circular moving window for the spatial filtering of overland flow distance maps. This results in a map of drainage texture at a scale that lies between two extremes, i.e., the purely local field (L) on one end, and the regional average or lumped drainage density on the other end. The natural length scale up to which the terrain shows autocorrelation is estimated by constructing variogram of the two overland flow distance maps. The variogram (figure 4) represents the variation (on the Y-axis) in the overland flow distance value as a function of lag distance (on the X-axis). At shorter

Figure 4. Autocorrelation of the surveyed (left) and simulated (right) maps of overland flow distance.
lags, L shows correlation with itself, after a certain threshold lag distance, the variogram stabilizes. This critical lag distance is the natural length scale upto which the overland flow distances is autocorrelated in this catchment. In this study area the length scales for the overland flow distance maps derived from field mapped or surveyed channel network and the DEM derived channel network were found to be 600 & 500 meters respectively (see figure 4). These were used to spatially filter the two overland flow distance maps and the resultant maps were treated using equation (3) to convert the overland flow distance values to drainage density values. The drainage density maps (figure 5) obtained using the above technique possess spatial variability at a scale that is comparable to the scale of geological features in the area.
In order to map the surface permeability anomalies in the catchment, the difference of the two drainage density maps is needed. To highlight the differences, a normalized difference map (figure 6(b)) was generated by dividing the arithmetic difference of the two maps with the arithmetic sum of the two maps. The normalized difference map displays the potential permeability anomalies in the catchment. In essence, this map highlights the zones that have suitable conditions of slope and upslope catchment area for runoff accumulation, but high surface permeability does not permit the generation of enough runoff to erode gullies and channels. Theoretically, the zones of high permeability anomalies are representative of permeable surface cover and these zones should also yield high field infiltration values. When compared with the pattern of infiltration obtained by the interpolation of point infiltration measurements, the normalized difference map shows a broadly similar pattern (figure 6). However, it is apparent that the normalized difference map representing the permeability anomaly possesses a greater small-scale variability as compared to the interpolated infiltration map.
A visual comparison of the two maps (interpolated infiltration map and the normalized difference map) shows broad similarity; however, visual map comparison is always subjective and often intuitive, so that the outcome of a visual map comparison may depend on the person performing the comparison. An objective measure of map similarity or dissimilarity is, thus, required for comparison of the maps. The use of a scatter-plot for this comparison seems awkward due to the large differences in the values at a few points, although the majority of points lie along a straight line. To overcome this problem, a fuzzy set comparison method has been used, that simulates the human judgment very closely. This technique yields an overall figure for similarity, the Fuzzy Kappa statistic, which is a numerical value aggregated from the detailed spatial results of fuzzy comparison between the two maps. The Fuzzy Kappa or Kfuzzy in short, is the expected percentage of agreement between two maps corrected for the fraction of agreement statistically expected from randomly relocating all cells in both maps. For this kind of comparison, a free tool “Map Comparison Kit” [42] was used.
A fuzzy kappa value of 0.7 has been obtained for the two maps. The high value of the Fuzzy Kappa confirms

Figure 5. Maps of drainage density derived from the spatial filtering of the overland flow distance maps. DD from surveyed channel network (left) and simulated channel network (right).
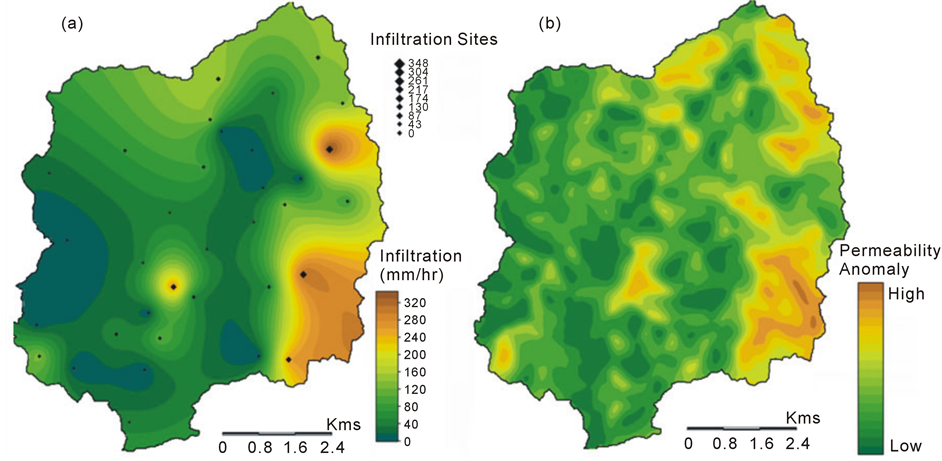
Figure 6. Map of infiltration capacity interpolated from point data (a); Normalized difference map representing the permeability anomaly in the catchment (b).
a strong similarity between the two maps indicating the usefulness of the drainage density anomalies in characterizing the spatial variability of infiltration. The detailed spatial variability of the permeability anomaly in the normalized difference map can be superimposed (using the external drift kriging technique) on the infiltration map to make the infiltration pattern richer and allow for better estimation of infiltration values at the unobserved sites. However, the variability introduced by the permeability anomaly map is only meaningful if it is able to predict the infiltration values with reasonable accuracy at unobserved sites. In order to perform such a validation, the infiltration value at each observation point was estimated. The estimation was done using simple kriging as well as kriging with external drift, permeability anomaly pattern being the external drift in this case. In this manner, each observation point has two estimated and one observed value of infiltration (figure 7).
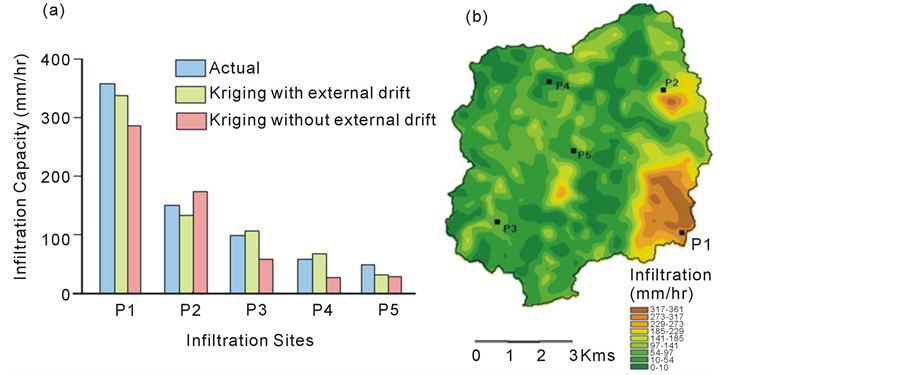
Figure 7. (a) Comparison of the actual field infiltration value, the value predicted by simple kriging interpolation, and the value predicted by using the permeability anomaly map as an external drift in kriging interpolation; (b) Map of spatial variability of infiltration obtained using the permeability anomaly map as an external drift in Kriging interpolation.
It is evident from figure 7 that the prediction of infiltration value at unobserved points is more reliable when the permeability anomaly pattern obtained from the present methodology is employed as an external drift or ancillary information source for kriging interpolation of the field infiltration data.
9. Conclusion and Recommendations
This study has demonstrated the links between drainage and infiltration patterns in a hard rock catchment. Results indicate that infiltration and drainage patterns are somewhat complementary to each other, as they evolve in response to the same set of conditions. An efficient method for the assessment of spatially variable infiltration is proposed using digital elevation data, which is best suited for use at catchment/regional scales in arid/semiarid hard rock terrain. In small first order catchments used for extensive hydrological research, acquiring infiltration patterns using high density of observations is quite meaningful, but at catchment scale and above, and for operational use, this may prove a costly and time consuming affair. For surface and groundwater modeling in large catchments, potential infiltration patterns can be quickly estimated using the present technique. The only field data required in using this approach is the infiltration measurements at a few points in the catchment. The point infiltration data can be interpolated by the kriging approach using the DEM based infiltration pattern as an external drift. The advantage of this approach over simply interpolating the point infiltration data without auxiliary (DEM based infiltration pattern) information is that it extracts the small-scale patterns from the auxiliary data in addition to using the large-scale, smoothly varying component from the original infiltration data, while a simple interpolation will neglect the small-scale variability. Thus, this approach is intended to be used in conjunction with some infiltration measurements. The technique is not intended to replace in situ measurements; rather it intends to reduce the number of infiltration measurements that have to be made to faithfully reproduce the spatial variability of infiltration patterns in a catchment. The potential infiltration patterns obtained using this technique will also be very useful for a broad assessment of catchment response before the actual data collection is initiated in surface water or groundwater modeling project especially at regional scales.
References
- Horton, R.E. (1933) The Role of Infiltration in the Hydrologic Cycle. American Geophysical Union, Transactions, 14, 446-460.
- Yair, A. and Lavee, H. (1981) Application of the Concept of Partial Area Contribution to Small Arid Watersheds. In: Singh, V., Ed., Proceedings International Symposium on Rainfall-Runoff Modeling, Mississippi State University, Mississippi Water Resource Publication, Ford Collins.
- Berndtsson, R. and Larson, M. (1987) Spatial Variability of Infiltration in a Semi-Arid Environment. Journal of Hydrology, 90, 117-133. http://dx.doi.org/10.1016/0022-1694(87)90175-2
- Scanlon, B.R., Langford, R.P. and Goldsmith, R.S. (1999) Relationship between Geomorphic Settings and Unsaturated Flow in an Arid Setting. Water Resource Research, 35, 983-999. http://dx.doi.org/10.1029/98WR02769
- Loague, K. and Gander, G.A. (1990) R-5 Revisited 1. Spatial Variability of Infiltration on a Small Rangeland Catchment. Water Resources Research, 26, 957-971. http://dx.doi.org/10.1029/WR026i005p00957
- Tricker, A.S. (1981) Spatial and Temporal Patterns of Infiltration. Journal of Hydrology, 49, 261-277. http://dx.doi.org/10.1016/0022-1694(81)90217-1
- Teixeira, J., Chamine, H.I., Espinha Marques, J., Gomes, A., Carvalho, J.M., Perez Alberti, A. and Rocha, F.T. (2008) Integrated Approach of Hydrogeomorphology and GIS Mapping to the Evaluation of Groundwater Resources—An Example from the Hydro Mineral System of Caldas da Cavaca, NW Portugal. In: Global Water Resource Management, Scientific Publishers, Jodhpur, 227-249.
- Raaflaub, L.D. and Collins, M.J. (2006) The Effect of Error in Gridded Digital Elevation Models on the Estimation of Topographic Parameters. Environmental Modelling & Software, 21, 710-732. http://dx.doi.org/10.1016/j.envsoft.2005.02.003
- O’Callaghan, J.F. and Mark, D.M. (1984) The Extraction of Drainage Networks from Digital Elevation Data. Computer Vision, Graphics and Image Processing, 28, 328-344. http://dx.doi.org/10.1016/S0734-189X(84)80011-0
- Fairfield, J. and Leymarie, P. (1991) Drainage Networks from Grid Digital Elevation Models. Water Resources Research, 27, 709-717. http://dx.doi.org/10.1029/90WR02658
- Quinn, P.F., Beven, K.J., Chevallier, P. and Planchon, O. (1991) The Prediction of Hillslope Flow Paths for Distributed Hydrological Modeling Using Digital Terrain Models. Hydrological Processes, 5, 59-79. http://dx.doi.org/10.1002/hyp.3360050106
- Lea, N.L. (1992) An Aspect Driven Kinematic Routing Algorithm. In: Parsons, A.J. and Abrahams, A.D., Eds., Overland Flow: Hydraulics and Erosion Mechanics, University College London Press, London, 393-407.
- Costa-Cabral, M.C. and Burges, S.J. (1994) Digital Elevation Model Networks (DEMON): A Model of Flow over Hillslopes for Computation of Contributing and Dispersal Areas. Water Resources Research, 30, 1681-1692. http://dx.doi.org/10.1029/93WR03512
- Tarboton, D. (1997) A New Method for the Determination of Flow Directions and Upslope Areas in Grid Digital Elevation Models. Water Resources Research, 33, 309-319.
- Dewandel, B., Lachassagne, P., Wyns, R., Maréchal, J.C. and Krishnamurthy, N.S. (2006) A Generalized 3-D Geological and Hydrogeological Conceptual Model of Granite Aquifers Controlled by a Single or Multiple Weathering. Journal of Hydrology, 330, 260-284. http://dx.doi.org/10.1016/j.jhydrol.2006.03.026
- Maréchal, J.C., Wyns, R., Lachassagne, P. and Subrahmanyam, K. (2004) Vertical Anisotropy of Hydraulic Conductivity in the Fissured Layer of Hard Rock Aquifers Due to Geological Structure of Weathering Profiles. Journal of the Geological Society of India, 63, 545-550.
- Williams, J. and Bonell, M. (1988) The Influence of Scale of Measurement of the Spatial and Temporal Variability of the Philip Infiltration Parameters—An Experimental Study in an Australian Savannah Woodland. Journal of Hydrology, 104, 33-51. http://dx.doi.org/10.1016/0022-1694(88)90156-4
- Jetten, V.G., Riezebos, H.T., Hoefsloot, F. and Van Rossum, J. (1993) Spatial Variability of Infiltration and Related Properties of Tropical Soils. Earth Surface Processes and Landforms, 18, 477-488. http://dx.doi.org/10.1002/esp.3290180602
- Ried, I. (1973) The Influence of Slope Orientation upon the Soil Moisture Regime, and Its Geomorphological Significance. Journal of Hydrology, 19, 309-321. http://dx.doi.org/10.1016/0022-1694(73)90105-4
- Jha, M.K., Chowdhury, A., Chowdary, V.M. and Peiffer, S. (2007) Groundwater Management and Development by Integrated Remote Sensing and Geographic Information Systems: Prospects and Constraints. Water Resource Management, 21, 427-467. http://dx.doi.org/10.1007/s11269-006-9024-4
- Montgomery, D.R. and Dietrich, W.E. (1988) Where Do Channels Begin? Nature, 336, 232-234. http://dx.doi.org/10.1038/336232a0
- Horton, R.E. (1945) Erosional Development of Streams and Their Drainage Basins: Hydrophysical Approach to Quantitative Morphology. Geological Society of America Bulletin, 56, 275-370. http://dx.doi.org/10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2
- Saraf, A.K., Choudhury, P.R., Roy, B., Sarma, B., Vijay, S. and Choudhury, S. (2004) GIS Based Surface Hydrological Modelling in Identification of Groundwater Recharge Zones. International Journal of Remote Sensing, 25, 5759-5770. http://dx.doi.org/10.1080/0143116042000274096
- Olaya, V. (2004) A Gentle Introduction to SAGA GIS. G?ettingen University, G?ettingen.�
- Journel, A.G. and Huijbregts, C.J. (1978) Mining Geostatistics. Academic Press, London, 600 p.
- Ahmed, S. and De Marsily, G. (1987) Comparison of Geostatistical Methods for Estimating Transmissivity Using Data on Transmissivity and Specific Capacity. Water Resource Research, 23, 1717-1737. http://dx.doi.org/10.1029/WR023i009p01717
- van Zyl, J. (2001) The Shuttle Radar Topography Mission (SRTM): A Breakthrough in Remote Sensing of Topography. Acta Astronautica, 48, 559-565.
- Jarvis, A., Rubiano, J., Nelson, A., Farrow, A. and Mulligan, M. (2004) Practical Use of SRTM Data in the Tropics: Comparisons with Digital Elevation Models Generated from Cartographic Data. Centro Internacional de Agricultura Tropical (CIAT) Working Document No. 198, Cali, 32 p.
- Band, L.E. (1986) Topographic Partition of Watersheds with Digital Elevation Models. Water Resources Research, 22, 15-24. http://dx.doi.org/10.1029/WR022i001p00015
- Tarboton, D.G., Bras, R.L. and Rodrigues-Iturbe, I. (1991) On the Extraction of Channel Networks from Digital Elevation Data. Hydrological Processes, 5, 81-100. http://dx.doi.org/10.1002/hyp.3360050107
- Montgomery, D.R. and Dietrich, W.E. (1992) Channel Initiation and the Problem of Landscape Scale. Science, 255, 826-830. http://dx.doi.org/10.1126/science.255.5046.826
- Montgomery, D.R. and Foufoula-Georgiou, E. (1993) Channel Network Source Representation Using Digital Elevation Models. Water Resource Research, 29, 3925-3934. http://dx.doi.org/10.1029/93WR02463
- Moore, I.D., Burch, G.J. and MacKenzie, D.H. (1988) Topographic Effects on the Distribution of Surface Soil Water and the Location of Ephemeral Gullies. American Society of Agricultural Engineers Transactions, 31, 1098-1107. http://dx.doi.org/10.13031/2013.30829
- Moore, I.D., O’Loughlin, E.M. and Burch, G.J. (1988) A Contour-Based Topographic Model for Hydrological and Ecological Applications. Earth Surface Processes and Landforms, 13, 305-320. http://dx.doi.org/10.1002/esp.3290130404
- Dietrich, W.E., Wilson, C.J., Montgomery, D.R., McKean, J. and Bauer, R. (1992) Erosion Thresholds and Land Surface Morphology. Geology, 20, 675-679. http://dx.doi.org/10.1130/0091-7613(1992)020<0675:ETALSM>2.3.CO;2
- Dietrich, W.E. and Dunne, T. (1993) The Channel Head. In: Beven K. and Kirkby M.J., Eds., Channel Network Hydrology, Wiley, New York, 175-219.
- Prosser, I.P. and Dietrich, W.E. (1995) Field Experiments on Erosion by Overland and Their Implication for a Digital Terrain Model of Channel Initiation. Water Resource Research, 31, 2867-2876. http://dx.doi.org/10.1029/95WR02218
- Howard, A.D. (1994) A Detachment-Limited Model of Drainage Basin Evolution. Water Resource Research, 30, 2261-2285. http://dx.doi.org/10.1029/94WR00757
- Broscoe, A.J. (1959) Quantitative Analysis of Longitudinal Stream Profiles of Small Watersheds. Office of Naval Research, Project NR 389-042, Technical Report No. 18, Department of Geology, Columbia University, New York.
- Tarboton, D.G. and Ames, D.P. (2001) Advances in the Mapping of Flow Networks from Digital Elevation Data. World Water and Environmental Resources Congress, May 20-24, 2001, Orlando.
- Tucker, G.E., Catani, F., Rinaldo, A. and Bras, R.L. (2001) Statistical Analysis of Drainage Density from Digital Terrain Data. Geomorphology, 36, 187-202. http://dx.doi.org/10.1016/S0169-555X(00)00056-8
- Visser, H. and de Nijs, T. (2006) The Map Comparison Kit. Environmental Modelling & Software, 21, 346-358. http://dx.doi.org/10.1016/j.envsoft.2004.11.013


