Journal of Modern Physics
Vol.07 No.06(2016), Article ID:65063,13 pages
10.4236/jmp.2016.76053
Newton’s Gravitational Constant Big G Is Not a Constant
Ilija Barukčić
Horandstrasse, Jever, Germany

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2016; accepted 25 March 2016; published 28 March 2016
ABSTRACT
Newton’s gravitational constant Big OG, appearing in both Newton’s law of gravity and Einstein’s general relativity, is essential for our today’s understanding of gravity. Thus far, despite of the very long history of measurements of Newton’s gravitational constant Big OG, a definite value is still not in sight. Surprisingly, the results of different experiments have varied by much more than would be expected due to systematic or random errors. Why do measurements of Newton’s gravi- tational constant Big OG vary so much? The purpose of this publication is to provide a logically and mathematically self-consistent theoretical proof that Newton’s gravitational constant Big OG is not a constant.
Keywords:
Quantum Theory, Relativity Theory, Unified Field Theory, Causality

1. Introduction
Today, Isaac Newton (1642-1727) is best known for his important contribution to the formulation of the theory of gravity. Newton’s Principia from a historical point of view was published in a philosophically tumultuous and rich time. As is well known, Philosophers at Newton’s time were “studying nature” often by studying texts (i.e. such as commentaries on Aristotle and other) rather than engaging in observations or conducting experiments. Philosophers at Newton’s time often did not employ mathematical techniques at all. Newton’s Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), published in 1686, marked a radical transformation from philosophy into a mathematically governed modern physical science. According to Newton’s universal law of gravitation [1] , two object with a certain mass (Om1 and Om2) will attract each other with a certain force OF. Newton’s force of gravitational attraction OF is proportional to the product of these two masses (Om1 ´ Om2) and the inverse square of the distance (Od²) between these two masses and a constant [1] of proportionality, called Newton’s gravitational constant Big OG. Newton’s gravitational constant Big OG has been measured about a dozen times over the last centuries. In 1798, Henry Cavendish [2] and co-workers obtained a value for Newton’s constant OG as 6.67 ´ 10−11 [Newton ´ m²/kg²]. Meanwhile, measurements of Newton’s gravitational constant Big OG were conducted below the surface of the earth (in mine shafts) [3] [4] , within boreholes [5] , in the deep ocean [6] and in an Airy-type geophysical experiment conducted in a 2-km-deep hole in the Greenland ice cap [7] at depths between 213 and 1673 m et cetera. The measurements of Newton’s gravitational constant Big OG even under the most optimistic conditions consistently documented a significant deviation of Newton’s gravitational constant Big OG from predictions based on Newton’s law of gravitation. Despite the difficulties in measuring Newton’s gravitational constant Big OG, the published experimental results of Newton’s gravitational constant Big OG have varied by much more than can be justified due to systematic or random errors. A systematic study [8] of changes in Newton’s gravitational constant Big OG at different times of day and night is found in 2002a clear daily rhythm. The measured Newton’s gravitational constant Big OG oscillates over time like a sine wave. Finally, the first theoretical evidence [9] that Newton’s gravitational constant Big OG was not a constant was published in the year 2015. Newton’s gravitational constant Big OG, essential for our today’s understanding of gravity, is appearing in both Newton’s law of gravity and Einstein’s theory of general relativity. In Einstein’s theory of general relativity, developed early in the 20th century, the curvature of space-time is proportional to Newton’s gravitational constant Big OG. A proof that Newton’s gravitational constant Big OG is not a constant would have influence on the unlimited validity of Einstein’s theory of general relativity too.
2. Material and Methods
2.1. Definitions
Definition: Proof by Contradiction (Reductio ad Absurdum)
The logical background of a proof by contradiction is Aristotle’s law of non-contradiction. A rigorous proof by contradiction proof of a theorem follows the standard method of contradiction used in science and mathematics and should be convincing as much as possible. For the first, we assume that a claim/a theorem/a proposition/a statement et cetera which has to be proved, is true. One then proceeds to demonstrate that a conclusion drawn from such a claim/a theorem/a proposition/a statement et cetera leads to a contradiction. Hence, the supposed claim/theorem/proposition/statement et cetera is deemed to be false. Consequently, we are then led to conclude that it was wrong to assume the claim/the theorem/the proposition/the statement was true. Thus far, the claim/the theorem/the proposition/the statement is proved to be false.
Definition: Thought Experiments
Properly constructed (real or) thought experiments (as devices of scientific investigation) can be used for diverse reasons in a variety of areas. Thought experiments can help us to investigate some basic properties of nature even under conditions when it is too difficult or too expensive to run a real experiment. Furthermore, a thought experiment can provide some evidence against or in favor of a theory. However, a thought experiment is not a substitute for a real experiment.
Definition: Newton’s Law of Gravitation from the Standpoint of a Moving Observer O
The influence of Isaac Newton’s masterpiece Philosophiae naturalis principia mathematica on the development of modern science, physics and astronomy is still of historical importance. Isaac Newton (1642-1727) published on 5 July 1686 in his work Philosophiae Naturalis Principia Mathematica on page 198 (Prop. LXXVI. Theor. XXXVI) his well known universal law of gravitation. Newton defines the force of gravity in the following way (Figure 1):
Figure 1. Philosophiae Naturalis Principia Mathematica, Prop. LXXVI. Theor. XXXVI, page 198.
Translated from the Latin into English.
“The attractive force of every point decreases in the duplicate ratio of the distance of the body attracted ; I say, that the whole force with which one of these spheres attracts the other will be reciprocally proportional to the square of the distance of the centres.”
For the first, Newton’s key word is proportional. Newton’s statement of proportionality is the source of Newton’s gravitational constant Big OG, known to physicists as Big OG. For the second, Newton himself is of the opinion, that his law of universal gravitation is valid under conditions of inertial frames of reference. Newton’s law of universal gravitation from the standpoint of a co-moving observer O in a special relativity consistent form written as an equation states
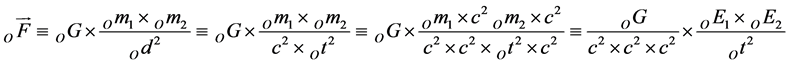 (1)
(1)
where OF is the force due to gravity between the two masses, OG is the gravitational constant as measured by a moving observer, Om1 is the mass of object 1, Om2is the mass of object 2. Thus far, Od = c ´ Ot is the distance between the centers of these two masses (Om1 and Om2) as measured by the moving observer O.
Scholium
Under conditions of inertial frames of reference invariant quantities are the same for all observers (an observerindependent quantity). In special relativity, the total force or the net force (the sum of forces acting on an object) is equal to zero. But this does not mean that there are no forces. In general, force is a vector quantity, which means force has a direction and a magnitude. Sometimes, force is denoted using boldface such as F.
Definition: Newton’s law of gravitation from the standpoint of a stationary observer
Let RF denote the force under conditions of special relativity as determined by a stationary observer R. Let Rm1 denote the “relativistic” mass as measured by a stationary observer R. Let Rm2 denote a second “relativistic” mass as measured by a stationary observer R. Let RG denote the Newtonian gravitational constant as determined by a stationary observer R. Let Rt denote the time as determined by a stationary observer R. Let c denote the speed of the light in vacuum. Let Rd = c ´Rt denote the distance between the centers of the two masses Rm1 and Rm2 as measured by the stationary observer R. Newton’s law of universal gravitation from the standpoint of a stationary observer R written as an equation states
 (2)
(2)
Scholium.
Under conditions of inertial frames of reference, we expect that a Newtonian gravitational constant which is determined by a stationary observer is equivalent with a Newtonian gravitational constant as measured by a moving observer. Especially, due to Newton’s third law, under conditions of special theory of relativity, we do expect that is OF = RF.
Definition: Rest mass Om and relativistic mass Rm
The relative motion between two inertial frames of reference, where Newton’s laws are valid, causes observers in those frames of reference to measure different values of the particle’s energy (mass) and time. Especially, the notion “relativistic mass” Rm of an object and the time is dependent on the relative velocity v of the observer and depends at the end on the observer’s frame of reference. Under circumstances where the relative velocity between two inertial frames of reference is equal to zero, observers will measures the same values for particle’s energy (mass) and time and distances too. Thus far, according to special relativity theory [10] - [12] it is
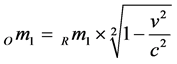 (3)
(3)
Scholium
Einstein special theory relativity defines mass at least in two different ways. The “rest mass” or “invariant mass” denoted as Om is an invariant quantity which is measured by an observer at rest relative to Om has the same value for all observers in all reference frames. The “rest mass” Om of an object is identical with the Newtonian mass as measured by an observer moving along with the object, while a rest relative to the moving object. The “relativistic mass” Rm is dependent on the velocity of the observer. The term “relativistic mass” Rm was first defined by Gilbert N. Lewis and Richard C. Tolman in 1909 [13] .
Definition: The time of a stationary observer Rt and the time of a co-moving observer Ot
Time is dependent on the observer’s reference frame. Especially, clocks moving at close to the speed of light c will slow down with respect to a stationary observer R (observer at rest). Thus far, let Rt denote the time as measured by a stationary observer, i.e. the relativistic time. Let Ot denote the time as measured by a moving observer. The relationship between the time Ot as measured by a clock moving at constant velocity v in relation to the time Rt as measured by a clock of a stationary observer is determined by Einstein’s relativistic time dilation [14] as
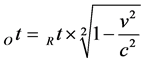 (4)
(4)
where Ot denotes time as measured by a moving observer, Rt denotes the time as measured by a stationary observer, v denotes the relative velocity and c denotes the speed of light in vacuum. Equally, it is
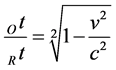 (5)
(5)
or
 (6)
(6)
Scholium
Coordinate systems can be chosen freely, deepening upon circumstances. In many coordinate systems, an event can be specified by one time coordinate and three spatial coordinates. The time as specified by the time coordinate is denoted as coordinate time. Coordinate time is distinguished from proper time. The concept of proper time, introduced by Hermann Minkowski in 1908 and denoted as Ot, incorporates Einstein’s time dilation effect. In principle, Einstein is defining time exclusively for every place where a watch measuring this time is located.
“... Definition ... der ... Zeit ... für den Ort, anwelchemsich die Uhr … befindet ...” [15] .
In general, a watch is treated as being at rest relative to the place where the same watch is located.
“Eswerdefernermittels der imruhenden System befindlichen ruhend en Uhren die Zeit t [Rt, author] des ruhenden Systems ... bestimmt, ebensowerde die Zeit τ [Ot, author] des bewegten Systems, in welchensichrelativzuletzteremruhendeUhrenbefinden, bestimmt...” [16] .
Only, the place where a watch at rest is located can move together with the watch itself. Therefore, due to Einstein, it is necessary to distinguish between clocks as such which are qualified to mark the time Rt when at rest relatively to the stationary system R, and the time Ot when at rest relatively to the moving system O.
“Wirdenkenunsfernereine der Uhren, welcherelativzumruhenden System ruhenddieZeit t [Rt, author], relativzumbewegten System ruhend die Zeit τ [Ot, author] anzugebenbefähigtsind ...” [17] .
In English:
“Further, we imagine one of the clocks which are qualified to mark the time t [Rt, author] when at rest relatively to the stationary system, and the time τ [Ot, author] when at rest relatively to the moving system….”.
In other words, we have to take into account that both observers have at least one point in common. The stationary observer R and the moving observer O are at rest, but at rest relative to what? The stationary observer R is at rest relative to a stationary co-ordinate system R, the moving observer O is at rest relative to a moving co- ordinate system O. Both co-ordinate systems can but must not be at rest relative to each other. The time Rt of the stationary system R is determined by clocks which are at rest relatively to that stationary system R. Similarly, the time Ot of the moving system O is determined by clocks which are at rest relatively to that the moving system O. What is the time marked by the clock when viewed from the stationary system? What is the time marked by the clock when viewed from the moving system? In last consequence, due to Einstein’s theory of special relativity, a moving clock (Ot) will measure a smaller elapsed time between two events than that measured by a non-moving (inertial) clock (Rt) between the same two events.
Definition: The normalized relativistic time dilation
As defined above, due to Einstein’s special relativity, it is
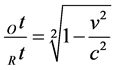 (7)
(7)
The normalized relativistic time dilation relation [18] follows as
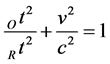 (8)
(8)
Definition: The distance Od and the distance Rd
In general, it is distance = speed ´ time. The time as such depends on the frame of reference in which it is measured or in other words a moving clock will more slowly. In general, it follows that
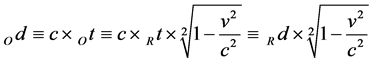 (9)
(9)
where Od denotes the distance as measured by a moving observer, Ot = Ot2 − Ot1 denotes the (period of) time as measured by a moving observer, Rd denotes the distance as measured by a stationary observer, Rt = Rt2 − Rt1 denotes the (period of) time as measured by a stationary observer, v denotes the relative velocity between the moving O and the stationary R observer and c denotes the speed of light in vacuum.
Definition: Einstein’s field equation
Newton’s theory of gravity has been superseded by Einstein’s (1879-1955) new theory of gravity but continues to be used as an approximation of the effects of gravitation. Leaving aside that Newton’s theory of gravity is under dispute, Newton’s gravitational constant is still of use and part even of Einstein’s general relativity theory [19] too. Einstein’s field equations are determined as
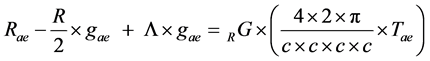 (10)
(10)
where RG denotes Newton gravitational constant. Einstein’s general relativity theory does seem to be the correct theory of gravitation at least at low energies. As can be seen, curvature of space-time is proportional to Newton’s constant of gravitation.
Definition: The relativistic Doppler effect
Redshift can be measured by determining the wavelength of a known transition, such as hydrogen a-lines for distant quasars, and finding the fractional shift compared to a stationary reference. The light from the stars or from distant galaxies has distinct spectral features i.e. due to the characteristics of the atoms in the gases around the stars. These spectra can be examined, they are found to be shifted (Doppler shift). The measured (red) shifts are usually stated in terms of a so called z parameter. The measured Doppler red shifts can be used to calculate the recession velocity v of stars or galaxies, presuming that the Hubble law is valid. We obtain
 (11)
(11)
A z value of 8.68 was measured by Zitrin et al. [20] .
2.2. Axioms: Axiom I. (Lex Identitatis).
The following theory is based on the axiom:
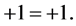 (12)
(12)
3. Results
3.1. Theorem. Newton’s Gravitational Constant Big G Is a Constant
Claim (Theorem. Proposition. Statement)
Under conditions of special relativity (inertial frames of reference) Newton’s gravitational constant is not a constant. In principle, a co-moving observer O and a stationary observer R will not agree on the value of Newton’s gravitational constant. In general, we must accept that
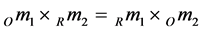 (13)
(13)
Proof.
In general, axiom I is determined as
 (14)
(14)
Multiplying this equation by the “rest mass” Om1, we obtain the mass as determined by co-moving observer as

According to Einstein’s theory of special relativity the laws of physics are the same in any inertial frame of reference. A stationary observer R will ascribe the value Rm1 to the same object. Due to special relativity we obtain

Multiplying this equation by Rm2, we obtain

Two different observers moving with constant velocity relative to each other will have a different view on the product of two masses. Due to special relativity, the equation before can be rearranged as

Quod erat demonstrandum
Scholium
Two different observers moving with constant velocity relative to each other will obtain the same value of the product of the two masses i.e. equation by
3.2. Theorem. Newton’s Gravitational Constant II
Claim (Theorem. Proposition. Statement)
Under conditions of the special theory of relativity, we must accept that

Proof
In general, it is

Multiplying this equation by the “rest mass” Om1 and by the “rest mass” Om2 we obtain

Dividing this equation by OG/Od² it is

Due to special relativity, this equation can be rearranged as

or as

In general, the equation simplifies as

Quod erat demonstrandum.
3.3. Theorem. Newton’s Gravitational Constant III
Claim (Theorem. Proposition. Statement)
Under conditions of the special theory of relativity, where the relative velocity between the mass Om1 and the mass Om2 is equal to v = 0 while moving at constant relative velocity v with respect to a stationary observer R, we must accept that

Proof
In general, it is

Multiplying this equation by Newton’s gravitational constant OG we obtain

At this point, our assumption is that Newton’s gravitational constant as determined by a stationary observer R and denoted by RG is identical with Newton’s gravitational constant OG as determined by the moving observer O. In general it is assumed, that Newton’s gravitational constant is independent of the frame of reference. Thus far, we change the equality above and do obtain

Multiplying this equation by (Om1 ´ Om2)/Od² it follows that

Due to special relativity, we rearrange this equation as

This equation simplifies as

Quod erat demonstrandum.
Scholium.
Let J denote the co-moving observer. Let L denote the stationary observer. Let denote mass 1, let denote mass 2. The relative velocity between the moving observer J and the mass and the mass is equal to v = 0. In other words, the moving observer J is at rest relative the mass and the mass . Mass and mass are moving at the same time with a constant relative velocity with respect to the stationary observer L. Table 1 may illustrate this experimental situation in more detail.
The moving observer J is at rest relative to the mass 1 denoted as and at the same time at rest relative to the mass 2 denoted as . The moving observer J ascribes to the mass the value Om1 and at the same time to the mass the value Om2. Within the frame of reference of the moving observer J, the relative velocity between the two masses is zero. At the same time, from the standpoint of the stationary observer L, both masses are moving with a certain relative and constant velocity v relative to the frame of reference of the stationary observer L. Therefore, the stationary observer L ascribes to the mass the value Rm1 and to the mass the value Rm2. Written as a mathematical formula, we obtain

Under these experimental conditions, it appears to be justified to conclude that Newton’s gravitational constant Big OG is a constant [21] .
3.4. Theorem. Newton’s Gravitational Constant IV
Claim (Theorem. Proposition. Statement)
Under conditions of special theory of relativity it is

Proof
In general, it is

Newton’s law of universal gravitation follows as

Consequently, due to Theorem 3.3, it is

or according to special relativity
Table 1. The relationship between two masses at rest from the standpoint of two observers.

This equation can be simplified as

which is equal to

Thus far, we obtain the relationship

Quod erat demonstrandum
Scholium
Let denote mass 1, let denote mass 2. Let J denote the co-moving observer. Let L denote the stationary observer. The moving observer J is at rest relative Om1. The stationary observer L is at rest relative Om2. The following 2 × 2 Table 2 may illustrate the relationships above.
Due to the constant relative velocity, which is different from zero, the moving observer J will ascribe the mass Rm2 to the mass . At the same time, the stationary observer L ascribes the mass Rm1 to the mass . This has no influence on the product of both masses. We obtain

The product of the two masses m1 and m2 as calculated by the moving observer is equivalent to the product of the two masses m1 and m2 as calculated by the stationary observer.
3.5. Theorem. Newton’s Gravitational Constant Big G Is Not a Constant
Claim (Theorem. Proposition. Statement)
Under conditions of special theory of relativity, it is
Table 2. The relationship between two masses from the standpoint of two observers.

Proof
In general, it is

Newton’s law of universal gravitation follows as

Consequently, due to Theorem 3.3, it is

or according to special relativity

This equation can be simplified as

which is equal to

Thus far, we obtain the relationship

According to the Theorem 3.2, we obtain equally

In general, it is

Rearranging this equation, it follows from the above that

We simplify this equation as

or as

In general, we obtain

Quod erat demonstrandum.
Scholium
The moving observer O and the stationary observer R will agree on the value on Newton’s gravitational constant Big G only if v = 0, otherwise not. The value of Newton’s gravitational constant Big G is reference frame dependent, Newton’s gravitational constant Big G is not a constant.
3.6. Theorem. Newton’s Gravitational Constant Big OG of a Distant Galaxy
Claim (Theorem. Proposition. Statement)
An international team of astrophysicists [20] discovered a distant galaxy, called EGSY8p7, with a spectroscopic redshift of z = 8.68 by observing its characteristic hydrogen signature. This red shift is equivalent to a recessional velocity of the distant galaxy EGSY8p7 as v = 0.9788812110358344´ c. Assuming that v is approximately identical with the relative velocity between the galaxy EGSY8p7 and our earth, Newton’s constant Big G of the distant galaxy EGSY8p7 oG can be calculated approximately as

Proof
Due to our theorem before, it is

The relative velocity of the distant galaxy is approximately v = 0.9788812110358344´ c as calculated in this paper while Newtons’s constant RG is about ~6.674 × 10-11 [N×m2/kg]. We obtain

We obtain

Quod erat demonstrandum.
4. Discussion
There is already some theoretical evidence [18] that Newton’s gravitational constant Big G is not a constant. On page 132 of the paper mentioned, there is a misprint within the Equation (12). The misprint free form of the Equation (12) of the paper mentioned is
to a achieve a correct result. Newton’s gravitational constant Big G is reference frame dependent. This can be proofed by a simple experiment. The orbital velocity of our earth with respect to the sun is different at perihelion than at aphelion. The difference in orbital velocity may be small but is big enough to make the proof whether Newton’s constant Big G is a constant or not. Newton’s constant Big G should be of the same value at perihelion and at aphelion. In contrast to expectation, the results measurements of Newton’s gravitational constant Big G performed first at perihelion and later at aphelion, or vice versa, will vary significantly and by much more than would be expected due to systematic or random errors.
5. Conclusion
Newton’s gravitational constant Big G is not a constant. Today, the constancy of Newton’s gravitational constant Big G is a constituting part of Einstein’s theory of general relativity. Consequently, it appears to be necessary to review the unrestricted validity of Einstein’s theory of general relativity [22] from the beginning.
Cite this paper
Ilija Barukčić, (2016) Newton’s Gravitational Constant Big G Is Not a Constant. Journal of Modern Physics,07,510-522. doi: 10.4236/jmp.2016.76053
References
- 1. Newton, I. (1686) Philosophiae Naturalis Principia Mathematica. Pepys, Londini, 198.
http://dx.doi.org/10.3931/e-rara-1237 - 2. Cavendish, H. (1798) Philosophical Transactions of the Royal Society of London, 88, 469-526.
http://dx.doi.org/10.1098/rstl.1798.0022 - 3. Holding, S.C. and Tuck, G. (1984) Nature, 307, 714-716.
http://dx.doi.org/10.1038/307714a0 - 4. Holding, S.C., Stacey, E.D. and Tuck, G. (1986) Physical Review D: Particles and Fields, 33, 3487-3494.
http://dx.doi.org/10.1103/PhysRevD.33.3487 - 5. Hsui, A.T. (1987) Science, 237, 881-883.
http://dx.doi.org/10.1126/science.237.4817.881 - 6. Stacey, E.D. and Tuck, G. (1981) Nature, 292, 230-232.
http://dx.doi.org/10.1038/292230a0 - 7. Ander, M.E., et al. (1989) Physical Review Letters, 62, 985-988.
http://dx.doi.org/10.1103/PhysRevLett.62.985 - 8. Gershteyn, M.L., et al. (2004) Gravitation & Cosmology, 8, 243-246.
- 9. Barukcic, I. (2015) International Journal of Applied Physics and Mathematics, 5, 126-136.
http://dx.doi.org/10.17706/ijapm.2015.5.2.126-136 - 10. Einstein, A. (1905) Annalen der Physik, 323, 639-641.
http://dx.doi.org/10.1002/andp.19053231314 - 11. Einstein, A. (1907) Annalen der Physik, 328, 384.
http://dx.doi.org/10.1002/andp.19073280713 - 12. Einstein, A. (1918) Annalen der Physik, 55, 241-242.
http://dx.doi.org/10.1002/andp.19183600402 - 13. Lewis, G.N. and Tolman, R.C. (1909) Proceedings of theAmerican Academy of Arts and Sciences, 44, 709-726.
http://dx.doi.org/10.2307/20022495 - 14. Einstein, A. (1905) Annalen der Physik, 322, 904.
- 15. Einstein, A. (1905) Annalen der Physik, 322, 893.
- 16. Einstein, A. (1905) Annalen der Physik, 322, 898.
- 17. Einstein, A. (1905) Annalen der Physik, 322, 903.
- 18. Barukcic, I. (2013) International Journal of Applied Physics and Mathematics, 3, 387-391.
http://dx.doi.org/10.7763/IJAPM.2013.V3.242 - 19. Einstein, A. (1916) Annalen der Physik, 354, 769-822.
http://dx.doi.org/10.1002/andp.19163540702 - 20. Zitrin, A., Labbé, I., Belli, S., Bouwens, R., Ellis, R.S., Roberts-Borsani, G., Stark, D.P., Oesch, P.A. and Smit, R. (2015) The Astrophysical Journal Letters, 810, Article ID: l12.
- 21. Barukcic, I. (2015) International Journal of Applied Physics and Mathematics, 5, 129-131.
http://dx.doi.org/10.17706/ijapm.2015.5.2.126-136 - 22. Barukcic, I. (2015) International Journal of Applied Physics and Mathematics, 5, 18-28.
http://dx.doi.org/10.17706/ijapm.2015.5.1.18-28




