Received 6 November 2015; accepted 27 December 2015; published 30 December 2015

ABSTRACT

With the development of fuzzy measure theory, the integral inequalities based on Sugeno integral are extensively investigated. We concern on the inequalities of Choquuet integral. The main purpose of this paper is to prove the Hölder inequality for any arbitrary fuzzy measure-based Choquet integral whenever any two of these integrated functions f, g and h are comonotone, and there are three weights. Then we prove Minkowski inequality and Lyapunov inequality for Choquet integral. Moreover, when any two of these integrated functions f₁, f₂, ∙∙∙, f_n are comonotone, we also obtain the Hölder inequality, Minkowski inequality and Lyapunov inequality hold for Choquet integral.

Keywords:

Choquet Integral, Fuzzy Measure, Comonotone, Hölder Inequality, Minkowski Inequality, Lyapunov Inequality

1. Introduction

The Choquet integral, introduced in [1] , of a nonnegative, 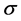-measurable function f, based on a fuzzy measure 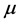on measurable set A, is defined as

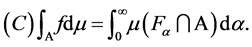
Ralescu and Adams [2] studied several equivalent definitions of fuzzy integral, while Pap [3] and Wang and Klir [4] provided an overview of fuzzy measure theory. The main properties of Choquet integral are monotonicity and positive homogeneity, see [3] [5] . Although the Choquet integral have the positive homogeneity,

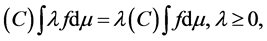
but it is generally nonlinear with respect to its integral due to the nonadditivity of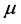. That is, we may have

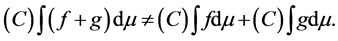
So, in some sense, the Choquet integral ia a kind of fuzzy integral. But, unlike the Sugeno integral [6] , the Choquet integral is a real generalization of the Lebesgue integral. In the special case when the monotone measure is -additive, the Choquet integral coincides with the Lebesgue integral since the definition of the Choquet integral is just an equivalent definition the Lebesgue integral. The main fields for application of the Choquet integral are engineering, soft computing, social sciences, patter recognition and decision analysis [7] [8] .

Integral inequalities are useful tools in several theoretical and applied fields. For more information on classical inequalities, we refer the reader to the distinguished monograph [9] [10] . Recently, Li and Sun [11] provided Hölder type inequalities for Sugeno integral. Some other classical inequalities have also been generalized to Sugeno integral by other authors (see, for example [12] [13] ). And Song have been proved the Berwald type inequality for extremal universal integrals based on -concave function in [14] and Song also provided fuzzy algebra in triangular norm system in [15] . Recently Li and Song [16] proved Hermite-Hadamard type inequality for Sugeno integrals based on 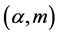-convex function. Then Li and Song [17] proved Generalization of Liyapunov type inequality for pseudo-integrals. In [18] we proved Sandor’s type inequality for fuzzy integrals based on 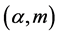-Convex function.

Section 2 consists of some preliminaries and notations about Choquet integral. In section 3, we prove the Hölder inequality for arbitrary fuzzy measure-based Choquet integral whenever any two of these integrated functions are comonotone. Then, we prove Minkowski inequalities and Lyapunov inequality for arbitrary fuzzy measure-based Choquet integral whenever any two of these integrated functions are comonotone. And including several examples. Finally, some conclusions are drawn.

2. Preliminaries

In this section we recall some basic definitions and previous results that will be used in the sequel.

As usual we denote by R the set of real numbers. Let X be a nonempty set, 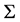be a -algebra of subsets of X, and 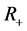denote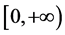. Also, let 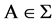and f be a nonnegative measurable function on, is a monotone measure.

Definition 1. ( [11] ) A set function is called a fuzzy measure if the following properties are satisfied:

(FM1);

(FM2) implies;

(FM3), implies

(FM4), and imply

When is a fuzzy measure, then the triple is called a fuzzy measure space.

Definition 2. ( [4] ) The Choquet integral of a nonnegative measurable function f with respect to monotone measure on measurable set A, denoted by, is defined by the formula

where for. When, is usually written as.

Since f in Definition 2 is measurable, we know that for and, therefore, so is well defined for all. Furthermore, is a class of sets that are nonincreasing with respect to and so are sets in. Since monotone measure is a nondecreasing set function, we know that is a nondecreasing function of and, therefore, the above Riemann integral makes sense. Thus, the Choquet integral of a nonnegative measurable function with respect to a monotone measure on a measurable set is well defined.

The Choquet integral has some properties of the Lebesgue integral. These properties are listed in the following theorem.

Theorem 1. ( [4] ) Let f and g be nonnegative measurable functions on. A and B be measurable sets, and a be a nonnegative real constant. Then,

1);

2);

3);

4) If on A, then;

5) If then,;

6).

Unlike the Lebesgue integral, the Choquet integral is generally nonlinear with respect to its integrand due to the nonadditivity of. That is, we may have

for some nonnegative measurable functions f and g. But when integrand f and g satisfying the properties of comonotone, then we have

(1)

This is the properties of Choquet integral of comonotone additivity. Then we give the definition of two functions comonotonicity.

Definition 3. ( [11] ) Let X be a nonempty set, two functions are said to be comonotone, if for all, then

Clearly, if f and g are comonotone, then for all nonnegative real numbers, either or. Indeed, if this assertion does not hold, then there are and. That is, and. And hence, , contradicting! Notice that constant function and any functions are comonotone, by (1) and Theorem 1 (2) we obtain,

3. Hölder Inequality for Choquet Integral

This section is devoted to providing Hölder inequality for Choquet integral, when there are three integrand and three weights. And these integrand satisfying the properties of comonotone additivity. Then we prove Hölder inequality for Choquet integral about a finite number of integrands and finite weights appears as its corollary.

In this paper, we suppose any two of these nonnegative measurable functions are comonotone, so we can easily obtained any two of f, g and h are comonotone.

Theorem 2 (Hölder inequality). Let be a fuzzy measure space, , f, g and h be nonnegative

measurable functions. When any two of f, g and h are comonotone, and,. Then, the Hölder inequality

(2)

holds.

Proof. By Theorem 3.1 [19] the Hölder inequality about two nonnegative measurable functions and two weights

(3)

holds. Let, then, When f and h are nonnegative measurable functions, then by

the product of a finite number of measurable functions still can be measurable, we have fg is nonnegative measurable function. And fg and h are comonotone for any can be easily proved. Then, the inequality

(4)

holds. Let, , then. Then the inequality

(5)

holds. Then, by the inequalities (4) and (5), we obtain

(6)

This completes the proof.

Then, let us review examples illustrating the previous result.

Example 1. Let, , , for. p = 6, q = 3 and r = 2. be

the class of all Borel sets in and for, where m is the lebesgue measure. We know the is a monotone measure on -algebra and f, g and h are nonnegative measurable functions on X, and any two of f, g and h are comonotone. According to Definition 2, the value of Choquet integral for fgh, f, g and h with respect to are

In a similar manner, we calculate that

, , and.

By the inequality

Then, we obtain

(7)

When the integrand of the integral cannot be expressed by an explicit algebraic expression of, or the expression is too complex, the value of the Choquet integral has to be approximately calculated by using some numerical method (e.g., the Simpson method).

Example 2. Let, , and,. And any two of f, g and h are comonotone, then

Then, we can calculate that

and

So by the inequality

where is defined as in Example 1. Then, we obtain

(8)

From the above two examples we can get, f, g and h be nonnegative measurable functions, when any two of f, g and h are comonotone, and,. Then, the Hölder inequality holds.

Hölder inequality for Choquet integral about a finite number of integrands and finite weights appears in the following corollary.

Corollary 1. Let be a fuzzy measure space, , and f_n be nonnegative measurable

functions. When any two of are comonotone, and, , then, the Hölder inequality for Choquet integral about a finite number of integrands and finite weights

holds.

As the application of Hölder inequality for Choquet integral, we will prove Minkowski inequality. First, we prove the following lemma.

4. Minkowski Inequality for Choquet Integral

Lemma 1. Let f, g and When any two of f, g and h are comonotone, then any two of these functions, and are comonotone, for any.

Proof. For any, we first prove and are comonotone. According to Definition 3 [11] , this is equivalent to prove that

(9)

If, then by any two of f, g and h are comonotone, we obtain,. And by nonnegativity of f, g and h and, we get

Then, the inequality (9) holds.

The case that when, the inequality (9) can be proved in a similar manner.

We have proved the inequality (9) holds, when. In a same way, we prove the inequality (9) holds, when,. And the inequality (9) obviously holds, when, and.

So, we obtain the functions and are comonotone. In a similar manner, we get the the functions and are comonotone.

As so far, we prove any two of these functions, and are comonotone.

This completes the proof.

Then the Minkowski inequality for Choquet integral is given in the following theorem.

Theorem 3 (Minkowski inequality). Let be a fuzzy measure space and, f, g and h: be measurable functions. When any two of f, g and h are comonotone, then the inequality

(10)

holds for any.

Proof. When, by any two of f, g and h are comonotone, we get

Obviously, the inequality (10) holds.

When, there exists, such that (i.e.). By the Lemma 2 and Theorem 2, we obtain

In the same method, we get

Hence,

(11)

This completes the proof.

Example 3 Let, , and, , when any two of f, g and h are comonotone. Where is defined as in Example 1. Then

In the same way,we calculate that

Then, we get

If there is a finite nonnegative measurable function, the Minkowski inequality for Choquet integral holds or not. First, we have to prove the following corollary.

Corollary 2. Let. When any two of are comonotone, then any two of

these functions are comonotone, for any.

Corollary 3. Let be a fuzzy measure space and, be measurable functions. When any two of are comonotone , then the inequality

(12)

holds, for any.

5. Lyapunov Inequality for Choquet Integral

Theorem 4 (Lyapunov inequality). Let be a fuzzy measure space and be a measurable set, be a measurable function. Let, , when satisfies this

equality,. Then the inequality

(13)

holds.

Proof. Let, , , then, for any. By Theorem 2, we have

And by, we get the inequality

(14)

Remark 1. Let be a fuzzy measure space and be a measurable set, we have

for any.

Corollary 4. Let be a fuzzy measure space, be a measurable set and be a measurable function. Let, , when satisfies

, and. Then, we have the inequality

(15)

6. Conclusion

In this paper, we prove the Hölder inequalities for any arbitrary fuzzy measure based on Choquet integral whenever any two of these integrated functions f, g and h are comonotone. As its application, we also prove Minkowski inequality and Lyapunov inequality for Choquet integral. Moreover, we also obtain whenever any two of these integrated functions are comonotone, the Hölder inequality, Minkowski inequality and Lyapunov inequality hold for Choquet integral.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 51374199).

Cite this paper

XiuliYang,XiaoqiuSong,LeileiHuang, (2015) Some General Inequalities for Choquet Integral. Applied Mathematics,06,2292-2299. doi: 10.4236/am.2015.614201

References

NOTES

^*Corresponding author.