Applied Mathematics
Vol.05 No.10(2014), Article ID:46516,8 pages
10.4236/am.2014.510137
Characterization of Self Dual Lattices in 
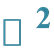 and
and 
Comlan de Souza1, David W. Kammler2
1Department of Mathematics, California State University at Fresno, Fresno, USA
2Department of Mathematics, Southern Illinois University at Carbondale, Carbondale, USA
Email: csouza@csufresno.edu, dkammler@siu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 19 March 2014; revised 19 April 2014; accepted 26 April 2014

ABSTRACT
This paper shows that the only self dual lattices in 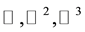 are rotations of
are rotations of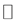 ,
,  and
and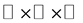 .
.
Keywords:
Self dual Lattice

1. Introduction
Let
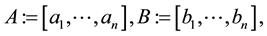
be nonsingular 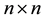 real matrices with column vectors
real matrices with column vectors 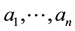 and
and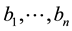 , respectively. Let
, respectively. Let
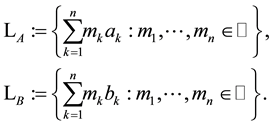
be the lattices in 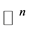 that are generated by the columns of
that are generated by the columns of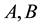 . The lattice
. The lattice 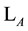 will be a subset of the lattice
will be a subset of the lattice 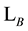 if and only if the generators
if and only if the generators 


for suitably chosen integers
i.e.,
is a matrix of integers. Analogously, the lattice 


if and only if both 
are matrices with integer elements. When this is the case, 

this implies that
Such a matrix is said to be unimodular. The above analysis (that can be found in [1] ) is summarized as follows.
Theorem 1 The lattices 
is a matrix of integers with
Corollary 1 Lattices are preserved under integer column operations.
Proof 1 Let 

be a strictly upper triangular matrix of integers. Then 
where
is a strictly upper triangular matrix of integers. The columns of
i.e.,
generate the same lattice as the columns of A. To see this we observe that
is a matrix of integers with unit determinant.
2. Dual lattices
Definition 1 Two linearly independent sets of real 


where 


and
are biorthogonal, we find
so that
This being the case, given linearly independent vectors 


The lattice 






is a matrix of integers with determinant
Suppose now that 
Let
be the generators of lattices 

we see that 




We are interested in characterizing those lattices 
This will be the case if and only if
is a matrix of integers with determinant
this will be the case only if
or equivalently
In this way we see that a lattice 



[2] [3] . Thus a lattice can be self dual only if each of its primitive cells, has unit volume.
Self dual lattices are preserved under orthogonal transformations. Indeed, let 

and let 



has columns
that generate the lattice






i.e., by
Thus the generators of the dual lattice 



so 

we see that the orthogonal transformation 

3. Main results
We will now show that the only self dual lattices in 


The case n = 1
Let 




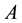


lattice 
i.e., if and only if
Thus the only self dual lattice in 
The case n = 2
Theorem 2 Every self dual lattice in 

Proof 2 Let 






where 

The lattice 







By hypothesis the lattice 

and
Since 


where

for some

for some 

Using these expressions with (1.2) we find
so
Using these expressions with (1.1) we find
and since
this implies that
It follows that 






A theorem of Minkowski [1] states that
where 


which implies that 


Another result in [4] states that if 

which leads to
The case n = 3
Theorem 3 Every self dual lattice in 

Proof 3 Let the self dual lattice 



Following the analysis from the previous section, we set
where 
with
By hypothesis the lattice 


Since the lengths of the generators of the lattice 


The columns of 


It can be verified that 
and after using 
Since 


and
for suitably chosen 


for some 

We also have


for some 
so that

Using (1.7) and (1.8)-(1.12) we find

Using (1.6) and (1.7) we see that,
which implies that
Again using (1.6) and (1.7) we see that,
which implies that
so that
Since 
or
In this way we see in turn that 


It follows that 






Suppose now that 

where
where the biorthogonal vectors 

if and only if 

Theorem 4 Let 

if and only if
for some orthonormal choice of the vectors
Analogously, we can prove the following 3-dimensional generalization.
Theorem 5 Let 

if and only if
for some orthonormal choice of the vectors
These results correspond to the familiar identity
III ˄= III
from univariate Fourier analysis. The possibility of rotations (other than reflections) in 
References
- Kannan, R. (1987) Minkowski’s Convex Body Theorem and Integer Programming. Mathematics of Operations Research, 12, 415-440.
- Strang, G. (1976) Linear Algebra and Its Applications. Academic Press, Inc., New York.
- Senechal, M. (1995) Quasicrystals and Geometry. Cambridge University Press, New York.
- Conway, J.H., Odlyzko, A.M. and Sloane, N.J.A. (1978) Extremal Self-Dual Lattices Exit Only in Dimensions 1 to 8, 12, 14, 15, 23, and 24.