Applied Mathematics
Vol.05 No.13(2014), Article ID:47688,9 pages
10.4236/am.2014.513184
Global 1 Estimation of the Cauchy Problem Solutions to the Navier-Stokes Equation
Asset Durmagambetov, Leyla Fazilova
Department Applied Mathematics and Informatics, Buketov Karaganda State University, Karaganda, Kazakhstan
Email: aset.durmagambet@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 April 2014; revised 28 May 2014; accepted 7 June 2014
ABSTRACT
The analytic properties of the scattering amplitude are discussed, and a representation of the potential is obtained using the scattering amplitude. A uniform time estimation of the Cauchy problem solution for the Navier-Stokes equations is provided. The paper also describes the time blowup of classical solutions for the Navier-Stokes equations by the smoothness assumption.
Keywords:
Schrödinger’s Equation, Potential, Scattering Amplitude, Cauchy Problem, Navier-Stokes Equations, Fourier Transform, Global Solvability and Uniqueness of the Cauchy Problem, Loss of Smoothness

1. Introduction
In this paper, we introduce important explanatory results presented in a previous study in [1] . We therefore restate the basic to clarify out understanding of them. We begin by considering some ideas about the potential in the inverse scattering problem, and this is then used to estimate solutions of the Cauchy problem for the Navier- Stokes equations. A similar approach has been developed for one-dimensional nonlinear equations [2] - [5] , but to date, there have been no results for the inverse scattering problem for three-dimensional nonlinear equations. This is primarily through difficulties in solving the three-dimensional inverse scattering problem. This paper is organized as follows: the study begin describing the inverse scattering problem, giving in a formula for the scattering potential. Using this potential, we obtain uniform time estimates in time for solutions to the Navier-Stokes equations, which suggest the global solvability of the Cauchy problem for the Navier-Stokes equations. Essentially, the present study expands the results for one-dimensional nonlinear equations with inverse scattering methods to multi-dimensional cases. Our main achievement is a relatively unchanged projection onto the space of solutions associated with the continuous spectrum for the nonlinear equations, which allows us to focus solely on the behavior associated with the decomposition of the solutions to the discrete spectrum. In the absence of a discrete spectrum, we obtain estimations for the maximum potential in the weaker norms, compared with the norms for the Sobolev spaces.
Consider the operators
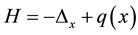 and
and
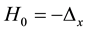 defined in the dense set
defined in the dense set
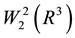 in the space
in the space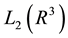 ; let q be a bounded fast-decreasing function. The operator
; let q be a bounded fast-decreasing function. The operator
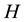 is called the Schrödinger operator. We consider the three-dimensional inverse scattering problem for the Schrödinger operator, i.e, the scattering potential must be reconstructed from the scattering amplitude. This problem has been studied by many researchers ( [6] - [9] , and references therein).
is called the Schrödinger operator. We consider the three-dimensional inverse scattering problem for the Schrödinger operator, i.e, the scattering potential must be reconstructed from the scattering amplitude. This problem has been studied by many researchers ( [6] - [9] , and references therein).
2. Results
Consider Schrödinger’s equation:
 . (1)
. (1)
Let
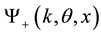 be a solution of (1) with the following asymptotic behavior:
be a solution of (1) with the following asymptotic behavior:
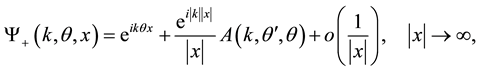 (2)
(2)
where
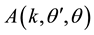 is the scattering amplitude and
is the scattering amplitude and
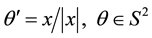 for
for
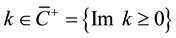
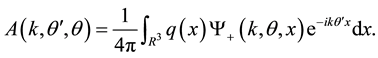 (3)
(3)
Let us also define the solution
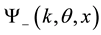 for
for
 as
as
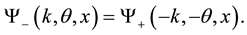
As is well known [2] :
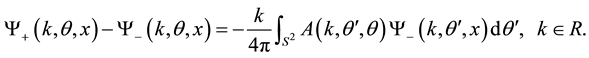 (4)
(4)
This equation is the key to solving the inverse scattering problem, and was first used by Newton [7] [8] and Somersalo et al. [9] .
Equation (4) is equivalent to the following:
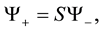
where S is a scattering operator with kernel
The following theorem was stated in [6] :
Theorem 1. (The energy and momentum conservation laws) Let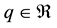
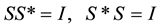

Definition 1. The set of measurable functions
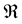
is recognized as being of Rollnik class.
As shown in [10] ,
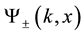
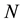

where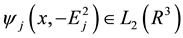
We present Povzner’s results [10] below:
Theorem 2. (Completeness) For both an arbitrary
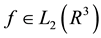
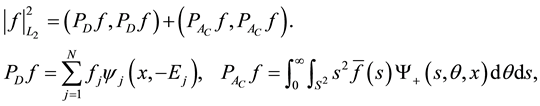
where
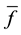
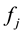
Theorem 3. (Birman-Schwinger estimation). Let
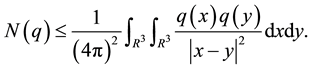
This theorem was proved in [11] .
Let us introduce the following notation:
For
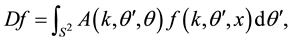

where
We define the operators


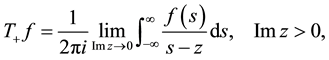
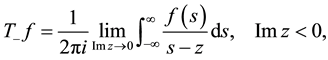
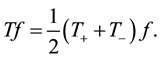
Consider the Riemann problem of finding a function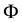
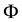
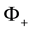

Lemma 1.
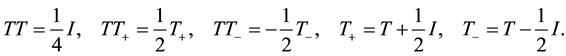
Theorem 4. Let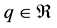
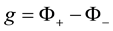

The proof of the above follows from the classic results for the Riemann problem.
Lemma 2. Let

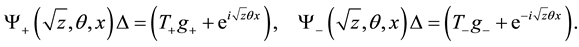
The proof of the above follows from the definitions of
Definition 2. Denote by
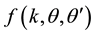
Definition 3. Denote by
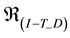
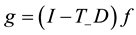

Lemma 3. Suppose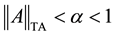
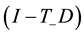
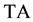
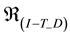
The proof of the above follows from the definitions of
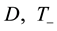
Lemma 4. Let
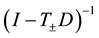
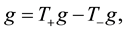
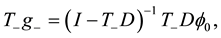

The proof of the above follows from the definitions of
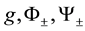
Lemma 5. Let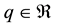
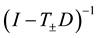
where

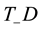
Proof: Using
and
We establish the proof.
Lemma 6. Let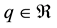
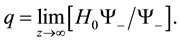
Lemma 7. Let
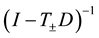
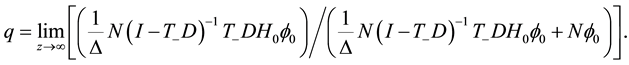
The proof of the above follows from the definitions of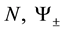
Lemma 8. Let
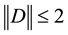
The proof of the above follows from the definition of
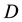
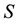
Lemma 9. Let


The proof of the above follows from the definitions of
Lemma 10. Let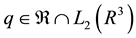
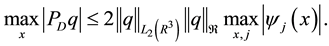
The proof of the above follows from the definition of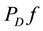
Lemma 11. Let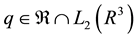
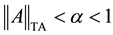
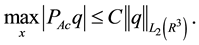
To prove this result, one calculates
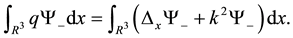
Using Lemma 5, the first approximation can be obtained in terms of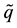

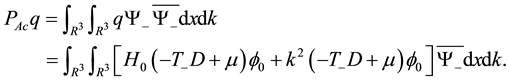
where
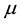

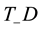
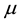
3. Conclusions for the Three-Dimensional Inverse Scattering Problem
This study has shown once again the outstanding properties of the scattering operator, which, in combination with the analytical properties of the wave function, enable an almost-explicit formula for the potential to be obtained from the scattering amplitude. Furthermore, this approach overcomes the problem of over-determination, resulting from the fact that the potential is a function of three variables, whereas the amplitude is a function of five variables. We have shown that it is sufficient to average the scattering amplitude to eliminate the two extra variables.
4. Cauchy Problem for the Navier-Stokes Equation
Numerous studies of the Navier-Stokes equations have been devoted to the problem of the smoothness of its solutions. A good overview of these studies is given in [13] -[17] . The spatial differentiability of the solutions is an important factor, this controls their evolution. Obviously, differentiable solutions do not provide an effective description of turbulence. Nevertheless, the global solvability and differentiability of the solutions has not been proven, and therefore the problem of describing turbulence remains open. It is interesting to study the properties of the Fourier transform of solutions of the Navier-Stokes equations. Of particular interest is how they can be used in the description of turbulence, and whether they are differentiable. The differentiability of such Fourier transforms appears to be related to the appearance or disappearance of resonance, as this implies the absence of large energy flows from small to large harmonics, which in turn precludes the appearance of turbulence.
Thus, obtaining uniform global estimations of the Fourier transform of solutions of the Navier-Stokes equations means that the principle modeling of complex flows and related calculations will be based on the Fourier transform method. The authors are continuing to research these issues in relation to a numerical weather prediction model; this paper provides a theoretical justification for this approach. Consider the Cauchy problem for the Navier-Stokes equations:
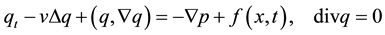
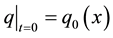
in the domain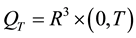

The problem defined by (28), (29), (30) has at least one weak solution
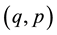
The following results have been proved [14] :
Theorem 5. If
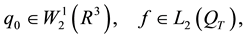
there is a single generalized solution of (28), (29), (30) in the domain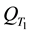

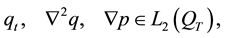
Note that
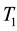
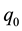
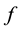
Lemma 12. Let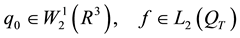
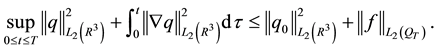
Our goal is to provide global estimations for the Fourier transforms of the derivatives of the solutions to the Navier-Stokes Equations (28), (29), (30) without requiring the initial velocity and force to be small. We obtain the following uniform time estimation. Using the notation
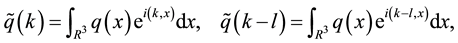

Assertion 1. The solution of (28) (30) according to Theorem 5 satisfies:
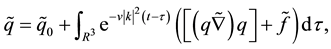
where
This follows from the definition of the Fourier transform and the theory of linear differential equations.
Assertion 2.The solution of (28) (30) satisfies:
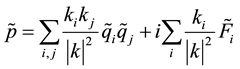
and the following estimations:
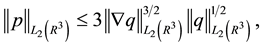
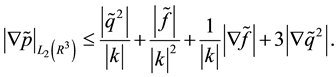
This expression for
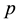
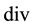
Lemma 13. The solution of (28), (29), (30) in Theorem 5 satisfies the following inequalities:
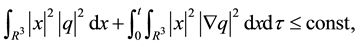
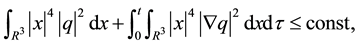
or

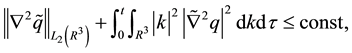
This follows from the Navier-Stokes equations, our first a priori estimation (Lemma 1), and Lemma 2.
Lemma 14. The solution of (28) (30) satisfies the following inequalities:
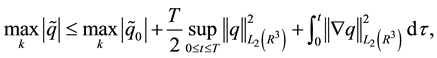
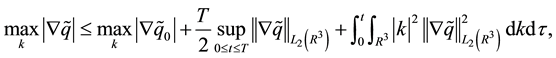
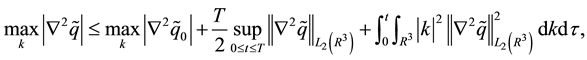
These estimations follow from (9), Parseval’s identity, the Cauchy-Schwarz inequality, and Lemma 3.
Lemma 15. The solution of (28) (30) according to Theorem 5 satisfies

This follows from our a priori estimation (Lemma 1) and the assertion of Lemma 3.
Lemma 16. The solution of (28) (30) according to Theorem 5 satisfies to the following inequalities:
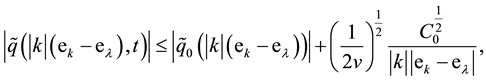
where
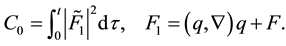
Proof. From (36), we have the inequality:
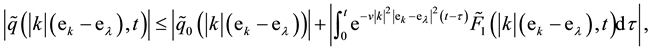
where
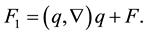
Using the notation
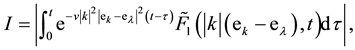
And Hölder’s inequality in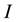
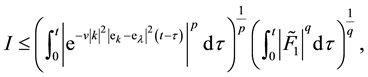
where
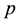
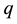
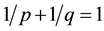
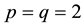
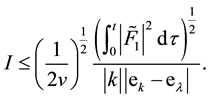
Using the estimation for
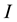
Lemma 17. Let
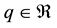
Then,
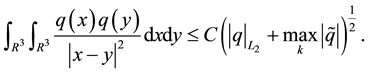
A proof of this lemma can be obtained using Plancherel’s theorem. For
consider the transformation of the Navier-Stokes:
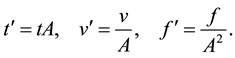
Lemma 18. Let
then
Proof. Using the definitions for

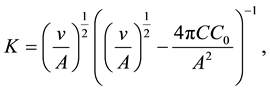
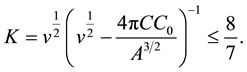
We now obtain uniform time estimations for Rollnik’s norms of the solutions of (28) (30). The following (and main) goal is to obtain the same estimations for
the velocity components of the Cauchy problem for the Navier-Stokes equations. We shall use Lemmas 6 and 11.
Theorem 6. Let
Then, there exists a unique generalized solution of (28) (30) satisfying the following inequality:
where the value of
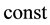
Proof. It suffices to obtain uniform estimates of the maximum velocity components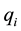
Because uniform estimates allow us to extend the local existence and uniqueness theorem over the interval in which they are valid. To estimate the velocity components, Lemma 10 can be used:
Using Lemmas (13)-(17) for
we can obtain
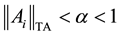

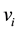

Theorem 6 asserts the global solvability and uniqueness of the Cauchy problem for the Navier-Stokes equations.
Theorem 7. Let
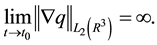
Then, there exists

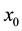
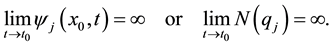
Proof. A proof of this lemma can be obtained using
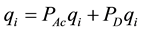
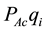
Theorem 7 describes the blowup of classical solutions for the Navier-Stokes equations.
5. Conclusion
Uniform global estimations of the Fourier transform of solutions of the Navier-Stokes equations indicate that the principle modeling of complex flows and related calculations can be based on the Fourier transform method. In terms of the Fourier transform, under both smooth initial conditions and right-hand sides, no apparent fluctuations appear in the speed and pressure modes. A loss of smoothness in terms of the Fourier transform can only be expected for singular initial conditions or unbounded forces in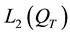
Acknowledgements
We are grateful to the Ministry of Education and Science of the Republic of Kazakhstan for a grant, and to the System Research “Factor” Company for joint efforts in this project. The work was performed as part of an international project, “Joint Kazakh-Indian studies of the influence of anthropogenic factors on atmospheric phenomena on the basis of numerical weather prediction models WRF (Weather Research and Forecasting)”, commissioned by the Ministry of Education and Science of the Republic of Kazakhstan.
References
- Durmagambetov, A.A. and Fazilova, L.S. (2014) Global Estimation of the Cauchy Problem Solutions’ the Navier- Stokes Equation. Journal of Applied Mathematics and Physics, 2, 17-25. http://dx.doi.org/10.4236/jamp.2014.24003
- Russell, J.S. (1844) Report on Wave. Report of the 14th Meeting of the British Association for the Advancement of Science, York, September 1844 (London 1845), Plates XLVII-LVII, 90-311.
- Russell, J.S. (1838) Report of the Committee on Waves. Report of the 7th Meeting of British Association for the Advancement of Science, John Murray, London, 417-496.
- Ablowitz, M.J. and Segur, H. (1981) Solitons and the Inverse Scattering Transform SIAM, 435-436.
- Zabusky, N.J. and Kruskal, M.D. (1965) Interaction of Solitons in a Collisionless Plasma and the Recurrence of Initial States. Physical Review Letters, 15, 240-243. http://dx.doi.org/10.1103/PhysRevLett.15.240
- Faddeev, L.D. (1974) The Inverse Problem in the Quantum Theory of Scattering. II. Itogi Nauki i Tekhniki. Ser. Sovrem. Probl. Mat., VINITI, Moscow, 93, 180.
- Newton, R.G. (1979) New Result on the Inverse Scattering Problem in Three Dimensions. Physical Review Letters, 43, 541-542. http://dx.doi.org/10.1103/PhysRevLett.43.541
- Newton, R.G. (1980) Inverse Scattering in Three Dimensions. Journal of Mathematical Physics, 21, 1698-1715. http://dx.doi.org/10.1063/1.524637
- Somersalo, E., et al. (1988) Inverse Scattering Problem for the Schrodinger’s Equation in Three Dimensions: Connections between Exact and Approximate Methods. http://conservancy.umn.edu/bitstream/4896/1/449.pdf
- Povzner, A.Y. (1953) On the Expansion of Arbitrary Functions in Characteristic Functions of the Operator
. Russian Matematicheskii Sbornik, 32, 109.>http://html.scirp.org/file/7-7402179x192.png" class="200" />. Russian Matematicheskii Sbornik, 32, 109.
- Birman, M.S. (1961) On the Spectrum of Singular Boundary-Value Problems. Russian Matematicheskii Sbornik, 55, 125.
- Poincare, H. (1910) Lecons de mecanique celeste. t. 3, 347-349.
- Leray, J. (1934) Sur le mouvement d’un liquide visqueux emplissant l'espace. Acta Mathematica, 63, 193-248. http://dx.doi.org/10.1007/BF02547354
- Ladyzhenskaya, O.A. (1970) Mathematics Problems of Viscous Incondensable Liquid Dynamics. M:Science, 288.
- Solonnikov, V.A. (1964) Estimates Solving Nonstationary Linearized Systems of Navier-Stokes’ Equations. Transactions Academy of Sciences USSR, 70, 213-317.
- Huang, X.D. and Li, J. and Wang, Y. (2013) Serrin-Type Blowup Criterion forFull Compressible Navier-Stokes System. Archive for Rational Mechanics and Analysis, 207, 303-316. http://dx.doi.org/10.1007/s00205-012-0577-5
- Terence Tao (2014) Finite Time Blowup for an Averaged Three-Dimensional Navier-Stokes Equation. arXiv:1402. 0290 [math. AP]


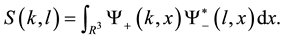
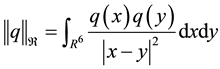
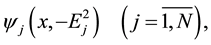

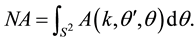
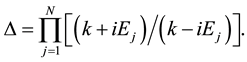
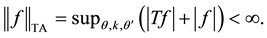
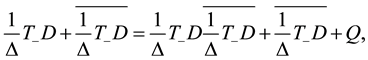
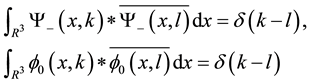
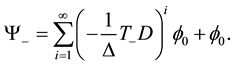
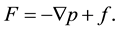
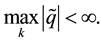


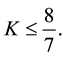
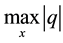
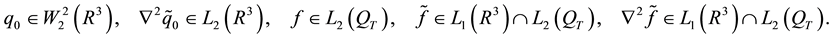

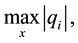
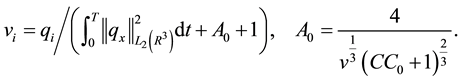
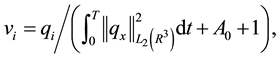
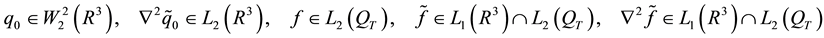
 . Russian Matematicheskii Sbornik, 32, 109.>http://html.scirp.org/file/7-7402179x192.png" class="200" />. Russian Matematicheskii Sbornik, 32, 109.
. Russian Matematicheskii Sbornik, 32, 109.>http://html.scirp.org/file/7-7402179x192.png" class="200" />. Russian Matematicheskii Sbornik, 32, 109.