Applied Mathematics
Vol.4 No.10C(2013), Article ID:38394,8 pages DOI:10.4236/am.2013.410A3007
Reformulation of Relativistic Quantum Mechanics Equations with Non-Commutative Sedeons
Institute for Physics of Microstructures of the Russian Academy of Sciences, Nizhniy Novgorod, Russia
Email: mironov@ipmras.ru
Copyright © 2013 Victor L. Mironov, Sergey V. Mironov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 22, 2013; revised June 22, 2013; accepted June 29, 2013
Keywords: Clifford Algebra; Sedeons; Relativistic Quantum Mechanics; Sedeonic Klein-Gordon and Dirac Equations
ABSTRACT
We present sixteen-component values “sedeons”, generating associative non-commutative space-time algebra. The generalized relativistic wave equations based on sedeonic wave function and space-time operators are proposed. We demonstrate that sedeonic second-order wave equation for massive field can be reformulated as the quasi-classical equation for the potentials of the field or in equivalent form as the Maxwell-like equations for the field intensities. The sedeonic first-order Dirac-like equations for massive and massless fields are also discussed.
1. Introduction
The application of multicomponent hypercomplex numbers and multivectors in classical and quantum field theory has a long history. In particular, the simplest generalization of electrodynamics and quantum mechanics was developed on the basis of quaternions [1-6]. The structure of quaternions with four components (scalar and vector) corresponds to the relativistic four-vector approach that allows one to reformulate relativistic relation in terms of quaternionic algebra. However, the essential imperfection of the quaternionic algebra is that the quaternions do not include pseudoscalar and pseudovector components. The consideration of space symmetry with respect to spatial inversion leads to the eight-component structures enclosing scalar, pseudoscalar, vector and pseudovector. There is a lot of works on application of different eight-component values such as biquaternions and octonions in classical electrodynamics and relativistic quantum mechanics [7-17]. However, a consistent relativistic approach implies equally the space and time symmetries that require the consideration of the extended sixteen-component space-time algebras.
There are a few approaches in the development of field theory on the basis of sixteen-component structures. One of them is the application of hypernumbers sedenions, which are obtained from octonions by Cayley-Dickson extension procedure [18-22]. But as in the case of octonions the essential imperfection of sedenions is their non-associativity. Another approach is based on the application of hypercomplex multivectors generating associative space-time Clifford algebras. The basic idea of such multivectors is an introduction of additional noncommutative time unit vector, which is orthogonal to the space unit vectors [23,24]. However, the application of such multivectors in quantum mechanics is considered in general as one of abstract algebraic schemes enabling the reformulation of Klein-Gordon and Dirac equations for the multicomponent wave functions but does not touch the physical entity of these equations.
Recently we have developed an alternative approach based on our scalar-vector concept [25-28] realized in eight-component octons and sixteen-component sedeons. In particular, in Ref. [28] we considered a variant of sixteen-component sedeonic space-time Clifford algebra with non-commutative vector basis and commutative space-time units that allowed us to reformulate the equations of relativistic quantum mechanics in terms of scalar-vector wave function. However, obtained equations have some asymmetry and contain the special non-sedeonic operators of space-time conjugation. In this paper we present a new version of the sedeonic space-time algebra with non-commutative bases and demonstrate some of its application to the symmetric reformulation of the basic equations of relativistic quantum mechanics as the equations for the field potentials and field intensities.
2. Sedeonic Space-Time Algebra
The sedeonic algebra encloses four groups of values, which are differed with respect to spatial and time inversion.
• Absolute scalars 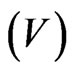 and absolute vectors
and absolute vectors 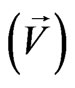 are not transformed under spatial and time inversion.
are not transformed under spatial and time inversion.
• Time scalars 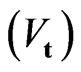 and time vectors
and time vectors 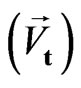 are changed (in sign) under time inversion and are not transformed under spatial inversion.
are changed (in sign) under time inversion and are not transformed under spatial inversion.
• Space scalars 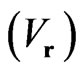 and space vectors
and space vectors 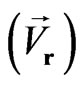 are changed under spatial inversion and are not transformed under time inversion.
are changed under spatial inversion and are not transformed under time inversion.
• Space-time scalars 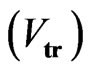 and space-time vectors
and space-time vectors 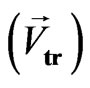 are changed under spatial and time inversion.
are changed under spatial and time inversion.
Here indexes 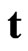 and
and 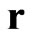 indicate the transformations (
indicate the transformations (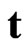 for time inversion and
for time inversion and 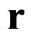 for spatial inversion), which change the corresponding values. All introduced values can be integrated into one space-time sedeon
for spatial inversion), which change the corresponding values. All introduced values can be integrated into one space-time sedeon , which is defined by the following expression:
, which is defined by the following expression:
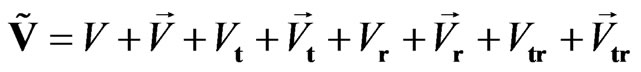 . (1)
. (1)
Let us introduce scalar-vector basis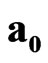 ,
, 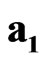 ,
, 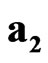 ,
, 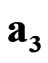 , where the value
, where the value 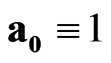 is absolute scalar unit and the values
is absolute scalar unit and the values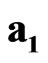 ,
, 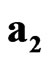 ,
, 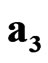 are absolute unit vectors generating the right Cartesian basis. We introduce also four spacetime scalar units
are absolute unit vectors generating the right Cartesian basis. We introduce also four spacetime scalar units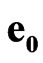 ,
, 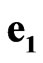 ,
, 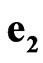 ,
, 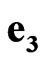 , where value
, where value 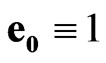 is a absolute scalar unit;
is a absolute scalar unit; 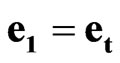 is a time scalar unit;
is a time scalar unit; 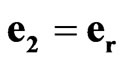 is a space scalar unit;
is a space scalar unit; 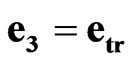 is a space-time scalar unit. Using space-time scalar units
is a space-time scalar unit. Using space-time scalar units 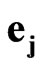
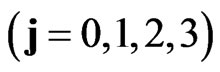 and scalar-vector basis
and scalar-vector basis 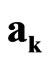
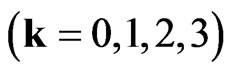 we can introduce unified sedeonic components
we can introduce unified sedeonic components 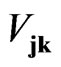 in accordance with the following relations:
in accordance with the following relations:
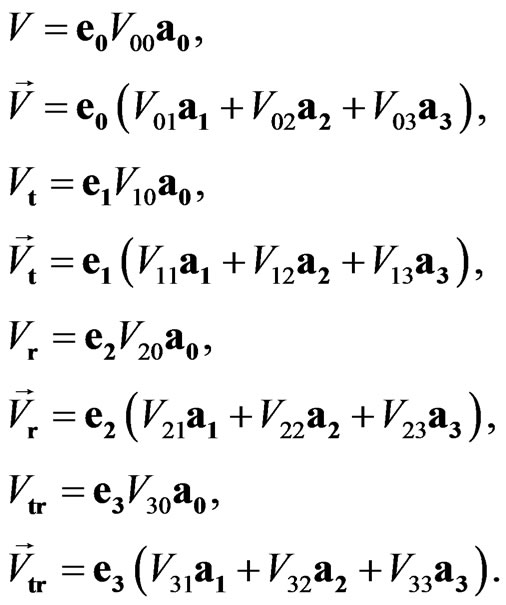 (2)
(2)
Then the sedeon (1) can be written in the following expanded form:
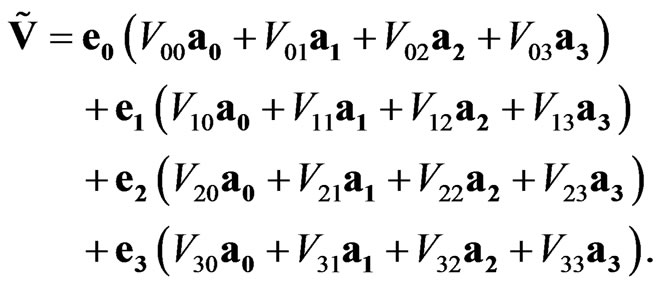 (3)
(3)
The sedeonic components 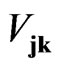 are numbers (complex in general). Further we will use symbol 1 instead of units
are numbers (complex in general). Further we will use symbol 1 instead of units 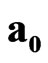 and
and 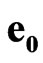 for simplicity.
for simplicity.
The multiplication and commutation rules for sedeonic absolute unit vectors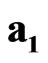 ,
, 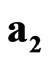 ,
, 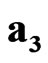 and space-time units
and space-time units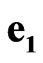 ,
, 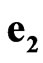 ,
, 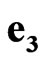 are presented in Tables 1 and 2 respectively.
are presented in Tables 1 and 2 respectively.
In the tables and further the value 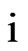 is the imaginary unit
is the imaginary unit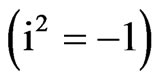 . Note that sedeonic units
. Note that sedeonic units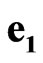 ,
, 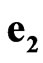 ,
, 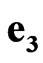 and unit vectors
and unit vectors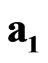 ,
, 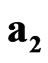 ,
, 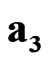 generate the anticommutative algebras:
generate the anticommutative algebras:
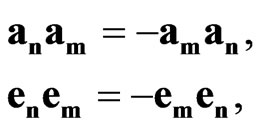 (4)
(4)
for 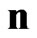 and
and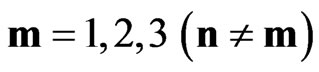 , but
, but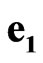 ,
, 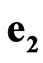 ,
, 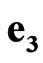 commute with
commute with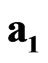 ,
, 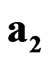 ,
,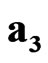 :
:
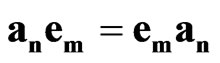 , (5)
, (5)
for any 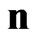 and
and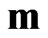 .
.
Thus the sedeon  is the complicated space-time object consisting of absolute scalar, time scalar, space scalar, space-time scalar, absolute vector, time vector, space vector and space-time vector.
is the complicated space-time object consisting of absolute scalar, time scalar, space scalar, space-time scalar, absolute vector, time vector, space vector and space-time vector.
Introducing the designations of scalar-vector values
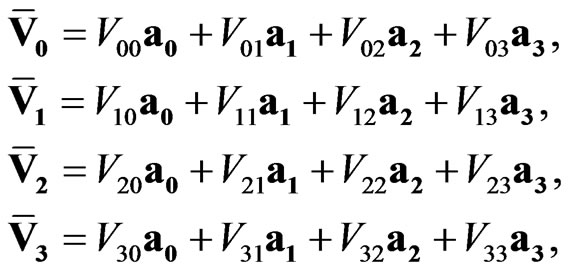 (6)
(6)
we can write the sedeon (3) in the compact form
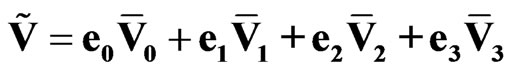 . (7)
. (7)
On the other hand, introducing the designations of space-time sedeon-scalars
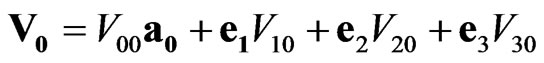 ,
,
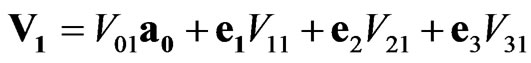 , (8)
, (8)

Table 1. Multiplication rules for absolute unit vectors.

Table 2. Multiplication rules for space-time units.
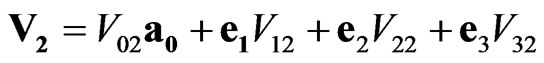 ,
,
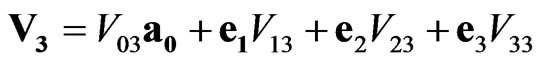 we can write the sedeon (3) in another form
we can write the sedeon (3) in another form
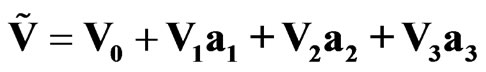 , (9)
, (9)
or introducing the sedeon-vector
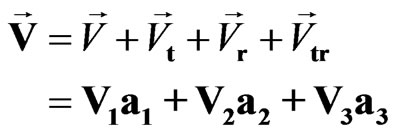 (10)
(10)
it can be represented in following compact form:
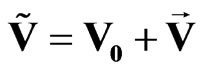 . (11)
. (11)
Further we will indicate the sedeon-scalars and the sedeon-vectors with the bold capital letters.
Let us consider the sedeonic multiplication in detail. The sedeonic product of two sedeons  and
and 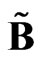 can be presented in the following form:
can be presented in the following form:
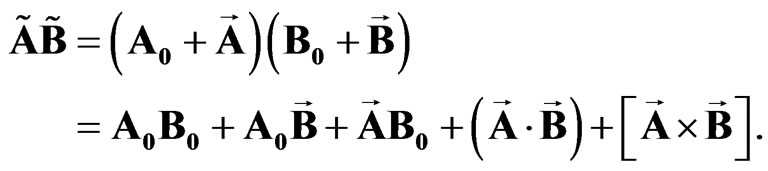 (12)
(12)
Here we denote the sedeonic scalar multiplication of two sedeon-vectors (internal product) by symbol “ ” and round brackets
” and round brackets
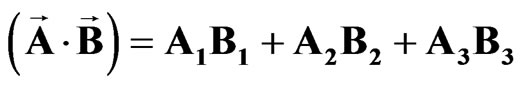 , (13)
, (13)
and sedeonic vector multiplication (external product) by symbol “ ” and square brackets
” and square brackets
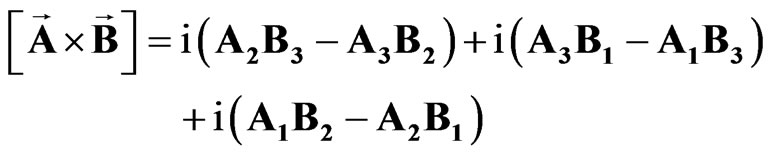 (14)
(14)
In Equations (13) and (14) the multiplication of sedeonic components is performed in accordance with Equation (8) and Table 2. Note that in sedeonic algebra the expression for the vector product (14) differs from analogous expression in Gibbs vector algebra. As a consequence, in sedeonic algebra the formula for the vector triple product of three absolute vectors ,
, 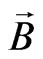 and
and 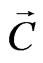 has the following form:
has the following form:
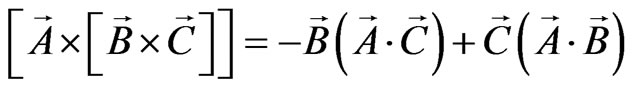 . (15)
. (15)
Thus, the sedeonic product
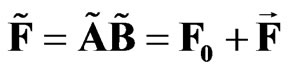
has the following components:
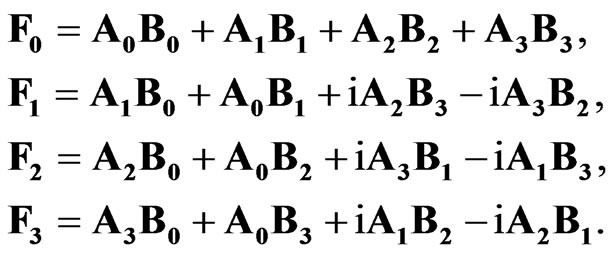 (17)
(17)
3. Sedeonic Spatial Rotation and Space-Time Conjugation
The rotation of the sedeon  on the angle
on the angle 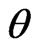 around the absolute unit vector
around the absolute unit vector 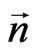 is realized by uncompleted sedeon
is realized by uncompleted sedeon
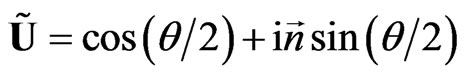 (18)
(18)
and by complex conjugated sedeon
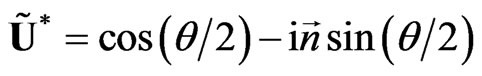 , (19)
, (19)
which satisfy the relation
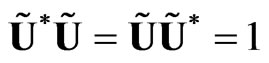 . (20)
. (20)
The transformed sedeon 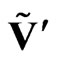 is defined as the sedeonic product
is defined as the sedeonic product
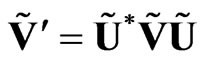 . (21)
. (21)
Thus the transformed sedeon 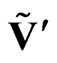 can be written in the following expanded form:
can be written in the following expanded form:
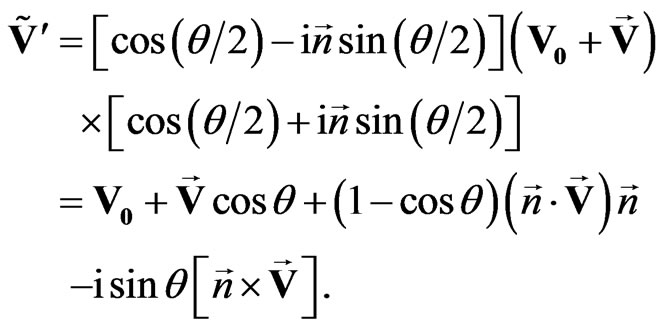 (22)
(22)
It is clearly seen that rotation does not transform the sedeon-scalar part, but sedeonic vector 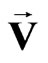 is rotated on the angle
is rotated on the angle 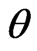 around
around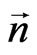 .
.
The operations of time conjugation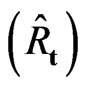 , space conjugation
, space conjugation 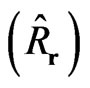 and space-time conjugation
and space-time conjugation 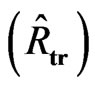 are connected with transformations in
are connected with transformations in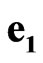 ,
, 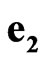 ,
, 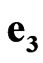 basis and can be presented as
basis and can be presented as
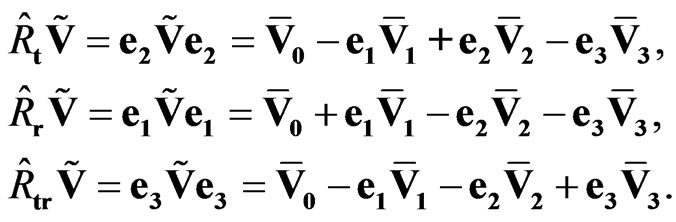 (23)
(23)
4. Sedeonic Lorentz Transformations
The relativistic event four-vector can be represented in the follow sedeonic form:
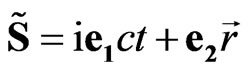 , (24)
, (24)
where 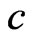 is the velocity of light,
is the velocity of light, 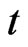 is the absolute scalar of time and
is the absolute scalar of time and 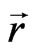 is the absolute radius-vector. The square of this value is the Lorentz invariant
is the absolute radius-vector. The square of this value is the Lorentz invariant
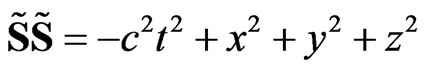 . (25)
. (25)
The Lorentz transformation of event four-vector is realized by sedeons
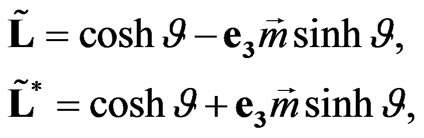 (27)
(27)
where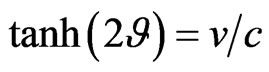 ;
; 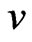 is velocity of motion along the absolute unit vector
is velocity of motion along the absolute unit vector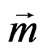 . Note that
. Note that
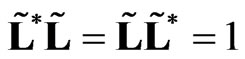 . (28)
. (28)
The transformed event four-vector 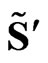 is written as
is written as
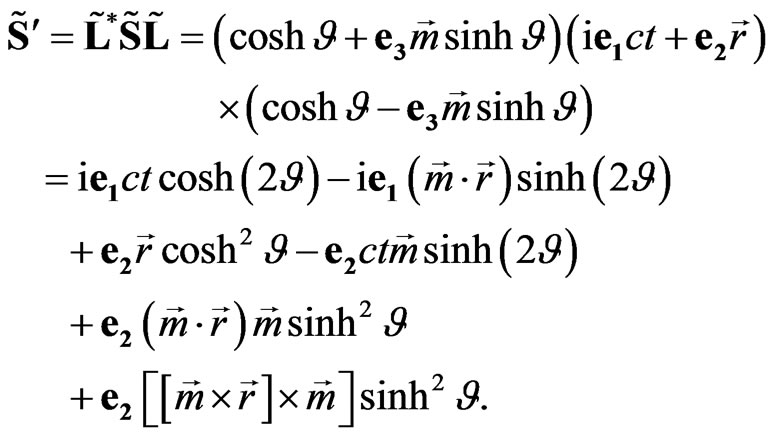 (29)
(29)
Separating the values with 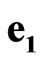 and
and 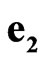 we get the well-known expressions for the time and coordinates transformations [29]:
we get the well-known expressions for the time and coordinates transformations [29]:
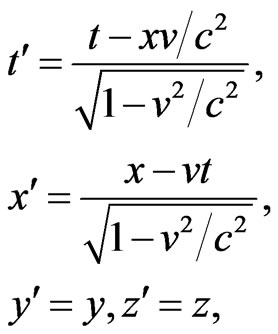 (30)
(30)
where 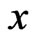 is the coordinate along the
is the coordinate along the 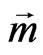 vector.
vector.
Let us also consider the Lorentz transformation of the full sedeon . The transformed sedeon
. The transformed sedeon 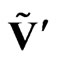 can be written as sedeonic product
can be written as sedeonic product
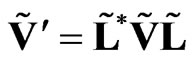 . (31)
. (31)
In expanded form:
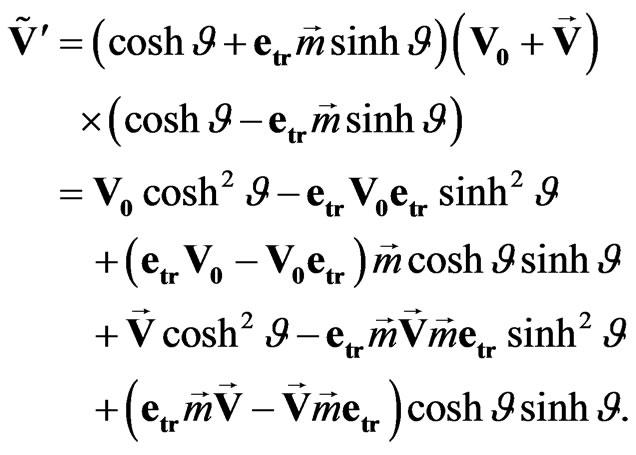 (32)
(32)
Rewriting the expression (32) with scalar (13) and vector (14) products we get
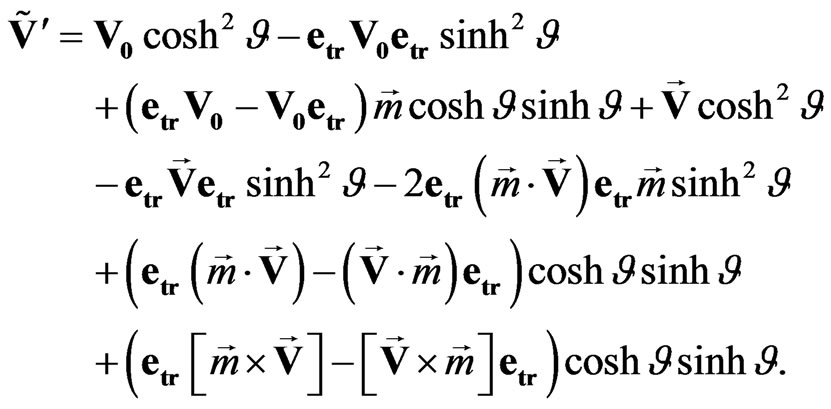 (33)
(33)
Thus, the transformed sedeon have the following components:
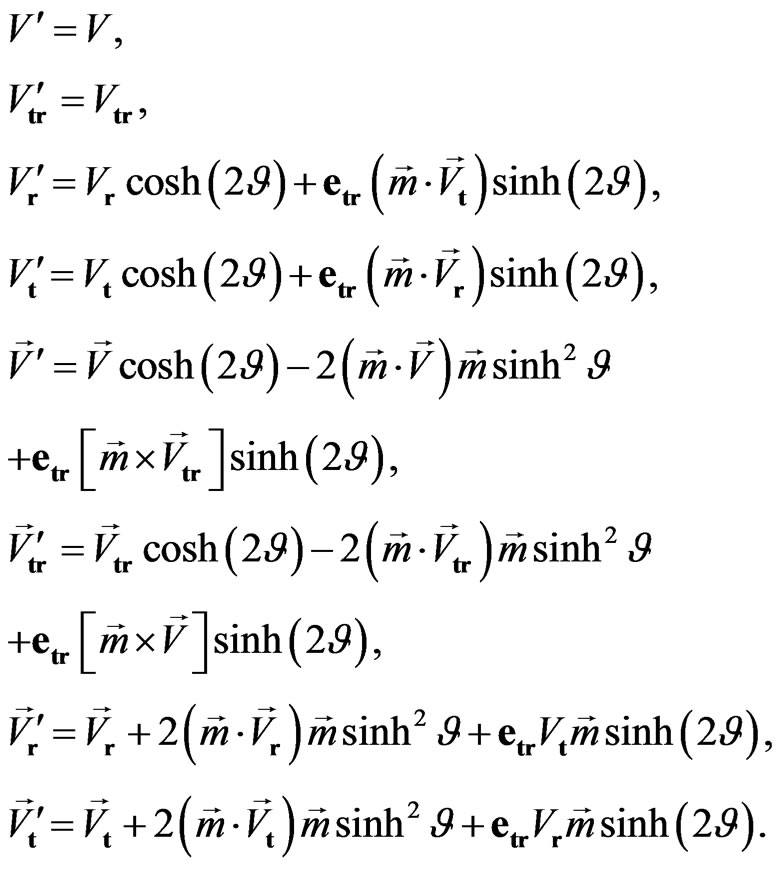 (34)
(34)
5. Generalized Sedeonic Wave Equation
The relativistic wave function should satisfy an equation, which is obtained from the Einstein relation between energy and momentum
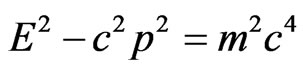 (35)
(35)
by means of changing classical energy 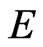 and momentum
and momentum 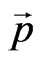 on corresponding quantum-mechanical operators [30]:
on corresponding quantum-mechanical operators [30]:
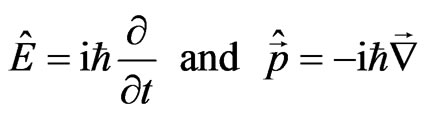 , (36)
, (36)
where 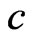 is the velocity of light,
is the velocity of light, 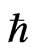 is the Planck constant. The absolute gradient vector has the following form:
is the Planck constant. The absolute gradient vector has the following form:
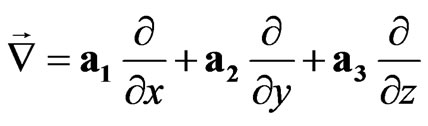 . (37)
. (37)
In sedeonic algebra the Einstein relation (35) can be written as
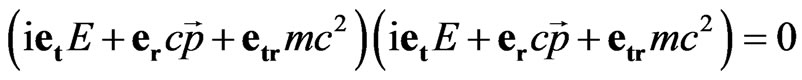 . (38)
. (38)
Let us consider the wave function in the form of space-time sedeon
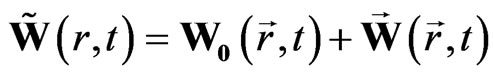 . (39)
. (39)
Then the generalized sedeonic wave equation is written in the following symmetric form
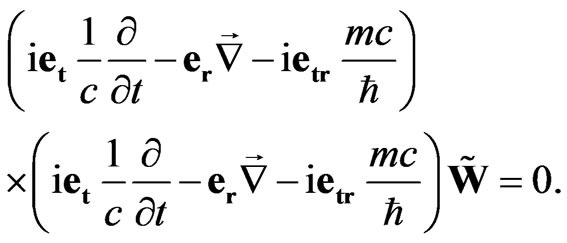 (40)
(40)
Redefining the operators
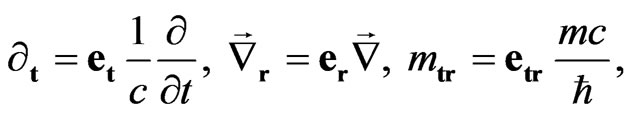 (41)
(41)
we can rewrite the Equation (40) in compact form:
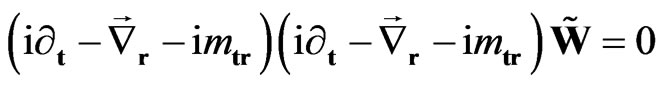 . (42)
. (42)
The sedeonic Equation (42) can be represented in the form of the system of Maxwell-like first-order equations. Let us consider the sequential action of operators. After the action of the first operator in the left part of Equation (42) we obtain
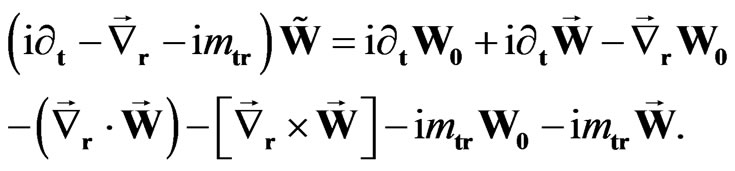 (43)
(43)
Introducing the scalar and vector field’s intensities
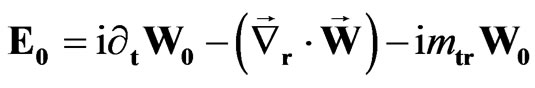 , (44)
, (44)
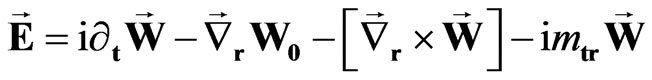 , (45)
, (45)
the relation (43) is presented as
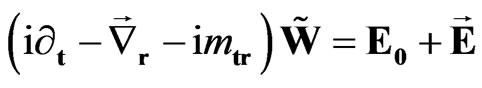 . (46)
. (46)
Then the wave Equation (42) can be rewritten in the following form:
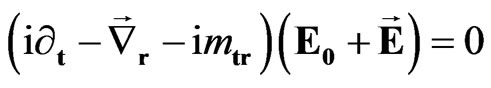 . (47)
. (47)
Performing sedeonic multiplication in expression (47) and separating sedeon-scalar and sedeon-vector parts we obtain the Maxwell-like system of first-order equations:
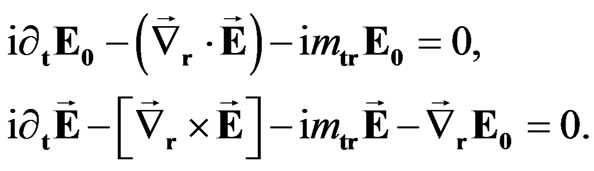 (48)
(48)
In the particular case of zero mass field the system (48) coincide with the Maxwell equations for electromagnetic field in a vacuum. Indeed, choosing sedeonic potential as
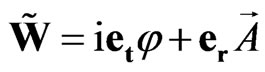 , (49)
, (49)
we get the following wave equation:
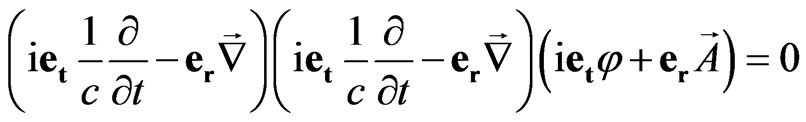 . (50)
. (50)
Here 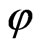 is scalar potential,
is scalar potential, 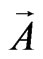 is vector potential. After the action of the first operator in the left part of Equation (50) we obtain
is vector potential. After the action of the first operator in the left part of Equation (50) we obtain
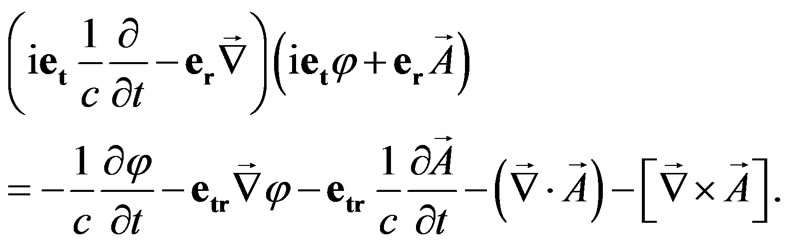 (51)
(51)
Using the sedeonic definitions of the electric and magnetic field’s intensities
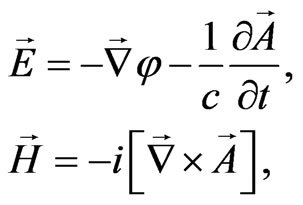 (52)
(52)
and taking into account Lorentz gauge condition
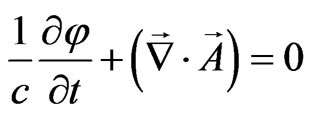 , (53)
, (53)
we can rewrite the expression (51) in the following form:
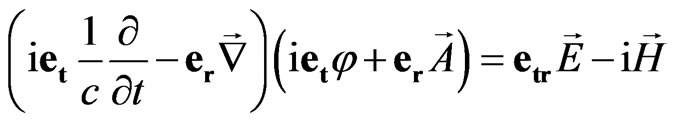 . (54)
. (54)
Then the wave Equation (50) can be represented as
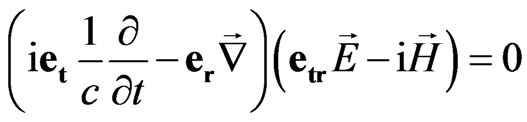 . (55)
. (55)
Performing sedeonic multiplication in the left part of equation (55) we get
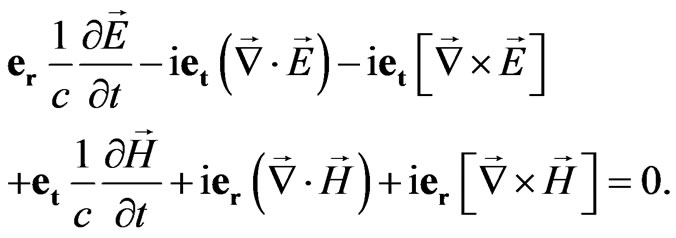 (56)
(56)
Separating space-time values we obtain the system of Maxwell equations in the following form:
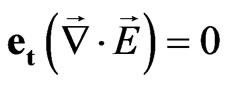 —time scalar,
—time scalar,
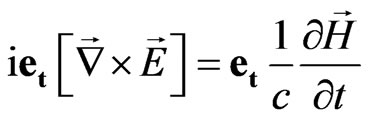 —time vector,
—time vector,
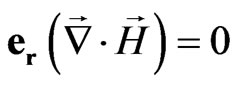 —space scalar,(57)
—space scalar,(57)
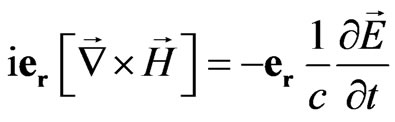 —space vector.
—space vector.
The system (57) coincides with Maxwell equations for free electromagnetic field.
6. Sedeonic Generalization of Dirac Equation
The sedeonic algebra enables the reformulation of the first-order Dirac equation [30] as a wave equation for the filed potential. In this case the homogeneous Dirac wave equation is written as
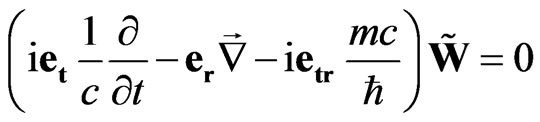 , (58)
, (58)
where the sedeonic wave function 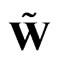 can be considered as the field potential. In fact, this equation describes the special massive field with zero field intensities
can be considered as the field potential. In fact, this equation describes the special massive field with zero field intensities 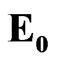 and
and 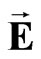 (see expression (46)). In Equation (58) the basis elements
(see expression (46)). In Equation (58) the basis elements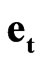 ,
, 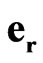 ,
, 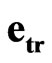 and
and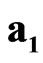 ,
, 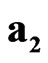 ,
, 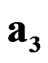 play the role of the space-time operators, which transform the sedeonic potential
play the role of the space-time operators, which transform the sedeonic potential 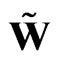 by means of component permutation.
by means of component permutation.
In particular, for the special case of zero mass the Equation (58) is written as
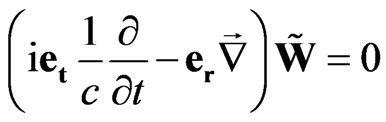 . (59)
. (59)
This equation describes the free massless electromagnetic field with field intensities 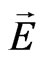 and
and 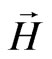 equal to zero (see the expression (54)).
equal to zero (see the expression (54)).
Let us consider the plane wave solution of Equation (59) in detail. We will seek the potential in the form:
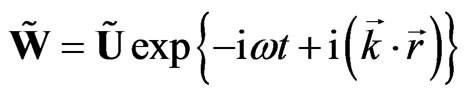 , (60)
, (60)
where 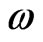 is a frequency,
is a frequency, 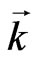 is an absolute wave vector and the wave amplitude
is an absolute wave vector and the wave amplitude 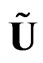 does not depend on coordinates and time. The dependence of the frequency on the wave vector has two branches:
does not depend on coordinates and time. The dependence of the frequency on the wave vector has two branches:
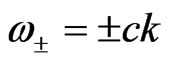 , (61)
, (61)
where 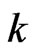 is the module of wave vector
is the module of wave vector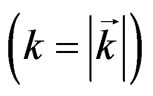 . Let us choose the amplitude of potential as
. Let us choose the amplitude of potential as
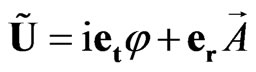 . (62)
. (62)
Then, substituting potential
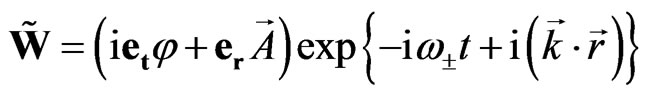 (63)
(63)
into (59) we obtain the following equation:
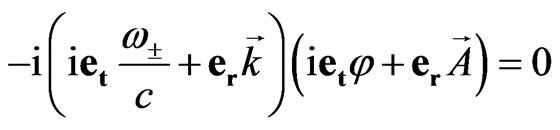 . (64)
. (64)
Introducing longitudinal 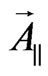 and perpendicular
and perpendicular 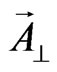 components of vector potential (with respect to the wave vector
components of vector potential (with respect to the wave vector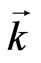 ) we get
) we get
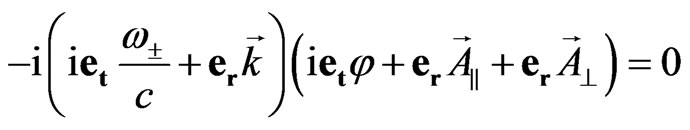 . (65)
. (65)
Performing multiplication in (65) and separating different space-time values we obtain the following relations:
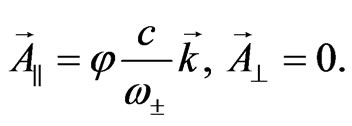 (66)
(66)
Then Equation (65) is rewritten as
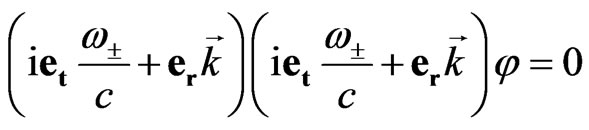 . (67)
. (67)
Thus the plane wave solution for the Equation (59) can be written in the following form:
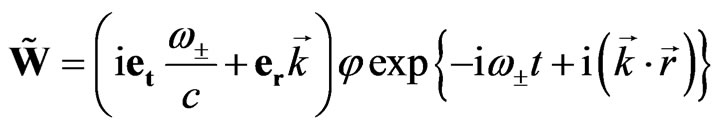 , (68)
, (68)
where 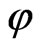 is arbitrary scalar constant and the expression in round brackets is so-called zero divisor:
is arbitrary scalar constant and the expression in round brackets is so-called zero divisor:
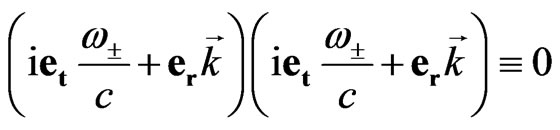 . (69)
. (69)
In general, the plane wave solution for the Equation (59) can be written in the following sedeonic form:
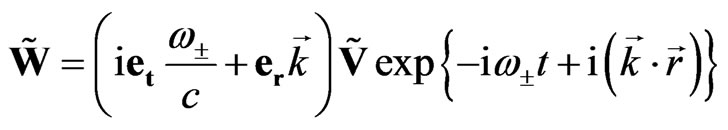 , (70)
, (70)
where  is an arbitrary sedeon with constant components. Note that the internal structure of this wave is changed under space and time conjugation.
is an arbitrary sedeon with constant components. Note that the internal structure of this wave is changed under space and time conjugation.
7. Discussion
The algebra of sedeons can be considered as the scalar-vector variant of complexified Clifford algebra with specific commutation and multiplication rules. The sedeonic basis elements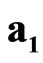 ,
, 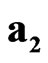 ,
, 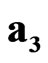 are responsible for the spatial rotation, while the elements
are responsible for the spatial rotation, while the elements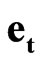 ,
, 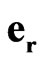 ,
, 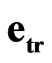 are responsible for the space-time inversions. Mathematically, these two bases are equivalent, and the different physical properties attributed to them are an important physical essence of our sedeonic hypothesis.
are responsible for the space-time inversions. Mathematically, these two bases are equivalent, and the different physical properties attributed to them are an important physical essence of our sedeonic hypothesis.
In contrast to the Heaviside-Gibbs vector algebra the multiplication rules for vector basis in sedeonic algebra contain the imaginary unit (see Table 1). It allows realizing scalar-vector algebra on which Clifford product is defined [25]. Apparently, such possibility of vector basis multiplication was pointed first by Macfarlane, A. [31]. Later the similar multiplication rules for matrix basis were applied by Pauli, W. [32] and Dirac, P.A.M. [33] in their spinor equations.
We emphasize that in present variant of sedeonic algebra the basis 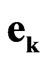 is non-commutative in contrast to the previously discussed [28]. This fact has far-reaching and important implications. Using non-commutative
is non-commutative in contrast to the previously discussed [28]. This fact has far-reaching and important implications. Using non-commutative 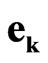 one can to write Einstein relation for energy and momentum, and as a consequence the second order wave equation, in a symmetric form as the product of two the same operators. It enables to exclude from the wave equations the nonsedeonic operators of space and time conjugation considered in [28].
one can to write Einstein relation for energy and momentum, and as a consequence the second order wave equation, in a symmetric form as the product of two the same operators. It enables to exclude from the wave equations the nonsedeonic operators of space and time conjugation considered in [28].
The important point is that the sedeonic basis elements simultaneously play a role of the operators and spacetime basis of the wave function. From a physical point of view, this allows us to reformulate the Klein-Gordon equation of relativistic quantum mechanics as the quasiclassical equation for the potentials of the field or in equivalent form as the Maxwell-like equations for the field intensities. At the same time the sedeonic first-order equations for massive and massless fields have very natural interpretation as the equations for the potentials corresponding to the fields with zero field intensities. Thus, the sedeonic formalism enables the development of a unified description of massive and massless fields on the basis of sedeonic space-time operators and scalarvector potentials.
8. Summary
Thus, in this paper we have presented the sixteen-component sedeons generating associative noncommutative space-time algebra. We proposed sedeonic second-order wave equation for massive field and demonstrated that this equation can be represented as the system of firstorder Maxwell-like equations for the field intensities.
The sedeonic Dirac-like first-order wave equations for massive and massless fields formulated in the sedeonic form were also considered. It was shown that these equations describe potential fields with zero field intensities.
The application of sedeonic approach to the description of massive baryon and lepton fields will be considered in our next paper.
9. Acknowledgements
The authors are very thankful to Mironova, G.V. for kind assistance and moral support. We also thank Köplinger, J. for the useful discussion.
REFERENCES
- S. L. Adler, “Quaternionic Quantum Mechanics and Quantum Fields,” Oxford University Press, New York, 1995.
- V. Majernik, “Quaternionic Formulation of the Classical Fields,” Advances in Applied Clifford Algebras, Vol. 9, No. 1, 1999, pp. 119-130. http://dx.doi.org/10.1007/BF03041944
- K. Imaeda, “A New Formulation of Classical Electrodynamics,” Nuovo Cimento, Vol. 32, No. 1, 1976, pp. 138- 162. http://dx.doi.org/10.1007/BF02726749
- A. J. Davies, “Quaternionic Dirac Equation,” Physical Review D, Vol. 41, No. 8, 1990, pp. 2628-2630. http://dx.doi.org/10.1103/PhysRevD.41.2628
- S. De Leo and P. Rotelli, “Quaternion Scalar Field,” Physical Review D, Vol. 45, No. 2, 1992, pp. 575-579. http://dx.doi.org/10.1103/PhysRevD.45.575
- C. Schwartz, “Relativistic Quaternionic Wave Equation,” Journal of Mathematical Physics, Vol. 47, No. 12, 2006, Article ID: 122301. http://dx.doi.org/10.1063/1.2397555
- Y.-F. Liu, “Triality, Biquaternion and Vector Representation of the Dirac Equation,” Advances in Applied Clifford Algebras, Vol. 12, No. 2, 2002, pp. 109-124. http://dx.doi.org/10.1007/BF03161242
- M. Gogberashvili, “Octonionic Electrodynamics,” Journal of Physics A: Mathematics in General, Vol. 39, No. 22, 2006, pp. 7099-7104. http://dx.doi.org/10.1088/0305-4470/39/22/020
- A. Gamba, “Maxwell’s Equations in Octonion Form,” Nuovo Cimento A, Vol. 111, No. 3, 1998, pp. 293-302.
- T. Tolan, K. Özdas and M. Tanişli, “Reformulation of Electromagnetism with Octonions,” II Nuovo Cimento B, Vol. 121, No. 1, 2006, pp. 43-55. http://dx.doi.org/10.1393/ncb/i2005-10189-9
- S. Demir and M. Tanisli, “A Compact Biquaternionic Formulation of Massive Field Equations in Gravi-Electromagnetism,” European Physical Journal Plus, Vol. 126, 2011, p. 115. http://dx.doi.org/10.1140/epjp/i2011-11115-8
- B. C. Chanyal, P. S. Bisht and O. P. S. Negi, “Generalized Octonion Electrodynamics,” International Journal of Theoretical Physics, Vol. 49, No. 6, 2010, pp. 1333-1343. http://dx.doi.org/10.1007/s10773-010-0314-5
- P. S. Bisht, G. Karnatak and O. P. S. Negi, “Generalized Gravi-Electromagnetism,” International Journal of Theoretical Physics, Vol. 49, No. 6, 2010, pp. 1344-1356. http://dx.doi.org/10.1007/s10773-010-0315-4
- V. Dzhunushaliev, “Nonassociativity, Supersymmetry and Hidden Variables,” Journal of Mathematical Physics, Vol. 49, No. 4, 2008, Article ID: 042108. http://dx.doi.org/10.1063/1.2907868
- M. Gogberashvili, “Octonionic Version of Dirac Equations,” International Journal of Modern Physics A, Vol. 21, No. 17, 2006, pp. 3513-3523. http://dx.doi.org/10.1142/S0217751X06028436
- S. De Leo and K. Abdel-Khalek, “Octonionic Dirac Equation,” Progress in Theoretical Physics, Vol. 96, No. 4, 1996, pp. 833-846. http://dx.doi.org/10.1143/PTP.96.833
- D. Hestenes, “Observables, Operators, and Complex Numbers in the Dirac Theory,” Journal of Mathematical Physics, Vol. 16, No. 3, 1975, pp. 556-572. http://dx.doi.org/10.1063/1.522554
- K. Imaeda and M. Imaeda, “Sedenions: Algebra and Analysis,” Applied Mathematics and Computations, Vol. 115, No. 2-3, 2000, pp. 77-88. http://dx.doi.org/10.1016/S0096-3003(99)00140-X
- K. Carmody, “Circular and Hyperbolic Quaternions, Octonions, and Sedenions,” Applied Mathematics and Computations, Vol. 28, No. 1, 1988, pp. 47-72. http://dx.doi.org/10.1016/0096-3003(88)90133-6
- K. Carmody, “Circular and Hyperbolic Quaternions, Octonions, and Sedenions—Further Results,” Applied Mathematics and Computations, Vol. 84, No. 1, 1997, pp. 27-47. http://dx.doi.org/10.1016/S0096-3003(96)00051-3
- J. Köplinger, “Dirac Equation on Hyperbolic Octonions,” Applied Mathematics and Computations, Vol. 182, No. 1, 2006, pp. 443-446. http://dx.doi.org/10.1016/j.amc.2006.04.005
- S. Demir and M. Tanişli, “Sedenionic Formulation for Generalized Fields of Dyons,” International Journal of Theoretical Physics, Vol. 51, No. 4, 2012, pp. 1239-1252. http://dx.doi.org/10.1007/s10773-011-0999-0
- W. P. Joyce, “Dirac Theory in Spacetime Algebra: I. The Generalized Bivector Dirac Equation,” Journal of Physics A: Mathematics in General, Vol. 34, No. 10, 2001, pp. 1991-2005. http://dx.doi.org/10.1088/0305-4470/34/10/304
- C. Cafaro and S. A. Ali, “The Spacetime Algebra Approach to Massive Classical Electrodynamics with Magnetic Monopoles,” Advances in Applied Clifford Algebras, Vol. 17, No. 1, 2006, pp. 23-36. http://dx.doi.org/10.1007/s00006-006-0014-7
- V. L. Mironov and S. V. Mironov, “Octonic Representation of Electromagnetic Field Equations,” Journal of Mathematical Physics, Vol. 50, No. 1, 2009, Article ID: 012901. http://dx.doi.org/10.1063/1.3041499
- V. L. Mironov and S. V. Mironov, “Octonic SecondOrder Equations of Relativistic Quantum Mechanics,” Journal of Mathematical Physics, Vol. 50, No. 1, 2009, Article ID: 012302. http://dx.doi.org/10.1063/1.3058644
- V. L. Mironov and S. V. Mironov, “Octonic First-Order Equations of Relativistic Quantum Mechanics,” International Journal of Modern Physics A, Vol. 24, No. 22, 2009, pp. 4157-4167. http://dx.doi.org/10.1142/S0217751X09045480
- V. L. Mironov and S. V. Mironov, “Sedeonic Generalization of Relativistic Quantum Mechanics,” International Journal of Modern Physics A, Vol. 24, No. 32, 2009, pp. 6237-6254. http://dx.doi.org/10.1142/S0217751X09047739
- L. D. Landau and E. M. Lifshits, “Classical Theory of Fields,” 4th Edition, Pergamon Press, New York, 1975.
- P. A. M. Dirac, “The Principles of Quantum Mechanics,” Clarendon Press, Oxford, 1958.
- A. Macfarlane, “Hyperbolic Quaternions,” Proceedings of the Royal Society at Edinburgh, 1899-1900 Sessions, pp. 169-181.
- W. Pauli, “Zur Quantenmechanik des Magnetischen Elektrons,” Zeitschrift für Physik, Vol. 43, No. 9-10, 1927, pp. 601-623. http://dx.doi.org/10.1007/BF01397326
- P. A. M. Dirac, “The Quantum Theory of the Electron,” Proceedings of Royal Society at London. Series A, Vol. 117, No. 778, 1928, pp. 610-624. http://dx.doi.org/10.1098/rspa.1928.0023

