Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24369,4 pages DOI:10.4236/apm.2012.26059
The p.q.-Baer Property of Fixed Rings under Finite Group Action
Department of Mathematics, College of Sciences, Yanbian University, Yanji, China
Email: *hljin98@ybu.edu.cn, hljin98@hanmail.net
Received August 21, 2012; revised September 30, 2012; accepted October 8, 2012
Keywords: p.q.-Baer Property; Fixed Ring; Group Action
ABSTRACT
A ring R is called right principally quasi-Baer (simply, right p.q.-Baer) if the right annihilator of every principal right ideal of R is generated by an idempotent. For a ring R, let G be a finite group of ring automorphisms of R. We denote the fixed ring of R under G by RG. In this work, we investigated the right p.q.-Baer property of fixed rings under finite group action. Assume that R is a semiprime ring with a finite group G of X-outer ring automorphisms of R. Then we show that: 1) If R is G-p.q.-Baer, then RG is p.q.-Baer; 2) If R is p.q.-Baer, then RG are p.q.-Baer.
1. Introduction
Throughout this paper all rings are associative with identity. Recall from [1] that a ring R is called right principally quasi-Baer (simply, right p.q.-Baer) if the right annihilator of every principal right ideal of R is generated, as a right ideal, by an idempotent of R. A left principally quasi-Baer (simply, left p.q.-Baer) ring is defined similarly. Right p.q.-Baer rings have been initially studied in [1]. For more details on (right) p.q.-Baer rings, see [1-6].
Recall from [7] (see also [8]) that a ring R is called quasi-Baer if the right annihilator of every right ideal is generated, as a right ideal, by an idempotent of R. A ring R is called biregular if for each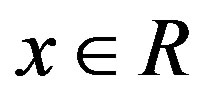 ,
, 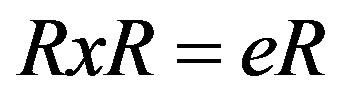 for some central idempotent
for some central idempotent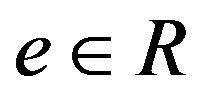 . We note that the class of right p.q.-Baer rings is a generalization of the classes of quasi-Baer rings and biregular rings.
. We note that the class of right p.q.-Baer rings is a generalization of the classes of quasi-Baer rings and biregular rings.
For a ring R, we use  to denote a fixed maximal right ring of quotients of R. According to [9] an idempotent
to denote a fixed maximal right ring of quotients of R. According to [9] an idempotent of a ring
of a ring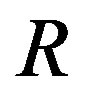 is called left (resp., right) semicentral if
is called left (resp., right) semicentral if 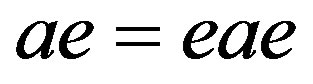 (resp.,
(resp.,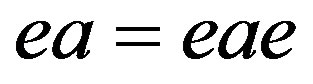 ) for all
) for all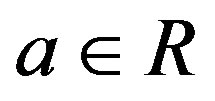 . Equivalently, an idempotent
. Equivalently, an idempotent is left (resp., right) semicentral if and only if eR (resp.,
is left (resp., right) semicentral if and only if eR (resp.,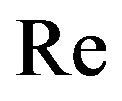 ) is a two-sided ideal of R. For a ring R, we let
) is a two-sided ideal of R. For a ring R, we let 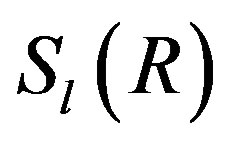 (resp.,
(resp.,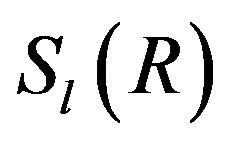 ) denote the set of all left (resp., right) semicentral idempotents. An idempotent
) denote the set of all left (resp., right) semicentral idempotents. An idempotent of a ring
of a ring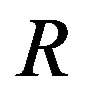 is called semicentral reduced if
is called semicentral reduced if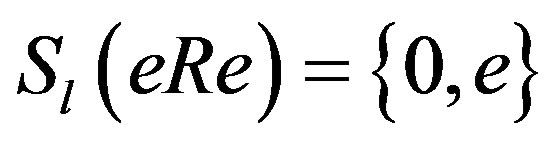 . Recall from [2] that a ring R is called semicentral reduced if
. Recall from [2] that a ring R is called semicentral reduced if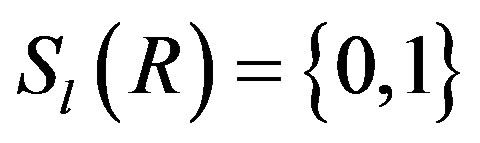 , i.e., 1 is a semicentral reduced idempotent of R.
, i.e., 1 is a semicentral reduced idempotent of R.
For a nonempty subset X of a ring R, we use 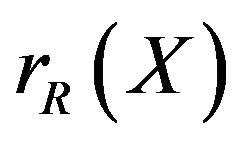 and
and 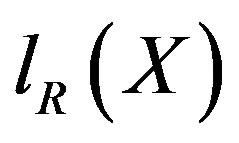 to denote the right annihilator and the left annihilator of X in R, respectively. If R is a semiprime ring and I is a two-sided ideal of R, then
to denote the right annihilator and the left annihilator of X in R, respectively. If R is a semiprime ring and I is a two-sided ideal of R, then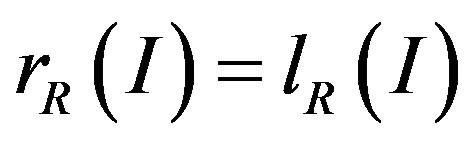 . For a right R-module
. For a right R-module and a submodule N of M, we use
and a submodule N of M, we use 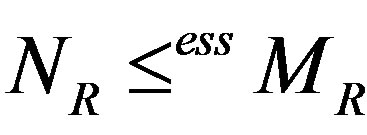 and
and  to denote that
to denote that 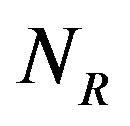 is essential in
is essential in 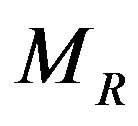 and
and 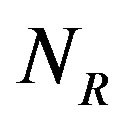 is dense in
is dense in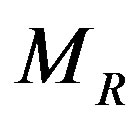 , respectively.
, respectively.
For a ring R, we let 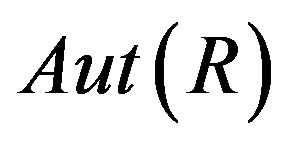 denote the group of ring automorphisms of R. Let
denote the group of ring automorphisms of R. Let 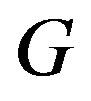 be a subgroup of
be a subgroup of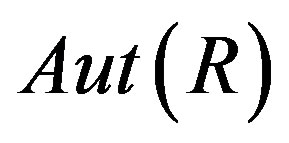 . For
. For  and
and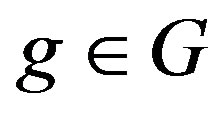 , we let
, we let 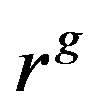 denote the image of r under g. We use
denote the image of r under g. We use 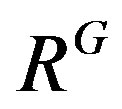 to denote the fixed ring of R under G, that is
to denote the fixed ring of R under G, that is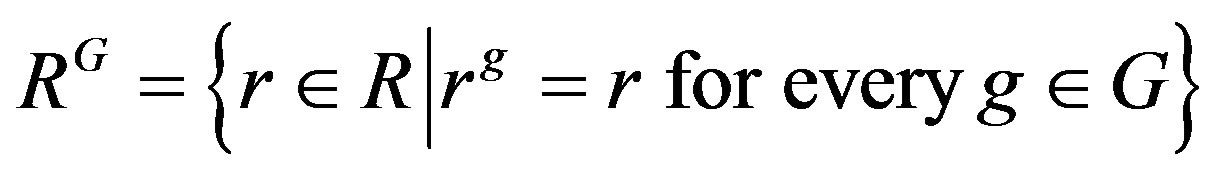 .
.
We begin with the following example.
2. Preliminary
Example 2.1. There exist a ring R and a finite group G of ring automorphisms of R such that R is right p.q.-Baer but RG is not right p.q.-Baer. Let 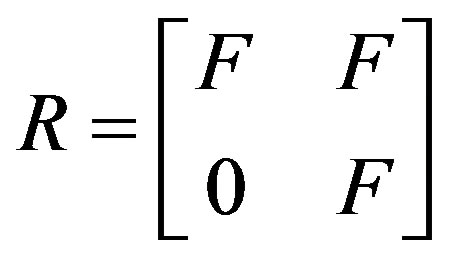 with a field F of characteristic 2. Then R is right p.q.-Baer. Define
with a field F of characteristic 2. Then R is right p.q.-Baer. Define 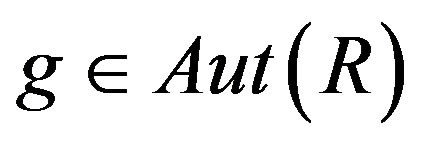 by
by
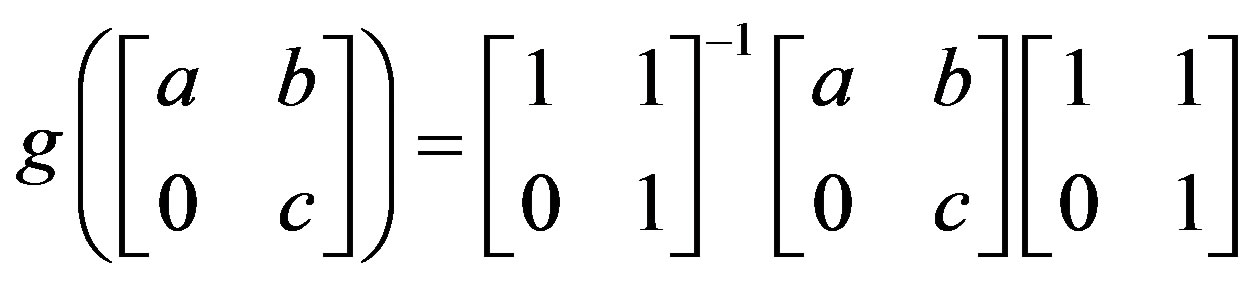
Then 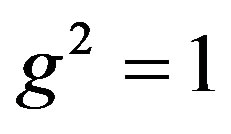 since the characteristic of F is 2.
since the characteristic of F is 2.
Now we show that RG is not right p.q.-Baer. The fixed ring under G is
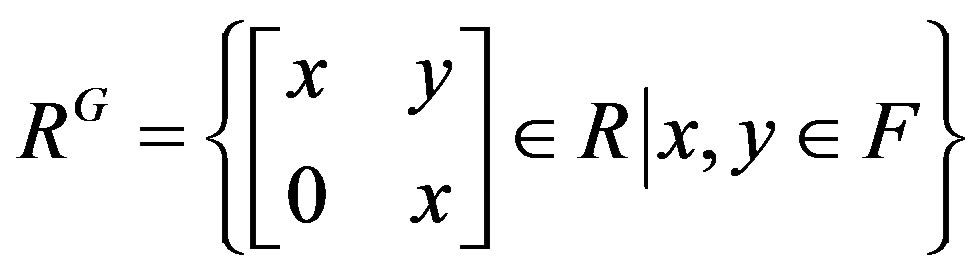
By computation we see that the idempotents of RG are only 0 and 1, thus RG is semicentral reduced. So if RG is right p.q.-Baer, then RG is a prime ring by [2, Lemma 4.2], a contradiction. Thus RG is not right p.q.-Baer.Also we can see that RG is not left p.q.-Baer.
Definition 2.2. Let R be a semiprime ring. For 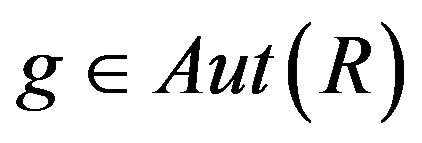 , let
, let
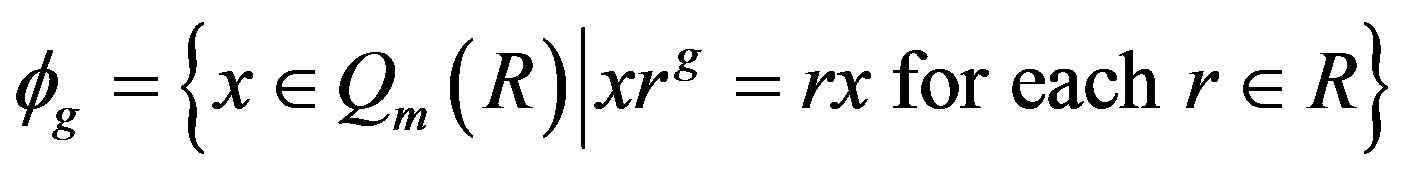 where
where 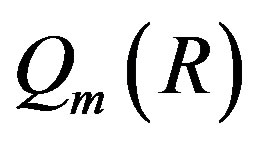 is the Martindale right ring of quotients of R (see [10] for more on
is the Martindale right ring of quotients of R (see [10] for more on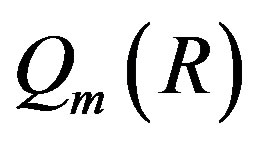 ). We say that
). We say that is Xouter if
is Xouter if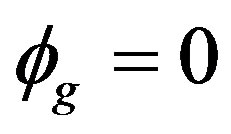 . A subgroup G of
. A subgroup G of 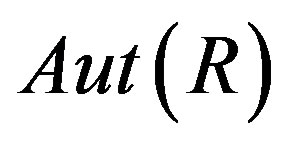 is called Xouter on R if every
is called Xouter on R if every 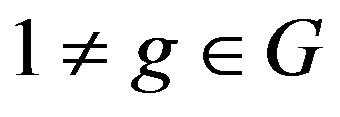 is X-outer. Assume that R is a semiprime ring, then for
is X-outer. Assume that R is a semiprime ring, then for , let
, let
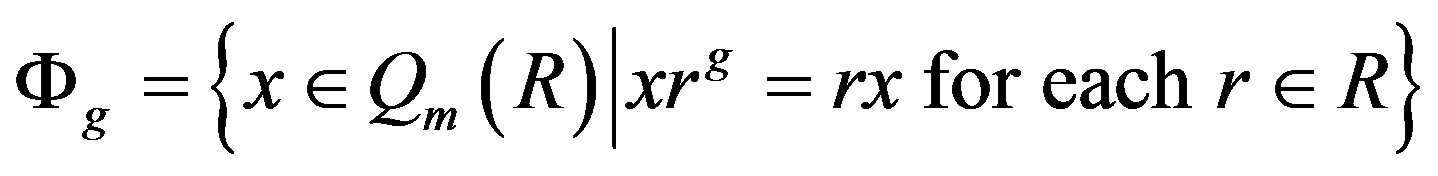 .
.
For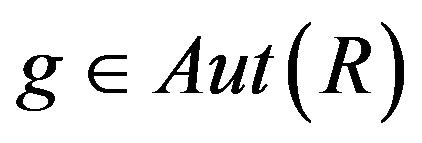 , we claim that
, we claim that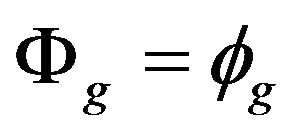 . Obviously
. Obviously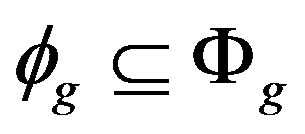 . Conversely, if
. Conversely, if 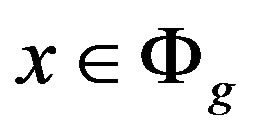 then
then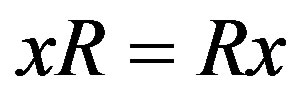 . There exists
. There exists 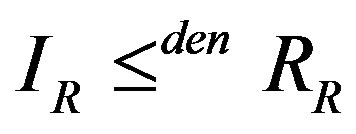 such that
such that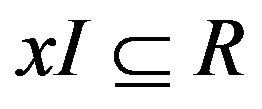 . Therefore
. Therefore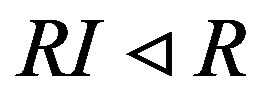 ,
, 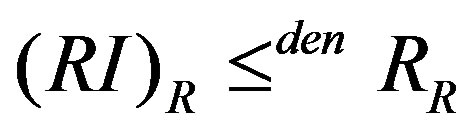 , and
, and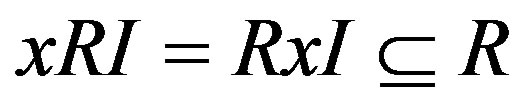 . Thus
. Thus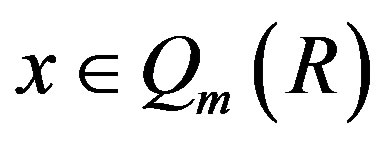 , hence
, hence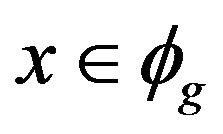 . Therefore
. Therefore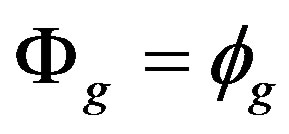 . So if G is X-outer on R, then G can be considered as a group of ring automorph-ismms of
. So if G is X-outer on R, then G can be considered as a group of ring automorph-ismms of 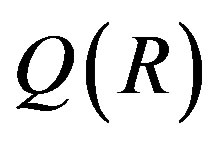 and G is X-outer on
and G is X-outer on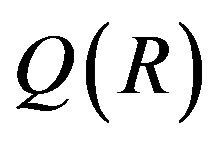 . For more details for X-outer ring automorphisms of a ring, etc., see [10, p. 396] and [11].
. For more details for X-outer ring automorphisms of a ring, etc., see [10, p. 396] and [11].
We say that a ring R has no nonzero n-torsion (n is a positive integer) if 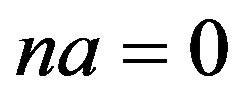 with
with 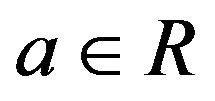 implies
implies .
.
Lemma 2.3. [12,13]
Let R be a semiprime ring and G a group of ring automorphisms of R. If 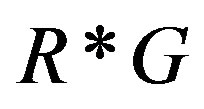 is semiprime, then
is semiprime, then 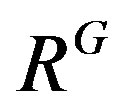 is semiprime.
is semiprime.
For a ring R, we use 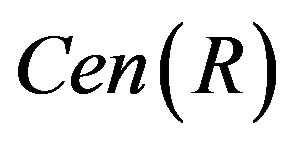 to denote the center of R.
to denote the center of R.
Lemma 2.4. For a semiprime ring R, let G be a group of X-outer ring automorphisms of R.
Then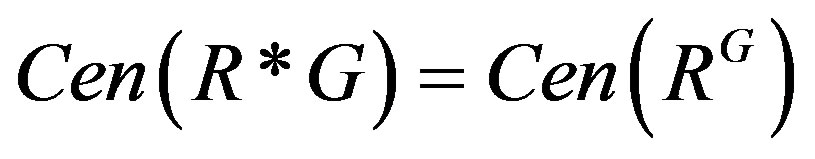 .
.
Proof.
Let 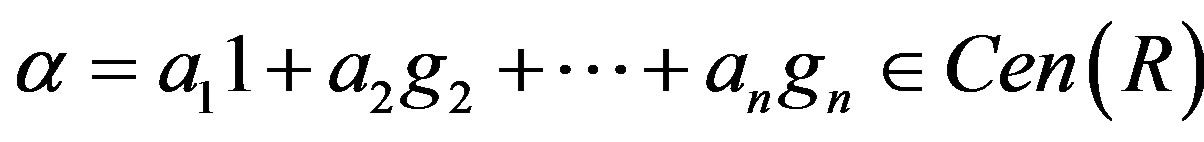 with
with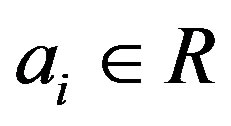 , 1 the identity of G, and
, 1 the identity of G, and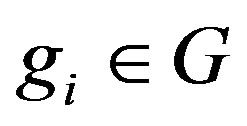 .
.
The 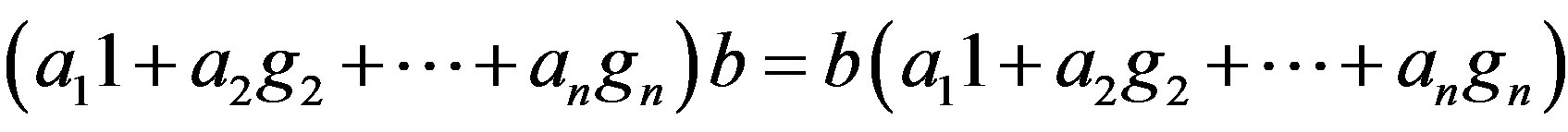 for all
for all . So
. So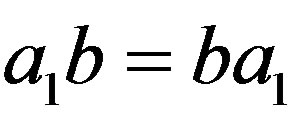 ,
, 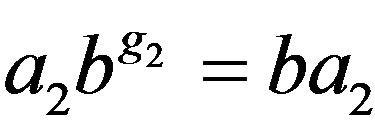 , ···,
, ···, 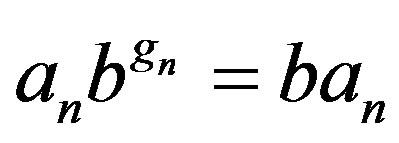 for all
for all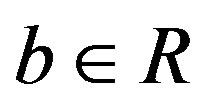 . Since G is X-outer, it follows that
. Since G is X-outer, it follows that
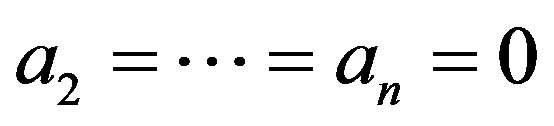 . Hence
. Hence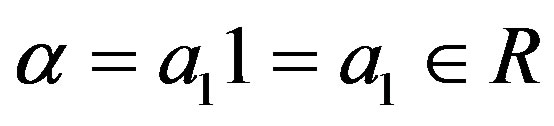 . Also since
. Also since 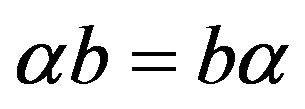 for all
for all , we have that
, we have that .
.
Note that for all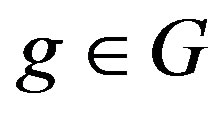 ,
, 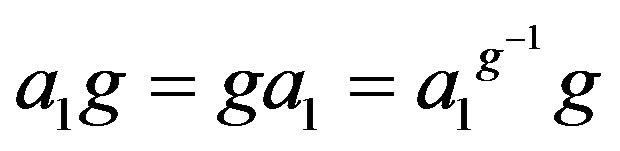 implies
implies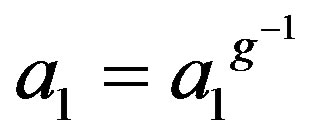 . So
. So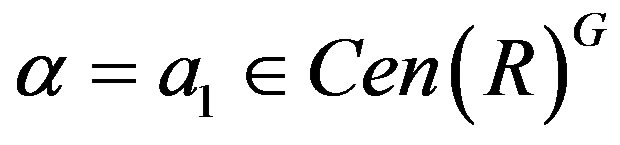 . Thus
. Thus
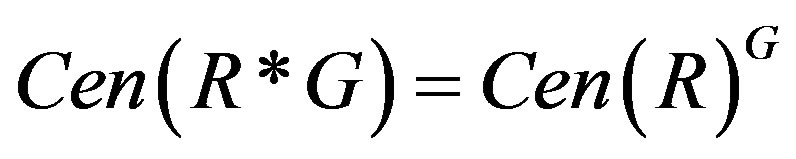 .
.
Conversely, 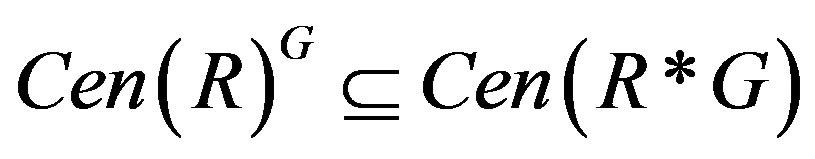 is clear.
is clear.
Therefore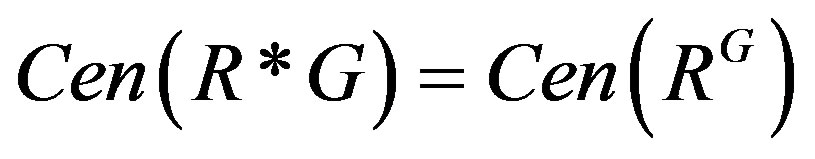 .
.
Lemma 2.5. [14] Assume that R is a semiprime ring and G is a finite group of X-outer ring automorphisms of R. Then .
.
Lemma 2.6. Assume that R is a semiprime ring and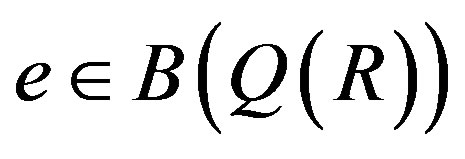 . Let
. Let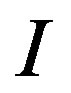 be a two-sided ideal of R such that
be a two-sided ideal of R such that 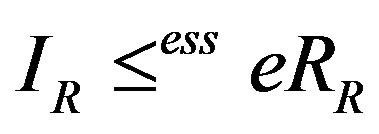 and
and 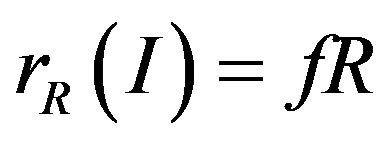 with
with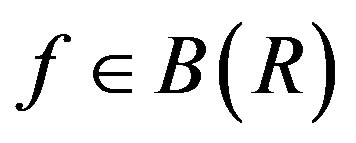 . Then
. Then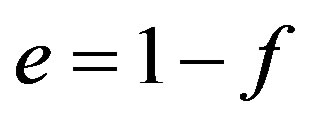 .
.
Proof. Since R is semiprime,
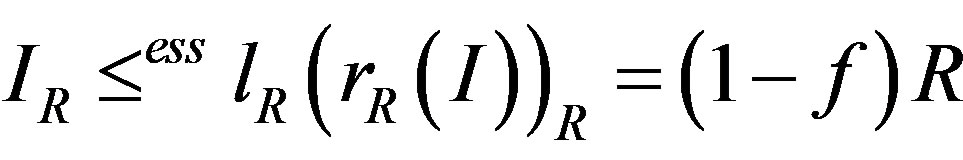 . Thus
. Thus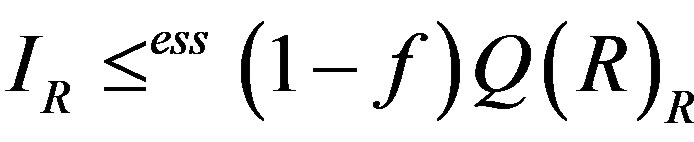 . As
. As ,
, . We note that e and
. We note that e and 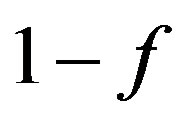 are in
are in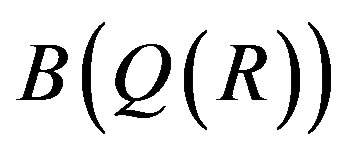 . So we have that
. So we have that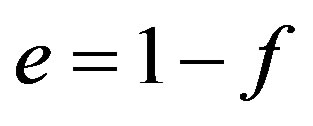 .
.
Lemma 2.7. [15] Let R be a semiprime ring with a finite group G of X-outer ring automorphisms of R.
1) For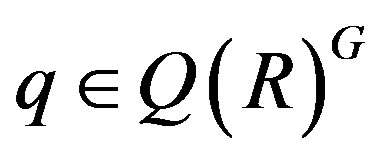 , let I be a dense right ideal I of RG such that
, let I be a dense right ideal I of RG such that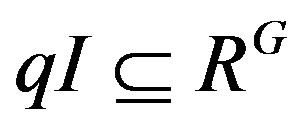 . Then IR is a dense right ideal of R and the map
. Then IR is a dense right ideal of R and the map  defined by
defined by
 , with
, with 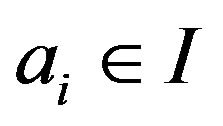 and
and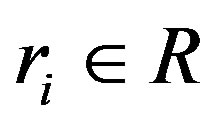 , is a right R-homomorphism. Moreover
, is a right R-homomorphism. Moreover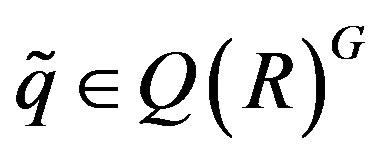 .
.
2) The map 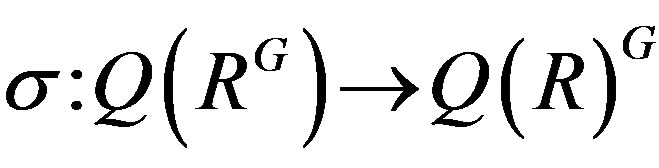 defined by
defined by 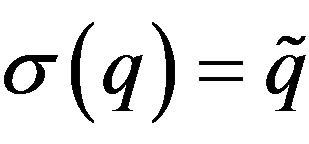 is a ring isomorphism.
is a ring isomorphism.
3) Let 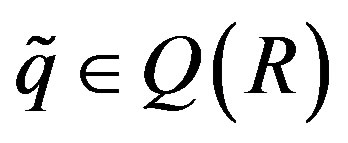 and K a dense right ideal of R such that
and K a dense right ideal of R such that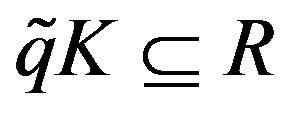 . Then
. Then 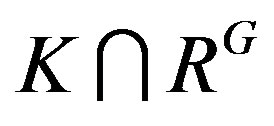 is a dense right ideal of RG
is a dense right ideal of RG
and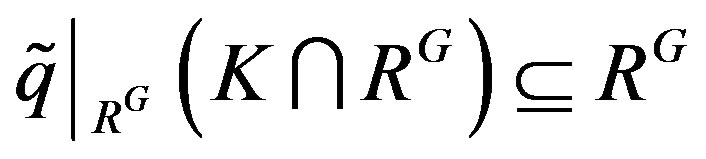 , where
, where 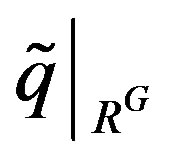 is the restriction of
is the restriction of 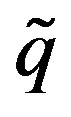 to RG. Thus
to RG. Thus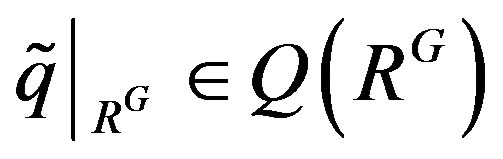 .
.
For a ring R with a group G of ring automorphism of R, we say that a right ideal I of R is G-invariant if 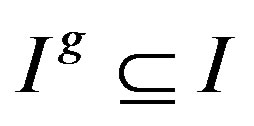 for every
for every , where
, where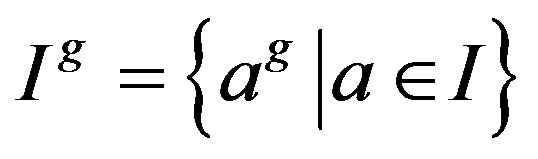 .
.
Proposition 2.8. [1] Let R be a semiprime ring. Then the followings are equivalent.
1) R is right p.q.-Baer;
2) Every principal two-sided ideal of R is right essential in a ring direct summand of R;
3) Every finitely generated two-sided ideal of R is right essential in a ring direct summand of R;
4) Every principal two-sided ideal of R that is closed as a right ideal is a direct summand of R;
5) For every principal two-sided ideal I of R, 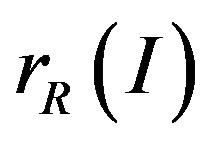 is right essential in a direct summand of R;
is right essential in a direct summand of R;
6) R is left p.q.-Baer.
For a ring R with a group G of ring automorphisms of R, we say that a right ideal I of R is G-invariant if 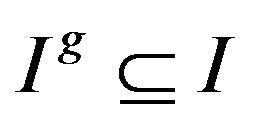 for every
for every , where
, where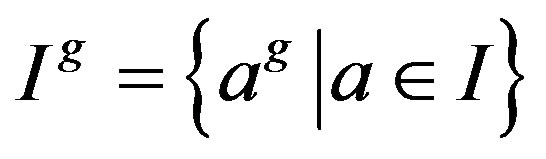 . Assume that R is a semiprime ring with a group G of ring automorphisms of R. We say that R is G-p.q.-Baer if the right annihilator of every finitely generated G-invariant two-sided ideal is generated by an idempotent, as a right ideal. By Proposition 8, if a ring R is semiprime p.q.- Baer with a group G of ring automorphisms of R, then R is G-p.q.-Baer.
. Assume that R is a semiprime ring with a group G of ring automorphisms of R. We say that R is G-p.q.-Baer if the right annihilator of every finitely generated G-invariant two-sided ideal is generated by an idempotent, as a right ideal. By Proposition 8, if a ring R is semiprime p.q.- Baer with a group G of ring automorphisms of R, then R is G-p.q.-Baer.
A ring R is called right Rickart if the right annihilator of each element is generated by an idempotent of R. A left Rickart ring is defined similarly. A ring R is called Rickart if R is both right and left Rickart. A ring R is said to be reduced if R has no nonzero nilpotent element. We note that reduced Rickart rings are p.q.-Baer rings.
We put
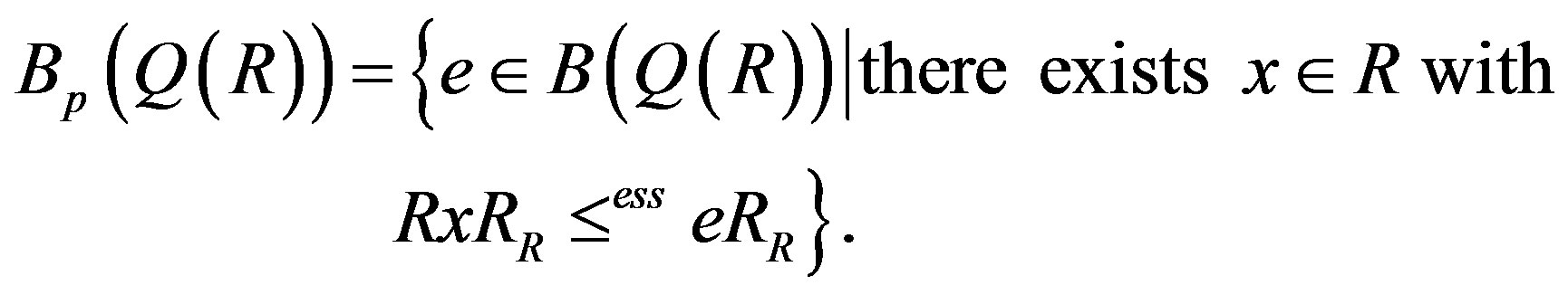
Let 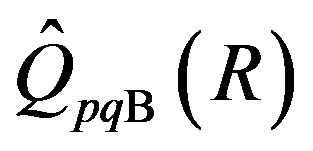 be the subring of
be the subring of 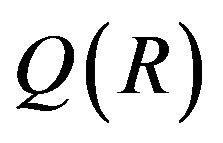 generated by R and
generated by R and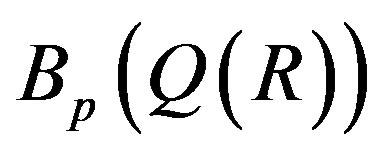 .
.
Lemma 2.9. [16] Assume that R is a semiprime ring. Then:
1) The ring 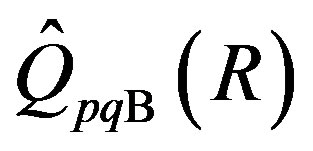 is the smallest right ring of quotients of
is the smallest right ring of quotients of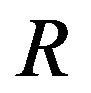 which is p.q.-Baer;
which is p.q.-Baer;
2) R is p.q.-Baer if and only if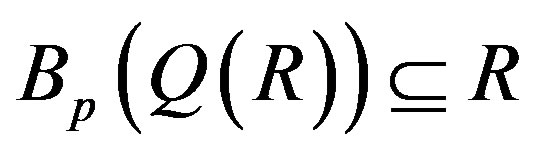 .
.
With these preparations, in spite of Example 1, we have the following result for p.q.-Baer property of RG on a semiprime ring R for the case when G is finite and X-outer.
3. Main Results
Theorem 3.1. Let R be a semiprime ring with a finite group G of X-outer ring automorphisms of R. Then:
1) If R is G-p.q.-Baer, then RG is p.q.-Baer.
2) If R is reduced G-p.q.-Baer, then RG is Rickart.
Proof. 1) Assume that R is G-p.q.-Baer. To show that RG is p.q.-Baer, it is enough to see that 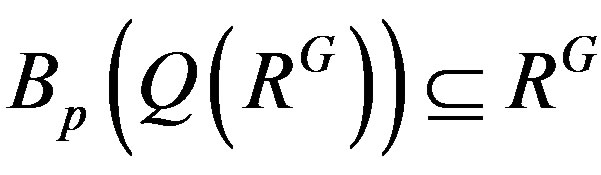 by Lemma 9 since RG is semiprime from Lemma 3. Let
by Lemma 9 since RG is semiprime from Lemma 3. Let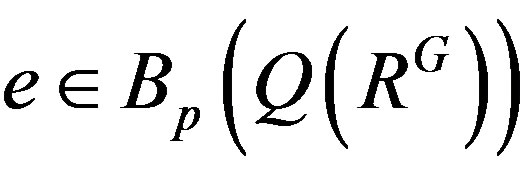 . Then
. Then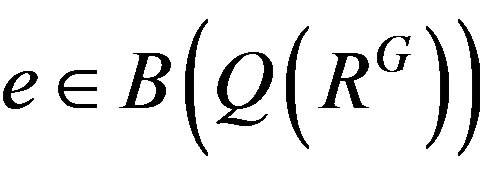 , so
, so 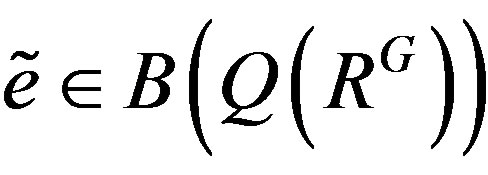 by Lemma 7. From Lemma 9, there exists
by Lemma 7. From Lemma 9, there exists 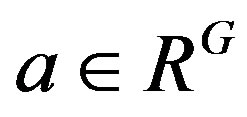 such that
such that 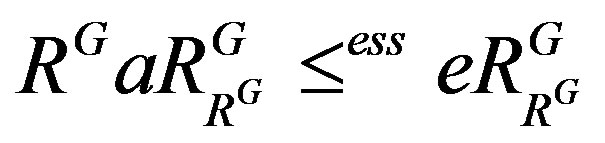 because
because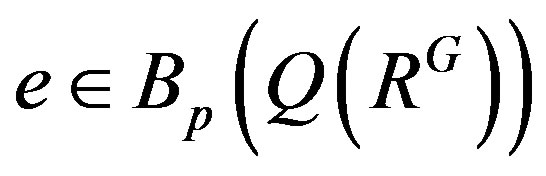 . Note that
. Note that .
.
We show that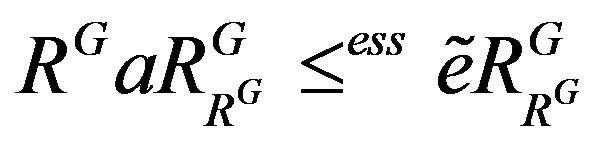 . To see this, say
. To see this, say
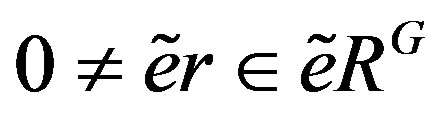 with
with . Then
. Then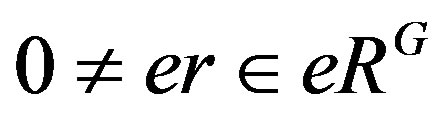 . So there exists
. So there exists 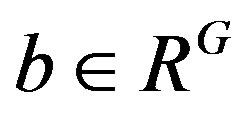 such that
such that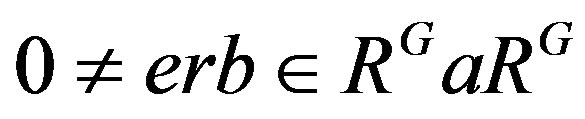 . Hence
. Hence 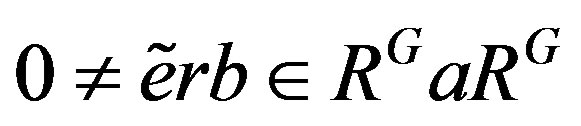 .
.
Observe that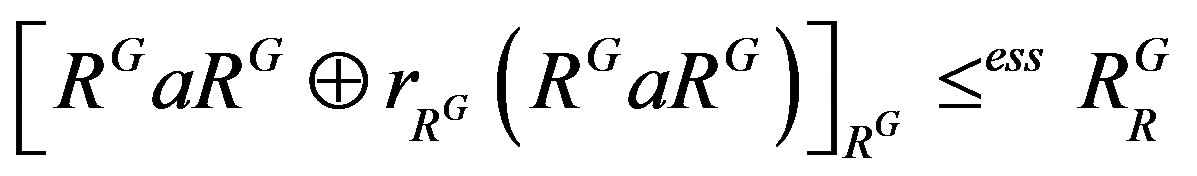 , as RG is semiprime from Lemma 3. So
, as RG is semiprime from Lemma 3. So 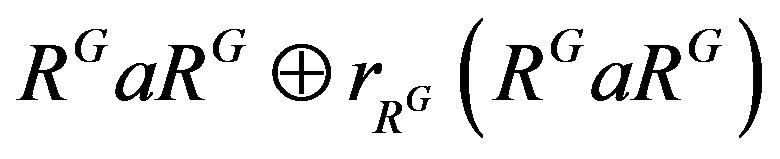 is a dense right ideal of RG since RG is semiprime. By Lemma 7,
is a dense right ideal of RG since RG is semiprime. By Lemma 7, 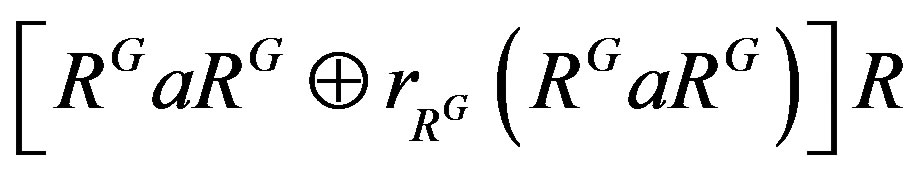 is a dense right ideal of
is a dense right ideal of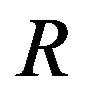 . So it is essential in
. So it is essential in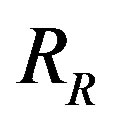 . Hence
. Hence
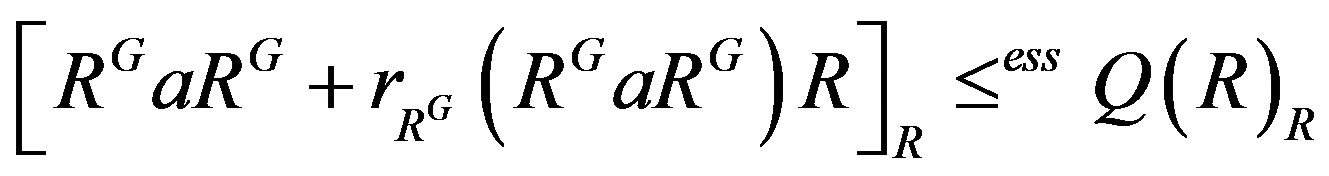 .
.
We claim that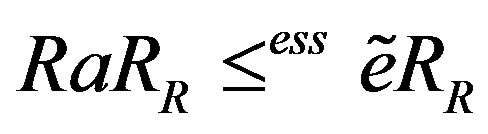 .
.
First note that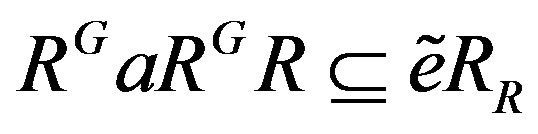 . For the claim, it is enough to show that
. For the claim, it is enough to show that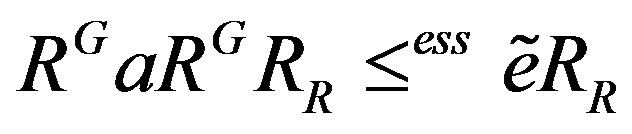 . Take
. Take
 with
with . Then there exists
. Then there exists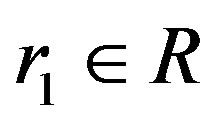 such that
such that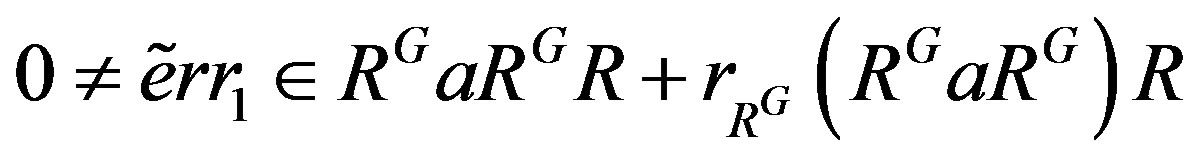 . Say
. Say
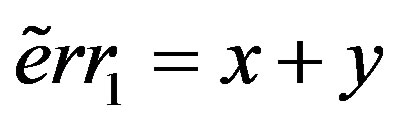 , where
, where 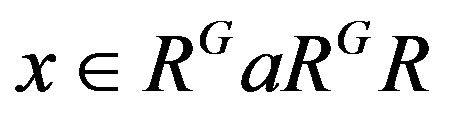 and
and 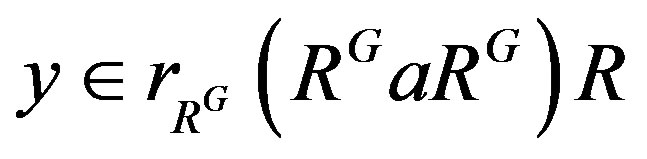 .
.
Then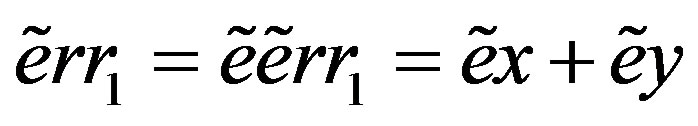 .
.
Put 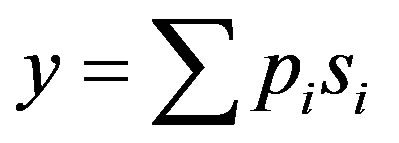 with
with 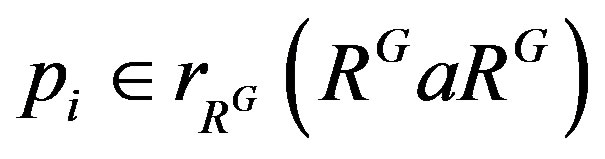 and
and . Then
. Then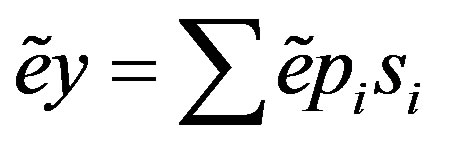 . In this case,
. In this case, 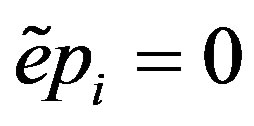 for all i. To see this, assume on the contrary that there is
for all i. To see this, assume on the contrary that there is 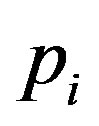 such that
such that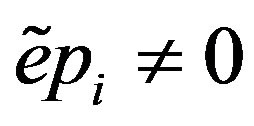 . Note that
. Note that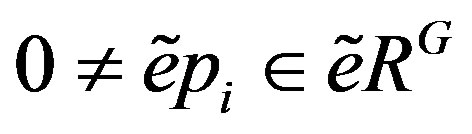 .
.
Thus there exists 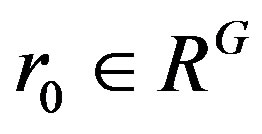 such that
such that 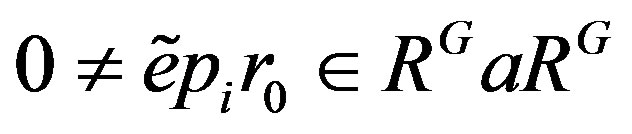 because
because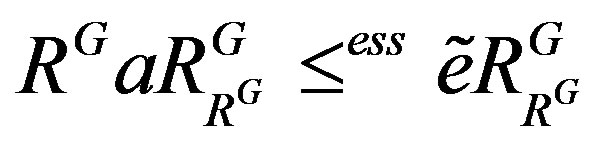 .
.
Also 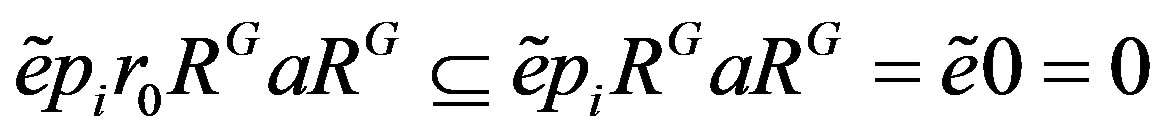 because
because 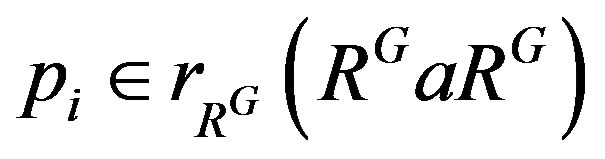 . Therefore we have that
. Therefore we have that 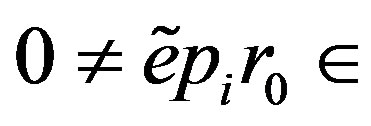
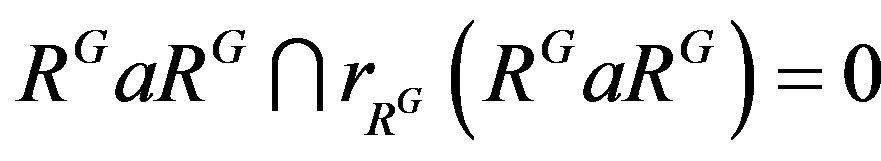 , a contradiction. Thus
, a contradiction. Thus 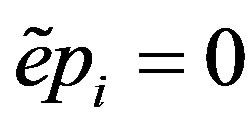 for all i, so
for all i, so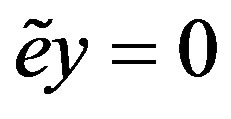 . Hence
. Hence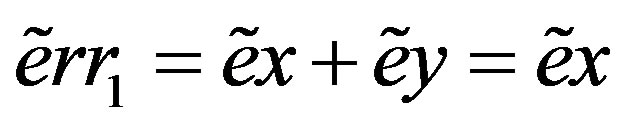 . Now since
. Now since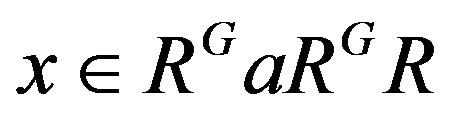 , write
, write 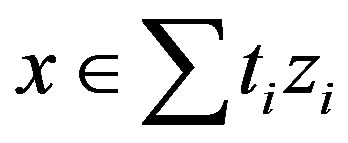 with
with 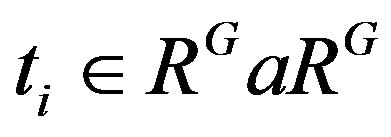 and
and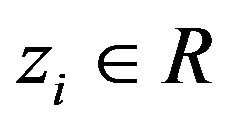 . Then
. Then  because
because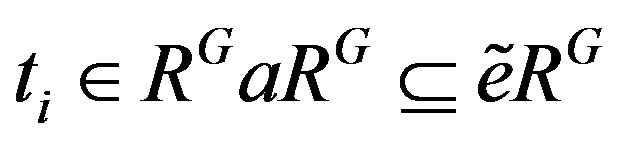 . So
. So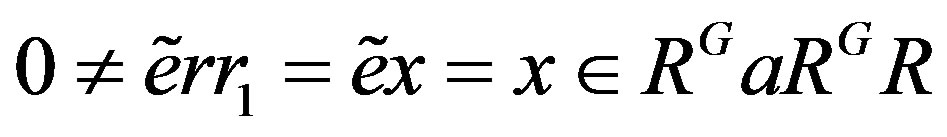 . Therefore
. Therefore . Note that
. Note that
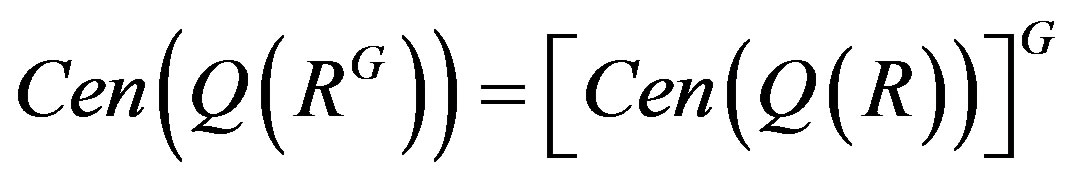 by Lemma 5. Therefore
by Lemma 5. Therefore
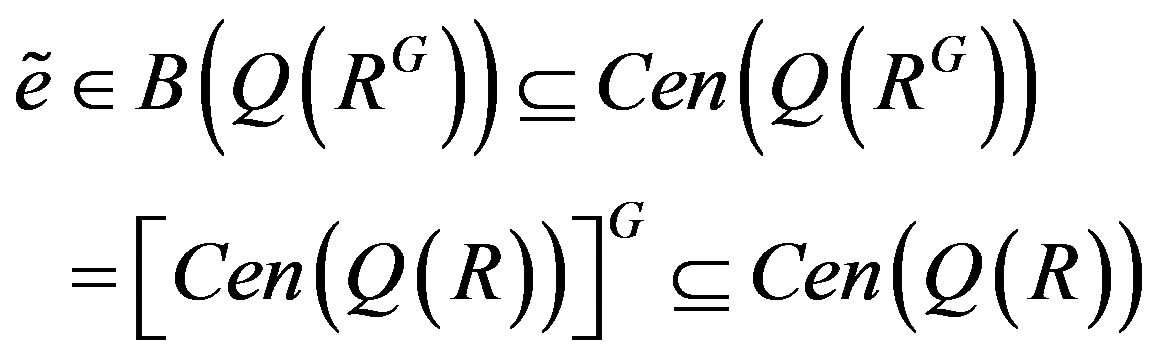
Hence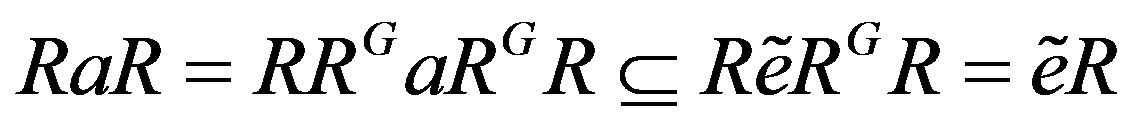 .
.
As RaR is a G-invariant two-sided ideal of R and R is R-p.q.-Baer, there is  such that
such that  . From [9],
. From [9],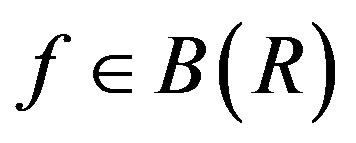 . As
. As 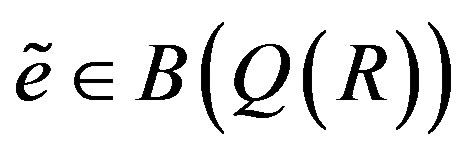 and
and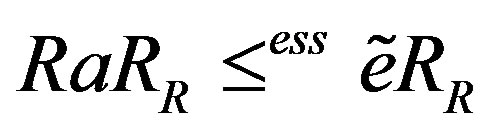 , it follows that
, it follows that 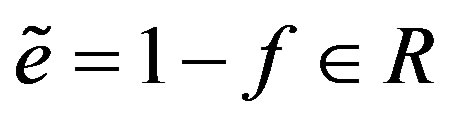 by Lemma 6, so
by Lemma 6, so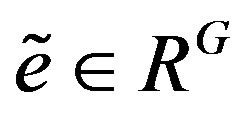 .
.
Therefore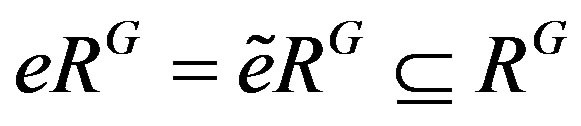 , and thus
, and thus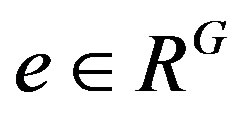 .
.
So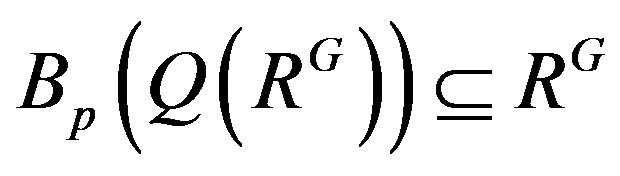 , and hence RG is p.q.-Baer by Lemma 9.
, and hence RG is p.q.-Baer by Lemma 9.
2) We recall that a reduced p.q.-Baer ring is Rickart. Thus if R is reduced G-p.q.-Baer, then RG is Rickart from 1).
4. Conclusion
In [14], the quasi-Baer property of fixed rings under finite group actions on a semiprime ring and their applications to C*-algebras have been studied (see also [17,18]). Motivated by investigations in [14], in this paper we investigate the right p.q.-Baer property of fixed rings under finite group actions on a given semiprime ring. Assume that R is a semiprime ring with a finite group G of X-outer ring automorphisms of R. Then we show that if R is G-p.q.-Baer, then RG is p.q.-Baer. Thus if R is a semiprime p.q.-Baer ring with finite group G of X-outer ring automorphisms of R, then RG is p.q.-Baer.
REFERENCES
- G. F. Birkenmeier, J. Y. Kim and J. K. Park, “Principally Quasi-Baer Rings,” Communications in Algebra, Vol. 29, No. 2, 2001, pp. 639-660. doi:10.1081/AGB-100001530
- G. F. Birkenmeier, H. E. Heatherly, J. Y. Kim and J. K. Park, “Triangular Matrix Representations,” Journal of Algebra, Vol. 230, No. 2, 2000, pp. 558-595. doi:10.1006/jabr.2000.8328
- G. F. Birkenmeier, J. Y. Kim and J. K. Park, “Quasi-Baer Ring Extensions and Biregular Rings,” Bulletin of the Australian Mathematical Society, Vol. 61, No. 1, 2000, pp. 39-52. doi:10.1017/S0004972700022000
- G. F. Birkenmeier, J. Y. Kim and J. K. Park, “A Sheaf Representation of Quasi-Baer Rings,” Journal of Pure and Applied Algebra, Vol. 146, No. 3, 2000, pp. 209-223. doi:10.1016/S0022-4049(99)00164-4
- G. F. Birkenmeier and J. K. Park, “Triangular Matrix Representations of Ring Extensions,” Journal of Algebra, Vol. 265, No. 2, 2003, pp. 457-477. doi:10.1016/S0021-8693(03)00155-8
- G. F. Birkenmeier, J. Y. Kim and J. K. Park, “Polynomial Extensions of Baer and Quasi-Baer Rings,” Journal of Pure and Applied Algebra, Vol. 159, No. 1, 2001, pp. 25- 42. doi:10.1016/S0022-4049(00)00055-4
- W. E. Clark, “Twisted Matrix Units Semigroup Algebras,” Duke Mathematical Journal, Vol. 34, No. 3, 1967, pp. 417-423. doi:10.1215/S0012-7094-67-03446-1
- A. Pollingher and A. Zaks, “On Baer and Quasi-Baer Rings,” Duke Mathematical Journal, Vol. 37, No. 1, 1970, pp. 127-138. doi:10.1215/S0012-7094-70-03718-X
- G. F. Birkenmeier, “Idempotents and Completely Semiprime Ideals,” Communications in Algebra, Vol. 11, No. 6, 1983, pp. 567-580. doi:10.1080/00927878308822865
- T. Y. Lam, “Lectures on Modules and Rings,” Springer, Berlin, 1998.
- J. W. Fisher and S. Montgomery, “Semiprime Skew Group Rings,” Journal of Algebra, Vol. 52, No. 1, 1978, pp. 241-247. doi:10.1016/0021-8693(78)90272-7
- M. Cohen, “Morita Context Related to Finite Automorphism Groups of Rings,” Pacific Journal of Mathematics, Vol. 98, No. 1, 1982, pp. 37-54.
- S. Montgomery, “Outer Automorphisms of Semi-Prime Rings,” Journal London Mathematical Society, Vol. 18, No. 2, 1978, pp. 209-220. doi:10.1112/jlms/s2-18.2.209
- H. L. Jin, J. Doh and J. K. Park, “Group Actions on Quasi-Baer Rings,” Canadian Mathematical Bulletin, Vol. 52, 2009, pp. 564-582. doi:10.4153/CMB-2009-057-6
- J. Osterburg and J. K. Park, “Morita Contexts and Quotient Rings of Fixed Rings,” Houston Journal of Mathematics, Vol. 10, 1984, pp. 75-80.
- G. F. Birkenmeier, J. K. Park and S. T. Rizvi, “Principally Quasi-Baer Ring Hulls,” Advances in Ring Theory, 2010, pp. 47-61. doi:10.1007/978-3-0346-0286-0_4
- G. F. Birkenmeier, J. K. Park and S. T. Rizvi, “Hulls of Semiprime Rings with Applications to C∗-Algebras,” Journal of Algebra, Vol. 322, No. 2, 2009, pp. 327-352. doi:10.1016/j.jalgebra.2009.03.036
- G. F. Birkenmeier, J. K. Park and S. T. Rizvi, “The Structure of Rings of Quotients,” Journal of Algebra, Vol. 321, No. 9, 2009, pp. 2545-2566. doi:10.1016/j.jalgebra.2009.02.013
NOTES
*Corresponding author.

