World Journal of Condensed Matter Physics
Vol.05 No.04(2015), Article ID:61515,13 pages
10.4236/wjcmp.2015.54032
Coexistence of Spin Density Wave (SDW) and Superconductivity in Ba1−xKxFe2As2
Haftu Brhane
Department of Physics, Haramaya University, Diredawa, Ethiopia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 28 March 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT
With the use of a model Hamiltonian and retarded double time green’s function formalism, we obtain mathematical expressions for spin density wave and superconductivity parameters. The model reveals a distinct possibility of the coexistence of magnetic phase and superconductivity, which are two usually irreconcilable cooperative phenomena. The work is motivated by the recent experimental evidences of coexistence of spin density wave and superconductivity in a number of FeAs-based superconductors. The theoretical results are then applied to show the coexistence of spin density wave and superconductivity in iron pnictide compound Ba1−xKxFe2As2 (0.2 ≤ x < 0.4).
Keywords:
Retarded Double Time Green’s Function Formalism, Spin Singlet and Triplet State, Spin Density Wave and Superconducting

1. Introduction
The interplay between superconductivity and magnetism has been an interesting topic in condensed mater physics which has been considered until very recently hostile and incompatible. Since the discovery of superconductivity in quaternary pnictide-oxides with critical temperatures (TC) up to 55 K a lot of tremendous interest has been generated in the study of coexistence of these two cooperative phenomena of superconductivity and magnetism. After first reports on superconductivity in undoped LaNiPO [1] [2] below 5 K, shortly after this discovery the breakthrough was a TC of 26 K in the F-doped arsenide LaO1−xFxFeAs system [3] .
In addition to this several groups reported an increase of TC values by replacing La with smaller-size rare- earth ions like CeO1−xFxFeAs [4] , and samarium-arsenide oxides Sm(O1−xFx)FeAs with a critical temperature TC of 55 K [5] [6] . The iron based superconductors promise interesting applications. While the interplay of superconductivity and magnetism, as well as their mechanisms remains the issues of active debates and studies, one thing in FeSC riddle is clear that it is the complex multi-band electronic structure of these compounds that determine their rich and puzzling properties. What is important and captivating is that this complexity seems to play a positive role in the struggle for understanding the FeSC physics and also for search of the materials with higher TC [7] .
The FeSC is quite promising for applications. Having much higher Hc than cuprates and high isotropic critical currents [8] they are attractive for electrical power and magnet applications, while the coexistence of magnetism and superconductivity makes them interesting for spintronics [9] . All the compounds share similar electronic band structure in which the electronic states at the Fermi level are occupied predominantly by the Fe 3d electrons [7] .
By combining transport, X-ray and neutron diffraction experiment studies, the first member of a new family of iron pnictide superconductors (Ba1−xKx)Fe2As2 with the ThCr2Si2-type structure was discovered a bulk superconductor with TC = 38 K and both the SDW and the superconducting orders coexist in the (Ba1−xKx)Fe2As2 (0.2 ≤ x < 0.4). The structural and electronic properties of the parent compound BaFe2As2 are closely related to LaFeAsO. The induced superconductivity by hole doping is found to have a significantly higher TC in comparison with hole doped LaFeAsO. In contrast to previously stated opinions, the results prove that hole doping is definitely a possible pathway to induce high-TC superconductivity, at least in the oxygen-free compounds [10] .
The above exciting discovery stimulated a lot of interest in the study of coexistence of superconductivity and magnetism. The proximity of the magnetic and superconducting (SC) phases suggests a close relationship between the two phenomena. It is generally believed that the magnetic couplings between the itinerant electrons and/or between the itinerant electron and local spin are essential to both spin density wave instability and superconductivity. Besides, other experimental and theoretical findings, especially the antiferromagnetic ground state and the SDW anomaly of LaFeAsO strongly suggest that the pairing mechanism of the electrons is likely to be connected with spin fluctuations, as it has been assumed for the cuprates [10] .
Triplet superconductivity appears provided that we have coexistence of singlet superconductivity and SDW. In many high
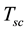 superconductors, superconducting mechanism is attributed to strong coulomb interactions of the electrons in the system, which can also be the cause for the appearance of SDW state. This suggests the existence of competition between the two states [11] . The properties of the unconventional triplet superconductivity and SDW with an emphasis on the analysis of their order parameter were reviewed.
superconductors, superconducting mechanism is attributed to strong coulomb interactions of the electrons in the system, which can also be the cause for the appearance of SDW state. This suggests the existence of competition between the two states [11] . The properties of the unconventional triplet superconductivity and SDW with an emphasis on the analysis of their order parameter were reviewed.
Research on superconducting iron arsenides has largely focused on ternary compounds with the ThCr2Si2-type structure, rather than arsenide oxides (LaFeAsO derivatives) [12] . This is because single-phase samples and also large single crystals of the ternary compounds are much easier to obtain. Partial replacement of barium for potassium (hole doping) induced superconductivity at 38 K in (Ba0.6K0.4)Fe2As2, [13] .
The relation between the spin-density-wave (SDW) and superconducting order is a central topic in current research on the superconducting iron pnictide based high TC superconductors. So, in this paper, we start with a model Hamiltonian which incorporates not only terms of the BCS but also by assuming the pairing interaction is due to spin fluctuations for iron pnictide superconductors Ba1−xKxFe2As2, to examine the coexistence of spin density wave and superconductivity.
2. Model Hamiltonian of the System
The purpose of this work is to study theoretically the co-existence of spin density wave and superconductivity properties in the compound Ba1−xKxFe2As2 in general and to find expression for transition temperature and order parameter in particular. For this purpose, we tried to find the mathematical expression for the superconducting critical temperature (TC), superconducting order parameter (∆sc) the magnetic order parameter (M) and SDW transition temperature (TSDW). Within the framework of the BCS model, the model of the Hamiltonian for coexistence SDW and superconductivity in the compound can be express as:
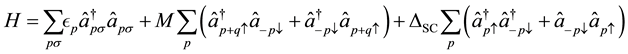 (1)
(1)
where
 are the creation (annihilation) operators of an electron having the wave number p and spin
are the creation (annihilation) operators of an electron having the wave number p and spin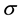 .
.
Whereas (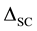 ) superconducting order parameter and (M) SDW order parameters. The Hamiltonian in (1) will be used to determine the equations of motion in terms of the Green function.
) superconducting order parameter and (M) SDW order parameters. The Hamiltonian in (1) will be used to determine the equations of motion in terms of the Green function.
2.1. Coupling of SDW and Superconducting Order Parameters
The Double time dependent Green’s function equal to the change of the average value of some dynamic quantity by the time t and useful because they can be used to describe the effect of retarded interactions and all quantities of physical interest can be derived from them. To get the equation of motion we use the double-time temperature dependent retarded Green function is given by Zubarev [14] :
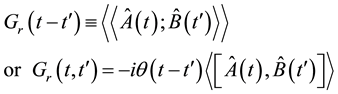 (2)
(2)
where
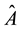 and
and
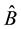 are Heisenberg operators and
are Heisenberg operators and
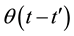 is the Heaviside step function. Now, using Dirac delta function and Heisenberg operators, we can write as:
is the Heaviside step function. Now, using Dirac delta function and Heisenberg operators, we can write as:
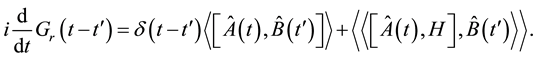
The Fourier transformation
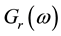 is given by
is given by
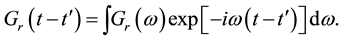 (3)
(3)
Taking the Fourier transform we get:
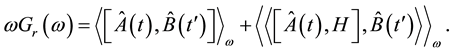 (4)
(4)
From (4), it follows that
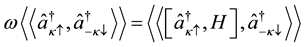 (5)
(5)
where the anti-commutation relation,
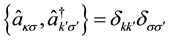 (6)
(6)
has been used. To derive an expression for

(1) and using the identities and

Solving the commutator in Equation (5) by using the Hamiltonian in e Equation (1), we get

After some lengthy but straightforward calculations; we arrive at the following results:


Substituting (8) in to (5), we get

The equation of motion for the correlation


Evaluating the commutator in Equation (10) using Hamiltonian:

After some lengthy but straightforward calculations; we arrive at the following results:


Substituting (11) in to (10), we get

Similarly as we did in the above the equation of motion for the correlation

is given by:

and

From Equation (12), we obtain:

And from Equation (14):

Plugging Equations (15) and (16) in (9), yields:

And insert Equations (15) and (16) in (13), we have:

Applying nesting condition



and

Let

Then Equations (19) and (20) respectively becomes:


Finally we can express:

Using the expression


To take into account the temperature dependence of order parameters, we shall write as:


where
Using Equation (24) into Equation (25), we obtain

Let us use

and

Plugging Equation (28) and Equation (29) in Equation (27), we get:

For mathematical convenience, we replace the summation in (27) by integration. Thus
where

The density of state
Assume



where
Finally we can write Equation (31) as:

From (32), it clearly follows that the order parameters

We now consider the equations of motion for SDW, we can write,

Doing a lot as we did in the above, we finally get:



and

Doing a lot as we did in the previous, we finally get:

Using Equation (38) in to Equation (26), the SDW order Parameter M is given by:

or

So, finally we get:

From (41), it is again evident that the order parameters

It is, therefore, possible that in some temperature interval, SDW and superconductivity can co-exist, although one phase has a tendency to suppress the critical temperature and the order parameter of the other phase.
2.2. Dependence of the Magnetic Order Parameter on the Transition Temperature for Spin Density Wave and Superconductivity
To study Equation (32), we consider the case, when
We can then replace
In (32) and get,
Using the integral relation,

the above equation reduces to,

from the BCS theory, the order parameter

using this result in (43), we obtain

To solve (45) numerically we use Debay temperature and the interband BCS coupling constant.
To estimate α, I consider the case

From (32), we then have

Putting



Using Laplacian’s transformation with Matsuber relation result we can write,
where



Using the fact that, for low temperature,




We can write (48) as,

Using L’Hospital’s rule, it is easy to show that
which can be neglected since

Substituting (49) in (46), we then obtain
This implies,

which can be used to estimate


energy.
To study how M depends on the magnetic transition temperature

proceeding as before, it is easy to show that,
Neglecting
This gives;

we can use (52) to draw the phase diagram for M and
2.3. Pairing of Spin Density Wave (SDW) and Triplet Superconductivity
In this section we want to drive an expressions for the order parameters of SDW, M, and triplet superconductivity,


where the superconducting order parameter is given by:

We now consider the equation of motion:

Doing a lot as we did in the above for the commutation and using the assumption


The nesting property of the Fermi surface that expected for low dimensional band structure and attributed to the SDW ordering gives as an expression
Finally:

Since we are dealing with only the triplet pair; we can ignore the singlet correlation.
The equation of motion for correlation in RHS of (57) is written as:

and

which can be rewritten, after solving the commutation relation and removing the singlet pair.
From Equations (58) and (59), we will get;

With help of Equation (60) and Equation (57):

which in turn can be written as:

Applying nesting condition



Using the expression

where
and
By taking an approximation over the superconducting order parameter, such that it is independent of wave vector, finally we get:

We now consider the equations of motion for SDW, we can write,

Doing a lot as we did in the above, we finally get:

So,

3. Results
Starting with a model Hamiltonian for the system and using Green’s function formalism, we obtained expressions for superconducting transition temperature (TC), magnetic order parameter (M) and spin density wave transition temperature (TSDW). Based on these result we found two very vital equations ((45) and (52)). Moreover, we scrutinized the effect of magnetic order parameter (M) on superconducting transition temperature (TC) and spin density wave transition temperature (TSDW) in Ba1−xKxFe2As2 by using the relevant parameters. For this purpose, we have used (45) which have been numerically solved using the relevant parameters to plot the phase diagram for magnetic order parameter (M) versus superconducting transition temperature (TC). In the same figure, we have also plotted the phase diagram of magnetic ordering (M) versus spin density wave transition temperature (TSDW), using (52). From the graph we observe TC decreases with increase in M, whereas TSDW increases with increase in M. The phase diagrams of M versus TC and M versus TSDW, were merged to obtain the region where both spin density wave and superconductivity co-exist. The regions of intersection of the two merged graphs showed in Figure 1 indicate co-existence of spin density wave and superconductivity for Ba1−xKxFe2As2.
4. Conclusion
Using a model Hamiltonian consisting of spin density wave and superconducting part and applying Green’s function formalism we have got an expression which shows the relation of the two order parameters and their variation with temperature. From Figure 1 we observe that TC decreases with increase in M, whereas TSDW increases with increase in M. The spin density wave and superconducting phases, therefore, resist each other. However, the present work shows that there is a small region of temperature, where both the phases may be in existence together, which is indicated by (SC + SDW) in the figure. In the absence of spin density wave the expression for both singlet and triplet cases reduces to the well known BCS result. My study explicitly shows that
Figure 1. Co-existence of spin density wave (SDW) and superconductivity in Ba1−xKxFe2As2.
spin density wave and superconductivity truly coexist in Ba1−xKxFe2As2 (0.2 ≤ x < 0.4) in some range of magnetic order.
Acknowledgements
I thank Prof. Amarendra Rajput for providing me constructive comments, suggestions and valuable support.
Cite this paper
HaftuBrhane, (2015) Coexistence of Spin Density Wave (SDW) and Superconductivity in Ba1-xKxFe2As2. World Journal of Condensed Matter Physics,05,319-331. doi: 10.4236/wjcmp.2015.54032
References
- 1. Watanabe, T., Yanagi, H., Kamiya, T., Kamihara, Y., Hiramatsu, H., Hirano, M. and Hosono, H. (2007) Nickel-Based Oxyphosphide Superconductor with a Layered Crystal Structure, LaNiOP. Inorganic Chemistry, 46, 7719-7721.
http://dx.doi.org/10.1021/ic701200e - 2. Tegel, M., Bichler, D. and Johrendt, D. (2008) Synthesis, Crystal Structure and Superconductivity of LaNiPO. Solid State Sciences, 10, 193-197.
http://dx.doi.org/10.1016/j.solidstatesciences.2007.08.016 - 3. Kamihara, Y., Watanabe, T., Hirano, M. and Hosono, H. (2008) Iron-Based Layered Superconductor La[O1-xFx]FeAs (x = 0.05 - 0.12) with Tc = 26 K. Journal of the American Chemical Society, 130, 3296-3297.
http://dx.doi.org/10.1021/ja800073m - 4. Chen, G.F., Li, Z., Wu, D., Li, G., Hu, W.Z., Dong, J., Zheng, P., Luo, J.L. and Wang, N.L. (2008) Superconductivity at 41-K and Its Competition with Spin-Density-Wave Instability in Layered CeO1-xFxFeAs. Physical Review Letters, 100, Article ID: 247002.
http://dx.doi.org/10.1103/PhysRevLett.100.247002 - 5. Ren, Z.A., Lu, W., Yang, J., Yi, W., Shen, X.L., Li, Z.C., Che, G.C., Dong, X.L., Sun, L.L., Zhou, F. and Zhao, Z.X. (2008) Superconductivity at 55 K in Iron-Based F-Doped Layered Quaternary Compound Sm[O1-xFx]FeAs. Chinese Physics Letters, 25, 2215.
http://dx.doi.org/10.1088/0256-307X/25/6/080 - 6. Kenji, I., Yusuke, N. and Hideo H. (2009) To What Extent Iron-Pnictide New Superconductors Have Been Clarified. Journal of the Physical Society of Japan, 78, Article ID: 062001.
- 7. Kordyuk, A.A. (2012) Iron-Based Superconductors: Magnetism, Superconductivity, and Electronic Structure. Low Temperature Physics, 38, 1119-1134.
http://dx.doi.org/10.1063/1.4752092 - 8. Putti, M., et al. (2010) New Fe-Based Superconductors: Properties Relevant for Applications. Superconductor Science and Technology, 23, Article ID: 034003.
http://dx.doi.org/10.1088/0953-2048/23/3/034003 - 9. Patel, U., et al. (2009) Growth and Superconductivity of FeSex Crystals. Applied Physics Letters, 94, Article ID: 082508.
http://dx.doi.org/10.1063/1.3093838 - 10. Rotter, M., Tegel, M. and Johrendt, D. (2008) Superconductivity at 38 K in the Iron Arsenide (Ba1-xKx)Fe2As2. arXiv:0805.4630v1 [cond-mat.supr-con]
- 11. Digor, D.F., et al. (2005) Moldavian Journal of the Physical Sciences, 4.
- 12. Rotter, M., Pangerl, M., Tegel, M. and Johrendt, D. (2008) Superconductivity and Crystal Structures of (Ba1-xKx)Fe2As2 (x = 0 - 1). Angewandte Chemie International Edition, 47, 7949-7952.
http://dx.doi.org/10.1002/anie.200803641 - 13. Rotter, M., Tegel, M. and Johrendt, D. (2008) Superconductivity at 38 K in the Iron Arsenide (Ba1-xKx)Fe2As2. Physical Review Letters, 101, Article ID: 107006.
http://dx.doi.org/10.1103/PhysRevLett.101.107006 - 14. Zubarev, D.N. (1960) Double-Time Green Functions in Statistical Physics. Uspekhi Fizicheskikh Nauk SSSR, 71, 7.
- 15. Hsian, P.C. (2011) Robust Based Band Reed Solomon Detection over Power Line Channel. Journal of Engineering Science and Technology, 6, 69-81.
- 16. Zhou, Y. and Gong, C.D. (2006) Unusual Behavior of Superconductivity Induced by Anisotropic Structure in the Ferromagnetic State. Europhysics Letters, 74, Article ID: 145150.
http://dx.doi.org/10.1209/epl/i2005-10495-1































