Atmospheric and Climate Sciences
Vol.4 No.1(2014), Article ID:40953,7 pages DOI:10.4236/acs.2014.41007
Precipitation Extremes Analysis over the Brazilian Northeast via Logistic Regression
Programa de Pós-Graduação em Ciências Climáticas, Centro de Ciências Exatas e da Terra, Universidade Federal do Rio Grande do Norte, Natal, Brazil
Email: *wlfcfm@hotmail.com, *pslucio@ccet.ufrn.br
Copyright © 2014 Washington Luiz Félix Correia Filho et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Washington Luiz Félix Correia Filho et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 12, 2013; revised November 10, 2013; accepted November 18, 2013
Keywords:Odds Ratio; ROC Curve; Outgoing Longwave Radiation; Semiarid Region
ABSTRACT
This work diagnosed the precipitation extremes over the Brazilian Northeast (NEB) based on logistic regression for obtaining associations between precipitation extremes and the meteorological variables by Odd Ratio (OR). Data of ten meteorological variables to the NEB (North (NNEB), East (ENEB), South (SNEB) and Semiarid (SANEB)) were used daily. The OR results evidenced that the outgoing longwave radiation was the key variable on the precipitation extremes detection in three sub-regions: ENEB with 2.91 times (95% confidence interval (CI): 2.11, 4.02), NNEB with 3.63 times (95% CI: 1.93, 6.83), and SANEB with 5.40 times (95% CI: 3.04, 9.61); while on SNEB, it was relative humidity with 3.88 times (95% CI: 2.89, 5.20) more chance to favor the precipitation extremes. The maximum temperature, zonal wind component, evaporation, specific humidity and RH also had influence on these extremes. Goodness-of-fit and ROC analysis demonstrated that all models had a good fit and good predictive capability.
1. Introduction
The increase of extreme events in a short period of time became in the society more vulnerable at weather and climate extremes variability, resulting in great socioeconomic losses [1]. These extremes are related to several environmental factors that favor the increase on their frequency and intensity: 1) ocean-atmospheric variables relationships, such as: air temperature [2], precipitation [3], wind speed [4] and sea surface temperature (SST) [5]; 2) regional micro-climate changes due to rapid urbanization of the cities without proper urban planning [6]; and 3) orographic effects [7]. These factors when combined at atmospheric circulation or meteorological systems in several spatiotemporal scales [8] can favor the extremes occurrence; the aim of this paper is to diagnose the precipitation extremes.
These extremes have motivated various researchers on seeking to detect associations between precipitation extremes and environmental factors, as [9] that investigated precipitation extremes to future scenarios and detected interaction between temperature and water vapor that propel the precipitation extremes, already in tropical regions these extremes are motivated by specific humidity saturation in low levels. The relationship of temperature and specific humidity was also found by [10].
On Brazilian Northeast, these extremes are related at precipitation by deficit (semiarid region) or excess (capitals or coast regions) found by several researchers [11- 13]. These extreme events directly or indirectly affect with great socioeconomic losses caused by flash floods or by prolonged droughts [14].
Several statistical methods have been implemented to extract patterns on these extremes, aboard of these papers generalized linear models (GLM) [15,16]. The GLM is a flexible generalization of ordinary linear regression that allows for response variables that have other than a normal distribution. Furthermore, these models are effective and robust that it will facilitate to obtaining the precipitation extremes by logistic regression models. In climate sciences, the logistic regression application is related to precipitation occurrence or amount models [17,18], and forecast skill verification of the climate models [19]. Thus, this approach via odds ratio (OR) will pretend to answer the questions:
1) Does SST determine the precipitation extreme occurrence?
2) Which is (are) variable(s) that favor(s) the precipitation extreme occurrence?
3) What is the magnitude of these associations via OR on extreme intensification?
4) What will be the OR’s behavior similar in all the NEB sub-regions?
In order to answer these questions, the goal of this article is to characterize the precipitation extremes on NEB via logistic regression model, using ten meteorological variables for 1979-2011.
2. Material and Methods
2.1. Study Area
The Brazil Northeast has 1.5 × 106 km2 of area ranging between 1 - 18˚S and 35 - 47˚W, the region is influenced by different meteorological systems with distinct characteristics. According to [20], the NEB precipitation pattern is divided in three sub-regions: Eastern (ENEB)—influenced by mesoscale convective systems (MCS), mesoscale convective complex (MCC) and easterly wave disturbance [21-23]; Southern (SNEB)—influenced by South Atlantic Convergence Zone (SACZ), Frontal Systems (FS) and Upper Tropospheric Cyclonic Vortex (UTCV) [24, 25]; and Northern (NNEB)—influenced by Intertropical Convergence Zone (ITCZ), easterly wave disturbance [22,26]; others meteorological systems also occur such as: sea breeze systems on the NNEB and ENEB and the South Atlantic Subtropical Anticyclone influences in all the sub-regions [24,25].
Cluster analysis was performed to characterize the new NEB precipitation pattern using Euclidean distance via Ward method, resulting in four sub-regions: ENEB, LNEB, SNEB and semiarid (SANEB) as the new sub-region shown on Figure 1.
2.2. Data
We use daily precipitation data from Climate Prediction Center—NOAA [27] with 0.5˚ × 0.5˚ grid resolution and resized 1.5˚ × 1.5˚, among the February-July months (rainy period) for 1979-2011 period.
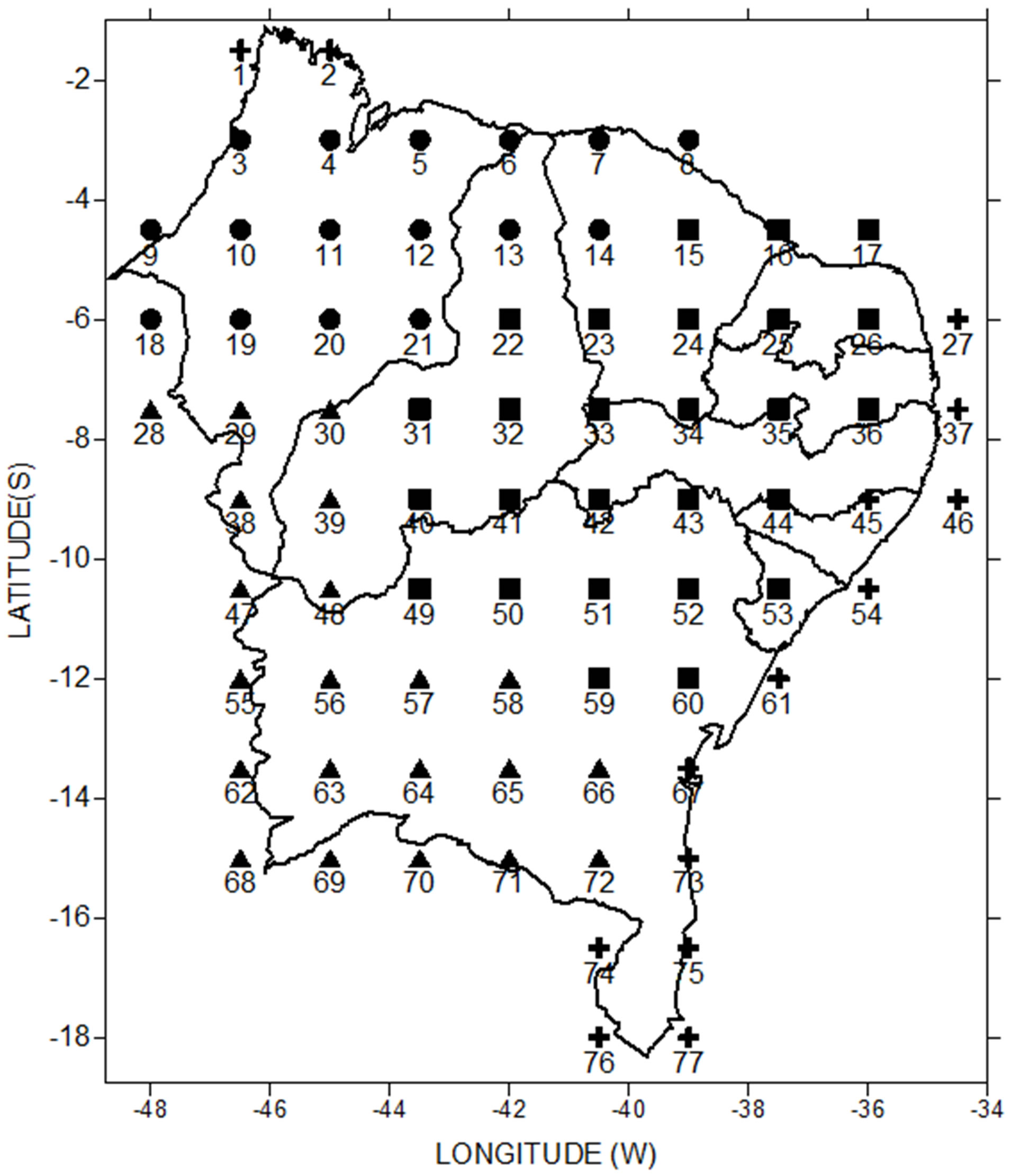
Figure 1. Grid points distribution on NEB which was divided in four sub-regions (symbols): NNEB (circle); ENEB (cross); SANEB (square) and SNEB (triangle).
On this analysis were used others variables: relative humidity (RH), minimum (TN) and maximum (TX) temperatures, evaporation (EV), zonal and meridional wind components (CompU and CompV), gust wind (GUST) and specific humidity (SHUM) provided from Era-Interim reanalyzes [28]; and interpolated satellite data of outgoing longwave radiation (OLR) provided from Earth System Research Laboratory-NOAA (ESRL-NOAA) [29]. All data are same grid resolution (1.5˚ × 1.5˚) shown on Figure 1.
It was generated 77 grid points, wherein it was used 4 points that represent each sub-region: NNEB—point 02 (northern of Maranhão); SANEB—point 45 (northeastern of Alagoas); SANEB—point 63 (southwestern of Bahia); and SNEB—point 75 (southeastern of Bahia).
2.3. PCA for Atlantic and Pacific Regions
We also use daily SST data of the two tropical regions: Atlantic Ocean (ATL) (21˚S - 21˚N, 57˚W - 15˚E) and Pacific Ocean (NINO), El Niño 1.2, 3, 3.4 and 4 regions (5˚S - 5˚N, 90˚W - 160˚E, and 10˚S - 0˚, 80˚W - 90˚W) provided from the Era-Interim reanalyzes. The SST in daily timescale is little used due at low degree variability, but will be important for Poisson regression build.
The SST data implementation of variables explanatory follows these stages: 1) The inclusion of lags for both basins: Atlantic—30 days, and Pacific—90 days due at ocean time response; 2) To calculate the anomalies for each SST regions; and 3) Principal Components Analysis (PCA) to extract the main pattern behavior.
The categorization of variables following two criteria: 1) precipitation data upper 95th percentile (>95 p) values was considered as extreme; 2) for OLR, OLR below 240 Wm−2 (OLR < 240) was considered as convective clouds; 3) for the others variables, the threshold was considered as abnormal those quartile that it obtain higher number occurrence, shown on Table 1.
2.4. Logistic Regression Models
After that PCA composition based on SST regions, we apply the cross correlation function (CCF) to identify lag of correlations between precipitation and the other variables to extract the lags. Then the logistic regression model was applied following two important criteria: 1) Given a set of independent variables, the propose is estimate the probability of precipitation extreme occurrence; and 2) To assess the magnitude of the influence of each meteorological variable on precipitation extremes obtained by odds ratio (OR). The logistic regression is expressed:
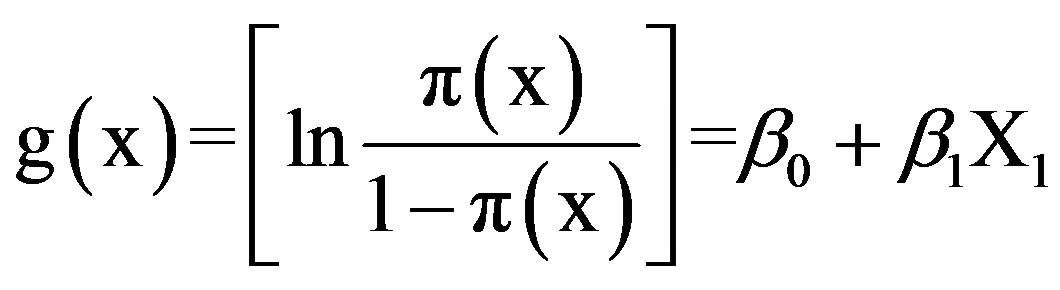 . (1)
. (1)
g(x) is precipitation extreme in dichotomous form (between 0’s e 1’s), and p is the precipitation extremes occurrence probability, given by:
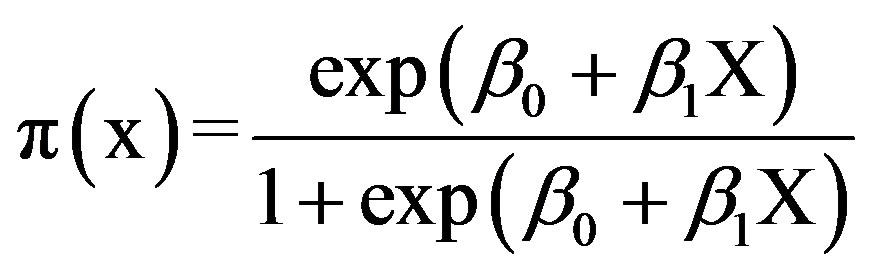 . (2)
. (2)
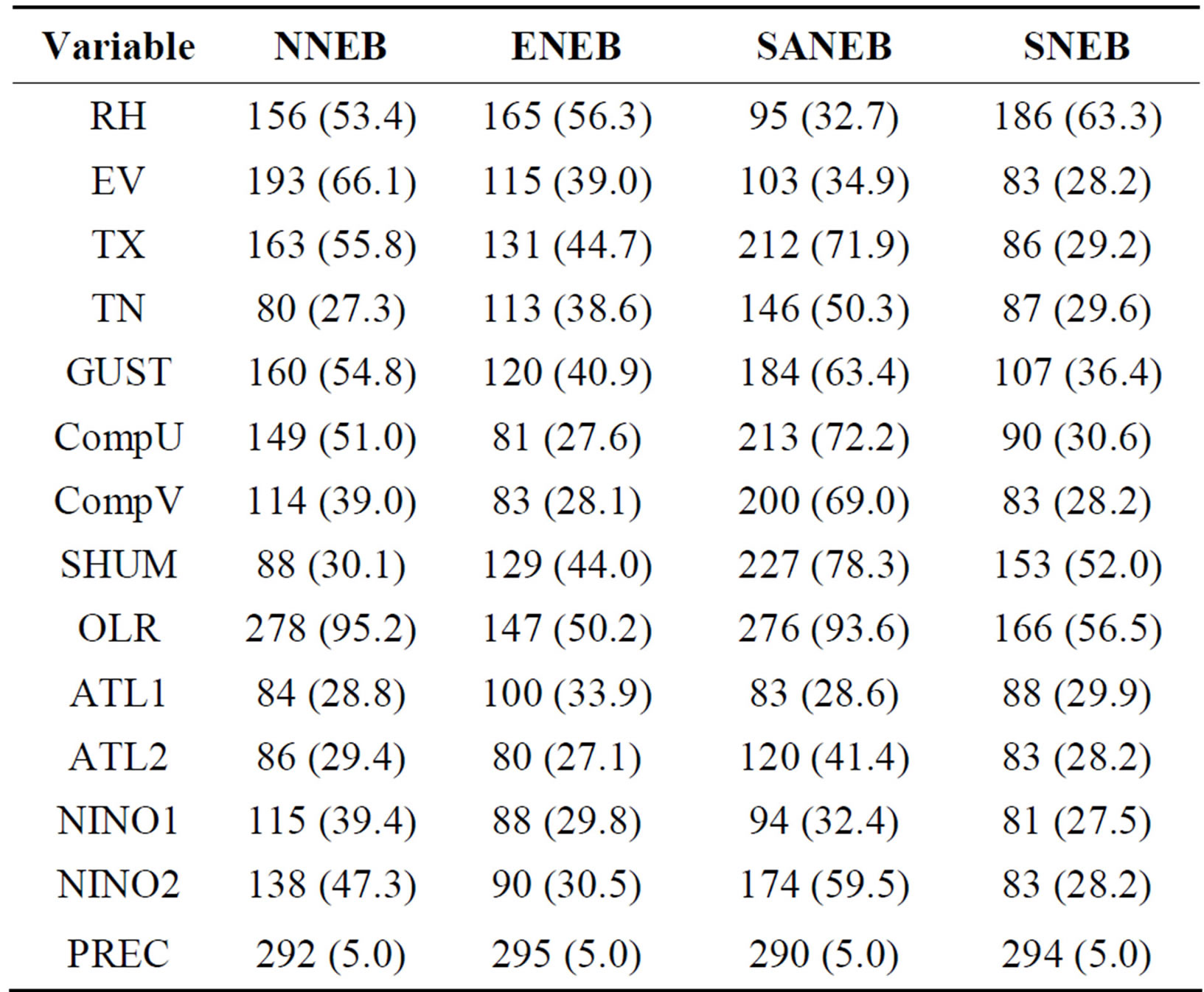
Table 1. Contingency table results generated by logistic regression model for four NEB sub-regions that exhibit the number confirmed of extreme precipitation cases of positive true ( n˚ cases in %).
2.5. Odds Ratio
Odds ratio (OR) was calculated for each variable, obtaining the association magnitude between precipitation extremes and the meteorological variables. For calculate the OR should get the odds, which is the natural measure more important in logistic regression and can be interpreted as the ratio between the odds of the precipitation extremes to occur to the odds of precipitation extremes not to occur. Both odds are dimensionless and non-negative, if the OR < 1 is described as exposure factor, the observed variable is not influence the precipitation extremes, while the OR > 1 is described as risk factor, thus the observed variable influence on the precipitation extremes. Thus, the OR depends of four probabilities that following:
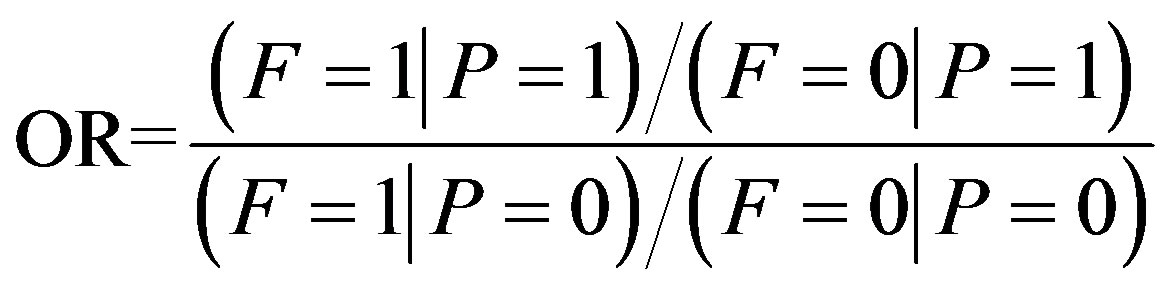 (3)
(3)
which F = 1 when the observed variable influences on precipitation extremes occur, F = 0 otherwise, P = 1 when the precipitation extreme occur, and P = 0 otherwise.
2.6. Goodness-of-Fit and ROC Curve
For goodness-of-fit (GOF) analysis [30] was used three methods: Deviance residual, AIC and p-value. Deviance Residual is the quality-of-fit statistic measure based on maximum likelihood using the sum of squared residuals in ordinary least squares. Akaike Information Criterion (AIC) is quality-of-fit measure wherein seek to select variables given a joint of variables that optimize the performance of the model with the minimum AIC value. Already the p-value is other measures that verify whether the variables contained on model has significance statistical, generally it used p < 0.005 value for reject the null hypothesis. For assess the accuracy of model it was used receiver operating characteristics (ROC) graph.
The ROC curve is a technique for visualizing, organizing and selecting classifiers, thus it evaluates the quality or performance of diagnostic tests [31,32].
Generally, the ROC analysis assesses the quality of model counting of occurrence or not precipitation extremes and the exposure factor presence or absent at an extreme condition. Thus, the common measure used is Area under Curve (AUC) that interpret the average value of sensibility for all values of specificity with aim to evaluate the overall performance of a diagnostic test, ranging between 0 and 1, wherein a bigger value suggests the better overall performance of a diagnostic test [31]. All results computations were generated on R software [33] with packages support: MASS [34], ROCR [35] and Epi [36].
3. Results and Discussions
The logistic regression model results, OR’s and goodness-of-fit analysis (deviance residual, AIC, p-value) are shown on Tables 2-5 for four NEB sub-regions (NNEB, ENEB, SANEB and SNEB) shown on Figure 2. The 5800 daily precipitation data upper >95 p were considered, corresponding 290 - 295 precipitation extremes cases obtained.
For goodness-of-fit was verified that the SANEB (Table 3) sub-region obtained the best values of AIC with 1386.1 and deviance residual of 1366.1.
The ROC curve analysis shown on Figure 3 was observed that all models showed were above 0.80, which shows that all the models have a good predictive ability,
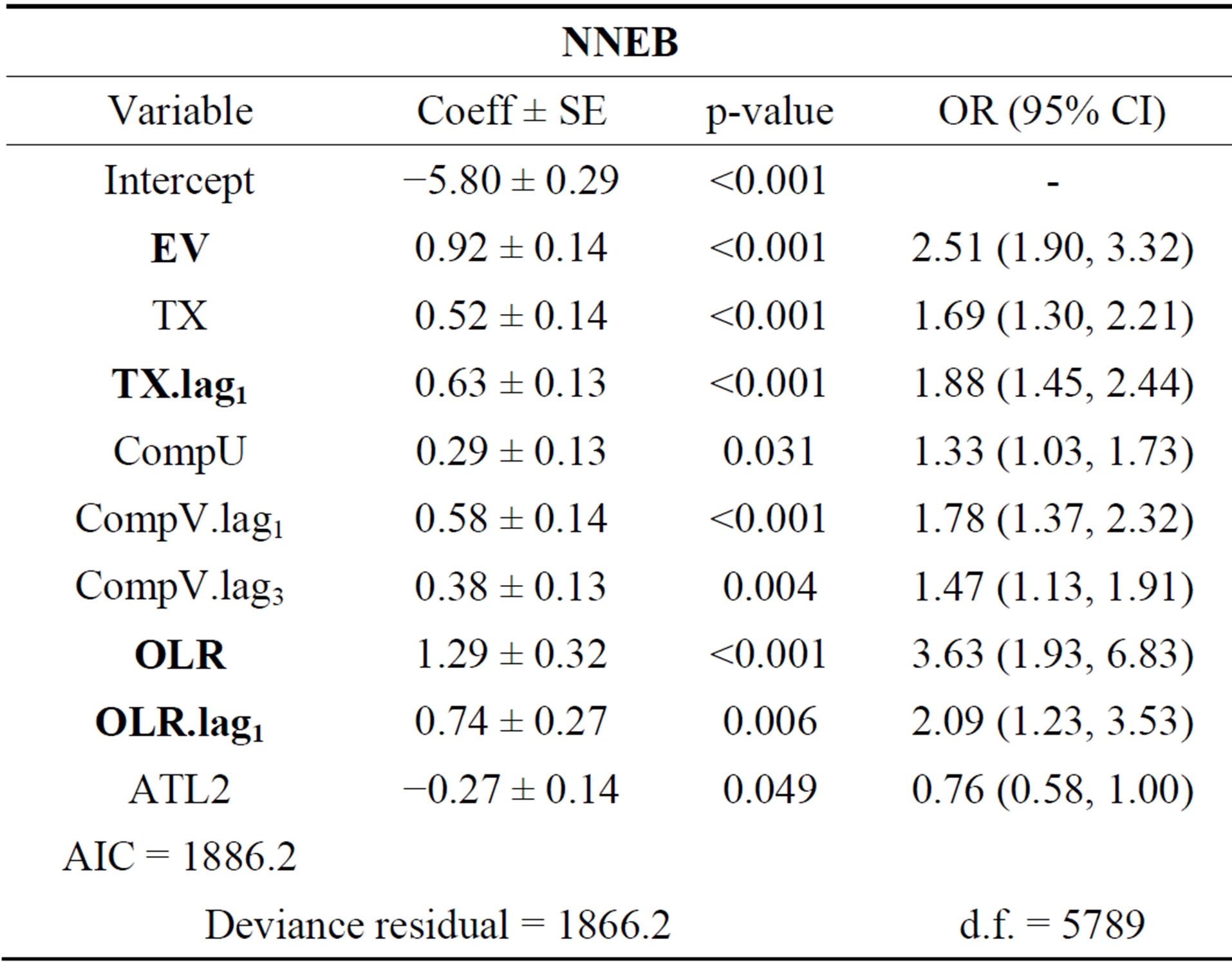
Table 2. Logistic regression models for NNEB. Coefficient regression (Coeff), Standard Error (SE), p-value, Odds Ratio (95% CI) and Goodness-of-fit (AIC test, Deviance residual and degrees of freedom (df)).
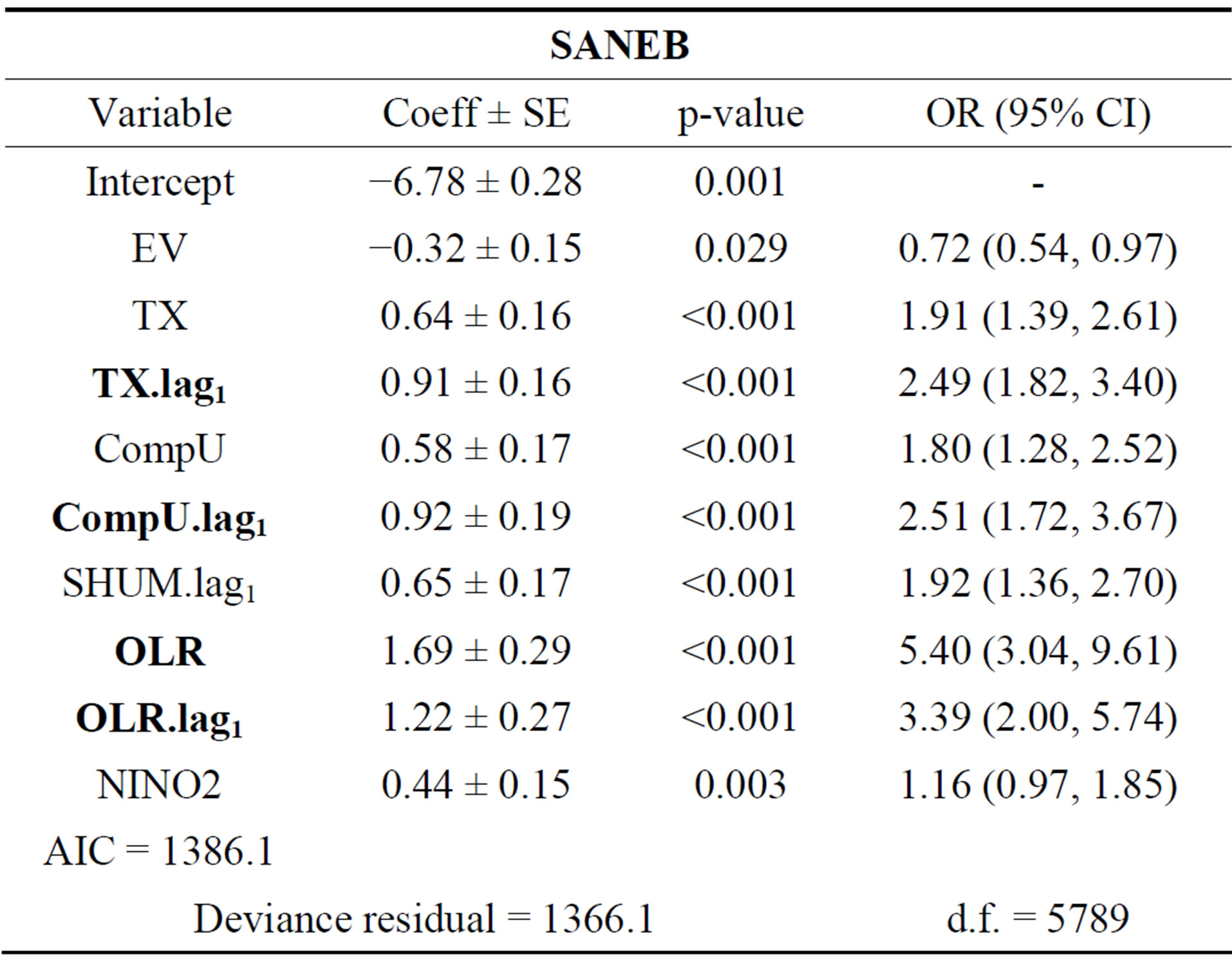
Table 3. Logistic regression models for SANEB. Coefficient regression (Coeff), Standard Error (SE), p-value, Odds Ratio (95% CI) and Goodness-of-fit (AIC test, Deviance residual and degrees of freedom (df)).
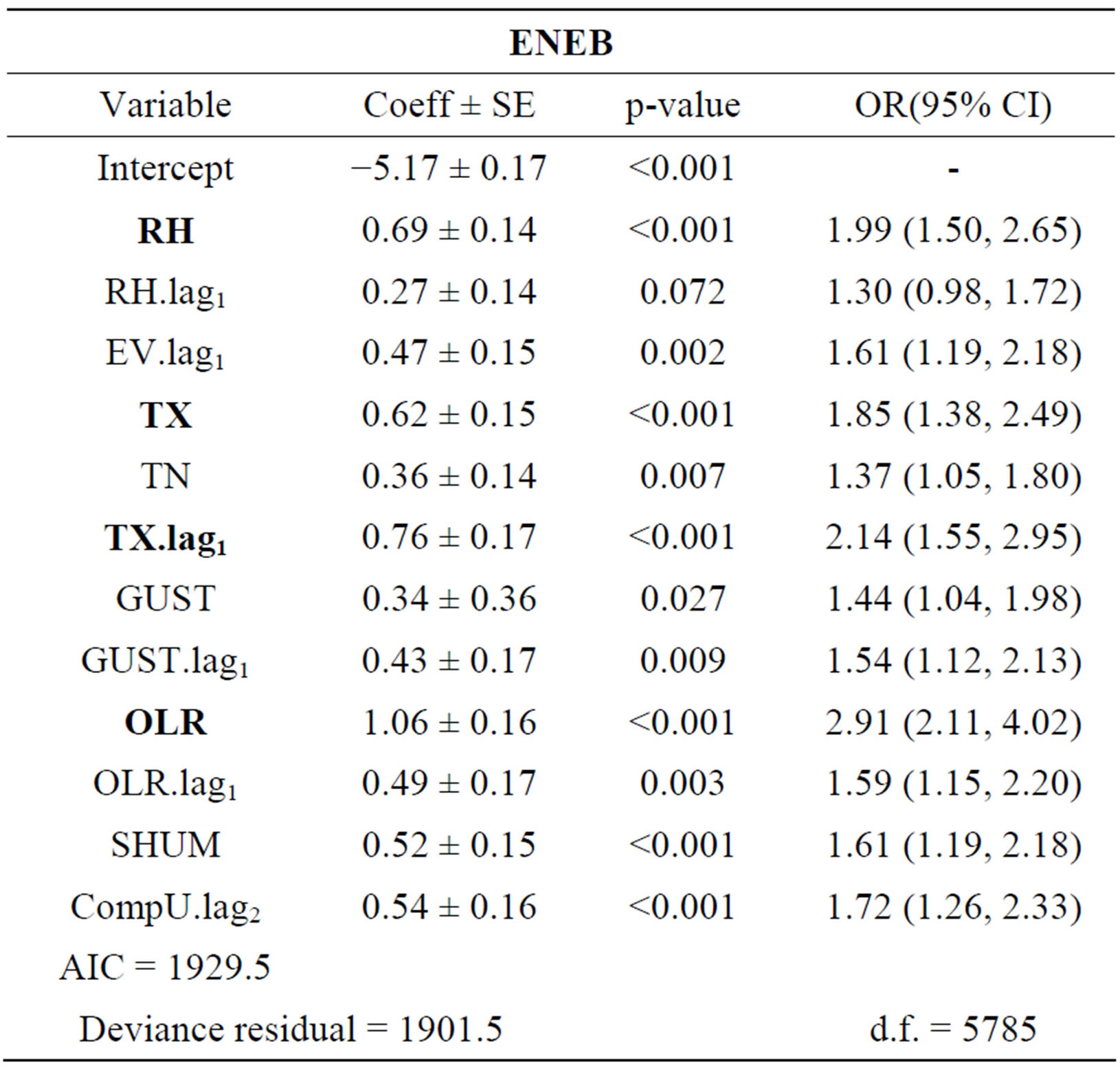
Table 4. Logistic regression models for ENEB. Coefficient regression (Coeff), Standard Error (SE), p-value, Odds Ratio (95% CI) and Goodness-of-fit (AIC test, Deviance residual and degrees of freedom (df)).
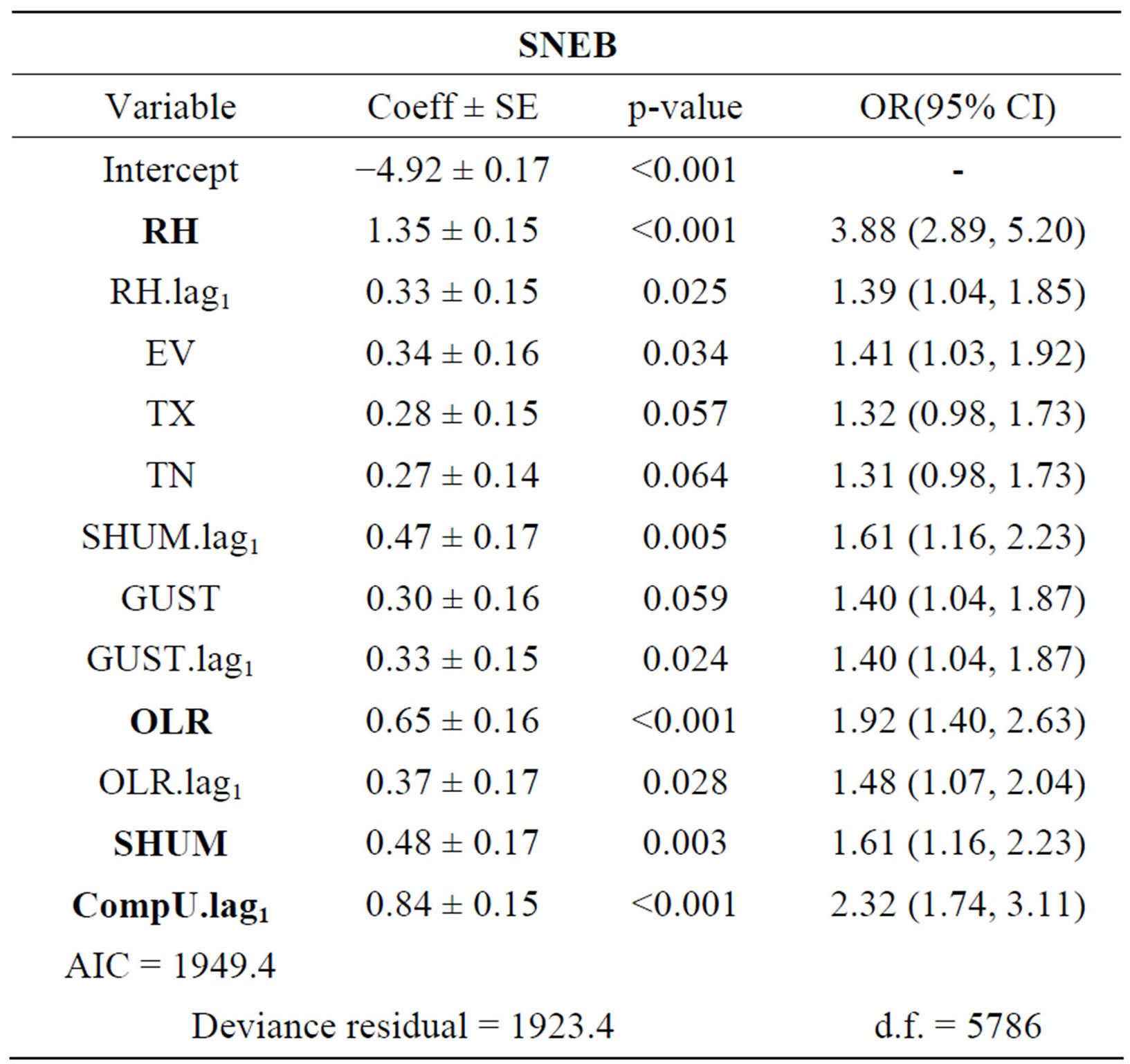
Table 5. Logistic regression models for SNEB. Coefficient regression (Coeff), Standard Error (SE), p-value, Odds Ratio (95% CI) and Goodness-of-fit (AIC test, Deviance residual and degrees of freedom (df)).
highlighting again the SANEB (Figure 3) sub-region that exhibit the best AUC value of 0.935.
The measure associations by Odds Ratio, on NNEB (Northern of Maranhão) there is evidence that the variables that contribute on precipitation extremes are EV, OLR, TX.lag1 and OLR.lag1; for the ENEB (Northeastern of Alagoas) are RH, OLR, TX and TX.lag1; already on SANEB (Southwestern of Bahia) are OLR, TX.lag1,
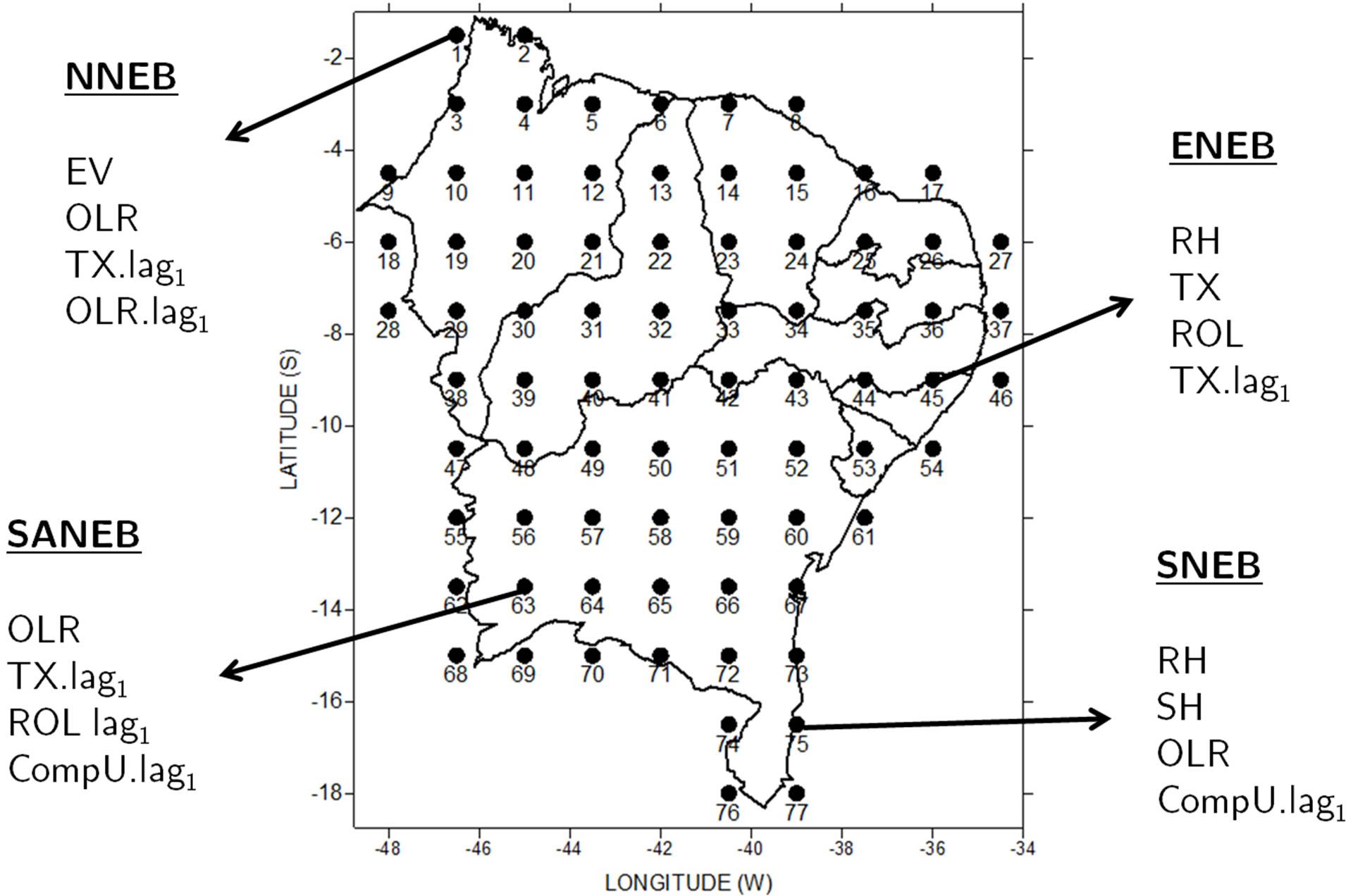
Figure 2. Meteorological variables that influenced on NEB precipitation extremes by logistic regression models.
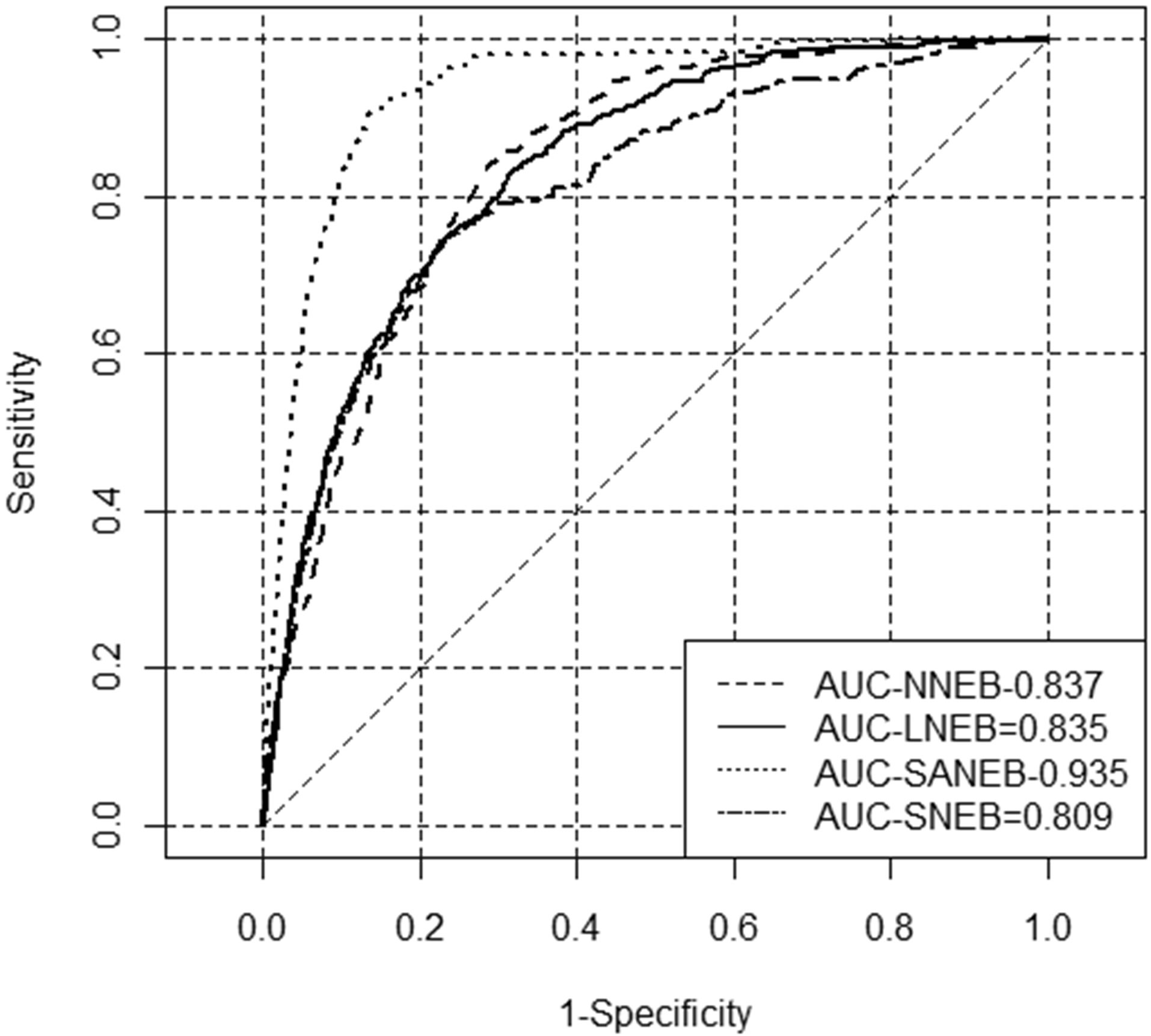
Figure 3. ROC curve for logistic models. AUC values on right bottom for each sub-regions: NNEB (solid line), ENEB (dashed line), SANEB (dotted line) and SNEB (dashed and dotted line).
OLR.lag1 and OLR.lag1; and on SNEB (Southeastern of Bahia) are RH, OLR, SHUM and CompU.lag1.
On OR analysis was evidenced that the OLR (Tables 2-5) is main variable on precipitation extremes detection, NNEB with 2.91 times (95% confidence interval (CI): 2.11, 4.02), on NNEB with 3.63 times (95% CI: 1.93, 6.83) and SANEB with 5.40 times (95% CI: 3.04, 9.61) more chance to favor the precipitation extremes; while on SNEB the highlight is RH with 3.88 times (95% CI: 2.89, 5.20) more chance to favor the precipitation extremes.
The OR results corroborate with [37], wherein the authors detected the OLR and extreme precipitation relationships on tropics using climate indices (rain > 10 mm and OLR < 180 Wm−2), this indices indicated that association favoring the convection formation by low-level moisture convergence causing the precipitation more intense suggested by [38]. It is noted that the precipitation extremes events is well distinct for each NEB subregion favored by several meteorological variable associated meteorological systems corroborating with [39] that describe is not only temperature has a cause-effect influence on precipitation intensity, but for a combination of different meteorological systems.
Analyzing the sub-regions in separate, the precipitation extremes on NNEB (Table 2) is linked at ITCZ displacement in north-south direction that transport heat and moisture into region, subside by TX and EV combined. On SANEB (Table 3), scarcity precipitation region in NEB, it was verified that TX.lag1, CompU, OLR and OLR.lag1 favor precipitation extremes boosted by temperature and moisture advection associated at easterly flow forming of deep convection caused by frontal systems [20] or north axis SACZ displacement [25] that penetrating on southern NEB.
On ENEB (Table 4), this extremes are strength by RH, TX and TX.lag1 combined with CompU.lag1, according to [13] the intense precipitation occurrence is favored for heat and moisture transport by easterly waves disturbances and boost the MCS and MCC formation about region which are largely responsible for maintaining the precipitation regime, contributing with 50% - 70% of annual regime. On SNEB (Table 5), the TX.lag1, U.lag1 and OLR were influenced in precipitation extremes arising from different meteorological systems: eastern influence—breeze systems and easterly wave disturbance, and southern influence—SACZ and frontal systems.
4. Conclusion
These initial conclusions show that Atlantic and Pacific SSTs in daily timescale do not significantly favor on precipitation extremes. The OLR is a key variable in extreme precipitation detection. The projection for future work is to evaluate the extreme precipitation occurrence in Northeast Brazil by relative risk via Poisson regression seeking to detect the behavior by count process.
Acknowledgements
The author thanks at CAPES for doctoral financial support; George Pedra and Naurinete Barreto by several contributions for this article. P. S. Lucio is sponsored by a PQ2 grant (Proc. 302493/2007-7) from CNPq (Brazil).
REFERENCES
- T. R. Karl and D. R. Easterling, “Climate Extremes: Selected Review and Future Research Directions,” Climatic Change, Vol. 42, 1999, pp. 209-325.
- G. C. Blain, “Modeling Extreme Minimum Air Temperature Series under Climate Change Conditions,” Ciência Rural, Vol. 41, 2011, pp. 1877-1883. http://dx.doi.org/10.1590/S0103-84782011001100005
- A. M. Grimm and R. G. Tedeschi, “ENSO and Extreme Rainfall Events in South America,” Journal of Climate, Vol. 22, No. 7, 2009, pp. 1589-1609. http://dx.doi.org/10.1175/2008JCLI2429.1
- P. Friederichs, M. Göber, S. Bentzien, A. Lenz and R. Krampitz, “A Probabilistic Analysis of Wind Gusts Using Extreme Value Statistics,” Meteorologische Zeitschrift, Vol. 18, No. 6, 2009, pp. 615-629. http://dx.doi.org/10.1127/0941-2948/2009/0413
- G. A. M. Silva and D. Mendes, “Comparison Results for the CFSv2 Hindcasts and Statistical Downscaling over the Northeast of Brazil,” Advances in Geosciences, Vol. 35, 2013, pp. 79-88. http://dx.doi.org/10.5194/adgeo-35-79-2013
- P. Willems, K. Arnbjerg-Nielsen, J. Olsson and V. T. V. Nguyen, “Climate Change Impact Assessment on Urban Rainfall Extremes and Urban Drainage: Methods and Shortcomings,” Atmospheric Research, Vol. 103, 2012, pp. 106-118. http://dx.doi.org/10.1016/j.atmosres.2011.04.003
- R. A. Houze Jr., “Orographic Effects on Precipitations Clouds,” Reviews of Geophysics, Vol. 50, 2012, Article ID: GR1001.
- F. Kucharski, D. Polzin and S. Hastenrath, “Teleconnection Mechanisms of Northeast Brazil Droughts : Modeling and Empirical Evidence,” Revista Brasileira de Meteorologia, Vol. 23, No. 2, 2008, pp. 115-125. http://dx.doi.org/10.1590/S0102-77862008000200001
- P. A. O. Gorman and T. Schneider, “The Physical Basis for Increases in Precipitation Extremes in Simulations of 21st-Century Climate Change,” Proceedings of the National Academy of Sciences, Vol. 106, 2009, pp. 14773- 14777. http://dx.doi.org/10.1073/pnas.0907610106
- P. Berg, C. Moseley, and J. O. Haerter, “Strong Increase in Convective Precipitation in Response to Higher Temperatures,” Nature Geoscience, Vol. 6, No. 3, 2013, pp. 181-185. http://dx.doi.org/10.1038/ngeo1731
- M. D. Oyama and C. A. Nobre, “Climatic Consequences of a Large-Scale Desertification in Northeast Brazil: A GCM Simulation Study,” Journal of Climate, Vol. 17, No. 16, 2004, pp. 3203-3213. http://dx.doi.org/10.1175/1520-0442(2004)017<3203:CCOALD>2.0.CO;2
- B. Liebmann, G. N. Kiladis, D. Allured, C. S. Vera, C. Jones, L. M. V. Carvalho, I. Bladé and P. L. M. Gonzáles, “Mechanisms Associated with Large Daily Rainfall Events in Northeast Brazil,” Journal of Climate, Vol. 24, No. 2, 2011, pp. 376-396. http://dx.doi.org/10.1175/2010JCLI3457.1
- Y. K. Kouadio, J. Servain, L. A. T. Machado and C. A. D. Lentini, “Heavy Rainfall Episodes in the Eastern Northeast Brazil Linked to Large-Scale Ocean-Atmosphere Conditions in the Tropical Atlantic,” Advances in Meteorology, Vol. 2012, 2012, pp. 1-16. http://dx.doi.org/10.1155/2012/369567
- S. Hastenrath, “Exploring the Climate Problems of Brazil’s Nordeste: A Review,” Climatic Change, Vol. 112, No. 2, 2011, pp. 243-251. http://dx.doi.org/10.1007/s10584-011-0227-1
- A. J. A. Nelder and R. W. M. Wedderburn, “Generalized Linear Models,” Journal of the Royal Statistical Society. Series A (General), Vol. 135, No. 3, 1972, pp. 370-384. http://dx.doi.org/10.2307/2344614
- Z. Yan, S. Bate, R. E. Chandler, V. Isham and H. Wheater, “Changes in Extreme Wind Speeds in NW Europe Simulated by Generalized Linear Models,” Theoretical and Applied Climatology, Vol. 83, No. 1-4, 2005, pp. 121- 137.
- J. Abaurrea and J. Asín, “Forecasting Local Daily Precipitation Patterns in a Climate Change Scenario,” Climate Research, Vol. 28, 2005, pp. 183-197. http://dx.doi.org/10.3354/cr028183
- M. K. Tippett, A. G. Barnston and A. W. Robertson, “Estimation of Seasonal Precipitation Tercile-Based Categorical Probabilities from Ensembles,” Journal of Climate, Vol. 20, No. 10, 2007, pp. 2210-2228. http://dx.doi.org/10.1175/JCLI4108.1
- T. M. Hamill, J. S. Whitaker and X. Wei, “Ensemble Reforecasting: Improving Medium-Range Forecast Skill Using Retrospective Forecasts,” Monthly Weather Review, Vol. 132, No. 6, 2004, pp. 1434-1447. http://dx.doi.org/10.1175/1520-0493(2004)132<1434:ERIMFS>2.0.CO;2
- V. E. Kousky, “Frontal Influences on Northeast Brazil,” Monthly Weather Review, Vol. 107, No. 9, 1979, pp. 1140-1153. http://dx.doi.org/10.1175/1520-0493(1979)107<1140:FIONB>2.0.CO;2
- L. C. B. Molion and S. de O. Bernardo, “Uma Revisão da Dinâmica das Chuvas no Nordeste Brasileiro,” Revista Brasileira de Meteorologia, Vol. 17, No. 1, 2002, pp. 1-10. http://dx.doi.org/10.1590/S0102-76382002000100002
- R. R. Torres and N. J. Ferreira, “Case Studies of Easterly Wave Disturbances over Northeast Brazil Using the Eta Model,” Weather and Forecasting, Vol. 26, No. 2, 2011, pp. 225-235. http://dx.doi.org/10.1175/2010WAF2222425.1
- H.-Y. Ma, X. Ji, J. D. Neelin and C. R. Mechoso, “Mechanisms for Precipitation Variability of the Eastern Brazil/SACZ Convective Margin,” Journal of Climate, Vol. 24, No. 13, 2011, pp. 3445-3456. http://dx.doi.org/10.1175/2011JCLI4070.1
- R. R. Chaves and I. F. A. Cavalcanti, “Atmospheric Circulation Features Associated with Rainfall Variability over Southern Northeast Brazil,” Monthly Weather Review, Vol. 129, No. 10, 2001, pp. 2614-2626. http://dx.doi.org/10.1175/1520-0493(2001)129<2614:ACFAWR>2.0.CO;2
- L. M. V. Carvalho, C. Jones and B. Liebmann, “The South Atlantic Convergence Zone : Intensity, Form, Persistence, and Relationships with Intraseasonal to Interannual Activity and Extreme Rainfall,” Journal of Climate, Vol. 17, 2004, pp. 88-108. http://dx.doi.org/10.1175/1520-0442(2004)017<0088:TSACZI>2.0.CO;2
- S. K. Mishra, V. B. Rao and M. A. Gan, “Structure and Evolution of the Large-Scale Flow and an Embedded Upper-Tropospheric Cyclonic Vortex over Northeast Brazil,” Monthly weather review, Vol. 129, No. 7, 2001, pp. 1673-1688. http://dx.doi.org/10.1175/1520-0493(2001)129<1673:SAEOTL>2.0.CO;2
- M. Chen, W. Shi, P. Xie, V. Silva, V. E. Kousky, R. Wayne Higgins and J. E. Janowiak, “Assessing Objective Techniques for Gauge-Based Analyses of Global Daily Precipitation,” Journal of Geophysical Research: Atmospheres (1984-2012), Vol. 113, No. D4, 2008.
- D. P. Dee, S. M. Uppala, A. J. Simmons, P. Berrisford, P. Poli, S. Kobayashi, U. Andrae, M. A. Balmaseda, G. Balsamo, P. Bauer, P. Bechtold, A. C. M. Beljaars, L. Van De Berg, J. Bidlot, N. Bormann, C. Delsol, R. Dragani, M. Fuentes and A. J. Geer, “The ERA-Interim Reanalysis : Configuration and Performance of the Data Assimilation System,” Quarterly Journal of the Royal Meteorology Society, Vol. 137, 2011, pp. 553-597. http://dx.doi.org/10.1002/qj.828
- B. Liebmann and C. A. Smith, “Description of a Complete (Interpolated) Outgoing Longwave Radiation Dataset,” Bulletin of the American Meteorological Society, Vol. 77, 1996, pp. 1275-1277.
- D. W. Hosmer, S. Taber and S. Lemeshow, “The Importance of Assessing the Fit of Logistic Regression Models: A Case Study,” American Journal of Public Health, Vol. 81, No. 12, 1991, pp. 1630-1635. http://dx.doi.org/10.2105/AJPH.81.12.1630
- S. H. Park, “Receiver Operating Characteristic (ROC) Curve : Practical Review,” Vol. 5, 2004, pp. 11-18.
- T. Fawcett, “An Introduction to ROC Analysis,” Pattern Recognition Letters, Vol. 27, No. 8, 2006, pp. 861-874. http://dx.doi.org/10.1016/j.patrec.2005.10.010
- R Development Core Team and Others, “R: A Language and Environment for Statistical Computing,” 2013.
- W. N. Venables, and B. D. Ripley, “Modern Applied Statistics with S-PLUS,” Vol. 250, Springer-Verlag, New York, 1994. http://dx.doi.org/10.1007/978-1-4899-2819-1
- T. Sing, O. Sander, N. Beerenwinkel and T. Lengauer, “ROCR: Visualizing Classifier Performance in R,” Bioinformatics, Vol. 21, No. 20, 2005, pp. 3940-3941. http://dx.doi.org/10.1093/bioinformatics/bti623
- B. Carstensen, M. Plummer, E. Laara and M. Hills, “{Epi}: A Package for Statistical Analysis in Epidemiology,” 2013.
- S. Sandeep and F. Stordal, “Use of Daily Outgoing Longwave Radiation (OLR) Data in Detecting Precipitation Extremes in the Tropics,” Remote Sensing Letters, Vol. 4, No. 6, 2013, pp. 570-578. http://dx.doi.org/10.1080/2150704X.2013.769284
- K. E. Trenberth, A. Dai, R. M. Rasmussen and D. B. Parsons, “The Changing Character of Precipitation,” Bulletin of the American Meteorological Society, Vol. 84, No. 9, 2003, pp. 1205-1217. http://dx.doi.org/10.1175/BAMS-84-9-1205
- S. C. Liu, C. Fu, C.-J. Shiu, J.-P. Chen and F. Wu, “Temperature Dependence of Global Precipitation Extremes,” Geophysical Research Letters, Vol. 36, No. 17, 2009, Article ID: L17702. http://dx.doi.org/10.1029/2009GL040218
NOTES
*Corresponding authors.

