Received 27 April 2015; accepted 5 June 2015; published 11 June 2015

ABSTRACT

We present a new model of cosmology which appears to show great promise. Our flat space cosmology model, using only four basic and reasonable assumptions, derives highly accurate Hubble parameter H₀, Hubble radius R₀ and total mass M₀ values for our observable universe. Our model derives a current Hubble parameter of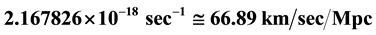, in excellent agreement with the newly reported (lower limit) results of the 2015 Planck Survey. Remarkably, all of these derivations can be made with only these basic assumptions and the current CMB radiation temperature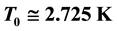. The thermodynamic equations we have generated follow Hawking’s black hole temperature formula. We have also derived a variety of other useful cosmo- logical formulae. These include angular velocity and other rotational formulae. A particularly useful hyperbolic equation, 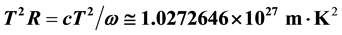, has been derived, which appears to be an excellent fit for the Planck scale as well as the current observable universe scale. Using the flat space Minkowski relativistic formula for Doppler effect, and a formula for staging our cosmological model according to its average mass-energy density at every Hubble time (universal age) in its expansion, a persuasive argument can be made that the observable phenomena attributed to dark energy are actually manifestations of Doppler and gravitational redshift. Finally, a theory of cosmic inflation becomes completely unnecessary because our flat space cosmology model is always at critical density.

Keywords:

Flat Space Cosmology, Cosmic Inflation, Dark Energy, Hubble Parameter, Critical Density, Angular Velocity, Light Speed Expansion, Light Speed Rotation, Redshift, Universe, CMBR

1. Introduction

Modern cosmology has recently struggled with modeling cosmic acceleration [1] and providing a reasonable explanation for the extreme flatness of the current observable universe. The ideas of a force in opposition to attractive gravity (dark energy) and of new physics required in the theory of cosmic inflation have been the source of much debate and consternation among cosmologists and astrophysicists. The authors have recently explored and published reports [2] - [5] of a new model of cosmology which appears to adequately address these problems without requiring new physics. Our model of flat space cosmology according to the Schwarzschild formula [6] , Hawking’s black hole temperature formula [7] and two other basic assumptions appears to discount the need for dark energy and the theory of cosmic inflation [8] entirely.

2. Basic Assumptions of Flat Space Cosmology

Our basic assumptions of flat space cosmology can be expressed as follows, for any scale from the Planck scale to the scale of our observable universe:

1) Cosmic radius R and total mass M follow the Schwarzschild formula 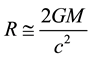at all times.

2) The cosmic event horizon translates at speed of light c with respect to its geometric center. Accordingly, the cosmic Hubble parameter H can be expressed as 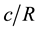and Hubble time (universal age) can be expressed as 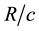for any stage of cosmic expansion.

3) The cosmic linear velocity of rotation is speed of light c at all Hubble times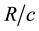. Thus, angular velocity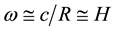, the Hubble parameter.

4) Following thermodynamics of Hawking’s black hole temperature formula, at any radius R the cosmic temperature T is inversely proportional to the geometric mean of cosmic total mass M and Planck mass.

3. Characteristic Equations of Flat Space Cosmology

The characteristic equations of flat space cosmology resulting from the above assumptions are:

A. Relations between cosmic radius, total mass and angular velocity:

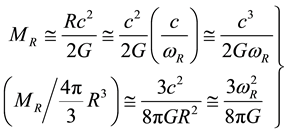(1)

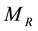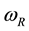where R, , and represent the cosmic radius, total mass and angular velocity (Hubble parameter), respectively. Average mass density (critical density) is derived in the second line.

B. Relations between temperature, mass, radius and angular velocity (thermodynamics):

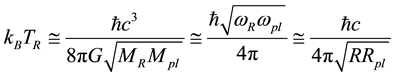(2)

where T_R is the cosmic temperature, 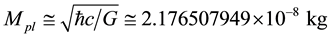is the Planck mass,

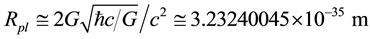is the Planck mass-associated cosmic radius and

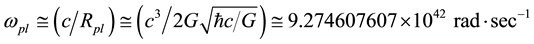is the Planck mass-associated angular velocity (also the Planck mass-associated Hubble parameter H_pl).

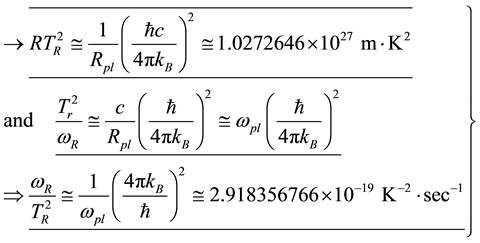(3)

4. Our Derivations of Current Cosmological Values

Using only our basic assumptions and the equations they generate above, derivations of current values for our observable universe are as follows:

Relations between universal current radius, current temperature, current angular velocity (also current Hubble parameter H₀), current total mass and current average mass density (critical density):

(4)

(5)

(6)

(7)

The above-derived radius and total mass values correspond to a current observable universe with a radius of 14.6 billion light-years and roughly 2 × 10²² visible stars plus 5x dark matter, or about 10⁵³ kg.

All of these derived current cosmological values are consistent with the 2015 Planck Survey data.

As per the 2015 Planck data [9] , the current value of the Hubble parameter H₀ is reported to be:

As per the 2015 Planck data, the current value of CMBR temperature is:

COBE/FIRAS CMBR temperature measurement [10] :

5. Practical Applications of Current Angular Velocity in Our Model

A. Galactic revolving speed:

For our current light speed rotating cosmic model, on the equatorial plane, galactic revolving speed can be expressed as:

(8)

Here, and represent the galactic distance from the cosmic center and galactic revolving speed corresponding to the cosmic angular velocity, respectively. The important point is that, even though

is always less than 1, the proposed velocity refers to galactic “revolution speed” about the cosmic center and the proposed distance refers to galaxy distance from the cosmic center. In contrast, in Hubble’s law [11] [12] , velocity refers to galactic “receding speed” and distance refers to “distance between galaxy and observer.” Importantly, actual galactic “revolving speeds” have never been confirmed by any direct cosmological observations. This is for further study.

B. Galactic receding speed:

In our current expanding cosmic model, on the equatorial plane, galactic receding speed can be expressed as:

(9)

Qualitatively, this relation also resembles the famous Hubble velocity-distance law. The point is that is the distance between galaxy and cosmic center and not the distance between galaxy and observer. Importantly, actual galactic “receding speeds” have never been confirmed by direct cosmological observations. This is for further study.

From the above, it is clear that, at the present time, on the equatorial plane, the magnitude of galactic revolving speed equals the magnitude of galactic receding speed. Hubble’s law appears to be a physical consequence of flat space cosmology.

C. Galactic centripetal acceleration:

1) For any revolving galaxy, galactic centripetal acceleration a_g can be expressed as:

(10)

2) For any satellite that is assumed to be revolving at a distance from the cosmic center, its centripetal acceleration a_satellite can be expressed as:

(11)

Based on the above applications, and by measuring actual galactic “revolving speeds” and galactic “recession speeds,” the current cosmic angular velocity can be estimated.

D. Galactic rotational curves:

The current dominant paradigm is that galaxies are embedded in halos of cold dark matter (CDM), made of non-baryonic weakly-interacting massive particles. However, an alternative way to explain the observed rotation curves of galaxies is the postulate that, for gravitational accelerations below a certain value , the true gravitational field strength g approaches, where is the usual Newtonian gravitational field strength (as calculated from the observed distribution of visible matter). This paradigm is known as modified Newtonian dynamics (MOND) [13] - [15] . MOND explains successfully many phenomena in galaxies, among which the following non-exhaustive list: 1) it predicted the shape of rotation curves of low surface-brightness (LSB) galaxies before any of them had ever been measured; 2) tidal dwarf galaxies (TDG),which should be devoid of collision-less dark matter, still exhibit a mass discrepancy in Newtonian dynamics, which is perfectly explained by MOND; 3) the baryonic Tully-Fisher relation, one of the tightest observed relations in astrophysics, is a natural consequence of MOND, both for its slope and its zero-point; 4) the first realistic simulations of galaxy merging in MOND were recently carried out, notably reproducing the morphology of the Antennae galaxies; 5) it naturally explains the universality of “dark” and baryonic surface densities within one core radius in galaxies.

So far, in the MOND model, the origin of acceleration constant is purely empirical and is unknown from first principles. By fitting the rotation curves, its magnitude is being determined empirically. The fundamental question to be answered is: Does MOND reflect the influence of cosmology on local particle dynamics at low accelerations? To understand the issue here, the authors assume:

1) The acceleration term is not a constant but a variable and depends on the galactic revolving speed about the cosmic center. The reasoning behind this guess is that each revolving galaxy will certainly experience a characteristic centripetal acceleration if the universe is rotating. This idea supports MOND concepts to some extent.

2) The magnitude of this acceleration variable can be assumed to be proportional to the current cosmic angular velocity and can be referred to as the “cosmological galactic acceleration”.

With reference to the MOND results, empirically, the revolving speed of a star about the galaxy is represented by the following relation:

(12)

where is the mass of the galaxy. By consider-

ing the galactic revolving speed about the cosmic center, the magnitude of galactic centripetal ac-

celeration can be assumed to vary as:

(13)

where is the distance between galaxy and the cosmic center. Now the rotational speed of a star in any galaxy can be represented as follows:

(14)

With an assumed universal proportionality ratio of 1, and by knowing the galactic mass and actual revolving speeds of galactic stars, galactic revolving speed and galactic distance from the cosmic center can be approximated in the following way:

(15)

By knowing our mother galactic mass and rotational curves, our galactic distance from the cosmic center can be approximated. By considering the different model-dependent proportionality ratios, and correlating all of the data, the correct magnitude of the proportionality ratio can be fitted. This is for further study.

6. Model Equations of Cosmic Redshift in Flat Space Cosmology

Given our stated basic assumptions, our expanding cosmic model shows average mass-energy density to be inversely proportional to. One way to look at this is that, the deeper an observer from Earth looks into space (and time), the greater the average mass-energy density stage of the cosmos one is observing. Thus, since each progressively denser stage of the cosmos is associated with higher average gravitational field strength, there must be associated gravitational time dilation effects. This conclusion is firmly grounded in general relativity. As such, it is conceivable that the progressively higher redshifts we observe with increasing look-back distances may be, in part, a manifestation of gravitational time dilation. In addition, because of this inverse square relationship over very long distances, plots of proximal galactic redshifts per unit of distance observed would be expected to look relatively linear (as seen by the weaker telescopes of the 1920s and 1930s) and deep space galactic redshifts per unit of distance observed would be expected to clearly fall away from linearity, along with decreasing luminosity, as redshifts extend into the infrared range (as seen in 1998 Type 1a supernovae observations) [16] .

In this section, in a semi-empirical approach, the authors propose a simple model equation for observed and predicted cosmic redshifts. It is for further research and analysis. The current model equation under study is:

(16)

where and represent past and current cosmic average mass-energy density, respectively.

The following graph (Figure 1), according to the above formula, shows expected observed cosmic redshift as a function of the above-defined average mass-energy density ratio pertaining to a particular astronomical observation. In this manner, increasingly greater redshifts would be expected to correspond with more distant galactic observations. However, notice the apparent near-linearity up to a density ratio of about 10⁴, and the increasingly nonlinear appearance with deeper space observations. The authors propose that something like this mathematical relationship could be responsible for the illusion of dark energy and, therefore, useful in modeling the results of progressively deeper space observations.

Of course, one must also factor in redshift as a function of relativistic Doppler effect. Since we are modeling flat space cosmology, the correct model formula is Minkowski’s relativistic Doppler formula for flat space:

(17)

In order to keep scaling similar to Figure 1, the velocity term v in the Minkowski formula can be substituted by where. The simplified relation can be expressed as follows.

(18)

Figure 2 shows redshift term Z as a function of a log scale of decreasing cosmic radius ratio pertaining to progressively deeper space observations. The reader should note that the CMBR redshift of 1089 corresponds with the place on the horizontal axis corresponding to log value −5.7738. Perhaps more importantly, however, the reader’s attention is directed to the place on the horizontal axis corresponding to log value −1.456. A greatly magnified portion of this region of Figure 2 would show the nonlinearity corresponding to the earliest visible galaxies which are moving away from us at about 0.95c.

It is now clearly apparent that a combination of gravitational time dilation (Figure 1) and flat space relativistic Doppler effect (Figure 2) could be the entire explanation for the nonlinearity of deep space Type 1a supernovae observations currently being attributed to “dark energy.” Our flat space cosmology model provides a reasonable explanation for current astronomical observations without the need to invoke a new type of force and energy.

7. Summary

Our flat space cosmology model, using only four basic and reasonable assumptions, generates highly accurate Hubble parameter, Hubble radius and total mass values for our observable universe. These values are in excellent agreement with the newly reported results of the 2015 Planck Survey and require only our assumptions and the current CMB radiation temperature to generate them. The thermo- dynamic equations we have generated, following Hawking’s black hole temperature formula, in conjunction with our basic assumptions, create a variety of useful cosmological formulae. These include angular velocity and other rotational formulae. Such rotational formulae should be correlated with further galactic observations, perhaps putting further constraints on dark matter.

Our results correlate nicely with a variety of astronomical observations. To take one example, one can roughly estimate the total mass, based upon observational estimates that there are approximately 10¹¹ visible galaxies times approximately 2 × 10¹¹ visible stars per galaxy times approximately 10³⁰ kg per star, totalling to approximately 2 × 10⁵² kg of visible (baryonic) mass. Multiplying this number by the roughly 5x expected dark matter gives a total mass observable of approximately 10⁵³ kg. Our model derives a value of appro- ximately 9.3 × 10⁵² kg from the Schwarzschild formula, after using a thermodynamic equation to derive (14.6 billion light-years). See equations 4 thru 7 for details. This is a remarkable achievement, since the only precise observational data our model requires is current CMB radiation temperature!

Dr. Stephen Hawking’s black hole temperature formula has been extremely useful in this undertaking. Since a picture is worth a thousand words, the following log graph (Figure 3) neatly summarizes our model relation- ships between Hubble time (universal age), Hubble radius, total mass and CMB radiation temperature.

One of the more useful thermodynamic equations generated with the help of Hawking’s black hole tem- perature formula is our hyperbolic equation:, which could, theoretically, apply all the way down to the Planck scale. Applicable numbers for current universal observations are shown at the extremes of the four axes.

One of the most interesting features of our model is that, by following the Schwarzschild formula and the assumption that is the appropriate Hubble parameter, the cosmic average mass density is always at critical density. The simple proof of this is that our derived cosmic average mass density formula is identical to the Friedmann critical density formula when is taken to be the Hubble parameter. Hence, our cosmic model is always “flat” (as defined by a universe at the Friedmann critical density) at every Hubble time stage of its growth.

The significance of the above revelation cannot be ignored. Ever since physicist Robert Dicke first made the observation [17] in 1969, cosmologists have been deeply puzzled as to how our universe appears to be expanding in a very precise way so as to perfectly balance out the attractive “force” of gravity. This is what is meant by a flat universe. In fact, as it was pointed out at the time, for such an apparent balance to be within observable error in the present, the presumably opposing forces in the very early universe (within a fraction of the first second after the Big Bang) must have been of equal magnitude to within one part in 10¹⁴. This has since been referred to as the “cosmological flatness problem.” There is an excellent discussion of this problem in Alan Guth’s book [18] , “The Inflationary Universe”. As one of the pioneers and early proponents of the theory of cosmic inflation, Dr. Guth makes it very clear in his book that the flatness problem is the primary reason a theory of cosmic inflation appears to be necessary.

One of the important requirements for a suitable theory of cosmic inflation is that it shows the very early universe to scale at least 25 logs of 10 in a tiny fraction of a second. However, one need only look at our summary log graph to see that such a “hyper-rapid exponential expansion” occurs within 10⁻¹⁷ of a second of Hubble time (universal age) in the very early growth of our flat space cosmos. Thus, a flat space cosmology which acts according to our basic assumptions, including light speed expansion and light speed rotation [19] [20] , naturally exhibits this cosmic inflation effect without requiring new physics.

Our model also suggests that the observational phenomena attributable to dark energy (especially the 1998 Type 1a supernovae data) may be entirely a manifestation of Minkowski flat space relativistic Doppler effect and gravitational time dilation, as explained in Section 6. Our mathematical model, as graphically represented in Figure 1 and Figure 2 of Section 6, clearly shows expected nonlinearity corresponding to our deepest space observations. It should be noted that the appearance of a very nearly perfectly balanced “force” in opposition to attractive gravity, as suggested by the 2015 Planck Survey value for the dark energy equation of state, could actually be an illusion produced by a constantly flat universe. Observations in support of a flat universe simply imply that no apparent net forces are acting on the universal system as a whole.

Finally, although currently formulated scientific laws appear to prevent one from ever observing the internal conditions of a black hole, we must at least consider the possibility that our own universe could be a particularly large evolved and evolving black hole (i.e., truly gargantuan in comparison to the known supermassive giant black holes). There appears to be nothing in general relativity which prevents such a possibility, however remote this possibility may seem to the reader at the present time.

8. Conclusion

Flat space cosmology, as introduced here, is one of the most exciting, interesting and productive new theories in cosmology. Given the few basic and reasonable assumptions of our model, it is astounding as to how well the resulting derivations fit with our current observable universe, as detailed in the 2015 Planck Survey results. The authors humbly request that the scientific community explore this fascinating subject in a true scientific spirit. Furthermore, the authors humbly request that the Nobel committee seriously consider honoring Drs. Stephen W. Hawking and Abhas Mitra for their invaluable work on black holes and cosmology in general.

Acknowledgements

The authors express their thanks to Dr. Abhas Mitra for his kind and valuable suggestions in developing this paper. One of the authors, Seshavatharam U.V.S., is indebted to professors K.V. Krishna Murthy, Chairman, Institute of Scientific Research in Vedas (I-SERVE), Hyderabad, India and Shri K.V.R.S. Murthy, former scientist IICT (CSIR), Govt. of India, Director, Research and Development, I-SERVE, for their valuable guidance and great support in developing this subject. Author Dr. E. Terry Tatum would also like to thank Dr. Rudy Schild, Harvard Center for Astrophysics, for his support and encouragement in developing this subject.

References