International Journal of Geosciences
Vol.07 No.01(2016), Article ID:63199,13 pages
10.4236/ijg.2016.71007
Quantification of the Diminishing Earth’s Magnetic Dipole Intensity and Geomagnetic Activity as the Causal Source for Global Warming within the Oceans and Atmosphere
David A. E. Vares1,2, Trevor N. Carniello2,3, Michael A. Persinger1,2,3
1Human Studies, Laurentian University, Sudbury, Canada
2Behavioural Neuroscience Programs, Laurentian University, Sudbury, Canada
3Biomolecular Sciences, Laurentian University, Sudbury, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 December 2015; accepted 26 January 2016; published 29 January 2016
ABSTRACT
Quantitative analyses of actual measurements rather than modeling have shown that “global warming” has been heterogeneous over the surface of the planet and temporally non-linear. Residual regression analyses by Soares (2010) indicated increments of increased temperature precede increments of CO2 increase. The remarkably strong negative correlation (r = −0.99) between the earth’s magnetic dipole moment values and global CO2-temperature indicators over the last ~30 years is sufficient to be considered causal if contributing energies were within the same order of magnitude. Quantitative convergence between the energies lost by the diminishing averaged geo- magnetic field strength and energies gained within the ocean-atmosphere interface satisfy the measured values for increased global temperature and CO2 release from sea water. The pivotal variable is the optimal temporal unit employed to estimate the total energies available for physical-chemical reactions. The positive drift in averaged amplitude of geomagnetic activity over the last 100 years augmented this process. Contributions from annual CO2 from volcanism and shifts in averaged geomagnetic activity, lagged years before the measured global temperature-CO2 values, are moderating variables for smaller amplitude perturbations. These results indicated that the increase in CO2 and global temperatures are primarily caused by major geophysical factors, particularly the diminishing total geomagnetic field strength and increased geomagnetic activity, but not by human activities. Strategies for adapting to climate change because of these powerful variables may differ from those that assume exclusive anthropomorphic causes.
Keywords:
CO2, Global Warming, Climate Change, Geomagnetic Field, Magnetic Dipole, Volcanic Activity

1. Introduction
“Global warming” is a term applied to the approximately 1˚C averaged increase in terrestrial surface temperature that has been measured over the last ~150 years [1] . According to Soares [2] , there has been an enhancement of this warming between approximately 1975 and 1998. There have been multiple concurrent solar and geophysical variables that have accompanied this mild increase in terrestrial surface temperature. They include lower cloud cover and hence greater total solar irradiance [3] , expansion of the solar corona and increased geomagnetic activity [4] , a 10% increase in water vapor within the atmosphere [1] and the physical chemical consequences of the earth’s magnetic dipole moment [5] . However, the primary explanation for generic global warming has been attributed to human activities, particularly the combustion of fossil fuels, that releases CO2 into the atmosphere. Predictions for future global temperature changes have been almost exclusively based upon models rather than extracting recondite relationships within actual measurements. Here we present quantitative evidence that although global warming has been occurring recently, the primary source may not be caused by release of CO2 from human activities but from physical processes strongly coupled to the diminishing magnetic dipole of the earth as well as enhanced geomagnetic activity due to shifting parameters within the movement of the solar system.
The visible representation of positive drifting of inferences of CO2 as ppm (parts per million) in the air or water temperature over the last half of a century has been a powerful persuasive tool. Although the graphs exhibit significant face validity, their construct validity is ambiguous. The limitations associated with the attribution of global warming primarily to human activity such as the combustion of fossil fuels are inaccuracies of the term and of the limited sampling of the key measurements. The changes in annual temperatures over the last century have not been linear (there was cooling in the 1960s and 1970s) which would not be typical of a “gradual loading” phenomenon. In addition, the changes in temperature are not homogeneously distributed globally. Knox and Douglass [6] challenged the global warming trend of 0.63 ± 0.28 W/m2 reported by Lyman et al. [7] during 1993-2008 by revealing the “flattening” that occurred around 2001 to 2002. Between the years 2003 and 2008 there was cooling, not warming, with a diminishment between 0.01 to 0.16 W/m2.
There are relatively few stations measuring CO2 which are then generalized to the planet even though about two-thirds of the land masses are in the northern hemisphere where high latitude regions exhibit the predominance of warming [2] . The strongest evidence that CO2 is not causing the incremental increase in global temperature is the direction of the quantitative relationship between residuals from regression analyses for years for temperature and CO2. If increments in CO2 were “causing” increments of increased temperature then the former must precede the later. However Soares [2] found the opposite quantitative relationship which would indicate, using the same criteria as do classic epidemiologists for cause and effect, that the causal factor for CO2 increases was temperature.
A global, physical perspective, without emphasizing a species-centric reference for cause, requires the consideration of all possibilities as well as all their dynamic combinations for the source of the recent increase in warming within the atmosphere and oceans. A solar-related source has been considered by many researchers [8] [9] . The sun and its system completes one orbit around the galactic center once every approximately 250 million years. This means from the perspective of human durations it has been moving through different space for the duration of the interval for which direct measurements and inferences of surface temperature have been collected [10] [11] .
The correlation between the solar semi-diameter, that could reflect the intrinsic structure of intergalactic space [12] and geomagnetic time series was reported by Neto et al. [13] . Lockwood et al. [4] demonstrated there has been a doubling of the solar coronal magnetic field during the past 100 years which has been associated with the increased average annual intensity of geomagnetic activity [14] . The inference by Fenton et al. [15] , based upon measurements of the albedo of planet Mars that its temperature had increased by about 0.7˚C over 20 years, strongly indicates that increased terrestrial increases in temperature may be related to processes other than its inhabitants. This approach is in marked opposition to the conclusions of Tett et al. [16] who excluded purely natural forcing of temperature change and attributed it “largely to the anthropogenic components”.
Courtillot et al. [5] have also pursued this approach and have suggested strong connections between the earth’s magnetic field and climate change, specifically the “archeomagnetic jerks” that are abrupt and about 100 years in duration. Geomagnetic activity which refers to the most disturbed components of the earth’s static magnetic field are in the range of about 1% (40 to 5000 nT, depending upon latitude) of the earth’s static magnetic field which is usually attributed with an average value of about 50,000 nT [17] . Changes in the magnitude of either the steady state (dc) or variable (ac) components are important because of a fundamental physical relationship involving energy (E), which is:
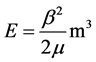 (1)
(1)
where B is the strength of the magnetic field, μ is the magnetic permeability (4π × 10−7 N/A2) and m3 is the volume being considered.
2. Geomagnetic Activity and Increased Global Temperatures
The ingenious analyses of El-Borie and Al-Thoryaib [14] indicated that the aa (average antipodal) index could be partially employed to predict global mean temperature. This was important because Stamper et al. [18] had found an unprecedented correlation of r = 0.97 within an optimal solar wind-magnetospheric coupling function. They argued that this coupling was directly associated over three solar cycles with increases in interplanetary magnetic field strength, solar wind speed and particle density. Persinger [19] calculated the dynamic pressure to be about 2.5 nPa which when multiplied by the volume of the lower troposphere (10 km thickness) with a volume of 5.1 × 1018 m3 would result in 1.2 × 1010 J/s or 3.8 × 1017 J per year within this gaseous volume.
By setting PV (pressure and volume) equal to the equation, Persinger [19] showed that the equivalent changes in average geomagnetic activity (about 16 nT) since around 1900 was the same order of magnitude of that which had been measured. The coefficients calculated by other researchers at ground level ranged from 13 nT∙nPa−0.5 [20] to 34 nT∙nPa−0.5 [21] . Over the extent of the analyses (100 years), the cumulative energy would have been 5.6 × 1019 J. Within 5.1 × 1024 cc (5.1 × 1018 m3) of sea water in the oceans this would have produced an increase of about 10−5˚C rather than the 0.1˚C to 1˚C that has been observed unless that increased geomagnetic activity-induced energy was displayed to a narrow depth between 100 m and 1 km at the ocean-atmospheric boundary.
Subsequent analyses by El-Borie et al. [22] analyzed the power spectral densities of data for global standardized temperature, aa (geomagnetic activity) and sunspot numbers for the years 1880 through 2008. They found that the correlation between global temperature and geomagnetic indicators was +0.66 while the concordance between global temperature and sunspot numbers was +0.38. The difference of magnitude between the two is statistically significant indicting that geomagnetic variability was the strongest. These authors emphasized the temporal displacements or lags between the classes of variables. Any change in aa indices was found to be associated with a change in the global standardized temperature. El-Borie’s previous work [14] had also demonstrated the presence of a 5 - 7 year lag in the quantitative changes in global geomagnetic activity and subsequent changes in temperature. The presence of significant peaks in the power spectral density for global temperature that included 21.3, 14.2, 11.6, 9.1, 7.5 and 6.4 years reinforced the contribution from solar-geomagnetic periodicities as well as their harmonics and potential beat frequencies.
Quantitative analyses of local measurements of sea water temperature and geomagnetic variations have supported these global values. Gang and Persinger [23] analyzed the values for the ocean water temperature and related parameters from the Victoria Experimental Network Under the Sea (VENUS) and demonstrated moderate strength (r = 0.60) correlations between global geomagnetic activity on days of and before small but discrete increases in sea water temperature, but not the second and thirds days before or the days afterwards. The multiple regression equation predicted that for every 10 nT increase in daily geomagnetic activity the water temperature increased by 0.1˚C. This meant that over the range occurring during the study (2 nT to 45 nT of geomagnetic activity) the average net increase should have been about 0.4˚C. However the standard error of the estimate placed the range between 0.1˚C to 0.7˚C. The actual change during this period as measured directly from subsurface sensors was ~1˚C.
3. Diminishment of the Absolute Intensity of Earth’s Magnetic Moment: Quantitative Solutions to Ocean-Atmosphere Energy Release
Unlike geomagnetic activity whose intensities wax and wane within durations of days, diminishment of the absolute intensity of the earth’s total geomagnetic field has been continuous and approximately 1000 times more intense than the daily fluctuations. The geomagnetic activity is superimposed upon this “quasi-static” source. Vares and Persinger [24] discerned from the data published by Pazur and Winklhofer [25] that over the last 32 years the earth’s magnetic dipole had diminished by ~2.9 × 10−6 T. This would have been associated with significant decrease in intrinsic magnetic energy that could be involved with maintaining the status of sequestering gases within sea water. The correlation between the diminishing magnetic dipole strength and the increase in global averaged CO2 was −0.997. Such strengths in most sciences would be considered causal or indicate that the same “source of variance” is being measured.
As shown in Figure 1 from Vares and Persinger [24] a decrease of ~2500 nT was associated with an increase of ~50 ppm of CO2 over this same period. The Boulder data were employed because they were a median value representative of the global shift. Within the 10 km thickness assumed to reflect the biosphere the application of Equation (1) indicated that over the 32 year period 1.72 × 1013 J would have been lost and hence potentially released as thermal energy. This assumes there were no recondite processes modifying the physical-chemical or quantal bases of the specific heat capacity of water. This energy matched the shift in CO2 levels as inferred by calculations. However assuming 4.18 J per 1 cc (10−6 m3) was that raise the temperature of the sea water 1˚C at standard temperature and pressure (STP), then the total energy within the 5.1 × 1018 m3 shell would be 2 × 1025 J rather than the value indicated on page 851 [24] . This discrepancy was recognized by a Discovery Magazine blogger [26] and produced a series of constructive corrections.
The potential discrepancy does not change the validity of the strong inverse correlation of −0.997 between diminished energy from the earth’s magnetic dipole moment and the rise in global temperature and CO2. What is required then is to discern the quantitative sources required to produce the convergence between the two systems. The most parsimonious missing variable would be duration assumed to maintain and dissipate the energy per unit molecular time. If the functional cumulative loss of energy occurred in increments of 1 s (the intrinsic unit for most dimensional analyses of these processes) then the total energy dissipated would be (1.72 × 1013 J per block) × (3.2 × 101 years per block) × (3.15 × 107 s per year) or 1.7 × 1022 J. To explore these implications we calculated the results again from a different perspective.
The energy associated with a magnetic field within a volume can be described by the relationship noted in
Figure 1. The strong inverse correlation (from vares and persinger [24] ) as a function of year for the boulder total field intensity (our inference of the diminishing geomagnetic dipole moment, blue line) and the increase in globally averaged CO2 levels (red line).
Equation (1). Vares and Persinger assumed an averaged depth within the oceans of 10 km and calculated the magnetic energy from this change in intensity of the magnetic dipole. Given a terrestrial surface area of 5.1 × 1014 m2 and an average depth of 104 m or 10 km (or a slightly less depth if the estimate that the oceans cover 70% of the surface is preferred), the functional volume would be 5.1 × 1018 m3 (Figure 2). According to (1) the energy shift (potential loss) within that volume associated with 10 km depth of ocean would be 1.72 × 1013 J.
Because the Earth is not a closed system, we assumed the magnetic energy within the volume must be maintained. As Vares and Persinger stated previously the “implicit assumption for J conversions is the temporal unit of one second.” Other researchers, such as Knox and Douglass [6] employing different assumptions and random sampling measurements have estimated a recent heat loss ranging from 0.01 to 0.5 W/m2 which is equivalent for the total surface to between 5 × 1012 J/s to ~2.5 × 1014 J/s (W). This range overlaps with our estimates from magnetic energy loss associated with the diminished dipole magnetic field intensity within the 10 km shell.
To estimate the cumulative energy that might maintain any temperature shift the temporal factor must be considered. This means that over the extent of 32 years with 3.15 × 107 s per year, there would be 1.72 × 1013 J/s multiplied by 1.01 × 109 s (32 years) or a cumulative effect of 1.73 × 1022 J (0.41 × 1022 calories). This would be consistent with the classical law of constant heat summation as described by Maass and Steachie [27] . We appreciate there would be some differential from the increasing drift of the diminishment of the dipole over that time.
For traditional approaches the amount of heat transfer is defined in terms of the mass of the water [28] . By infusing 1 calorie into 1 gram (1 cc) of water there is an increase of 1˚C. For the same mass a loss of 1˚C would be associated with the potential removal (or conversion) by transfer of 1 calorie. When applied to the present problem there would be energy transfer due to the loss of 0.41 × 1022 calories coupled to the diminishing dipole strength within the 10 km volume (5.1 × 1024 cc) of ocean water. With these values there would be a potential loss of 0.08 × 10−2˚C per cc of water. Because there are 18 cc per mole of water, this would be equivalent to a loss of 1.44 × 10−2˚C per mole of water.
The value of the release of intrinsic energy from the diminished dipole strength that is equivalent to ±0.001˚C is based upon the volume of oceans with an average of 10 km depth. If this energy were displaced to a smaller volume such as only the thin shell of 1 km below the surface of the ocean which constitutes the major interface
Figure 2. The radius of the Earth is 6.37 × 106 m (center to green line). Assuming a thin 10 km spherical shell depth of the oceans (blue), is a relative 0.3% of the total Earth radius. Taking the surface area of the Earth’s oceans to be 5.1 × 1014 m2 and the 10 km depth yields an applicable ocean volume of 5.1 × 1018 m3. Similarly, the functional volume of the atmosphere shell (red) can also be approximated by the differences with similar coefficients of ~5.1 × 1018 m3. The green line therefore depicts the ocean-atmosphere gas exchange boundary. Note: the ocean and atmosphere shells are not to scale.
with the gaseous atmosphere, the increase would be within the +1˚C range. Our data and calculations indicate that a major mode by which this energy is dissipated from the ocean water into the atmosphere is by the release of the CO2 from the ocean reservoir. Current estimates indicate that about 93% of CO2 is contained within the oceans.
We assumed the loss of energy from the ocean water coupled to the diminishing energy from the earth’s magnetic dipole was dissipated into the adjacent gas within the atmosphere. The energy assumed to increase a gas by 1˚C is 1 J per gram. The major constituent of the earth’s atmosphere is diatomic Nitrogen with a gram molecular weight of 28 g. Hence the energy required to raise the temperature 1˚C would be 28 J. One mole of a gas at STP is 22.4 L. This volume is equivalent to 2.24 × 10−2 m3 and the energy required would be the ratio or 1.25 × 103 J/m3.
The total energy that was available from the diminishment of the magnetic dipole was calculated to be 1.73 × 1022 J. When this value is divided by 1.25 × 103 J/m3, the affected volume (assuming no dissipation elsewhere) would be 1.38 × 1019 m3. This solution is within the same order of magnitude as the assumed volume (based upon 10 km depth) of atmosphere which matches the ocean volume from which the dissipating energy from the diminishing magnetic dipole was calculated. This quantity of energy within the volume occupied by a 10 km thick shell of atmosphere within which there has been an increase by 50 ppm or 0.13 × 1023 CO2 molecules per cubic meter is significant. Within the 5.1 × 1018 m3 shell there would be 6.7 × 1040 CO2 molecules. Hence the energy per molecule contributed by the loss of 1.73 × 1022 J from the diminished dipole would be about 2.58 × 10−18 J per CO2 molecule or some equivalent molecule. This is well within the energy range of many bond energies. It may be relevant that the wavelength associated with the quantum frequency (by dividing by Planck’s constant) of this increment of energy is within the range (121.6 nm) attributed to the dissociation of water by sunlight that according to Clary [29] occurs continuously within the earth’s atmosphere.
Noting the estimated gas exchange coefficient varies with a number of environmental variables and ranges between 8 and 18 mol/m2 per year, and assuming a value of 3.35 × 1014 m2 for the surface area of oceans, the increase of 50 ppm over the 32 years for CO2 and the 0.67 × 1040 CO2 molecules, there would have been a net excess of +1 mol/m2 per year between the ocean and atmosphere carbon cycle. This is within the same order of magnitude as model-estimated variance.
The involvement of proportions of dissociation of water by sunlight directly due to the energies released from molecular reactions subsequent to the declining earth’s magnetic dipole moment would support the water vapor hypothesis by Soares [2] . Aptly reiterating water vapor’s potential to absorb about 63% of radiating long wave energy compared to the 22% and 2% absorption rates for CO2 and CH4, respectively, he calculated that the net retention of 11 W/m2 would correspond to an amplifying greenhouse effect of 3.5%. This would be equivalent to a global warming of an average 1.3˚C. This is also within the range of observed values.
The symmetry of reversibility of the relationship between CO2 levels and temperature is important to appreciate. Soares’ [2] results that indicated temperature correlated strongest with increased CO2 changes about one-half to one year later, which he inferred indicated that temperature was “the driver” and not CO2. However there was an absence of correlation between the two variables for periods of decreases in temperature indicating the process was not reversible and that the physical chemical mechanisms for uptake of this gas into oceans is complex and may involve multiple mechanisms that are quite different than elementary degassing.
4. Experimental Simulation of Reduced Static Geomagnetic Field-Increased CO2 Release from Salt Water
The correlational analyses reported by Vares and Persinger [24] and the Pazur and Winklhaufer [25] sea water solubility study showed a negative correlation of −0.99 between the rising CO2 and the declining magnetic dipole strength of the earth over the last approximately three decades. Between 1980 and 2013 the concentrations of the gas in the atmosphere increased by ~50 ppm while the magnetic field strength decreased by ~2.9 μT. We designed an experiment to support a causal bases to this relationship. Although local laboratory experiments do not necessarily simulate the complexity and emergent phenomena associated with large mass effects, such as those occurring over the surface of a planet, quantitative results obtained by experiment and direct manipulation of key variables can be supportive or reflective of “proof in principle”.
We experimentally examined if the reduction of the local geomagnetic field intensity at the magnitudes associated with global diminishments could produce increases in release of carbon dioxide from simulated sea water. Beakers containing 100 cc of NaCl at concentrations typical of sea water were extracted from 1 L initial preparations. The beaker was placed in the middle of a custom-constructed 10 cm by 10 cm by 10 cm plastic box that we have employed to study the effects of complex patterned magnetic fields upon the growth of aberrant cells [30] . Pairs of solenoids (Reed switches) in each plane generated magnetic fields from a digital to analogue (DAC) converter whose values were determined by Complex software developed by Professor Stanley Koren [31] . The magnetic field patterns and strengths can be determined by converting a series of numbers from 0 thru 256 to equivalent voltages between −5 V and +5 V.
The unique feature of the Koren process is that the generation of the programmable magnetic field is derived from reconverting the diminishment of the ambient geomagnetic field. In other words the background geomagnetic field is “bucked” by the application of the dc magnetic fields between the pairs of solenoids. This effect was considered optimal to test the feasibility of local static geomagnetic reduction upon the release of CO2 from salt water. The pattern “negpo”, which is the negative half of a sine wave, was selected from our field pattern library. It is composed of 200 points all with values below 127 or negative polarity. The point duration of each value was set at 3 ms in light of its efficacy for affecting proton related processes in cells, particularly those associated with hydronium ions [32] [33] . Our quantitative calculations for the energy loss associated within sea water and its release into the atmosphere of CO2 as well as the increase in temperature from the diminishment of the earth’ magnetic dipole moment assumes a central role of this ion. Because the point duration was 3 ms and there were 200 points in the half wave the frequency was 1.67 Hz. However the intrinsic variation from the 3 ms point durations which involve the shifts in current values would have been 333.3 Hz.
A USB Probe Meter (CM-004) CO2 sensor was placed over the top of the beaker. CO2 in ppm was measured automatically by the accompanying Gaslab V2.0.8.9 software by a laptop (Core i5, Thinkpad) computer once every 30 s. The total number of cycles of repetition of the field (“negpo”) was 9999 (maximum possible for software). This means that the duration of the field exposure in all three spatial planes through the 3 pairs of solenoids was 100 min (6 × 103 s). Direct measurements by a MEDA FVM 400 Vector Magnetometer (Macintyre Electronic Design Associates) indicated that the strongest component (the vertical field strength) of the geomagnetic field inside the space occupied by the volume of water diminished by between 1.7 and 3.7 μT when the field was activated. Four measurements on separate nights between 04 and 06 hours local time with no lights operating in the laboratory were completed. Two field and two non-field conditions were completed on alternative nights. During two control (sham field) nights the program was not activated although the system was operating.
The means and SDs (in parentheses) for CO2 in ppm for the two control runs were 600 (4), 603 (16). For the two magnetic field trials on alternative nights theses values were 618 (39) and 624 (42) ppm. The mean difference between the field and no field conditions was about 19 ppm. The source of the relatively small coefficient of variation for the first control trial is unclear, although we have measured similar narrow dispersions on other days within “natural” background geomagnetic field intensities.
The magnetic energy according to Equation (1) within that volume of 100 cc would have been between 1.2 and 5.5 × 10−10 J. Assuming 19 ppm then (1.9 × 10−5) × 6.023 × 1023 molecules per Mole and 5.5 Moles of water in 100 cc, there would be 6.29 × 1019 molecules of CO2 released from that volume. That would be equivalent to 1.8 to 8.7 × 10−30 J per molecule of CO2. Vares and Persinger [24] have calculated that the diminished effect within a 10 km shell of seawater from the declining dipole strength was 2.56 × 10−27 J per CO2 molecule. However the experimental field was activated for 6 × 103 s which means the cumulative dynamic energy would have been 1.1 to 5.2 × 10−26 J per molecule. Thus the magnitudes of the energies for the calculated estimates for the planet and the experimental measurements were approaching the same order of magnitude. The two estimates would have converged after about 1400 s to 300 s of experimental exposure.
5. Recondite Power Oscillations for Potential Ocean-Air CO2-Temperature Coupling
The relationship between the diminishment of the earth’s magnetic dipole moment and the increase in atmosphere temperature and CO2 involves increments of years. Chemical processes such as the life time of the hydronium ion involves durations of picoseconds [34] while asymptotes for chemical reactions may involve milliseconds to seconds. Fundamental spheroidal modes or background free oscillations of the entire earth, such as spectral power densities for solid earth-atmospheric acoustic oscillations, occur at 4.5 mHz and 3.7 mHz. They are the fundamental spheroidal modes 0S29 and 0S37 [35] [36] . Large scale gravitational effects involve periods in the orders of tens of minutes with a particular dissociation around 30 min [37] [38] .
These may be masked spectral densities of interests within the ocean-atmosphere processes that could facilitate coupling in a manner similar to the diminished energy required to “connect” the two systems if they share resonance. The means of the spectral power densities of the laboratory measured CO2 levels recorded once every 30 s with and without the presence of the reduced 3.7 μT geomagnetic fields revealed a marked increase in spectral power density of CO2 release within periodicities starting around 2000 s or 33.3 minutes. The profiles are shown in Figure 3. If that value (in seconds) is multiplied by the lower limit of about 10−30 J per molecule the value would be within the range of 2.76 × 10−27 J per molecule. Previous measurements in our laboratory have indicated that about one-half an hour is the inflection point for the escalating random power density for photon counts and gravity variations. The presence of the approximately 30 min periodicity in this gas emission from laboratory prepared salt water during an experimentally produced diminishment of the earth’s magnetic field requires consideration of gravitational factors in the declining dipole-increasing CO2 connection.
The intrinsic resonance of the ocean depth-atmosphere height parameters are temporal variables of pivotal significance because they involve universal values and specific solutions. Magnetic diffusivity, a concept employed perspicaciously by Ryskin [39] is the inverse of the conductivity of the solvent and magnetic permeability. Assuming the conductivity of sea water to be ~4.8 S and knowing magnetic permeability is 4π × 10−7 N/A2, the diffusivity would be 0.17 × 106 m2/s. When multiplied by the inflection point of the period for the spectral power density (Figure 3) that occurs when the static magnetic field is reduced experimentally, the area is approximately 4.1 × 108 m2. This is equivalent to a linear distance of 20 km or the width of the two shells of ocean depth and atmosphere we have assumed in our approach.
The assumption of an average depth of 10 km for oceans and 10 km for function coupled atmosphere is consistent with empirical estimates. Potential resonance between the ocean-atmosphere because of intrinsic properties associated with the reduction of the geomagnetic field has quantitative support. Each water molecule displays a Debye unit of 1.86 or 6.2 × 10−30Asm. When multiplied by the decrease in magnetic field strength over the measurement period, 2.9 × 10−6 T, the resulting momentum term is 1.8 × 10−35 kg m/s. The force resulting from the application of the hydrogen line (1.42 GHz), which is conspicuously measured over large bodies of
Figure 3. Averaged spectral densities for fluctuations in amplitudes of CO2 “gasing out” values in ppm for 100 cc quantities of salt water exposed to the normal geomagnetic field (blue) or to an experimentally reduced geomagnetic field (red) to intensity reflecting the global diminishment of the dipole magnetic moment over the last 32 years.
water, is 2.55 × 10−26 N. This may appear to be a small force and when applied over the distance of a single O-H bond (0.96 × 10−10 m) results in 2.45 × 10−36 J. Because of the homogeneity of these quantities within all water molecules, a relatively focused frequency would emerge at the quantum level. When this value is divided by Planck’s constant (6.626 × 10−34 J s) the emergent frequency is 0.37 × 10−2 Hz or 3.7 mHz. This is one of the peak frequencies of earth-atmospheric coupling as measured by Nishida et al. [36] . It may be relevant that quantum-level phenomena may be expressed within macro-geophysical phenomena that include specific energetic bands of global seismicity [40] .
6. Multivariate Contributors Analysis: Inclusive Data Sources
In order to assess the magnitude (effect size) by which other variables could contribute to the CO2-temperature enhancements, additional complex analyses were completed. Data employed previously were retrieved [24] and updated including the annual total field intensities (F), annual globally averaged CO2 (ppm) levels, and annual global (Land and Ocean and combined) anomalies (degrees C).
Annual total field intensities (F) as measured in nanoTesla (nT) were retrieved from the United States Geological Survey (USGS), Boulder Observatory (BOU) (http://geomag.usgs.gov/) for the years between 1964-2012. The Boulder Observatory was selected as a global representative of the variable field intensities. Annual Globally Averaged CO2 (ppm) levels were retrieved from the National Oceanic & Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL) (http://www.esrl.noaa.gov/) for the years between 1980- 2012. The Annual Global (Land and Ocean combined) Anomalies (degrees C) expressed as departures from the 20th century average (1901-2000) measures were retrieved from the National Oceanic & Atmospheric Administration (NOAA) National Centers for Environmental Information (NCEI) (https://www.ncdc.noaa.gov/) formerly the National Climatic Data Center (NCDC), for the years between 1970-2012. Additional volcanic activity data was queried from the joint Smithsonian Institution National Museum of Natural History Global Volcanism Program (http://volcano.si.edu/) and the United States Geological Survey (USGS), retrieving data for total eruptions per year.
The annual data were formatted using Matlab software and computational values entered into SPSS software for statistical relationship investigation. Zero-order relationship analysis was conducted on the three annual measures, followed by lag-lead relationship analysis (±5 years) and partial correlation for residual analysis. Table 1 presents the results of a lag/lead±5 years, stepwise multiple regression analysis for the various predictive models of global land, ocean and combined land + ocean temperatures.
The results indicate a temporal order of the average values for geomagnetic activity (aa) strength 2 years prior to temperature changes, with associated CO2 levels 1 year following. Graphing the land and ocean combined temperature variations, after controlling for the geomagnetic field measures 2 years prior, revealed a slight smoothing of the trend curve (Figure 4). The visual congruence of the coherence between raw temperature increases and the residuals of global geomagnetic activity (aa) two years previously dissociated around 2005. This is the same period when Knox and Douglass [6] showed no increase in global temperature and technically a
Table 1. Results of multivariate analyses of contemporary and lagged data for primary variables.
mild cooling effect. The flattening effect after the year 2001 is also apparent for raw surface temperature values.
In addition there is evidence that the diminishing residuals after 2005 for the average amplitude of geomagnetic activity (a strong solar coupled phenomenon) is associated with no further increase in raw temperature and in fact a potential trend for cooling. This would be consistent with other quantitative data.
Investigations of all energetic possibilities indicated that multiple contributors were potentially superimposed upon the magnetic dipole diminishment effects. Expanding upon predictive models and the temporal order of geomagnetic field strength 2 years prior to temperature changes with associated CO2 levels 1 year following, a lag/lead relationship analysis was conducted with all variables (geo/solar) as well as the total global volcanic activity. The only statistically significant relationships were connected to the magnitude of volcanism and are presented in Figure 5.
These results again point to the dynamic nature of the Earth’s non-closed system and temporal dependency before any relation is observable. To illustrate the importance of time delays, Figure 6 presents the statistically significant relationship of volcano eruptions with CO2 levels 4 years later.
7. Conclusions
There are correlations and causes for the fluctuations in global temperature within the last century. Although
Figure 4. Annual global temperature anomalies for the combined land and ocean departures from the 20th century average, and the residual global temperature anomalies values after controlling for the aa index from 2 years prior.
Figure 5. The total volcano eruptions displayed a moderate positive relationship with carbon dioxide levels for two, three, four and five years after the epoch year. Volcano activity was not related to the other global or solar activity values.
Figure 6. Shows the relationship between annual total volcanic activity and the subsequent globally averages carbon dioxide levels 4 years later.
general consensus has concluded a causal connection between elevations of carbon dioxide in the atmosphere and increases in ocean and atmospheric temperature, the inferences are made primarily from models with minimal convergent quantification. The strongest data-based causal inferences for the elevated carbon dioxide levels in the atmosphere are related to the diminishing intensity of the earth’s magnetic field strength (the magnetic dipole moment) with modulations from solar driven geomagnetic activity and volcanism.
The complex lag effects, analogous to time constants and reluctance phenomena in smaller physical systems, can obscure this relationship when only bivariate graphs are viewed and year-to-year residuals are not considered. The quantitative convergence of the energies associated with the changes in the ambient magnetic fields within the interface between the oceans and atmosphere, supports the validity of a causal connection. The quantitative connection between diminished ambient magnetic field strengths and carbon dioxide releases from salt water within the laboratory by experimentation is consistent with the global correlation data. Reliance exclusively upon the belief that human activities are primarily responsible for the recent elevations of carbon dioxide and temperature could result in allocating global resources erroneously and initiating technologies that would be ineffective. The allocation would not facilitate optimal species adaptation to these geophysical changes.
Acknowledgements
Thanks to Professor Lukasz Karbowski for technical contributions and to Dr. Linda St. St-Pierre, Laurentian University Faculty Association (LUFA) and CAUT (Canadian Association of University Teachers) for defending our academic freedom to pursue the controversial, the “politically incorrect” and the unknown.
Cite this paper
David A. E.Vares,Trevor N.Carniello,Michael A.Persinger,11, (2016) Quantification of the Diminishing Earth’s Magnetic Dipole Intensity and Geomagnetic Activity as the Causal Source for Global Warming within the Oceans and Atmosphere. International Journal of Geosciences,07,78-90. doi: 10.4236/ijg.2016.71007
References
- 1. Landscheidt, T. (2000) Solar Wind near Earth: Indicator of Variation of Variation in Global Temperature. European Space Agency Special Publication, 463, 497-500.
- 2. Soares, P.C. (2010) Warming Power of CO2 and H2O: Correlations with Temperature Changes. International Journal of Geosciences, 1, 102-112. http://dx.doi.org/10.4236/ijg.2010.13014
- 3. Kristjansoon, J.E., Staple, A. and Kristiansen, A. (2002) A New Look at Possible Connections between Solar Activity, Clouds and Climate. Geophysical Research Letters, 29, 2107-2111.
http://dx.doi.org/10.1029/2002GL015646 - 4. Lockwood, M., Stamper, R. and Wild, M.M. (1999) Doubling of the Sun’s Solar Coronal Magnetic Field during the Past 100 Years. Nature, 399, 437-439. http://dx.doi.org/10.1038/20867
- 5. Courtillot, V., Gallet, Y., Le Mouel, J.-L., Fluteau, F. and Genevey, A. (2007) Are There Connections between the Magnetic Field Variations and Climate? Earth and Planetary Science Letters, 253, 328-329. http://dx.doi.org/10.1016/j.epsl.2006.10.032
- 6. Knox, R.S. and Douglass, D.H. (2010) Recent Energy Balance on Earth. International Journal of Geosciences, 1, 99-101. http://dx.doi.org/10.4236/ijg.2010.13013
- 7. Lyman, et al. (2010) Robust Warming of the Global Upper Ocean. Nature, 465, 334-337.
http://dx.doi.org/10.1038/nature09043 - 8. Erlykin, A.D., Sloan, T. and Wolfendale, A.W. (2009) Solar Activity and Mean Global Temperature. Environmental Research Letters, 4, Article ID: 014006. http://dx.doi.org/10.1088/1748-9326/4/1/014006
- 9. Haigh, J.D. (1996) The Impact of Solar Variability on Climate. Science, 272, 981-984.
http://dx.doi.org/10.1126/science.272.5264.981 - 10. Persinger, M.A. (2014) Conversion Energy from the Movement of the Solar System through Universal Pressure: Reflections in Seismic Events and Global Temperatures. International Letters of Chemistry, Physics and Astronomy, 17, 78-86. http://dx.doi.org/10.18052/www.scipress.com/ILCPA.36.78
- 11. Persinger, M.A. and Vares, D.A.E. (2014) The Asteroid Belt as a Consequence of Resonance Density Convergence From Solar Velocity Around the Galaxy and Universal Dynamic Pressure. International Letters of Chemistry, Physics and Astronomy, 15, 73-79.
http://dx.doi.org/10.18052/www.scipress.com/ILCPA.34.73 - 12. Persinger, M.A. (2014) Discrepancies between Predicted and Observed Intergalactic Magnetic Field Strengths from the Universe’s Total Energy: Is it Contained within Submatter Spatial Geometry? International Letters of Chemistry, Physics and Astronomy, 11, 18-23.
http://dx.doi.org/10.18052/www.scipress.com/ilcpa.30.18 - 13. Neto, E.R., et al. (2012) Correlation between Solar Semi-Diameter and Geomagnetic Time Series. International Journal of Geosciences, 3, 321-328. http://dx.doi.org/10.4236/ijg.2012.32034
- 14. El-Borie, M.A. and Al-Thoyaib, S.S. (2006) Can We Use the aa Geomagnetic Activity Index to Predict Partially the Variability in Global Mean Temperatures? International Journal of Physical Sciences, 1, 67-74.
- 15. Fenton, L.K., Geissler, P.E. and Haberie, R.M. (2007) Global Warming and Climate Forcing by Recent Albedo Changes on Mars. Nature, 446, 646-649. http://dx.doi.org/10.1038/nature05718
- 16. Tett, S.F.B., Stott, P.A., Allen, M.R., Ingram, W.J. and Mitchell, J.F.B. (1999) Causes of Twentieth-Century Temperature Change near the Earth’s Surface. Nature, 399, 569-572.
http://dx.doi.org/10.1038/21164 - 17. Campbell, W.H. (1997) Introduction to Geomagnetic Fields. Cambridge University Press, Cambridge.
- 18. Stamper, R., Lockwood, M., Wild, M.N. and Clark, T.D.G. (1999) Solar Causes of the Long-Term Increase in Geo-Magnetic Activity. Journal of Geophysical Research, 104, 325-328.
http://dx.doi.org/10.1029/1999JA900311 - 19. Persinger, M.A. (2009) The Possible Role of Dynamic Pressure from the Interplanetary Magnetic Field on Global Warming. International Journal of Physical Sciences, 4, 44-46.
- 20. Siscoe, G.L., Formisano, V. and Lazarus, V. (1968) A Calibration of the Magnetopause. Journal of Geophysical Research, 73, 4869-4874. http://dx.doi.org/10.1029/JA073i015p04869
- 21. Su, S.Y. and Konradi, A. (1975) Magnetic Field Depression at the Earth’s Surface Calculated from the Relationship between the Size of the Magnetosphere and the Dst Values. Journal of Geophysical Research, 80, 195-199. http://dx.doi.org/10.1029/JA080i001p00195
- 22. El-Borie, M.A., Shafik, E., Abdel-halem, A.A. and El-Monier, S.Y. (2010) Spectral Analysis of Solar Variability and Their Possible Role in Global Warming. Journal of Environmental Protection, 1, 111-116. http://dx.doi.org/10.4236/jep.2010.12014
- 23. Gang, N. and Persinger, M.A. (2012) Correlations between Ocean Water Temperature and Related Parameters from the Victoria Experimental Network under the Sean (VENUS) and Geomagnetic Activity: Implications for Climate Change. International Journal of the Physical Sciences, 7, 660-663.
- 24. Vares, D.A.E. and Persinger, M.A. (2015) Earth’s Diminishing Magnetic Dipole Moment Is Driving Global Carbon Dioxide Levels and Global Warming. International Journal of Geosciences, 6, 846-852.
http://dx.doi.org/10.4236/ijg.2015.68068 - 25. Pazar, A. and Winklhofer M. (2008) Magnetic Effect on CO2 Solubility in Seawater: A Possible Link between Geo-Magnetic Field Variations and Climate. Geophysical Research Letters, 35, L16710.
- 26. Magnetism: From Neuroscience to Climate Change?—Neuroskeptic. 16 October 2015.
http://blogs.discovermagazine.com/neuroskeptic/2015/10/16/magnetism-neuroscience-to-climate-change/#more-6886 - 27. Maass, O. and Steachie, E.W.R. (1939) An Introduction to the Principles of Physical Chemistry. John Wiley & Sons, London.
- 28. White, F.M. (1988) Heat and Mass Transfer. Addison-Wesley, Reading, MA.
- 29. Clary, D.C. (1999) Interfering with Water. Science, 285, 1218-1219.
http://dx.doi.org/10.1126/science.285.5431.1218 - 30. Karbowski, L.M., Murugan, N.J., Koren, S.A. and Persinger, M.A. (2015) Seeking the Source of Transcience for a Unique Magnetic Field Pattern that Completely Dissolves Cancer Cells in Vitro. Journal of Biomedical Science and Engineering, 8, 531-543. http://dx.doi.org/10.4236/jbise.2015.88050
- 31. Koren, S.A., Bosarge, W.E. and Persinger, M.A. (2015) Magnetic Fields Generated by Optical Coupler Circuits May Also Be Containment Loci for Entanglement of P-N Junction-Plasma Cell Membrane Photons within Exposed Living Systems. International Letters of Chemistry, Physics and Astronomy, 3, 84-105.
- 32. Persinger, M.A. (2015) Thixotropic Phenomena in Water: Quantitative Indicators of Casimir-Magnetic Transformations from Vacuum Oscillations (Virtual Particles). Entropy, 17, 6200-6212.
http://dx.doi.org/10.3390/e17096200 - 33. Koren, S.A., Dotta, B.T. and Persinger, M.A. (2014) Experimental Photon Doubling as a Possible Local Inference of the Hubble Parameter. The Open Astronomy Journal, 7, 1-6.
http://dx.doi.org/10.2174/1874381101407010001 - 34. Decoursey, T.E. (2003) Voltage-Gated Proton Channels and Other Proton Transfer Pathways. Physiology Reviews, 83, 475-579. http://dx.doi.org/10.1152/physrev.00028.2002
- 35. Tanimoto, T., Ulm, J., Nishida, K. and Kobayashi, N. (1998) Earth’s Continuous Oscillations Observed on Seismically Quiet Days. Geophysical Letters, 25, 1553-1563. http://dx.doi.org/10.1029/98GL01223
- 36. Nishida, K., Kobayahsi, N. and Fukao, Y. (2000) Resonant Oscillations between the Solid Earth and the Atmosphere. Science, 287, 2244-2246. http://dx.doi.org/10.1126/science.287.5461.2244
- 37. Quinn, T., Parks, H., Speake, C. and Davis, R. (2013) Improved Determination of G Using Two Methods. Physics Review Letters, 111, Article ID: 101102. http://dx.doi.org/10.1103/PhysRevLett.111.101102
- 38. Persinger, M.A. (2014) Potential Gravitational-Solar Electromagnetic Spectral Radiance Interaction as the Source of the Earth’s Background Free Oscillations. International Letters of Chemistry, Physics and Astronomy, 2, 11-14.
- 39. Ryskin, G. (2009) Secular Variation of the Earth’s Magnetic Field: Induced by Ocean Flow? New Journal of Physics, 11, Article ID: 063015. http://dx.doi.org/10.1088/1367-2630/11/6/063015
- 40. Vares, D.A.E. and Persinger, M.A. (2013) The ~3.6 to 3.7 M Paucity in Global Earthquake Frequency: Potential Coupling to Zero Point Fluctuation Force and Quantum Energies. International Journal of Geosciences, 4, 1321-1325. http://dx.doi.org/10.4236/ijg.2013.410127








