International Journal of Modern Nonlinear Theory and Application
Vol.05 No.04(2016), Article ID:72334,17 pages
10.4236/ijmnta.2016.54020
Approximate Inertial Manifold for a Class of the Kirchhoff Wave Equations with Nonlinear Strongly Damped Terms
Chengfei Ai, Huixian Zhu, Guoguang Lin
Department of Mathematics, Yunnan University, Kunming, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 8, 2016; Accepted: November 26, 2016; Published: November 29, 2016
ABSTRACT
This paper is devoted to the long time behavior of the solution to the initial boundary value problems for a class of the Kirchhoff wave equations with nonlinear strongly damped terms: 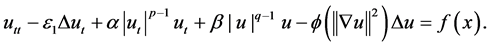 Fir- stly, in order to prove the smoothing effect of the solution, we make efficient use of the analytic property of the semigroup generated by the principal operator of the equation in the phase space. Then we obtain the regularity of the global attractor and construct the approximate inertial manifold of the equation. Finally, we prove that arbitrary trajectory of the Kirchhoff wave equations goes into a small neighbourhood of the approximate inertial manifold after large time.
Fir- stly, in order to prove the smoothing effect of the solution, we make efficient use of the analytic property of the semigroup generated by the principal operator of the equation in the phase space. Then we obtain the regularity of the global attractor and construct the approximate inertial manifold of the equation. Finally, we prove that arbitrary trajectory of the Kirchhoff wave equations goes into a small neighbourhood of the approximate inertial manifold after large time.
Keywords:
Kirchhoff Wave Equation, Global Attractor, The Smoothing Effect, The Regularity, Approximate Inertial Manifold

1. Introduction
It is well known that we are studying the long time behavior of the infinite dimensional dynamical systems of the nonlinear partial differential equations, and the concept of the inertial manifold plays an important role in this field. In 1985, G. Foias, G. R. Sell and R. Teman [1] first put forward the concept of the inertial manifold; it is an invariant finite dimensional Lipschitz manifold; it is exponentially attracting trajectory and contains the global attractor. But to ensure that existing conditions are very harsh for inertial manifolds (For instance, spectral interval condition), the existence of a large number of important partial differential equations is still not solved. Therefore, people naturally think of using an approximate, smooth and easy to solve the manifolds to approximate the global attractor and inertial manifolds, which is the approximate inertial manifold.
Approximate inertial manifolds are finite dimensional smooth manifolds, and each solution of the equation is in a finite time to its narrow field. In particular, the global attractor is also included in its neighbourhood. The existence of approximate inertial manifolds of a large number of dissipative partial differential equations has been studied [2] - [7] .
In this paper, we are concerned a class of the Kirchhoff wave equations with nonlinear strongly damped terms referred to as follows:
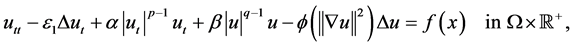 (1.1)
(1.1)
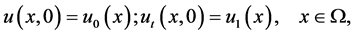 (1.2)
(1.2)
 (1.3)
(1.3)
where  is a bounded domain in
is a bounded domain in 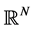 with smooth boundary
with smooth boundary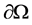 , and
, and 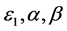 are positive constants, and the assumptions on
are positive constants, and the assumptions on 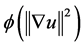 will be specified later.
will be specified later.
In [8] , G. Kirchhoff firstly proposed the so called Kirchhoff string model in the study nonlinear vibration of an elastic string. Kirchhoff type wave equations have been studied by many scholars (see [9] [10] [11] ). In reference [12] , the long time behavior of solutions for the initial value problems (1.1) - (1.3), the existence of global attractor corresponding to the semigroup operator 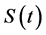 and the dimension estimation of glo- bal attractor, have been researched.
and the dimension estimation of glo- bal attractor, have been researched.
In [13] , Dai Zhengde, Guo Boling, Lin Guoguang studied the fractal structure of attractor for the generalized Kuramoto-Sivashinsky equations:
 (1.4)
(1.4)
 (1.5)
(1.5)
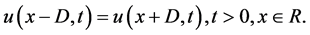 (1.6)
(1.6)
where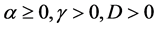 .
.
In [14] , Li Yongsheng, Zhang Weiguo studied regularity and approximate of the attractor for the strongly damped wave equation:
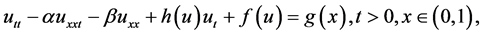 (1.7)
(1.7)
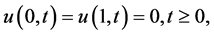 (1.8)
(1.8)
 (1.9)
(1.9)
where 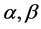 are positive constants.
are positive constants.
Luo Hong, Pu Zhilin and Chen Guanggan [15] studied regularity of the attractor and approximate inertial manifold for strongly damped nonlinear wave equation:



where 
Wang Lei, Dang Jinbao and Lin Guoguang [16] also studied the approximate inertial manifolds of the fractional nonlinear Schrödinger equation:



where 
i is the imaginary unit.
Recently, Sufang Zhang, Jianwen Zhang [17] studied approximate inertial manifold of strongly damped wave equation:



where 




There have many researches on approximate inertial manifolds for nonlinear wave equations (see [18] - [24] ). In order to construct the approximate inertial manifolds for the initial boundary value problems, in the references [14] to [15] , the regularity of the global attractor is studied, and then the approximate inertial manifold is constructed. In [18] , Tian Lixin, Lin Yurui construct approximate inertial manifolds under spline wavelet basis in weakly damped forced KdV equation. In infinite-dimensional dynamical systems, Kirchhoff type wave equation is a class of very important equation. However, the approximate inertial manifold and inertial manifold of the Kirchhoff wave equation with nonlinear strong damping term are rarely studied. Based on the current research situation of Kirchhoff wave equations, in this paper, we first study the regularity of the global attractor for a class of the Kirchhoff wave equations with nonlinear strongly damped terms, and then construct its approximate inertial manifold.
The paper is arranged as follows. In Section 2, we state some assumptions, notations and the main results are stated. In Section 3, through the estimation of solution smoothness of higher order, then we obtain the regularity of the global attractor. In Section 4, by constructing a smooth manifold, namely the approximate inertial manifold, we approximate the global attractor for the problems (1.1) - (1.3).
2. Statement of Some Assumptions, Notations and Main Results
For convenience, we denote the norm and scalar product in 








Let














We present some assumptions and notations needed in the proof of our results as follows:
(G1) From reference [12] , we set some constants:
such that

(G2) Let


Theorem 2.1 From reference [12] , due to (G1), (G2) hold,
(i) Let





(ii) Let




3. The Regularity of Global Attractor
In order to obtain the regularity of global attractor, we need to give a higher order uniform a priori estimates for the solution.
Let


Let

where
Further, we rewrite the problems (1.1) - (1.3):

From references [26] [27] , 



Lemma 3.1 From references [14] [15] , due to (G1), (G2) hold, let
Each

And there exist 

where


Proof. By the first conclusion (i) of theorem 2.1, when






Meanwhile, 


Then

Based on the reference [27] , the analytic properties of the semigroups generated by 









Since



then




Next, we multiply 



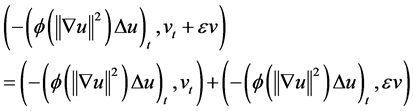
where from the hypothesis (G2),





where
By using Gagliardo-Nirenberg’s embedding inequality, Hölder’s inequality:

Similar to the relation (3.20):

By using Hölder’s inequality, Young’s inequality and Sobolev’s embedding inequality:




In reference [12] , 

So we get:

From above, we have


Taking


At last, we get:

Let



By using Poincaré’s inequality, we get

We take proper
Then

From the relation (3.36), we can get

By using Gronwall’s inequality, we obtain:

Taking


where

Meanwhile, we once again take proper
So there are

where


Lemma 3.2 From references [14] [15] , due to (G1), (G2) hold, let



And there exist


Proof. Take proper T, such that













Similar to lemma (3.1), we are now considering





where from the hypothesis (G2),
Similar to lemma 3.1


By using Hölder’s inequality, Young’s inequality and Sobolev’s embedding inequality:
Through similar methods above
From above, we have


Taking
At last, we get:

Let



By using Poincaré’s inequality, we get

We take proper






Then

From the relation (3.53), we can get

By using Gronwall’s inequality, we obtain:

Taking


where

Meanwhile, we once again take proper

So there are

where 

Similar to above discussions, there are


where 

Using the original Equation (1.1), we obtain

Next, using the elliptic property of the operator A, we get:

where 

So there are


where 

According to Lemmas 3.1, 3.2, we can get the following theorem :
Theorem 3.1 From reference [14] , let 




The proof of theorem 3.1 see ref. [14] , is omitted here.
4. The Approximate Inertial Manifold for the Global Attractor
In this section, we first construct a smooth manifold


Let




For the solution u of the problems (1.1) - (1.3), let










Let



From above, we have








Theorem 4.1 From references [14] [15] [16] , according to lemmas 3.1, 3.2 and the theorem 3.1, let 










Remark 4.1. For the problem (4.66), if we do not consider 






Then



Theorem 4.2 From references [14] [15] [16] , according to lemmas 3.1, 3.2 and the theorems 3.1, 4.1, then



















Proof. Firstly, let




From the relation (4.68), we can obtain:


Then from the hypothesis (G1),



We put 


Therefore


Then

So, we obtain

A similar method in reference [14] , we immediately get the semigroup 












where the 

Remark 4.2. This article is based on the references [14] [15] [16] , by estimating the higher regularity of the global attractor, then we construct its approximate inertial manifold. Approximate inertial manifold, which is a kind of nonlinear, finite dimensional and has certain smoothness. It is of great significance to study the long time behavior of the dissipative equations and the structure of the attractors. On the basis of this article, then we are likely to consider the inertial manifold of the global attractor for the problems (1.1) - (1.3).
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper. This work is supported by the Nature Science Foundation of China (No. 11561076).
Cite this paper
Ai, C.F., Zhu, H.X. and Lin, G.G. (2016) Approximate Inertial Manifold for a Class of the Kirchhoff Wave Equations with Nonlinear Strongly Damped Terms. International Journal of Modern Non- linear Theory and Application, 5, 218-234. http://dx.doi.org/10.4236/ijmnta.2016.54020
References
- 1. Foias, G., Sell, G.R. and Teman, R. (1985) Varities Inertilles des Equations Differentielles Dissipatives. Comptes Rendus de l’Académie des Sciences, 301, 139-142.
- 2. Margolin, L.G. and Jones, D.A. (1992) An Approximate Inertial Manifold for Computing Burgers’ Equation. Physica D, 60, 175-184.
https://doi.org/10.1016/0167-2789(92)90234-E - 3. Chueshov, I.D. (1996) On a Construction of Approximate Inertial Manifolds for Second Order in Time Evolution Equations. Nonlinear Analysis, Theory, Methods and Applications, 26, 1007-1021.
https://doi.org/10.1016/0362-546X(94)00191-4 - 4. Jolly, M.S., Kevrekidis, I.G. and Titi, E.S. (1990) Approximate Inertial Manifolds for the Kuramoto-Sivashinsky Equation: Analysis and Computations. Physica D, 44, 38-60.
https://doi.org/10.1016/0167-2789(90)90046-R - 5. Babin, A.V. and Vishik, M.I. (1992) Attractors of Evolution Equations. Studies in Mathematics and Its Applications, 25, North-Holland, New York.
- 6. Lin, G.G. (2011) Nonlinear Evolution Equation. Yunnan University Press, Kunming.
- 7. Dai, Z.D. and Guo, B.L. (2000) Inertial Manifold and Approximate Inertial Manifold. Science Press.
- 8. Kirchhoff, G. (1883) Vorlesungen Uber Mechanik. Teubner, Leipzig.
- 9. Nakao, M. (2009) An Attractor for a Nonlinear Dissipative Wave Equation of Kirchhoff Type. Journal of Mathematical Analysis and Applications, 353, 652-659.
https://doi.org/10.1016/j.jmaa.2008.09.010 - 10. Yang, Z.J., Ding, P.Y. and Liu, Z.M. (2014) Global Attractor for the Kirchhoff Type Equations with Strong Nonlinear Damping and Supercritical Nonlinearity. Applied Mathematics Letters, 33, 12-17.
https://doi.org/10.1016/j.aml.2014.02.014 - 11. Hirosawa, F. (2015) A Class of Non-Analytic Functions for the Global Solvability of Kirchhoff Equation. Nonlinear Analysis, 116, 37-63.
https://doi.org/10.1016/j.na.2014.12.016 - 12. Ai, C.F., Zhu, H.X. and Lin, G.G. (2015) The Global Attractors and Dimensions Estimation for the Kirchhoff Type Wave Equations with Nonlinear Strongly Damped Terms. Journal of Advances in Mathematics, 12, 6087-6102.
- 13. Dai, Z.D., Guo, B.L. and Lin, G.G. (1998) The Fractal Structure of Attractor for the Generalized Kuramoto-Sivashinsky Equations. Applied Mathematics and Mechanics, 19, 243-256.
- 14. Li, Y.S. and Zhang, W.G. (2000) Regularity and Approximate of the Attractor for the Strongly Damped Wave Equation. Acta Mathematica Scientia, 20, 342-350.
- 15. Luo, H., Pu, Z.L. and Chen, G.G. (2002) Regularity of the Attractor and Approximate Inertial Manifold for Strongly Damped Nonlinear Wave Equations. Journal of Sichuan Normal University (Natural Science), 25, 459-463.
- 16. Wang, L., Dang, J. and Lin, G. (2009) The Approximate Inertial Manifolds of the Fractional Nonlinear Schrodinger Equation. Journal of Yunnan University, 31, 373-377.
- 17. Zhang, S. and Zhang, J. (2015) Approximate Inertial Manifold of Strongly Damped Wave Equation. Pure Mathematics, 5, 278-283.
https://doi.org/10.12677/PM.2015.56040 - 18. Tian, L. and Lin, Y. (1999) Approximate Inertial Manifolds by Spline Wavelet Basis in Weakly Damped Forced KdV Equation. Acta Mathematica Scientia, 19, 379-386.
- 19. Shang, Y. and Guo, B. (1999) Approximate Inertial Manifolds for the Nonlinear Sobolev-Galpern Equations. Acta Mathematica Scientia, 24, 105-115.
- 20. Debussche, A. and Marion, M. (1992) On the Construction of Families of Approximate Inertial Manifolds. Journal of Differentital Equations, 100, 173-201.
https://doi.org/10.1016/0022-0396(92)90131-6 - 21. Li, Y., Wang, B. and Yang, B. (1997) Regularity and Approximate Inertial Manifolds for a Class of Evolutionary Equations. Journal of Lanzhou University, 33, 10-16.
- 22. Showwalter, R.E. (1976) Regularization and Approximation of Second Order Evolution Equations. SIAM Journal on Mathematical Analysis, 7, 461-472.
https://doi.org/10.1137/0507037 - 23. Li, H., Pu, Z. and Chen, G. (2008) Approximate Inertial Manifolds for the Suspension Bridge Equations. Journal of Sichuan Normal University, 31, 25-30.
- 24. Guo, B. and Lin, G. (1999) Approximate Inertial Manifolds of Non-Newtonian Viscous Incompressible Fluids. Journal of Mathematical Study, 32, 328-340.
- 25. Teman, R. (1998) Infinite Dimensional Dynamics Systems in Mechanics and Physics. Springer, New York.
- 26. Massat, P. (1983) Limiting Behavior for Strongly Damped Nonlinear Wave Equations. Journal of Differentital Equations, 48, 334-349.
https://doi.org/10.1016/0022-0396(83)90098-0 - 27. Pazy, A. (1983) Semigroup of Linear Operators and Applications to Partial Differential Equations. Springer, Berlin.
https://doi.org/10.1007/978-1-4612-5561-1















