Open Journal of Discrete Mathematics
Vol.1 No.2(2011), Article ID:5889,7 pages DOI:10.4236/ojdm.2011.12011
Lattice Paths and Rogers Identities
Center for Advanced Study in Mathematics, Panjab University, Chandigarh, India
E-mail: aka@pu.ac.in, meghagoyal2021@gmail.com
Received April 21, 2011; revised May 21, 2011; accepted June 2, 2011
Keywords: lattice paths, colored partitions, generating functions, combinatorial interpretations
Abstract
Recently we interpreted five q-series identities of Rogers combinatorially by using partitions with “n + t copies of n” of Agarwal and Andrews [1]. In this paper we use lattice paths of Agarwal and Bressoud [2] to provide new combinatorial interpretations of the same identities. This results in five new 3-way combinatorial identities.
1. Introduction Definitions and the Main Results
In the literature we find that several 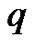 -identities such as given in Slater’s compendium [3] have been interpreted combinatorially using ordinary partitions by several authors (for example, see Connor [4], Subbarao [5], Subbarao and Agarwal [6] and Agarwal and Andrews [7]). In the early nineteen eighties Agarwal and Andrews introduced a new class of partitions called “
-identities such as given in Slater’s compendium [3] have been interpreted combinatorially using ordinary partitions by several authors (for example, see Connor [4], Subbarao [5], Subbarao and Agarwal [6] and Agarwal and Andrews [7]). In the early nineteen eighties Agarwal and Andrews introduced a new class of partitions called “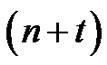 -color partitions” or partitions with “
-color partitions” or partitions with “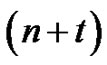 copies of
copies of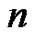 ”. Using these new partitions many more
”. Using these new partitions many more 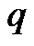 -identities have been interpreted combinatorially in [8-12].
-identities have been interpreted combinatorially in [8-12].
Recently in [13] we interpreted combinatorially the following 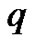 -identities of Rogers [14] by using colored partitions:
-identities of Rogers [14] by using colored partitions:
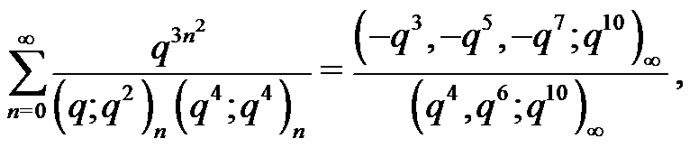 (1.1)
(1.1)
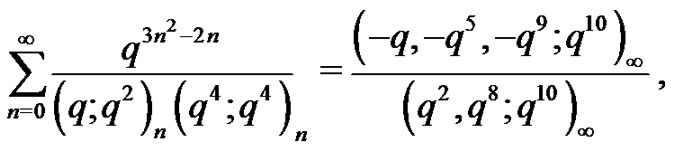 (1.2)
(1.2)
 (1.3)
(1.3)
 (1.4)
(1.4)
and
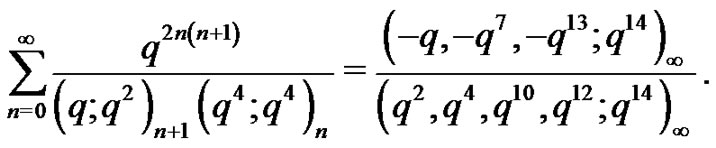 (1.5)
(1.5)
In Equations (1.1)-(1.5),  is a rising
is a rising  -factorial which in general is defined as follows :
-factorial which in general is defined as follows :

If  is a positive integer, then obviously
is a positive integer, then obviously
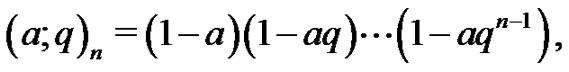
and
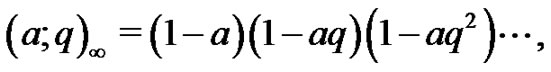
and 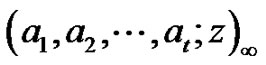 is defined by
is defined by

We remark that Identities (1.1) and (1.2) were also derived by Bailey [15] and appear in [1], Identities (1.3)-(1.5) are also referred as Rogers-Selberg identities (see [3,14,16]).
In this paper we interpret the left-hand sides of (1.1)- (1.5) as generating functions for certain weighted lattice path functions defined by Agarwal and Bressoud in [17]. First we recall the definitions of the partitions with “ copies of
copies of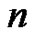 ” (also called
” (also called 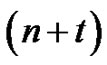 -color partitions) and their weighted difference from [12]:
-color partitions) and their weighted difference from [12]:
Definition 1. A partition with “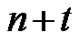 copies of
copies of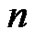 ”,
”, 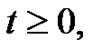 is a partition in which a part of size
is a partition in which a part of size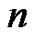 ,
, 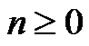 , can come in
, can come in 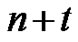 different colors denoted by subscripts:
different colors denoted by subscripts: 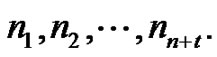
Thus, for example, the partitions of 2 with “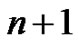 copies of
copies of ” are
” are
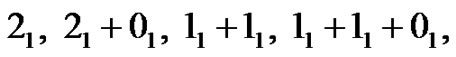
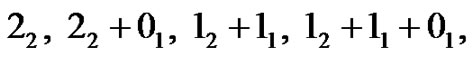

Note that zeros are permitted if and only if 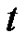 is greater than or equal to one.
is greater than or equal to one.
Definition 2. The weighted difference of two elements 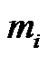 and
and ,
, 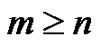 , is defined by
, is defined by 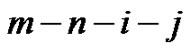 and is denoted by
and is denoted by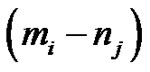 .
.
Next, we recall the following description of lattice paths from [17] which we shall be considering in this paper:
All lattice paths will be of finite length lying in the first quadrant. All paths will begin on the y-axis and terminate on the x-axis. Only three moves are allowed at each step:
northeast: from  to
to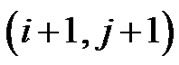 southeast: from
southeast: from 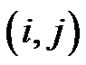 to
to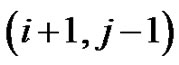 , only allowed if
, only allowed if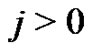 horizontal: from
horizontal: from 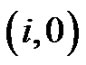 to
to , only allowed along x-axis.
, only allowed along x-axis.
All lattice paths are either empty or terminate with a southeast step: from 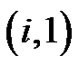 to
to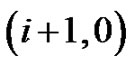 .
.
In describing lattice paths, we shall use the following terminology:
PEAK: Either a vertex on the y-axis which is followed by a southeast step or a vertex preceded by a northeast step and followed by a southeast step.
VALLEY: A vertex preceded by a southeast step and followed by a northeast step. Note that a southeast step followed by a horizontal step followed by a northeast step does not constitute a valley.
MOUNTAIN: A section of the path which starts on either the xor y-axis, which ends on the x-axis, and which does not touch the x-axis anywhere in between the end points. Every mountain has at least one peak and may have more than one.
PLAIN: A section of path consisting of only horizontal steps which starts either on the y-axis or at a vertex preceded by a southeast step and ends at a vertex followed by a northeast step.
Example: The following path has five peaks, three valleys, three mountains and one plain.
The HEIGHT of a vertex is its y-coordinate. The Weight of a vertex is its x-coordinate. The WEIGHT OF A PATH is the sum of the weights of its peaks.
In the example given above, there are two peaks of height three and three of height two, two valleys of height one and one of height zero.

Figure 1. contains five peaks, three valleys, three mountains and one plane.
The weight of this path is 
Recently in [13] we showed that the identities (1.1)- (1.5) have their colored partition theoretic interpretations in the following theorems, respectively:
Theorem 1. Let 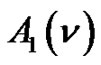 denote the number of
denote the number of 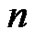 - color partitions of
- color partitions of 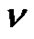 such that even parts appear with even subscripts and odd with odd, all subscripts are greater than 2, if
such that even parts appear with even subscripts and odd with odd, all subscripts are greater than 2, if 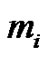 is the smallest or the only part in the partition, then
is the smallest or the only part in the partition, then  and the weighted difference of any two consecutive parts is nonnegative and is
and the weighted difference of any two consecutive parts is nonnegative and is . Let
. Let
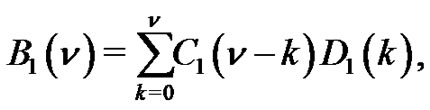
where 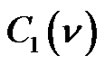 is the number of partitions of
is the number of partitions of  into parts
into parts 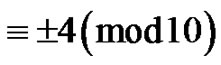 and
and  denotes the number of partitions of
denotes the number of partitions of 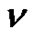 into distinct parts
into distinct parts  Then
Then
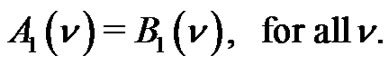
Example. 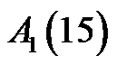 = 6, since the relevant partitions are
= 6, since the relevant partitions are ,
, 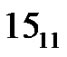 ,
, 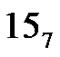 ,
, 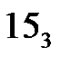 ,
, 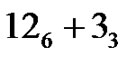 ,
,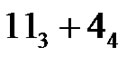 .
.
Also,
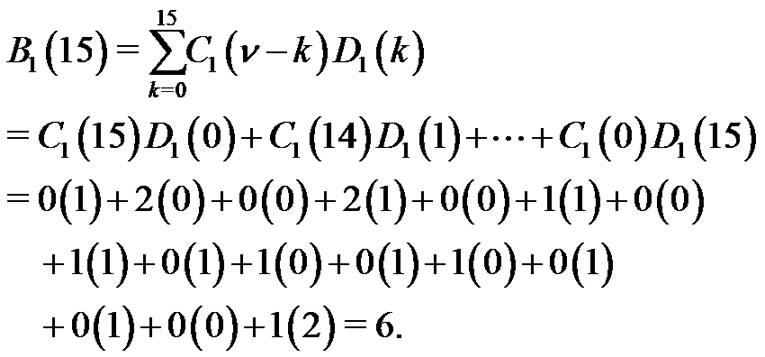
Theorem 2. Let 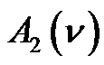 denote the number of
denote the number of 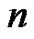 -color partitions of
-color partitions of  such that even parts appear with even subscripts and odd with odd, if
such that even parts appear with even subscripts and odd with odd, if 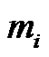 is the smallest or the only part in the partition, then
is the smallest or the only part in the partition, then  and the weighted difference of any two consecutive parts is
and the weighted difference of any two consecutive parts is  and is
and is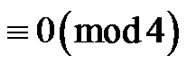 . Let
. Let
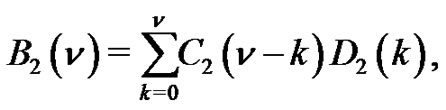
where  is the number of partitions of
is the number of partitions of  into parts
into parts 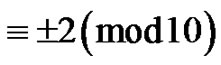 and
and 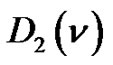 denotes the number of partitions of
denotes the number of partitions of 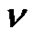 into distinct parts
into distinct parts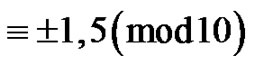 . Then
. Then
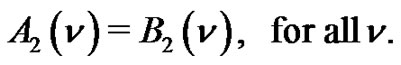
Theorem 3. Let  denote the number of
denote the number of  - color partitions of
- color partitions of  such that even parts appear with even subscripts and odd with odd
such that even parts appear with even subscripts and odd with odd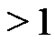 , if
, if 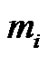 is the smallest or the only part in the partition, then
is the smallest or the only part in the partition, then  and the weighted difference of any two consecutive parts is nonnegative and is
and the weighted difference of any two consecutive parts is nonnegative and is 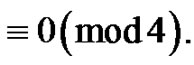 Let
Let
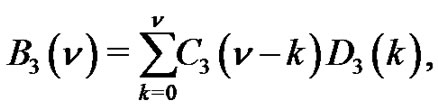
where  is the number of partitions of
is the number of partitions of  into parts
into parts 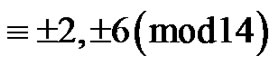 and
and  denotes the number of partitions of
denotes the number of partitions of  into distinct parts
into distinct parts 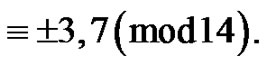 Then
Then

Theorem 4. Let 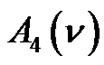 denote the number of
denote the number of 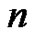 - color partitions of
- color partitions of 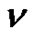 such that even parts appear with even subscripts and odd with odd, all subscripts are
such that even parts appear with even subscripts and odd with odd, all subscripts are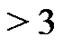 , if
, if 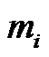 is the smallest or the only part in the partition, then
is the smallest or the only part in the partition, then  and the weighted difference of any two consecutive parts is
and the weighted difference of any two consecutive parts is 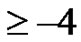 and is
and is  Let
Let
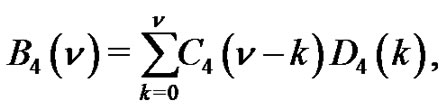
where 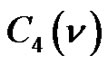 is the number of partitions of
is the number of partitions of 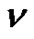 into parts
into parts  and
and 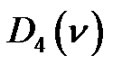 denotes the number of partitions of
denotes the number of partitions of 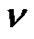 into distinct parts
into distinct parts 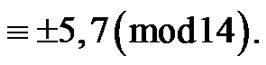 Then
Then
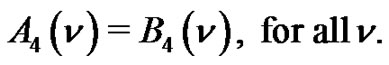
Theorem 5. Let 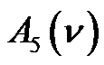 denote the number of partitions of
denote the number of partitions of  with “
with “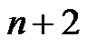 copies of
copies of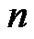 ” such that the even parts appear with even subscripts and odd with odd, all subscripts are
” such that the even parts appear with even subscripts and odd with odd, all subscripts are 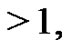 if
if 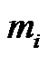 is the smallest or the only part in the partition, then
is the smallest or the only part in the partition, then 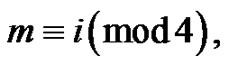 for some
for some 
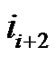 is a part and the weighted difference of any two consecutive parts is nonnegative and is
is a part and the weighted difference of any two consecutive parts is nonnegative and is 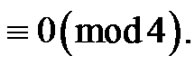 Let
Let
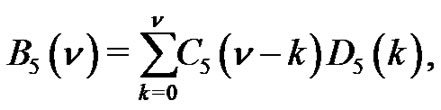
where 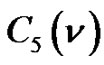 is the number of partitions of
is the number of partitions of 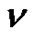 into parts
into parts 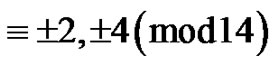 and
and 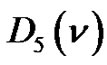 denotes the number of partitions of
denotes the number of partitions of 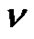 into distinct parts
into distinct parts 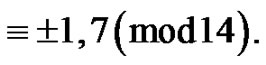 Then
Then
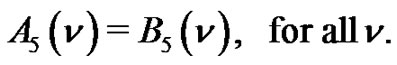
In this paper we prove the following combinatorial interpretations of the identities (1.1)-(1.5) in terms of lattice paths:
Theorem 6. Let 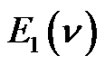 denote the number of lattice paths of weight
denote the number of lattice paths of weight 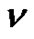 which start from
which start from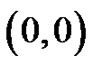 , have no valley above height 0, the lengths of the plains, if any, are
, have no valley above height 0, the lengths of the plains, if any, are 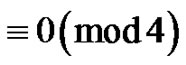 and the height of each peak is greater than 2. Then
and the height of each peak is greater than 2. Then
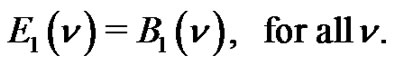
Example.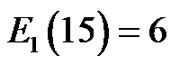 , since the relevant lattice paths are:
, since the relevant lattice paths are:
Theorem 7. Let 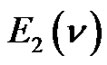 denote the number of lattice paths of weight
denote the number of lattice paths of weight 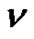 which start from
which start from , have no valley above height 0, the lengths of the plains are
, have no valley above height 0, the lengths of the plains are  and there is a plain of length
and there is a plain of length  between any two peaks. Then
between any two peaks. Then 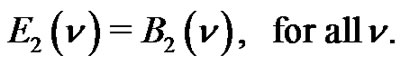

Figure 2. contains one peak of height fifteen.

Figure 3. contains one peak of height fifteen.
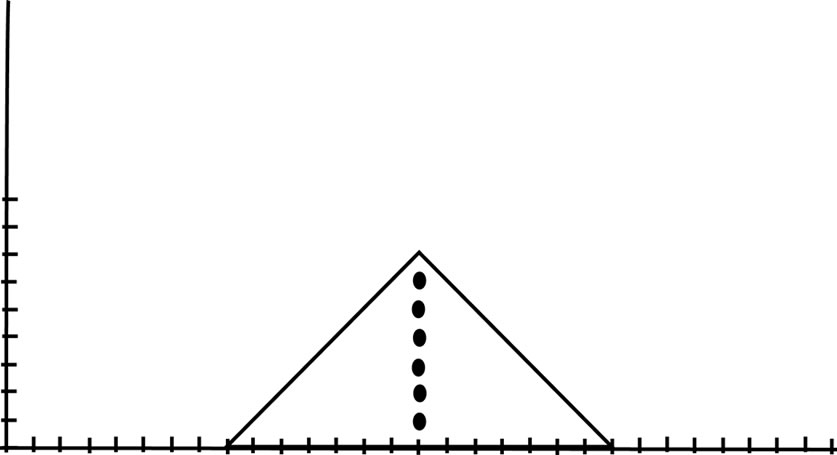
Figure 4. contains one plain of length eight and one peak of height seven.

Figure 5. Contains one plain of length eight and one peak of height seven.
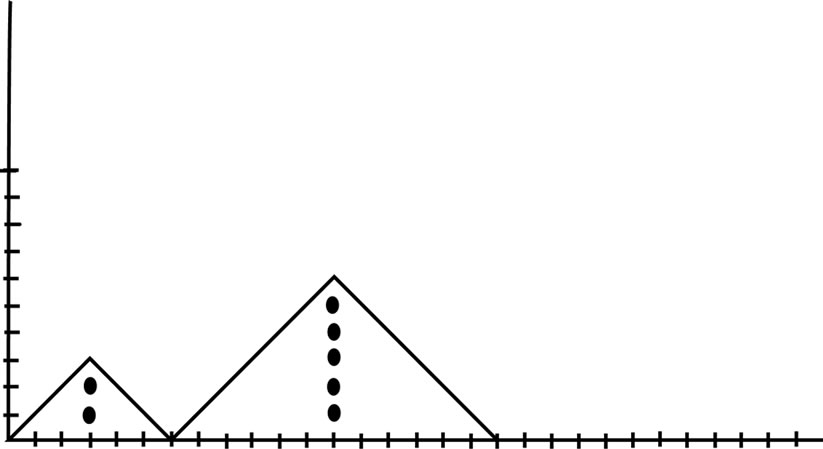
Figure 6. Contains one plain of length eight and one peak of height seven.
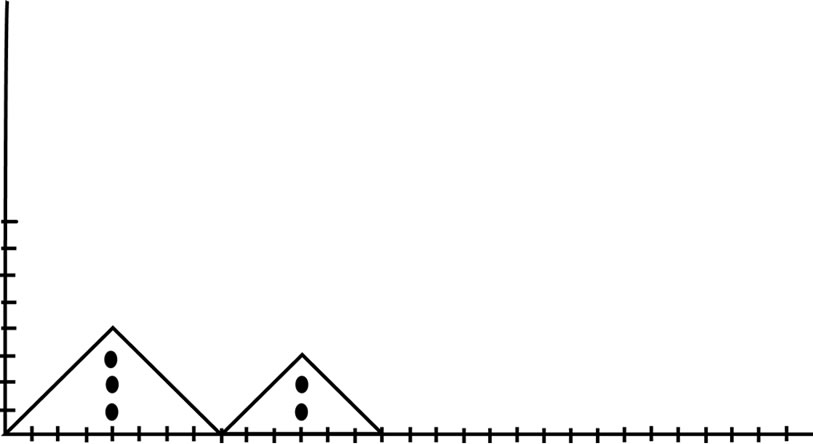
Figure 7. Contains two peaks of height four, three and one valley at height zero.
Theorem 8. Let 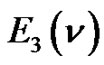 denote the number of lattice paths of weight
denote the number of lattice paths of weight 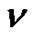 which start from
which start from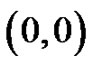 , have no valley above height 0, the lengths of the plains, if any, is
, have no valley above height 0, the lengths of the plains, if any, is  and the height of each peak is greater than 1. Then
and the height of each peak is greater than 1. Then

Theorem 9. Let 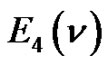 denote the number of lattice paths of weight
denote the number of lattice paths of weight  which start from
which start from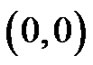 , have no valley above height 0, the height of each peak is
, have no valley above height 0, the height of each peak is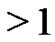 , there is a plain of length
, there is a plain of length  in the beginning of the path and the lengths of the other plains, if any, are
in the beginning of the path and the lengths of the other plains, if any, are 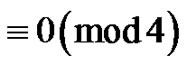 Then
Then
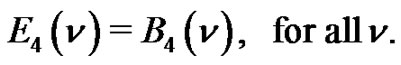
Theorem 10. Let 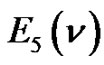 denote the number of lattice paths of weight
denote the number of lattice paths of weight 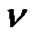 which start from
which start from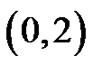 , have no valley above height 0, the height of each peak is
, have no valley above height 0, the height of each peak is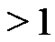 , the lengths of the plains, if any, are
, the lengths of the plains, if any, are 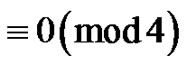 Then
Then
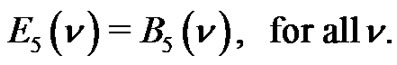
Theorems 6-10 lead to the following 3-way extension of Theorems 1-5:
Theorem 11. For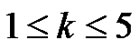 , we have
, we have
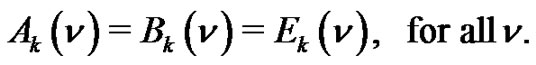
In [13] we have shown that for  the lefthand side of the Equation
the lefthand side of the Equation 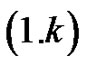 generates
generates 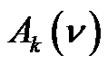 and consequently
and consequently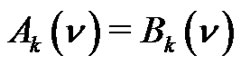 . Here we shall prove that the left-hand side of equation
. Here we shall prove that the left-hand side of equation 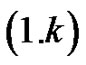 generates
generates  also. We shall also show bijectively that
also. We shall also show bijectively that 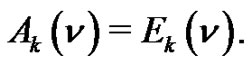
Furthermore, since each of these five cases is proved in a similar way, we provide the details for 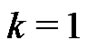 in our next section and sketch the changes required to treat the remainder in Section 3.
in our next section and sketch the changes required to treat the remainder in Section 3.
2. Proof of Theorem 6
In 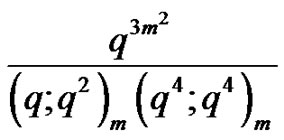 the factor
the factor 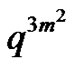 generates the lattice path of m peaks each of height 3 starting at (0,0) and terminating at
generates the lattice path of m peaks each of height 3 starting at (0,0) and terminating at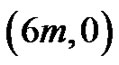 .
.
If m = 4, the path begins as:The factor 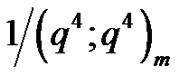 generates m-nonnegative multiples of 4, say
generates m-nonnegative multiples of 4, say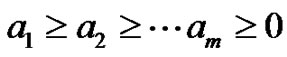 , which are encoded by inserting
, which are encoded by inserting  horizontal steps in front of the first mountain and
horizontal steps in front of the first mountain and 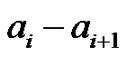 horizontal steps in front of the
horizontal steps in front of the 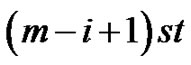 mountain,
mountain, 
If a1 = 8, a2 = 4, a3 = 4, a4 = 0, then our above graph becomes:
The factor  generates nonnegative multiples of (2i
generates nonnegative multiples of (2i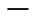 1),
1),  say,
say,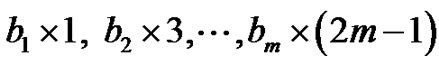 . This is encoded by having the ith peak grow to height
. This is encoded by having the ith peak grow to height
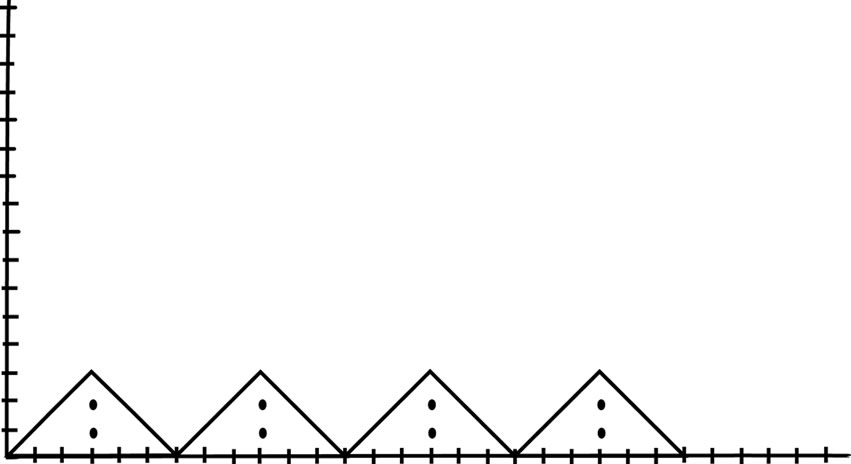
Figure 8. Contains four peaks each of height three and three valleys each at height zero.
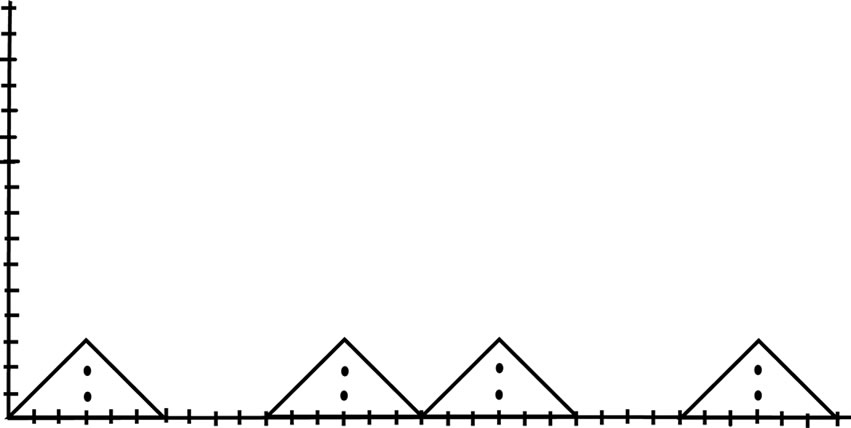
Figure 9. Contains two plains each of length four and four peaks each of height three and one valley at height zero.
 . Each increase by one in the height of a given peak increases its weight by one and the weight of each subsequent peak by two.
. Each increase by one in the height of a given peak increases its weight by one and the weight of each subsequent peak by two.
If b1 = 3, b2 = 1, b3 = 2, b4 = 0, then our example becomes:
In the Graph-8, we consider two successive peaks, say  th and
th and 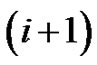 th and denote them by
th and denote them by 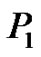 and
and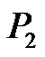 , respectively Now, due to the impact of the factor
, respectively Now, due to the impact of the factor , the Figure 11 changes to Figure 12 Again by taking into consideration, the impact of the factor
, the Figure 11 changes to Figure 12 Again by taking into consideration, the impact of the factor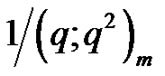 , the Figure 12 changes to Figure 13 or Figure 14 depending on whether
, the Figure 12 changes to Figure 13 or Figure 14 depending on whether  or
or 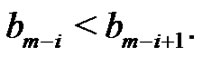 In the case when
In the case when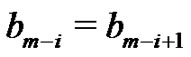 , the new graph will look like Figure 12.
, the new graph will look like Figure 12.
Every lattice path enumerated by 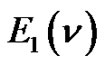 is uniquely generated in this manner. This proves that the L.H.S. of (1.1) generates
is uniquely generated in this manner. This proves that the L.H.S. of (1.1) generates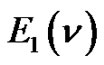 .
.
We now establish a 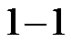 correspondence between the lattice paths enumerated by
correspondence between the lattice paths enumerated by  and the
and the 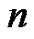 -color partitions enumerated by
-color partitions enumerated by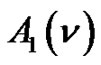 .
.
We do this by encoding each path as the sequence of the weights of the peaks with each weight subscripted by the height of the respective peak.
Thus, if we denote the two peaks in Figure 13 (or Figure 14) by 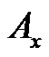 and
and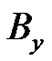 , respectively, then
, respectively, then

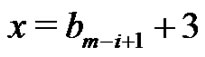
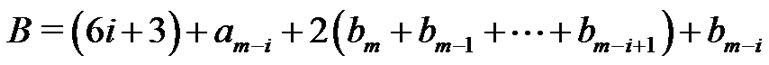
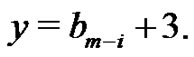
If we look at the  -color part
-color part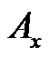 , we find that the parity of both
, we find that the parity of both  and
and 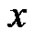 is determined by
is determined by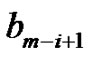 . If
. If 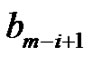 is odd, then both
is odd, then both 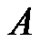 and
and  are even and if
are even and if 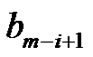 is even, then both
is even, then both 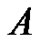 and
and 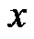 are odd. This proves that even parts appear with even subscripts and odd with odd. Clearly, all subscripts
are odd. This proves that even parts appear with even subscripts and odd with odd. Clearly, all subscripts 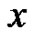 are
are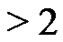 .
.
The weighted difference of these two consecutive parts is
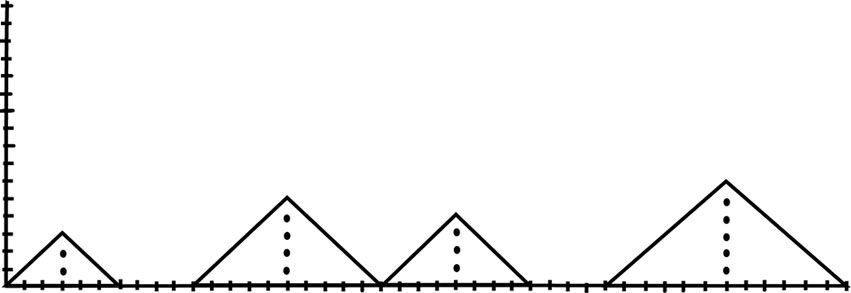
Figure 10. Contains two plains each of length four and four peaks of height three, five, four, six respectively and one valley at height zero.

Figure 11. Contains two peaks of same height.

Figure 12. Contains two peaks separated by a plane and length of the plane is a multiple of four.
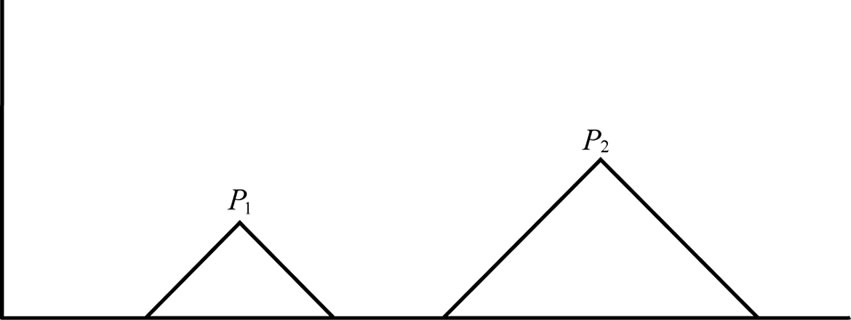
Figure 13. Contains two peaks of which height differs by an odd number and separated by a plane, P2 has more height than P1.

Obviously, if 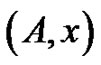 is the first peak in the lattice path then it will correspond to the smallest part in the corresponding
is the first peak in the lattice path then it will correspond to the smallest part in the corresponding 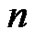 -color partition or to the singleton part if the
-color partition or to the singleton part if the  -color partition has only one part and in both cases
-color partition has only one part and in both cases
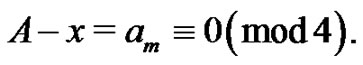
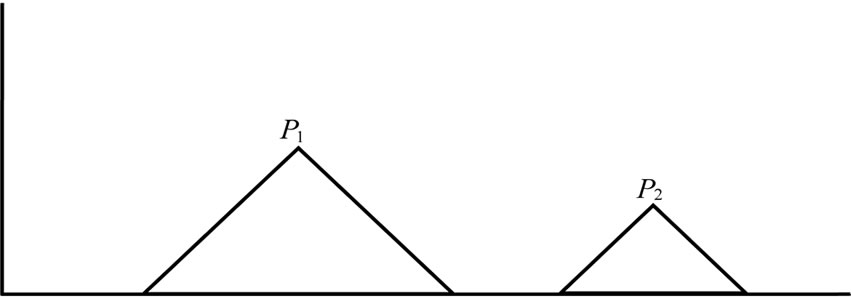
Figure 14. Contains two peaks of which height differs by an odd number and separated by a plane, P1 has more height than P2.
To see the reverse implication, we consider two  -color parts of a partition enumerated by
-color parts of a partition enumerated by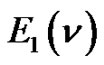 , say,
, say,  and
and .
.
Let  and
and 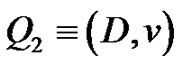 be the corresponding peaks in the associated lattice path.
be the corresponding peaks in the associated lattice path.
The length of the plain between the two peaks is  which is the weighted difference between the two parts
which is the weighted difference between the two parts  and
and  and is therefore nonnegative and
and is therefore nonnegative and 
Also, there can not be a valley above height 0. This can be proved by contradiction.
Suppose, there is a valley V of height 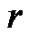
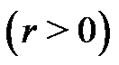 between the peaks
between the peaks 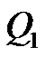 and
and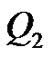 .
.
In this case there is a descent of 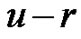 from
from 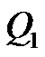 to V and an ascent of
to V and an ascent of  from V to
from V to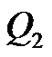 . This implies
. This implies
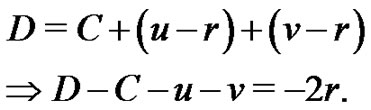
But since the weighted difference is nonnegative, therefore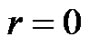 .
.
Also, 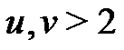 imply that the height of each peak is atleast 3. This completes the proof of Theorem 6.
imply that the height of each peak is atleast 3. This completes the proof of Theorem 6.
3. Sketch of the Proofs of Theorems 7-10
Case 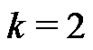 is treated in exactly the same manner as the first case except that now the path begins with
is treated in exactly the same manner as the first case except that now the path begins with 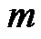 peaks each of height 1 and with a plain of length
peaks each of height 1 and with a plain of length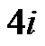 ,
,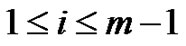 between ith and
between ith and 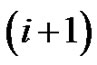 th peak.
th peak.
In the Case , the only point of departure from the first case is that the path begins with
, the only point of departure from the first case is that the path begins with 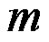 peaks each of height 2.
peaks each of height 2.
Case 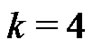 is treated in exactly the same manner as the previous case except that the extra factor
is treated in exactly the same manner as the previous case except that the extra factor  puts a plain of length of 2 in front of the first peak. This increases the weight of each peak by 2 and so the weight of the lattice path is increased by
puts a plain of length of 2 in front of the first peak. This increases the weight of each peak by 2 and so the weight of the lattice path is increased by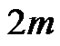 .
.
Comparing the case 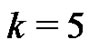 with the case
with the case , we see that in this case there are two extra factors, viz.,
, we see that in this case there are two extra factors, viz., 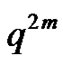 and
and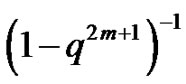 . The extra factor
. The extra factor 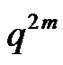 puts two south east steps: (0,2) to (1,1) and (1,1) to (2,0). Thus there are now
puts two south east steps: (0,2) to (1,1) and (1,1) to (2,0). Thus there are now 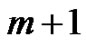 peaks starting from (0,2) and the extra factor
peaks starting from (0,2) and the extra factor
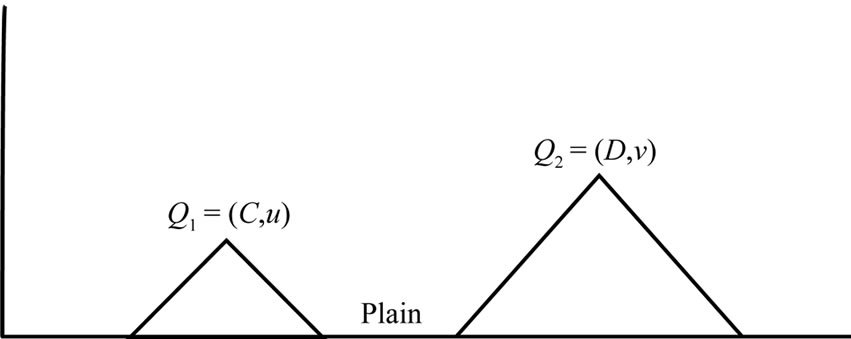
Figure 15. Contains two peaks separated by a plain.

Figure 16. Contains two peaks and a valley at height r.
 introduces a nonnegative multiple of
introduces a nonnegative multiple of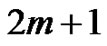 , say
, say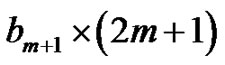 . This is encoded by having the first peak grow to height
. This is encoded by having the first peak grow to height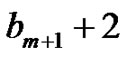 . Clearly,
. Clearly,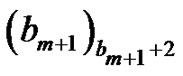 which is of the form
which is of the form 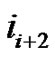 will be the colored part corresponding to the first peak.
will be the colored part corresponding to the first peak.
4. Conclusions
The sum-product identities like (1.1) to (1.5) are generally known as Rogers-Ramanujan type identities. They have applications in different areas such as Orthogonal polynomials, Lie-algebras, Combinatorics, Particle physics and Statistical mechanics.
The most obvious question arising from this work is:
Do Theorems 1.6-1.10 admit generalization analogous to the generalized results of [12,17]?
5. References
[1] A. K. Agarwal and G. E. Andrews, “Rogers-Ramanujan Identities for Partitions with ‘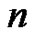 Copies of
Copies of ’,” Journal of Combinatorial Theory, Vol. 45, No. 1, 1987, pp. 40-49. doi:10.1016/0097-3165(87)90045-8
’,” Journal of Combinatorial Theory, Vol. 45, No. 1, 1987, pp. 40-49. doi:10.1016/0097-3165(87)90045-8
[2] A. K. Agarwal and D. M. Bressoud, “Lattice Paths and Multiple Basic Hypergeometric Series,” Pacific Journal of Mathematics, Vol. 136, No. 2, 1989, pp. 209-228.
[3] L. J. Slater, “Further Identities of the Rogers-Ramanujan Type,” Proceedings of the London Mathematical Society, Vol. s2-54, No. 1, 1952, pp. 147-167. doi:10.1112/plms/s2-54.2.147
[4] W. G. Connor, “Partition Theorems Related to Some Identities of Rogers and Watson,” Transactions of the American Mathematical Society, Vol. 214, 1975, pp. 95-111. doi:10.1090/S0002-9947-1975-0414480-9
[5] M. V. Subbarao, “Some Rogers-Ramanujan Type Partition Theorems,” Pacific Journal of Mathematics, Vol. 120, 1985, pp. 431-435.
[6] M. V. Subbarao and A. K. Agarwal, “Further Theorems of the Rogers-Ramanujan Type,” Canadian Mathematical Bulletin, Vol. 31, No. 2, 1988, pp. 210-214. doi:10.4153/CMB-1988-032-3
[7] A. K. Agarwal and G. E. Andrews, “Hook Differences and Lattice Paths,” Journal of Statistical Planning and Inference, Vol. 14, No. 1, 1986, pp. 5-14. doi:10.1016/0378-3758(86)90004-2
[8] A. K. Agarwal, “Partitions with ‘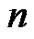 Copies of
Copies of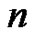 ’, Lecture Notes in Math.,” Proceedings of the Colloque de Combinatoire Énumérative, Université du Québec à Montréal, Berlin, May 28-June 1, 1985, no. 1234, pp. 1-4.
’, Lecture Notes in Math.,” Proceedings of the Colloque de Combinatoire Énumérative, Université du Québec à Montréal, Berlin, May 28-June 1, 1985, no. 1234, pp. 1-4.
[9] A. K. Agarwal, “Rogers-Ramanujan Identities for nColor Partitions,” Journal of Number Theory, Vol. 28, No. 3, 1988, pp. 299-305. doi:10.1016/0022-314X(88)90045-5
[10] A. K. Agarwal, “New Combinatorial Interpretations of Two Analytic Identities,” Proceedings of the American Mathematical Society, Vol. 107, No. 2, 1989, pp. 561-567. doi:10.1090/S0002-9939-1989-0979216-7
[11] A. K. Agarwal, “New Classes of Infinite 3-Way Partition Identities,” ARS Combinatoria, Vol. 44, 1996, pp. 33-54.
[12] A .K. Agarwal and G. E. Andrews, “Rogers-Ramanujan Identities for Partitions with ‘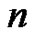 Copies of
Copies of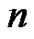 ’,” Journal of Combinatorial Theory, Series A, Vol. 45, No. 1, 1987, pp. 40-49. doi:10.1016/0097-3165(87)90045-8
’,” Journal of Combinatorial Theory, Series A, Vol. 45, No. 1, 1987, pp. 40-49. doi:10.1016/0097-3165(87)90045-8
[13] M. Goyal and A. K. Agarwal, “Further Rogers-Ramanujan Identities for n-Color Partitions,” Utilitas Methematica, Winnipeg. (In Press)
[14] L. J. Rogers, “Second Memoir on the Expansion of Certain Infinite Products,” Proceedings of the London Mathematical Society, Vol. s1-25, No. 1, 1894, pp. 318-343. doi:10.1112/plms/s1-25.1.318
[15] W. N. Bailey, “Some Identities in Combinatory Analysis,” Proceedings of the London Mathematical Society, Vol. s2-49, No. 1, 1947, pp. 421-435. doi:10.1112/plms/s2-49.6.421
[16] A. Selberg, “Über Einige Arithmetische Identitäten,” Avhandlinger Norske Akad, Vol. 8, 1936, pp. 1-23.
[17] A. K. Agarwal and D. M. Bressoud, “Lattice Paths and Multiple Basic Hypergeometric Series,” Pacific Journal of Mathematics, Vol. 136, No. 2, 1989, pp. 209-228.

