1. 引言

众所周知，保险公司的资产在随机经济环境中将会导致两种风险，通常称其为保险风险和金融风险 [1] 。其中，保险风险是因传统保险理赔业务引起的责任险，而金融风险是因保险公司用其持有的部分资产在金融市场上作风险投资引起的投资风险。在随机经济环境的前提下，根据保险实务和金融市场规律，需要作如下假设 [1] [2] ：保险公司在周期i的保费收入为 $C_i>0$ 支出为 $A_i>0$ 且 $C_i,A_i$ 为随机变量；时间 $i-1$ 到i的随机通胀因子为 $B_i$ ；保险公司的初始资本为 $x\left(x>0\right)$ ，综上，记保险公司在有限时间n的资本累积为U_n，则我们可得：

$U_0=x$ , $U_n=x{\displaystyle \prod _{i=1}^n{B}_i}+{\displaystyle \sum _{i=1}^n\left(C_i-A_i\right){\displaystyle \prod _{j=1+i}^n{B}_j}}.$

为了处理方便，记 ${\displaystyle \prod _{j=1+i}^i{B}_j=1}$ 。现在引入 $X_i=A_i-C_i$ ，则X_i为保险公司的净损失，即人们称的保险风

险；设时间i到 $i-1$ 的随机贴现因子为Y_i，则 $Y_i=1/B_i$ ，也就是人们称的金融风险，现用 ${\stackrel{⌢}{U}}_n$ 表示有限时间n的资本累积U_n的贴现值，则

${\stackrel{⌢}{U}}_n=U_n{\displaystyle \prod _{j=1}^n{Y}_j}=\left(x{\displaystyle \prod _{i=1}^n{B}_i}-{\displaystyle \sum _{i=1}^n{X}_i{\displaystyle \prod _{j=1+i}^n{B}_j}}\right){\displaystyle \prod _{j=1}^n{Y}_j}=x-{\displaystyle \sum _{i=1}^n{X}_i{\displaystyle \prod _{j=1}^i{Y}_j}}.$ (1.1)

现在假设保险公司的风险投资比例系数为 $p,p\in \left[0,1\right]$ ， $W_i$ 表示投资组合的价值，于是 $W_i=p{W}_{i-1}\left(1+r_i\right)+\left(1-p\right)W_{i-1}\left(1+r\right)$ ，则随机累积因子 $B_i=W_i/W_{i-1}=\left(1-p\right)\left(1+r\right)+P\left(1+r_i\right)$ ，从而对应的贴现因子(金融风险) $Y_i=1/\left[\left(1-p\right)\left(1+r\right)+p\left(1+r_i\right)\right]$ ，这里r为利率，r_i为投资回报率 [2] 。

在上式中若 $x<{\displaystyle \sum _{i=1}^n{X}_i{\displaystyle {\prod }_{j=1}^i{Y}_j}}$ ，则称保险公司破产了，这里的破产只是针对数学范畴而言的。在保险实务中，即使保险公司资产为负，也有机会恢复正常运营。本文感兴趣的是在数学范畴内用概率的方法来研究有限时间 $n<\infty$ 和无限时间 $n\to \infty$ 时保险公司发生破产情况，令 $S_n={\displaystyle \sum _{i=1}^n{X}_i{\displaystyle \prod _{j=1}^i{Y}_j}}$ ，那么有限时间n的破产概率表示为 [1] ：

$\psi \left(x,n\right)=\mathrm{Pr}\left(x-S_n<0\right)=\mathrm{Pr}\left(S_n>x\right)$ (1.2)

记 $M_n=\underset{1\le m\le n}{\max }{S}_m>x$ ，则有限时间n的破产概率表示为：

$\psi \left(x,n\right)=\mathrm{Pr}\left(\underset{1\le m\le n}{\inf }\left(x-S_m\right)<0\right)=\mathrm{Pr}\left(\underset{1\le m\le n}{\max }{S}_m>x\right)=\mathrm{Pr}\left(M_n>x\right).$ (1.3)

同时，我们可得无限时间 $n\to \infty$ 的破产概率表示为：

$\psi \left(x\right)=\underset{n\to \infty }{\lim }\psi \left(x,n\right)=\underset{n\to \infty }{\lim }\mathrm{Pr}\left(x-S_n<0\right)=\mathrm{Pr}\left(S_{\infty }>x\right)$ (1.4)

和

$\psi \left(x\right)=\underset{n\to \infty }{\lim }\psi \left(x,n\right)=\underset{n\to \infty }{\lim }\mathrm{Pr}\left(\underset{1\le m\le n}{\max }{S}_m>x\right)=\mathrm{Pr}\left(M_{\infty }>x\right).$ (1.5)

显然，在(1.3)式中 $0\le M_n\le {\displaystyle \sum _{i=1}^n\left(X_i\vee 0\right){\displaystyle \prod _{j=1}^i{Y}_j}}$ ，如果 $\left\{\left(X_1,Y_1\right),\left(X_2,Y_2\right),\cdots \right\}$ 构成的独立同分布的随机对序列

满足 $-\infty \le E\ln Y_1<0$ 和 $E\ln \left(X_1\vee 1\right)<\infty$ ，则相对应的 $S_n,M_n$ 是收敛的 [3] 。

在保险风险的研究中，对其理赔额的历史数据分析中，我们发现“占理赔总次数20%的那些理赔的数额之和往往达到历次理赔总额的80%，甚至更多！”(著名的二八定律)这些以很小概率发生的理赔竟然对保险公司的业务产生如此巨大的影响，不能不引起大家的关注。如何用概率方法来刻画和解释这类现象？ 研究应用概率的学者们发现重尾分布族可以很好的解释其理赔事件和理赔额的关系，重尾分布族更贴近实际，因此，重尾分布族成了保险风险研究的重点、热点之一，本文所研究的破产概率渐近等价式也是在重尾分布族这个条件下进行的。事实上，有关重尾分布族的破产概率研究已经取得一些不错的成果，如文献 [1] [2] [4] - [12] ，不过这些学者们大都集中在研究不同重尾分布族时的保险风险与金融风险独立的情形，如文献 [2] [4] - [6] 。这类文章具有典型代表是Tang & Tsitsiashvili [1] 总结归纳了一些学者的成果，在这个基础上研究保险风险和金融风险在 $\mathcal{L}\cap \mathcal{D}$ 族的破产概率问题，得到了有限时间内的保险公司破产概率的渐近等价式，接着其他学者在Tang & Tsitsiashvili [1] 的基础上对其进行了广泛的研究，如

文献 [4] - [12] 等。其中，Zhang [6] 设 $\Theta ={\displaystyle \prod _{j=1}^i{Y}_j}$ ，于是上述问题就可以简化为研究独立随机变量的随机加权

和问题，并且这里 $\Theta$ 可为任意相依结构，推导出保险风险在 $\mathcal{C}$ 族分布下的有限时间的破产概率渐近等价式。然而，上述研究的成果都不能很好的反映保险公司的实际运作情况，比如在汽车保险中大额的车损理赔往往带有人员的医疗理赔，又如金融危机造成的利率、金融市场不稳定等对保险业的影响，也就是说保险实务中各种风险之间是存在一定关系的，学者们考虑独立情形是为了数学上处理的方便。因此，我们需要研究相依风险模型，目前刻画保险风险相依关系最有效的方法和手段之一是用Copula函数(Ali-Mikhail-Haq，FGM，广义FGM等)，Copula函数在刻画相依关系具有以下几个方面的优势 [14] ：描述随机变量相关性只需要从联合分布函数构建；可以描述随机变量的协同性；构造多维随机变量分布函数等，比如下文中介绍的文献 [7] - [12] 等都采用了Copula函数方法。其中，Chen [7] 研究了保险风险与金融风险在 $\mathcal{S},{\mathcal{R}}_{-\alpha }$ 族分布下的破产概率，她假设保险风险与金融风险之间构成独立同分布的随机对序列且满足FGM分布(系数 $\theta$ 取值范围为(−1, 1])，她得到了有限时间下的破产概率一般渐近等价式并给出了具体的、严谨的证明。Chen [8] 在她Chen [7] 的基础上对其做了进一步完善，考虑FGM相依分布中系数 $\theta =-1$ 的特殊情形，获得了与她Chen [7] 相类似的结论。事实上，国内学者Jiang & Tang [10] 发表的论文中早已经研究了基于广义FGM分布的保险风险与金融风险相依问题，并获得了类似于Chen (2011) 的结果，只是由于某些原因而没有获得广泛关注。最近，Li & Tang [11] 考虑保险风险与金融风险构成的凸组合是强正则变化族 $\left({\mathcal{R}}_{-\alpha }^{\ast }\right)$ 下，研究了独立和FGM相依情形的破产概率，得到了在一个假设条件下(下文中假设a)的有限和无限时间的破产概率的渐近等价式。

本文在Li & Tang [11] 等基础上，考虑由保险风险X与金融风险Y构成的凸组合是强正则变化族 $\left({\mathcal{R}}_{-\alpha }^{\ast }\right)$ ，在广义FGM分布的条件下，推导出有限时间和无限时间的破产概率渐近等价式，推广了Li & Tang [11] 的研究成果。接下来的文章的结构安排如下，第二部分介绍一些准备工作和引理，第三部分是主要结论以及一些证明过程。

2.准备工作和引理

本文在没有特殊说明的情况下，以下关系式都表示 $x\to \infty$ 时成立。设两个正函数 $f\left(x\right),g\left(x\right)$ ：如果 ${\lim }_{x\to \infty }\sup f\left(x\right)/g\left(x\right)\le 1$ 成立，记： $f\left(x\right)\lesssim g\left(x\right)$ 或者 $g\left(x\right)\gtrsim f\left(x\right)$ ；如果 $f\left(x\right)\lesssim g\left(x\right)$ 且 $f\left(x\right)\gtrsim g\left(x\right)$ 成立，记： $f\left(x\right)\sim g\left(x\right)$ ；如果 $f\left(x\right)=O\left(g\left(x\right)\right)$ 且 $g\left(x\right)=O\left(f\left(x\right)\right)$ ，记： $f\left(x\right)\asymp g\left(x\right)$ ；除此之外，对实数x，记 $x_{+}=x\vee 0$ 和 $x_{-}=-\left(x\wedge 0\right)$ 。

2.1. 重尾分布族

定义2.1：(重尾分布 [12] )在 $ℝ$ 上的分布F，如果对任意的 $\alpha >0$ 有 ${\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{\alpha x}}F\left(\text{d}x\right)=\infty$ ，则称分布F是重尾的，记作 $F\in \mathcal{K}$ 。

定义2.2：( $\mathcal{S}\left(\alpha \right)$ 族 [13] )在 $\left[0,\infty \right)$ 上的分布F，如果对 $\alpha >0$ 有 $\underset{x\to \infty }{\lim }\frac{\overline{F^{2*}}\left(x\right)}{\overline{F}\left(x\right)}=2c<\infty$ ， $c=E{\text{e}}^{\alpha X}$ 且对所有的 $t\in ℝ$ ，有 $\underset{x\to \infty }{\lim }\frac{\overline{F\left(x-t\right)}}{\overline{F}\left(x\right)}={\text{e}}^{\alpha t}$ ，则称分布F是卷积等价的(Convolution-equivalent)，记作 $\mathcal{F}\in \mathcal{S}\left(\alpha \right)$ 。

定义2.3：( ${\mathcal{R}}_{-\alpha }$ 族 [13] )在 $ℝ$ 上的分布F，如果对任意的 $y>0$ 有 $\underset{x\to \infty }{\lim }\frac{\overline{F}\left(xy\right)}{\overline{F}\left(x\right)}=y^{-\alpha },\alpha \ge 0$ ，则称分布F是正则变化尾的(Regularly varying tailed)，记作 $\mathcal{F}\in {\mathcal{R}}_{-\alpha }$ 。

定义2.4：( ${\mathcal{R}}_{-\alpha }^{*}$ 族 [11] )在 $ℝ$ 上的分布F，如果对任意的 $x\in ℝ$ 有 $V\left(x\right)=1-\frac{\overline{F}\left(e^x\right)}{\overline{F}\left(0\right)}$ 属于 $\mathcal{S}\left(\alpha \right)\left(\alpha \ge 0\right)$ ，则称分布F是强正则变化尾的(Strongly regular variation tailed)，记作 $\mathcal{F}\in {\mathcal{R}}_{-\alpha }^{*}$ 。

根据定义2.2-2.4，有 ${\mathcal{R}}_{-\alpha }^{*}\subset {\mathcal{R}}_{-\alpha }\subset \mathcal{S}\left(\alpha \right)$ 成立 [11] ，更多关于重尾分布族的定义性质可阅读文献资料 [13] 等。

2.2. 广义FGM分布

设随机向量 $\left(X,Y\right)$ ，具有如下形式的联合分布函数：

$\Pi \left(x,y\right)=F\left(x\right)G\left(y\right)\left[1+\theta A\left(F\left(x\right)\right)B\left(G\left(y\right)\right)\right]$ (2.1)

其中， $\theta \in \left[-1,1\right]$ ，F, G是随机变量X, Y的边缘分布函数，这里“核”函数 $A\left(x\right),B\left(y\right)$ 满足 $\underset{x\to 1}{\lim }A\left(x\right)=0,$ $\underset{y\to 1}{\lim }B\left(y\right)=0$ 和一些正则性条件，使得 $\Pi \left(x,y\right)$ 为适当的二维分布。我们称(2.1)式表示的分布为广义Farlie-Gumbel-Morgenstern分布，简称为广义FGM分布 [10] 。根据Nelsen [14] 的研究，记：

$C\left(u,v\right)=uv\left[1+\theta A\left(u\right)B\left(v\right)\right]$ (2.2)

称(2.2)式为广义FGM Copula函数。若 $A\left(u\right)=1-u,B\left(v\right)=1-v$ ，则(2.2)式就是我们熟知的标准的FGM Copula函数，根据2.1式知边缘分布的相依程度取决于参数 $\theta$ 和函数 $A(\cdot ),B(\cdot )$ 。

2.3. 若干引理

接下来我们需要介绍几个引理，这几个引理在下文定理的证明中起着至关重要的作用，有关这些引理的详细证明可以阅读文献 [11] 。

引理2.1：设在 $ℝ$ 上的分布 $F_1,\cdots ,F_n$ ，如果对每一个 $q\in \Delta ,\Delta =\left\{\left(q_1,\cdots ,q_n\right)\in {\left(0,1\right)}^n:{\displaystyle {\sum }_{i=1}^n{q}_i=1}\right\},$ 有 $F_q={\displaystyle {\sum }_{i=1}^n{q}_i{F}_i}\in R_{-\alpha }^{*},\alpha \ge 0$ ，则 $F_1\ast \cdots \ast F_n\in \mathcal{S}\left(\alpha \right)$ 且

$\overline{F_1\ast \cdots \ast F_n}\in \mathcal{S}\left(\alpha \right)~{\displaystyle \sum _{i=1}^n\left({\displaystyle \prod _{j=1,j\ne i}^n{\widehat{F}}_j\left(\alpha \right)}\right){\overline{F}}_i\left(x\right).}$ (2.3)

引理2.2：设 $X_1,\cdots ,X_n\left(n\ge 2\right)$ 是独立非负的随机变量， $X_1,\cdots ,X_n$ 对应的分布分别为 $F_1,\cdots ,F_n$ 。如果对每个 $q\in \Delta$ 有 $F_q={\displaystyle {\sum }_{i=1}^n{q}_i{F}_i}\in R_{-\alpha }^{\ast },\alpha \ge 0$ ，则 ${\displaystyle \prod _{i=1}^n{X}_i}$ 属于 ${\mathcal{R}}_{-\alpha }^{*}\left(\alpha \ge 0\right)$ 且

$\mathrm{Pr}\left({\displaystyle \prod _{i=1}^n{X}_i}>x\right)~{\displaystyle \sum _{i=1}^n\left({\displaystyle \prod _{j=1,j\ne i}^{n}E{X}_j^{\alpha }}\right){\overline{F}}_i\left(x\right)}$ (2.4)

引理2.2与Breiman’s定理形式上相似。当 $n=2$ 时，引理2.2就得到最简单的形式：

$\mathrm{Pr}\left(X_1{X}_2>x\right)~E{X}_1^{\alpha }{\overline{F}}_2\left(x\right)+E{X}_2^{\alpha }{\overline{F}}_1\left(x\right).$

3. 主要结论及其证明

为了得到我们的结果，我们需要作如下假设：

假设a：由 $F,G$ 构成的凸组合是强正则变化族 $\left({\mathcal{R}}_{-\alpha }^{*}\right)$ ，即

$bF+\left(1-b\right)G\in {\mathcal{R}}_{-\alpha }^{*},$

其中 $b\in \left(0,1\right)$ 。事实上，假设a包含以下3种情形，具体如下 [11] ：

1) $F\in {\mathcal{R}}_{-\alpha }^{*}$ ， $\overline{G}\left(x\right)=o\left(\overline{F}\left(x\right)\right)$ ;

2) $F\in {\mathcal{R}}_{-\alpha }^{*}$ ， $G\in {\mathcal{R}}_{-\alpha }$ 且 $\overline{G}\left(x\right)=O\left(\overline{F}\left(x\right)\right)$ ;

3) $F\in {\mathcal{R}}_{-\alpha }^{*}$ ， $G\in {\mathcal{R}}_{-\alpha }^{*}$ 且函数 $a\left(x\right)=\frac{\overline{F}\left(e^x\right)}{\overline{G}\left(e^x\right)},$ 对任意的 $y>0,$ 有 $a\left(xy\right)\asymp a\left(x\right)$ 。

根据引言介绍，我们知道研究带有保险风险和金融风险的破产概率问题，实质上是研究随机变量乘积的尾部渐近性。因此，我们设两个随机变量X与Y，这里X表示保险风险，Y表示金融风险，其对应的边缘分布函数分别为F, G且由随机变量X与Y构成的随机向量 $\left(X,Y\right)$ 服从广义FGM分布(2.1式)。记H表示随机向量 $\left(X,Y\right)$ 的乘积分布(H表示随机变量XY的分布)，我们的目标就是研究随机变量X与Y之间的相依结构对其乘积尾分布 $\overline{H}$ 的影响。延续文献 [7] 等表示方法，设随机向量 $\left(X^{*},Y^{*}\right)$ 是随机向量 $\left(X,Y\right)$ 独立复制，即随机向量 $\left(X^{*},Y^{*}\right)$ 与随机向量 $\left(X,Y\right)$ 具有相同的分布但 $\left(X^{*},Y^{*}\right)$ 具有独立分量，于是，记H^*表示随机向量 $\left(X^{*},Y^{*}\right)$ 的乘积分布(H^*表示随机变量 $X^{*}{Y}^{*}$ 的分布)。最后，在给出定理之前先引入两个的新随机变量X_A和Y_B，其对应分布函数分别为：F_A, G_B，定义 [10] ：

$F_A\left(x\right)\triangleq F\left(x\right)\left[1-A\left(F\left(x\right)\right)\right],G_B\left(y\right)\triangleq G\left(y\right)\left[1-B\left(G\left(y\right)\right)\right],x,y\ge 0$ (3.1)

再设 ${\eta }_A,{\eta }_B$ 为函数 $A\left(u\right),B\left(v\right)$ 在 $u=1,v=1$ 时的左导数且 $\left|{\eta }_A\right|\vee \left|{\eta }_B\right|\le 1$ ，我们约定 ${\frac{A\left(u\right)}{1-u}|}_{u=1}=-{\eta }_A$ ， ${\frac{B\left(v\right)}{1-v}|}_{v=1}=-{\eta }_B$ ，根据研究可推得如下结论。

定理3.1：设两个随机变量X与Y，其对应的边缘分布为F, G，由随机变量X与Y构成的随机向量 $\left(X,Y\right)$ 服从广义FGM分布(2.1式)，若F, G满足假设a且 $E{Y}^{\alpha }<\infty$ ，则：

$\overline{H}\left(x\right)~\left[\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right]\overline{F}\left(x\right)+\left[\left(1+{\eta }_B\theta \right)E{X}^{\alpha }-{\eta }_B\theta E{X}_A^{\alpha }\right]\overline{G}\left(x\right).$ (3.2)

证明：根据文献 [10] 的研究和广义FGM分布的定义式，给出的定义(3.1)式是合理的。现在设随机向量 $\left(X_A^{*},Y_B^{*}\right)$ 是 $\left(X_A,Y_B\right)$ 独立的情形，即随机向量 $\left(X_A^{*},Y_B^{*}\right)$ 与随机向量 $\left(X_A,Y_B\right)$ 具有相同分布且 $\left(X_A^{*},Y_B^{*}\right)$ 具有独立分量，随机向量 $\left(X_A^{*},Y_B^{*}\right)$ 与随机向量 $\left(X_{}^{*},Y_{}^{*}\right)$ 也独立. 若 $E{Y}^{\alpha }$ 存在，则 $E{Y}_B^{\alpha }$ 也存在，证明见文献 [10] 。根据(3.1)式可得：

$A\left(F\left(x\right)\right)=1-\frac{F_A\left(x\right)}{F\left(x\right)},B\left(G\left(y\right)\right)=1-\frac{G_B\left(y\right)}{G\left(y\right)},x,y\ge 0$

代入到(2.1)式可得：

$\Pi \left(\text{d}s,\text{d}t\right)=\left(1+\theta \right)F\left(\text{d}s\right)G\left(\text{d}t\right)-\theta F_A\left(\text{d}s\right)G\left(\text{d}t\right)-\theta F\left(\text{d}s\right)G_B\left(\text{d}t\right)+\theta F_A\left(\text{d}s\right)F_B\left(\text{d}t\right)$ (3.3)

再对等式3.3两边积分可得：

$\begin{array}{c}\overline{H}\left(x\right)=\mathrm{Pr}\left(XY>x\right)\\ ={\displaystyle \int {\displaystyle {\int }_{st>x,s>0,t>0}{\displaystyle \prod \left(\text{d}s,\text{d}t\right)}}}\\ =\left(1+\theta \right){\overline{H}}^{*}\left(x\right)-\theta \mathrm{Pr}\left(X_A^{*}{Y}^{*}>x\right)-\theta \mathrm{Pr}\left(X^{*}{Y}_B^{*}>x\right)+\theta \mathrm{Pr}\left(X_A^{*}{Y}_B^{*}>x\right)\end{array}$ (3.4)

对(3.4)式，应用引理2.2得：

$\begin{array}{c}\overline{H}\left(x\right)~\left(1+\theta \right)\left[E{Y}^{\alpha }\overline{F}\left(x\right)+E{X}^{\alpha }\overline{G}\left(x\right)\right]-\theta \left[E{Y}^{\alpha }\mathrm{Pr}\left(X_A^{*}>x\right)+E{X}_A^{\alpha }\overline{G}\left(x\right)\right]\\ -\theta \left[E{Y}_B^{\alpha }\overline{F}\left(x\right)+E{X}^{\alpha }\mathrm{Pr}\left(Y_B^{*}>x\right)\right]+\theta \left[E{Y}_B^{\alpha }\mathrm{Pr}\left(X_A^{*}>x\right)+E{X}_A^{\alpha }\mathrm{Pr}\left(Y_B^{*}>x\right)\right]\end{array}$ (3.5)

又根据 $F_A\left(x\right)$ 和 $G_B\left(x\right)$ 的定义可得：

${\overline{F}}_A\left(x\right)~\left(1-{\eta }_A\right)\overline{F}\left(x\right)$ , ${\overline{G}}_B\left(x\right)~\left(1-{\eta }_B\right)\overline{G}\left(x\right)$ (3.6)

把(3.6)式代入(3.5)式，整理得：

$\overline{H}\left(x\right)~\left[\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right]\overline{F}\left(x\right)+\left[\left(1+{\eta }_B\theta \right)E{X}^{\alpha }-{\eta }_B\theta E{X}_A^{\alpha }\right]\overline{G}(\; x\; )$

即，定理3.1成立。

定理3.2：设 $\left\{\left(X_1,Y_1\right),\left(X_2,Y_2\right),\cdots ,\left(X_n,Y_n\right)\right\}$ 是独立同分布随机对序列并服从广义FGM分布(见(2.1)式)， $X_i,Y_i$ 的边缘分布分别为 $F,G$ ，若 $F,G$ 满足假设a且 $E{Y}^{\alpha }<\infty$ ，则：

$\psi \left(x,n\right)=\mathrm{Pr}\left(M_n>x\right)~A_n\overline{F}\left(x\right)+B_n\overline{G}\left(x\right)$ (3.7)

其中， $A_n=\left(\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right){\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}},$

$B_n={\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}}\left[(1+{\eta }_B\theta )E{(M_{n-i}+X_{n-i+1})}_{+}^{\alpha }-{\eta }_B\theta E{(M_{n-i}+X_{A,n-i+1})}_{+}^{\alpha }\right].$

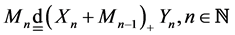证明：首先，设( $\underset{\_}{\underset{\_}{\text{d}}}$ 表示等价的意思)，下用数学归纳法证明定理3.2成立。

当 $n=1$ 时，显然， $\psi \left(x,1\right)=\mathrm{Pr}\left(M_1>x\right)=\mathrm{Pr}\left(X_{1,+}{Y}_1>x\right)=\overline{H}\left(x\right)$ ，即 $n=1$ 成立;

现在假设 $n=n-1\ge 1$ 时成立，根据假设条件，我们可知 $X_n,M_n,M_{n-1},X_n+M_{n-1},Y_n$ 都属于 ${\mathcal{R}}_{-\alpha }^{*}\subset \mathcal{S}\left(0\right)$ 。应用引理2.1(令 $\alpha =0$ )，可得：

$\mathrm{Pr}\left(X_n+M_{n-1}>x\right)~\left(1+A_{n-1}\right)\overline{F}\left(x\right)+B_{n-1}\overline{G}\left(x\right)$ (3.8)

于是，结合 $M_n$ 的等价定义有：

$\begin{array}{c}\psi \left(x,n\right)=\mathrm{Pr}\left(M_n>x\right)=\mathrm{Pr}\left({\left(X_n+M_{n-1}\right)}_{+}{Y}_n>x\right)\\ =\left(1+\theta \right)\mathrm{Pr}\left({\left(X_n^{*}+M_{n-1}\right)}_{+}{Y}^{*}>x\right)-\theta \mathrm{Pr}\left({\left(X_{A,n}^{*}+M_{n-1}\right)}_{+}{Y}^{*}>x\right)\\ -\theta \mathrm{Pr}\left({\left(X_n^{*}+M_{n-1}\right)}_{+}{Y}_B^{*}>x\right)+\theta \mathrm{Pr}\left({\left(X_{A,n}^{*}+M_{n-1}\right)}_{+}{Y}_B^{*}>x\right)\end{array}$ (3.9)

根据引理2.1，则(3.9)式等价于

$\begin{array}{c}\psi \left(x,n\right)~\left(1+\theta \right)\left[E{\left(X_n+M_{n-1}\right)}_{+}^{\alpha }\overline{G}\left(x\right)+E{Y}^{\alpha }\mathrm{Pr}\left({\left(X_n^{*}+M_{n-1}\right)}_{+}>x\right)\right]\\ -\theta \left[E{\left(X_{A,n}+M_{n-1}\right)}_{+}^{\alpha }\overline{G}\left(x\right)+E{Y}^{\alpha }\mathrm{Pr}\left({\left(X_{A,n}^{*}+M_{n-1}\right)}_{+}>x\right)\right]\\ -\theta \left[E{\left(X_n+M_{n-1}\right)}_{+}^{\alpha }\mathrm{Pr}\left(Y_B^{*}>x\right)+E{Y}_B^{\alpha }\mathrm{Pr}\left({\left(X_n^{*}+M_{n-1}\right)}_{+}>x\right)\right]\\ +\theta \left[E{\left(X_{A,n}+M_{n-1}\right)}_{+}^{\alpha }\mathrm{Pr}\left(Y_B^{*}>x\right)+E{Y}_B^{\alpha }\mathrm{Pr}\left({\left(X_{A,n}^{*}+M_{n-1}\right)}_{+}>x\right)\right]\end{array}$

结合(3.6)式、(3.8)式，计算得：

$\begin{array}{l}\psi (x,n)~\left[\left(1+\theta {\eta }_A\right)E{Y}^{\alpha }-\theta {\eta }_{A}E{Y}_B^{\alpha }+E{Y}^{\alpha }{A}_{n-1}\right]\overline{F}(x)\\ +\left[(1+\theta {\eta }_B)E{(X_n+M_{n-1})}_{+}^{\alpha }-\theta {\eta }_{B}E{(X_{A,n}+M_{n-1})}_{+}^{\alpha }+E{Y}^{\alpha }{B}_{n-1}\right]\overline{G}(\; x\; )\end{array}$

整理得：

$\psi \left(x,n\right)=\mathrm{Pr}\left(M_n>x\right)~A_n\overline{F}\left(x\right)+B_n\overline{G}\left(x\right)\text{.}$

即定理3.2成立。

定理3.3：设 $\left\{\left(X_1,Y_1\right),\left(X_2,Y_2\right),\cdots ,\left(X_n,Y_n\right)\right\}$ 是独立同分布随机对序列并服从广义FGM分布(见(2.1)式)， $X_i,Y_i$ 的边缘分布分别为 $F,G$ ，若 $F,G$ 满足假设a且 $E{Y}^{\alpha }<\infty$ ，则

$\psi \left(x,n\right)=\mathrm{Pr}\left(S_n>x\right)~A_n\overline{F}\left(x\right)+C_n\overline{G}\left(x\right)$ (3.10)

其中， $A_n=\left(\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right){\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}},$

$C_n={\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}}\left[(1+{\eta }_B\theta )E{(S_{n-i}+X_{n-i+1})}_{+}^{\alpha }-{\eta }_B\theta E{(S_{n-i}+X_{A,n-i+1})}_{+}^{\alpha }\right].$

证明：设 ( $\underset{\_}{\underset{\_}{\text{d}}}$ 表示等价的意思)，可用数学归纳法证明定理3.3成立，事实定理3.3证明与定理3.2证明相类似，这里都不再展开。

注记3.1：若我们取 $A\left(u\right)=1-u,B\left(v\right)=1-v$ ，此时， ${\eta }_A={\eta }_B=-1$ ，则：

$\psi \left(x,n\right)=\mathrm{Pr}\left(M_n>x\right)~{A^{\prime }}_n\overline{F}\left(x\right)+{B^{\prime }}_n\overline{G}\left(x\right)$ (3.11)

和

$\psi \left(x,n\right)=\mathrm{Pr}\left(S_n>x\right)~{A^{\prime }}_n\overline{F}\left(x\right)+{C^{\prime }}_n\overline{G}\left(x\right)$ (3.12)

其中， ${A^{\prime }}_n=\left(\left(1-\theta \right)E{Y}^{\alpha }+\theta E{Y}_B^{\alpha }\right){\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}}$ ,

$B_n^{\text{'}}={\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}}\left[(1-\theta )E{(M_{n-i}+X_{n-i+1})}_{+}^{\alpha }+\theta E{(M_{n-i}+X_{A,n-i+1})}_{+}^{\alpha }\right],$ ,

$C_n^{\text{'}}={\displaystyle \sum _{i=1}^n{\left(E{Y}^{\alpha }\right)}^{i-1}}\left[(1-\theta )E{(S_{n-i}+X_{n-i+1})}_{+}^{\alpha }+\theta E{(S_{n-i}+X_{A,n-i+1})}_{+}^{\alpha }\right].$

即Li & Tang [11] 文中的推论2.1(a)。

推论3.1：在定理3.2的前提下，如果 $E{Y}^{\alpha }<1$ ，则 $n\to \infty$ 有：

$\psi \left(x\right)=\mathrm{Pr}\left(M_{\infty }>x\right)~A_{\infty }\overline{F}\left(x\right)+B_{\infty }\overline{G}\left(x\right)$ (3.13)

其中， $A_{\infty }=\frac{1}{1-E{Y}^{\alpha }}\left(\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right),$

$B_{\infty }=\frac{1}{1-E{Y}^{\alpha }}\left[(1+{\eta }_B\theta )E{(M_{\infty }+X)}_{+}^{\alpha }-{\eta }_B\theta E{(M_{\infty }+X_A)}_{+}^{\alpha }\right].$

推论3.2：在定理3.3的前提下，如果 $E{Y}^{\alpha }<1$ 且 $E\ln \left(X_{-}\vee 1\right)<\infty$ ，则 $n\to \infty$ 有：

$\psi \left(x\right)=\mathrm{Pr}\left(S_n>x\right)~A_{\infty }\overline{F}\left(x\right)+C_{\infty }\overline{G}\left(x\right)$ (3.14)

其中， $A_{\infty }=\frac{1}{1-E{Y}^{\alpha }}\left(\left(1+{\eta }_A\theta \right)E{Y}^{\alpha }-{\eta }_A\theta E{Y}_B^{\alpha }\right)$ ,

$C_{\infty }=\frac{1}{1-E{Y}^{\alpha }}\left[(1+{\eta }_B\theta )E{(S_{\infty }+X)}_{+}^{\alpha }-{\eta }_B\theta E{(S_{\infty }+X_A)}_{+}^{\alpha }\right].$

注记3.2：在推论3.1，3.2中，若 $A\left(u\right)=1-u,B\left(v\right)=1-v$ ，则推论3.1，3.2即Li&Tang [11] 文中对应的推论2.1(b)(c)。

参考文献 (References)

[1] Tang, Q. and Tsitsiashvili, G. (2003) Precise Estimates for the Ruin Probability in Finite Horizon in a Discrete-Time Model with Heavy-Tailed Insurance and Financial Risks. Stochastic Processes and Their Applications, 108, 299-325. http://dx.doi.org/10.1016/j.spa.2003.07.001

[2] Liu, F. (2013) Heavy-Tailed Distribution in the Presence of Dependence in Insurance and Finance. Doctoral Dissertation, University of Liverpool, Liverpool. http://repository.liv.ac.uk/14419/

[3] Vervaat, W. (1979) On a Stochastic Difference Equation and a Representation of Non-Negative Infinitely Divisible Random Variables. Advances in Applied Probability, 11, 750-783. http://www.jstor.org/stable/1426858

[4] Tang, Q. and Tsitsiashvili, G. (2004) Finite- and Infinite-Time Ruin Probabilities in the Presence of Stochastic Returns on Investments. Advances in Applied Probability, 36, 1278-1299. http://dx.doi.org/10.1239/aap/1103662967

[5] Chen, Y.Q. and Xie, X.S. (2005) The Finite Time Ruin Probability with the Same Heavy-Tailed Insurance and Financial Risks. Acta Mathematicae Applicatae Sinica, 21, 153-156. http://link.springer.com/article/10.1007%2Fs10255-005-0226-y

[6] Zhang, Y., Shen, X. and Weng, C. (2009) Approximation of the Tail Probability of Randomly Weighted Sums and Applications. Stochastic Processes and Their Applications, 119, 655-675. http://dx.doi.org/10.1016/j.spa.2008.03.004

[7] Chen, Y. (2011) The Finite-Time Ruin Probability with Dependent Insurance and Financial Risks. Journal of Applied Probability, 48, 1035-1048. http://dx.doi.org/10.1239/jap/1324046017

[8] Chen, Y., Liu, J. and Liu, F. (2015) Ruin with Insurance and Financial Risks Following the Least Risky FGM Dependence Structure. Insurance: Mathematics and Economics, 62, 98-106. http://dx.doi.org/10.1016/j.insmatheco.2015.03.007

[9] Yi, L., Chen, Y. and Su, C. (2011) Approximation of the Tail Probability of Randomly Weighted Sums of Dependent Random Variables with Dominated Variation. Journal of Mathematical Analysis and Applications, 376, 365-372. http://dx.doi.org/10.1016/j.jmaa.2010.10.020

[10] Jiang, J. and Tang, Q. (2011) The Product of Two Dependent Random Variables with Regularly Varying or Rapidly Varying Tails. Statistics & Probability Letters, 81, 957-961. http://dx.doi.org/10.1016/j.spl.2011.01.015

[11] Li, J. and Tang, Q. (2015) Interplay of Insurance and Financial Risks in a Discrete-Time Model with Strongly Regular Variation. Bernoulli, 21, 1800-1823. http://arxiv.org/pdf/1507.07673.pdf

[12] 杨洋, 王开永. 保险风险管理中的破产渐近分析[M]. 北京: 科学出版社, 2013.

[13] Embrechts, P., Klüppelberg, C. and Mikosch, T. (2013) Modelling Extremal Events: For Insurance and Finance. Vol. 33, Springer Science & Business Media, Berlin.

[14] Nelsen, R.B. (2007) An Introduction to Copulas. Springer Science & Business Media, Berlin.