Open Access Library Journal
Vol.02 No.10(2015), Article ID:68765,23 pages
10.4236/oalib.1101921
A Constructive Model of Newtonian Gravitation
Raghubansh P. Singh
Herndon, Virginia, USA
Email: raghu.singh@verizon.net
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 30 September 2015; accepted 22 October 2015; published 29 October 2015

ABSTRACT
The paper explores whether Newtonian gravitation is mediated by force fields, and, if so, whether it can explain known gravitational phenomena. In conformity with the historical and conventional practice, the paper presents a physical model in which gravitational forces among objects are mediated by those force fields which are associated with the mass and momentum properties of the objects. The model explains: gravitational forces among masses, between mass and light, among photons, and among electromagnetic waves; gravity’s effect on spectral lines, time periods of atomic clocks, rays of light, and lengths of material rods. The model addresses: Mercury’s orbital precession rate; the pioneer anomaly; gravitational radiation from accelerating masses. It advances suggestions for detecting gravitational radiation and measuring its speed. The model re-discovers: gravitational deflection of light rays, shift of spectral lines, and dilation of time periods of atomic clocks; gravitational shrinking of elliptical orbits. The literature reveals that the Newtonian gravitational field can account for Mercury’s orbital precession rate. The model finds that all or a portion of the pioneer anomaly can be due to minute changes in gravity at the spacecraft. It estimates gravitational radiation energy emissions from the moon, the planet Mars, and the Hulse-Taylor binary pulsars. It proposes that a lunar satellite may serve as a platform for detecting the gravitational radiation and measuring its speed.
Keywords:
Gravitation, Gravitational Interaction, Gravitational Force, Gravitational Constant, Mass Field, Momentum Field, Gravitational Field, Gravitational Wave, Gravitational Radiation
Subject Area: Classical Physics

1. Introduction
Newton discovers the law that gravitational attraction between two bodies is proportional directly to their masses and inversely to the square of their separation distance. This action-at-distance force law conveys how gravity behaves, but not how it is mediated [1] .
The strong, the weak, and electromagnetic interactions are mediated respectively by the strong, the weak, and electromagnetic fields associated respectively with the color, the weak, and electrical charge properties of the objects. The strong and the weak interactions are mediated at the microscopic levels; electromagnetic interactions are mediated at the microscopic through macroscopic levels; gravitational interactions are known to occur at the macroscopic levels. At microscopic levels, the fields are fundamentally discrete (quanta); at macroscopic levels, the fields are effectively continuous (with values at each space-time point).
Following the aforementioned theme underlying the fundamental interactions, the model will be developed in three parts, of which this paper is the first:
1) Part 1: Classical gravitation theory. Gravitational interaction among objects will be formulated in terms of their pertinent static and dynamic properties and associated fields―at the macroscopic level.
Mass, as gravitational charge, is an inherent property of objects. Momentum, as gravitational current, is a dynamic property of objects.
Non-gravitational and other extraneous effects will be ignored; gauge symmetries will not be extracted; special relativity will be considered in principle only; quantum theory will be used elementarily; analogy with electrodynamics will be invoked as applicable.
Coordinate systems will be used only for the convenience of representing and analyzing gravitational phenomena [2] .
2) Part 2: Classical gravitational field theory.
3) Part 3: Quantum gravitational field theory.
2. Assumptions
We make two assumptions regarding masses (gravitational charges) and momenta (gravitational currents):
1) Mass has an envelope of mass field.
2) Momentum has an envelope of momentum field.
3. The Gravitation Model
We define mass field and momentum field of Assumptions (1) and (2).
The mass field M at a distance r from an object of mass m is defined as:
 , (1)
, (1)
where S is the mass-field coefficient, which is the strength of the mass field of an object of 1 kg mass at 1 m. The mass field extends out to infinity and is uniform in all directions.
The momentum field P at a distance r from an object of momentum p is defined as:
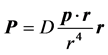 , (2)
, (2)
where D is the momentum-field coefficient, which is the strength of the momentum field of an object of 1 kg-m/s momentum at 1 m in the direction of momentum. The momentum field is not uniform in all directions.
The effective momentum field rangeq of an object with momentum p is defined as:
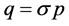 (3)
(3)
where σ is the momentum field range coefficient. An object with momentum of 1 kg-m/s has an effective momentum field range of σ m.
The sum of momentum field range q1 of object-1 and q2 of object-2 is thus:
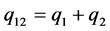 (4)
(4)
Gravitational force Fs between object-1 and object-2 with mass m1 and mass m2 respectively is mediated by their mass fields as defined in (1):
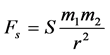 (5)
(5)
In analogy with electrodynamics, as like charges repel, so would like gravitational charges. That is, Fs is repulsive.
Gravitational force Fd between object-1 and object-2 with momentum p1 and momentum p2 respectively is mediated by their momentum fields as defined in (2):
 (6)
(6)
In analogy with electrodynamics, as parallel currents attract, so would parallel gravitational currents. That is, Fd is attractive or repulsive as the angle between p1 and p2 is acute or obtuse.
The dimension of S/D is of the square of speed, which we denote by b. In electrodynamics, the speed of light depends on the constants of the media: 1/(ε0μ0) = c2, where ε0 is electric permittivity, μ0 is magnetic permeability, and c is the speed of electric-magnetic (electromagnetic) wave in vacuum. By analogy, as the constants of the media in this model are S and D, the speed (b) of mass-momentum (gravitational) wave may be expressed by:
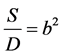 (7)
(7)
Estimations and measurements of constants S, D, b, and σ will be presented in later sections.
3.1. Universal Gravitation
Figure 1 shows an arbitrary sector of the universal sphere with center at the Primordial Point O, the space-time “point” where the universe originated. The Primordial Point is the primary space-time reference point for all objects in the universe. Objects O1 and O2 are at distances r1 and r2 from O. The angle between r1 and r2 at O is α. The objects have momentum vectors p1 and p2 relative to O.
At r ≤ q12, momentum fields are effective. From (6), gravitational force between objects O1 and O2 is:
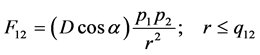 (8)
(8)
For non-zero-mass objects, we set p = mu, where m is mass and u is speed, and re-express (8) as:
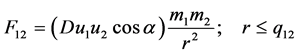 (9)
(9)
At r>q12, mass fields are predominant. From (5), (6), and (7), gravitational force between objects O1 and O2 is:
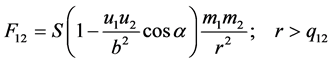 (10)
(10)
Equations (8), (9), and (10) are the Universal laws of gravitation. The terms in the three brackets are the universal gravitational “constants,” which are not constant as they vary with velocities u. That is, the universal gra-
Figure 1. Objects O1 and O2 with their momenta p1 and p2 relative to the Primordial Point O.
vitational forces have been evolving across space and with time since the universe began.
We simplify (8), (9), and (10), because the present-day velocity u of the solar system, or of the Milky Way galaxy, is not known. The age of the universe is large (about 14 BY). So, in Figure 1, r1 → ∞, r2 → ∞, and cos α → 1. There are no evidences of the solar system or the Milky Way galaxy flying apart at present, so, we set u1 ≈ u ≈ u2. Under these present conditions, Equations (8), (9), and (10) respectively become:
 (11)
(11)
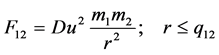 (12)
(12)
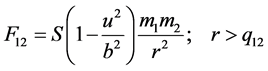 (13)
(13)
Equations (8), (9), and (10), or simplified (11), (12), and (13), are the three Newtonian laws of gravitational forces for zero-mass and non-zero-mass objects in the universe.
Equation (12) is the familiar classical Newton’s law, where the classical gravitational constant G ≡ Du2.
The active G and Γ ≡ S(1 − u2/b2) vary with u2; however, on the human space-time scale, as u is virtually constant, G and Γ are virtually constant.
Based on (12) and (13), Table 1 shows the signs of gravitational interaction between non-zero-mass objects: attractive if r ≤ q12 regardless of the value of u; and repulsive, attractive, or zero if r > q12 depending on u/b.
3.2. Matter-Energy Gravitational Interaction
A matter object of mass m and an energy object of energy E gravitationally interact via their momentum fields. Using (11), with p1 = mu and p2 = E/c, the gravitational force between them is:
 , (14)
, (14)
where κ is mass-energy gravitational coefficient:
 (15)
(15)
3.3. Gravitational Interaction between Electromagnetic Waves and between Photons
Photons and electromagnetic waves do not possess mass, but they have momentum.
Gravitational force between photons (p = E/c) is mediated by their momentum fields. From (11), the force is:
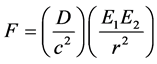 (16)
(16)
Gravitational force between electromagnetic waves (p = h/λ, h is Planck’s constant) is mediated by their momentum fields. From (11), the force is:

Table 1. Signs of gravitational interaction between non-zero masses.
We take photons of E ~ 106 MeV or electromagnetic waves of λ ~ 10?18 m, separated by r ~ 10?18 m. From (16) and (17), gravitational force between the photons or between the electromagnetic waves is of the order 10?22 nt.
Equations (8)-(15) hold at arbitrary velocities (υ) and moment a (p) as well.
4. Vibrating Particle in Gravitational Field
We derive the change in frequency (ν) of vibration of a particle as its position relative to a mass (m) changes. The mass, at r = 0, is a perfect sphere of radius R. The particle’s energy E is proportional to ν. Their momentum fields mediate the gravitational attraction between the mass and particle in accordance with (14).
4.1. Vibrating Particle outside the Mass
As the particle is moved from r = r ≥ R to r = (r + x), the change in its energy is given by:

Carrying out the integration, we have:

The fractional term > 1, thus νr < νx. The particle vibrates at lower frequency closer to the mass.
Using (19), we estimate κ. The details are in Appendix B, which shows:

As x → ∞, Equation (19) reduces to:

If the vibrating particle serves as an emitter of light, its wavelength (λ) at the sun and at infinity, from (21), (20), and data A(c, d), are related by:

or, (λR?λ∞)/λ∞ = 4.433 × 10?6. That is, spectral lines produced at the sun are redshifted by about 4.433 × 10?6 of their wavelengths compared to those produced at infinity. Wavelengths as emitted are longer closer to the mass.
If the vibrating particle serves as an atomic clock, its time period (τ) at the earth and at infinity, from (21), (20), and data A(e, f), are related by:

or, (τR?τ∞)/τ∞ = 1.454 × 10?9. That is, the interval between adjacent beats of an atomic clock at the earth is dilated by about 1.454 × 10?9 of the interval between adjacent beats at infinity. Time runs slower closer to the mass.
4.2. Vibrating Particle inside the Mass
As the particle is moved from r = 0 to r = r ≤ R, the change in its energy is given by:

where mr = (4/3)πr3ρ is the mass contained within r = r ≤ R, and ρ is mass density.
Carrying out the integration, we have:

The term in the bracket < 1 but > 0, thus ν0 < νr. The particle vibrates at lower frequency closer to the center of the mass.
Light wavelength at the surface and at the center of the sun, from (25), (20), and data A(c, d), are related by:

or, (λ0?λR)/λR = 2.22 × 10?6. That is, spectral lines produced at the sun’s center are redshifted by about 2.22 × 10?6 of their wavelengths compared to those produced at its surface. Wavelengths as emitted are longer closer to the center of the mass.
An atomic clock’s time period at the surface and at the center of the earth, from (25), (20), and data A(e, f), are related by:

or, (τ0?τR)/τR = 7.27 × 10?10. That is, the interval between adjacent beats of an atomic clock at the earth’s center is dilated by about 7.27 × 10?10 of the interval between adjacent beats at the surface. Time runs slower closer to the center of the mass.
4.3. Material Rod near a Mass
We address the change in the length of a rod of mass m' as its position relative to another mass m (?m') changes from r = r ≥ R to r = ∞.
We consider an ideal rod constituted of atoms of mass δm' (=m') and charge e spaced equally by d. Such an atom, under the electrostatic forces of its neighboring atoms, undergoes oscillations with period τ as given by:

where n is a parameter characteristic of the rod. (Appendix C, by example, shows that n = 3 for a one-dimen- sional rod.)
The gravitational field of mass m affects the oscillations of δm' according to (21). Substituting (28) in (21), we get:

In (29), dr > d∞. The rod is longer closer to the mass.
A thin wire (n = 3) is longer at the earth’s surface by about 9.7 × 10?10 of its length at infinity. If the gravitational field is uneven over the rod, it elongates unevenly.
4.4. Vibrating Particle and Point-Dense Mass
A mass of infinitely high point-density may be indicated by m/R → ∞. An example of such a mass would be a so-called black hole.
From (21), as m/R → ∞, τR/τ∞ → ∞. Time period at the surface tends to infinity; time virtually stops running.
From (21), as m/R → ∞, λR/λ∞ → ∞, subject to λRvR = c. At the surface, light travels at c with nearly flat waveform.
From (29), as m/R → ∞, dR/d∞ → ∞. At the surface, rod flattens to the point where it disintegrates.
4.5. Vibrating Particle and No Mass
For a vanishing mass, its point density m/R → 0/0, which is an indeterminate. From (21), as m/R → 0/0, (τR‑τ∞)/τ∞ → 0/0. One plausible interpretation would be τR → τ∞ → 0; that is, time periods may cease to exist in the absence of mass.
The effect of other fundamental fields on time and length is not known.
5. Constants and Parameters
We estimate S, D, b, σ, Γ, and u; κ was estimated in (20).
1) Appendix B has the details on the u and D estimates:


2) We estimate σ using the sun’s momentum field range. From (3), (30), and data A(c, g), we have:

That is, a mass with momentum of 1 kg-m/s has an effective momentum field range of the order 10?24 m.
From (3), (30), (32), and datum A(h), the black hole at the center of the Milky Way would have mass of 6.3 × 1036 kg.
3) We take electrical force (Fe) and gravitational force (Fg) between two particles of charge e (1.602 × 10?19 coul) and mass m (4.0 × 10?29 kg), intermediate between a proton and an electron. From Appendix D, the speed (b) of gravitational radiation is copied below, where Q is Coulomb’s constant:

From (33), (7), (31), and data A(i, j), we calculate:






The speed (b) of gravitational radiation is about 22.22% of the speed (c) of light.
The present-day primordial speed (u) is about 48% of the speed (c) of light and about 2.15 times the speed (b) of gravitational radiation. That is, from Table 1, present-day gravitational forces between non-zero masses are attractive.
4) Estimates of κ, u, D, b, S, and Γ are independent of σ.
6. Select Gravitational Phenomena
We address the following select gravitational phenomena.
6.1. Gravitational Deflection of Light at a Mass
In Appendix E, Equation (E.9) shows that the gravitational deflection θ of a ray of light with impact parameter d at a mass m is given by:

For small deflections: θ ≈ (2Gm)/(duc); from (38), as u ≈ c/2, θ ≈ (4Gm)/(dc2).
For a ray of light grazing the sun, we have, from (40), (20), and data A(c, d), the gravitational deflection angle θ ≈ 1.83 arc-secs.
(The 1919 expedition determined the deflection to be 1.75 arc-secs [3] ; the 1929 expedition yielded 2.2 arc-secs [4] ; later measurements ranged from 1.5 to 3 arc-secs [5] ; and recent experiments support 1.75 arc-secs [6] .)
From (40) we may infer that light with impact parameter d ≤ R at a black hole might turn back toward its source.
6.2. Escape Radius for Light near a Mass
To escape a mass m, light must be outside a critical impact parameter Re, which, from (40), is given by:

From (41), (20), (30), (32), and datum A(h), the black hole at the center of the Milky Way has Re ≈ 1010 m. As if they were points, the sun and the earth would have Re ≈ 3 km and 1 cm respectively.
6.3. Mercury’s Orbital Precession Rate
An observer measures Mercury’s orbital precession rate to be 5600 arc-secs/century. After filtering out the observer-planet relative motions, a 575 arc-secs/century is left over, which has been accounted for:
1) Price and Rush [7] show that the cumulative Newtonian gravity of planets Venus through Saturn contributes about 532 arc-secs/century. Each planet is replaced by a ring of uniform linear mass density to get a fairly accurate time-averaged effect of the moving planets. The force exerted by each planet on Mercury is directed outward, opposite to the force exerted by the sun.
2) Biswas [8] shows that a Lorentz covariant modification of the Newtonian potential contributes about 43 arc-secs/century. A second-rank symmetric tensor is introduced into special relativity as a potential rather than a metric.
3) Barwacz [9] shows that using an object’s total energy rather than its rest mass in a Newtonian gravitational field predicts Mercury’s orbital precession rate as observed.
6.4. The Pioneer Anomaly
The masses in the universe do not have exactly the same primordial velocity u; that is, G and Γ are not constant across space and over time. Even an infinitesimal change in u changes G and Γ, which leads to the perturbation of trajectories and orbits. A change in u may be caused by a local force, such as of gravitational, electromagnetic, thermal or other origin.
From (12), a small change Δu in u of a mass at r from another mass leads to a small change ΔG in G and a small change Δa in a (acceleration) as given by:

We now address the Pioneer anomaly. The Pioneer-10 and Pioneer-11 spacecraft, after they passed about 20 AU on their trajectories, were observed to have an additional acceleration of Δa ≈ (8.74 ± 1.33) × 10?10 m/s2 toward the sun [10] [11] . From (42), an increase of 0.00296% in u of the spacecraft leads to an increase of 0.00592% in G at their sites resulting in additional acceleration of Δa = 8.74 × 10?10 m/s2 toward the sun. That is, even a small variation in u (or G) at the site can account for all or a portion of the observed additional acceleration.
7. Gravitational Radiation from an Accelerating Mass
We derive gravitational Larmor’s formula. We follow Thomson’s treatment of electromagnetic radiation from accelerating charges [12] .
Figure 2 shows a mass m of momentum p at time t = 0, which accelerates at a for dt, gains speed by dυ (=υ), and continues for t (?dt). We examine the effects of acceleration a on the momentum field P and its components. A field vector is continuous and changes to it propagate at a finite speed (b). So, momentum-field component 0-A-B at t = 0 turns into t-C-A-B at t = t. We resolve momentum-field section C-A into radial momentum field Pr. and transverse momentum field Pt. Radial Pr drifts at υ but propagates radially at b. Transverse Pt changes from zero to amplitude Pt and back to zero in dt; this is gravitational radiation pulse propagating outwardly at speed b.
The geometrical ratio of transverse to radial momentum fields is:

where the radial momentum field Pr is given by (2) as:
Figure 2. Mass m with its momentum-field vector P.

Substituting (44) in (43) and using t = r/b and dυ/dt = a, we get:

Radial momentum field Pr varies with 1/r2, and transverse momentum field Pt with 1/r. That is, transverse Pt survives over radial Pr at greater distances.
We define gravitational Poynting intensity I (watt/m2):

Substituting (45) in (46), we get gravitational radiation intensity It due to transverse Pt:

Gravitational radiation intensity It falls off as 1/r2 and its angular variation is shown in Figure 3(a), which is a four-lobed quadrupole pattern. Figure 3(a), in turn, shows that gravitational radiation accelerates a mass at 45˚ to its propagation direction.
In contrast, the angular variation of electromagnetic radiation pulse intensity is shown in Figure 3(b), which, in turn, shows that electromagnetic radiation accelerates a charge at 90˚ to its propagation direction.
Gravitational radiation power (Ω) emitted is given by integrating (47) over all directions as follows:

If p and a are orthogonal, the magnitude of p stays constant, but its direction changes uniformly; that is, no momentum-field pulses develop. Thus, circular orbits are gravitationally stable, as masses in circular orbits do not emit gravitational radiation. Masses in motion in eccentric orbits or on arbitrary trajectories gravitationally radiate.
In contrast, a charge even in a circular orbit emits electromagnetic radiation.
Carrying out the integration in (48), we get gravitational Larmor’s formula:

A mass with motive power of pa ≈ 1025 watts emits gravitational radiation power of about one watt. A charge emits electromagnetic radiation power proportional to (ea)2.
7.1. Gravitational Radiation from Elliptical Orbits
We address gravitational radiation from masses in elliptical orbits. Figure 4(a) shows mass m2 in an elliptical orbit around mass m1. The elliptical orbit is given by semimajor axis A and eccentricity ε.

Figure 3. (a)Variation with φ in the intensity I of gravitational radiation; (b) Variation with φ in the intensity I of electromagnetic radiation.

Figure 4. (a) Mass m2 in an elliptical or bit around mass m1; (b) Variation of gravitational radiation power emission Ω with θ.
Appendix F details the derivations of Equations (50)-(55).
From (49), gravitational radiation power Ω emitted from a point (r, θ) on the orbit is given below:

From (50), peak gravitational radiation power Ωmax is emitted at a pair of angles θ+:

From (50) and (51), the variation of Ω with θ is shown in Figure 4(b), which shows the emission of gravitational radiation power in a pair of pulses with peaks Ωmax at θ+ and θ? in an orbital period.
Gravitational radiation energy Eo emitted in an orbital period τ is given by integrating Ω(θ) in (50) as follows:

or,

this is similar to the Peters’ formula [13] .
Change ΔA in A and change Δτ in τ due to the loss of gravitational radiation energy Eo per orbital period τ are:


7.2. Gravitational Radiation Power from Orbiting Bodies
Appendix G has the details on the emissions of gravitational radiation power from the moon, Mars, and the Hulse-Taylor binary pulsars (PSR B1913+16).
The moon emits peak gravitational radiation power at about 2306 watts. The semimajor axis is shrinking at 4.34 × 10−15 m/period.
Mars emits peak gravitational radiation power at, very low, less than one watt.
Pulsars PSR B1913+16 emit peak gravitational radiation power at about 1.67 × 1026 watts. Consequently, the semimajor axis is shrinking at 3.71 mm/period. The observed shrinking rate is 3.1 mm/period [14] .
8. Measurements
We suggest measurements for b, u, and σ:
1) Appendix H has the outlines for measuring b.
2a) Appendix B presents two approaches for determining the magnitude of velocity u.
2b) We are unable to make a suggestion for determining the direction of u of the solar system or the Milky Way.
3) Measurements of the momentum field range qm of a mass m yield the value of σ. From (3), σ = qm/(mu), where u comes from 2a) above. (The farthest extent of the solar system may be taken as the sun’s qm.)
4) The rest may be calculated using b, u, and G: D = G/u2; S = Db2; κ = Du/c; and Γ = S (1 − u2/b2).
Gravity elongates a rod. Measurements may be made of Bragg’s reflection/diffraction of X-rays from a crystal at the earth and at an altitude. The spacings between the atoms of the crystal would be relatively larger at the earth. Equations (19) and (28) and Bragg’s law are applicable.
9. Antimatter Gravitation
Antimatter has the same mass property as its counterpart matter but equal and opposite value of some other property. Negative mass is considered to be nonexistent. The model applies as is to antimatter-antimatter gravitational interactions. The model applies to matter-antimatter gravitational interactions; however, if antimatter mass were negative, Equations (5) and (6) would have their signs reversed.
10. Conclusions
Newtonian gravitation can be mediated by mass fields and momentum fields. There are three forms of Newtonian gravitational forces, which are applied to zero-mass and non-zero-mass objects in the universe.
Appendix I lists the results, including the new predictions. The model agrees on the observed values directionally and correctly and within an order of magnitude. Several ancillary deductions and inferences found in the literature are consistent with the model. On gravitational radiation, however, the model differs from the “accepted” views.
11. Epilogue
Faraday introduced the concept of field in physics. Classical physics introduced (classical) gravitational field and electromagnetic field. Modern physics introduced the strong nuclear field and the weak nuclear field. General relativity introduced space-time geometry field for gravity. This model introduces mass-momentum field for gravity.
Electromagnetic and gravitational interactions are similar in some aspects. They are repulsive and attractive and mediated by respective electric-magnetic and mass-momentum fields associated respectively with the mass and charge properties of the interacting objects. Charge fields extend out to infinity, so do mass fields.
Electromagnetic and gravitational interactions are not similar in some other aspects. Electromagnetic interactions occur when charge is present; so do gravitational interactions when mass is present, but they can occur even if the mass is zero. Charge is positive or negative, but mass is known to be positive only. Current has its magnetic field extending out to infinity; momentum has its momentum field, which is effectively (not finitely) limited in range and direction. Positive and negative charges and magnetic poles are equally abundant in nature; positive masses are abundant in nature, but negative masses are known to be non-existent; that is, electric and magnetic forces can be shielded, but gravitational forces may not be.
In strength, gravitational force differs starkly from electromagnetic force: the former is about 104˚ times weaker than the latter. Mass (momentum) fields are about 103˚ times weaker than electric (magnetic) fields. That is, mass fields and momentum fields are not as noticeable on the earth as are electric fields and magnetic fields.
As the Primordial velocity u has been varying across space and with time, so have been the gravitational forces. That is, gravitational forces have been evolving more or less differently in different regions of the universe since the universe began and are attractive present-day. Only in localized space-time regions, respective G and Γ are constant.
In the literature, more than one theory has been advanced to explain the Pioneer anomaly―thermal recoil has the most support [11] ―but none considers minute variations in the gravity (or G) at the spacecraft.
Our extensive knowledge of gravitation notwithstanding, detecting and deciphering gravitational radiation has been not satisfactory. More than one theory can explain several gravitational phenomena, but one and only one theory shall explain gravitational radiation. There are indirect evidences of the existence of gravitational radiation but no direct evidences so far on the physics (speed, structure, polarization, propagation, emission, and absorption) of gravitational radiation. A measure of the speed of gravitational radiation is as crucial to understanding gravitation as was the speed of light to understanding electrodynamics. The model suggests experiments for detecting gravitational radiation and measuring its speed.
Beyond microscopic levels, besides electric-magnetic fields and associated objects, the universe is filled with mass fields and momentum fields and associated objects.
We had set the boundaries for this part of the model. We now present our rationale:
1) Non-gravitational and other extraneous effects were ignored. Measurements of such astronomical phenomena as spectral shifts, deflections of light rays, the Pioneer anomaly, and the shrinking of the orbits of binary stars have been performed with high accuracy. However, it has been not possible to place complete confidence in the accounting and contributions of non-gravitational and other extraneous effects to those measurements― especially when the associated magnitudes are very small and in astronomical settings. (Examples of non-gravi- tational effects: electric, magnetic, etc. Examples of extraneous effects: systemic, Doppler, thermal, stellar accelerations, etc.)
2) Gauge symmetries were not extracted. These are useful in developing field/wave equations, which is an objective in the next part. Gauge symmetries may or may not make a theory more (or less) physical.
3) Special relativity was considered in principle only, because the speed of gravitational radiation has not been measured. If the speed of gravitational radiation were less that the speed of electromagnetic radiation, the development of gravitational field theories would have to resolve whether the equations should be covariant under additional transformation as well.
Mass-energy equivalence principle was not invoked. Light has momentum but no mass. So, for light we used p = E/c, not m = E/c2, to formulate light-mass and light-light gravitational interactions. As regards p = E/c, it is derived in the classical treatment of electromagnetic radiation pressure as well.
4) Quantum theory was used elementarily. The relationship that the energy of a vibrating particle is proportional to its frequency as advanced by Planck to explain black-body radiation sufficed.
Not imposing the boundaries will improve agreements with observations, but, at this starting point, the model will be unnecessarily complex at the cost of the basic physical insight. In the next parts, quantum theory and applicable covariance principles will be considered.
Cite this paper
Raghubansh P. Singh, (2015) A Constructive Model of Newtonian Gravitation. Open Access Library Journal,02,1-23. doi: 10.4236/oalib.1101921
References
- 1. Newton, I. (1687) Philosophiae Naturalis Principia Mathematica, 1687. (Translated and Reprinted by Cambridge University Press: Mathematical Principles of Natural Philosophy, 1934.)
The next evolution of the theory of gravitation occurs in 1915. Albert Einstein publishes a general relativity theory, according to which gravitation is due to the curvature which matter (or energy) creates in the field of spacetime geometry. The field of spacetime geometry is the gravitational field. The theory obviates the concept of (gravitational) force and its conventional mediation.
The linearized version of general relativity is strikingly similar to classical electromagnetism. Charges are not known to induce any distortions in the field of spacetime geometry. In reality, electromagnetic forces are mediated by electromagnetic fields. That is, in this limiting case, general relativity presents a non-force which is very similar to the mediated force! In the limiting case where the spacetime geometry field is weak, Newtonian gravity works very well. Thus, it is natural (not arbitrary) to explore whether Newtonian gravity could be mediated as well by gravitationally pertinent fields. - 2. Milne, E.A. (1935) Relativity Gravitation and World-Structure. Oxford University Press, Oxford.
Milne holds that “geometry can be selected primarily by the nature of underlying phenomenon and the convenience of representing and analyzing that phenomenon; and transformations of coordinates alone are but translations of language and have not necessarily much to do with phenomena.” - 3. Dyson, F.W., Eddington, A.S. and Davidson, C. (1920) A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919. Philosophical Transactions of the Royal Society of London, 332, 291-333.
http://dx.doi.org/10.1098/rsta.1920.0009 - 4. Freundlich, E., Klüber, H.V. and Brunn, A.V. (1931) Uber die Ablenkung des Lichtes im Schwerefeld der sonne (About the Deflection of Light in the Strong Field of the Sun). Zeitschrift fur Astrophysik, 3, 171.
- 5. Adler, R., Bazin, M. and Schiffer, M. (1965) Introduction to General Relativity. McGraw-Hill Book Company, New York, 188-202.
http://dx.doi.org/10.1063/1.3047725
Adler, Bazin, and Schiffer follow the arguments of Schiff and derive the equation for gravitational deflection of light by a mass using classical optics, the principle of equivalence, and special relativity. For Schiff’s arguments, see: Schiff, L.I. (1960) On Experimental Tests of the General Theory of Relativity. American Journal of Physics, 28, 340.
http://dx.doi.org/10.1119/1.1935800 - 6. Shapiro, S., et al. (2004) Measurement of the Solar Gravitational Deflection of Radio Waves Using Geodetic Very-Long-Baseline Interferometry Data, 1979-99. Physical Review Letters, 92, Article ID: 121101.
- 7. Price, M.P. and Rush, W.F. (1979) Nonrelativistic Contribution to Mercury’s Perihelion Precession. American Journal of Physics, 47, 531.
http://dx.doi.org/10.1119/1.11779 - 8. Biswas, T. (1994) Special Relativistic Newtonian Gravity. Foundations of Physics, 24, 513-524.
http://dx.doi.org/10.1007/BF02058061 - 9. Barwacz, D. (2014) Orbital Precession without GRT. Galilean Electrodynamics, 25, 93.
- 10. Anderson, J.D., et al. (1998) Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration. Physical Review Letters, 81, 2858-2861.
http://arxiv.org/abs/gr-qc/9808081
http://dx.doi.org/10.1103/physrevlett.81.2858 - 11. Turyshev, S.G., et al. (2012) Support for the thermal origin of the Pioneer Anomaly. Physical Review Letters, 108, Article ID: 241101.
http://arxiv.org/abs/1204.2507
http://dx.doi.org/10.1103/physrevlett.108.241101 - 12. Longair, M.S. (1981) High Energy Astrophysics, Volume 1, Cambridge University Press, Cambridge.
Pre-Maxwell, Thomson derived an equation for electric-magnetic power emission from accelerating charges. Post-Maxwell, Longair revived it for its simplicity and related physical insight. - 13. Peters, P.C. and Mathews, J. (1963) Gravitational Radiation from Point Masses in a Keplarian Orbit. Physical Review, 131, 435-440.
http://dx.doi.org/10.1103/PhysRev.131.435
The linearized version of general relativity is strikingly similar to classical electrodynamics, according to which charges in arbitrary motions radiate electromagnetic energy. Based on that understanding, Peters and Mathews formulate gravitationally radiated energy from masses in elliptical orbits. The equation, called Peters’ formula, predicts the decrease rate of the major axes of the binary pulsars PSR B1913+16’s orbits well.
Our derivation of gravitational Larmor’s formula and its applications are based on and consistent with the works of Thomson, Longair, and Peters and Mathews. - 14. Johnston, W.R. (2004) Data on the PSR B1913+16 System.
www.johnstonsarchive.net/relativity/binpulsar.html
The binary pulsar PSR B1913+16 are also known as the Hulse-Taylor pulsars. The pulsars are highly magnetic neutron stars. Each star is about 43% more massive than the sun.
The Johnston archive website has a consolidated table of data on the pulsars and their orbits. - 15. Ridpath, I., Ed. (2003) Oxford Dictionary of Astronomy. Oxford University Press, Oxford.
- 16. Isaacs, A., Ed. (2003) Oxford Dictionary of Physics. Oxford University Press, Oxford.
- 17. Pound, R.V. and Rebka Jr., G.A. (1959) Gravitational Redshift in Nuclear Resonance. Physical Review Letters, 3, 439-441.
http://dx.doi.org/10.1103/PhysRevLett.3.439 - 18. Pound, R.V. and Rebka Jr., G.A. (1960) Apparent Weight of Photons. Physical Review Letters, 4, 337-341.
http://dx.doi.org/10.1103/PhysRevLett.4.337 - 19. Goldstein, H. (1959) Classical Mechanics (79). Addison-Wesley Publishing Company, Reading.
- 20. Abbott, B.P., et al. (2009) Search for Gravitational Waves from Low Mass Compact Binary Coalescence in 186 Days of LIGO’s Fifth Science Run, ligo-p0900009-v11.
http://arxiv.org/pdf/0905.3710.pdf
Appendix A: Physical Data
The following data [15] [16] are used in the calculations. They are referenced as datum A(x) or data A(x, y).
a) Speed of light (c): 2.998 × 108 m/s.
b) Newton’s constant (G): 6.672 × 10?11 nt-m2/kg2.
c) Sun’s mass: 1.989 × 103 kg.
d) Sun’s radius: 6.963 × 108 m.
e) Earth’s mass: 5.976 × 1024 kg.
f) Earth’s radius: 6.378 × 106 m.
g) Farthest Kuiper Belt bodies from the sun: ~103 AU.
h) Diameter of the Milky Way galaxy: ~105 ly.
i) Coulomb’s constant (Q): 8.988 × 109 nt-m2/coul2.
j) Ratio of electrical to gravitational force: 1040.
Appendix B: Estimation of κ, u, and D
We present two approaches to estimating κ, u, and D.
B-1 Estimation of κ, u, and D based on the Pound-Rebka Experiment
From (19): light produced at the surface of the earth is relatively red shifted compared to light produced at a height.
In the Pound-Rebka experiment [17] [18] , gamma rays emitted from Fe57 at the bottom of a 22.5-m tower travel to absorber Fe57 at the top; the emitter is moved upward at a just speed so that a compensating Doppler shift is produced which allows resonant absorption by the absorber. That is:

where x and R indicate the tower’s height and the earth’s radius respectively, and the relative shift Δ = 5.13 × 10?15.
From (19), we have:

Comparing (B.1) with (B.2), we get:

Solving (B.3) for κ, we get:

Substituting in (B.4) x = 22.5 m and Δ = 5.13 × 10?15 from the experiment and m and R from data A(e, f), we get:

Equations (15) and (B.5), expression G ≡ Du2, and data A(a, b) yield:


B-2 Estimation of κ, u, and D with Gravitational Deflection of Light
From (E.9), the gravitational deflection θ of light with impact parameter d at a mass m is given by:

or,
We calculate κ, u, D, and ∆ for θ = 1.75, 1.83, and 2.2 arc-secs.
From (B.9), if m is the sun’s mass, d the impact parameter of light passing by the sun, and θ the gravitational deflection, we get κ.
Substituting κ from above in (15), we get u and D.
From (B.3), if m and R are Earth’s mass and radius, x = 22.5 m the height of the tower in the Pound-Rebka experiment, and κ as calculated above, we get ∆.
The results of calculations are listed in Chart 1.
The observed value of ∆ = 5.13 × 10?15 supports θ = 1.83 arc-secs gravitational deflection in the framework of the model.
B-3 We opted for Section B-1 over B-2, because in terrestrial experiments non-gravitational and other extraneous effects could be satisfactorily accounted for, controlled, and measured.
Appendix C: One-Dimensional Rod
We derive a mathematically simple relationship between the frequency (ν) of oscillations of atoms (or ions) which constitute a rod and the spacings (d) between them.
Picture 1 shows a one-dimensional rod of mass m constituted of atoms of mass δm (=m) and charge e spaced equally by d. Such an atom at O, under the electrostatic forces of its neighboring atoms at O? and O+, oscillates between points i and j with frequency ν and displacement ε (
Electrostatic force on δm when it is at point i is given below, where Q is the Coulomb’s constant:

Similarly, the electrostatic force on δm when it is at point j is given by:

From (C.1) and (C.2), atom δm has acceleration a directed toward the neutral point O, as given by:

The standard equation for a simple harmonic motion is:
Comparing this equation with (C.3), we get:
That is, for a rod of a given constitution (δm and d), we get:

Chart 1. Magnitudes of κ, u, D, and ∆ for selected values of θ.
Picture 1. An atom (δm, e) at O under the electrostatic forces of the neighboring atoms at O? and O+.
That is, ν2 is inversely proportional to d3.
C-1 Equation (C.5) is remarkably similar to Kepler’s third law of orbital motions.
Appendix D: Comparative Strengths of Gravitational and Electrical Forces
We consider two particles, separated by distance r, each of mass m and charge e.
Static gravitational force between the particles, from (5) and (7), is given by:

Static electrical force between the particles is given by:

where Q is the Coulomb’s constant.
From (D.1) and (D.2), we get:

That is, Fe/Fg is proportional to (e/m)2.
Appendix E: Gravitational Deflection of Light Rays by Mass
Picture 2(a) shows a light ray (ν) at impact parameter d from mass m. The light ray traces a hyperbola and has initial momentum pi and final momentum pf = pi + Δp. The gravitational force F between the light ray and the mass is mediated by their momentum fields. Picture 2(b) shows the vectorial relationships among the momenta.
Change (Δp) in momentum (p) of the light ray, from Picture 2(b) , is given by:

where p is the magnitude of initial and final momenta.
Angular momentum (J) of the light ray of energy Eν before and after the deflection is given by:

or,
By definition, force (F) is given by:

where, in this case, F will be the gravitational force between mass (m) and light ray (Eν), as given by (14):


(a) (b)
Picture 2. (a) Deflection of a light ray (ν) by a mass m. (b) Momentum vectors of the light ray.
From Picture 2(a) and Equation (E.4), we get:

Substituting (E.5) and (E.3) in (E.6), and noting that α = (π ? θ)/2 in Picture 2(a) , we get:
or,
Equating (E.7) to (E.1) and using Ev = pc, we get:

Rearranging (E.8), we get:

For small deflections,

Appendix F: Gravitational Radiation Emission from Mass in Elliptical Orbit
Picture 3 shows a mass m2 in an elliptical orbit around another mass m1. The elliptical orbit is given by semimajor axis A and eccentricity ε. We derive gravitational radiation power emission from the orbiting mass. The reduced-mass frame will be used. The reduced mass at m2 is μ = (m1m2)/(m1 + m2), and the compensated mass at m1 is (m1 + m2). Masses participating in gravitational interactions are neither reduced nor compensated.
From the geometry of the ellipse, we have:



Angular momentum vector (J), by definition, is given below, where p is momentum vector:

or,
Picture 3. A mass m2 in elliptical orbit around another mass m1.
The angular momentum (J) of m2 in an elliptical orbit is a constant of motion as given by [19] :

From (49), the gravitational Larmor’s formula, we have:

where acceleration a = Gm1/r2.
With (F.5), (F.6), and (F.7), we get from physics:

Using (F.8), (F.3), and (F.1), we get gravitational radiation power emission from a point (r, θ) on the orbit:

From (F.9), we get peak gravitational radiation power (Ωmax) from the points on the orbit at angles θ+ and θ?:

that is, power emission is maximum when the orbiting mass is θ+ or θ? away from the periastron.
Gravitational radiation energy (Eo) emission in one orbital period (τ) is given by integrating (F.9) as shown below:

Carrying out the integration, we get:

Substituting p = μυ in (F.5), we get speed υ of m2 at (r, θ):

From (F.2), (F.6), and (F.13), we get:

We use (F.1) in the r-term of (F.14) to get the θ-term:

From (F.14) and (F.15), the speed (υ) of m2 at a point (r, θ) on the ellipse is given by:

Kinetic energy (T) of m2 per orbital period is given below, where υ2(θ) comes from (F.16):
or,
Emission of gravitational radiation power (Ω) reduces kinetic energy (T). Changes ΔT, ΔJ, ΔA, and Δε in one orbital period (τ) ar


Substituting (F.6) and (F.17) in (F.18) and (F.19), we get changes ΔA and Δε per orbital period:


Kepler’s third law applies to binary systems as well:

From (F.22), first-order change in the orbital period (Δτ) per orbital period (τ) is given by:

where ΔA comes from (F.20).
Appendix G: Gravitational Radiation Emissions from Selected Binary Systems
We use (50)-(55) to estimate the magnitudes of gravitational radiation from the moon, Mars, and pulsars PSR B1913+16. We recall that as the eccentricity of an orbit goes to zero, so does the emission of gravitational radiation power.
G-1 Gravitational Radiation from Moon
We will use the following data: [15]
Mass of the earth: m1 = 5.976 × 1024 kg;
Mass of the moon: m2 = 7.348 × 1022 kg;
Semimajor axis of lunar orbit: A = 3.844 × 108 m;
Eccentricity of lunar orbit: ε = 0.055; and
Lunar orbital period: τ = 27.322 days.
From (50), the variation of Ω with θ is plotted in Figure 4(b), which shows the emission of gravitational radiation power in a pair of pulses at peaks Ωmax = 2.306 watts at θ = ± 83˚.8 away from the perihelion at approximately 14.6 days apart and then at 12.7 days apart per orbital period of 27.3 days.
From (53), gravitational radiation energy emitted in an orbital period is Eo = 2.702 × 106 joules.
From (54), the semimajor axis is decreasing at 4.338 × 10?15 m an orbital period.
From (55), the orbital period is decreasing at 4.0 × 10?17 sec in an orbital period.
Even though the moon has low orbital eccentricity, its mass is as much as 0.0123 times that of the earth. That is, the moon barely manages to emit gravitational radiation power at peaks of low but appreciable 2306 watts when it is at ± 83˚.8 away from its perihelion. The peak power emission of 2306 watts falls off to intensity of the order 10?15 watts/m2 at the earth, which may be too weak to be detectable. However, this power of about 2300 watts could be detectable by a detector in an artificial satellite at a calculated distance from the moon.
G-2 Gravitational Radiation from Mars
We will use the following data: [15]
Mass of the sun: m1 = 1.989 × 103 kg;
Mass of Mars: m2 = 6.5736 × 1023 kg;
Semimajor axis of Martian orbit: A = 2.278 × 1011 m;
Eccentricity of Martian orbit: ε = 0.093374; and
Martian orbital period: τ = 5.94 × 107 secs.
From (50), the variation of Ω with θ is plotted in Figure 4(b), which shows the emission of gravitational radiation power in a pair of pulses at peaks Ωmax = 0.45 watts at θ = ± 79˚.75 away from the perihelion.
G-3 Gravitational Radiation from Other Solar Planets
As in the case of Mars, the planets of the sun have low orbital eccentricities and small masses compared to the sun’s mass. That is, the planets emit no appreciable gravitational radiation while orbiting the sun.
G-4 Gravitational Radiation from PSR B1913+16
The neutron stars are orbiting each other around their center of mass. Their physical and orbital data are: [14]
Mass of the first star: m1 = 2.866 × 1030 kg;
Mass of the second star: m2 = 2.759 × 1030 kg;
Semimajor axis of each orbit: A = 1.95 × 109 m;
Eccentricity of each orbit: ε = 0.617131;
Orbital period: τ = 2.791 × 104 secs (7.752 hours); and
Distance from Earth: 21,000 light years.
From (50), the variation of Ω with θ is plotted in Figure 4(b), which shows the emission of gravitational radiation power in a pair of pulses at peaks Ωmax = 1.674 × 1026 watts at θ = ± 53˚.85 away from the periastron at approximately 6.58 hours apart and then at 1.17 hours apart per orbital period of 7.752 hours.
From (53), gravitational radiation energy emitted in one orbital period is Eo = 1.645 × 1030 joules.
From (54), due to the emission of gravitational radiation, the semimajor axis is decreasing at 3.71 mm per orbital period. The eccentricity is decreasing at 9.71 × 10?13 per orbital period. From (55), orbital period is decreasing at 7.987 × 10?8 sec per orbital period.
The peak power emission of 1.674 × 1026 watts falls off to intensity of the order 10?16 watts/m2 at the earth, which may be too weak to be detectable.
Appendix H: Determination of the Speed of Gravitational Radiation
Picture 4 shows a mass m2 in elliptical orbit about another mass m1. The ellipse is given by semimajor axis A and eccentricity ε.
Figure 4(b)shows variation with θ of gravitational radiation power Ω from m2. Peak gravitational radiation power Ωmax is emitted when m2 is either at (r+, θ+) or (r−, θ−). Angles θ+ are given by (F.10) in Appendix F.
We outline the steps to help carry out the measurement:
1) Determine the distance of m2 from the detector: d.
Picture 4. Mass m2 around mass m1 in elliptical orbit.
2) Detect by electromagnetic signals as m2 arrives at point (r+, θ+) and note the time (tc).
3) Note the time (tg) when peak gravitational power Ωmax from (r+, θ+) is detected. The peak power emission could have come from one of the previous orbital periods. (We note that no object can exceed the speed of light.)
4) If the electromagnetic signal comes from a specific orbital period, and the peak gravitational power signal comes from a prior nth orbital period (τ), we have:

or,
5) Repeat steps 1 - 4 for the next peak gravitational power Ωmax from point (r?,θ?).
We now apply (H.2) to the two astronomical binary systems: the moon and PSR B1913+16.
1) PSR B1913+16. This binary system is 21,000 light-years away; and each star has an orbital period of 2.791 × 104 secs. That is, there are at least 2.0 × 107 orbital periods during the time light travels from the stars to the detector. Extraneous agents between the stars and the detector would affect gravitational radiation and electromagnetic radiation differently. Therefore, it is not possible to ascertain n. That is, Equation (H.2) is not applicable.
According to Appendix G-4, peak gravitational radiation power emitted by the orbiting pulsars is 1.674 × 1026 watts. When received at the earth, it would be about 10?16 watts/m2, which may be too weak to be detectable. It is not probable either to send a gravitational-radiation detector close enough to the pulsars.
2) Earth-Moon. The moon is 1.2813 light-seconds away; its orbital period is 27.322 days. That is, the moon has barely moved along its orbit (≈10?7 of a period) in the time light travels to a detector on the earth. Extraneous agents between the moon and the earth would affect gravitational radiation and electromagnetic radiation differently but insignificantly. That is, Equation (H.2) is applicable here as n = 0. Equation (H.2) then becomes:

According to Appendix G-1, the gravitational radiation emission from the moon arriving at the earth is very low (of the order 10?15 watts/m2). Therefore, the detector should be placed in an artificial satellite around the moon.
Appendix I: Results and Predictions from the Model
Chart 2 lists the results and predictions from the model. They do not include any non-gravitational and other extraneous effects. These effects, known or unknown, are out of scope of this paper. The model’s results and predictions are due only to gravitational effects.
The measured values of spectral shift, time-period dilation, deflection of light, Mercury’s orbital precession, the classical gravitational constant, the Pioneers’ anomalous acceleration, and the PSR B1913+16’s orbital shrinking rate include non-gravitational and other extraneous effects.
Chart 2. Results and predictions from the model.
So far, no gravitational radiation has been detected [20] . There are indirect evidences of the existence of gravitational radiation but no direct evidences so far on the physics of gravitational radiation. In the literature, the speed of gravitational radiation is considered, without any evidence, to be equal to the speed of light in vacuum.
The model predicts spectral shift, time-period dilation, deflection of light rays, and the shrinking rate of the pulsars PSR B1913+16’s orbits directionally correctly and well within an order of magnitude―with only theoretical estimates of b, u, and κ.
The model makes new predictions:
1) Gravitational interactions are attractive or repulsive.
2) Classical gravitational constant is not universally constant.
3) Electromagnetic waves gravitationally interact; so do photons.
4) Rods get longer closer to mass.
5) Accelerating masses generate gravitational radiation which has a four-lobed quadrupole pattern and propagates at less than the speed of light.
We opted not to compare the model’s results with those from other theories, because the literature searches found little on its assumptions and predictions. Such comparisons would have little significance anyway until at least the speed of gravitational radiation has been measured.
Appendix J: Nomenclature
a acceleration
A semimajor axis of an ellipse
b speed of gravitational radiation
c speed of electromagnetic radiation
d impact parameter; arbitrary space interval
D momentum-field coefficient
e electrical charge
E energy
F force
G classical gravitational constant (G = Du2)
I gravitational Poynting intensity
J angular momentum
m mass (gravitational charge)
M mass-field vector
p momentum (gravitational current)
P momentum-field vector
q momentum field range of an object
q12 sum of q1 of object-1 and q2 of object-2
Q Coulomb’s constant
r arbitrary distance from an object
R radius
S mass-field coefficient
u velocity relative to the Primordial Point
Γ Γ = S (1 − u2/b2)
ε eccentricity of an ellipse; infinitesimal parameter
κ mass-energy gravitational coefficient
λ wavelength
μ reduced mass of a two-body system
ν frequency
σ momentum field range coefficient
τ period
υ arbitrary velocity
Ω power











