Open Access Library Journal
Vol.02 No.03(2015), Article ID:68132,10 pages
10.4236/oalib.1101389
Against Geometry: Nonstandard General Relativity
Günter Scharf
Physics Institute, University of Zürich, Zürich, Switzerland
Email: scharf@physik.uzh.ch
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 February 2015; accepted 14 March 2015; published 18 March 2015
ABSTRACT
We show that the Schwarzschild solution can be embedded in a class of nonstandard solutions of the vacuum Einstein’s equations with arbitrary rotation curves. These nonstandard solutions have to be taken as physical, if dark matter as needed in the standard theory cannot be found. As a consequence general relativity is considered as a classical field theory in Minkowski space and not as a geometric theory in the sense of Einstein. Assuming an asymptotically flat rotation curve and introducing a material disk into this model we find a matter density in accordance with the Tully- Fisher relation.
Keywords:
Dark Matter, General Relativity
Subject Areas: Modern Physics

1. Introduction
General relativity is a classical gauge theory. This implies that the fundamental fields, as the metric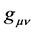 , are not directly observable. Therefore, in investigating gravitational effects it is important to identify the observable quantities which are actually measurable. Every observable is defined by a measuring process, the coordinate system included. A change of the coordinates, although mathematically possible, is dangerous for physical reasons: one may lose the contact with the measurable observables. Therefore, we choose physically defined coordinates once and for all and do not change them. On the scale of galaxies one most important observable is the circular velocity
, are not directly observable. Therefore, in investigating gravitational effects it is important to identify the observable quantities which are actually measurable. Every observable is defined by a measuring process, the coordinate system included. A change of the coordinates, although mathematically possible, is dangerous for physical reasons: one may lose the contact with the measurable observables. Therefore, we choose physically defined coordinates once and for all and do not change them. On the scale of galaxies one most important observable is the circular velocity 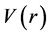 of stars or gas which can be measured by the Doppler shift of spectral lines (r is the radius of the circular orbit). This observable plays an important role in the following: we will use it to fix the gauge.
of stars or gas which can be measured by the Doppler shift of spectral lines (r is the radius of the circular orbit). This observable plays an important role in the following: we will use it to fix the gauge.
In standard general relativity one is tempted to interpret the metric 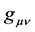 geometrically, for example by using it to measure the circumference of a circle in space. We reject this because, similarly as in electrodynamics, the
geometrically, for example by using it to measure the circumference of a circle in space. We reject this because, similarly as in electrodynamics, the 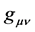 are the gravitational potentials and as such they are not observable. A nice way to see this is to consider electrodynamics and general relativity side by side. The electromagnetic fields
are the gravitational potentials and as such they are not observable. A nice way to see this is to consider electrodynamics and general relativity side by side. The electromagnetic fields 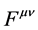 are defined by their effect on the motion of charged test bodies according to the equation of motion
are defined by their effect on the motion of charged test bodies according to the equation of motion
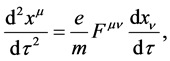 (1.1)
(1.1)
here the Lorentz force appears on the r.h.s. The corresponding equation of motion for test bodies in a gravitational field is the geodesic equation
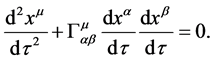 (1.2)
(1.2)
Consequently the Christoffel symbols are the gravitational field strengths. The field equations for the 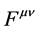 are the inhomogeneous Maxwell’s equations
are the inhomogeneous Maxwell’s equations
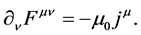 (1.3)
(1.3)
The field equations for the 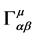 are Einstein’s equations
are Einstein’s equations
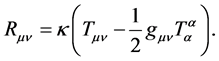 (1.4)
(1.4)
These are first order partial differential equations as (1.3), because the Ricci tensor is given by
 (1.5)
(1.5)
However (1.3) are only four equations for the 6 components of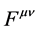 . The gap is filled by introducing the vector potential
. The gap is filled by introducing the vector potential
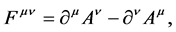 (1.6)
(1.6)
which is a consequence of the homogeneous Maxwell’s equations. Similarly (1.4) are only 10 equations for the 40 components of . The gap is filled by introducing the metric according to
. The gap is filled by introducing the metric according to
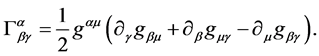 (1.7)
(1.7)
Since the electromagnetic potentials are not observable quantities, the same must be true for the metric tensor which, therefore, has no direct physical interpretation in general. Consequently, we do not interprete 
In the theoretical analysis one should try to relate the observables to the metric

The paper is organized as follows. As preliminaries we first consider the rotation curve in a general spherically symmetric gravitational field. Although this may be known we do not know a good reference. In Section 3 we solve the vacuum Einstein’s equations in our general spherically symmetric setting and express the metric tensor by the circular velocity

2. The Circular Velocity in General Relativity
We consider a star moving in an arbitrary static gravitational field. Following Weinberg ( [3] , Chapter 3/2) we introduce the freely falling coordinate system 

because in the locally inertial coordinates special relativity holds. Here 




where 


Since the local inertial coordinates 

for

and

In the following we assume that the non-diagonal elements 
we find

where (2.7) is used.
We want to specialize this for circular motion r = const choosing spherical coordinates


Taking the circular orbit 


and from (2.8) we finally obtain the important relation

In the following we consider static spherically symmetric metrics of the form

where 

here the prime means

It is not hard to integrate the geodesic equations for the metric (2.12) completely. Then one finds that there exist circular orbits for every radius 
Instead of using 

3. Solution of the Vacuum Equation
The metric functions a, b, c appearing in (2.12) must satisfy differential equations which follow from Einstein’s equations. In standard general relativity one puts c = 0. This is a special choice of gauge which leads to Birkhoff’s theorem and the Schwarzschild metric. This works well in the solar system, but obviously not on the galactic scale. The standard way out is to abandon the vacuum equations and assume some hypothetical dark matter. As long as this dark matter is not convincingly recorded one should also study the other possibility of retaining

Since the circular velocity 



The non-vanishing components of the Ricci tensor for the metric (2.12) are the diagonal elements [6]




the prime always denotes



As usual 
It is not hard to see that there are only two independent field equations. Indeed, using (3.6) b can be expressed by a and c. Eliminating b in (3.5) and (3.7) there results one second order differential equation for a and c:

Introducing the new metric function

where 

This can immediately by integrated

On the other hand the circular velocity squared (2.14) becomes

It is the velocity squared 

Differentiating and eliminating 

we find

This gives the first diagonal element of the metric

where 

where 


We have succeeded in expressing the metric by the circular velocity squared



That means the Schwarzschild metric is embedded in a class of nonstandard solutions. We emphasize that these solutions describe different physics because the corresponding circular velocities squared 
Now comes a pitfall for the well informed reader. In the books (e.g. [3] , Equation (8.1.4)) the line element (2.12) is transformed to the so-called “standard form” by redefining the radial coordinate as follows

according to (3.17). With an additional scale transformation

our metric (3.16-18) assumes the Schwarzschild form

Mathematically the class of nonstandard solutions has collapsed to the Schwarzschild solution. What does this mean physically? As discussed in the introduction we reject to interpret the metric (3.22) physically. Instead we consider the observable


where (3.19) has been used. This is just the Schwarzschild expression in the new coordinate






As far as the vacuum equations are concerned we are not able to predict the circular velocity; it must be given. But then from (3.16-18) we are able to predict other observable quantities which can be computed from the metric, for example lensing data [8] . In this way the theory can be tested. Another test is investigated in the next section.
4. Thin Material Disk with a Dark Halo
We study a simple model of a spiral galaxy by assuming that the normal matter is concentrated in the equatorial plane 



and have the normal vector

Then the finite discontinuities in the first partial derivatives of 

where + and − mean the limiting values from both sides of S. This follows from the decomposition of the gradient into normal and tangential components. The corresponding jumps in the Christoffel symbols then are

The Ricci tensor

contains derivatives of


Then it follows from (4.4) that

with

This is in agreement with Equation (2.14) of Taub [9] , note that his convention for the Ricci tensor is the negative of our (4.5).
In the Einstein’s equations these singular distribution must be compensated by a distribution valued energy- momentum tensor

where

If the jumps 



where
Now we come to our simple galaxy model where the normal matter is concentrated in the plane 


Then the metric (2.12) assumes the following non-diagonal form
with

For simplicity we still write r, but our admissible coordinates are

where the determinant D is equal to

To construct the metric with the material disk we apply the widely used displace, cut, and reflect method which goes back to Kuzmin [10] and since then has been used by many authors. Following the procedure of Voigt and Letelier [11] we take the metric (3.7) in the half space





The jumps (4.3) in the normal derivatives on 

where the prime always means 

with
we finally obtain

Here we have to put 

Now we must specify the circular velocity squared 


for large r. Then it follows from (3.16-18)

where by (3.17)

Using this in (4.18) the leading order comes from the last term

This is proportional to the density of normal matter because we consider a static energy-momentum tensor. Taking (4.21) into account we find that

for large R. This is in accordance with the baryonic Tully-Fisher relation for galaxies [3] [4] , which states that the total baryonic mass M is proportional to




The radial pressure 

5. Concluding Remarks
Our finding is that in the solar system the right gauge is


Obviously on small scales as the solar system or the binary pulsars the standard theory based on the geometric interpretation is the right one. But on the galactic scale which is a factor 108 bigger, the non-geometric aspect of general relativity becomes visible. In both cases we are observing geodesics in a gravitational field. On the small scale this field can be described geometrically, on the large scale this is not the appropriate picture.
Our solutions in Section 3 seem to be the right ones to describe the dark halo of galaxies, if some dark matter cannot be found experimentally. The Tully-Fisher relation found in the last section is a central relation in modified Newtonian dynamics (MOND) [13] . This suggests that nonstandard GR is in accordance with MOND in contrast to standard GR. As far as the vacuum equations are concerned this is obviously true because nonstandard GR does not predict the circular velocity

Cite this paper
Günter Scharf, (2015) Against Geometry: Nonstandard General Relativity. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1101389
References
- 1. Poincaré, H. (1952) Science and Hypothesis. Dover Publications, Inc., New York.
- 2. Xenon 100 Collaboration, 2012, arXiv 1207.5988
- 3. Weinberg, S. (1972) Gravitation and Cosmology. John Wiley & Sons, Hoboken.
- 4. Tully, R.B. and Fisher, J.R. (1977) A New Method of Determining Distances to Galaxies. Astronomy and Astrophysics, 54, 661-673.
- 5. McGaugh, S.S., Schombert, J.M., Bothun, G.D. and de Blok, W.J.G. (2000) The Baryonic Tully-Fisher Relation. The Astrophysical Journal, 533, L99-L102.
- 6. Scharf, G. (2011) Dark Matter in Galaxies According to the Tensor-Four-Scalars Theory. Physical Review D, 84, Article ID: 084045.
http://dx.doi.org/10.1103/PhysRevD.84.084045 - 7. Corbelli, E. (2003) Dark Matter and Visible Baryons in M33. Monthly Notices of the Royal Astronomical Society, 342, 199-207.
http://dx.doi.org/10.1046/j.1365-8711.2003.06531.x - 8. Bräunlich, G. and Scharf, G. (2010) Gravitational Lensing and Rotation Curve. General Relativity and Gravitation, 43, 143-154.
- 9. Taub, A.H. (1980) Space-Times with Distribution-Valued Curvature Tensors. Journal of Mathematical Physics, 21, 1423.
- 10. Kuzmin, G.G. (1956) Astron. Zh., 33, 27
- 11. Voigt, D. and Letelier, P.S. (2003) Exact General Relativistic Perfect Fluid Disks with Halos. Physical Review D, 68, Article ID: 084010.
http://dx.doi.org/10.1103/PhysRevD.68.084010 - 12. Scharf, G. (2012) Dark Matter in Galaxies According to the Tensor-Four-Scalars Theory III. arXiv 1205.4309.
- 13. Milgrom, M. (1983) A Modification of the Newtonian Dynamics—Implications for Galaxy Systems. Astrophysical Journal, 270, 384.
http://dx.doi.org/10.1086/161132 - 14. Scharf, G. (2012) Nonstandard General Relativity II. arXiv 1210.1496.
- 15. Bekenstein, J.D. (2004) Revised Gravitation Theory for the Modified Newtonian Dynamics Paradigm. Physical Review D, 70, Article ID: 083509.








