Open Access Library Journal
Vol.02 No.01(2015), Article ID:68019,13 pages
10.4236/oalib.1100945
Comprehention of Coils Overlappings Effects
―Magnetic Resonance Imaging
Mohammadreza Shiravi Khoozani1, Homayoun Meshgin Kelk1, Abolfazl Shiravi Khoozani2
1Department of Electrical Engineering, University of Tafresh, Tafresh, Iran
2Department of Medicine, Tehran University of Medical Sciences, Tehran, Iran
Email: mohammadreza.shiravi@gmail.com, Mediresearch12@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 January 2015; accepted 24 January 2015; published 28 January 2015
ABSTRACT
A typical medical Magnetic Resonance Imaging (MRI) contains a Local transmit/receive coil. Magnetic coil design is very important in study of the human brain and for neurological therapeutics technique. Precise spatial localization of stimulation sites is the key of efficient functional magnetic stimulations. Others have examined this issue at radio frequencies. This paper develops circular coils, figure-of-8 coils and coil array elements in order to realize a transcranial magnetic stimulator, and analyses the coil properties. The tests are done here with the applied DC excitation. The results show that different coils have different focus. The most important feature of these simulations is the ability to expand it. With these tests, the procedure of construction is determined. I simulate all procedures by MAXWELL 16.0.
Keywords:
Magnetic Resonance Imaging (MRI), Coil Array Element, Finite Element Methods
Subject Areas: Drugs & Devices, Electric Engineering

1. Introduction
Two Keyes factors in array element coil design are field homogeneity and cost. In terms of field homogeneity, we could apply two coil design methods: one is optimizing distance between two circular coil; another is array element coil design. Now, my idea is applying different configuration of coils to achieve best strength and uniformity in MRI. With this simulation, the cost also decreases clearly.
The studies done on this field include: In reference [1] , the authors reported that one can describe the use of a computational method for determining the overlap distance minimizing the mutual interaction between two adjacent coils that constitute a part of a phased array system used in MRI. The method is based upon the method of moments, and the analysis is carried out at a target imaging frequency to obtain the overlap distance. For a variety of complex RF phased array coils, one can determine, using the proposed approach, the overlap distance between the nearest neighbor block element RF coils such that the mutual interaction is nullified or minimized. One can give experimental results to validate the proposed approach. When compared with the experimental data, our theoretical prediction is in excellent agreement. In reference [2] , a coil design termed as broadside- coupled loop (BCL) coil and based on the broadside-coupled split ring resonator (BC-SRR) is proposed as an alternative to a conventional loop design at 7T. The BCL coil has an inherent uniform current which assures the rotational symmetry of the radio-frequency field around the coil axis. A comparative analysis of the signal-to- noise ratio provided by BCL coils and conventional coils has been carried out by means of numerical simulations and experiments in a 7T whole body system. In reference [3] , the author argues that besides single surface coil, multiple coil system is simulated, too. One can choose a two-square-surface coil system to verify the validity of mutual inductance effects by our algorithm. Testing functions for simulating this array system are two distinct loops along two surface coils, and base functions are identical to testing functions. Since one can tune the position of this two-surface coil system resonating at Larmor frequency.
Here I introduce this resource that I have expressed to the reader that operating coils overlap, the stimulation of DC and AC excitation effects are common.
2. MRI Scanner Components
The MRI scanner produces three types of magnetic fields that interact with the proton spins to produce images. First, the primary field 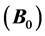 is generated by a superconducting coil surrounded by liquid helium (label A, Figure 1).
is generated by a superconducting coil surrounded by liquid helium (label A, Figure 1). 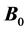 is the static field directed axially through the scanner Tunel (the
is the static field directed axially through the scanner Tunel (the  axis) that causes spin precession, and consequently, the net magnetization of each voxel. Ideally, the main magnet in the scanner would produce a uniform
axis) that causes spin precession, and consequently, the net magnetization of each voxel. Ideally, the main magnet in the scanner would produce a uniform 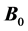 field throughout the entire imaging volume. Since this is rarely the case in a commercial scanner, “shim” coils (label B, Figure 1) are strategically installed to broaden the region of uniformity. The shim coils themselves produce magnetic fields that interact with
field throughout the entire imaging volume. Since this is rarely the case in a commercial scanner, “shim” coils (label B, Figure 1) are strategically installed to broaden the region of uniformity. The shim coils themselves produce magnetic fields that interact with 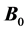 by superposition to correct known field in homogeneities. The second type of magnetic field applied by the scanner is an RF pulse referred to as the
by superposition to correct known field in homogeneities. The second type of magnetic field applied by the scanner is an RF pulse referred to as the 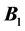 field. This field is produced by the body coil within the scanner (label D of Figure 1) or by a transmit coil local to the imaging volume (label E, Figure 1). Finally, the third type of field in the scanner is produced by a specially-designed coil within the scanner called the gradient coil (label C, Figure 1). When activated, this coil generates three different gradient fields that combine with the primary
field. This field is produced by the body coil within the scanner (label D of Figure 1) or by a transmit coil local to the imaging volume (label E, Figure 1). Finally, the third type of field in the scanner is produced by a specially-designed coil within the scanner called the gradient coil (label C, Figure 1). When activated, this coil generates three different gradient fields that combine with the primary 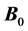 field by superposition [4] .
field by superposition [4] .
3. Calculations of Coil Design
Coil design methods are divided into three groups. The first two categories, discrete wires, such as Helmholtz coil, and current density techniques (distributed windings), are considered as classical methods. The remaining techniques are included in a third group termed as new methods.
Figure 1. Cut-away view of an MRI scanner. A: Primary field 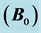 magnet in liquid helium bath B: Shim coil C: Gradient coil D: Body transmit/receive coil E: Local transmit/receive coil. Adapted from.
magnet in liquid helium bath B: Shim coil C: Gradient coil D: Body transmit/receive coil E: Local transmit/receive coil. Adapted from.
A number of studies have investigated coil design with DC and AC excitations [5] - [7] .
Now it is essential to mention some Magneto-statics. The Maxwell's equations that describe magnetic phenomena in the static regime are Gauss’s Law
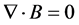 (1)
(1)
and Ampere’s Law
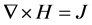 (2)
(2)
where  is the current density, that is the source of the magnetic field,
is the current density, that is the source of the magnetic field,  , which can be related to the magnetic induction,
, which can be related to the magnetic induction,  , through the constitutive equation.
, through the constitutive equation.
 (3)
(3)
here  is a characteristic of the medium known as the magnetic permeability. For nonmagnetic material Equation (3) reduces to
is a characteristic of the medium known as the magnetic permeability. For nonmagnetic material Equation (3) reduces to

and with little summation I have

This is the well-known Biot-Savart Law. Since the surface integral of the current density is the total current intensity, I, passing through a closed curve, C, the last equation can also be expressed as

The Biot-Savart law as applied to a circular wire loop in the XY plane is shown in Figure 2. The Biot-Savart Equation (6) can be easily integrated to obtain the axial (Z axis) magnetic field Bz

Combining terms, 

Magnetic field


Figure 2. Geometric configuration for the Biot-Sauart law.
The following approximation for the inductance of a single-turn wire loop is very accurate for small wires


Relation to Magnet coil design, the design of MRI magnet structures is complicated. In the design of conventional magnet structures, the analyst solves the ‘‘direct’’ problem in which the geometry and magnetization are given, and the field distribution is determined. In MRI, the analyst is faced with the more difficult ‘‘inverse’’ problem in which the field strength and uniformity are specified across the imaging region and the geometry and magnetization of the structure need to be determined. There is no unique solution to such problems in that a specified field distribution within a closed region can be obtained using an infinite number of different structures [8] .
4. The Exact Dimensions of the Model
Here, there are two coil configurations shown in Figure 12 and Figure 17, and their geometric parameters are shown in Table 1.
The RLC circuit is shown in Figure 3. 





where

5. Circular Coils
5.1. Circular Coils: Model 1
Figure 4 shows geometric configuration in Maxwell software. In all simulation except last case direction of current is anticlockwise. Figure 5 shows x-y and y-z plane for magnitude of magnetic field density. Figure 6 shows also this in x-z plane. According to this plot close the coil density is the strongest. Figure 7 shows 


Figure 9 shows geometric configuration of two coil. Figure 10 shows the magnitude of the magnetic flux density at distance 100 mm along z-axis from −50 mm blow to 50 mm above the coil. Figure 11 shows 
Figure 12 shows configuration of model 1. Figure 13 shows 
Figure 15 and Figure 16 show contrasting among previous states.
Table 1. The geometric parameters of two wire loop of the magnetic stimulation coil in Figure 17.
Figure 3. The RLC circuit.
Figure 4. Single coil.
Figure 5. Field density distribution.
Figure 6. View on X-Z plane.
Figure 7. Bz for y = 0, x = 0, on the Z axis.
5.2. Circular Coils: Model 2
Figure 17 shows configuration of model 2. Figure 18 shows Bz at center and edge of coil. Density is became bigger than model 1.
Figure 8. Bz for y = 23.5, x = 0, on the z axis.
Figure 9. Dual coil.
Figure 10. Bz for y = 0, x = 0.
Figure 11. Bz for y = 23.5, x = 0.
Figure 12. Model 1.
Figure 13. Bz for y = 0, x = 0.
Figure 14. Bz for y = 23.5, x = 0.
Figure 15. Bz for y = 0, x = 0.
Figure 16. Bz for y = 23.5, x = 0.
Figure 17. Model 2.
Figure 18. Abs(Bz) for y = 23.5, Bz for y = 0.
5.3. Comparisons between Models 1, 2
Figure 19 shows the magnitude of the magnetic flux density at 5 cm in the direction of the axis. Model 1 has bigger intension of magnetic field.
Figure 20 shows the magnitude of the magnetic flux density at radial 5 cm on the surface at x-y plane. The focus ability of model 2 is better than model 2.
6. Figure-of-8 Coils
The parameters of the figure-of-8 coils are the same as Table 1.
In Figures 21(a)-(c), the interval of axis of the two coils is D/4, 2D/4, 3D/4 respectively. D is the outer-di- ameter of coil; in (d), the two coils are no interval and not in the same plane; in (e), the two coils are no interval and in the same plane. In Figures 24(a)-(e) have the same means in Figure 21. Figure 22 and Figure 25 are the
Figure 19. Axial distribution of magnetic flux density.
Figure 20. Radial distribution of magnetic flux density.


Figure 21. Figure-of-8 coil configurations. (a) Type 1-model-1; (b) Type 2-model-1; (c) Type 3-model-1; (d) Type 4- model-1; (e) Type 5-model-1.
radial distributions of magnetic flux density 3 mm below the coil 1 of types of model 1 and model 2 with the currents in the same direction respectively. Figure 23 and Figure 26 are the radial distributions of magnetic flux density 3 mm below the coils of types of model 1 and model 2 along X axial. The currents are both anticlockwise. The mutual coupling could induce currents at adjacent coils, which could influence the spatial localization of the stimulation when the coil array has a high magnetic coupling configuration.
Figure 22. Radial distribution of magnetic flux density 3 mm below the coil 1 in the types of model 1. The currents are both anticlockwise.
Figure 23. Radial distribution of magnetic flux density 3 mm below the coils in the types of model 1 along X axial. The currents are both anticlockwise.


Figure 24. Figure-of-8 coil configurations. (a) Type 1-model-2; (b) Type 2-model-2; (c) Type 3-model-2; (d) Type 4- model-2; (e) Type 5-model-2.
The mutual coupling could induce currents at adjacent coils, which could influence the spatial localization of the stimulation when the coil array has a high magnetic coupling configuration. However, the coupling effect can be compensated by proper control of the charge voltages [9] . When the figure-of-8 coils have the current of
Figure 25. Radial distribution of magnetic flux density at 3 mm below the coil1 in the types of model 2. The currents are both anticlockwise.
Figure 26. Radial distribution of magnetic flux density at 3 mm below the coils in the types of model 2 along X axial. The currents are both anticlockwise.
the same direction, different type has different focality. The type 2-model-2 has the max numerical value and better focality. At other positions, magnetic field which produced by figure-of-8 coils are less uniform; type 1- model-1 and type 5-model-1 have two different focuses, so I should consider the position of the coils. If controlling the radius of the coil properly, the precision of focus should be able to reach millimeter, which is very useful in MRI; and the figure-of-8 coils of model 2 can produce several focuses, it can stimulate several targets at the same time, which are very useful in coils array elements. But Figure 22 and Figure 23 show better view with variety overlapping between tow coil. So I chose model 1 for research on array element coil.
7. Coil Array Element
To perform efficient to localize stimulation sites more precisely in brain studies, multichannel magnetic stimulations are desired. By using multicoils with which separate driving channels are connected, the stimulation site can be moved without any physical movements of the coils and the spatial localization in the stimulation can be achieved more precisely than by a conventional single coil-based system.
Figure 27 shows two kinds of coil array element constructions. Two figure-of-8 coils are difference in the direction. That is, coil array element 1 is with anticlockwise and the other with clockwise and coil array element 2 are both anticlockwise.
From Figure 28, the conclusions are the following: array element 1 has better focus than array element 2; the array element has better ability of focus than circular loop coil. If the current direction in a coil array element is controlled properly, they can produce several focuses, and also can produce many kinds of magnetic fields, which is useful in nerve imaging.

Figure 27. The coil array elements composed by two figure-of-8 coils. (a) Coil array element 1; (b) Coil array element 2.
Figure 28. Radial distribution of two coil array elements at 3 mm below the coils (dot) and centre of array (solid).
8. Conclusion
As was seen, all simulation was done successfully by MAXWELL 16.0. One can realize that Key properties of MRI magnets are three types of coils: Field generation, Field shaping, Stray-field containment coils. In this paper, the focality and stimulation depth of two circular models, five types of 8-shaped coils and two array elements have been discussed. The performance of model 2 is better than the others. The current direction has little effect on the stimulation depth. When the current directions in two coils are both anticlockwise, the 8-shaped coils can produce several focuses. The array element has better ability of focus than circular loop coil and figure-of-8 coils. Those are a well basis for our further work. In the next work, one will make his great efforts to analyze multichannel magnetic stimulation coils array.
Cite this paper
Mohammadreza Shiravi Khoozani,Homayoun Meshgin Kelk,Abolfazl Shiravi Khoozani, (2015) Comprehention of Coils Overlappings Effects —Magnetic Resonance Imaging. Open Access Library Journal,02,1-13. doi: 10.4236/oalib.1100945
References
- 1. Fujita, H., Missal, J.W. and Morich, M.A. (2000) Moment Method Analysis of Mutual Interaction in MRI Phased Array Coils. Magnetic Resonance Materials in Physics, Biology and Medicine, 10, 84-92.
- 2. Freire, M.J., Lopez, M.A., Meise, F., Algarin, J.M., Jakob, P.M., Bock, M. and Marques, R. (2013) A Broadside-Split-Ring Resonator-Based Coil for MRI at 7 T. IEEE Transactions on Medical Imaging, 32, 1081-1084.
- 3. Chen, J.-H., Jeng, S.-K., Lin, F.-H. and Kuan, W.-P. (1999) Quantitative Analysis of Magnetic Resonance Radio-Frequency Coils Based on Method of Moment. IEEE Transactions on Magnetics, 35, 2118-2127.
- 4. Robb Phillip, M. (2010) A Twenty-Eight Channel Coil Array for Improved Optic Nerve Imaging. M.S. Thesis, The University of Utah, Salt Lake City.
- 5. Lin, V.W.-H., Hsiao, I.N. and Dhaka, V. (2000) Magnetic Coil Design Considerations for Functional Magnetic Stimulation. IEEE Transactions on Biomedical Engineering, 47, 600-610.
- 6. Sanchez, C.C. (2008) Forward and Inverse Analysis of Electromagnetic-Elds for MRI Using Computational Techniques. University of Nottingham, Nottingham.
- 7. Kennedy, M.W. (2013) Magnetic Fields and Induced Power in the Induction Heating of Aluminium Billets. Licentiate Thesis in Materials Science and Engineering, Stockholm.
- 8. Thompson, M.T. (1999) Inductance Calculation Techniques. Power Control and Intelligent Motion.
- 9. Han, B.H., Chun, I.K., Lee, S.C. and Lee, S.Y., Member, Multichannel Magnetic Stimulation System (2004) Design Considering Mutual Couplings Among the Stimulation Coils. IEEE Transactions on Biomedical Engineering, 51, 812-817.




































