Paper Menu >>
Journal Menu >>
 Journal of Intelligent Learning Systems and Applications, 2011, 3, 155-170 doi:10.4236/jilsa.2011.33017 Published Online August 2011 (http://www.scirp.org/journal/jilsa) Copyright © 2011 SciRes. JILSA 155 Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Igor Chikalov1, Peggy Yao2, Mikhail Moshkov1, Jean-Claude Latombe3 1Mathematical and Computer Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia; 2Bio-Medical Informatics, Stanford University, Stanford, USA; 3Computer Science Department, Stanford University, Stanford, USA. Email: igor.chikalov@kaust.edu.sa Received March 7th, 2011; revised March 24th, 2011; accepted April 2nd, 2011. ABSTRACT Hydrogen bonds (H-bonds) play a key role in both the formation and stabilization of protein structures. H-bonds in- volving atoms from residues that are close to each other in the main-chain sequence stabilize secondary structure ele- ments. H-bonds between atoms from distant residues stabilize a protein’s tertiary structure. However, H-bonds greatly vary in stability. They form and break while a protein deforms. For instance, the transition of a protein from a non- functional to a func tional state may require some H-bonds to break and others to form. The intrinsic strength of an in- dividual H-bond has been studied from an energetic viewpoint, but energy alone may not be a very good predictor. Other local interactions may reinforce (or weaken) an H-bond. This paper describes inductive learning methods to train a protein-ind ep endent pro bab ilistic mod el o f H-bond stab ility from mo lecula r dynamics (MD) simulation trajecto- ries. The training data describes H-bond occurrences at successive times along these trajectories by the values of at- tributes called predictors. A trained model is constructed in the form of a regression tree in which each non-leaf node is a Boolean test (split) on a predictor. Each occurrence of an H-bond maps to a path in this tree from the root to a leaf node. Its predicted stability is associated with the leaf node. Experimental results demonstrate that such models can predict H-bond stability qu ite well. In particular, their performance is roughly 20% better than that of models based on H-bond energy alone. In addition, they can accurately identify a large fraction of the least stable H-bonds in a given conformation. The pape r discuss es sever al exte nsions that may yield further improvements. Keywords: Molecular Dynamics, Machine Learning, Regression Tree 1. Introduction A hydrogen bond (H-bond) corresponds to the attractive electrostatic interaction between a covalent pair D—H of atoms, in which the hydrogen atom H is bonded to a more electronegative donor atom D, and another non- covalently bound, electronegative acceptor atom A. Most H-bonds in a protein are of the form N—HO or O—HO, but other forms are possible. Due to their strong directional character, short distance ranges, and relatively large number in a folded protein, H-bonds play a key role in both the formation and stabilization of pro- tein structures [1-3]. While H-bonds involving atoms from residues that are close to each other in the main- chain sequence stabilize secondary structure elements, H-bonds between atoms from distant residues stabilize a protein’s tertiary structure [1,3-5]. In particular, the later ones shape loops and other irregular features that may contain functional sites. Unlike covalent bonds, H-bonds greatly vary in stabil- ity. They form and break while the conformation1 of a protein deforms. For instance, the transition of a folded protein from a non-functional meta-stable state into a functional (e.g. binding) state may require certain H- bonds to break and others to form [6]. The intrinsic strength of an individual H-bond has been studied from an energetic view point [7-11]. However, potential en- ergy alone may not be a very good predictor of H-bond stability. Other local interactions may reinforce or weaken an H-bond. Moreover, several “redundant” H-bonds may 1A protein conformation defines the relative positions of all the atoms in the protein.  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 156 contribute to rigidify the same group of atoms. To better understand the possible deformation of a protein in its folded state, it is desirable to create models that can re- liably predict the stability of an H-bond not just from its energy, but also from its local environment. Such a model can then be used in a variety of ways, e.g. to study the kinematic deformability of a folded protein confor- mation (by detecting its rigid components) and sample new conformations [12]. In this paper we apply inductive learning methods to train a protein-independent probabilistic model of H-bond stability from a training set of molecular dynam- ics (MD) simulation trajectories of various proteins. The input to the training procedure is a data table in which each row gives the value of several (32) attributes, called predictors, of an H-bond and its local environment at a given time t in a trajectory, as well as the measured stability of this H-bond over an interval of time ,t t . The output is a function of a subset of pre- dictors that estimates the probability that an H-bond pre- sent in the conformation c achieved by a protein will be present in any conformation achieved by this protein within a time interval of duration . The value of defines the timescale of the prediction. MD simulation trajectories provide huge amount of data yielding training data tables made of several hun- dred thousand, or more, rows. To build regression trees from such tables we propose methods that run in logOab a time, where a is the number of rows and b is the number of predictors. Tests demonstrate that the models trained with these methods can predict H- bond stability roughly 20% better than models based on H-bond energy alone. The models can also accurately identify a large fraction of the least stable H-bonds in a given conformation. In most tests, about 80% of the 10% H-bonds predicted as the least stable are actually among the 10% truly least stable. Section 2 gives a precise statement of the problem ad- dressed in this paper. Section 3 presents the machine learning approach that is used to solve this problem. Sec- tion 4 describes details of the training algorithm. Section 5 discusses test results obtained with models trained us- ing software implementing this algorithm. Section 6 suggests future developments that may lead to improving trained models. 2. Problem Statement Let c be the conformation of a protein P at some time considered (with no loss of generality) to be 0 and H be an H-bond present in c. Let M c be the set of all physically possible trajectories of P passing through c and π be the probability distribution over this set. We define the stability of H in c over the time interval by: 0 :,, 0,1, 1 ,,,,d π, qMc Hc H cIqHttq (1) where ,, I qHt is a Boolean function that takes value 1 if H is present in the conformation qt at time t along trajectory q, and 0 otherwise. The value ,,Hc can be interpreted as the probability that H will be present in the conformation of P at any specified time 0,t , given that P is at conforma- tion c at time 0. Our goal is to design a method for generating good approximations of . We also want these ap- proximations to be protein-independent, i.e., the argu- ment c may be a conformation of any protein. 3. General Approach We use machine learning methods to train a stability model s from a given set Q of MD simulation trajecto- ries of various proteins. Each trajectory qQ is a dis- crete sequence of conformations of a protein. These conformations are reached at times i ti , 0,1,i 2, , called ticks, where is typically on the order of the picoseconds2. We detect the H-bonds3 which are pre- sent in each conformation 1 qt using the geometric criteria given in [13] (see Appendix A). Note that an H- bond in a given protein is uniquely identified (across different conformations) by its donor, acceptor, and hy- drogen atoms. So, we call the presence of a specific H- bond H in a conformation 1 qt an occurrence of H in 1 qt . For each occurrence of an H-bond H in 1 qt we compute a fixed list of predictors, some numerical, oth- ers categorical. Some are time-invariant, like the types of the donor and acceptor atoms and the number of residues along the main-chain between the donor and acceptor atoms. Others are time-dependent. Among them, some describe the geometry of H in 1 qt , e.g. the distance between the hydrogen and the donor atoms and the angle made by the donor, hydrogen, and acceptor atoms. Oth- ers describe the local environment of H in 1 qt , e.g. the number of other H-bonds within a certain distance from the mid-point of H. The complete list of predictors used in our work is given in Appendix C. In total, it con- tains 32 predictors. 2MD simulation trajectories are computed by integrating the equations of motion with a time step on the order of the femtoseconds (10–15 s) in order to take into account high-frequency thermal vibrations. However, to reduce the amount of stored data, they are usually sub-sampled at a time step on the order of the picoseconds (10–12 s). 3We only consider H-bonds inside a protein. We ignore H-bonds be- tween a protein and the solvent. 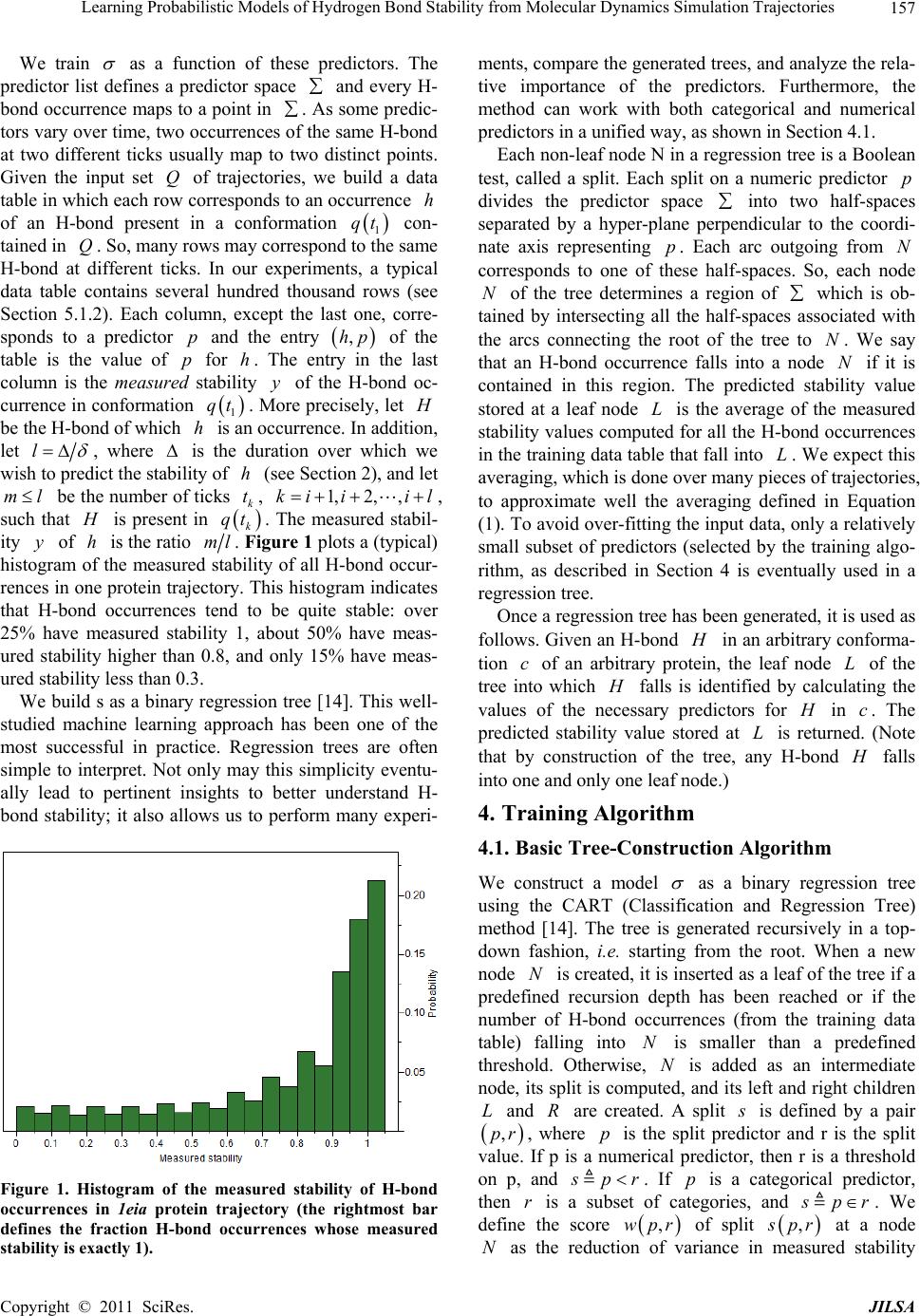 Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 157 We train as a function of these predictors. The predictor list defines a predictor space and every H- bond occurrence maps to a point in . As some predic- tors vary over time, two occurrences of the same H-bond at two different ticks usually map to two distinct points. Given the input set Q of trajectories, we build a data table in which each row corresponds to an occurrence h of an H-bond present in a conformation 1 qt con- tained in Q. So, many rows may correspond to the same H-bond at different ticks. In our experiments, a typical data table contains several hundred thousand rows (see Section 5.1.2). Each column, except the last one, corre- sponds to a predictor p and the entry ,hp of the table is the value of p for h. The entry in the last column is the measured stability y of the H-bond oc- currence in conformation 1 qt . More precisely, let H be the H-bond of which h is an occurrence. In addition, let l , where is the duration over which we wish to predict the stability of h (see Section 2), and let ml be the number of ticks k t, 1,2, ,ki iil , such that H is present in k qt . The measured stabil- ity y of h is the ratio ml. Figure 1 plots a (typical) histogram of the measured stability of all H-bond occur- rences in one protein trajectory. This histogram indicates that H-bond occurrences tend to be quite stable: over 25% have measured stability 1, about 50% have meas- ured stability higher than 0.8, and only 15% have meas- ured stability less than 0.3. We build s as a binary regression tree [14]. This well- studied machine learning approach has been one of the most successful in practice. Regression trees are often simple to interpret. Not only may this simplicity eventu- ally lead to pertinent insights to better understand H- bond stability; it also allows us to perform many experi- Figure 1. Histogram of the measured stability of H-bond occurrences in 1eia protein trajectory (the rightmost bar defines the fraction H-bond occurrences whose measured stability is exactly 1). ments, compare the generated trees, and analyze the rela- tive importance of the predictors. Furthermore, the method can work with both categorical and numerical predictors in a unified way, as shown in Section 4.1. Each non-leaf node N in a regression tree is a Boolean test, called a split. Each split on a numeric predictor p divides the predictor space into two half-spaces separated by a hyper-plane perpendicular to the coordi- nate axis representing p. Each arc outgoing from N corresponds to one of these half-spaces. So, each node N of the tree determines a region of which is ob- tained by intersecting all the half-spaces associated with the arcs connecting the root of the tree to N. We say that an H-bond occurrence falls into a node N if it is contained in this region. The predicted stability value stored at a leaf node L is the average of the measured stability values computed for all the H-bond occurrences in the training data table that fall into L. We expect this averaging, which is done over many pieces of trajectories, to approximate well the averaging defined in Equation (1). To avoid over-fitting the input data, only a relatively small subset of predictors (selected by the training algo- rithm, as described in Section 4 is eventually used in a regression tree. Once a regression tree has been generated, it is used as follows. Given an H-bond H in an arbitrary conforma- tion c of an arbitrary protein, the leaf node L of the tree into which H falls is identified by calculating the values of the necessary predictors for H in c. The predicted stability value stored at L is returned. (Note that by construction of the tree, any H-bond H falls into one and only one leaf node.) 4. Training Algorithm 4.1. Basic Tree-Construction Algorithm We construct a model as a binary regression tree using the CART (Classification and Regression Tree) method [14]. The tree is generated recursively in a top- down fashion, i.e. starting from the root. When a new node N is created, it is inserted as a leaf of the tree if a predefined recursion depth has been reached or if the number of H-bond occurrences (from the training data table) falling into N is smaller than a predefined threshold. Otherwise, N is added as an intermediate node, its split is computed, and its left and right children L and R are created. A split s is defined by a pair ,pr , where p is the split predictor and r is the split value. If p is a numerical predictor, then r is a threshold on p, and s pr . If p is a categorical predictor, then r is a subset of categories, and s pr . We define the score ,wpr of split , s pr at a node N as the reduction of variance in measured stability  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 158 that results from s. More formally: ,Var Var1 Var N LL LR wpr Y nn YY nn (2) where: N Y is the distribution of the measured stability of the H-bond occurrences in the training data table falling into N, L Y and R Yare the distributions of the measured sta- bility of the H-bond occurrences falling into L and R, respectively, when split s is applied, Var Y is the variance of distribution Y, n is the number of H-bond occurrences falling into N, L n is the number of H-bond occurrences falling into L when split s is applied. The algorithm chooses the split—both the predictor and the split value—that has the largest score. The com- putation of the split value for each predictor is done as follows (where we denote by N H the subset of H-bond occurrences in the training data table that fall into N): 1) For a numerical predictor, the values of this predic- tor in N H are sorted in ascending order. All midpoints between two distinct consecutive values are used as can- didate split values. The one with the largest split score is used as the split value. This value is clearly optimal. 2) For a categorical predictor, for every possible value v of this predictor in N H , we first compute the mean N Yv of the measured stability of all the H-bond oc- currences in N H where the predictor has value v. We then sort the possible values of the predictor into a list 12 ,,, K vv v ordered by N i Yv All the 1 K splits that divide this list into two contiguous sub-lists—e.g. 12 ,,, j vv v and 12 ,,, jj K vv v —are considered. The one with the best score is selected. Statement 8.16 in [14] proves that no other split can give a better score. Since the number of values of a numerical predictor in N H may often be large, it is worth noticing that an in- cremental procedure can compute split scores efficiently. Consider two consecutive candidate split values i s and 1i s in Step 1. Assume that we have computed the split score for i s and that we now want to compute the score for 1i s . We can easily identify the H-bond occurrences that are shifting from L to R. Then we can update VarLYand VarRYby only considering these occur- rences, in time linear in their number, as shown in Ap- pendix B. As a result we can compute the scores of all the candidate split values in time linear in the number of values of the considered numerical predictor in N H . For a categorical predictor, the computation of the scores of all the candidate split values is also linear in the number of categorical values. At each layer of the tree the total number of samples does not exceed the number of rows in the training table. So, building each layer takes linear time in the table size. Since we limit the depth of a regression tree by a rela- tively small constant (see Section 4.3), the complexity of the tree construction algorithm is dominated by the initial sorting of the table rows for each predictor. So, a tree is built in logOab a time, where a is the number of rows in the training data table and b is the number of predictors. This makes it possible to process tables with dozens of attributes and several hundred thousand rows using an off-the-shelf computer. 4.2. Violation of IID Property One important issue to deal with is the violation of the IID (independent, identically distributed) property in the training data table. The IID property would require that H-bond occurrences follow a certain fixed probability distribution, and that each row of a data table input to the learning algorithm is sampled according to this distribu- tion, independent of the other rows. The satisfaction of this property is critical for the trained model to pre- dict reliably the stability of H-bonds in new protein con- formations. However, it is likely to be violated, mainly because several H-bond occurrences in a data table cor- respond to the same H-bond. More specifically, two oc- currences of the same H-bond along the same trajectory are more likely to be similar (or even the same, in the case of time-independent predictors) along several di- mensions of the predictor space than two occur- rences of distinct H-bonds, especially if these bonds be- long to different proteins. This may result into correla- tions between predictor values and measured stability that are bond-specific and thus do not extend to other bonds. To illustrate this point, Figure 2 plots the histo- gram of the mean measured stability of all the distinct H- bonds occurring in one MD simulation trajectory. The figure shows that distinct H-bonds can have very differ- ent mean measured stability. It also shows that many H- bonds are unstable. These bonds contribute few bond occurrences in the training data table, which leads the histograms in Figures 1 and 2 to have “inverse” shapes. While Figure 1 indicates that most H-bond occurrences are quite stable, Figure 2 indicates that many H-bonds are unstable. To address this issue, we apply a two-step split calcu- lation procedure [17]. The training data table is divided at random into two tables 1 T and 2 T. The split predic- tor p and the split value r at a node N are com- puted separately, using one of these two tables: 1) The best split value * p r is computed for each pre-  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 159 Figure 2. Histogram of the mean measured stability of H- bonds in 1eia protein trajectory. dictor p using 1 T: * 1 arg max, pr rwpr, where 1,wpr denotes the score of split ,pr on 1 T. 2) The best split predictor * p is computed using 2 T with the best split values computed at the previous step: ** 2 arg max, pp pwpr, where * 2, p wpr denotes the score of split * , p pr on 2 T. 3) The selected split is ** , p pr . Assume that the best split value computed in the first step is obtained for some predictor p. If this best value results from a bond-specific correlation between p and measured stability in 1 T, then this correlation is unlikely to happen again in 2 T, since 1 T and 2 T have been separated at random. So, in the second step, predic- tor p will likely have a small score * 2,p wpr and so will not be selected as the split predictor. To reduce the risk that the same bond-specific correlation exists in both 1 T and 2 T, we divide the training data in such a way that all occurrences of the same H-bond end up in the same table. 4.3. Tree Pruning To prevent model overfitting, we limit the size of a re- gression tree by bounding its maximal depth by a rela- tively small constant (5 in most of our experiments). We also define a minimal number of H-bond occurrences that must fall into a node for this node to be split. How- ever, it is usually better to set these thresholds rather lib- erally and later prune the obtained tree using an adaptive algorithm, as described below. We initially set aside a fraction 3 T of the training data table that has no overlap with the subsets 1 T and 2 T used in Section 4.2. Once a tree has been constructed using 1 T and 2 T, pruning is an iterative process. At each step, one non-leaf node N whose split has mini- mal score (on 1 T) becomes a leaf node by removing the sub-tree rooted at N. This process continues until the pruned tree only contains the root node. It creates a se- quence of trees with decreasing numbers of nodes. We then estimate the prediction error of each tree as the mean square error of the predictions made by this tree on 3 T. The tree with the smallest error is selected. 3 T is selected so that it does not contain occurrences of H- bonds also represented in 1 T or 2 T. 5. Test Results In Section 5.1 we present the experimental setup with which the test results reported in Section 5.2 have been obtained. In Section 5.3 we analyze and discuss the con- tents of regression trees generated in our experiments. 5.1. Experimental Setup 5.1.1. MD Tra jectori e s In the experiments reported below, we used 6 MD simu- lation trajectories picked from different sources. We call these trajectories 1c90A, 1e85A, 1g90A_1 and 1g90A_2 from [18], and 1eia and complex from [19]. In all of them the time interval between two successive ticks is 1 ps. Table 1 indicates the protein simulated in each trajectory, its number of residues, the force field used by the simulator, and the duration of the trajectory. Each trajectory starts from a folded conformation resolved by X-ray crystallography. Trajectories obtained with different proteins allow us to test if a model trained with one protein can pre- dict H-bond stability in another protein. Similarly, tra- jectories generated with different force fields allow us to test a model trained with one force field can predict H-bond stability in trajectories generated with another force field. We did additional experiments with a larger set of trajectories, but the results were similar to those reported below. 5.1.2. Data Ta bl es From each of the 6 trajectories we derived a separate data table in which the rows represent the detected H- bond occurrences and the columns give the values of the predictors and H-bond measured stability. Table 2 lists the number of distinct H-bonds detected in each trajec- tory and the total number of H-bond occurrences ex- tracted. Since most H-bonds are not present at all ticks, the number of H-bond occurrences is smaller than the number of distinct H-bonds multiplied by the number of ticks. So, for example, the data table generated from tra- jectory 1e85A consists of 1,253,879 rows, 32 columns for predictors, and one column for measured stability. Note that complex was generated for a complex of two molecules. All H-bonds occurring in this complex are taken into account in the corresponding data table. The 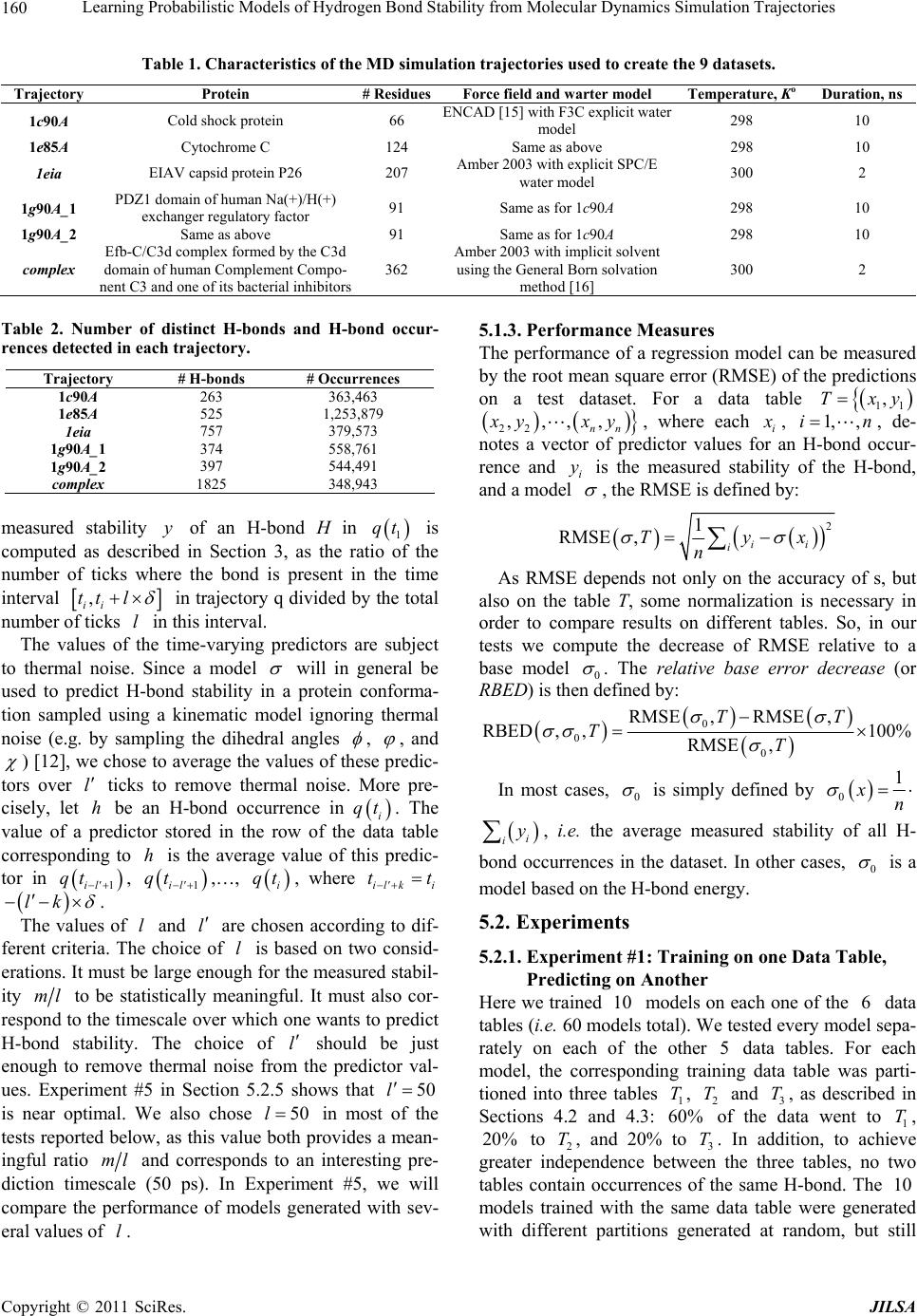 Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 160 Table 1. Characteristics of the MD simulation trajectories used to create the 9 datasets. Trajectory Protein # ResiduesForce field and warter model Temperature, Ko Duration, ns 1c90A Cold shock protein 66 ENCAD [15] with F3C explicit water model 298 10 1e85A Cytochrome C 124 Same as above 298 10 1eia EIAV capsid protein P26 207 Amber 2003 with explicit SPC/E water model 300 2 1g90A_1 PDZ1 domain of human Na(+)/H(+) exchanger regulatory factor 91 Same as for 1c90A 298 10 1g90A_2 Same as above 91 Same as for 1c90A 298 10 complex Efb-C/C3d complex formed by the C3d domain of human Complement Compo- nent C3 and one of its bacterial inhibitors 362 Amber 2003 with implicit solvent using the General Born solvation method [16] 300 2 Table 2. Number of distinct H-bonds and H-bond occur- rences detected in each trajectory. Trajectory # H-bonds # Occurrences 1c90A 263 363,463 1e85A 525 1,253,879 1eia 757 379,573 1g90A_1 374 558,761 1g90A_2 397 544,491 complex 1825 348,943 measured stability y of an H-bond H in 1 qt is computed as described in Section 3, as the ratio of the number of ticks where the bond is present in the time interval , ii tt l in trajectory q divided by the total number of ticks l in this interval. The values of the time-varying predictors are subject to thermal noise. Since a model will in general be used to predict H-bond stability in a protein conforma- tion sampled using a kinematic model ignoring thermal noise (e.g. by sampling the dihedral angles , , and ) [12], we chose to average the values of these predic- tors over l ticks to remove thermal noise. More pre- cisely, let h be an H-bond occurrence in q i t. The value of a predictor stored in the row of the data table corresponding to h is the average value of this predic- tor in 1il qt , 1il qt ,…, i qt , where il ki tt lk . The values of l and l are chosen according to dif- ferent criteria. The choice of l is based on two consid- erations. It must be large enough for the measured stabil- ity ml to be statistically meaningful. It must also cor- respond to the timescale over which one wants to predict H-bond stability. The choice of l should be just enough to remove thermal noise from the predictor val- ues. Experiment #5 in Section 5.2.5 shows that 50l is near optimal. We also chose 50l in most of the tests reported below, as this value both provides a mean- ingful ratio ml and corresponds to an interesting pre- diction timescale (50 ps). In Experiment #5, we will compare the performance of models generated with sev- eral values of l. 5.1.3. Pe r formance Measures The performance of a regression model can be measured by the root mean square error (RMSE) of the predictions on a test dataset. For a data table 11 ,Txy 22 ,,,, nn x yxy, where each i x , 1,,in, de- notes a vector of predictor values for an H-bond occur- rence and i y is the measured stability of the H-bond, and a model , the RMSE is defined by: 2 1 RMSE ,ii i Tyx n As RMSE depends not only on the accuracy of s, but also on the table T, some normalization is necessary in order to compare results on different tables. So, in our tests we compute the decrease of RMSE relative to a base model 0 . The relative base error decrease (or RBED) is then defined by: 0 0 0 RMSE,RMSE , RBED , ,100% RMSE , TT TT In most cases, 0 is simply defined by 0 1 xn i i y , i.e. the average measured stability of all H- bond occurrences in the dataset. In other cases, 0 is a model based on the H-bond energy. 5.2. Experiments 5.2.1. Experiment #1: Training on one Data Table, Predicting on Another Here we trained 10 models on each one of the 6 data tables (i.e. 60 models total). We tested every model sepa- rately on each of the other 5 data tables. For each model, the corresponding training data table was parti- tioned into three tables 1 T, 2 T and 3 T, as described in Sections 4.2 and 4.3: 60% of the data went to 1 T, 20% to 2 T, and 20% to 3 T. In addition, to achieve greater independence between the three tables, no two tables contain occurrences of the same H-bond. The 10 models trained with the same data table were generated with different partitions generated at random, but still  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 161 satisfying the previous ratios and condition. In all cases the maximal depth of a tree was set to 5. Table 3 gives the mean value of RBED for each pair of data tables and Table 4 gives estimated standard de- viation. More specifically, the chart of Figure 3 shows the distribution of the RBED values for the 10 models trained with 1c90A on each data table (so each of the 10 models contributes 6 points in the chart). These results show that, on average, a model trained with one trajec- tory predicts H-bond stability in another trajectory rea- sonably well, even if the two trajectories were generated using different energy functions. However, we note that the variance of the 10 RBED values for each test data table is rather large. We also note that the mean RBED values are generally lower for models tested on complex, while the mean RBED values for models trained on complex and tested on other tables (last column of Table 3) are comparable to other values. Recall that the trajectory complex was generated for a complex made of a protein and a ligand, while every other trajectory was generated for a single protein. So, it is likely that complex contains H-bonds in situations that did not occur in any of the other trajecto- ries. Figures 4 and 5 show trees trained with the data table 1c90A and complex. We will comment on gener- ated trees in Section 5.3. 5.2.2. Experiment #2: Training on Data from Multiple Trajectories Here, we trained models on data tables obtained by mix- ing subsets of 5 data tables and we tested these models on the remaining data table. For each combination of 5 data tables, we trained 10 models by mixing different fractions of the 5 data tables. For each model, the mixed data table was partitioned into three tables 1 T, 2 T and 3 T as in Experiment #1: 60% of the data went to 1 T, 20% to 2 T, and 20% to 3 T. Again, no two tables contain occurrences of the same H-bond. Furthermore, we trained 4 groups of models varying in the tree’s maximal depth (5 or 15) and in the fraction of H-bond occurrences taken from each data table (10% or 50%). So, in total, 240 models were generated in this experi- ment. Table 5 shows the mean RBED value for each com- bination of data tables and each group of models and Table 6 shows estimated standard deviation. In columns 3 through 8 we indicate the data table used for testing the models trained on a combination of the 5 other data ta- bles. Figure 6 shows the distribution of the RBED val- ues for the models built with the settings of in the first row of Table 5 (i.e. maximal depth of 5 and 10% from each data table). We note that the RBED values are significantly higher than in Experiment #1, meaning that models trained us- ing data from several trajectories are more accurate than models trained using data from a single trajectory. This is not surprising, since a training data table generated from several trajectories is likely to provide richer data Figure 3. Distribution RBED values for the 10 models gen- erated with 1c90A (Experiment #1). The horizontal line shows the average of all 50 RBED values. Table 3. Mean values of RBED for each pair of data tables (Experiment #1). Test\Train 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex 1c90A 37.89 42.87 11.72 37.04 38.70 35.44 1e85A 44.91 58.82 31.67 53.04 53.10 42.20 1eia 34.41 38.18 41.52 34.55 37.69 40.19 1g90A_1 40.06 44.83 27.75 41.89 47.52 34.36 1g90A_2 34.69 40.79 35.11 37.52 38.72 34.54 complex 28.41 34.75 34.14 28.46 32.81 39.00 Average 36.72 43.37 30.31 38.75 41.42 37.62 Table 4. Standard deviation values of RBED for each pair of data tables (Experiment #1). Test\Train 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex 1c90A 8.27 6.35 35.58 11.57 11.49 6.06 1e85A 14.64 3.99 28.99 5.68 8.29 8.48 1eia 5.85 1.85 3.46 5.86 3.55 1.93 1g90A_1 9.04 7.69 14.95 11.99 9.07 11.70 1g90A_2 12.00 4.87 11.94 10.97 8.36 3.57 complex 5.00 1.62 2.49 7.83 3.09 2.58  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 162 Figure 4. Regression tree trained with 1c90A (Experiment #1). Figure 5. Regression tree (only the top 3 layers are shown) trained with complex (Experiment #1). Table 5. Mean RBED values obtained in Experiment #2. Fraction of data Max tree depth 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex Average 0.1 5 46.92 59.37 42.60 50.93 45.29 37.90 47.17 0.5 5 47.07 59.59 43.15 50.69 45.45 38.08 47.34 0.1 15 47.24 59.03 43.35 51.42 45.65 38.07 47.46 0.5 15 46.87 59.04 43.46 51.38 45.89 38.38 47.50 Table 6. Standard deviation of RBED values obtained in Experiment #2. Fraction of data Max tree depth 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex 0.1 5 0.25 0.60 0.64 0.54 0.31 0.63 0.5 5 0.25 0.36 0.83 0.66 0.22 0.48 0.1 15 0.57 1.00 0.84 0.42 0.50 0.85 0.5 15 1.27 1.10 1.00 0.62 0.59 0.60  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 163 about H-bond stability than a table derived from a single trajectory. Furthermore, the variance of RBED values is now very small, meaning that the training process yields models that are stable in performance. Finally, like in Experiment #1, the RBED values are again lower for models tested on complex. All these results suggest that we should try to train models with a larger set of trajec- tories. We actually did some experiments using a few additional trajectories, but with no noticeable improve- ment. Most likely these trajectories did not contain enough H-bonds in situations that did not already occur in the trajectories of Table 1. Another observation is that both deeper trees and lar- ger data fractions tend to improve model accuracy, but the very small gain is not worth the additional model or computation complexity. Table 6 shows that standard deviation is higher for deeper trees that is an expected result of increasing model complexity. Figures 7 and 8 show two partial trees trained with combinations of all tables, except 1c90A (in Figure 7) and 1e85A (in Figure 8). Figure 6. Distribution RBED values for the models built with settings specified in the first row of Table 5. Figure 7. Top 3 layers of a tree trained with combination of all tables, except 1c90A (Experiment #2). The actual tree has 5 layers (55 nodes). Figure 8. Top 3 layers of a tree trained with combination of all tables, except 1e85A (Experiment #2). The actual tree has 5 complete layers (63 nodes).  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 164 5.2.3. Experiment #3: Comparison with FIRST-Energy Model Here, the models are the same as those generated in Ex- periment #2 in the first row of Table 5 (maximal depth of 5 and 10% from each data table). But we now com- pare them to a regression tree 0 built from the same training data using FIRST_energy as the only predictor (predictor #32 in Appendix C). FIRST_energy is the value of the function used in FIRST [10] to evaluate the energy of an H-bond occurrence; it is a slightly modified version of the Mayo energy [7]. We compute RBED values as defined in Section 5.1.4 where 0 is the sim- ple regression tree. Table 7 shows the mean RBED val- ues. Tests on all 6 data tables show that the more com- plex models are significantly more accurate that the model based on FIRST_energy only. Overall, these re- sults confirm that the stability of an H-bond occurrence depends not only on its energy, but also on other pa- rameters. See Section 5.3 for more comments. 5.2.4. Experiment #4: Identification of Least Stable H-Bonds Most H-bond occurrences tend to be stable. So, accu- rately identifying the weakest ones is important if one wishes to predict the possible deformation of a protein [12]. Here, we measure how well the models generated in Experiment #2 (again, in the first row of Table 5) identify the least stable H-bonds occurrences in the test data table. In each test table T, we first identify the subset S of the 10% least stable H-bond occurrences (i.e., the H-bond occurrences with the smallest measured stability). Using a regression tree trained with a combination of data from the 5 other tables, we then sort the H-bond occurrences in T in ascending order of predicted stability and we compute the fraction 0, 1w of S that is contained in the first 100 %u occurrences in this sorted list, for successive values of 0,1u. We call the function wu the identification curve of the least stable H-bonds for . Figure 9 plotsidentification curves for each of the 6 test tables. Each plot consists of three curves: the red curve is the ideal identification curve (the one that would be obtained with a model that perfectly predict the 10% least stable H-bonds), the blue curve is obtained with one (randomly picked) regression tree computed in Experi- ment #2, and the green curve is obtained by sorting H- bond occurrences in decreasing values of FIRST_en ergy. One can see that the models computed in Experiment #2 perform well in general. For models tested on data tables Table 7. Mean values of RBED computed in Experiment #3. 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex 26.36 27.95 5.65 22.63 19.63 19.42 other than complex, about 80% of the 10% H-bond oc- currences predicted as the least stable are actually among the 10% truly least stable. However, several curves show a rather long tail of poorly ranked unstable bonds. For example, the set of the 50% least stable bonds predicted by the model tested on 1eia still misses about 5% of the truly least stable bonds. Not surprisingly, the results for complex are much less satisfactory. The regression mod- els generated in Experiment #2 perform consistently bet- ter than the FIRST_energy-only models, but for 1eia the difference is small. 5.2.5. Experiment #5: Models for Different Averaging and Prediction Windows Here the testing setup is the same as for Experiment #2 (first row of Tabl e 5), but we let the numbers of ticks l and l vary. Recall from Section 5.1.b that l is the number of ticks over which bond stability is measured, while l is the number of ticks over which predictor values are averaged. First, we set l to 50 ticks (50 ps), and we built and tested models for predictor averaging windows of suc- cessive lengths l = 2, 5, 10, 20, 50, 100, 200, and 500 ticks. So, in total we built 400 models. Table 8 shows the mean RBED value for each test table and each value of l . Figure 10 shows the distribution of the RBED values for the models tested on 1c90A (10 models for each value of l ). An averaging window length of l = 50 ticks gives the best results. Shorter lengths fail to elimi- nate thermal noise in predictor values, but longer win- dows tend to smooth out important changes in predictor values. Next, we set l to 50 ticks (50 ps) and we built and tested models for prediction windows of successive lengths l = 10, 20, 50, 100, 200, and 500 ticks (so here we built 300 models). Table 9 shows the mean RBED value for each test table and each value of l. Figure 11 shows the distribution of the RBED values for the models tested on 1c90A. Again, a 50-tick predic- tion window gives the best results. With shorter windows measured stability is less reliable. But longer windows lead to making predictions too far beyond an observed Table 8. Mean RBED values for different lengths l' of the predictor averaging window (Experiment #5). 'l1c90A1e85A1eia 1g90A_1 1g90A_2 complex 228.15 39.55 22.71 36.39 24.72 7.18 538.71 48.65 31.08 43.75 38.05 22.03 1042.78 54.18 36.31 46.50 42.37 29.53 2045.58 57.43 40.48 49.40 44.66 34.78 5047.13 59.72 43.88 51.48 45.76 39.05 10046.58 59.44 43.81 50.96 45.52 38.54 20045.18 58.91 43.21 49.95 43.38 36.20 50041.40 56.25 41.81 46.94 37.99 30.69 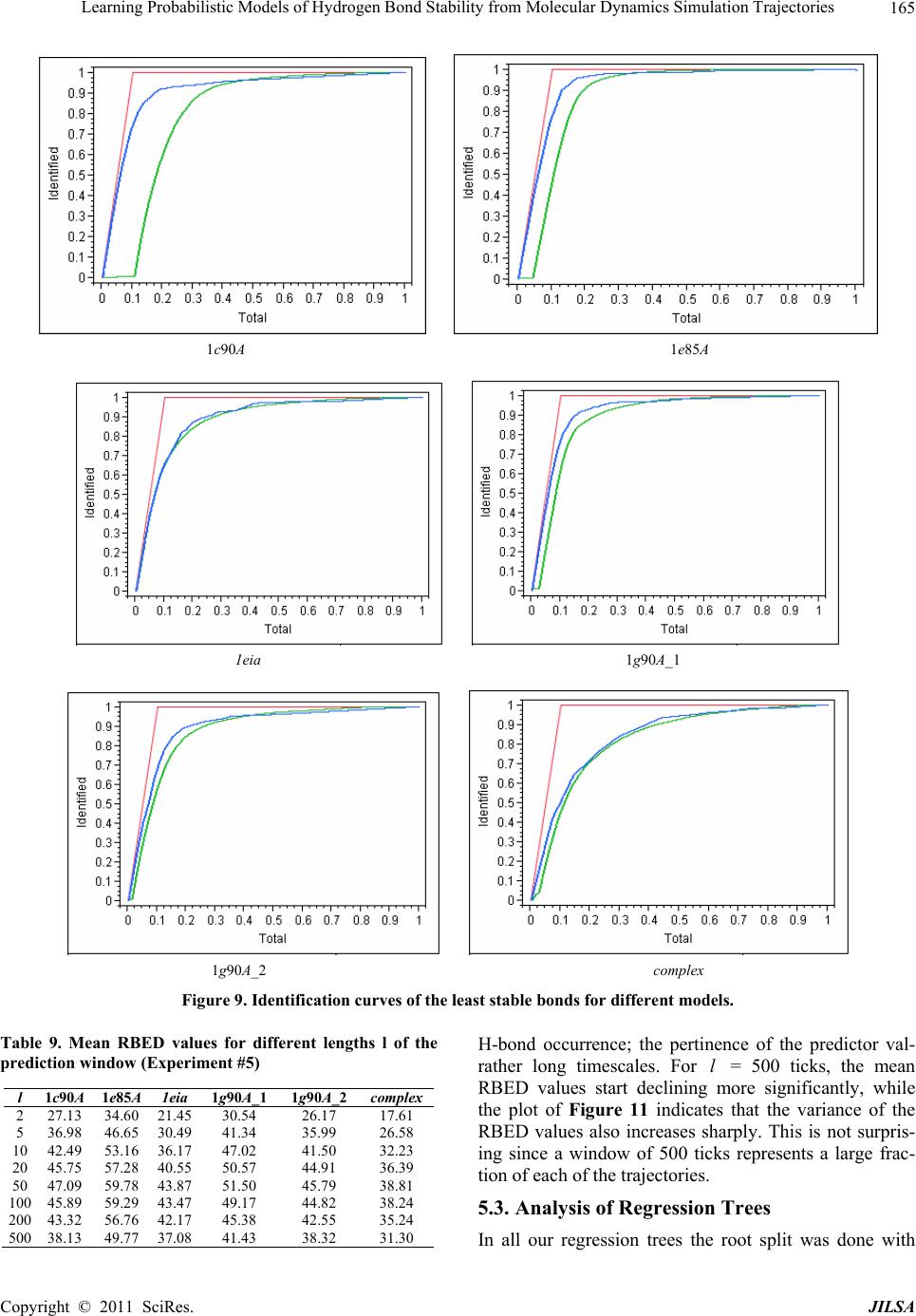 Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 165 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex Figure 9. Identification curves of the least stable bonds for different models. Table 9. Mean RBED values for different lengths l of the prediction window (Experiment #5) l 1c90A 1e85A 1eia 1g90A_1 1g90A_2 complex 2 27.13 34.60 21.45 30.54 26.17 17.61 5 36.98 46.65 30.49 41.34 35.99 26.58 10 42.49 53.16 36.17 47.02 41.50 32.23 20 45.75 57.28 40.55 50.57 44.91 36.39 50 47.09 59.78 43.87 51.50 45.79 38.81 100 45.89 59.29 43.47 49.17 44.82 38.24 200 43.32 56.76 42.17 45.38 42.55 35.24 500 38.13 49.77 37.08 41.43 38.32 31.30 H-bond occurrence; the pertinence of the predictor val- rather long timescales. For l = 500 ticks, the mean RBED values start declining more significantly, while the plot of Figure 11 indicates that the variance of the RBED values also increases sharply. This is not surpris- ing since a window of 500 ticks represents a large frac- tion of each of the trajectories. 5.3. Analysis of Regression Trees In all our regression trees the root split was done with  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 166 Figure 10. Distribution of RBED values for models tested on 1c90A for different lengths l’ of the predictor averag- ing window (Experiment #5). Figure 11. Distribution of RBED values for models tested on 1c90A for different lengths l of the prediction window (Experiment #5). predictor Dist_H_A (the distance between the H and ac- ceptor atoms), which therefore appear as the single most discriminative attribute to predict H-bond stability. The mean measured stability of the two children of the root node differs by a ratio ranging from 1.5 to 2 depending on the specific tree. The importance of the distance be- tween the H and the acceptor is consistent with previous findings. Levitt [8] found that most stable H-bonds have Dist_H_A less than 2.07Å. Jeffrey and Saenger [20] also suggested that Dist_H_A is a key attribute affecting H-bond stability, with a value less than 2.2Å for moder- ate to strong H-bonds. Consistent with these previous findings, the split values of the deepest Dist_H_A nodes in our re gression trees vary slightly around 2.1Å. This distance was observed in [8] to sometimes fluctuate by up to 3Å in stable H-bonds, due to high-frequency atomic vibration. This observation supports our decision to average predictor values over windows of l ticks, as it would be easy to incorrectly predict the stability of an H-bond from the value of Dist_H_A at a single tick. Predictor FIRST_energy, a modified Mayo potential [7] implemented in FIRST (a protein rigidity analysis soft- ware) [10], is often used in splits close to the root. This is not surprising since it is a function of several other per- tinent predictors: Dist_H_A, Angle_D_H_A, Angle_H_ A_AA, and Hybrid_state (hybridization state of the bond). Some other distance-based predictors (Dist_D_AA, Dist_ D_A, Dist_H_D), angle-based predictors and Ch_type predictor appear often in regression trees, but closer to the leaf nodes. They nevertheless play a significant role in predicting H-bond stability. For example, as shown in Figures 7 and 8, if Angle_H_A_AA is at least 105˚, an H- bond has very high stability (about 0.96); otherwise, the stability drops to 0.71. The preference for larger angle matches well with the well-known linearity of H-bonds [20,21]. Other predictors that are used in splits only occasion- ally have a less obvious role. A number of predictors (such as, Atom_type_A, Atom_type_AA, Resi_type_H, Rgd_type) never appeared in our trees. Either they have no or very small impact on H-bond stability, or they are highly correlated with other more discriminative predic- tors. In order to get a more quantitative measure of the rela- tive impact of the predictors on H-bond stability, let us define the importance of a predictor p in a regression tree by: p sN I pwsns where p N is the set of nodes where the split is made using p, ws is the score of the split s , and ns is the number of H-bond occurrences falling into the node where split s is made4. We trained 10 models on data tables combining 10% of each the 1c90A, 1e85A, 1eia, 1g90A_1, 1g90A_2 and complex data tables. Im- portance scores for each predictor were averaged over these models and then linearly scaled to adjust the score of the least important predictor (with non-zero average importance) equal to 1. The average importance of every predictor appearing in at least one model is shown in Figure 12. The figure confirms that distance-based and angle-based predictors, as well as FIRST_energy, are the most important. It also shows that a number of other pre- dictors—including Resi_name_H, Resi_name_A and Range (difference in residue numbers of donor and ac- ceptor)—have less, but still significant importance. Overall, we observe that predictors that describe the local environment of an H-bond occurrence play a rela- tively small role in predicting its stability. In particular, 4This measure is not perfect because some predictors are correlated. For instance, the value of FIRST_energy is correlated with other pre- dictors. A better, but more complicated, measure of predictor impor- tance uses ensembles of trees of a special form [17].  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 167 Figure 12. Predictor importance scores. we had expected that descriptors such as #29 (Num_hb_ spaceNbr ) and #30 (Num_hb_spaceRgdNbr), which count the number of other H-bonds located in the neighbor- hood of the analyzed H-bond, would have had more im- portance. However, this may reflect the fact that the MD simulation trajectories used in our tests are too short to contain enough information to infer the role of such pre- dictors. Indeed, while transitions between meta-stable states are rare in those trajectories, predictors describing local environments may have greater influence on the stability of H-bonds that must break for such transitions to happen. So, longer trajectories may eventually be needed to better model H-bond stability. 6. Conclusions and Future Work In this paper we have described machine learning meth- ods to train regression trees modeling H-bond stability in a protein. The training and test data are in the form of tables whose rows describe H-bond occurrences at suc- cessive times along Molecular Dynamics simulation tra- jectories and columns give the values of various predic- tors. Each node in a regression tree is a Boolean test on a predictor. Each row (H-bond occurrence) in a data table determines a path in the tree from the root to a leaf node. A predicted stability is associated with each leaf node. The generated trees are relatively small and easily under- standable. Trees can be built to predict H-bond stability over different time scales. Test results demonstrate that trained models can pre- dict H-bond stability quite well. In particular, we have shown that their performance is significantly better (roughly 20% better) than that of a model based on H- bond energy alone. We have also shown that they can accurately identify a large fraction of the least stable H- bonds in a given conformation. However, our results also suggest that better results could be obtained with a richer set of MD simulation trajectories. In particular, the tra- jectories used in our experiments might be too short to characterize the stability of H-bonds that break and form during a transition between meta-stable states. We believe that the training methods could be im- proved in several ways: To eliminate thermal noise, predictor values are aver- aged over time windows of 50 ticks, independent of the elapsed time between two ticks (see Section 5.2.5). It would be better to averaging predictor values before sub-sampling MD simulation trajectories (see Foot- note 2). This would result in a much shorter averaging window, hence it would greatly reduce the risk of fil- tering out changes in predictor values that are impor- tant for H-bond stability. Unfortunately, in our trajec- tories we only had access to the data after sub-sam- pling. More sophisticated learning techniques could be used. For example, instead of generating a single tree, we could generate an ensemble of trees, such as Gradient Boosting Trees [22] or Random Forests [23]. A re- gression tree could also be enriched by using splits on linear combinations of predictors and by fitting linear regression models at the leaves. We could use rigidity analysis methods such as those described in [12] to decompose a protein into rigid groups of atoms (based on distance constraints im- posed by covalent and hydrogen bonds present in the current conformation). This would allow us to apply Bayesian techniques to align the predicted stability of individual H-bonds in the same rigid group. By doing so, we could better predict the collective behavior of related H-bonds and avoid solitary incorrect predic- tions. Finally, the notion of stability itself could be refined, for example by distinguishing between the case where an H-bond frequently switches on and off during a prediction window and the case where it rarely switches. Overall, we believe that considerable progress can still be made in learning more accurate and robust models of H-bond stability. 7. Acknowledgements The authors thank Lydia Kavraki (Rice University), Vijay Pande (Stanford), Michael Levitt (Stanford) and Jerry Wang Tsai (University of the Pacific) for providing us MD simulation trajectories and for useful comments during our work. 8. References [1] E. N. Baker, “Hydrogen Bonding in Biological Macro- molecules,” International Tables for Crystallography,  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 168 Vol. F, No. 22, 2006, pp. 546-552. [2] A. R. Fersht and L. Serrano, “Principles in Protein Stabil- ity Derived from Protein Engineering Experiments,” Cur- rent Opinion in Structural Biology, Vol. 3, No. 1, 1993, pp. 75-83. doi:10.1016/0959-440X(93)90205-Y [3] D. Schell, J. Tsai, J. M. Scholtz and C. N. Pace, “Hydro- gen Bonding Increases Packing Density in the Protein In- terior,” Proteins: Structure, Function, and Bioinformatics, Vol. 63, No. 2, 2006, pp. 278-282. doi:10.1002/prot.20826 [4] B. Honing, “Protein Folding: From the Levinthal Paradox to Structure Prediction,” Journal of Molecular Biology, Vol. 293, No. 2, 1989, pp. 283-293. doi:10.1006/jmbi.1999.3006 [5] C. N. Pace, “Polar Group Burial Contributes More to Protein Stability than Nonpolar Group Burial,” Biochem- istry, Vol. 40, No. 2, 2001, pp. 310-313. doi:10.1021/bi001574j [6] Z. Bikadi, L. Demko and E. Hazai, “Functional and Structural Characterization of a Protein Based on Analy- sis of Its Hydrogen Bonding Network by Hydrogen Bonding Plot,” Archives of Biochemistry and Biophysics, Vol. 461, No. 2, 2007, pp. 225-234. doi:10.1016/j.abb.2007.02.020 [7] B. I. Dahiyat, D. B. Gordon and S. L. Mayo, “Automated Design of the Surface Positions of Protein Helices,” Pro- tein Science, Vol. 6, No. 6, 2007, pp. 1333-1337. doi:10.1002/pro.5560060622 [8] M. Levitt, “Molecular Dynamics of Hydrogen Bonds in Bovine Pancreatic Trypsin Unhibitor Protein,” Nature, Vol. 294, 1981, pp. 379-380. doi:10.1038/294379a0 [9] K. Morokuma, “Why do Molecules Interact? The Origin of Electron Donor-Acceptor Complexes, Hydrogen Bonding, and Proton Affinity,” Accounts of Chemical Re- search, Vol. 10, No. 8, 1997, pp. 294-300. doi:10.1021/ar50116a004 [10] A. J. Rader, B. M. Hespenhelde, L. A. Kuhn and M. F. Thorpe, “Protein Unfolding: Rigidity Lost,” Proceedings of the National Academy of Sciences, Vol. 99, No. 6, 2002, pp. 3540-3545. doi:10.1073/pnas.062492699 [11] M. A. Spackman, “A Simple Quantitative Model of Hy- drogen Bonding,” Journal of Chemical Physics, Vol. 85, No. 11, 1986, pp. 6587-6601. doi:10.1063/1.451441 [12] M. F. Thorpe, M. Lei, A. J. Rader, D. J. Jacobs and L. A. Kuhn, “Protein Flexibility and Dynamics Using Con- straint Theory,” Journal of Molecular Graphics and Modeling, Vol. 19, No. 1, 2001, pp. 60-69. doi:10.1016/S1093-3263(00)00122-4 [13] I. K. McDonald and J. M. Thornton, “Satisfying Hydro- gen Bonding Potential in Proteins,” Journal of Molecular Biology, Vol. 238, No. 5, 1994, pp. 777-793. doi:10.1006/jmbi.1994.1334 [14] L. Breiman, J. H. Friedman, R. A. Olshen and C. J. Stone, “Classification and Regression Trees,” CRC Press, Boca Raton, 1984. [15] M. Levitt, M. Hirshberg, R. Sharon and V. Daggett, “Po- tential Energy Function and Parameters for Simulations of the Molecular Dynamics of Proteins and Nucleic Acids in Solution,” Computer Physics Communications, Vol. 91, 1995, No. 1-3, pp. 215-231. doi:10.1016/0010-4655(95)00049-L [16] J. Srinivasan, M. Trevathan, P. Beroza and D. Case, “Ap- plication of a Pairwise Generalized Born Model to Pro- teins and Nucleic Acids: Inclusion of Salt Effects,” Theo- retical Chemistry Accounts, Vol. 101, No. 6, 1999, pp. 426-434. doi:10.1007/s002140050460 [17] E. Tuv, A. Borisov and K. Torkokola, “Best Subset Fea- ture Selection for Massive Mixed-Type Problems,” Lec- ture Notes in Computer Science, Springer, Vol. 4224, 2006, pp. 1048-1056. doi:10.1007/11875581_125 [18] H. Joo, X. Qu, R. Swanson, C. M. McCallum and J. Tsai, “Modeling the Dependency of Residue Packing upon Backbone Conformation Using Molecular Dynamics Simulation,” Computational Biology and Chemistry, Ac- cepted, 2010. [19] N. Haspel, D. Ricklin, B. Geisbrecht, J. D. Lambris and E. K. Lydia, “Electrostatic Contributions Drive the Interac- tion between Staphylococcus Aureus Protein Efb-C and Its Complement Target C3d,” Protein Science, Vol. 17, No. 11, 2008, pp. 1894-1906. doi:10.1110/ps.036624.108 [20] G. A. Jeffrey and W. Saenger, “Hydrogen Bonding in Biological Structures,” Springer-Verlag, 1991. [21] W. W. Clenland, P. A. Frey and J. A. Gerlt, “The Low Barrier Hydrogen Bond in Enzymatic Catalysis,” Journal of Biological Chemistry, Vol. 273, 1998, pp. 25529- 25532. doi:10.1074/jbc.273.40.25529 [22] J. H. Friedman, “Greedy Function Approximation: A Gradient Boosting Machine,” Annals of Statistics, Vol. 29, No. 5, 2000, pp. 1189-1232. doi:10.1214/aos/1013203451  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 169 Appendix A: H-bond Identification We use the geometric criteria proposed in [13] to identify H-bonds in a protein conformation. These criteria, shown in Figure A.1., specify conditions on distances and an- gles that must be satisfy by the atoms H (hydrogen), D (donor), A (acceptor), and AA (the atom covalently bonded to A) for the H-bond to be considered present. Figure A.1. Constraints on H-bond geometry. Appendix B: Computing the Split Score for a Numerical Predictor. Consider Step 1 (computation of the optimal split value of a numerical predictor) in Section 4.1. Let i s and 1i s be two consecutive candidate split values. Assume that we have computed the split score for i s and that we now want to compute the score for 1i s . As we mentioned in Section 4.1, we can easily find the H-bond occurrences that are shifting from the left child L of node N to its right child R. Assume for simplicity, all predictor values are different. Then only one bond oc- currence shifts. Let i y be measured stability for this occurrence. We keep sum of response values (SL, SR) and sum of square response values (QL, QR) for left and right node, and do the simple update: 1iii SLSL y ; 1iii SRSR y ; 2 1 iii QLQLy ; 2 1 iii QRQRy Having these sum updated we immediately calculate variance of the response in left and right child as mean of the squares minus the square of the mean 2 11 11 ii L QL SL Var Yii ; 2 11 11 ii R QR SR Var Yni ni . The response variance in the root node does not de- pend on the split point, so we can easily calculate split score now 1 11 ** iN LR ini WVarYVar YVarY nn . As a result we can calculate split score in a constant time. Appendix C: List of Predictors # Feature Name Feature Meaning Type Distance-related 1 Dist_H_D Distance between H and donor (covalent bond length) F 2 Dist_H_A Distance between H and acceptor (H-bond length) F 3 Dist_A_AA Distance between acceptor and the atom it covalently bonded to F 4 Dist_D_A Distance between donor and acceptor F 5 Dist_D_AA Distance between donor and AA F 6 Dist_H_AA Distance between H and AA F Angle-related 7 Ang_D_H_A Angle Donor-H-Acceptor F 8 Ang_H_A_AA Angle H-acceptor-the atom the acceptor covalently bonded to F 9 Ang_D_A_AA Angle donor-acceptor-the atom the acceptor covalently bonded to F 10 Ang_planar Angle between plane D-H-A and H-A-AA F Atom 11 Atom_type_D Donor atom type (e.g. O, N, S, C) C 12 Atom_type_A Acceptor atom type (e.g. N, O, S) C 13 Atom_type_AA AA atom type (e.g. P, C, S) C  Learning Probabilistic Models of Hydrogen Bond Stability from Molecular Dynamics Simulation Trajectories Copyright © 2011 SciRes. JILSA 170 Residue 14 Resi_name_H Donor residue name (3 letter code) C 15 Resi_name_A Acceptor residue name (3 letter code) C 16 Resi_type_H Donor residue type. Nonpolar (Ala, Val, Leu, Ile, Trp, Met, Pro), Polar_acidic (Asp, Glu), Polar_uncharged (Gly, Ser, Thr, Cys, Tyr, Asn, Gln), Polar_basic (Lys, Arg, His)C 17 Resi_type_A Acceptor residue type C 18 Resi_sch_size_H Donor residue side-chain size, i.e. number of atoms in the side-chain F 19 Resi_sch_size_A Acceptor residue side-chain size F Bond structure type 20 Sec_type Secondary structure of the H-bond. MA (H-atom and O-atom are in same helix, middle portion), MB (same strand, middle), EA (same helix, end), EB (same strand, end), AL (helix-loop), BL (helix-loop), DA (different helices), SL (same loop), DL (different loops). Don't have DB (different strands) because it's hard to know which strand pairs with which strand to form the sheet. C 21 Ch_type H and O are on mch or sch: MM (mch-mch), MS (mch-sch), SS (sch-sch) C 22 Rgd_type SR (H and A are in the same rigid body), DR (different rigid body) C 23 Range Difference in the residue numbers of donor and acceptor, i.e. abs(Residonor-Resiacceptor) F 24 Hybrid_state Hybridization state (sp2-sp2, sp2-sp3, sp3-sp2, sp3-sp3) C 25 Num_furcated_H Number of H-bonds share the H-atom as this H-bond F 26 Num_furcated_A Number of H-bonds share the acceptor as this H-bond F Environment 27 Num_potential_As Number of potential acceptors (N, O, or S) in 3Å of H (but not covalently bonded to it) besides the current acceptor F 28 Num_hb_seqNbr Number of sequence-neighboring H-bonds, i.e., number of H-bonds of residues ±2 of Residonor and Resiacceptor F 29 Num_hb_spaceNbr Number of space-neighboring H-bonds, i.e., number of H-bonds within 5Å of the mid-point of this H-bond F 30 Num_hb_spaceRgdNbr Number of space-neighboring H-bonds in the same rigid-body, i.e., number of Num_hb_spaceNbr in the same rigid-body as this H-bond (cross-rigid = –100)5 F 31 Surface Average surface percentage of the H atom and acceptor F Energy 32 FIRST_energy Modified Mayo potential implemented in FIRST [10] F 5Here, we first use the FIRST software [TLR + 01] to decompose the p rotein into rigid groups of atoms based on distance constraints im- p osed by covalent and hydrogen bonds present in the current confor m a- tion. Num_hb_spaceRgdNbr is the number of H- b onds located within 5Å of the mid-point of the analyzed H-bond in the same rigid compo- nent. |

