Applied Mathematics, 2011, 2, 953-958
doi:10.4236/am.2011.28131 Published Online August 2011 (http://www.SciRP.org/journal/am)
Application of He’s Variational Iteration Method and
Adomian Decomposition Method to Solution for the Fifth
Order Caudrey-Dodd-Gibbon (CDG) Equation
Mehdi Safari
Department of Mechanical Engineering, Aligoodarz Branch, Islamic Azad University, Aligoodarz, Iran
Received June 14, 2010; revised June 26, 2011; accepted July 4, 2011
Abstract
In this work we use the He’s variational iteration method and Adomian decomposition method to solution
N-soliton solutions for the fifth order Caudrey-Dodd-Gibbon (CDG) Equation.
Keywords: Variation Iteration Method, Adomian Decomposition Method, Caudrey-Dodd-Gibbon (CDG)
Equation
1. Introduction
The theory of solitary waves has attracted much interest
in recent years for treatment of PDEs describing nonlin-
ear and evolution concepts. Nonlinear phenomena appear
in many areas of scientific fields such as solid state
physics, plasma physics, fluid dynamics, mathematical
biology and chemical kinetics. The nonlinear problems
are characterized by dispersive effects, dissipative effects,
convection-advection, and diffusion process. A broad
class of analytical solutions methods, such as inverse
scattering method, Ba¨cklund transformation method,
Hirota’s bilinear scheme [1-6], Hereman’s method [7,8],
pseudo spectral method, Jacobi elliptic method,
Painleve´ analysis [9], and other methods, were used to
handle these problems. However, some of these analyti-
cal solutions methods are not easy to use because of the
tedious work that it requires. This paper is concerned
with the multiple-soliton solutions of the fifth order non-
linear Caudrey-Dodd-Gibbon (CDG) equation [10,11]
2
30 30 1800
txxxxxxxxx xxx
uuuu uuuu  (1)
with is a sufficiently often differentiable func-
tion. It is well-known that this equation is completely
integrable. This means that it has multiple-soliton solu-
tions. The CDG equation possesses the Painleve´ prop-
erty as proved by Weiss in [9]. A useful study is intro-
duced in [9] using the Painleve´ property and the
Ba¨cklund transformation in handling the CDG equation
and other equations as well. It was found in [9] that the
CDG Equation (1) has the Backlund transformation

,uxt
2
2
2lnu
x
u


 (2)
where satisfies the CDG equation, and
2
u
1
26
x
xx
x
u   (3)
and

22
2;4;
t
x
xx
x
0

 
 (4)
The last two equations can be expressed as the Lax pair
62 0
xxx xxx
u

 (5)

2
22
186 620
txxx x
uuuxx

  (6)
The objective of this work is to further complement
other studies related to the CDG equation. The tanh
method [12-17], and the tanh-coth method [18,19] will
be used to stress its power in the determination of single-
soliton solution and other travelling wave solutions. We
aim to use Adomian decomposition method and variation
iteratin method to solve this equation.
2. Basic Idea of He’s Variational Iteration
Method
To clarify the basic ideas of VIM, we consider the fol-

954 M. SAFARI
lowing differential equation:

LuNug t (7)
where is a linear operator, a nonlinear operator
and L

N
g
t an inhomogeneous term.
According to VIM, we can write down a correction
functional as follows:
  
10d
t
nnn n
ututLu Nu g


  

(8)
where

is a general Lagrangian multiplier which can
be identified optimally via the variational theory. The
subscript indicates the nth approximation and
is considered as a restricted variation
nn u

0
n
u


.
a. VIM Implement f or this Equa tion:
We first consider the application of VIM Caudrey-
Dodd-Gibbon(CDG) equ a tion:
2
30 30 1800
txxxxxxxxx xxx
uuuu uuuu  (9)
with the initial conditions of:
 
22
0,secuxth x

  (10)
To earn general Lagrangian multiplier ()

we put
coeficient of tor u
x
u equal zero.where prime indicates
a differential with respect to x and dot denotes a differen-
tial with respect to t. We earn

respect to . After
some calculations, we obtain the following stationary
conditions in Equations(10a) and (10b):
t

1
t 


0 (10a)

1   (10b)
Its correction variational functional in x and t can be
expressed, respectively, as follows:
 
  

5
15
0
2
2
32
3
,, ,
30,, 30,
,180,,d
t
nnnn
nn n
nnn
uxtuxtu xtu xt
x
uxt uxtuxt
xx
uxtuxt uxt
x x
 ,



 







 



(9)
We start with the initial approximation of


,0ux
given by Equation (4). Using the above iteration formu-
las (9), we can directly obtain the other components as
follows:






25
13
cosh+32 tsinh
,cosh
x
x
uxt x


 (11)
  
 




 

8
2
210
7
5
5
15 3
3
15 3
2
20 4
4
20 420 4
15 3
8
10 210 2
1
,(coshx
cosh x
+32sinhxtcoshx
+163840sinhxt coshx
614400sinhxt coshx
7372800t coshx
+ 2949120tcoshx+ 4423680t
+ 491520sinhxtcoshx
+512t coshx768tcosh
uxt μμ
μ
μμ μ
μμ μ
μμ μ
μμ
μμ μ
μμ μ
μμμ





6
xμ
(13)
and continue then we show the last result in Figure 1(a).
3. Basic Idea of Adomian Decomposition
Method
We begin with the equation


LuRuFugt 

(14)
where L is the operator of the highest-ordered derivatives
with respect to t and R is the remainder of the linear op-
erator. The nonlinear term is represented by


F
u. Thus
we get


Lug tR uFu 

(15)
The inverse 1
L

is assumed an integral operator given
by

1
0d
t
L

t (16)
The operating with the operator on both sides of
Equation (15) we have
1
L
 


1
0
uf LgtRuFu

  (17)
where 0
f
is the solution of homogeneous equation
0Lu  (18)
involving the constants of integration. The integration
constants involved in the solution of hom ogeneous Eq ua-
tion (18) are to be determined by the initial or boundary
condition according as the problem is initial-value prob-
lem or boundary-value problem.
The ADM assumes that the unknown function


,uxt

M. SAFARI
955
,
can be expressed by an infinite series of the form
 
0
,
n
n
uxtu xt


 (19)
and the nonlinear operator


F
u can be decomposed by
an infinite series of polynomials given by

0n n
F
u


A

(20)
where will be determined recurrently, and

,
n
uxt n
A
are the so-called polynomials of defined by
01
,,,
n
uu u
00
1d ,0,1,2,
!d
n
i
ni
n
n
AFun
n







 




 (21)
It is now well known in the literature that these poly-
nomials can be constructed for all classes of nonlinearity
according to algorithms set by Adomian [10,15] and re-
cently developed by an alternative approach in [8,9,
16,17].
b. ADM Implement for This Equation
We solve this equation
  
 



5
5
0
23
23
2
,,30
,30 ,,
180,, d
t
n+1n n
nn n
nn
uxtux ux
x x
ux uxux
xx
ux ux
x
,






 









 (22)
We solve with this way CDG equation and continue
 

7
13
32 sinh
,cosh
tx
uxt
x


 (23)
  


 
 
 
 
 

4
12 210 2
210
2
10 210 2
5
5
3
5
5
86
42
1
,128t(23040t cosh
cosh
57600 tcosh+34560 t
+1280 sinhtcosh
7680 sinhtcosh
+7680 sinhtcosh
+ 4cosh126cosh
+ 420cosh315cosh
uxt x
x
x
xx
xx
xx
xx
xx


 
 
 
 








(24)
 

 


 
 
 
 

7
22
3
4
12 210 2
10
2
10 210 2
5
5
3
5
5
86
4
32t sinh
,sech+ cosh
1
+128t(23040tcosh
cosh
57600t cosh+34560t
+1280sinhtcosh
7680 sinhtcosh
+7680 sinhtcosh
+4cosh 126cosh
+420cosh 315co
x
uxt= xx
x
x
x
xx
xx
xx
xx
x

 


 
 
 
 








2
sh x 

(25)
We sum in Equation (25) and earn the results ac-
cording to i
u
i1,1.5,2, 3


in Figures 1-4.
We compared 2-D figures of VIM and ADM for dif-
ferent values of

in Figure 5.
4. Conclusions
In this paper, He’s variational iteration method has been
successfully applied to find the solution CDG equations.
(a)
(b)
Figure 1. For the solitary wave solution with the first initial
conditions (4) of Equation (1), VIM result for


uxt, is,
respectively (b) and ADM(b),with μ = 1.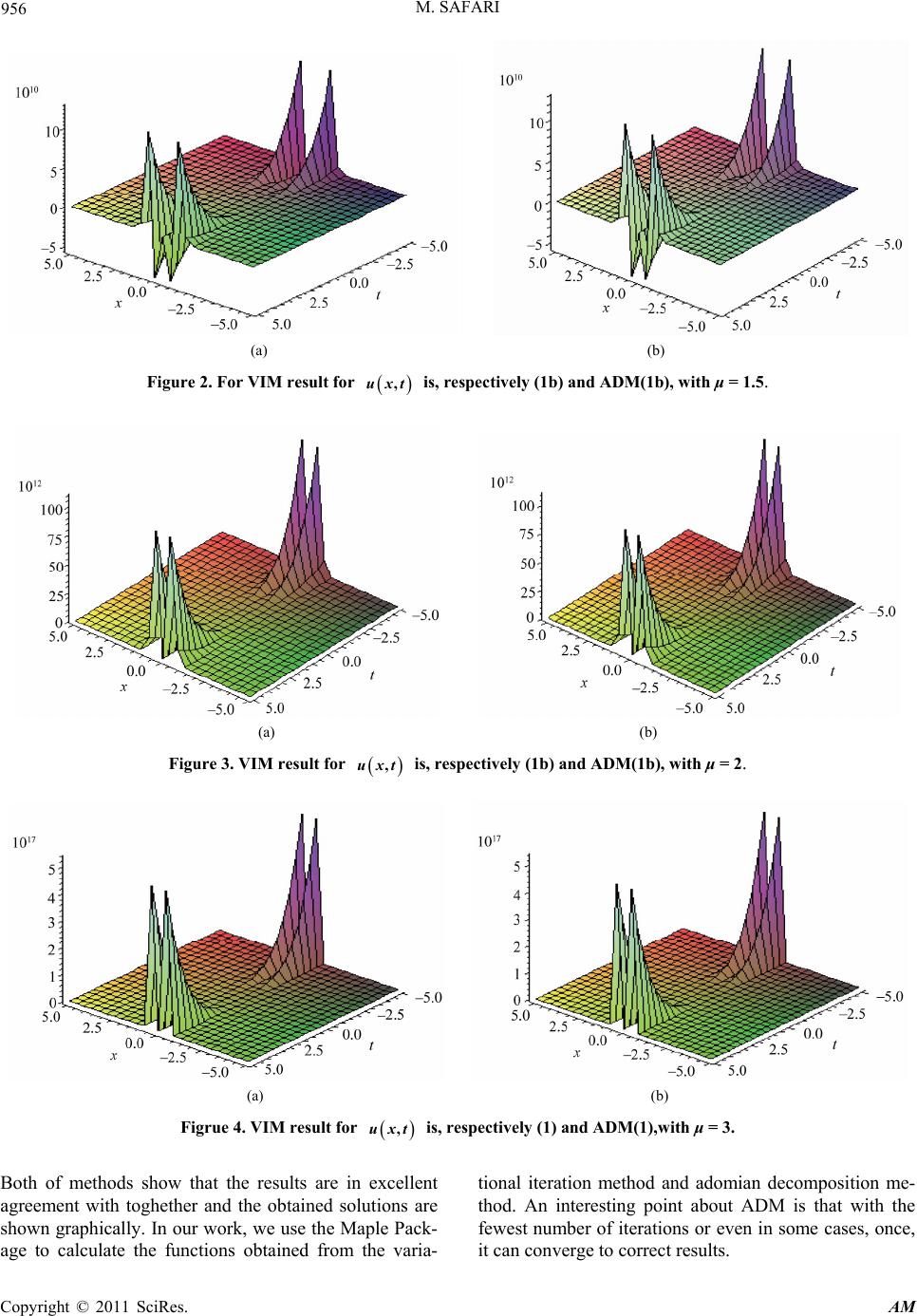

M. SAFARI
956
(a) (b)
Figure 2. For VIM result for


uxt, is, respectively (1b) and ADM(1b), with μ = 1.5.
(a) (b)
Figure 3. VIM result for


uxt, is, respectively (1b) and ADM(1b), with μ = 2.
(a) (b)
Figrue 4. VIM result for


uxt, is, respectively (1) and ADM(1),with μ = 3.
Both of methods show that the results are in excellent
agreement with toghether and the obtained solutions are
shown graphically. In our work, we use the Maple Pack-
age to calculate the functions obtained from the varia-
tional iteration method and adomian decomposition me-
thod. An interesting point about ADM is that with the
fewest number of iterations or even in some cases, once,
it can converge to correct results.

M. SAFARI
957
Figure 5. Comparison 2-D figures of VIM and ADM for different values of μ.
5. References
[1] R. Hirota, “The Direct Method in Soliton Theory,” Cam-
bridge University Press, Cambridge, 2004.
[2] R. Hirota, “Exact Solutions of the Korteweg-de Vries
Equation for Multiple Collisions of Solitons,” Physical
Review Letters, Vol. 27, No. 18, 1971, pp. 1192-1194.
doi:10.1103/PhysRevLett.27.1192
[3] R. Hirota, “Exact Solutions of the Modified Korteweg-de
Vries Equation for Multiple Collisions of Solitons,” Jour-
nal of the Physical Society of Japan, Vol. 33, No. 5, 1972,
pp. 1456-1458. doi:10.1143/JPSJ.33.1456
[4] R. Hirota, “Exact Solutions of the Sine-Gordon Equation
for Multiple Collisions of Solitons,” Journal of the Physi-
cal Society of Japan, Vol. 33, No. 5, 1972, pp. 1459-
1463. doi:10.1143/JPSJ.33.1459
[5] J. Hietarinta, “A Search for Bilinear Equations Passing
Hirota’s Three-Soliton Condition. I. KdV-Type Bilinear
Equations,” Journal of Mathematical Physics, Vol. 28,
No. 8, 1987, pp. 1732-1742. doi:10.1063/1.527815
[6] J. Hietarinta, “A Search for Bilinear Equations Passing
Hirota’s Three-Soliton Condition. II. mKdV-Type Bilin-
ear Equations,” Journal of Mathematical Physics, Vol. 28,
No. 9, 1987, pp. 2094-2101. doi:10.1063/1.527421
[7] W. Hereman and W. Zhaung, “Symbolic Software for
Soliton Theory,” Acta Applicandae Mathematicae, Phys-
ics Letters A, Vol. 76, 1980, pp. 95-96.
[8] W. Hereman and A. Nuseir, “Symbolic Methods to Con-
struct Exact Solutions of Nonlinear Partial Differential
Equations,” Mathematics and Computers in Simulation,
Vol. 43, 1997, pp. 13-27.
doi:10.1016/S0378-4754(96)00053-5

958 M. SAFARI
[9] J. Weiss, “On Classes of Integrable Systems and the
Painleve´ Property,” Journal of Mathematical Physics,
Vol. 25, No. 1, 1984, pp. 13-24. doi:10.1063/1.526009
[10] P. J. Caudrey, R. K. Dodd and J. D. Gibbon, “A New
Heirarchy of Korteweg-de Vries Equations,” Proceedings
of the Royal Society A, Vol. 351, 1976, pp. 407-422.
doi:10.1098/rspa.1976.0149
[11] R. K. Dodd and J. D. Gibbon, “The Prolongation Struc-
ture of a Higher Order Korteweg-de Vries Equations,”
Proceedings of the Royal Society A, Vol. 358, 1977, pp.
287-300.
[12] W. Malfliet, “The Tanh Method: A Tool for Solving Cer-
tain Classes of Nonlinear Evolution and Wave Equa-
tions,” Journal of Computational and Applied Mathe-
matics, Vol. 164-165, 2004, pp. 529-541.
doi:10.1016/S0377-0427(03)00645-9
[13] W. Malfliet, “Solitary Wave Solutions of Nonlinear
Wave Equations,” American Journal of Physics, Vol. 60,
No. 7, 1992, pp. 650-654. doi:10.1119/1.17120
[14] W. Malfliet and W. Hereman, “The Tanh Method: I. Ex-
act Solutions of Nonlinear Evolution and Wave Equa-
tions,” Physica Scripta, Vol. 54, 1996, pp. 563-568.
doi:10.1088/0031-8949/54/6/003
[15] W. Malfliet and W. Hereman, “The Tanh Method: II.
Perturbation Technique for Conservative Systems,” Phy-
sica Scripta, Vol. 54, 1996, pp. 569-575.
doi:10.1088/0031-8949/54/6/004
[16] A. M. Wazwaz, “The Tanh Method for Travelling Wave
Solutions of Nonlinear Equations,” Applied Mathematics
and Computation, Vol. 154, No. 3, 2004, pp. 713-723.
doi:10.1016/S0096-3003(03)00745-8
[17] A. M. Wazwaz, “Partial Differential Equations: Methods
and Applications,” Balkema Publishers, The Netherlands,
2002.
[18] A. M. Wazwaz, “The Extended Tanh Method for New
Solitons Solutions for Many Forms of the Fifth-Order
KdV Equations,” Applied Mathematics and Computation,
Vol. 184, No. 2, 2007, pp. 1002-1014.
doi:10.1016/j.amc.2006.07.002
[19] A. M. Wazwaz, “The Tanh-Coth Method for Solitons and
Kink Solutions for Nonlinear Parabolic Equations,” Ap-
plied Mathematics and Computation, Vol. 188, 2007, pp.
1467-1475. doi:10.1016/j.amc.2006.11.013