Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:65449,4 pages
10.4236/jamp.2016.44072
On the Implementation of Exponential B-Splines by Poisson Summation Formula
Sinuk Kang
Division of Mathematics and Informational Statistics, College of Natural Sciences, Wonkwang University, Iksan, South Korea



Received 8 January 2016; accepted 6 April 2016; published 13 April 2016
ABSTRACT
Polynomial splines have played an important role in image processing, medical imaging and wavelet theory. Exponential splines which are of more general concept have been recently investigated.We focus on cardinal exponential splines and develop a method to implement the exponential B-splines which form a Riesz basis of the space of cardinal exponential splines with finite energy.
Keywords:
Exponential Splines, B-Splines, Poisson Summation Formula

1. Introduction
During the past decade, there have been an increasing number of papers devoted to the use of polynomial splines in signal processing [1]-[4]. The interest in these techniques grew after it was shown that most classical spline- fitting problems on a uniform grid (interpolation, least squares, and smoothing splines) could be solved efficiently using recursive digital filtering techniques. These spline-based algorithms have been found to be quite advantageous for image processing and medical imaging, especially in the context of high-quality interpolation, where it has been demonstrated that they yield the best cost-quality tradeoff among all linear techniques [5]-[8]. Polynomial splines have also been shown to play a fundamental role in wavelet theory [9].
Although there are a few applications of polynomial splines in continuous-time signal processing, splines have apparently had less impact in this area. Part of the reason may be that (piecewise) polynomials do only appear marginally in basic systems theory. The most prominent functions in continuous-time signal-and-systems theory are the exponentials, which correspond to the modes of differential systems (analog filters and circuits). Having made this observation and motivated by the search for a unification between the continuous and discrete-time approaches to signal processing, Unser [10] deals with the task of extending the previously mentioned formulation to the enlarged class of exponential splines. These splines, as their name suggests, are made up of exponential segments that are connected together in a smooth fashion. They form a natural extension of the polynomial splines and have been characterized mathematically in relatively general terms [11] [12].
The kind of splines that are the most appropriate for signal processing are the cardinal ones, which are defined on a uniform grid. Mathematically, this corresponds to the simplest possible setup, which goes back to the pioneering work of Schoenberg on polynomial splines in 1946 [13]. In his early paper, it was shown that every cardinal polynomial spline has a unique and stable representation in terms of B-spline expansion. For cardinal exponential spline which is general concept of polynomial spline, Unser showed that if one excludes the pathological case of improperly spaced imaginary roots, then every cardinal exponential spline with suitable parameter has a unique and stable representation in terms of its B-spline expansion [10].
We present several methods to implement exponential B-splines. The paper is organized as follows. In Section 2, we begin with abrief introduction of exponential B-splines and notations needed throughout the paper. In Section 3, the methods will be presented. The conclusion is given in Section 4.
2. Preliminaries
2.1. Notations
Vectors are marked with an arrow and are used to represent N-tuples, i.e.,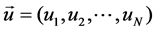 .
.
The Fourier transform of 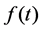 is denoted by
is denoted by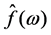 . For
. For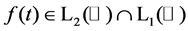 , it is given by
, it is given by
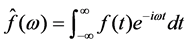 ;
;
otherwise, it is defined in the distributional sense. The Laplace transform of a causal (possibly exponentially increasing) function 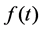 is defined as
is defined as
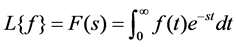 .
.
The one-sided power function is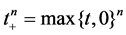 . The discrete signal
. The discrete signal ,
, 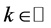 , is characterized by its z-transform
, is characterized by its z-transform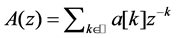 .
.
2.2. Exponential B-Splines (E-Splines)
Let us consider the generic differential operator of order N

with constant coefficients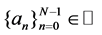 ,whose argument is some continuously varying time function
,whose argument is some continuously varying time function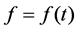 . Here,
. Here, 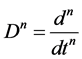 denotes the nth-order derivative, and
denotes the nth-order derivative, and  is the identity operator. The operator L is also characterized by the roots of its characteristic polynomial
is the identity operator. The operator L is also characterized by the roots of its characteristic polynomial
 .
.
We will therefore use the notation

Definition 2.1. An exponential spline with parameter 


where the sequence 

The cardinal exponential splines correspond to the specialized case where the knots are at the integer, i.e.,
We now introduce the exponential B-spline 
Theorem 2.2. [10] The set of functions 


Thus, if one excludes the pathological cases of improperly spaced imaginary roots first identified by Ron [14], this means that every cardinal exponential spline with parameter 

The E-splines are localized, that is compactly supported and shortest possible, versions of the Green functions that generate the exponential splines. The way in which such E-splines are constructed is especially easy to understand in the first-order case. One takes the green function 



Note that this first-order E-spline is supported in [0, 1), irrespective of


The higher order E-splines are obtained by successive convolution of lower order ones:
which is a process that is justified by the convolution relation of the corresponding Green functions.
3. Method to Implementing E-Splines
In general, E-splines with parameter 


From the Poisson summation formula of E-splines, we take a finite number of terms of the summation as an approximation of E-splines and find its truncation error bound as follows:
Theorem 3.1. Define (


and let
Proof. Since

we get
The proof completes by
4. Conclusion
In this paper, we present the method to implement exponential B-splines by its Poisson summation formula. We achieve an explicit formula on the truncation error bound for exponential B-spline. As the future work, one can generalize de Boor’s order recursion for the calculation of B-splines [15] into that for E-splines.
Acknowledgements
The author thanks Prof. Michael Unser for useful comments and suggestions during the preparation of the manuscript.
Cite this paper
Sinuk Kang, (2016) On the Implementation of Exponential B-Splines by Poisson Summation Formula. Journal of Applied Mathematics and Physics,04,637-640. doi: 10.4236/jamp.2016.44072
References
- 1. Unser, M. (2000) Sampling-50 Years after Shannon. Proc. IEEE, 88, 569-587. http://dx.doi.org/10.1109/5.843002
- 2. Unser, M. (1999) Splines: A Perfect Fit for Signal and Image Processing. IEEE Signal Process. Mag., 16, 22-38. http://dx.doi.org/10.1109/79.799930
- 3. Unser, M., Aldroubi, A. and Eden, M. (1993) B-Spline Signal Processing: Part 1—Theory. IEEE Trans. Signal Process., 41, 821-832. http://dx.doi.org/10.1109/78.193220
- 4. Unser, M., Aldroubi, A. and Eden, M. (1993) B-Spline Signal Processing: Part 2—Efficient Design and Applications. IEEE Trans. Signal Process., 41, 834-848. http://dx.doi.org/10.1109/78.193221
- 5. Meijering, E.H.W., Niessen, W.J. and Viergever, M.A. (2001) Quantitative Ecaluation of Convolution-Based Methods for Medical Image Interpolation. Med. Image Anal., 5, 111-126. http://dx.doi.org/10.1016/S1361-8415(00)00040-2
- 6. Thevenaz, P., Blu, T. and Unser, M. (2000) Interpolation Revisited. IEEE Trans. Med. Imag., 19, 739-758. http://dx.doi.org/10.1109/42.875199
- 7. Lehmann, T.M., Gonner, C. and Spitzer, K. (1999) Survey: Interpolation Methods in Medical Image Processing. IEEE Trans. Med. Imag., 18, 1049-1075. http://dx.doi.org/10.1109/42.816070
- 8. Lehmann, T.M., Gonner, C. and Spitzer, K. (2001) Addendum: B-Spline Interpolation in Medical Image Processing. IEEE Trans. Med. Imag., 20, 660-665. http://dx.doi.org/10.1109/42.932749
- 9. Unser, M. and Blu, T. (2003) Wavelet Theory Demystified. IEEE Trans. Signal Process., 51, 470-483. http://dx.doi.org/10.1109/TSP.2002.807000
- 10. Unser, M. and Blu, T. (2005) Cardinal Exponential Splines: Part 1—Theory and Filtering Algorithms. IEEE Trans. Signal Process., 53, 1425-1438. http://dx.doi.org/10.1109/TSP.2005.843700
- 11. Schumaker, L.L. (1981) Spline Functions: Basic Theory.
- 12. Dahmen, W. and Micchelli, C.A. (1987) On Theory and Application of Exponential Splines. In: Chui, C.K., Shumaker, L.L. and Utreras, F.I., Eds., Topics in Multivariate Approximation, Academic, New York, 37-46. http://dx.doi.org/10.1016/b978-0-12-174585-1.50008-7
- 13. Schoenberg, I.J. (1946) Contribution to the Problem of Ap-proximation of Equidistant Data by Analytic Functions. Quart. Appl. Math., 4, 45-99.
- 14. Ron, A. (1992) Linear Indepen-dence of the Translates of an Exponential Box Splines. Rocky Mountian J. Math., 22, 331-351. http://dx.doi.org/10.1216/rmjm/1181072814
- 15. De Boor, C. (1972) On Calculation with B-Splines. J. Approx. Theory, 6, 50-62. http://dx.doi.org/10.1016/0021-9045(72)90080-9







