Circuits and Systems, 2011, 2, 225-236
doi:10.4236/cs.2011.23032 Published Online July 2011 (http://www.SciRP.org/journal/cs)
Fast Signed-Digit Multi-operand Decimal Adders
Jeff Rebacz, Erdal Oruklu, Jafar Saniie
Department of Electrical and Computer Engineering, Illinois Institute of Technology, Chicago, USA
Received April 14, 2011; revised May 22, 2011; accepted May 29, 2011
Abstract
Decimal arithmetic is desirable for high precision requirements of many financial, industrial and scientific
applications. Furthermore, hardware support for decimal arithmetic has gained momentum with IEEE 754-
2008, which standardized decimal floating-point. This paper presents a new architecture for two operand and
multi-operand signed-digit decimal addition. Signed-digit architectures are advantageous because there are
no carry-propagate chains. The proposed signed-digit adder reduces the critical path delay by parallelizing
the correction stage inherent to decimal addition. For performance evaluation, we synthesize and compare
multiple unsigned and signed-digit multi-operand decimal adder architectures on 0.18 μm CMOS VLSI
technology. Synthesis results for 2, 4, 8, and 16 operands with 8 decimal digits provide critical data in de-
termining each adder’s performance and scalability.
Keywords: Computer Arithmetic, Decimal Arithmetic, Signed-Digit, Multi-operand Adder, BCD
1. Introduction
Translating a decimal fraction into a finite floating-point
representation is prone to losing precision as a result of
rounding errors. In almost all financial settings, decimal
arithmetic is desired to guarantee balances are calculated
correctly and lawfully. Some industrial and scientific
applications require high-precision decimal arithmetic as
well. Software packages have been available for most
programming languages so that decimal numbers could
be evaluated with decimal arithmetic to avoid error [1,2].
IBM recently departed from this software solution by
incorporating a decimal floating-point arithmetic unit in
the Power6 [3] and z10 processors [4]. A compelling
reason to do such is a report [5] showing that 55% of the
numbers stored in the databases of 51 major organiza-
tions are decimal. One study shows that for a set of five
benchmarks, a 1.3 to 12.8 speedup factor was obtained
by simulating a processor using virtual decimal arithme-
tic hardware against software routines [6]. Applications
that spend a large proportion of the time consuming
decimal calculation stand to benefit from hardware-based
decimal operations. Therefore, research into decimal
arithmetic has gained momentum. Decimal renditions of
binary carry-save [7,8] and carry-lookahead adders [9-11]
have been proposed. Decimal floating-point addition is
treated in [12-14]. New decimal multipliers [15-18] and
dividers [19-21] have also been proposed. In [17], new
decimal encodings improve the latency and area for de-
cimal partial product generation and reduction for multi-
plication. Similarly, in [22], a new redundant digit set is
used with special encodings called two-valued digits
(twits), resulting in a faster implementation of both addi-
tion and subtraction.
The main motivation behind this paper is to introduce
a new signed-digit architecture and objectively compare
it with signed and unsigned digit adders. Signed-digit
decimal adders have the benefit of carry-free addition
although a carry-propagate adder must be used to trans-
form the signed-digit sum into an unsigned sum. In the
next two sections, we will present the theory of decimal
encodings and signed-digit decimal numbers. In the sub-
sequent sections, brief descriptions of other adders are
given: the nonspeculative multi-operand adder [7], mixed
binary and BCD adder [23], reduced delay BCD adder
[10], dynamic decimal CLA [11], Svoboda adder [24],
speculative signed-digit adder [25], decimal carry-free
adder [26] and Redundant Binary Coded Decimal
(RBCD) adder [27,28]. Then, the proposed method for
signed-digit addition is discussed. A constant addition
technique will be applied to both the correction step in
signed-digit decimal addition and conversion to binary-
coded decimal (BCD). Multi-operand decimal addition
based on signed-digit addition will follow. Finally, the
synthesis results will be discussed.
The notation used throughout this paper is as follows:

226 J. REBACZ ET AL.
Variables are represented with a name and a subscript.
Take xi for example, x is the label and i indicates the digit
position. If no subscript is present, x will refer to the
word-wide variable across all digit positions. Numbers
enclosed in square brackets index the bit position. For
example, the second bit of sum at the first digit position
is sum0 [1].
2. Decimal Encodings
A discussion of decimal encodings is related to signed
digit arithmetic because the primary motivation for both
are similar, i.e. they are concerned with achieving better
performance by leveraging a more convenient number
representation for certain tasks. For example, Binary-
Coded Decimal (BCD) is the representation usually used
for decimal arithmetic. A BCD digit is the binary repre-
sentation of a decimal number [0,9] with 4 bits. BCD is
convenient for arithmetic, but is not optimal for storage
because 4 bits for 10 decimal digits wastes 6 encodings.
In IEEE 754-2008, storage of decimal floating-point
numbers is specified to be in Densely Packed Decimal
(DPD) form. In DPD, 3 decimal digits are encoded with
10 bits, which is much more efficient for storage.
For multiplication, several signed and unsigned repre-
sentations have been developed to increase performance.
In [15], it is shown how a signed-digit representation can
reduce the number of partial products in a decimal mul-
tiplier. These partial products can be efficiently accumu-
lated with a signed digit adder. In [15], the classic Svo-
boda adder [24] is used for partial product reduction, yet,
it will be shown that the proposed signed digit represen-
tation can yield better performance. On the other hand,
unsigned representations in multiplications are also
gaining track. In [17], traditional BCD or BCD-8421 is
recoded to BCD-5421, BCD-4221 and BCD-5211 to
efficiently generate partial products and reduce the par-
tial product reduction tree. One of the advantages of this
scheme is that multiplying by two from one encoding to
another may simply require a left shift. Another advan-
tage of the encoding is that it allows the reuse of a binary
radix-4 multiplier, sharing components to save area.
These new encodings also have advantages over BCD-
8421 in division, as demonstrated in [20].
Unsigned decimal adders usually work with BCD
numbers, but that is not required. The partial product
adder in [29] uses the Overloaded Decimal Representa-
tion (ODR), a redundant unsigned 4-bit encoding to store
and add intermediate partial products in a carry-save
format. In ODR, a decimal digit may take on values 0
through 15. In iterative operations, the decimal correc-
tion vector of +6, which is usually required for unsigned
decimal addition, is easier to detect and less costly to add.
The correction is only needed when a digit exceeds 16,
which is easily detected by inspecting the digit’s carry
out. When the carry out is detected, adding 6 occurs in
the next iteration, which shortens the critical path.
Another adder that leverages encodings other than
BCD is the mixed binary and BCD multi-operand adder.
The mixed binary and BCD multi-operand adder [23],
which will later be described in more detail and imple-
mented, uses both binary and BCD representations and
operations. Binary addition occurs for a column of BCD
digits. The binary result is then converted back to BCD
number. The process will repeat until there are two rows
of BCD numbers to be inputted into a 2-operand BCD
adder.
In signed-digit adders, there appear to be three popular
representations: the Svoboda code [24], the two’s com-
plement representation (used in the proposed method),
and the positive/negative component representation.
The Svoboda code uses 5-bits to represent numbers in
the set [−6,6]. A positive number xi is represented in
Svoboda code as 3
ii
X
x


31 3
i
while a negative number is
represented as i
X
x

 . For example, positive
decimal numbers 1 and 6 are represented in Svoboda
code as 110 = 00011 and 610 = 10010 respectively; nega-
tive decimal numbers −1 and −6 are represented in Svo-
boda code as −110 = 11100 and −610 = 01101 respectively.
There are two representations for zero (00000 and
11111). The Svoboda code allows for quick addition, but
the encoding may be difficult to work with or costly to
convert to and from.
The two’s complement representation for signed-digit
numbers is used in the RBCD adder [27,28] and in this
work. In RBCD, the digits are 4-bits wide and represent
numbers between 7 and −7 inclusive. RBCD’s number
range requires BCD numbers to go through a conversion
step (since 8 and 9 must be recoded). Our proposed adder
does not require a conversion step because we use 5-bits
to represent a signed decimal digit in the range of [−9,9].
This convenience is a key feature of our design.
In [25,26], a signed-digit is represented as the sum of
one positive 4-bit binary vector x+ and one negative 4-bit
binary vector x−. This positive/negative component rep-
resentation may store −2 in various ways: as x+ = 0001
and x− = 0011 or as x+ = 0010 and x− = 0100. With this
representation, numbers can be easily inverted by swap-
ping x+ and x−. Additionally, no conversion from BCD is
needed. However, there are 8 bits to a digit. Though this
fact does not automatically imply more area consumption,
the results do suggest it.
3. Decimal Signed-Digit Theory
The decimal signed-digit number system used here has

J. REBACZ ET AL.
227

all the properties and limitations set forth in [30]. A de-
cimal signed-digit set D is a special case of general
signed-digit sets when r = 10 (r is the radix or base).
3 13 5 2

,,1,0,D

   (1)
where α, β and r are related by (2).
1r

  (2)
Usually, symmetric signed-digit sets are used (α = β).
The signed-digit set is said to be redundant (any number
has multiple representations) if (3) holds.
1
2
r


 (3)
The decimal signed-digit set used in this work is [−9,9]
or −9 to 9 inclusive (r = 10, α = 9). With this decimal
signed-digit set, to add two decimal signed-digits xi and
yi, three quantities must be added together: the interme-
diate sum ui (i.e., interim sum), the carry ci (i.e., transfer)
which can take values in {−1,0,1}, and the correction
. The intermediate sum ui is xi + yi and ranges
from −18 to 18 inclusive with the digit set [−9,9]. The
carry ci is generated using a rule set such that −8 ≤ ui −
≤ 8 holds. Determining ci is done by comparing
ui to comparison constants. For the decimal signed-digit
set used, one comparison constant is in [−8,−1], the other
in [1,8], and are usually chosen to minimize hardware
complexity [31]. If −1 and 1 were the comparison con-
stants, then ci is −1 when ui is less than −1; ci is 1 when
ui is greater than 1; ci is zero when ui is −1, 0 or 1. The
correction is and adds to the intermediate sum
ui along with the previous digit’s carry to obtain the sum.
Note that i
is between −8 and 8 inclusive, so
an input carry of −1 or 1 will never cause a carry to
propagate to the next decimal digit. The above is ex-
pressed in (4)-(6).
10 i c
10 i
c
10 i c
10
i
uc
iii
uxy (4)
1
10
ii ii
s
ucc

 (5)
1if1
1if 1
0otherwise
i
ii
u
cu









(6)
An example demonstrates that the signed-digit tech-
nique still produces carries, but never propagates them.
In other words, a digit’s carry out is not a function of its
carry in. In this example, the operands are absent of neg-
ative digits only to facilitate demonstration. The com-
parison constants are −1 and 1. For the least significant
digit column, the intermediate sum is 8 + 8 = 16. Since
16 > 1, c0 = 1 is added to the next column and –10 is the
correction for the least significant column.
8
+ 3 4 7 8
3 16 9 9 16 u vector
−10 0 −10 −10 −10 −10 correction vector
1 0
11 1 1 c vector
1 −72−30 0 6 s vector
The general algorithm is as follows:
1) For each digit, add the two operands to get the in-
termediate sum, ui. The range for ui is −18 to 18 inclu-
sive.
2) If ui > 1, set correctioni = −10 and ci =1. If ui < −1,
set correctioni = 10 and ci = −1. In the example, the c
vector is shifted one digit position to the left so that addi-
tion occurs within each column.
3) Find the sum of the three vectors, u, correction and
c. This operation, as those before, will not propagate
carries because the method guarantees: −9 ≤ si ≤ 9.
4. Prior Work in Unsigned-Digit Decimal
Addition
4.1. Nonspeculative Multi-operand Adder
In [7], a nonspeculative multi-operand adder is presented
that can sum up to 16 operands. For each digit column,
M operands are added using a linear array of M-2 binary
carry-save adders. Carries outside the 4-bit range for
each digit are transferred to the next column, and saved
for later use. A 4-bit CPA finds a 5-bit uncorrected in-
termediate sum after the carry-save adders. This uncor-
rected intermediate sum together with the saved carries
are inputted into combinational logic to find the carry out
and a 4-bit correction vector. Another 4-bit CPA adds the
correction vector to the uncorrected intermediate sum to
yield the corrected intermediate sum. Finally, the carry-
outs and the corrected intermediate sum must be added
with a word-wide carry-propagation adder. In this work,
multioperand adders requiring decimal carry-propagation
addition use the dynamic decimal CLA [10] because it
gives the best delay and area usage.
4.2. Mixed Binary and BCD Multi-operand
Adder
This adder, proposed in [23], presents a scalable scheme
to realize any N-operand addition. First, for each digit
column, the N operands are added with N:2 reduction
and a CPA. Each column sum is then converted into a
decimal number with a network of binary to decimal
converter cells. Depending on the number of decimal
digits this conversion process produces, another stage of
binary addition and binary to decimal conversion may
ensue. When the digits of the converted decimal sum is
two, a fast decimal carry-propagation adder (in this work,

228 J. REBACZ ET AL.
the dynamic decimal CLA adder [10]) is used to obtain
the final decimal sum.
For 3 to 11 operands, only one stage is needed because
maximum number of digits for the sum of a digit column
with 11 operands is . Thus, 2-operand ad-
dition follows to calculate the final sum. For 12 to 111
operands, two stages are needed because the maximum
decimal sum for a digit column is 999, which is three
digits. Adding three digits across each digit column is
3-operand addition, and necessitates another stage.
2:9 1199
4.3. The Reduced Delay BCD Adder
In [10], the 2-operand decimal adder is composed of a
4-bit binary adder, an analyzer circuit, a carry network,
and another 4-bit binary adder to add the correction vec-
tor. Using the intermediate sum from the first 4-bit bi-
nary adder, the analyzer circuit finds the generate and
propagate signals for that digit. The signals from all dig-
its are passed to a Kogge-Stone carry network to find the
carries. Appropriately wiring the generated carries to the
final 4-bit adder will add the correction vector (0, 6, 1 or
7), which depends on the carry in and the carry out for
that digit.
4.4. The Dynamic Decimal Adder Using Carry
Lookahead
Like the reduced delay BCD adder, the dynamic decimal
CLA adder [11] is a 2-operand adder that finds digit
propagate and generate signals to be used in a carry loo-
kahead scheme for fast carry propagation. These signals
are generated per digit using combinational logic on the
bit propagate and generate signals of the two input BCD
digits. The sum bits are calculated as a function of the bit
generate and propagate signals, the carry in, and the car-
ry out. A speculation technique is used for the upper two
bits of each digit to speed up the addition time. With
dynamic logic, this technique can yield impressive speed.
5. Prior Work in Signed-Digit Decimal
Addition
5.1. Svoboda Adder
The Svoboda adder [24] was an early 2-operand design
that added digits from −6 to 6 inclusive. The Svoboda
adder uses the Svoboda code described in Section 2. This
code helps simplify decimal addition. On the other hand,
converting BCD operands into the Svoboda code and
back requires overhead.
BCD to Svoboda code conversion begins by trans-
forming each input BCD digit to a 5-bit vector corre-
sponding to the Svoboda code of that digit minus 4. Then,
a Svoboda adder adds 4 to the Svoboda code of all digits.
To convert back to BCD, a similar, but reversed proc-
ess is used. Constants are iteratively added with a
Svoboda adder until all the digits are between –4 and 5
inclusive. The worst case (i.e., the number of times the
loop is executed) depends on the number of digits. We
have implemented the Svoboda adder with the suggested
BCD to Svoboda code conversion scheme but without
the suggested Svoboda code to BCD conversion scheme.
Instead, we have replaced it with a faster carry-looka-
head conversion scheme. First, the Svoboda code is
transformed into a two’s complement number ranging
from −6 to 6 inclusive. Second, generate and propagate
signals are detected and used in a Kogge-Stone prefix
network to generate carries so that the proper corrections
can be applied to each digit. Also, the Svoboda adder
was originally designed with two stages of chained full
adders with end-around-carries. In the experiment, we
have replaced the full adder chains with prefix adders in
order to improve speed performance.
5.2. Speculative SD Adder
This architecture [25] is rather complex as it implements
a clever speculation technique that facilitates the addition
of input carries. The input operands are in the positive/
negative component representation. For example, −3
would be represented like this (let the two vectors be
expressed as (x+, x−):



25 3
0010,0101


 
Internally, the speculative SD adder uses compressors
to add the input operands. These compressors resemble
carry-save addition, but are modified to handle negative
bits. The two comparison constants are 1 and −1. A sign
detection unit is necessary to determine the carry out.
Once the carry out is found, a correction is added if nec-
essary.
No input conversion is necessary since BCD is within
the speculative SD’s digit set. The adder is speculative
because it prepares two pairs of sums, one which can be
easily incremented by one and another that can be easily
decremented by one. The last step of this adder involves
adding a correction vector according to the digit posi-
tion’s carry out.
For conversion back to BCD, the negative component
is subtracted from the positive component to yield a 5-bit,
two’s-complement number between −9 and 9. This num-
ber is inputted into an analyzer circuit to find generate
and propagate signals to use in a carry-lookahead scheme.
Once the carries are known, the right constants can be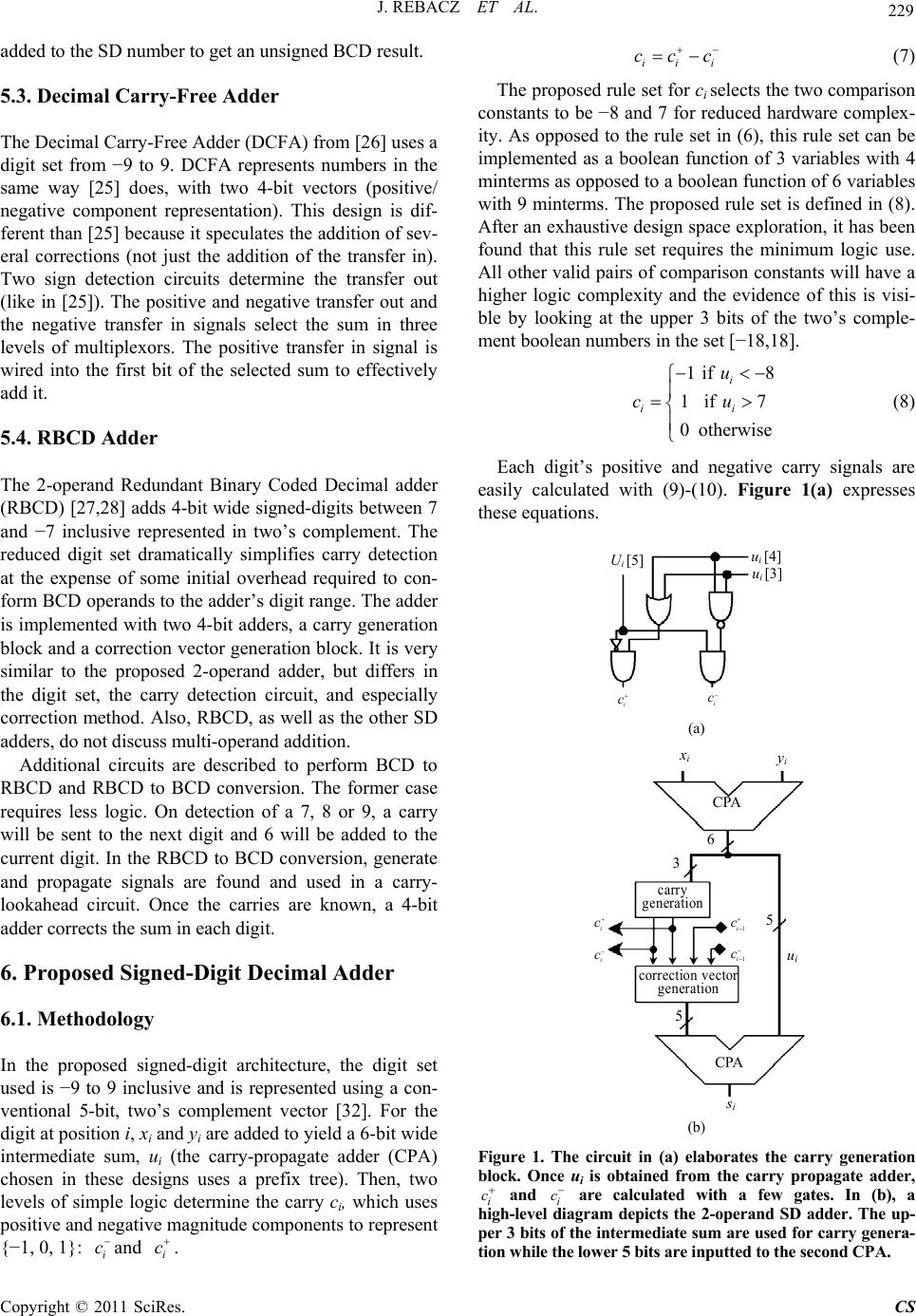

J. REBACZ ET AL.
229
added to the SD number to get an unsigned BCD result.
5.3. Decimal Carry-Free Adder
The Decimal Carry-Free Adder (DCFA) from [26] uses a
digit set from −9 to 9. DCFA represents numbers in the
same way [25] does, with two 4-bit vectors (positive/
negative component representation). This design is dif-
ferent than [25] because it speculates the addition of sev-
eral corrections (not just the addition of the transfer in).
Two sign detection circuits determine the transfer out
(like in [25]). The positive and negative transfer out and
the negative transfer in signals select the sum in three
levels of multiplexors. The positive transfer in signal is
wired into the first bit of the selected sum to effectively
add it.
5.4. RBCD Adder
The 2-operand Redundant Binary Coded Decimal adder
(RBCD) [27,28] adds 4-bit wide signed-digits between 7
and −7 inclusive represented in two’s complement. The
reduced digit set dramatically simplifies carry detection
at the expense of some initial overhead required to con-
form BCD operands to the adder’s digit range. The adder
is implemented with two 4-bit adders, a carry generation
block and a correction vector generation block. It is very
similar to the proposed 2-operand adder, but differs in
the digit set, the carry detection circuit, and especially
correction method. Also, RBCD, as well as the other SD
adders, do not discuss multi-operand addition.
Additional circuits are described to perform BCD to
RBCD and RBCD to BCD conversion. The former case
requires less logic. On detection of a 7, 8 or 9, a carry
will be sent to the next digit and 6 will be added to the
current digit. In the RBCD to BCD conversion, generate
and propagate signals are found and used in a carry-
lookahead circuit. Once the carries are known, a 4-bit
adder corrects the sum in each digit.
6. Proposed Signed-Digit Decimal Adder
6.1. Methodology
In the proposed signed-digit architecture, the digit set
used is −9 to 9 inclusive and is represented using a con-
ventional 5-bit, two’s complement vector [32]. For the
digit at position i, xi and yi are added to yield a 6-bit wide
intermediate sum, ui (the carry-propagate adder (CPA)
chosen in these designs uses a prefix tree). Then, two
levels of simple logic determine the carry ci, which uses
positive and negative magnitude components to represent
{−1, 0, 1}: and .
i
c
i
c
ii i
cc c



 (7)
The proposed rule set for ci selects the two comparison
constants to be −8 and 7 for reduced hardware complex-
ity. As opposed to the rule set in (6), this rule set can be
implemented as a boolean function of 3 variables with 4
minterms as opposed to a boolean function of 6 variables
with 9 minterms. The proposed rule set is defined in (8).
After an exhaustive design space exploration, it has been
found that this rule set requires the minimum logic use.
All other valid pairs of comparison constants will have a
higher logic complexity and the evidence of this is visi-
ble by looking at the upper 3 bits of the two’s comple-
ment boolean numbers in the set [−18,18].
1if8
1if7
0otherwise
i
ii
u
cu









(8)
Each digit’s positive and negative carry signals are
easily calculated with (9)-(10). Figure 1(a) expresses
these equations.
u
i
[4]
i
c

i
c
u
i
[3]
U
i
[5]
(a)
x
i
y
i
CPA
3
6
5
i
c

i
c

1i
c

1i
c

CPA
u
i
s
i
5
correction vecto
r
generation
carry
generation
(b)
Figure 1. The circuit in (a) elaborates the carry generation
block. Once ui is obtained from the carry propagate adder,
i
c

and i c

are calculated with a few gates. In (b), a
high-level diagram depicts the 2-operand SD adder. The up-
per 3 bits of the intermediate sum are used for carry genera-
tion while the lower 5 bits are inputted to the second CPA.

230 J. REBACZ ET AL.
 


543
ii ii
cu uu
 (9)
 


543
iii i
cuuu
  (10)
After ui and ci are found, the correction vector must be
found and added. The correction vector corresponds to
from (5). However, since the incoming carry
from the previous digit, ci-1, must eventually be added to
ui as well, it is convenient to think of the correction vec-
tor as 1. The correction vector (which is
simply the constant term to be added to ui) is tabulated
for every possible input combination in Table 1. Addi-
tion between ui and this correction vector will result in a
5-bit sum, si. Note that because of the rule set chosen, the
final sum for each digit will fall in [−9, 8] meaning that
the carry-out of the last CPA will always be 0.
10 i c
10 ii cc


The proposed SD decimal adder is shown in Figure 1
(b). The carry generation block of the proposed adder is
shown in Figure 1(a). It is apparent in this figure that
carries only propagate to the next digit. There is no ripple
effect since carry generation does not depend on the car-
ry in. This design is a necessary precursor to the im-
proved version in the next section.
6.2. Parallel Addition of the Correction Vector
The previously proposed adder’s correction generation
block and correction vector CPA can be replaced by a
parallel speculative structure to reduce delay since the
bits of ui are available before the carries. In these parallel
adders, speculative addition of the correction vector and
incoming carry take place in one or two stages of logi-
cally minimized constant addition. For one stage, the
addition of the constants −11, −10, −9, −1, 0, 1, 9, 10, 11
are precomputed and selected with ci and ci-1 in a multi-
plexor.
Table 1. Correction vector generation.
i
c i c 1i c
 1i
c
 Correction Vector
0 0 0 0 000002 (010)
0 0 0 1 111112 (–110)
0 0 1 0 000012 (110)
0 1 0 0 010102 (1010)
0 1 0 1 010012 (910)
0 1 1 0 010112 (1110)
1 0 0 0 101102 (–1010)
1 0 0 1 101012 (–1110)
1 0 1 0 101112 (–910)
For two stages, the addition of −10, 0 and 10 are pre-
computed and selected by ci in one stage; −1, 0 and 1 are
precomputed and selected by ci-1 in the other stage [32].
Depending on the method of constant addition chosen,
certain optimizations can be made. For example, the
proposed parallel adder uses a method of constant addi-
tion such that the addition of x + c, where x is the 5-bit
input and c is the constant, produces a vector f that indi-
cates which bits in x need to be inverted to obtain the
sum. So, five XOR gates are needed to invert r for any
constant addition. Hardware can be reduced by placing
the XOR gates after the multiplexor instead of having
groups of XOR gates for each constant before the multi-
plexor.
The terminology and concept of the constant addition
used were derived from the flag inversion cell (fic) se-
quences in [33]. The method in [33] describes adding
two variables and a constant. For this architecture, only
one variable and a constant are added. A detailed de-
scription of the constant addition mechanism can be
found in [33].
In the two-stage parallel adder, the intermediate sum,
ui, is fed to two constant addition blocks for adding and
subtracting 10. A 3-to-1 multiplexer will select f for
adding −10, 0 or 10 according to the selects: i
c

and
i
c

. The multiplexer’s output is XORed with ui to invert
the flagged bits. This inversion yields .
10
ii
uc
The remaining step is to add the incoming carry. Two
more constant addition blocks are used to add or subtract
1 from i
u10
i
c

. Another 3-to-1 multiplexer is used
with XOR gates after it to invert another flagged set of
bits and yield the sum. Breaking the addition up into two
stages seems to sacrifice speed. However, the two levels
involve a very small amount of logic. Both circuits (one-
stage and two-stage implementations) have a better area-
delay product with parallel constant addition than with-
out.
The one-stage parallel adder is shown in Figure 2.
This design takes advantage of the fact that ui is calcu-
lated before any of the carries. In fact, the correction
vector speculative addition starts as soon as ui[0] arrives.
Therefore, it can be seen that this type of speculation can
improve performance. Most other decimal signed-digit
adders do not speculate the constant addition.
7. SD and BCD Conversion
Any SD number can be converted to BCD, and vice-
versa [30]. The proposed SD adders must extend an un-
signed BCD number by one bit for BCD to SD conver-
sion. On the other hand, a carry-propagation operation
must be performed for SD to BCD conversion. A Kogge-
Stone prefix network is used to accelerate the carry-
propagation. The propagate signal pi is set when the SD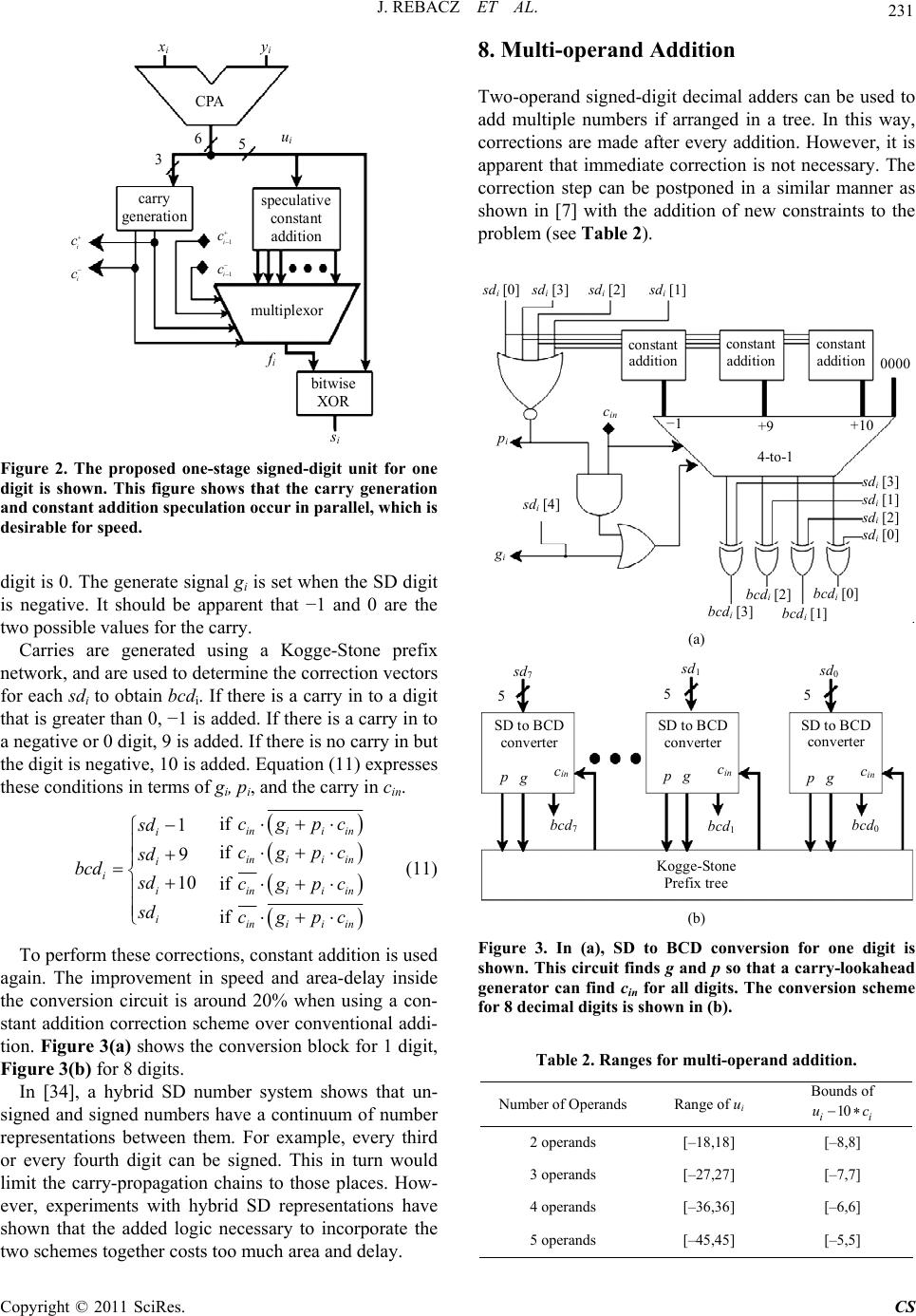

J. REBACZ ET AL.
231
carry
generation
x
i
y
i
CP
A
u
i
f
i
s
i
speculative
constant
addition
multi ple xo
r
bitwise
XOR
3
6 5
i
c
i
c
1i
c

1i
c

Figure 2. The proposed one-stage signed-digit unit for one
digit is shown. This figure shows that the carry generation
and constant addition speculation occur in paralle l, which is
desirable for speed.
digit is 0. The generate signal gi is set when the SD digit
is negative. It should be apparent that −1 and 0 are the
two possible values for the carry.
Carries are generated using a Kogge-Stone prefix
network, and are used to determine the correction vectors
for each sdi to obtain bcdi. If there is a carry in to a digit
that is greater than 0, −1 is added. If there is a carry in to
a negative or 0 digit, 9 is added. If there is no carry in but
the digit is negative, 10 is added. Equation (11) expresses
these conditions in terms of gi, pi, and the carry in cin.




if
1
if
9
10 if
if
inii in
i
inii in
i
i
iinii in
iinii in
cgpc
sd
cgpc
sd
bcd sd cgpc
sd cgpc










(11)
To perform these corrections, constant addition is used
again. The improvement in speed and area-delay inside
the conversion circuit is around 20% when using a con-
stant addition correction scheme over conventional addi-
tion. Figure 3(a) shows the conversion block for 1 digit,
Figure 3(b) for 8 digits.
In [34], a hybrid SD number system shows that un-
signed and signed numbers have a continuum of number
representations between them. For example, every third
or every fourth digit can be signed. This in turn would
limit the carry-propagation chains to those places. How-
ever, experiments with hybrid SD representations have
shown that the added logic necessary to incorporate the
two schemes together costs too much area and delay.
8. Multi-operand Addition
Two-operand signed-digit decimal adders can be used to
add multiple numbers if arranged in a tree. In this way,
corrections are made after every addition. However, it is
apparent that immediate correction is not necessary. The
correction step can be postponed in a similar manner as
shown in [7] with the addition of new constraints to the
problem (see Table 2).
sd
i
[0]
constant
addi t i on
sd
i
[3]sd
i
[2]sd
i
[1]
sd
i
[4]
constant
addition
co n stant
addition 0000
sd
i
[1]
sd
i
[3]
sd
i
[2]
sd
i
[0]
+10 +9
−1
4-to-1
bcd
i
[1]
bcd
i
[2]
bcd
i
[3]
bcd
i
[0]
p
i
c
in
g
i
(a)
sd
7
sd
1
sd
0
555
SD to BCD
converter
pgc
in
bcd
7
pg c
in
bcd
1
SD to BCD
converter
SD to BCD
converter
p gc
in
bcd
0
Kogge-Stone
Prefix tree
(b)
Figure 3. In (a), SD to BCD conversion for one digit is
shown. This circuit finds g and p so that a carry-lookahead
generator can find cin for all digits. The conversion scheme
for 8 decimal digits is shown in (b).
Table 2. Ranges for multi-operand addition.
Number of Operands Range of ui Bounds of
10
ii
uc


2 operands [–18,18] [–8,8]
3 operands [–27,27] [–7,7]
4 operands [–36,36] [–6,6]
5 operands [–45,45] [–5,5]

J. REBACZ ET AL.
232
c
7
n
The operations for n-operand addition for a digit in the
ith position can be summarized in (12)-(14) (ai,n repre-
sents the nth input for the ith digit position). These show
that an intermediate sum can be calculated from multiple
operands and a similar correction procedure can be used
to obtain the sum. Equation (14) must be satisfied for a ci
in order for carry-free decimal signed-digit addition to
work. For example, for three operand addition,
–7≥ i ≥ 7, for all possible ui in [−27,27], a ci
value can be found that makes true.
Note that (14) finds the maximum bounds, but tighter
bounds are possible so long as the bounds can represent
all decimal digits.
10
i
u
710
ii
uc 
,1 ,2,ii ii
ua aa (12)
1
10
ii ii
s
ucc

 (13)

:1010 10
iii
cnuc 

n (14)
with the maximally redundant digit set of [−9,9], 6 or
more operands cannot be added without an intermediate
correction since adding 5 carries restricts to
[−4, 4]. This condition cannot hold for such ui as −5, 5, 15.
10
ii
uc
Therefore, only 2, 3, 4 and 5-operand signed-digit ad-
ders are possible with the present scheme (see Figure 4).
Furthermore, only the 2-operand adder can make use of
the parallel addition technique; delay cannot be improved
since the greater number of parallel additions increases
the multiplexer size and the load.
CPA
correction vector
generation
c
i
c
i−1
3 : 2 reduction
carry
generation
u
i
CPA
(3, 4 or 5) : 2 reduction
Figure 4. The proposed signed-digit multi-operand addition
unit for one digit is shown. This scheme is limited for addi-
tion of 3, 4 or 5 operands.
The combinational logic for carry generation becomes
more constrained and more complex as n increases. For
2-operand addition, there is a lot of flexibility in choos-
ing the rule set as evidenced by the logic minimization
obtained in (8). For 5 operands, fewer rule sets are
available to choose from. Since adding 5 SD numbers
may result in 45 or −45 (maximum carry in of 4 or −4),
the rule set must ensure that . The
2-operand correction logic requires the 3 upper bits from
ui whereas the 5-operand correction logic requires all bits
from ui and many more minterms.
510
ii
uc5
For multi-operand addition requiring multiple modules
(i.e. n > 5), combining reduction where possible can
yield better performance [35]. The lower part of the SD
adder that reduces and adds ui, ci−1 and can be
combined with the earlier part of the next level’s SD
adder that reduces and adds n operands. The operation
for these parts is addition, so the property of associativity
can be exploited.
10 i c
As an example of multi-operand addition as well as
this optimization technique, a 16-operand adder is shown
in Figure 5(a). Three 5-operand adders add the first 15
input operands. The 16th input operand is added on the
second level with the three sums from the first level us-
ing a 4-operand adder. The circuit can be improved by
considering the three parallel 5-operand adders together,
and summing their internal ui, c
i-1, and terms
together instead of separately. Basically, instead of per-
forming three separate 3:2 reductions followed by a CPA
for each 5-operand adder, one large 9:2 reduction fol-
lowed by a CPA is performed. Adding the 16th input at
this stage only involves growing the reduction circuit to
10:2. Furthermore, only one CPA is needed to produce ui
for the 4-operand circuit instead of four (one at the end
of each 5-operand adder and one near the beginning of
the 4-operand adder). This optimized 16-operand adder
is shown in Figure 5(b). The reduction circuit should be
organized to reduce the terms that become available first.
First, the intermediate sums and leftover operands should
be reduced. When the carries become available, their
reduction should be merged with the intermediate sums.
Likewise, reduction of the correction vector should be
merged when it becomes available.
10 i c
9. Results
All designs were written in Verilog HDL. Synthesis re-
sults for area and timing were obtained from Synopsys
Design Compiler using MOSIS TSMC 0.18μm standard
cell technology. Each design was compiled as an 8-digit
(decimal) adder. Several of the designs are 2-operand
only, but are arranged in a parallel tree to obtain multi-
operand addition.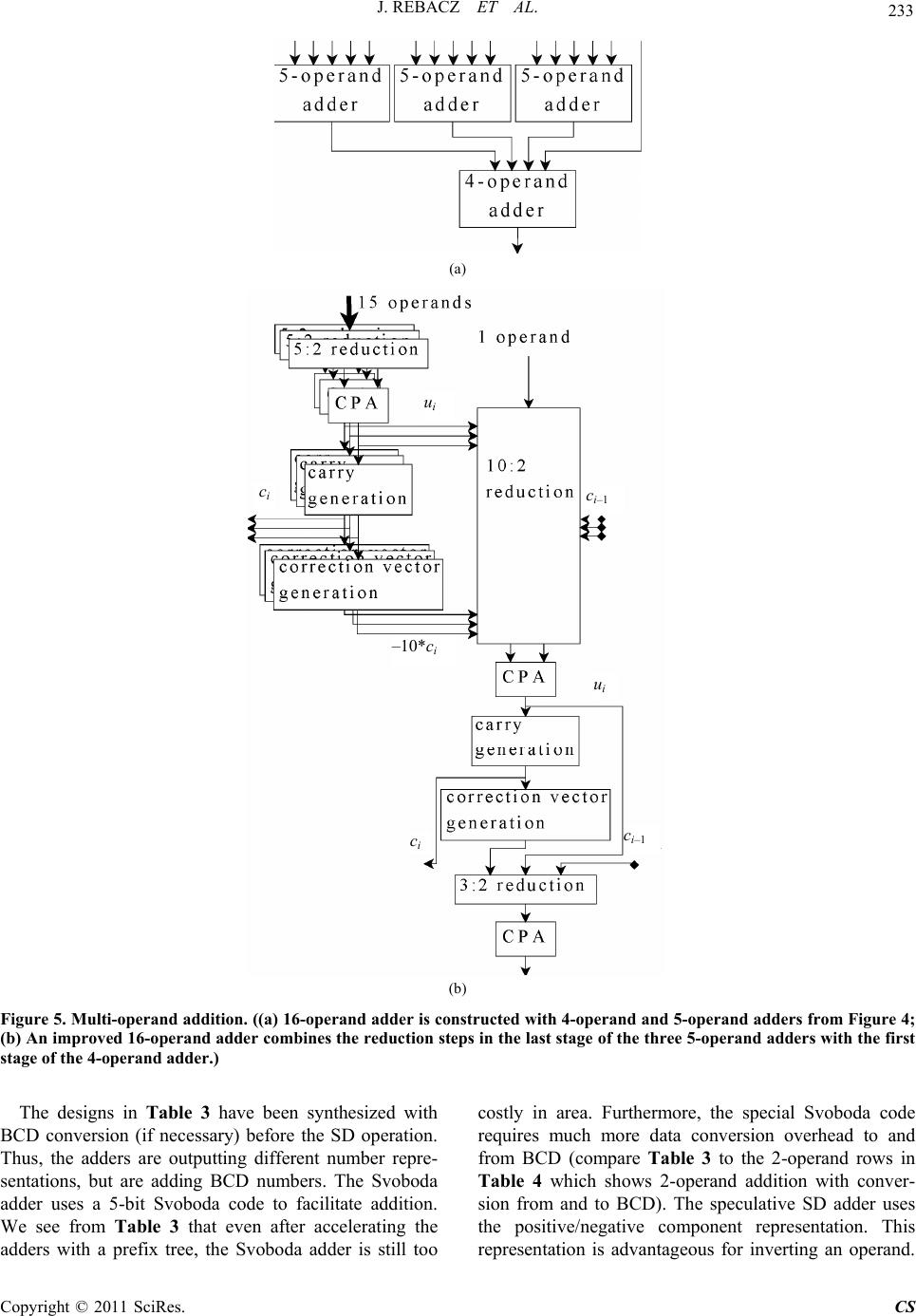

J. REBACZ ET AL.
233
(a)
ui
ci ci–1
–
10*ci
ui
ci–1
ci
(b)
Figure 5. Multi-operand addition. ((a) 16-operand adder is constructed with 4-operand and 5-operand adders from Figure 4;
(b) An improved 16-operand adder combines the reduction steps in the last stage of the three 5-operand adders with the first
stage of the 4-operand adder.)
The designs in Table 3 have been synthesized with
BCD conversion (if necessary) before the SD operation.
Thus, the adders are outputting different number repre-
sentations, but are adding BCD numbers. The Svoboda
adder uses a 5-bit Svoboda code to facilitate addition.
We see from Table 3 that even after accelerating the
adders with a prefix tree, the Svoboda adder is still too
costly in area. Furthermore, the special Svoboda code
requires much more data conversion overhead to and
from BCD (compare Table 3 to the 2-operand rows in
Table 4 which shows 2-operand addition with conver-
sion from and to BCD). The speculative SD adder uses
the positive/negative component representation. This
representation is advantageous for inverting an operand.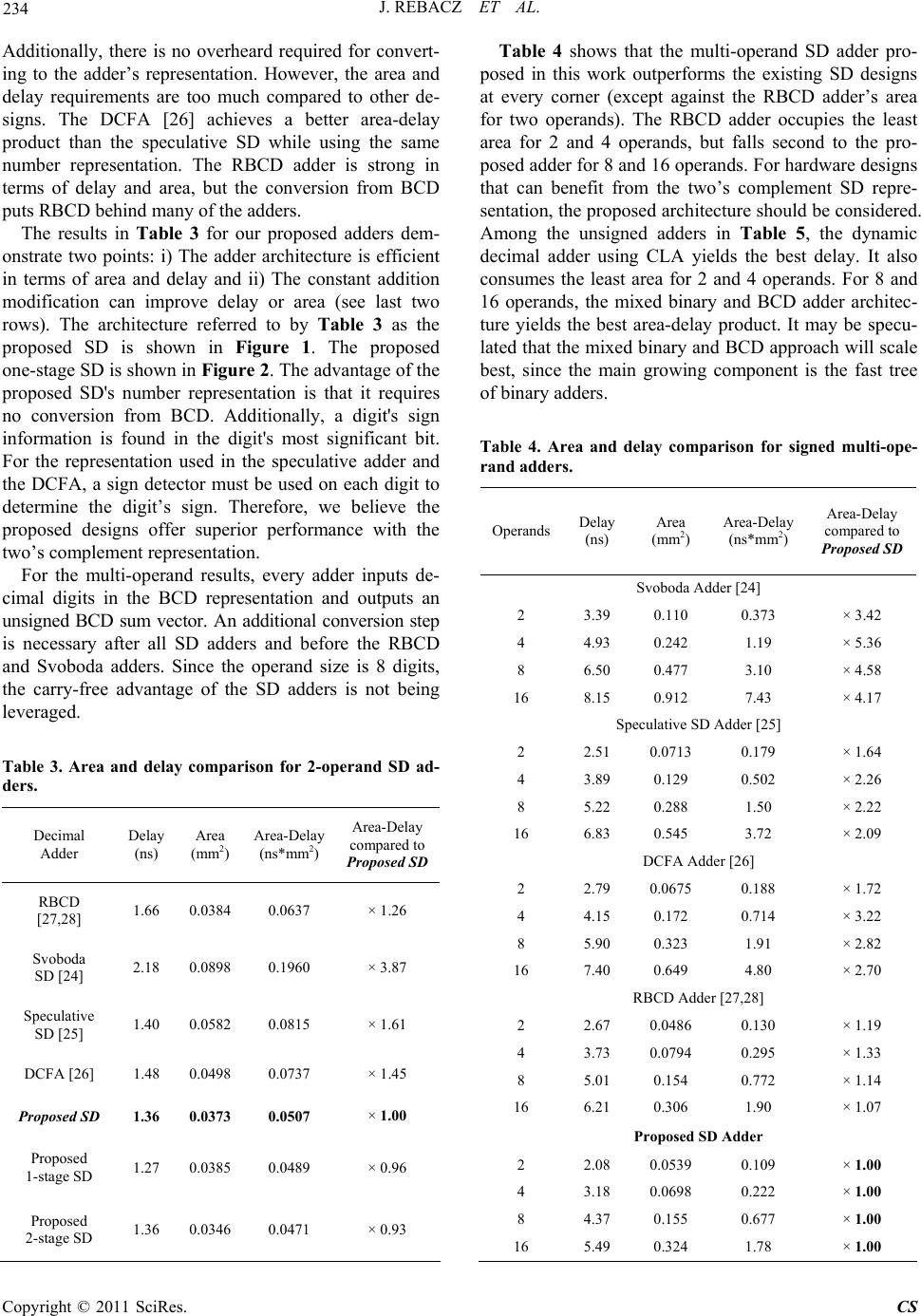

234 J. REBACZ ET AL.
Additionally, there is no overheard required for convert-
ing to the adder’s representation. However, the area and
delay requirements are too much compared to other de-
signs. The DCFA [26] achieves a better area-delay
product than the speculative SD while using the same
number representation. The RBCD adder is strong in
terms of delay and area, but the conversion from BCD
puts RBCD behind many of the adders.
The results in Table 3 for our proposed adders dem-
onstrate two points: i) The adder architecture is efficient
in terms of area and delay and ii) The constant addition
modification can improve delay or area (see last two
rows). The architecture referred to by Table 3 as the
proposed SD is shown in Figure 1. The proposed
one-stage SD is shown in Figure 2. The advantage of the
proposed SD's number representation is that it requires
no conversion from BCD. Additionally, a digit's sign
information is found in the digit's most significant bit.
For the representation used in the speculative adder and
the DCFA, a sign detector must be used on each digit to
determine the digit’s sign. Therefore, we believe the
proposed designs offer superior performance with the
two’s complement representation.
For the multi-operand results, every adder inputs de-
cimal digits in the BCD representation and outputs an
unsigned BCD sum vector. An additional conversion step
is necessary after all SD adders and before the RBCD
and Svoboda adders. Since the operand size is 8 digits,
the carry-free advantage of the SD adders is not being
leveraged.
Table 3. Area and delay comparison for 2-operand SD ad-
ders.
Decimal
Adder
Delay
(ns)
Area
(mm2)
Area-Delay
(ns*mm2)
Area-Delay
compared to
Proposed SD
RBCD
[27,28] 1.66 0.03840.0637 × 1.26
Svoboda
SD [24] 2.18 0.08980.1960 × 3.87
Speculative
SD [25] 1.40 0.05820.0815 × 1.61
DCFA [26] 1.48 0.04980.0737 × 1.45
Proposed SD 1.36 0.03730.0507 × 1.00
Proposed
1-stage SD 1.27 0.03850.0489 × 0.96
Proposed
2-stage SD 1.36 0.03460.0471 × 0.93
Table 4 shows that the multi-operand SD adder pro-
posed in this work outperforms the existing SD designs
at every corner (except against the RBCD adder’s area
for two operands). The RBCD adder occupies the least
area for 2 and 4 operands, but falls second to the pro-
posed adder for 8 and 16 operands. For hardware designs
that can benefit from the two’s complement SD repre-
sentation, the proposed architecture should be considered.
Among the unsigned adders in Table 5, the dynamic
decimal adder using CLA yields the best delay. It also
consumes the least area for 2 and 4 operands. For 8 and
16 operands, the mixed binary and BCD adder architec-
ture yields the best area-delay product. It may be specu-
lated that the mixed binary and BCD approach will scale
best, since the main growing component is the fast tree
of binary adders.
Table 4. Area and delay comparison for signed multi-ope-
rand adders.
Operands Delay
(ns)
Area
(mm2)
Area-Delay
(ns*mm2)
Area-Delay
compared to
Proposed SD
Svoboda Adder [24]
2 3.39 0.110 0.373 × 3.42
4 4.93 0.242 1.19 × 5.36
8 6.50 0.477 3.10 × 4.58
16 8.15 0.912 7.43 × 4.17
Speculative SD Adder [25]
2 2.51 0.0713 0.179 × 1.64
4 3.89 0.129 0.502 × 2.26
8 5.22 0.288 1.50 × 2.22
16 6.83 0.545 3.72 × 2.09
DCFA Adder [26]
2 2.79 0.0675 0.188 × 1.72
4 4.15 0.172 0.714 × 3.22
8 5.90 0.323 1.91 × 2.82
16 7.40 0.649 4.80 × 2.70
RBCD Adder [27,28]
2 2.67 0.0486 0.130 × 1.19
4 3.73 0.0794 0.295 × 1.33
8 5.01 0.154 0.772 × 1.14
16 6.21 0.306 1.90 × 1.07
Proposed SD Adder
2 2.08 0.0539 0.109 × 1.00
4 3.18 0.0698 0.222 × 1.00
8 4.37 0.155 0.677 × 1.00
16 5.49 0.324 1.78 × 1.00

J. REBACZ ET AL.
235
Table 5. Area and Delay Comparison for unsigned multi-
operand adders.
Operands Delay (ns) Area (mm2) Area-Delay (ns*mm2)
Nonspeculative Adder [7]
2 1.29 .0246 .0317
4 3.15 .0614 .193
8 4.03 .147 .592
16 6.78 .280 1.90
Mixed Binary and BCD Adder [23]
2 1.29 .0246 .0317
4 2.71 .0535 .145
8 3.41 .101 .344
16 4.45 .187 .832
Reduced Delay BCD Adder [10]
2 1.34 .0284 .0381
4 2.57 .0644 .166
8 3.68 .143 .526
16 4.84 .278 1.34
Dynamic Decimal using CLA Adder [11]
2 1.29 .0246 .0317
4 2.38 .0598 .142
8 3.01 .123 .370
16 3.82 .236 .902
Proposed SD multi-operand addition with conversion
to BCD does not outperform the best unsigned multi-
operand scheme. However, the SD adders’ larger func-
tional domain must not be overlooked. That is, the ease
at which subtraction can be performed with an SD adder
over an unsigned adder strengthens the SD adder’s posi-
tion.
10. Applications
The ideal target applications for the proposed signed-
digit schemes would leverage signed-digit advantages.
One benefit is the elimination of carry propagation addi-
tion with long words (64 or 128 bits) operated on itera-
tively. If the application does not require iterative com-
putations, then immediate conversion back to an un-
signed representation will negate the carry-free addition
performance. However, if the application requires know-
ledge of sign at each iterative step, which signed-digit
addition easily provides, then signed-digit addition is
promising. Moreover, applications that can conveniently
use the signed-digit representation for other operations as
well as addition/subtraction stand to benefit. The itera-
tive multiplier in [15] uses a signed-digit adder because
an earlier step (partial product generation) found that the
signed-digit representation can increase performance. In
SRT division, division is executed iteratively and the sign
of the dividend is necessary at each iteration. Therefore,
the proposed 2-operand adders can potentially serve a
core role in division. For the proposed multi-operand
scheme, adding multiple partial products to reduce cycles
in iterative multiplication appears promising. Finally,
advanced financial algorithms may stand to benefit.
11. Conclusions
In this study, new signed-digit two operand and multi-
operand decimal adders are proposed. Performance of re-
cent decimal adder architectures have been investigated
and compared. The proposed SD adder excels in speed
and area usage among previously proposed SD adders.
The use of constant addition for speculation and the merg-
ing of adjacent modules with sharable operations enable
efficient implementation of two operand and multi-op-
erand decimal addition.
12. References
[1] BigDecimal, 2008. http://java.sun.com/products.
[2] DecNumber, AlphaWorks, 2008.
http://www.alphaworks.ibm.com/tech/decnumber.
[3] L. Eisen, et al., “IBM POWER6 Accelerators: VMX and
DFU,” IBM Journal of Research and Development, Vol.
51, No. 6, 2007, pp. 663-683. doi:10.1147/rd.516.0663
[4] C. Webb, “IBM z10: The Next-Generation Mainframe
Microprocessor,” IEEE Micro, Vol. 28, No. 2, 2008, pp.
19-29. doi:10.1109/MM.2008.26
[5] A. Tsang and M. Olschanowsky, “A Study of Database 2
Customer Queries,” Technical Report TR-03.413, IBM
Santa Teresa Laboratory, San Jose, USA, 1991.
[6] L.-K. Wang, C. Tsen, M. Schulte and D. Jhalani,
“Benchmarks and Performance Analysis of Decimal
Floating-Point Applications,” 5th International Confer-
ence on Computer Design, Lake Tahoe, 7-10 October
2007, pp. 164-170. doi:10.1109/ICCD.2007.4601896
[7] R. Kenney and M. Schulte, “High-Speed Multioperand
Decimal Adders,” IEEE Transactions on Computers, Vol.
54, No. 8, 2005, pp. 953-963. doi:10.1109/TC.2005.129
[8] I. D. Castellanos and J. E. Stine, “Compressor Trees for
Decimal Partial Product Reduction,” GLSVLSI’08: Pro-
ceedings of the 18th ACM Great Lakes Symposium on
VLSI, ACM, Orlando, 4-6 May 2008, pp. 107-110.
[9] I. S. Hwang, “High Speed Binary and Decimal Arithme-
tic Unit,” USA Patent No. 4,866,656.
[10] A. Bayrakci and A. Akkas, “Reduced Delay BCD Ad-
der,” IEEE International Conference on Application Spe-
cific Systems, Architectures and Processors, Montreal,
9-11 July 2007, pp. 266-271.
[11] Y. You, Y. D. Kim and J. H. Choi, “Dynamic Decimal
Adder Circuit Design by Using the Carry Lookahead,”

J. REBACZ ET AL.
236
IEEE Design and Diagnostics of Electronic Circuits and
Systems, Prague, 18-21 April 2006, pp. 242-244.
doi:10.1109/DDECS.2006.1649627
[12] L.-K. Wang and M. Schulte, “A Decimal Floating-Point
Adder with Decoded Operands and a Decimal Lead-
ing-Zero Anticipator,” 19th IEEE Symposium on Com-
puter Arithmetic, Portland, 8-10 June 2009, pp. 125-134.
[13] A. Vazquez and E. Antelo, “A High-Performance Sig-
nificand BCD Adder with IEEE 754-2008 Decimal
Rounding,” 19th IEEE Symposium on Computer Arith-
metic, Portland, 8-10 June 2009, pp. 135-144.
[14] L.-K. Wang and M. Schulte, “Decimal Floating-Point
Adder and Multifunction Unit with Injection-Based
Rounding,” 18th IEEE Symposium on Computer Arith-
metic, Montpellier, 25-27 June 2007, pp. 56-68.
[15] M. Erle, E. Schwarz and M. Schulte, “Decimal Multipli-
cation with Efficient Partial Product Generation,” 17th
IEEE Symposium on Computer Arithmetic, Cape Cod,
27-29 June 2005, pp. 21-28.
[16] M. Erle, M. Schulte and B. Hickmann, “Decimal Float-
ing-Point Multiplication via Carry-Save Addition,” 18th
IEEE Symposium on Computer Arithmetic, Montpellier,
25-27 June 2007, pp. 46-55.
[17] A. Vazquez, E. Antelo and P. Montuschi, “A New Family
of High-Performance Parallel Decimal Multipliers,” 18th
IEEE Symposium on Computer Arithmetic, Montpellier,
25-27 June 2007, pp. 195-204.
[18] G. Jaberipur and A. Kaivani, “Improving the Speed of
Parallel Decimal Multipliers,” IEEE Transactions on
Computers, Vol. 58, No. 11, 2009, pp. 1539-1552.
doi:10.1109/TC.2009.110
[19] T. Lang and A. Nannarelli, “A Radix-10 Digit-Recurrence
Division Unit: Algorithm and Architecture,” IEEE Trans-
actions on Computers, Vol. 56, No. 6, 2007, pp. 727-739.
doi:10.1109/TC.2007.1038
[20] A. Vazquez, E. Antelo and P. Montuschi, “A Radix-10
SRT Divider Based on Alternative BCD Codings,” 25th
International Conference on Computer Design, Lake
Tahoe, 7-10 October 2007, pp. 280-287.
[21] H. Nikmehr, B. Phillips and C. Lim, “Fast Decimal
Floating-Point Division,” IEEE Transactions on Very
Large Scale Integration (VLSI) Systems, Vol. 14, No. 9,
2006, pp. 951-961.
[22] A. Kaivani and G. Jaberipur, “Fully Redundant Decimal
Addition and Subtraction Using Stored-Unibit Encod-
ing,” Integration, the VLSI journal, Vol. 43, No. 1, 2010,
pp. 34-41.
[23] L. Dadda, “Multioperand Parallel Decimal Adder: A
Mixed Binary and BCD Approach,” IEEE Transactions
on Computers, Vol. 56, No. 10, 2007, pp. 1320-1328.
doi:10.1109/TC.2007.1067
[24] A. Svoboda, “Decimal Adder with Signed Digit Arithme-
tic,” IEEE Transactions on Computers, Vol. C-18, No. 3,
1969, pp. 212-215. doi:10.1109/T-C.1969.222633
[25] J. Moskal, E. Oruklu and J. Saniie, “Design and Synthesis
of a Carry-Free Signed-Digit Decimal Adder,” IEEE In-
ternational Symposium on Circuits and Systems, New
Orleans, 27-30 May 2007, pp. 1089-1092.
[26] H. Nikmehr, B. Phillips and C. Lim, “A Decimal Car-
ry-Free Adder,” Smart Structures, Devices, and Sys-
tems-II, Sydney, 13 December 2005, pp. 786-797.
[27] B. Shirazi, D. Yun and C. Zhang, “RBCD: Redundant
Binary Coded Decimal Adder,” IEE Proceedings on
Computers and Digital Techniques, Vol. 136, No. 2, 1989,
pp. 156-160. doi:10.1049/ip-e.1989.0021
[28] B. Shirazi, D. Yun and C. Zhang, “VLSI Designs for
redundant Binary-Coded Decimal Addition,” 7th Annual
International Phoenix Conference on Computers and
Communications, Scottsdale, 16-18 March 1988, pp.
52-56. doi:10.1109/PCCC.1988.10042
[29] R. Kenney, M. Schulte and M. Erle, “A High-Frequency
Decimal Multiplier,” IEEE International Conference on
Computer Design: VLSI in Computers and Processors,
San Jose, 11-13 October 2004, pp. 26-29.
doi:10.1109/ICCD.2004.1347893
[30] A. Avizienis, “Signed Digit Number Representations for
Fast Parallel Arithmetic,” IRE Transactions on Electronic
Computers, Vol. EC-10, No. 3, 1961, pp. 389-400.
doi:10.1109/TEC.1961.5219227
[31] B. Parhami, “Generalized Signed-Digit Number Systems:
A Unifying Framework for Redundant Number Repre-
sentations,” IEEE Transactions on Computers, Vol. 39,
No. 1, 1990, pp. 89-98. doi:10.1109/12.46283
[32] J. Rebacz, E. Oruklu and J. Saniie, “High Performance
Signed-Digit Decimal Adders,” IEEE International Con-
ference on Electro/Information Technology, Windsor, 7-9
June 2009, pp. 251-255. doi:10.1109/EIT.2009.5189621
[33] V. Dave, E. Oruklu and J. Saniie, “Design and Synthesis
of a Three Input Flagged Prefix Adder,” IEEE Interna-
tional Symposium on Circuits and Systems, New Orleans,
27-30 May 2007, pp. 1081-1084.
doi:10.1109/ISCAS.2007.378197
[34] D. Phatak and I. Koren, “Hybrid Signed-Digit Number
Systems: A United Framework for Redundant Number
Representations with Bounded Carry Propagation Chains,”
IEEE Transactions on Computers, Vol. 43, No. 8, 1994, pp.
880-891. doi:10.1109/12.295850
[35] J. Rebacz, E. Oruklu and J. Saniie, “Performance Evalua-
tion of Multi-Operand Fast Decimal Adders,” 52nd IEEE
International Midwest Symposium on Circuits and Sys-
tems, Cancun, 2-5 August 2009, pp. 535-538.
doi:10.1109/MWSCAS.2009.5236036