Journal of Water Resource and Protection
Vol. 2 No. 6 (2010) , Article ID: 2068 , 11 pages DOI:10.4236/jwarp.2010.26062
Fuzzy Approach Based Management Model for Irrigation Planning
1Department of Civil Engineering, Government College of Engineering, Aurangabad, India
2Government College of Engineering, Aurangabad, India
3Department of Civil Engineering, Amrutvahini College of Engineering, Sangamner, India
E-mail: dgregulwar@rediffmail.com, jyotiba.gurav@rediffmail.com
Optimal Cropping Pattern
Received March 5, 2010; revised April 6, 2010; accepted May 4, 2010
Keywords: Linear Programming (LP), Multi Objective Fuzzy Linear Programming (MOFLP),
ABSTRACT
The objective of this paper is to develop the irrigation planning model and to apply the same in the form of Multi Objective Fuzzy Linear Programming (MOFLP) approach for crop planning in command area of Jayakwadi Project Stage I, Maharashtra State, India. To formulate MOFLP model various Linear Programming (LP) models are developed to optimize the Net Benefits (NB), Crop/Yield Production (YP), Employment Generation (EG) and Manure Utilization (MU) for which the objective function and constraints are crisp in nature. From the results of these LP models the linear membership function for each individual objective function has been developed. Considering the decision makers satisfaction level (λ), all the four objectives are maximized simultaneously. The results of the MOFLP and LP are compared. The MOFLP model concentrates on satisfying four objectives simultaneously. The present model will be helpful for the decision maker to take decision under conflicting situation when planning for different objectives simultaneously. The degree of satisfaction λ, works out to be 0.58. Compromised solution provides Net Benefits 1503.73 Million Rupees, Crop Production 319563.50 Tons, Employment Generation/Labour Requirement 29.74 Million Man days and Manure Utilization 154506.50 Tons respectively.
1. Introduction
Water resources systems planning development and management is the area in which irrigation planning problem involves with multiple possible and valuable planning objectives. Some of them, one can represent in terms of monetary returns and a few which one cannot, are social upliftment, environmental status, ecological balance, conservation of natural resources etc. The objectives expressed in terms of monetary returns can be easily imposed in the form of objective functions. Irrigation planning is the area which is associated with many monetary and nonmonetary objectives. Some of the monetary objectives are crop production, total net benefits, manure utilization, labour requirement, water utilization and land utilization. The crop planning study is normally practiced for the determination of type of crops that should be taken and the area to be utilized for those crops. To decide these two parameters various other parameters are influencing such as type of crop suitable to particular soil, water availability, land availability, labour availability, manure requirement, etc. Crop planning problem is formulated in the form of linear programming model with number of objective functions and set of constraints. Focusing on only one objective does not satisfy the different desires of people/farmers of region. Some of the multiple objectives in crop planning problem may conflict with one another. This may be because of all these objectives share the same type of resources which used for any one objective it may not available for other objectives [1]. Single optimal solutions do not yield in case of multiple objective analyses, but which are more useful for the determination of the trade-offs among noncommensurabe objectives. The crop production study that provides the maximum net benefits is not likely to generate the highest employment of labour, nor it may produce the maximum yield or return in terms of foreign exchange from agricultural exports. Considering the case of developing countries these objectives may be more important than the maximization of net benefits. Every development objective uses the same available resources, but not in equal amount [2]. Irrigation planning problem becomes more complicated, if uncertainty is included in the form of drought and floods, fluctuations in the market price of crops and its yields, non availability of right type of labour at right time and inflow variation from season to season. To tackle such kind of vagueness in planning with multiple objectives and the imprecision involved in the parameter values; the fuzzy set theory is considered as an alternative approach. Many advantages of the Fuzzy Linear Programming (FLP) are considered over the other existing multiobjectvie optimization methods, especially constraint and weighting methods. When the numbers of objectives are greater than three these two methods may become computationally disadvantages. Also in case of weighting method, the specification of weight plays a vital role which is difficult to quantify and sometimes the solution is sensitive to weights. However the nondominated alternatives are generated in case of constraint method. To make the selection of suitable alternative the existing Multi Criterion Decision Making (MCDM) tools are used and which does not yield the same alternative. To check the robustness of ranking, an extensive sensitivity analysis is required. On the other hand, in case of FLP for each additional objective function only one constraint is required. The flexibility of converting the fuzzy model into existing optimization software makes the approach more useful.
Morales et al. [3] have developed a simulation model for planning the conjunctive use of irrigation water from a single multipurpose reservoir and an aquifer and allocation of cropped areas within an irrigation district. Raman et al. [4] have developed a decision support for planning of crop during droughts for Bhadra reservoir command area of Karnataka state, India. Mannocchi and Mecarelli [5] have discussed the optimization criteria for deficit irrigation of a farm. Srinivasa Raju and Nagesh Kumar [6] have discussed linear programming (LP) irrigation planning model for evaluation of irrigation development strategy for the case study of Sri Ram Sagar project, in Andhra Pradesh of India. Srinivasa Raju and Nagesh Kumar [7] developed the Fuzzy Linear Programming (FLP) for three conflicting objectives of Sri Ram Sagar project, in Andhra Pradesh of India. Sethi et al. [8] developed optimization model to find optimal cropping pattern and area allocation in relation with availability of water resources for different season. Itoh et al. [9] have presented crop planning problem with profit coefficients for agricultural products as discrete random variable. Sonmez and Altin [10] have developed the optimum cropping pattern for adequate and deficit water supply for mid size farm in Harran Plain Firat irrigation district. Sahoo et al. [11] have developed the linear programming and fuzzy optimization models for three conflicting objectives of irrigation planning in Mahanadi-Kathajodi delta in eastern India. Regulwar and Anand Raj [12] have presented the monthly Multi Objective Genetic Algorithm Fuzzy Optimization (MO-GAFUOPT) for two conflicting objectives of Multireservoir in Godavari Sub basin, in Maharashtra state of India. Mohaddes and Mohayidin [13] have developed fuzzy mathematical programming model for tackling three objectives simultaneously, which are maximization of profit, maximization of employment and minimization of soil erosion. A monthly Multi Objective Multireservoir operation model solved by Genetic algorithm under Fuzzy environment has been developed by Regulwar and Anand Raj [14].
The objective of this paper is to develop the irrigation planning model and to apply the same in the form of Multi Objective Fuzzy Linear Programming (MOFLP) approach for crop planning in command area of Jayakwadi Project Stage I, Maharashtra State, India. The objective of MOFLP model is to develop an optimal cropping pattern that maximizes Net Benefits, Yield/Crop production, Employment Generation/Labour Requirement and Manure Utilization simultaneously.
2. Description of the Case Study Area
The lower Godavari River Basin, Maharashtra State, India is taken under consideration. The Jayakwadi project stage-I is located across eastward flowing river Godavari, Maharashtra state, India. The irrigable command area is 1416.40 km2. The catchment area of the reservoir is up to the dam site 21774 km2. The length of the dam is 10280m and its maximum height is 37.73 m. The gross storage of the reservoir is 2909 Mm3 and live storage is 2170 Mm3.Total installed capacity for power generation is 12 MW (Pumped storage plant). Figure 1 shows index map of Jayakwadi project, Maharashtra state, India.
3. Methodology and Model Development
The objective is to find out optimal cropping pattern for 75% dependable yield in command area. The problem has been formulated as an optimization model based on deterministic inflows. In the formulation of the problem the following assumptions have been made:
Crops are considered to be grown throughout the year. The irrigation intensity adopted is 22% in Kharif season, 45% in Rabi season and 28% in two seasonal, H. W. crop 3%, Perennial 4.5% and that becomes a total irrigation intensity of 102.5%. Ground water usage is not considered in the command area. Only surface water has been considered for irrigation. The soil of the study area is homogeneous in nature. Various relationships within the models are based on the framework of lineariry.
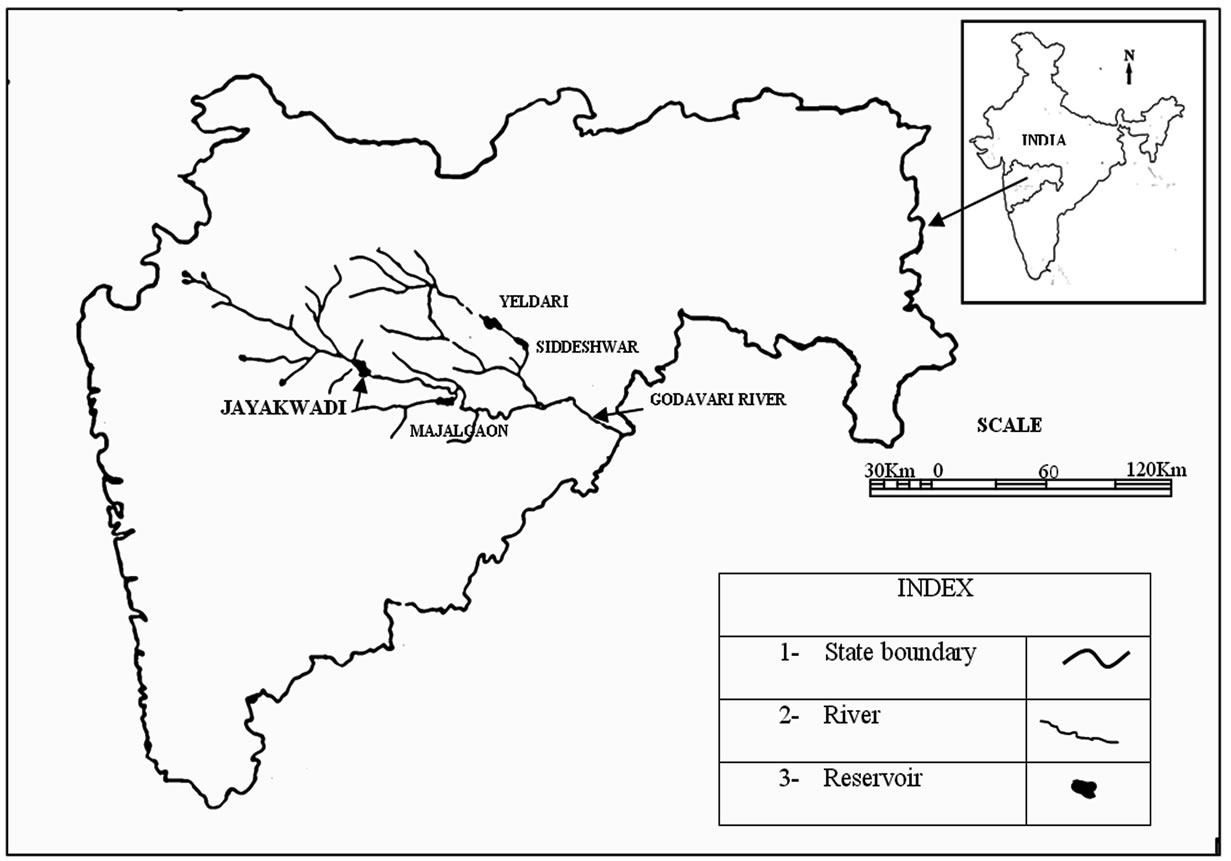
Figure 1. Index map of Maharashtra State of India.
Same management practice has been applied for a particular crop event under each land and hence, the crop/ yield production, net benefits, labour/employment generation and manure utilization under particular crop activity is constant. The duration and timings of the cropping activity are considered as a constant and do not vary over years. There are three seasons for growing crops (viz. Kharif, Rabi, and two seasonal) without any overlapping. Under certain overlapping situations, care is taken by adding specific constraints. The input cost for each crop is considered as twenty percent of the total gross benefits to be gained.
3.1. Objective Function
The four objectives are considered in the present study.
3.1.1. Maximization of Net Benefits (NB)
Maximization of Net benefits can be expressed as; (canonical form of LP)
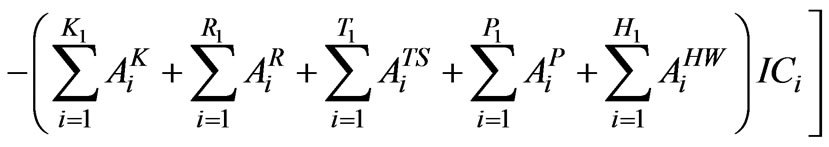
 (1)
(1)
[In which i = crop index. 1 = Sugarcane (P), 2 = Banana (P), 3 = Chilies (TS), 4 = L S Cotton (TS), 5 = Sorghum (K), 6 = Paddy (K), 7 = Sorghum (R), 8 = Wheat (R), 9 = Gram (R) and 10 = Groundnut (HW) and ha = 10000 m2]
The net benefits (NB) coefficients from the irrigated area under various crops are obtained by subtracting the input cost (20% of gross benefit) from gross benefit for different crops. The Gross benefits are calculated by multiplying the average yield of a crop per ha and current market price of that crop. The crop production (CP) coefficients are taken as the average yield of a crop per ha. (Commissionerate of Agriculture Maharashtra State, 2006, Agricultural Statistical Information Maharashtra State, India part-II [15]).
3.1.2. Maximization of Yield or Crop Production (CP)
Focusing on the food sufficiency of the region, the crop production is to be maximized and can be expressed in canonical form as follows;
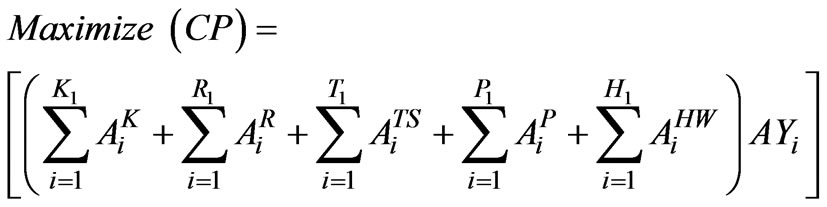 (2)
(2)
3.1.3. Maximization of Employment Generation (EG) or Labour Requirement
Keeping in mind the socio-economic development, the policy maker has to concentrate on the maximization of employment generation or labour requirement.
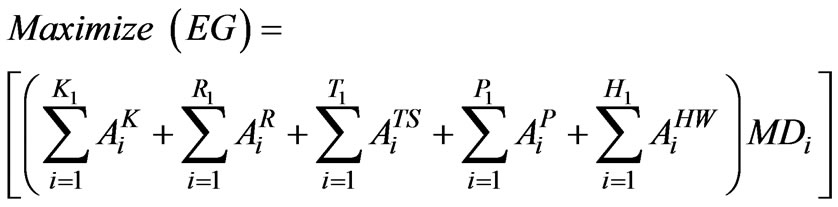 (3)
(3)
The labour requirement or numbers of Man Days (MD) for a particular crop per ha are considered through discussion with farmers and experts from agricultural fields.
3.1.4. Maximization of Manure Utilization (MU)
In order to maintain the fertility and nutrient sufficiency of soil in proper manner, one should concentrate on maximization of use of manures.
 (4)
(4)
The Requirement of Manure (MU) for a crop per ha are considered through discussion with farmers and experts from agricultural fields.
3.2. Constraints
3.2.1. Sowing Area Constraint
3.2.1.1. Total Sowing Area Constraint The total area constraint for various crops for the present study is considered to take care of total area available for cultivation in command area during different crop seasons. The total sowing area constraint is given by,
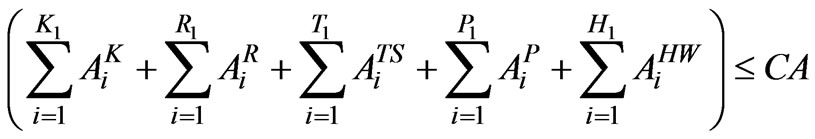 (5)
(5)
3.2.2. Maximum Sowing Area Constraint (According to Existing Cropping Pattern)
The maximum sowing area constraint for various crops is defined to account for maximum sowing area available for cultivation during various crop seasons according to existing cropping pattern of the project. The maximum sowing area constraint is given byKharif
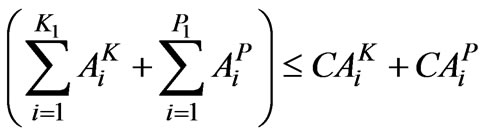 (6)
(6)
Rabi
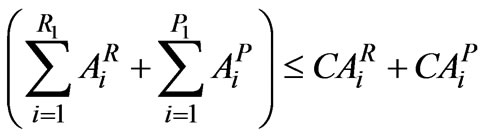 (7)
(7)
Hot Weather and Perennial
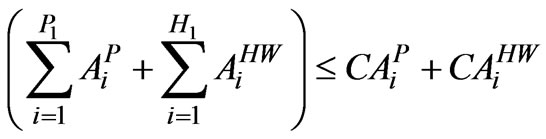 (8)
(8)
3.2.3. Affinity Constraint
The farmers of the region are having a tendency to grow cash crops and other crops according to their interest and benefits. To safeguard the interest of the food requirement of the region according to the storage capacity of the reservoir the following limitation (upper limit using the existing cropping pattern) for various crops are incorporated as constraintsPerennial
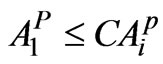 (9)
(9)
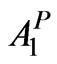 = Area under perennial crop Sugarcane in ha
= Area under perennial crop Sugarcane in ha
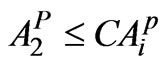 (10)
(10)
 = Area under perennial crop Banana in ha Two Seasonal
= Area under perennial crop Banana in ha Two Seasonal
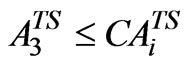 (11)
(11)
 = Area under two seasonal crop Chilies in ha
= Area under two seasonal crop Chilies in ha
 (12)
(12)
 = Area under two seasonal crop L S Cotton in ha Kharif
= Area under two seasonal crop L S Cotton in ha Kharif
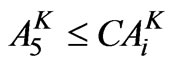 (13)
(13)
 = Area under kharif crop Sorghum in ha
= Area under kharif crop Sorghum in ha
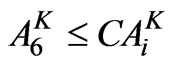 (14)
(14)
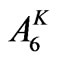 = Area under kharif crop Paddy in ha Rabi
= Area under kharif crop Paddy in ha Rabi
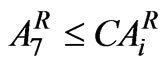 (15)
(15)
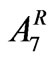 = Area under rabi crop Sorghum in ha
= Area under rabi crop Sorghum in ha
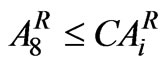 (16)
(16)
 = Area under rabi crop Wheat in ha
= Area under rabi crop Wheat in ha
 (17)
(17)
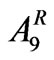 = Area under rabi crop Gram in ha Hot Weather
= Area under rabi crop Gram in ha Hot Weather
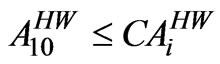 (18)
(18)
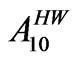 = Area under hot weather crop Groundnut in ha
= Area under hot weather crop Groundnut in ha
3.2.4. Labour Availability
To tackle the problem of uncertainty of avoiding the labour from outside the region, the labour requirement should not exceed the total labour availability during that intervalKharif
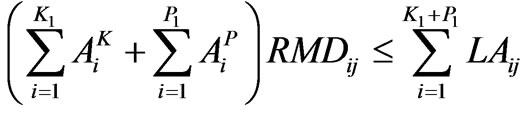 (19)
(19)
Rabi
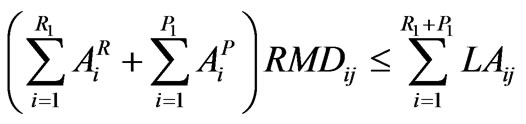 (20)
(20)
Perennial and hot weather
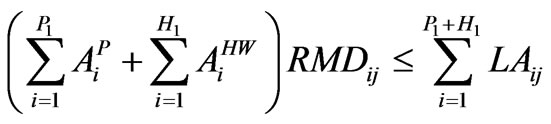 (21)
(21)
3.2.5. Manure Availability
In order to keep the fertility of soil in rich condition, the total manure requirement should not exceed the total availability of the manure in that season.
Kharif
 (22)
(22)
Rabi
 (23)
(23)
Perennial and Hot Weather
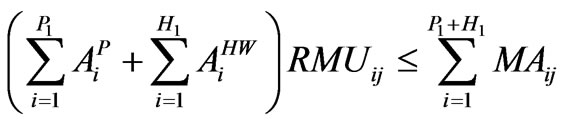 (24)
(24)
3.2.6. Water Availability Constraint
The total water requirement of different crop should not exceed the total water availability in the reservoir,
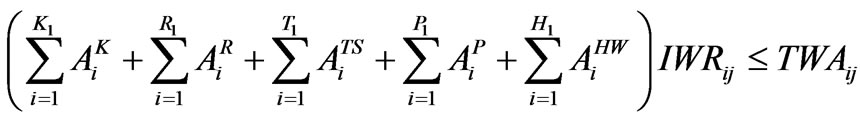 (25)
(25)
3.2.7. Non Negativity Constraint
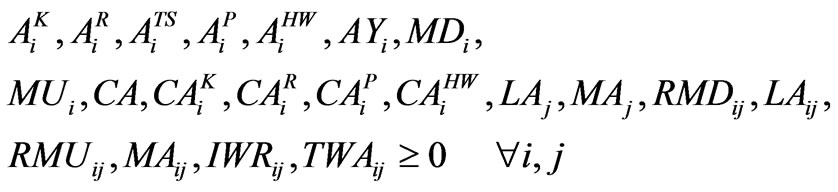 (26)
(26)
3.3. Fuzzy Linear Programming Algorithm (FLP Algorithm)
In brief it is divided into following steps:
1) Considering only one objective at a time, solve the problem as a linear programming problem.
2) Focusing on the results obtained in the step 1, work out the corresponding values of each objective from the solution obtained.
3) Comparing the values of objective function obtained in step 2; find out (ZU) and (ZL) for each objective under consideration.
4) Keeping in view the values of (ZU) and (ZL) for each objective; establish the linear membership function.
5) Introducing the dummy variable (λ), now the objective function changes to maximize the dummy variable (λ) subjected to the additional constraints due to the fuzziness in the value of the objective functions and original constraints.
6) Develop the equivalent Linear Programming (LP) model as a Multiobjective Fuzzy Linear Programming model (MOFLP).
7) With degree of truth (λ) work out compromised solution.
The schematic representation of fuzzy approach model for compromised solution is as shown in Figure 2.
4. Result Analysis
The objective function of the present study considering the Equations (1) to (4) of the linear programming planning (LPP) model are to maximize the net benefits, yield/crop production, employment generation and ma-
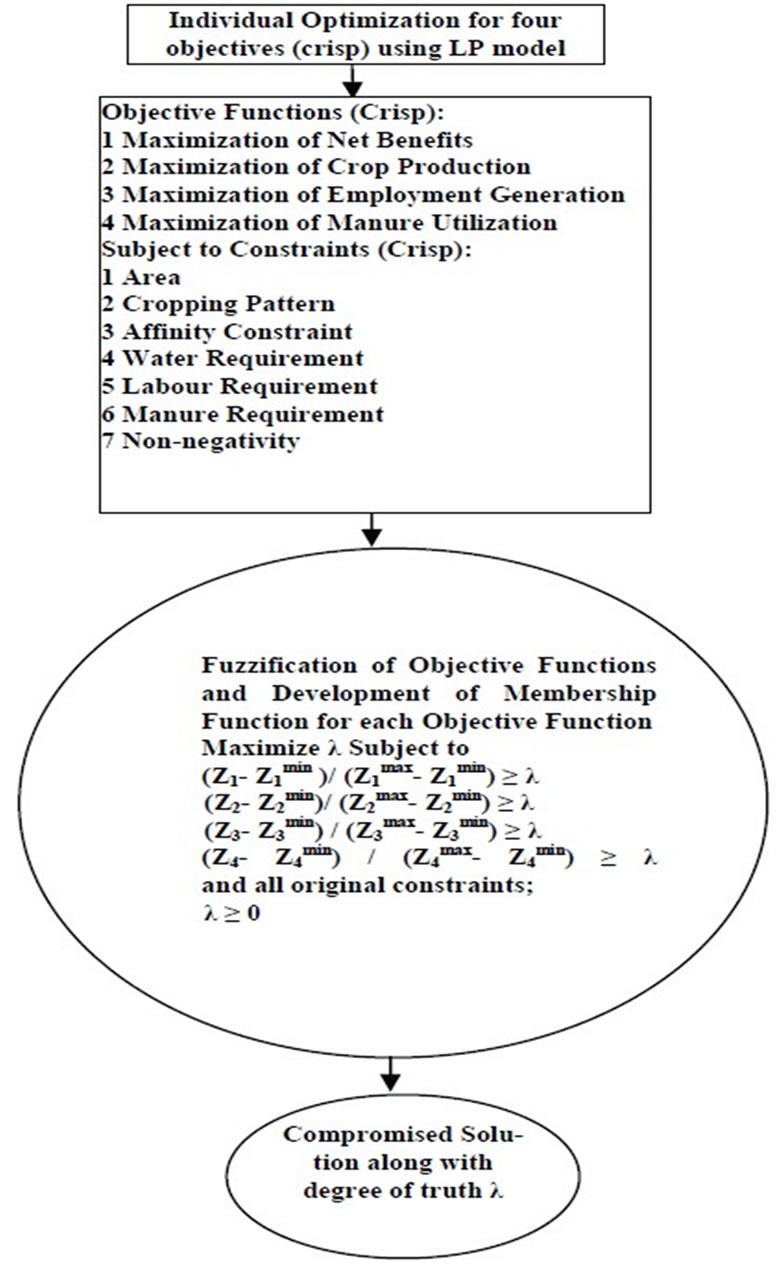
Figure 2. Schematic representation of fuzzy approach model for compromised solution.
nure utilization for the command area of the Jayakwadi Project stage-I. These objective functions are maximized separately subjected to constraints (Equations (5) to (26)) using the LINGO (Language for INteractive General Optimization). The results of this individual maximization of the four different objectives are used to develop the membership function for each objective taking the help of the best (+) and worst (-) value of the same. The membership functions are shown graphically in Figures (3-6). The same membership functions are written in the form of mathematical Equations (27) to (30). The results are shown in Table 1. Also the results are shown graphically

Figure 3. Membership function for Z1 (in Million Rupees).

Figure 4. Membership function for Z2 (in Tons).

Figure 5. Membership function for Z3 (in Million Man days).
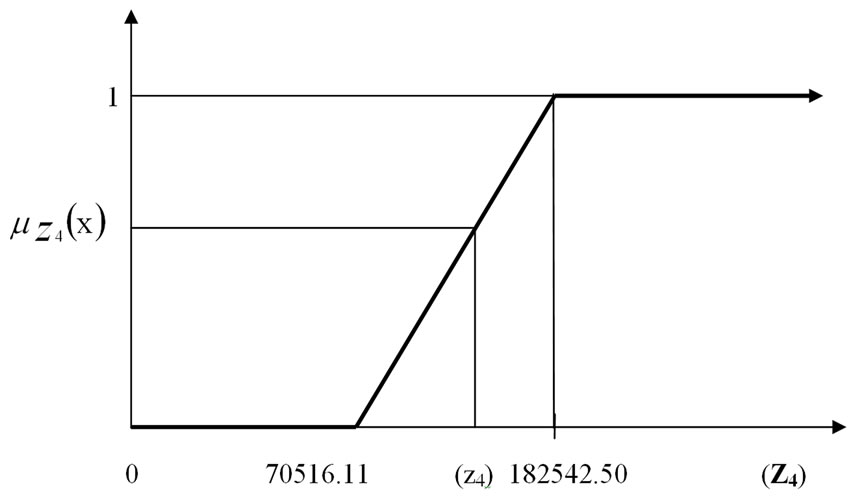
Figure 6. Membership function for Z4 (in Tons).
in Figures (7-11).
The membership functions µ1(X), µ2(X), µ3(X) and µ4(X) of the fuzzy sets characterizing the objective functions rise linearly from 0 to 1 at the highest achievable value of Z1 = 1683.04 Million Rs, Z2 = 473464.40 tons, Z3 = 34.44 Million Man days and Z4 = 182542.50 tons respectively. The level of satisfaction associated with net benefits rises from 0 if the net benefit is 1255.69 million Rs or less to 1 if the total net benefits is Z1 = 1683.04 Million Rs or more. The level of satisfaction with respect to crop/yield Production rises from 0 if the crop/yield production is 106674.40 Tons or less to 1 if the crop/ yield production is Z2 = 473464.40 tons or more and the satisfaction level associated with employment generation rises from 0 for 23.25 million man days or less to 1 for employment generation Z3 = 34.44 Million Man days and more. Similarly the level of satisfaction associated with manure utilization rises from 0 if the manure utilization is 70516.11 tons or less to 1 if the manure utilization is Z4 = 182542.50 tons or more. The maximum satisfaction level from the membership functions of four participating/conflicting objectives has been designated as the ‘best’ achieved/compromised solution.
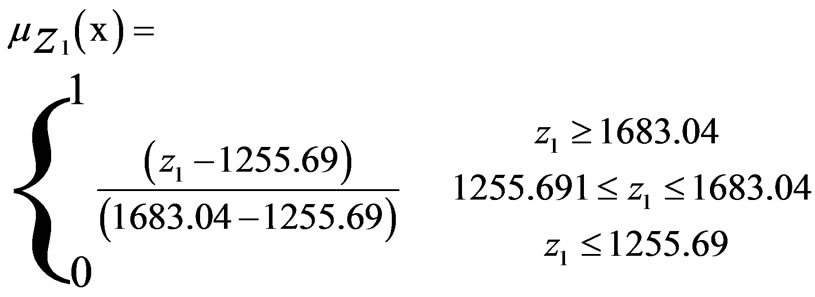 (27)
(27)
 (28)
(28)
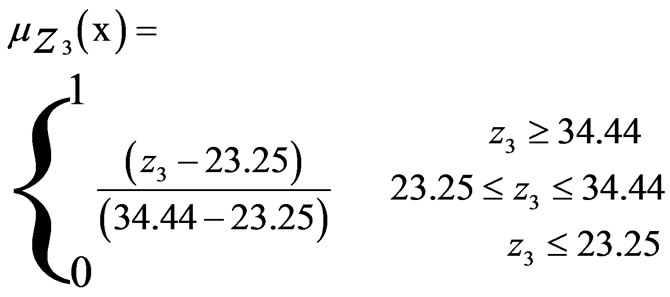
![]()
![]() (29)
(29)
 (30)
(30)
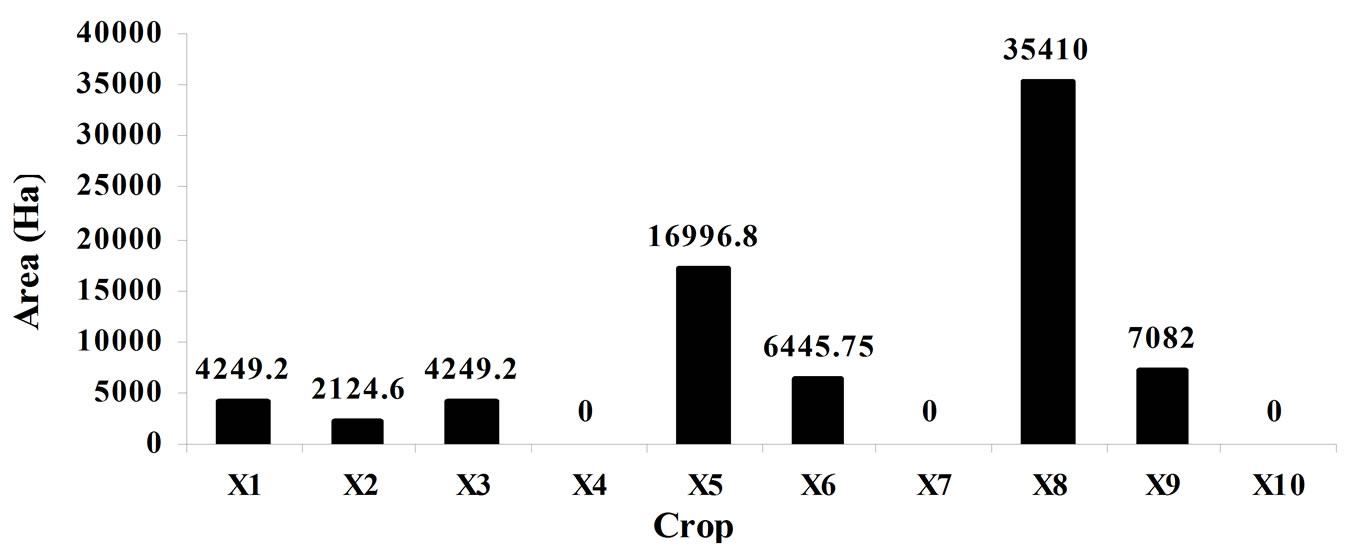
Figure 7. Cropping pattern for maximization of net benefits.
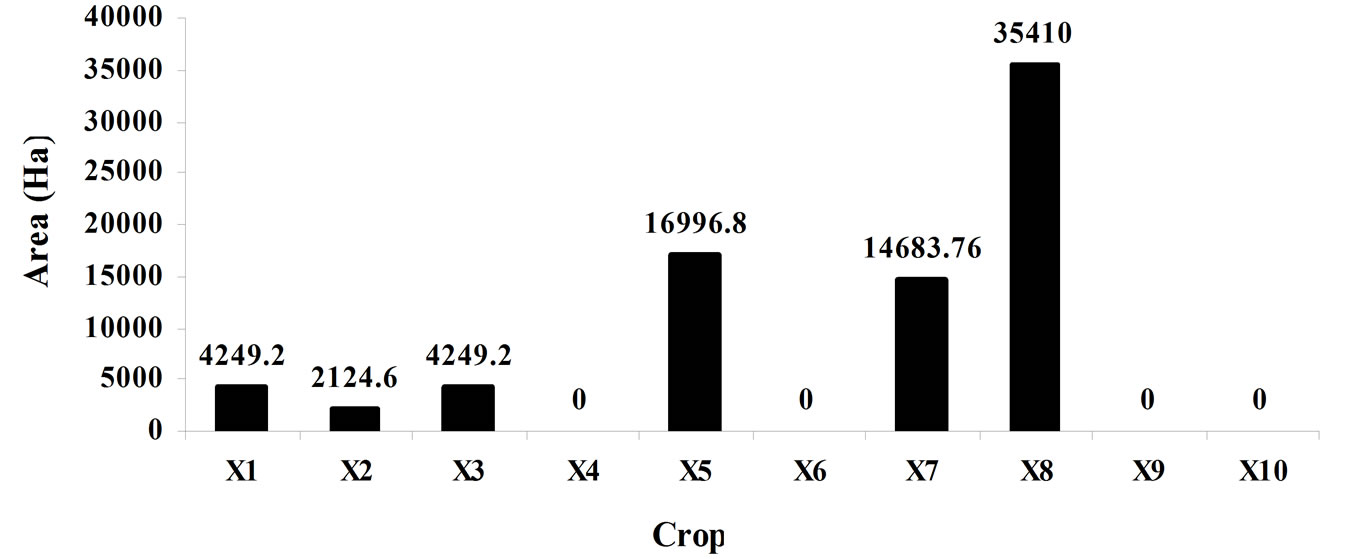
Figure 8. Cropping pattern for maximization of crop production.
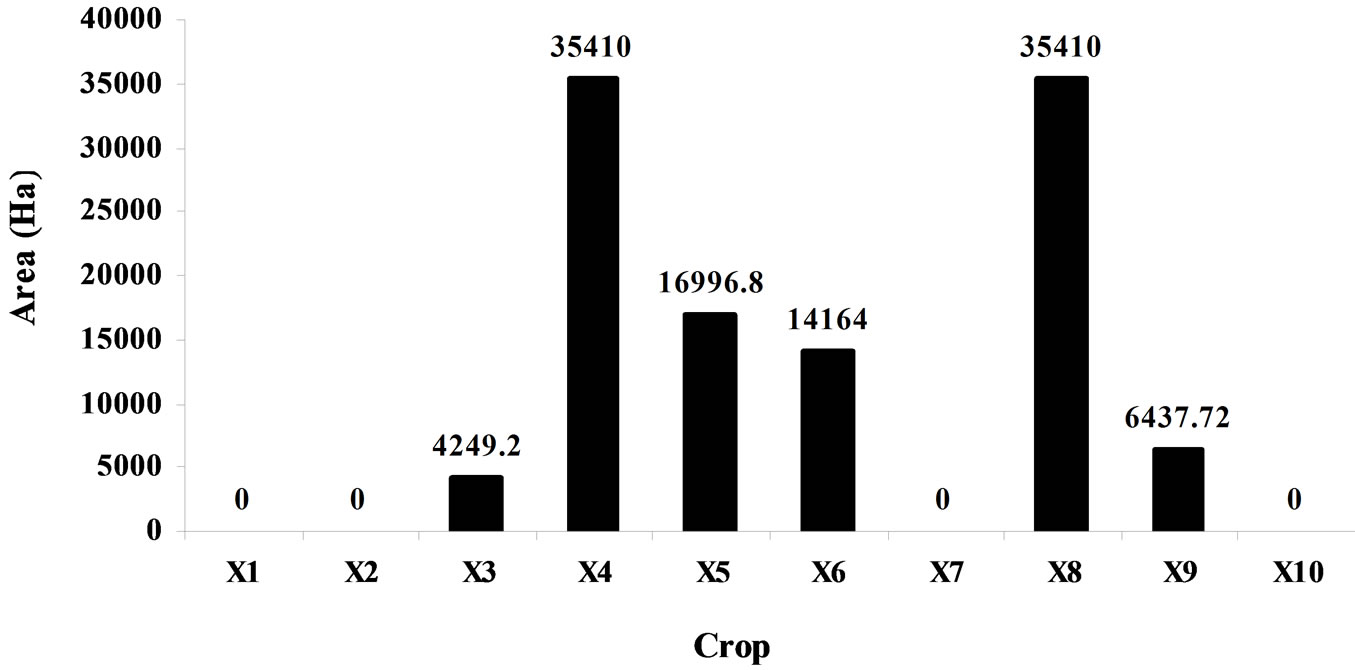
Figure 9. Cropping pattern for maximization of employment generation.
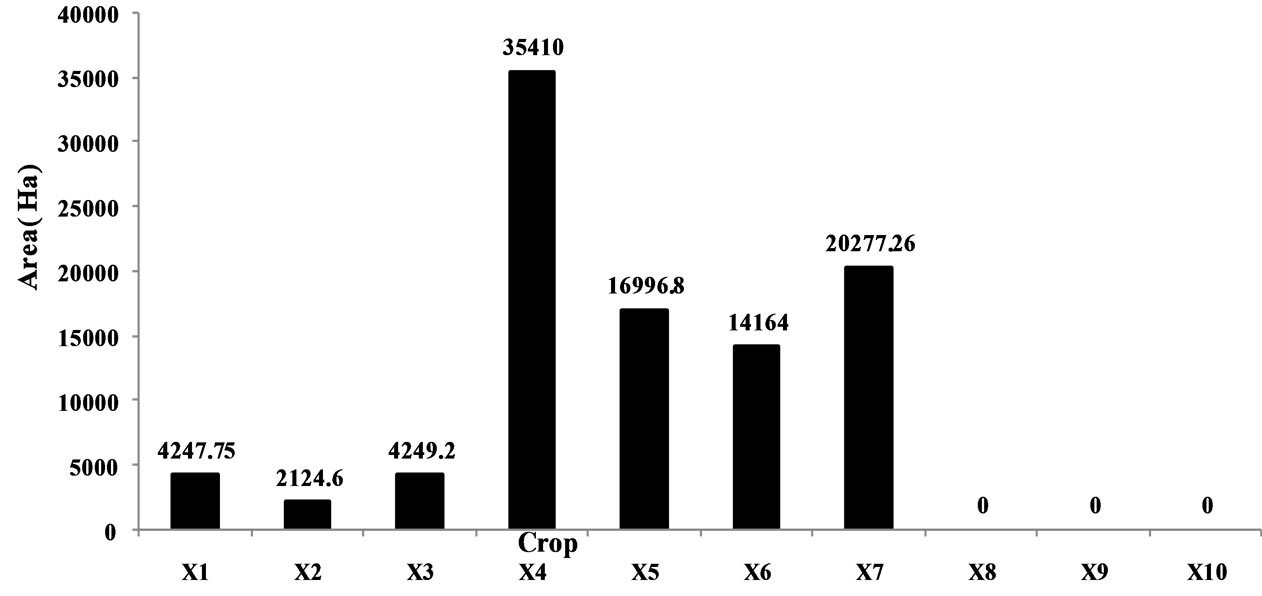
Figure 10. Cropping pattern for maximization of manure utilization.

Figure 11. Cropping pattern in the form of compromised solution for four conflicting objectives under fuzzy environment.
Finally the modified form of the optimization problem (MOFLP) by introducing the dummy variable λ = min [µ1(X), µ2(X), µ3(X), µ4(X)] such that the objective is to Maximize λ
Subject to(Z1–1255.69 × 106) / (1683.04 × 106–1255.69 × 106) ≥ λ
(Z2–106674.40) / (473464.40–106674.40) ≥ λ
(Z3–23.25 × 106) / (34.44 × 106–23.25 × 106) ≥ λ
(Z4–70516.11) / (182542.50–70516.11) ≥ λ
and all other original constraint given (Equations (5) to (26)) in the model; λ ≥0.
The solution of MOFLP is presented in Table 1. From this solution it is observed that the area to be irrigated is constant in case of Chilies (TS) and Sorghum (K) under LP model and MOFLP model solution. When the Net Benefit is to be maximized then the area under irrigation is zero for LS Cotton (TS), Sorghum (R) and Groundnut (HW) because the benefit coefficient is low for these crops. Similarly when the Crop Production is to be maximized then the area under irrigation is zero for LS Cotton (TS), Paddy (K), Gram (R) and Groundnut (HW).
Also when the Employment Generation/Labour Requirement is to be maximized then the area under irrigation is zero for sugarcane (P), Banana (P), Sorghum (R) and Groundnut (HW). This is due to the labour requirement per ha is low and also due to the limited area under existing cropping pattern. On the other hand when manure utilization is to be maximized then the area under irrigation is zero for wheat (R) ,Gram (R) and Groundnut (HW) as manure requirement per ha is low and also due to the limited area under existing cropping pattern. Area under irrigation is zero for Sorghum (R) and Groundnut (HW) if four conflicting objectives are considered simultaneously under MOFLP environment.
In case of individual optimization for four objectives separately the irrigation intensity is 54.05%, 54.86%, 79.54% and 68.81% respectively, while in case of MOFLP it is 70.02%. In case of MOFLP the irrigation intensity is more by 15.97%, 15.15%, 1.21% if we compare with individual optimization for net benefits, crop production and manure utilization respectively and less by 9.52% if we compare with individual optimization for employment generation.
The degree of truth for compromised solution for four

Table 1. Solution for the net benefits, crop yield/ production, employment generation and manure utilization crop areas of LPP model and MOFLP.
conflicting objectives under fuzzy environment is works out to be λ=0.58. MOFLP compromise solution provides Net Benefits 1503.73 (Million Rupees), Crop Production 319563.50 (Tons), Employment Generation/Labour Requirement 29.74 (Million Man days) and Manure Utilization 154506.50 (Tons) respectively.
5. Conclusions
The irrigation planning and their environmental and social aspects are focused under the present case study. The objective of the study is to develop an optimal cropping pattern that maximizes Net Benefits, Crop Production, Employment Generation/Labour Requirement and Manure Utilization simultaneously. For this, MOFLP approach has been developed and applied to Jayakwadi Project Stage I, Maharashtra State, India. This study proposes a basis for irrigation planning as an integrated approach. The degree of truth for compromised solution for four conflicting objectives under fuzzy environment is works out to be λ = 0.58. MOFLP compromised solution provides Net Benefits 1503.73 Million Rupees, Crop Production 319563.50 Tons, Employment Generation/ Labour Requirement 29.74 Million Man days and Manure Utilization 154506.50 Tons respectively. The present model will be helpful for the decision maker to take decision under conflicting situation when planning for different objectives simultaneously. This model is capable to trace out an integrated irrigation planning with prime consideration for economic, social and environmental issue. The results obtained under the present study are sensitive to the changes in the market price of crop, cost of crop production, unit labour cost, and unit manure cost and water availability.
6. Acknowledgements
The authors would like to express their sincere thanks to Command Area Development Authority, Aurangabad, Maharashtra State, India and Mahatma Phule Krishi Vidyapeeth Rahuri, Ahmednagar, Maharashtra State, India for providing necessary data for analysis.
REFERENCES
- S. Vedula and P. P. Mujumdar, “Water Resources Systems Modelling Techniques and Analysis,” Tata-McGraw Hill, New Delhi, 2005.
- D. P. Loucks, J. R. Stedinger and D. A. Haith, “Water Resources Systems Planning and Analysis,” Prentice-Hall, Englewood Cliffs, New Jersey, 1981.
- J. C. Morales, M. A. Marino and E. A. Hozapfel, “Planning Simulation Model of Irrigation District,” Journal of Irrigation and Drainage Engineering, Vol. 118, No. 1, 1992, pp. 74-87.
- H. Raman, S. Mohan and N. C. V. Rangacharya, “Decision Support System for Crop Planning during Droughts,” Journal of Irrigation and Drainage Engineering, Vol. 118, No. 2, 1992, pp. 229-241.
- F. Mannocchi and P. Mecarelli, “Optimization Analysis of Deficit Irrigation Systems,” Journal of Irrigation and Drainage Engineering, Vol. 120, No. 3, 1994, pp. 484- 503.
- K. S. Raju and D. N. Kumar, “Optimum Cropping Pattern for sri Ram Sagar Project: A Linear Programming Approach,” Journal of Applied Hydrology, Vol. 8, No. 1-2, 2000, pp. 57-67.
- K. S. Raju and D. N. Kumar, “Irrigation Planning of sri Ram Sagar Project Using Multi Objective Fuzzy Linear Programming,” ISH Journal of Hydraulic Engineering, Vol. 6, No. 1, 2000, pp. 55-63.
- L. N. Sethi, D. Nagesh Kumar, S. N. Panda and B. C. Mal, “Optimal Crop Planning and Conjunctive Use of Water Resources in a Coastal River Basin,” Water Resource and Management, Vol. 16, No. 3, 2002, pp. 145-169.
- T. Itoh, H. Ishii and T. Nanseki “A Model of Crop Planning under Uncertainty in Agricultural Management,” International Journal of Production Economics, Vol. 81-82, 2003, pp. 555-558.
- F. K. Sonmez and M. Altin, “Irrigation Scheduling and Optimum Cropping Pattern with Adequate and Deficit Water Supply for Mid-Sized Farms of Harran Plain,” Pakistan Journal of Biological Sciences, Vol. 7, No. 8, 2004, pp. 1414-1418.
- B. Sahoo, A. K. Lohani and R. K. Sahu, “Fuzzy Multiobjective and Linear Programming Based Management Models for Optimal Land-Water-Crop Systems Planning,” Water Resource and Management, Vol. 20, 2006, pp. 931-948.
- D. G. Regulwar and P. Anand Raj, “Development of 3-D Optimal Surface for Operation Policies of a Multireservoir in Fuzzy Environment Using Genetic Algorithm for River Basin Development and Management,” Water Resource and Management, Vol. 22, No. 5, 2008, pp. 595- 610.
- S. A. Mohaddes and M. G. Mohayidin, “Application of the Fuzzy Approach for Agricultural Production Planning in a Watershed, a Case Study of the Atrak Watershed Iran,” American-Eurasian Journal of Agriculture & Environment Science, Vol. 3, No. 4, 2008, pp. 636-648.
- D. G. Regulwar and P. Anand Raj, “Multi Objective Multireservoir Optimization in Fuzzy Environment for River Basin Development and Management,” Journal of Water Resource and Protection, Vol. 1, No. 4, 2009, pp. 271-280.
- Commissionerate of Agriculture Maharashtra State, “Agricultural Statistical Information Maharashtra State,” India Part-II, 2006.
Notations
The following symbols are used in this paper
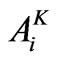 Area of ith
Area of ith crop in kharif season (ha);
crop in kharif season (ha);
 Area of ith
Area of ith crop in rabi season (ha);
crop in rabi season (ha);
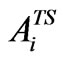 Area under two seasonal crop (ha);
Area under two seasonal crop (ha);
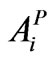 Area under perennial crop (ha);
Area under perennial crop (ha);
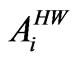 Area under hot weather crop (ha);
Area under hot weather crop (ha);
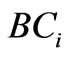 Benefit coefficient for ith crop;
Benefit coefficient for ith crop;
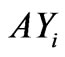 Average yield of ith crop;
Average yield of ith crop;
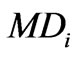 Number of man days for ith crop per ha;
Number of man days for ith crop per ha;
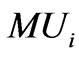 Manure utilization/Requirement of manure in tons for ith crop per ha;
Manure utilization/Requirement of manure in tons for ith crop per ha;
 Total command area for all season for ith crop (ha);
Total command area for all season for ith crop (ha);
 Command area for kharif season for ith crop (ha);
Command area for kharif season for ith crop (ha);
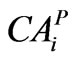 Command area under perennial crop (ha);
Command area under perennial crop (ha);
 Command area under hot weather crop (ha);
Command area under hot weather crop (ha);
 Command area for rabi season for ith crop (ha);
Command area for rabi season for ith crop (ha);
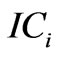 Input cost for ith Crop;
Input cost for ith Crop;
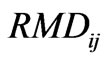 Requirement of man days or labour for ith crop in jth interval;
Requirement of man days or labour for ith crop in jth interval;
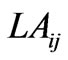 Labour availability for ith crop in jth interval;
Labour availability for ith crop in jth interval;
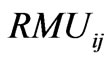 Requirement of manure utilization for ith crop in jth interval;
Requirement of manure utilization for ith crop in jth interval;
 Manure availability for ith crop in jth interval;
Manure availability for ith crop in jth interval;
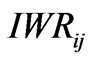 Irrigation water requirement for ith crop in jth interval;
Irrigation water requirement for ith crop in jth interval;
 Total water availability for ith crop in jth interval;
Total water availability for ith crop in jth interval;
i Crop index;
H1 Hot weather crops;
R1 Crops under rabi season;
R Rabi;
T1 Two seasonal crops;
P1 Perennial crops;
K1 Crops under kharif season;
X1… X10 Area under cultivation of a particular crop ‘i’ (ha);
µ (X) Membership function;
λ Degree of truth/Level of satisfaction

