Journal of Biomedical Science and Engineering
Vol. 5 No. 12 (2012) , Article ID: 25775 , 6 pages DOI:10.4236/jbise.2012.512092
An endothelial cell model containing cytoskeletal components: Suspension and adherent states
![]()
Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran
Email: kiumarsi@mech.sharif.edu, *mssaidi@sharif.edu, firoozabadi@sharif.edu
Received 3 September 2012; revised 4 October 2012; accepted 15 October 2012
Keywords: Endothelial Cell; Plasma Membrane; Cytoskeleton; Cell Adhesion; Force-Deformation Behavior of the Cell
ABSTRACT
Endothelium is the interior layer of an artery made up of tremendous number of endothelial cells which are located side by side. Finding the effective parameters that cause the cells to obtain mechanical strength in different morphologies is an important issue in cell biomechanics. In this work a numerical model for a single endothelial cell is developed. This model includes cell’s plasma membrane and nucleus using the traingular network of spectrin level approach. Cytoskeleton main components such as intermediate and actin filaments as well as microtubules are the other important subsets of the simulated model. Mass and spring theory is utilized in cytoskeleton components simulation. A spreading model is applied on the cell in order to simulate the adhesion on a substrate and test the model’s qualitative performance and the result is verified by the experiment. Also deformation of the cell caused by an external compressive force is another quantitative test which is predicted by the model and the results are validated with an experimental AFM test. The two most popular morphologies of the cells resulted from this work are the cell suspension morphology which is the result of no external forces and the cell adherent morphology which is the result of cell adhesion to the extracellular matrix. The mechanical stiffness of the endothelial cell is obtained in this simulation.
1. INTRODUCTION
Discovering the mechanical behavior of an adherent cell (a cell which is connected to the extracellular matrix) is one of the important goals in prevention and also treatment of the cardiovascular diseases. During cell’s feeding, migration, growth and death, apoptosis, proliferation, etc., endothelial cells need regular changes in their cell cytoskeleton structure. Several numerical models have been developed to help scientists to discover cells behavior under different loading conditions but more studies are needed for completing the weakness points of these models.
Working on cell mechanics has become popular in the last two decades. Recognizing the mechanism of arterial diseases like arteriosclerosis, heart attack requires discovering of cell’s behavior in different conditions especially for adherent-cell responses to mechanical stimulations [1]. These issues have got the attention of researchers modeling adherent forms of the cells [2]. Several methods are utilized in these models including continuum, molecular dynamics, and mass and spring methods. Experimental works have also been performed comprehensively over the last two decades. Experiment is a key approach for discovering the cell’s behavior and also its geometry. It has been used vastly in cell mechanics before any other approaches. For example scanning cell membranous and cytoskeletal structure [3] is one of the earliest experimental works done using scanning tunneling microscope. Imaging the main filaments inside the cell and showing the components such as hilly structure were the main purposes of their work, although the observed structure could not be fully characterized in that time so more imaging seemed to be needed for identifying certain molecular structure influenced in imaging process. Helmke et al. [4] used high resolution four dimensional fluorescent measurements to observe the cytoskeleton behavior in hemodynamic external forces. They analyzed the endothelial biomechanics and discussed the role of the cytoskeleton in a decentralized model of endothelial mechanotransduction process, as well. Moreover, they summarized the effects of external fluid stresses on strain distribution inside the cytoskeleton. Finally, they suggested the mechanisms for force transmission and transduction in their work.
Modeling a single cell membrane have been done by Fedosov et al. [5]. They developed a stress free erythrocyte model using a numerical coarse grained method. Bending stiffness, macroscopic elastic properties, area and volume constraints of the membrane have been considered in their model. Cytoskeleton is simulated in several studies too. For example, nucleus, actin filaments (or microtubules), focal adhesion site and also cell to cell adhesion proteins are considered in Mazzag et al.’s work [6]. They modeled the cell as a simple linear viscoelastic Kelvin body. Despite of these widespread efforts in single cell simulation, including all effective parameters is not possible in a numerical simulation. Moreover, studying adherent cell responses to the mechanical stimulation is critical because the adhesion of the cells to the extracellular matrix can be disrupted in high pulsatile flows as the result of the nature of these flows. One of the earliest works in disruption of the cell adhesion is Kong et al.’s work [7]. Thresholds of mechanical forces which disrupt cell adhesion molecules are analyzed in their microscopic model. Two threshold values of the traction forces applied to the cell can be obtained from their work; the first one indicates the region where the focal adhesion proteins grow in order to endure the traction force and the second value indicates the threshold of the rupture. In another similar work of cell modeling McGarry et al. [8] created a three dimensional eukaryotic cell model using finite element techniques and tensegrity network of interconnected links to simulate microtubules. Reaching the adherent cell non-linear structural behavior was the main goal of their work.
This study presents a mechanical endothelial cell model using the combination of mass and spring method and also spectrin level theory. To accredit the model, a cell was stimulated to adhere to a flat substrate and spread on it. Also for quantitative validation, a specific amount of force was applied to one node of the cell membrane and deformation of the mentioned node was observed, then the results were compared with that of AFM test. The model considers cytoskeletal forces with nucleus and outer membrane interactions. The magnitude of these forces is converted to reduced scale. This simulation tries to manifest a more comprehensive cell model by using a more complete cell structure in comparison with the previous cell models. Cell membrane, nucleus, actin filaments, microtubules, and intermediate filaments are some of the main organelles inside living cells which have been simulated in this work. Considering all these components will help the model to be more realistic and trustworthy but adding other sub-proteins such as actinins and filamins to the model will help it to show more precise behavior. The Spectrinlevel theory has been justified before [5,9,10]. Also mass and spring theory is one of the basic and popular tools in cell mechanics. The integration of the interactions among different organelles is a noticeable issue. In our model all the existing forces are converted to a reduced scale based on DPD1 method, then summation of forces in all nodes are checked to be zero in every time-step. The final outcome of this work is two major morphologies of a stable cell, cell suspension and cell adherent morphologies.
2. ENDOTHELIAL CELL MODEL
2.1. Cell Membrane Model
Membrane model is made up of two-dimensional traingulated networks with desired points in vertices. It is designed for 27,344 vertices (see Fedosov et al. [5] for more information). System energy is the sum of four independent energies, specified for any point {xi} as below: [5]
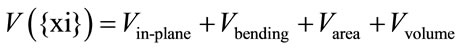 (1)
(1)
Vin-plane indicates elastic form energies of the system similar to spring. Worm like chain and finitely extensible non-linear elastic (FENE) are two most popular forms of this kind. The worm like chain elastic energy is the only one that has been selected for this model.
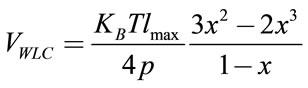 (2)
(2)
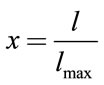 (3)
(3)
In this relation  is the maximum length of each link,
is the maximum length of each link, 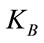 is Boltzmann constant,
is Boltzmann constant, 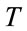 is the absolute temperature, and
is the absolute temperature, and 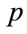 is the persistence length.
is the persistence length.
Bending energy prevents the deviation of angle between two adjacent triangles from equilibrium magnitude 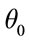 and conform to the following relation:
and conform to the following relation:
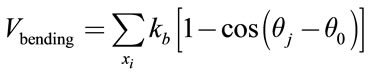 (4)
(4)
Area and volume free energies constraint membrane area and volume and enforce them to remain in their equilibrium state. It is assumed that the surrounded volume and surface area of the cell are approximately constant.
2.2. Nucleus Model
Nucleus is initially made of a spherical membrane designed in spectrin-level network and is shown in Figure 1. The nucleus model is similar to the cell plasma membrane (CPM) with the same potentials but with geometrically and physically different parameters. This membrane is stiffer than CPM (about ten times in bending stiffness) and is designed for 3000 vertices. Area and volume constraint ratios are considered as
 and
and , respectively.
, respectively.
In most of prior works nucleus is simulated as a hard spherical element which could not be deformed [11] but in this work the nucleus is designed as a deformable membrane with real nucleus physical parameters.
2.3. Cytoskeleton Model
The cytoskeleton supplies stiffness of the cell. It comprises three main protein filaments namely actin filaments, microtubules and intermediate filaments. These filaments are considered in our endothelial cell model.
Actins are about 5 - 8 nm in diameter with an elastic modulus of 2.2 GPa. These elements sustain extension of mechanical forces [12,13]. In microtubules α- and β- tubulin creates a tube like link with a natural resistance to both compression and torsion. Cross section of this filament is larger than actins (about 7.7 nm2) with elastic modulus of 1.2 GPa [11]. Intermediate filaments are other fibers whose size and physical properties are between actins and microtubules.
Our model links microtubule origin points, named centrosome, with other parts of the membrane using appropriate physical parameters. Centrosome is placed at a point close to the cell nucleus. In this model, it is assumed to be fixed relative to the nucleus; however, it actually can displace relative to the nucleus in large deformations. Also intermediate filaments are designed as springs that are making effective connections between nucleus and CPM. Intermediate filaments fill most of the inner cell space. Also actin filaments are assumed to connect two different points of the cell outer membrane so they can form the downward structure of cell membrane and provide more strength to it; as a result, the
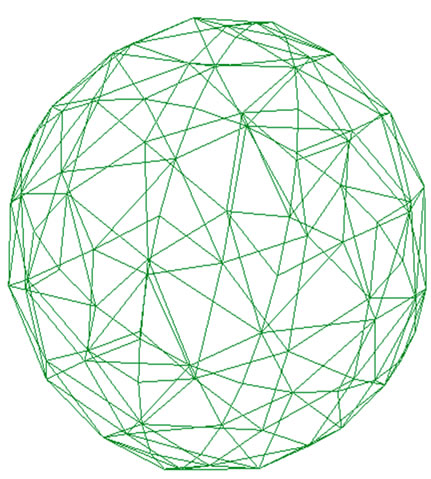
Figure 1. Spectrin-level network of nucleus.
dispersion of actin filaments in outer parts of the cell is more than other locations.
2.4. Adhesion Model
Cells are said to be in suspension morphology when they have not been connected to the extracellular matrix (ECM). In this condition the cells work in an isolated manner but the endothelial cells tend to reach their adherent morphology to be in a more stable condition. For doing some of the biological processes such as migration and proliferation the cells need to adhere to ECM. Indeed focal adhesion sites provide required mechanical linkages between cell cytoskeleton and its outer environment.
In this model, to simulate cell adhesion, a 6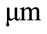 diameter suspended spherical cell is selected as initial condition using the results of Yamada et al., 2010. Adhesion to a flat plate known as ECM starts from the most bottom point of the cell. Next microtubules are lengthened from centrosome with a velocity of Vpol. Lengthening goes on until the end of the microtubule reaches to the flat plate (see Figure 2).
diameter suspended spherical cell is selected as initial condition using the results of Yamada et al., 2010. Adhesion to a flat plate known as ECM starts from the most bottom point of the cell. Next microtubules are lengthened from centrosome with a velocity of Vpol. Lengthening goes on until the end of the microtubule reaches to the flat plate (see Figure 2).
When the end point of a microtubule reaches the substrate, some integrin receptors sense the substrate so that the cell makes a connection with the ECM via a mediator protein named integrin.
Microtubules force compression applied to the outer membrane is calculated from Equation 5 [11]:
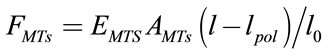 (5)
(5)
where  is the initial length of microtubule and
is the initial length of microtubule and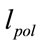 is the length of microtubule due to polymerization.
is the length of microtubule due to polymerization.
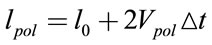 (6)
(6)
The effects of other factors like membrane force, actin tension and tensional components causes the real length of microtubule ( ) to be less than
) to be less than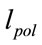 .
.
In the next stage a specific amount of force was applied to the model and its deformation was tracked. The objective of this test is measuring the cell stiffness. The AFM test is a common experimental procedure for obtaining the cell stiffness therefore the results of our
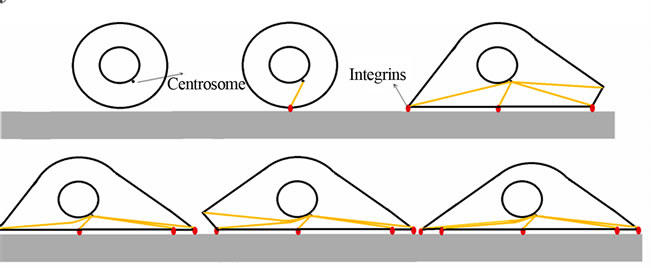
Figure 2. Schematic steps of focal adhesion. From left-top (suspended) and right-bottom (fully adherent cell). Using [11].
numerical solution are compared with experimental AFM tests [14]. The amounts of cross section and Young module used in this work are shown in Table 1. These values are obtained by considering the following references: [11-13,15].
3. RESULTS AND CONCLUSION
3.1. Results
In the first step, the simulated cell is released from an initial optional condition without any external force (suspension morphology was expected in this step). Intermediate filaments and membrane potentials as well as nucleus potentials are activated. Reaching the minimum level of system energy, the cell obtains its suspension morphology, while suspension is a morphology in which the cell faces just interior interactions and no other external part adheres to it (see Figure 3). Cell’s spherical configuration is in good agreement with Caille et al. [16] results.
In the second numerical simulation, a spherical 6 diameter cell, started from suspension state, adheres to a flat plate which is in a 0.05
diameter cell, started from suspension state, adheres to a flat plate which is in a 0.05 distance under the cell’s lowest point. Microtubules start lengthening and the cell spreads until adheres to the substrate (see Figure 4). Other views are shown in Figures 5 and 6.
distance under the cell’s lowest point. Microtubules start lengthening and the cell spreads until adheres to the substrate (see Figure 4). Other views are shown in Figures 5 and 6.
A cell starts from the suspension state and the microtubules exert compression forces to plasma membrane
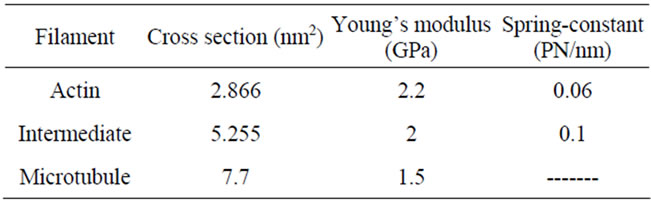
Table 1. Physical constants of different filaments.
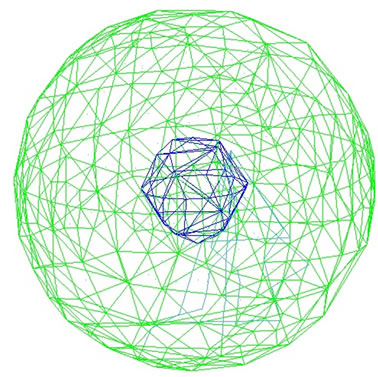
Figure 3. Minimum energy state of the system of an endothelial cell, when no external force is applied. Blue links display nucleus network and greens are for cell membrane.
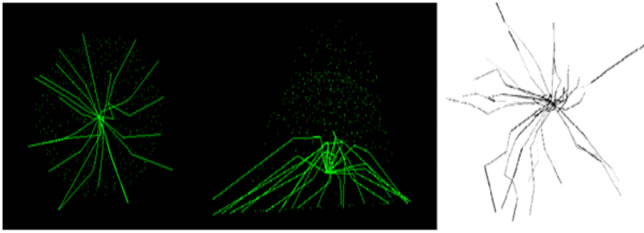
until full adhesion is achieved. A comparison has been made between simulated model and Wendling et al. (2000) experiment (cited in Maurin’s paper, 2008) (see Figure 5). This figure shows an acceptable agreement with the mentioned work. A same comparison has been made in microtubule lengthening shape confirming the simulation results (see Figure 6).
The change of lengthening force of the microtubules
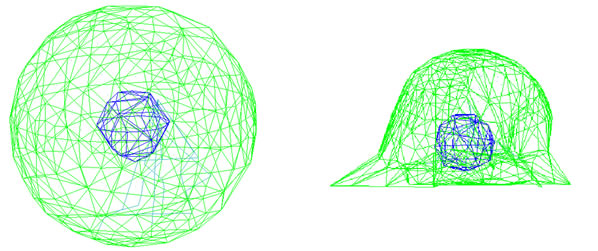

Figure 4. Cell focal adhesion steps, cell start from an initial condition (left) and after microtubules lengthening, it reaches to an adherent shape (right).
 (a)
(a)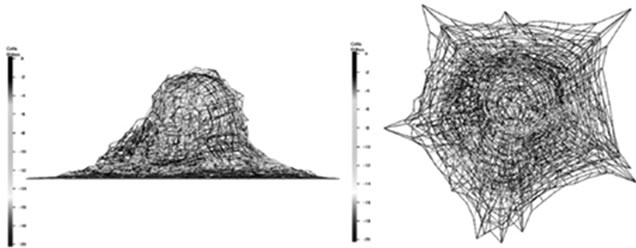 (b)
(b)
Figure 5. Cell final adhesion isometric (left) and top view (right) our simulation (a) and Maurin’s work (b).
 (a) (b)
(a) (b)
Figure 6. Microtubules growth during cell adhesion: (a) top and lateral view, our simulation; (b) and Maurin’s result.
in an adhesion process is shown in Figure 7. After cell spreading, the amount of the force approaches the asymptotic value which represents the cell static equilibrium.
3.2. Stiffness Measurement Results
An analogy between experimental atomic force microscopy and numerical test displaying force-deformation curves is done (see Figures 8 and 9). Experimental results are taken from Sato et al. work [14] which is performed in bovine cultured endothelial cells. In this work the force is applied to two different points of the cell, the topmost point and a point in the neighborhood of the middle height region. These two points are selected from the nodes of the spectrin network of the cell’s membrane. The results of the topmost point (displayed in Figure 8) are extracted by tuning the stiffness of the cell-components in their allowable range and their amounts are
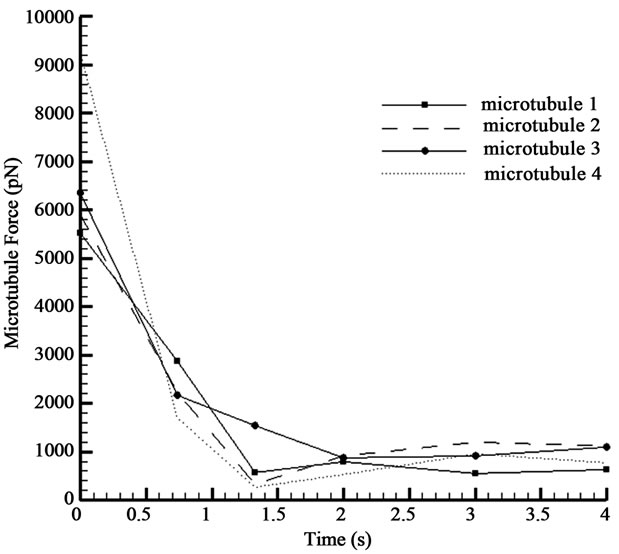
Figure 7. Microtubule force acted to the membrane.
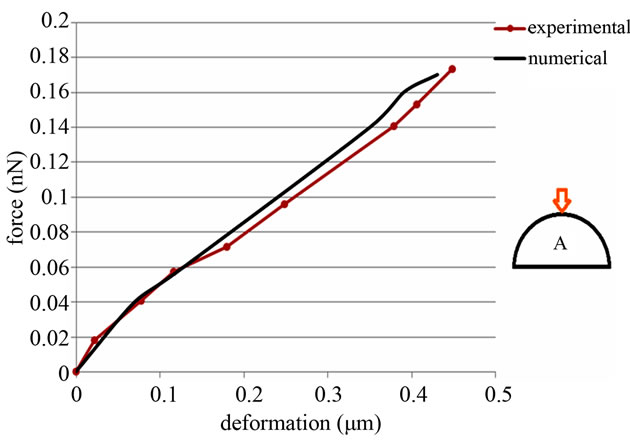
Figure 8. Force-deformation curve, comparison simulated model with Sato et al.’s experiments (2000). Force is applied to the topmost point.
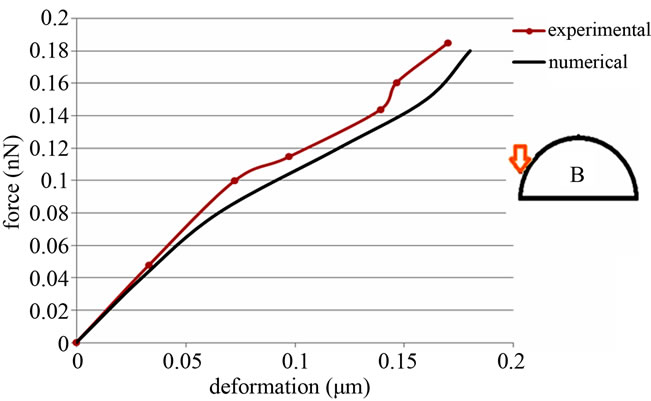
Figure 9. Force-deformation curve, comparison simulated model with Sato et al.’s experiments (2000). Force is applied to an adjacent point.
shown in Table 1. In the next test no tuning is done and the same quantities of the first test have been used. The results shown in Figure 9 illustrate the simulated model’s reliability.
It can be noticed that a cell is more flexible in its top point and cell-stiffness increases in the adjacent regions. Considering the experimental errors and the amount of uncertainty in involved parameters, these results confirm the Sato et al.’s work [14].
Considering Figures 8 and 9, it is noticed that there is a mismatch between the experimental and numerical data to some degree. This can be explained as follows. First of all, it should be noted that cell is a living being with varying properties in response to external stimuli. The degree to which the properties change is dependent on the specific strength of a given stimulus. These changes in properties introduce some uncertainty to numerical as well as experimental results. In addition, the model that we have developed for the cell is a simplified model of the real cell. This simplification and cumulative error in numerical simulations may have contributed considerably to the observed deficiency. It is also to mention that Sato et al. performed experiments on bovine endothelial cells, while the present model is developed based on human cells. Therefore, one may not expect to obtain numerical results in full agreement with the corresponding experimental data. To this end, it should be noted that the experimental measurement errors could be a source on mismatch. Regarding the aforementioned discussion, it should be said the main comparable feature between our numerical results and the referred experimental data may be the variation trends, which are in good agreement with each other.
3.3. Conclusions
The main and important target of this paper is to study the mechanical behavior of an endothelial cell by developing a numerical model. Required values (stiffness and other necessary parameters) were searched in prior works comprehensively, but no particular quantity for cellparameters was obtained with certainty, which means that there is a range of values available for these parameters. Therefore by changing the amount of coefficients in the admissible range the model can be used for human, bovine and other existing endothelial cells. The best result (in 27,344 vertices of membrane’s network) was obtained for a nucleus with 3000 vertices. Microtubules and actins are designed as mechanical columns and cables; which could bear compression and extension, respectively. For validation, the cell adhering on a flat substrate is simulated. Results are in an acceptable agreement with other similar numerical and experimental results.
This model could be applied to some other simulations too. One of the most important questions in biology is the cell migration mechanism. This mechanism could be observed easily using actin cytoskeleton regulation using this numerical model.
4. ACKNOWLEDGEMENTS
The authors gratefully acknowledge Mr. A. Mahboudi and Mr. Amir H. Khalighi for their contribution in computer programming.
REFERENCES
- Khazaei, M., Afshari, F.M. and Laher, I. (2008) Vascular endothelial function in health and diseases. Pathophysiology, 15, 49-67. doi:10.1016/j.pathophys.2008.02.002
- Zeng, X. and Li, S. (2011) Multiscale modeling and simulation of soft adhesion and contact of stem cells. Journal of the Mechanical Behavior of Biomedical Materials, 4, 180-189.
- Ruppersberg, J.P., Hober, H.J.K., Gerber, C. and Gert, B. (1989) Imaging of cell membraneous and cytoskeletal structures with a scanning tunneling microscope. FEB 08715, 257, 460-464.
- Helmke, B.P. and Davies, P.F. (2002) The cytoskeleton under external fluid mechanical forces: Hemodynamic forces acting on the endothelium. Annals of Biomedical Engineering, 30, 284-296. doi:10.1114/1.1467926
- Fedosov, D.A., Caswell, B. and Karniadakis, G.E. (2010) Systematic coarse-graining of spectrin-level red blood cell models. Computer Methods in Applied Mechanics and Engineering, 199, 1937-1948. doi:10.1016/j.cma.2010.02.001
- Mazzag, B. and Barakat, A.I. (2010) The effect of noisy flow on endothelial cell mechanotransduction: A computational study. Annals of Biomedical Engineering, 39, 911-921. doi:10.1007/s10439-010-0181-5
- Kong, D., Ji, B. and Dai, L. (2010) Stabilizing to disruptive transition of focal adhesion response to mechanical forces. Journal of Biomechanics, 43, 2524-2529. doi:10.1016/j.jbiomech.2010.05.019
- McGarry, J.G. and Prendergas, P.J. (2004) A three-dimensional finite element model of an adherent eukaryotic cell. European Cells and Materials, 7, 27-34.
- Discher, D.E., Boal, D.H. and Boey, S.K. (1998) Simulations of the erythrocyte cytoskeleton at large deformation. II. micropipette aspiration. Biophysical Journal, 75, 1584-1597.
- Li, J., Dao, M., Lim, C.T. and Suresh, S. (2005) Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophysical Journal, 88, 3707-3719. doi:10.1529/biophysj.104.047332
- Maurin, B., Canadas, P., Baudriller, H., Montcourrier, P. and Bettache, N. (2008) Mechanical model of cytoskeleton structuration during cell adhesion and spreading. Journal of Biomechanics, 41, 2036-2041. doi:10.1016/j.jbiomech.2008.03.011
- Shin, J.H., Mahadevan, L., So, P.T. and Matsudaira, P. (2004) Bending stiffness of a crystalline actin bundle. Journal of Molecular Biology, 337, 255-261. doi:10.1016/j.jmb.2004.01.028
- Palmer, A., Cha, B. and Wirtz, D. (1998) Structure and dynamics of actin filament solution in the presence of latrunculin A. Journal of Polymer Science, 36, 3007-3015.
- Sato, M., Nagayama1, K., Kataoka, N., Sasaki, M. and Hane, K. (2000) Local mechanical properties measured by atomic force microscopy for cultured bovine endothelial cells exposed to shear stress. Journal of Biomechanics, 33, 127-135. doi:10.1016/S0021-9290(99)00178-5
- Kreplak, L. and Fudge, D. (2006) Biomechanical properties of intermediate filaments: From tissues to single filaments and back. BioEssays, 29, 26-35. doi:10.1002/bies.20514
- Caille, N., Thoumine, O., Tardy, Y. and Meister, J.J. (2002) Contribution of the nucleus to the mechanical properties of endothelial cells. Journal of Biomechanics, 35, 177-187.
NOTES
*Corresponding author.
1Dissipative Particle Dynamics.

