Materials Sciences and Applications
Vol. 4 No. 1 (2013) , Article ID: 27073 , 13 pages DOI:10.4236/msa.2013.41006
Li Mold Thermo-Mechanical Rigidity Criterion for Surface Quality of Continuous Casting of Steel
![]()
Royal Institute of Technology, Stockholm, Sweden
Email: moelbealy@hotmail.com
Received October 9th, 2012; revised November 8th, 2012; accepted December 1st, 2012
Keywords: Continuous Casting of Steel; Surface Quality; Solid Shell Resistance
ABSTRACT
A theoretical investigation of heat flow, solidification and solid shell resistance “Ic” has been undertaken by using a mathematical model and previous plant trials. The ultimate purpose is to develop operating conditions and therefore to improve the surface quality for continuously cast steel slabs. A new simple criterion called mold thermo-mechanical rigidity “MTMR” has been proposed to evaluate and to improve these purposes. The parameters of MTMR and its non-dimensional number which use to control the surface defects are present in this investigation. Previous plant trails of slab surface defects formation have been investigated thermo-mechanically with this criterion. The predications show that this criterion is very sensitive of operating parameters and is a significant qualitative tool to evaluate the surface quality. From examination of the behavior of MTMR, the susceptibility and mechanism of surface defects formations with MTMR have been primarily discussed.
1. Introduction
Nowadays the continuous casting technology is still undergoing important developments due to the facts that the requirements on product quality, increasing the productivity, saving the energy and recently on the needs of clean environment are continuously being increased. These developments incorporate not only equipment revamps or updates in the installation setups and in their process controls but also in the strategies developments of zero defects by helping the computational models. Computational models of heat transfer, solid shell resistance, interdendritic strain, and micro/macrosegregation are powerful and reliable tools to help of avoiding the defects formation in different cooling zones.
The first requirement to develop a successful zero defects strategy to avoid defects formation is to gain insight into thermal fields during solidification especially in the mold zone and to have an in-depth knowledge of mechanisms of many complex phenomena associated with mold heat transfer and therefore the mechanisms behind the surface defects formation and breakouts. Figure 1(a) shows a schematic of these mechanisms [1]. Liquid metal flows into the mold cavity through a submerged entry nozzle and is directed by the angle and geometry of nozzle ports [2]. Mold powder added to the free surface of the liquid steel melts and flows between the steel and the mold wall to act as a lubricant [3,4]. Shrinkage of steel shell away from the mold walls may generate contact resistances or air gaps, which act as a further resistance to heat flow, especially after the slag is completely solid and unable to flow into the gaps. Finally, the flow of cooling water through vertical slots in the copper mold walls withdraws the heat and controls the temperature of the copper mold walls. After exiting the mold, the steel shell moves between successive sets of alternating support rolls and spray nozzles in the spray zones. The accompanying heat extraction causes surface temperature variations while the shell continues to solidify. It is obvious that many diverse phenomena simultaneously control the complex sequence of events which govern heat transfer and therefore result in formation of surface and subsurface defects.
In the present work, it has been undertaken to develop a fast, simple and flexible criterion to predict and evaluate the surface defects formations in continuously cast steel slabs. Subsequently, this study has been conducted as theoretical investigation with previous metallurgical studies on the plant trials of early solidification stages in continuously cast steel slabs to clarify the mechanism of “MTMR” with different effects of operating conditions based on the nature of surface defects formation.
2. Model Formulation
The present work computes 1-D transient heat flow, so-

Figure 1. Schematic of (a) mold and upper spray zones phenomena of continuous casting process [1], (b) 1-D grid of computation and (c) superheat flux conditions [1].
lidification and solid shell resistance through the solidifying shell and mushy zone. This because the Pèclet number [5] (Pe = vLmoldrCp/l) in the directions of z and y of this process are high and are equal to (Pez = 2.406 × 103) and (Pey = 5.697 × 103), respectively [5]. Therefore, a 3-D problem can simplify it into full 1-D problem. Subsequently, 1-D mathematical model domain represented schematically in Figure 1(b) is for middle of the long transverse cross-section moving downward with steel shell by the slab casting speed.
Superheat from liquid steel was evaluated by using the same approach developed by Huang et al. [6]. This approach was used to estimate the superheat flux “qsh” tabulated in Table 1. It was found that this flux varies linearly with superheat temperature difference as shown in Figure 1(c) and is almost directly proportional to casting speed. Figure 1(c) represents results for a typical bifurcated, downward directed nozzle. The influence of this function is insignificant to shell growth over most of the wide face, where the superheat flux is small and contact with mold is good [6]. This model then has been developed based upon the general frame work for governing equations as presented by Poirier and his co workers of thermal analysis [7].
In order to calculate the different phases of low and peritectic carbon steels, the solidification behaviors of different steels can be classified into three modes as shown in Figures 2(a)-(c). The same approach developed by Rogberg [8], for calculating delta phase of different carbon steel alloys whereas Fredriksson and Stjerndahl [9], approach was used to calculate the different interdendritic liquid and dendritic solid phases dur-
Table 1. Heat flow conservation equations and the boundary conditions [5,7].
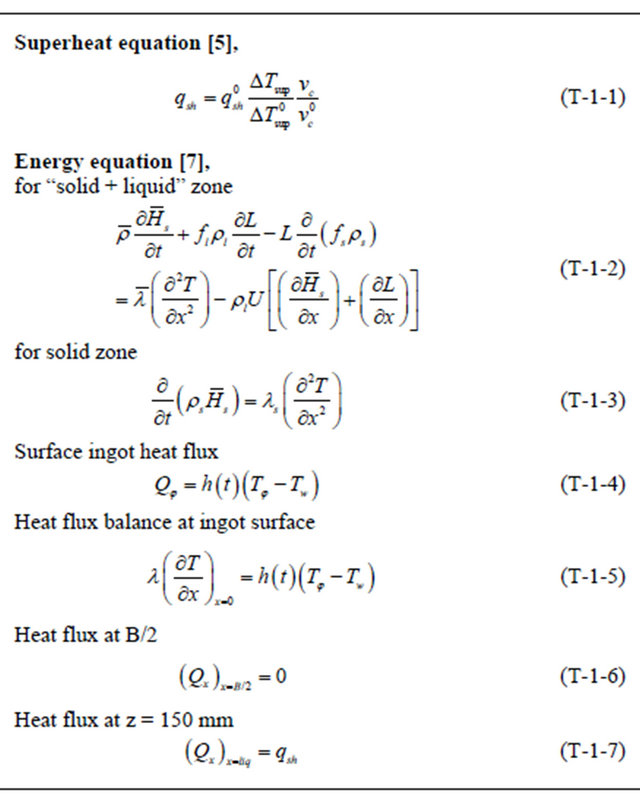
ing solid phase transformation or during peritectic reactions [9,10]. Also, Miyazawa and Schwerdtferger [11] proposed an approach to model the resistance of coherent solid shell against the thermo-mechanical stresses subjected to slab as shown in Figures 3(a) and (b). This approach was modified by El-Bealy [12,13] to involve
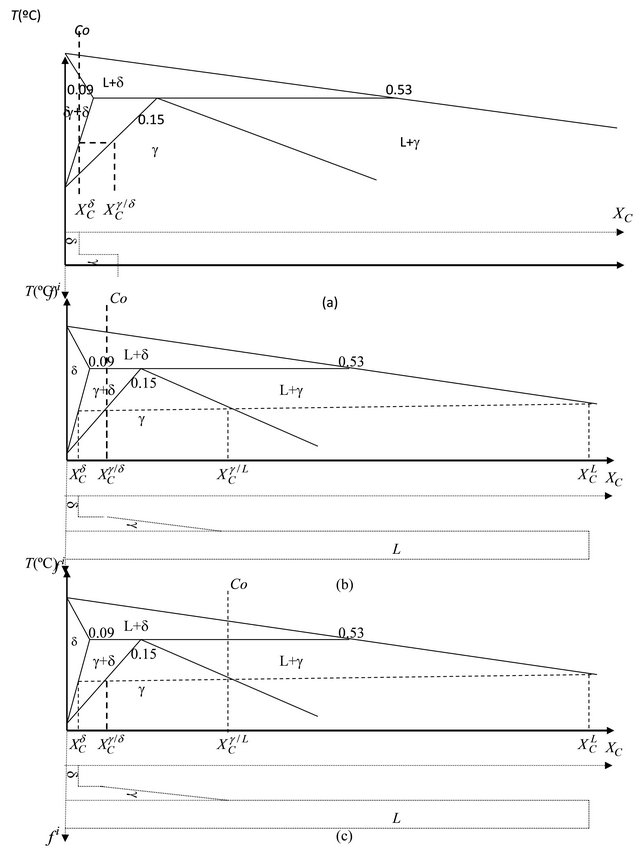
Figure 2. Carbon concentrations during phase transformations, (a) mode 1, (b) mode 2 and (c) mode 3 of Fe-C alloys [13].
the effect of different solid dendritic phases on the solid shell resistance as illustrated in Figures 3(c) and (d). Tables 1-3 summarize the model governing equations and its supplementary relations. Only few explanations are provided here, and the reader is referred to the originnal references for the details of the model and assumptions made in the derivations of its governing equations.
However, In order to examine a mold quality criterion of continuously cast steel slab, a new criterion called mold thermo-mechanical rigidity “MTMR” has been proposed to reveal slab macro/micro-surface defects level such as macrosegregation level, interdendritic cracks, oscillation marks, bulging and related defects formed in the mold zone [14]. This concept can be defined by computing the non-dimensional MTMR number to define the thermomechanical shell resistance against different types of stresses in the mold as follows [14];
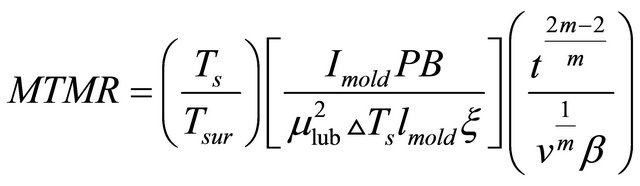 (1)
(1)
The first part of Equation (1) is pure thermal part which consists of the ratio  between steel solidus temperature “Ts” and the surface temperature “Tsur”. Ts covers the effects of composition and macro segregation whereas Tsur includes the effects of cooling conditions and steel type on MTMR and therefore on the thermo-mechanical resistance of different stresses. The
between steel solidus temperature “Ts” and the surface temperature “Tsur”. Ts covers the effects of composition and macro segregation whereas Tsur includes the effects of cooling conditions and steel type on MTMR and therefore on the thermo-mechanical resistance of different stresses. The
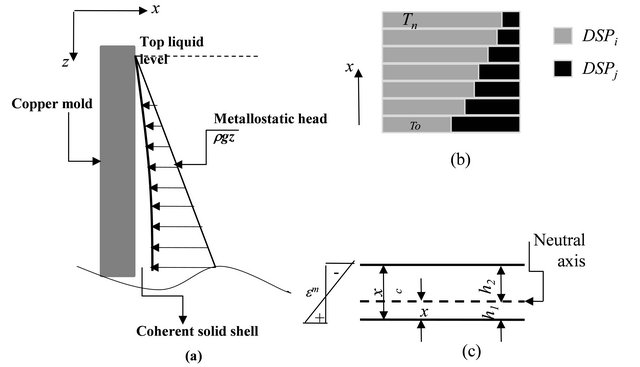
Figure 3. Schematic representation of (a) metallostatic head, (b) dendritic solid phases distributions and (c) neutral axis cross section [44].
Table 2. Conservation equations of solidification phenomena of carbon steels [8,9].

metallurgical studies and measurements by Brimacombe et al. [16], they concluded that the surface cracks are interdendritic, high positive segregated and thus their dendrites behave brittle [16]. Equation (1) indicates that MTMR is inversely proportional to Ts and therefore to the level of macrosegregation which it agrees well with Brimacombe et al. metallurgical examinations [16].
The second part is thermo-mechanical part and consists of several parameters in the nominator and dominator of Equation (1). In the nominator of Equation (1), it includes Imold which contains the indirect effects of cool-
Table 3. Solid shell resistance equations and creep strain relations [11,29].

ing conditions [16], solidification behavior of alloy [13], and macrosegregation level on MTMR. This agree well with the metallurgical studies and measurements by Brimacombe et al. [16]. This may give an explanation for different categories of surface crack morphology especially the changes in the crack width and its depth. The second factor in the nominator of this part is ferro-static. It helps to push the solid shell out into the mold wall and compensates the air gap width. Consequently, this may improve the heat flow performance from slab surface into the mold wall and may reduce the surface reheating degree. B is a last parameter and helps to resist the thermo-mechanical stresses based on stress analysis on the slab geometry. However, the increasing in B may reduce the susceptible to surface crack formation based on the type of contact with mold wall [17]. Irving and Perkins [18] have suggested that thin slabs are more susceptible to surface crack formation than thick slabs. But, they have cautioned against this observation such a conclusion because thinner slabs are normally casted at a higher speed.
In dominator of the second part of Equation (1), the mold powder viscosity which normally adds to the free surface of the liquid steel affects MTMR. It melts and then flows into the mold wall with liquid steel to act as lubricant which results in decreasing in the thermal conductivity of steel compound and reduces the heat flow from steel compound into mold wall. This causes to delay the dissipation of superheat stored in the liquid steel which affects the surface temperature and the solid shell growth. Based on the melting temperature and viscosity of mold powder, therefore, the square of mlub is inversely proportional to the degree of resistance of thermo-mechanical stresses or to MTMR. The support for this mechanism was found in the scanning cracked samples and their micrographs by Brimacombe et al. [16] where concentrations of elements Si, Al, Ca, K and Na, which contained in the mold powder were found in all cracks studied even at the root. They concluded that the crack must has nucleated and formed when the mold powder was liquid and able to penetrate to the crack root [16]. The second parameter in the dominator of this part is melt superheat “DTs” which it’s increasing decreases MTMR. This agrees well with reports by Larsen and Moss [17]. They concluded that the severity of surface cracks especially longitudinal mid surface cracks increases with increasing the melt superheat. The third parameter in the dominator of second part is mold length lmold. Previous work by Dippenaar et al. [19], Watanabe et al. [20] and Chandra et al. [21] pointed out that in the upper region of mold, the air gap is considerably less than a millimeter wide but, many cases accounts for as much as 80% - 90% of the total resistance to heat flow. This mechanism agrees well with scanning micrographs by Brimacombe et al. [16] where the white line or structure change due to the air gap formation and its position can give a clear answer about the sudden change into a high positive macro-segregation level. Therefore, this width increases with increasing the mold length resulted in a high positive segregation level. This leads to decrease in the resistance to thermo-mechanical stresses and therefore it is inversely proportion to MTMR as shown in Equation (1). Finally, the last parameter in the dominator of this part is chill roughness “x”. The laboratory scale experiments by Muojekwu et al. [22] are evident that heat extraction increases with increasing surface smoothness of chill, resulting in an increase in shell thickness and a decrease in secondary dendrite arm spacing. This means that the increasing in the chill roughness decreases the resistance of thermo-mechanical stresses and therefore is inversely proportion to MTMR as illustrated in Equation (1).
Finally, the material part in Equation (1) reveals mold dwell time “t” and casting speed “v” in nominator and dominator of Equation (1), respectively, for non-dimensional mathematical requirements. Also, different materials formula of exponent creep material m appeared in both the nominator and dominator of Equation (1) represented the effect of different types of steels on MTMR. Wherever, Morozenskii et al. [22] have reported that steel containing 0.17% C to 0.2% C has a minimum strain to fracture compared to the steels with higher or lower carbon levels where the creep properties varies with carbon content of different types of steel alloys. This affects the solidification and shell formation and therefore, affects resistance of thermo-mechanical stresses [22,23]. Equation (1) shows also the effect of thermal linear expansion coefficient “β” revealed in its dominator where it was concluded that the shape and width of the air gap which has a large responsibility about the mold heat flow depends mainly on β and local temperature distribution [23,24]. Therefore, the value of β affects directly the resistance of thermo-mechanical stresses where the increasing in β may decrease MTMR.
Heat transfer at ingot surface was assumed to follow a generalised Newtonian law and the initial and boundary conditions were described in detail in Refs. [15,25,26] and the equations used in these computations are summarized in Table 1. However, El-Bealy and Fredriksson [27] approach was used to determine the mold cooling condition.
The model requires simultaneous solution of governing equations in Tables 1-3. The simulation starts by stetting the initial steel to the pouring temperature. Then, each time step begins by estimating the new casting temperature distribution Different dendritic phase fractions and thermo-physical properties of steel were then calculated. The initial Newtonian heat transfer coefficient is then estimated based on the previous experience. In order to evaluate thermal fields, the heat flow equations in Table 1 are solved where these steps repeat until solutions converge. Applying the temperature distribution to calculate the thermo-mechanical curves, the model then analyzes the thermo-visco-elastic and mechanical deformation behavior of the steel and calculates the strains in different zones. Then, the model calculates the macro-segregation distribution and these steps repeat until the error between the measurements and predicted segregation are within ±5%. The results use then as initial conditions with different mold parameters for calculating the mold thermo-mechanical criterion which solve Equation (1).
Also, work adopts temperature-dependent steel properties chosen to be as realistic as possible. The actual liquidus and solidus temperatures of multi-components alloy are summarized in Ref. [28] whereas the functions for calculating the equilibrium partition, diffusion coefficients and thermo-physical properties are illustrated in Refs. [29-33]. The temperature-dependent conductivity and enthalpy functions for multi-component alloying elements or impurities for plain steels and their different phases are fitted from measured data compiled by Harste [32]. Although, the density of steel and its changes with temperature is very feeble of different phases of plain carbon steels but the effect of composition seems important in this work as well as the need to compute the molar volume of different phases. These functions can be calculated from the relations summarized in Ref. [34]. However, the exponent creep material “m” in Equations. [T-III-2] and [T-III-5] of steel alloys are determined experimentally from uniaxial tests and its values are summarized in Ref. [32].
3. Pervious Plant Trials & Measurements
The simulated slab casters are based on two actual Industrial casting machines and the reader is referred to the original references for the details of cooling and operating conditions [16]. Table 4 gives the composition and casting conditions of slabs from the defect samples were taken. The superheat “DTs” was taken constant and is equal to 20˚C for different heats. Two mold powders were examined in these trials and their viscosity were summarized in Table 5 with temperature [25].
4. Simulated Results & Comparisons
The model developed in the previous sections in this paper was applied to simulate the continuous casting of steel in two different molds where previous experimental measurements had been made as described in the a series of previous papers [16,25].
Table 4. Composition and casting conditions of defect slab samples [16].
Mold thickness is average, 240 mm.
Table 5. Mold powder used in Trials [21].
4.1. Case 1
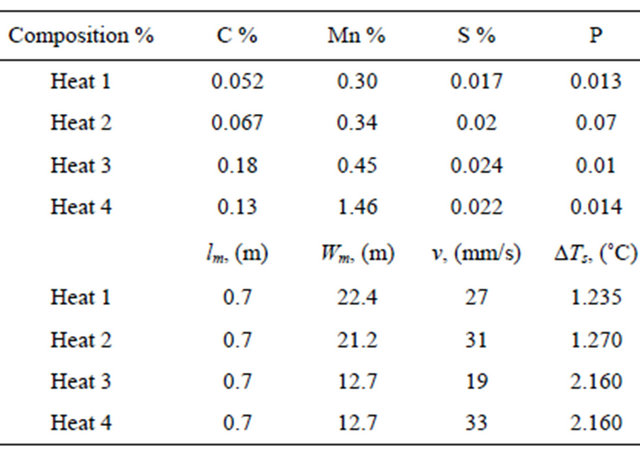
Figures 4(a)-(d) show the comparisons between the predicted heat fluxes “Qf” surface temperatures “Tf”, coherent solid shell resistances “Ic and mold thermo-mechanical rigidity criterion “MTMR”, respectively, for case 1.
Figure 4(a) shows the variation of surface heat flux “Qf” with distance from meniscus for different heats. At pouring temperature, it is considered that heat transfer controlled by turbulent convection streams in liquid region where liquid metal flows into the mold through a submerged entry nozzle and directed by the nozzle characteristics. Therefore, it can be seen that the initial value of Qf of the initial sub-region of BAGF is always within 1200 kW/m2 for different heats 1 and 2. These values decrease slightly and reach a minimum value of 800 kW/m2 at distance 175 mm beneath the meniscus where the direction of the steel jet controls and concentrates the heat flux of turbulent fluid flow on the solidified shell. [1,2] This affects delivery of superheat to the solid/liquid interface of the growing shell. This agrees with the predications and measurements of Panaras et al. [35] and might help to explain the mechanisms of different mechanisms of surface defects formation. As solidification starts, the dendrites begin to grow and the heat transfer mode changes [36]. Consequently, Qf increases slowly based on the solidification behavior, cooling and fluid flow conditions until the coherent temperature. At the initial coherent sub-region, it is obvious that Qf rises rapidly from initial contact values of 800 until peak values 2000 and 1620 kW/m2 at 200 mm for heats 1 and 2, respectively. This is due to a changing in the heat transfer mode from convection/conduction into a conduction mode [36]. Once the solidifying shell becomes self supporting, it contracts in accordance with thermo-mechanical and shrinkage properties of casting, while the mold wall may expand. The relative magnitude of the casting contract, shrinkage and the chill expansion, together with any pressure acting on the interface determines the type of contact between the mold wall and slab and therefore controls the heat transfer flux in AAGF. Subsequently, the peak values decline sharply to 650 kW/m2 for different heats as shown in Figure 4(a). A further slight decreasing in heat flux occurs as the width of gap grows, coupled with increasing thermal resistance between the solidified shell and mold wall. From the onset of a steadily growing gap, the air gap increases very slowly [35,36] which results in a slight fluctuation of heat flux due to the effect of increasing in the ferrostatic head effect. This is associated with very slight decreasing in Qf until minimum value at mold exit 100 kW/m2. In general, the predications point out that there is no observed difference between the heat fluxes of heats 1 and 2 expect in initial coherent region where the difference is observed between peak values and also at the mold exit.
The surface temperature profiles shown in Figure 4(b) illustrate the effect of various mold cooling zones on the surface temperature “Tf”. These profiles demonstrate that Tf falls by different cooling rates based on the natural of cooling region in the mold zone. Subsequently, in initial BAGF, the slab surface cools gradually into 1320˚C when the molten steel is still in the liquid zone. As solidification starts, the cooling rate reduces slightly until 1300˚C where the latent heat of fusion starts to dissipate during solidification process. Based on the magnitude of coherence temperature, Tf cools rapidly into 1200˚C. When the air gap begins to form, the solid shell separates from the mold wall in AAGF. This results in a complete changing in the heat transfer mode and the slab surface reheats into 1225˚C. This is followed by a gradual reheating of slab surface until 1244˚C at 500 mm beneath the meniscus. Tf cools again and leaves the mold by different values where Tf in the case of heat 2 is higher than Tf in the case of heat 1. This agrees with experimental work and measurements performed by Brimacombe et al. [16] where heat 2 reveals a higher depth from slab surface of longitudinal mid-face surface cracks than its depth in heat 1.
Simulation of Ic is also often used as criterion for measuring the resistance against different thermo-metallurgical and mechanical stresses subjected to the slab in different cooling zones [11,29]. Recently, this criterion affects significantly the mold heat transfer especially in AAGF and therefore the air gap width profile. This quantity was studied here under various mold cooling conditions and solidification phenomena for its importance. Therefore, to examine the influence of various operating conditions of different heats on the ability of coherent shell to resist different thermo-mechanical stresses and therefore, to control the mold thermo-mechanical rigidity, the model was used to simulate Ic and its results are shown in Figure 4(c) for different heats 1 and 2. Subsequently, the model predications show that Ic increases continuously with distance from meniscus by different growth rates where the same profiles for different heats were observed. The results show there is no any significant resistance within the first 200 mm. Then, when the slab shell becomes coherently, Ic begins to increase by different growth rates based on the various mold cooling conditions. The model predications show also that there is no observed difference in Ic between two heats until 400 mm. Then, this difference starts to enlarge gradually until the mold exit. This is due to a difference in the surface reheating temperatures for heats 1 and 2. These change the temperature gradients of solid shell and mushy zone which control the growth rates of different isotherms [29].

Figure 4. Variations of (a) mold heat fluxes, (b) surface temperature, (c) mold solid shell resistance and (d) mold thermomechanical rigidity number with distance from meniscus for heats 1 and 2.
It has been suggested that the mold thermo-mechanical rigidity criterion “MTMR” for different mold cooling conditions can be related to surface quality of continuously cast steel slabs [14]. Also, it helps the steel Industries men to deepen their understanding of complex mechanisms of the different defects formation and to prevent them [37-39]. Therefore, in order to check, the validity of this criterion, solution of Equation (1) to compute MTMR with distance from meniscus is graphically represented in Figure 4(d) for heats 1 and 2. The model results illustrate that MTMR grows from very small values close to meniscus until 240 mm beneath the meniscus. As indicated in the various studies of industrial practices conducted by Brimacombe et al. [16] and Morozenskii et al. [40], it is common practice that the formation of longitudinal mid-face surface cracks start to nucleate in the area beneath the meniscus directly and within the first 100 - 200 mm [41]. This is due to a generation of the thermo-metallurgical interdendritic strain only as shown in Figure 4(d) [43]. After 250 mm, MTMR begins to grow exponentially by the same trend as Ic growth shown in Figure 4(c). The effect of Tf and Ic on MTMR is clearly observed at mold exit where the value of MTMR of heat 1 is higher than its value of heats 2 and the effect of mechanical stress due to ferro-static head begins to consider [16].
4.2. Case 2
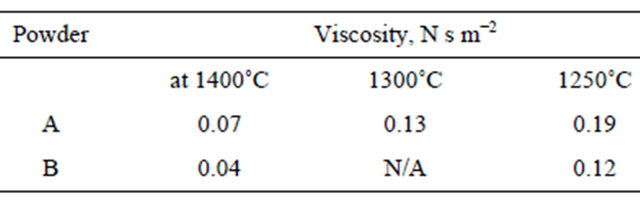
In the case of peritectic carbon steels, the comparisons between the behaviors of the heat fluxes “Qf” surface temperatures “Tf”, coherent solid shell resistances “Ic” and mold thermo-mechanical rigidity “MTMR” for case 2 are shown in Figures 5(a)-(d), respectively.
Figure 5(a) shows the comparisons of predicted Qf in the mold zone for different heats 3 and 4. Overall, it can be seen from this figure that Qf follows the same trend in various mold cooling regions. Consequently, the quantitative differences appear due to the changes in type of steel alloy and low casting speeds [42,43]. In initial BAGF, the predications demonstrate that the initial value Qf decreases slightly from initial value 1200 into 800 kW/m2 within 200 mm for different heats due to the effect of turbulent flow and superheat. Consequently, the situation changes completely at the coherent region where Qf raises rapidly from initial value of 800 until peak values of 1400 and 1600 kW/m2 at 250 mm for heats 3 and 4, respectively. This is followed by a steep drop in Qf into 720 kW/m2 in AAGF. As air gap continues to grow, Qf decreases gradually by different rates into minimum values at mold exit associated with slight fluctuations. Not surprisingly, Qf reveals no difference between the heat fluxes of heats 3 and 4 expect in initial coherent region where the difference only is observed between the peak values. This agrees with measurements by Singh and Blazek [42], as well as the measurements by Samarasekera et al. [43] The differences between the previous measurements and present results are due the different in the mold cooling conditions [42,43].
The profiles of Tf shown in Figure 5(b) illustrate the comparisons between Tf histories for heats 3 and 4. It can be seen, the similar trend is observed of surface temperature profiles in the mold zone. Tf cools or reheats by different rates in the mold regions. In initial BAGF, the surface cools into 1300˚C within the first 150 mm. As solidification starts, the cooling rate reduces due to the effect of the latent heat of fusion and therefore the surface slightly cools into 1250˚C. As solidification continues, Tf drops again into 1170˚C within 250 mm from meniscus. When the air gap forms and solid shell starts to separate from mold wall, surface begins to reheat into 1200˚C. This is followed by a gradual cooling by different cooling rates for different heats. Then, the surface reheats again into 1170˚C and 1130˚C for heats 3 and 4, respectively. This is followed by slight surface reheating of 1190˚C for heat 3 whereas the heat 4 reveals small and gradual cooling into 1110˚C until the mold exit.
The calculations of profile of Ic for heats 3 and 4 are shown in Figure 5(c). The same trend similar to case 1 is observed. Although, Figure 5(c) illustrates that Ic increases continuously in the various mold cooling regions by different growth rates. But, the predicted results show noticeable drop at 570 mm from meniscus for all heats. This drop is due to the sufficient surface reheating associated with air gap formation. This is followed by a continuous growth of Ic exponentially until mold exit. It is interesting to note that in the case of heat 4, Ic is higher than Ic in the case of heat 3. Another interesting observation arises from examination of Ic profiles shown in Figures 4(c) and 5(c). The model predications exhibit a clear observed difference between the values of Ic at mold exit where the magnitudes of Ic in the case of heats 3 and 4 (Case 2) are higher by three into seven times than their magnitudes in the case of heats 1 and 2 (Case 1). This agrees well the industrial practices and many investtigations and may explain the destructive and unproductive effect of different casting speeds on the surface and inner qualities of continuously cast steel slabs [2,14-16].
Figure 5(d) shows the comparisons of computed MTMR for case 2. The similar trend of MTMR is observed similar to case 1. It is interesting to note that the MTMR of heat 3 is higher than MTMR of heat 4 at the mold exit whereas the depth of crack of heat 3 (12.6 mm) is deeper than its depth of heat 4 (9.2 mm) [16]. This is due to the effect of position of neutral axis on the mechanical stress distribution in the coherent shell [33]. Another reason comes from examination of the computed MTMR histories where the effect of surface reheating reduces the growth rate of MTMR based upon the reheating degree as shown in Figure 5(d) [6,15,44]. This results in a decreasing in Ic against the thermo-mechanical stresses.
5. General Discussion
5.1. Mechanism of Mold Thermo-Mechanical Rigidity Criterion with Surface Defects Formation
The results of MTMR calculations, combined with knowledge of effects of mold operating parameters, leads to an importance and a consistent mechanism for MTMR with surface defects formation. Figure 6 illustrates the position of white line (curve 1) or structure change, end of longitudinal mid-face surface crack depth (curve 2) and depression depth (curve 3) with respect MTMR for the different heats examined.
In the curve 1 of Figure 6, the position of white line observed to be zero for the first three heats and within MTMR values from 700 ´ 10−3 to 2100 ´ 10−3 whereas in the case of heat 4 increases into 3 mm for MTMR values greater than 2800 ´ 10−3. With small values of MTMR, the ferro-static pressure (see Figures 3(a)-(c)) may take the coherent solid shell and close the air gap between the slab surface and mold wall. This mechanism helps to draw the dendrites tips (see Figure 3(d)) away from the steel nozzle axis or from the effective area of its convection streams. With increasing the distance from meniscus, the effect of steel nozzle convection streams declines and the white line phenomenon disappears. However, in the case of high MTMR values, the coherent solid shell resists the ferro-static pressure and the displacements of dendrite tips are small. Therefore, the ferro-static pressure cannot draw the dendrite tips away from the steel nozzle axis. Therefore, the effect of its convection streams becomes considerable and the white line phenomenon is observed.
In the case of curve 2 in Figure 6, another important observation can be noted where the depth of mid-face surface cracks vary from 9 into 17 mm with range of MTMR from 720 ´ 10−3 to 3230 ´ 10−3 [16]. This curve reveals generally that the increasing in MTMR decreases the occurrence of mid-face surface cracks and its depth. This is because the coherent solid shell can resist the mechanical stresses generated due to the ferro-static pressure (see Figure 3(a)). This controls the position of neutral axis (see Figure 3(d)), and its distance from slab surface [44]. This distance controls the stress distribution through the coherent solid shell and then controls the propagation of mid-face surface crack and its morphology characteristics such as its depth and width of crack.
Also, the curve 3 in Figure 6 shows that the depth of surface depression varies from 0.5 to 2.8 mm within the same range of MTMR [16]. This curve show a slight and fluctuated effect of MTMR on the surface depression formation and its depth. This is because that the parameters controlled the surface depression formation defer significantly from the parameters control MTMR. But still, the mechanism of increasing of MTMR resists the
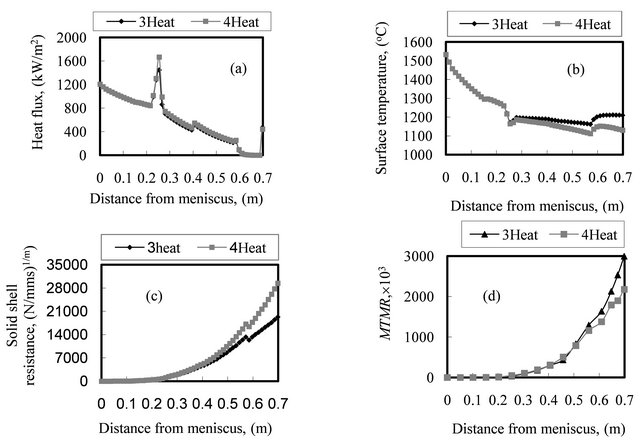
Figure 5. Variations of (a) mold heat fluxes, (b) surface temperature, (c) mold solid shell resistance and (d) mold thermomechanical rigidity with distance from meniscus for heats 3 and 4.

Figure 6. Variations of mold thermo-mechanical rigidity with different surface defects.
surface depression formation generally and then its depth. This is related to the fact that the high strength shell has a high possibility for resisting the plastic deformations.
In general, one can state further that the increasing in MTMR decreases the occurrence of surface defects formation. Also, it is concluded from these results that MTMR is a good quantitative indicator to examine the surface quality. Subsequently, its history can define the reason behind the defect formation and its value may determine the characteristics and morphology of defect. The disagreement in this comparison illustrated in Figure 6 is due to the complexity and differences of many mold phenomena and their imprecise interactions mechanisms governed the heat flow and solidification processes in the mold zone. Some of these phenomena or their interactions do not include with many mold conditions used in Equation (1). Also, this disagreement may be due to the fact that surface defects nucleate metallurgically close to the meniscus [16].
6. Conclusions
A transient, one-dimensional model has been developed to quantify the temperature, solidification and coherent solid shell resistance. A simple criterion of evaluation of surface quality of continuously cast steel slabs called mold thermo-mechanical rigidity “MTMR” has been proposed. The model predications are validated by extensive comparisons with different previous and well published experimental measurements and observations. The key findings of this study are summarized below.
1) The operating parameters especially those affect the solid shell resistance “Imold” have significant, direct and indirect effects on MTMR and therefore, on the surface quality.
2) The solid shell resistance “Imold” plays a major role to control MTMR and therefore to classify the surface quality.
3) MTMR is considered as qualitative indicator of surface quality and this criterion includes the most mold operating conditions and may help to explain complex mechanisms affect the surface defects formation.
7. Acknowledgements
The author sincere gratitude to Prof. Hasse Fredriksson, Royal Institute of Technology, Institute of Materials Processing, Dept. of Casting of Metals, Stockholm, Sweden for his considerable supervision, guidance, helpful discussions throughout the work and valuable assistance (1990-1995). Also, this work was sponsored partial by the Companies’ Chair of Swedish Iron Masters Association, Stockholm, for which the author is grateful.
REFERENCES
- Y. Meng and B. G. Thomas, “Heat Transfer and Solidification Model of Continuous Slab Casting: CON1D,” Materials Transactions B, Vol. 34B, No. 5, 2003, pp. 685- 705.
- F. M. Najjar, B. G. Thomas and D. E. Hershey, “Numerical Study of Steady Turbulent Flow through Bifurcated Nozzles in Continuous Casting,” Metallurgical and Materials Transactions B, Vol. 26, No. 4, 1995, pp. 749- 765. doi:10.1007/BF02651721
- K. C. Mills, “A Review of ECSC Funded Research on Mould Flux,” Steel Technology International, Vol. 16, No. 3, 1994, pp. 161-166.
- Y. Kashiwaya, C. E. Cicutti and A. W. Cramb, “An Investigation of the Crystallization of a Continuous Casting Mold Slag Using the Single Hot Thermocouple Technique,” The Iron and Steel Institute of Japan International, Vol. 38, No. 4, 1998, pp. 357-365. doi:10.2355/isijinternational.38.357
- C. Li and B. G. Thomas, “Thermomechanical FiniteElement Model of Shell Behavior in Continuous Casting of Steel,” Metallurgical and Materials Transactions B, Vol. 35, No. 6, 2004, pp. 1151-1172.
- X. Huang, B. G. Thomas and F. M. Najjar, “Modeling Superheat Removal during Continuous Casting of Steel Slabs,” Metallurgical Transactions B, Vol. 23, 1992, pp. 339-356. doi:10.1007/BF02656290
- D. R. Poirier, P. J. Nandapurkar and S. Ganesan, “The Energy and Solute Conservation Equations for Dendritic Solidification,” Metallurgical Transactions B, Vol. 22, 1991, pp. 889-900. doi:10.1007/BF02651165
- B. Rogberg, “High Temperature Properties of Steels and their Influence on the Formation of Defects in Continuous Casting,” Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 1982.
- H. Fredriksson and J. Stjerndahl, “Solidification of IronBase Alloys,” Metal Science, Vol. 16, No. 12, 1982, pp. 575-580. doi:10.1179/030634582790427136
- M. El-Bealy and B. G. Thomas, “Modeling of Solidification Behaviors and Interdendritic Strain for Low Alloy Steel Casting Processes,” Proceedings of 54th Electric Furnace Conference, Dallas, 9-12 December 1996, pp. 565-576.
- K. Miyazawa and K. Schwerdtferger, “Computation of Bulging of Continuously Cast Slabs with Simple. Bending Theory,” Ironmaking & Steelmaking, Vol. 6, 1979, pp. 68-74.
- M. El-Bealy, “Monotonic and Fluctuated Cooling Approaches in Secondary Cooling Zones during Continuous Casting,” Canadian Metallurgical Quarterly, Vol. 36, No. 1, 1997, pp. 49-56. doi:10.1179/000844397795515706
- M. El-Bealy, “Modeling of Phase Transformations and Solid Shell Resistance in Continuously Cast Steel Slabs,” Proceeding of 80th Steelmaking Conference of ISS Conference, Chicago, 1997.
- M. O. El-Bealy, “On the Mechanism of Mold ThermoMechanical Rigidity for Surface Quality of Continuously Cast Steel Slabs,” Journal of Egyptian Society of Mechanical Engineers, Vol. 111, 2011, pp. 42-51.
- M. O. El-Bealy, “Journal of Egyptian Society of Mechanical Engineers,” Steel Research International, Vol. 82, No. 10, 2011, pp. 1187-1206. doi:10.1002/srin.201000301
- J. K. Brimacombe, F. Weinberg and E. B. Hawbolt, Metall, “Formation of Longitudinal, Midface Cracks in Continuously-Cast Slabs,” Metallurgical Transactions B, Vol. 10, No. 2, 1979, pp. 279-292. doi:10.1007/BF02652472
- G. L. Larson and T. E. Moss, “Mechanism of Air Gap Formation,” Open Hearth Proceed, Vol. 57, 1974, pp. 211-225.
- W. R. Irving and A. Perkins, “Metals Society/IRSID Conference on Continuous Casting,” Biarritz, 1976.
- R. J Dippenaar, I. V. Samarasekera and J. K. Brimacombe, “Mould Taper in Continuous. Casting Billet Machines,” Trans-Lunar Space Tug and The International Space Station, Vol. 7, 1986, pp. 31-43.
- S. Watanabe, K. Harada, N. Fujita, T. Tamura and K. Noro, “Solidification of Continuious Casting,” The Iron and Steel Institute of Japan, Vol. 5B, No. 11, 1972, pp. S393-S394.
- S. Chandra, J. K. Brimacombe and I. V. Samarasekera, “Mould Heat Transfer and Continuously Cast Billet Quality with Mould Flux Lubricant: Part 2. Lubrication and Oscillation Mark Formation,” Ironmaking & Steelmaking, Vol. 20, 1993, pp. 104-112.
- C. A. Muojekwu, V. Samarasekera and J. K. Brimacombe, “Heat Transfer and Microstructure during the Early Stages of Metal Solidification,” Metallurgical Transactions B, Vol. 26B, No. 2, 1995, pp. 361-382.
- M. Wolf and W. Kurz, “The Effect of Carbon Content on Solidification of Steel in the Continuous Casting Mold,” Metallurgical Transactions B, Vol. 12B, 1981, pp. 85-93. doi:10.1007/BF02674761
- Y. Ueshima, S. Mizoguchi, T. Matsumiya and H. Kajioka, “Analysis of Solute Distribution in Dendrites of Carbon Steel with δ/γ Transformation during Solidification,” Metallurgical Transactions B, Vol. 17, No. 4, 1986, pp. 845- 859. doi:10.1007/BF02657148
- C. A. M. Pinheiro, I. V. Samarasekera, J. K. Brimacombe and B. N. Walker, “Mould Heat Transfer and Continuously Cast Billet Quality with Mould Flux Lubrication Part 1 Mould Heat Transfer,” Ironmaking & Steelmaking, Vol. 27, No. 1, 2000, pp. 37-54. doi:10.1179/030192300677363
- A. Grill, K. Sorimachi and K. Brimacombe, “Heat Flow, Gap Formation and Break-Outs in the Continuous Casting of Steel Slabs,” Metallurgical Transactions B, Vol. 7B, No. 2, 1976, pp. 177-189.
- M. El-Bealy and H. Fredriksson, “On the Formation of a Fluctuated Macrosegregation Phenomenon in Continuous Casting Processes,” Scandinavian Journal of Metallurgy, Vol. 23, 1994, pp. 140-150.
- M. O. El-Bealy and A. M. Hussein, “Cracking Breakouts Susceptibility Function ‘CBSF’ New Technique to Control the Productivity and Quality in Continuously Cast Steel Slabs,” Proceeding of AIST Annual Meeting, 2007, Indianapolis.
- M. El-Bealy, “On the Mechanism of Halfway Cracks and Macrosegregation of Continuously Cast Steel Slabs,” Part I & II, Scandinavian Journal of Metallurgy, Vol. 24, 1995, pp. 63-80, 106-120.
- I. Jimbo and A. A. W. Cramb, “The Density of Liquid Iron-Carbon Alloys,” Metallurgical Transactions B, Vol. 24, No. 1, 1993, pp. 5-10. doi:10.1007/BF02657866
- Y. Meng and B. G. Thomas, “Modeling Transient SlagLayer Phenomena in the Shell/Mold Gap in Continuous Casting of Steel,” Metallurgical Transactions B, Vol. 34, No. 5, 2003, pp. 685-605.
- K. Harste, “Untersuchung zur Schrumpfung und zur Entstehung von Blöcke aus Fe-C-Legierungen,” Ph. D. Thesis, Technical University of Clausthal, Germany, 1989.
- J. Miettinen, “Calculation of Solidification-Related Thermophysical Properties for Steels,” Metallurgical Transactions B, Vol. 28, No. 2, 1997, pp. 281-297. doi:10.1007/s11663-997-0095-2
- M. O. El-Bealy, “A Mathematical Model of Interdendritic Thermo-Metallurgical Strain for Dendrirtic Solidification Processes,” Metallurgical Transactions B, Vol. 42, No. 6, 2011, pp. 1280-1296.
- G. A. Panaras, A. Theodorakakos and G. Bergeles, “Numerical Investigation of the Free Surface in a Continuous Steel Casting Mold Model,” Metallurgical Transactions B, Vol. 29, No. 5, 1998, pp. 1117-1126.
- M. O. El-Bealy and R. M. Hammouda, “On the Mechanism of Natural Convection and Equiaxed Structure during Dendritic Solidification Processes,” Steel Research International, Vol. 78, 2007, pp. 602-611.
- M. O. El-Bealy, “Air-Water Mist Nozzle for ThermoMechanical Rigidity of Continuously Cast Steel Slabs,” Proceeding of International Convention of Asia Scholars, Guilin City, 2010.
- M. O. El-Bealy, “Thermo-Mechanical Rigidity of High Performance and Life Improvements for Caster Roll in Continuous Casting Machines,” 16th Design of Manufacturing and lifecycle Conference, ASME Conference, Washington DC, 28-31 August 2011.
- J. E. Kelly, K. P. Michalek, T. G. O’OConnor, B. G. Thomas and J. A. Dantzig, “Initial Development of Thermal and Stress Fields in Continuously Cast Steel Billets,” Metallurgical Transactions A, Vol. 19, No. 10, 1988, pp. 2589-2602.
- L. I. Morozenskii, O. A. Mitenev and V. K. Krutikov, Stal, “Method for Calculating Shrinkage Deformations and Creep of Claydite Concrete,” Stal Engineering, Vol. 5, No. 4, 1965, pp. 272-276.
- Y. Matoba, K. Okamura, T. Murakami and K. Yamamoto, “Solid Mechanics and Material Engineering,” JSME International Journal Series A, Vol. 48, No. 3, 2005, pp. 163-170. doi:10.1299/jsmea.48.163
- S. N. Singh and K. E. Blazek, “Heat Transfer and Skin Formation in a Continuous-Casting Mold as a Function of Steel Carbon Content,” Journal of Metals, Vol. 10, 1974, pp. 17-27.
- I. V. Samarasekera, J. K. Brimacombe and R. Bommaraju, “Mould Behaviour and Solidification in the Continuous Casting of Steel Billets: Ii. Mould Heat Extraction, Mould-Shell Interaction and Oscillation-Mark Formation,” Trans-Lunar Space Tug and the International Space Station, Vol. 5, 1984, pp. 79-94.
- M. O. El-Bealy, “Interdendritic Strain and Macrosegregation Coupled Phenomena for Interdendritic Crack Formation during Solidification in Direct Chill Cast Sheet Ingots,” Metallurgical and Materials Transactions B, Vol. 43, No. 3, 2012, pp. 635-656.
Nomenclature
A : unity elementary area of volume element in plane x (m2);
AAGF: after air gap formation cooling region;
 : material coefficient of Equations. 6(b) and (c) and 7 of k-phase at temperature T;
: material coefficient of Equations. 6(b) and (c) and 7 of k-phase at temperature T;
B : slab thickness (mm);
BAGF: before air gap formation cooling region;
Cp: specific heat capacity (kJ/kgK);
D : diffusion coefficient (cm2/s);
f : fraction of phase;
fcoh: coherence constant;
h1: distance from surface to neutral axis (mm);
h2: distance from the coherent isotherm to neutral axis (mm);
h : Newtonian heat-transfer coefficient (W/m2k);
h(t): Newtonian heat-transfer coefficient at time t (W/m2k);
 : enthalpy (kJ/kg);
: enthalpy (kJ/kg);
 : average enthalpy (kJ/kg);
: average enthalpy (kJ/kg);
Ic: resistance of coherent solid shell to creep (N(mm s)1/m);
k: phase;
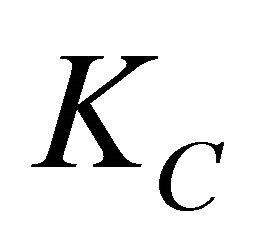 : partition coefficient of carbon for multi components system;
: partition coefficient of carbon for multi components system;
lmold : mold length (m);
L: latent heat of fusion (kJ/kg);
MTMR: mold thermo-mechanical rigidity;
 : exponent of Equations. (6) and (7) of k-solid phase N: number of solid phases;
: exponent of Equations. (6) and (7) of k-solid phase N: number of solid phases;
P: ferro-static pressure head (N/m2);
 : superheat-flux profile from database case from 3-D fluid flow model (kW/m2);
: superheat-flux profile from database case from 3-D fluid flow model (kW/m2);
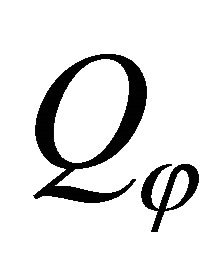 : surface heat flux (kW/m2);
: surface heat flux (kW/m2);
Qx: heat flux at distance x from surface (kW/m2);
Pe : Pèclet number;
t : time (s);
T: temperature (˚C);
Tl,Tcoh,Ts: liquius, coherence and solidus temperatures (˚C);
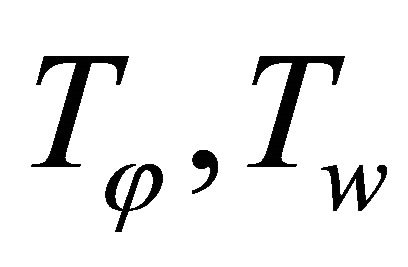 : surface and cooling fluid temperatures (˚C);
: surface and cooling fluid temperatures (˚C);
U: superficial Interdendritic velocity (m/s);
v: casting speed (m/s);
 : molar volume (cm3/mol);
: molar volume (cm3/mol);
x,y,z: Cartesian co-ordinates (m).
Greek Symbols
β: thermal linear expansion coefficient (1/˚C);
 : concentration (wt pct);
: concentration (wt pct);
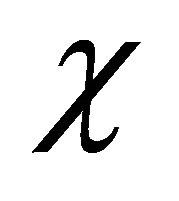 : thermal conductivity (W/mK);
: thermal conductivity (W/mK);
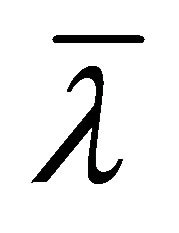 : average thermal conductivity (W/mK);
: average thermal conductivity (W/mK);
ρ: density (kg/m3);
 : average density of control volume element (kg/m3);
: average density of control volume element (kg/m3);
m: viscosity (N s/m2 );
x: chill roughness (mm);
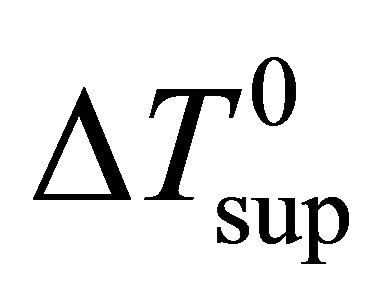 : superheat temperature difference at casting speed
: superheat temperature difference at casting speed 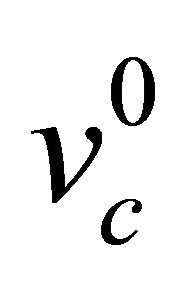 (˚C);
(˚C);
DTs: superheat (˚C).
Superscript Symbols
C: carbon;
d : delta;
g”: gamma;
®: transformation;
/: interface.
Subscribe Symbols
coh: coherence;
eff: effective;
pour: pouring;
pr: peritectic;
l: liquid;
Lub: lubricant;
out: mold exit;
s: solid;
x,y,z: Cartesian co-ordinates (m).

