Journal of Modern Physics
Vol.07 No.11(2016), Article ID:68672,14 pages
10.4236/jmp.2016.711119
Cosmogonic Speculations: Particle Creation from Energy Conservation in the Universe Evolution
Paolo Christillin
Dipartimento di Fisica, Università di Pisa and I.N.F.N., Sezione di Pisa, Pisa, Italy

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 June 2016; accepted 17 July 2016; published 20 July 2016
ABSTRACT
Information about the Universe from Hubble’s law is consistent with that coming from the evaluation of inertial forces, supporting the picture of a steady state expansion of a black hole Universe. Backed up also by the consideration of the black body self energy, the post big bang temperature decrease is consistent with particle creation if energy conservation applies at every scale. This process is shown to provide a gravitational repulsive force which can counterbalance gravitational attraction thus allowing the possibility of a steady non-inflationary expansion. That seems to provide an alternative coherent scheme for our picture of the Universe evolution, disposing of the cosmological term, of dark energy and of the bulk of dark matter.
Keywords:
Cosmogony, Black Holes, Particle Creation, Self Energy, Inertial Forces

1. Introduction
The present scenario for our Universe evolution is based first of all on two sound experimental facts: Hubble’s law [1] and the CMB [2] (although the latter was predicted semiquantitatively by Alpher, Herrman and Gamow [3] ). In more recent times finer details have come from BOOMERAanG [4] , Cobe [5] , Planck [6] and the Supernovae data [7] [8] which hint at an accelerated expansion.
The prevailing fit is based on the GR equations where the theoretical interpretation of the notorious cosmological term seems to represent a formidable problem. Quoting e.g. Susskind [9] “the best efforts of the best physicists, using our best theories predict the cosmological constant… equivalent to the vacuum energy... incorrectly by 120 orders of magnitude”.
That its theoretical treatment leaves many people unsatisfied is reflected e.g. in Perlmutter’s words [10] : “Dark energy has now been added to the already perplexing question of dark matter [11] . One is tempted to speculate that these ingredients are add-ons, like the Ptolemaic epicycles, to preserve an incomplete theory”.
In that respect, let also quote Feynman’s [12] words “Although in ordinary circumstances a physicist would rebel against a theory which so cavalierly ignores our cherished laws about the conservation of matter and energy, one must remember that here we are not dealing with an ordinary problem but with a cosmological problem”. Although these words were referring to the steady state theory of Hoyle [13] , the warning applies in general.
That a revision is needed had also already been pointed out in [14] in connection with the treatment of one of our theoretical milestones i.e. black body radiation. Indeed at cosmological scales the gravitational interaction of photons cannot be neglected and this results in a substantial role of the self energy, especially in the radiation dominated era.
If we enforce energy conservation at any scale, one is thus forced to admit photon (and particle) non-con- servation, which explains the non-gravitational collapse of the Universe. This provides an alternative scheme where our causal Universe has evolved from a total zero energy quantum fluctuation at the Planck scale to the present dimensions, again with total zero energy, without any need to invoke inflation.
The crucial points will be :
1) energy vs. particle number conservation,
2) the presence of a gravitational repulsive force due to particle creation,
3) the black body handling,
4) the consideration of inertial forces.
2. Present Picture: The Unity of the Universe
a) inertial forces
We summarize the results of the calculations backing up the conjecture put forward mainly by Sciama [15] and further developed by Berry [16] concerning the constraints provided by the inertial forces on the mass of the Universe.
Consider first how the Coriolis force is generated in the rotating frame by the counter rotating Universe. Since a rotating matter distribution produces a gravitomagnetic field  (according to the parameter free effective vector formulation of gravitation [17] ) proportional to the angular velocity of rotation
(according to the parameter free effective vector formulation of gravitation [17] ) proportional to the angular velocity of rotation 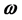
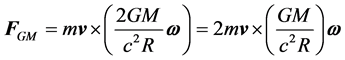 (1)
(1)
the Coriolis force on a mass m
 (2)
(2)
is recovered
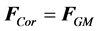 (3)
(3)
if for the Universe,
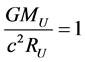 . (4)
. (4)
The relevant point in this argument is that in the relative rotation, the magnetic field generated by distant layers of matter goes as 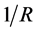 i.e. the same behavior of radiation, rather than the usual
i.e. the same behavior of radiation, rather than the usual 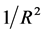 of Newtonian forces. Therefore a relative more important role even of distant stars is a matter of fact.
of Newtonian forces. Therefore a relative more important role even of distant stars is a matter of fact.
As regards linear inertial forces, the same effective vector gravitation accounts for them via a different mechanism i.e. dipole radiation [18] .
It is well known that in the non inertial frame  of a particle
of a particle 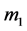 attracted by another M, where the said particle is at rest and manifestly
attracted by another M, where the said particle is at rest and manifestly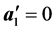 , non inertial forces have to be introduced. They come from all other particles which acquire the opposite acceleration
, non inertial forces have to be introduced. They come from all other particles which acquire the opposite acceleration 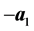 generating an additional force given by
generating an additional force given by
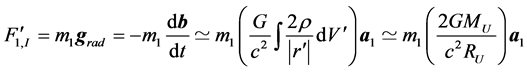 (5)
(5)
where I stands for inertial and 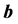 for the gravitomagnetic vector potential. Therefore if
for the gravitomagnetic vector potential. Therefore if
 (6)
(6)
the inertial force generated in the non inertial reference frame 
rest of the Universe exactly compensates the “true” Newtonian (N) force

Thus the two previous conditions on the energy content of the Universe, which taken at their face value seem to be contradictory, confirm instead at a semiquantitative level the fact that we are indeed living inside a black hole. All the more so since they come from two different mechanisms.
Let us now come to an apparently disconnected issue i.e. the cosmological expansion.
b) the gross features of the expansion
Hubble’s law [1] of the recession velocity of galaxies reads

where 

Whether our Universe would eventually contract or keep expanding should depend on a critical density

the particles inside the sphere with potential energy
The steady state thus takes place when these two energies balance each other or

In this case

and


It is evident that these considerations represent a rough non relativistic schematization of the process. As a matter of fact in the energy density no trace of the kinetic energy of the expanding particles within the sphere appears nor their contribution to the potential energy because of the mass energy equivalence; the mass M is just an “effective” static source which is thought to represent reality and hence to determine the motion of m.
Nevertheless data seem to confirm [4] to the percent the critical value for the density.
Let us then check the consistency of Equation (11) with the results from inertial forces by using Hubble’s relation predictively at 

whence

which implies that the total mass is balanced by its gravitational self energy (up to a factor of 2) to make the total energy of the Universe zero.
We thus see that the extrapolation of Hubble’s law to the whole of our causal Universe, circumventing critical estimates of the contribution of distant regions to the critical density, yields the same black hole condition entering the evaluation of inertial forces and validates Feynman’s conjecture that the critical density is just about the best density to use in cosmological problems because it allows for free particle creation [12] , the mass being swallowed by its gravitational self energy. Thus Hubble’s law is not only fundamental in its vector form in proving that there is no center in the Universe but its extrapolation is paramount in determining its fate.
Let us then see how mass creation embodied in the previous equation enters consistently the equation of motion for the acceleration. We differentiate with respect to t to get from
the velocity

the acceleration

This last equation differs fundamentally from the standard treatment rewriting completely our picture of the Universe. Indeed whereas the first term in the r.h.s. yields the Newtonian (and GR) attractive acceleration due to the mass M enclosed within the radius R, the second term gives a repulsive effect due to matter creation. Therefore even without a cosmological term we have a built-in repulsive gravitational term which may make the Universe not to collapse, without dark energy i.e.

The preceding energy conserving cosmogonic equations (ECCE) represent the minimal parameter-free self- consistent model of the gross features of the Universe in which extra parameters may be introduced only if necessary for fitting finer details of its evolution. In the r.h.s. of Equation (16) the two terms can indeed compensate thus yielding a steady state evolution if

equivalent to

The scale factor which links mass and radius is manifestly 
Notice that although the equation of energy conservation looks like the traditional one, the consistency requirement coming from the acceleration, implies a totally different scenario. In other words whereas in a traditional picture (without the cosmological term) the fate of the Universe resembles the description of the motion of a body thrown up in the air in a gravitational field, so that according to how its velocity compares to the escape velocity determined by the density it will collapse or not, here the expansion velocity is

It follows that

implying at the same time for the density evolution

which is still another way to express the linear relation between mass and radius of a black hole, confirming the flatness of space. The previous relation can be also directly got from Equation (14) by imposing total energy conservation for the interacting Universe at all times

This has to be contrasted with the requirement one gets from thermodynamic considerations as well as from GR

which expresses matter conservation (i.e. essentially particle number) as it can be simply obtained by imposing

and by taking into account the energy content of pressure (which plays a role essentially only for radiation) with the well known behaviors for matter (m) and radiation (rad)

The ratio of pressure to density
In conclusion the standard scenario has to cope with the problem of energy conservation, the proposed one clashes with our belief of particle number conservation. However this picture does not at all correspond to Hoyle’s [13] . There, particle creation is invoked to obtain a steady constant density state and to disprove the big bang. The present proposal rather somewhat resembles, apart from the fundamental difference due to particle creation, to the primeval egg by Lemaître [21] .
Just to get an order of magnitude, the estimated number of particles would have resulted from

(which we get allowing for creation of the present number minus the negligible Planck one over the age of the Universe) i.e. the creation of only ten hydrogen atom per cubic kilometer per year (since it has been referred to the present dimensions the creation rate would have been higher in the past). Therefore in that respect the present proposal does not go against any experimental evidence.
3. Self Energies: The Planck Scale
The fundamental Planck quantities are



As well known one way to derive them is to ask in which units our “fundamental” coupling constants 
In another derivation they are determined by requiring the Compton wavelength of a particle to coincide with its Schwarzschild radius. Thus the Planck energy corresponds to the energy contained in the minimum (because it cannot be compressed farther without violating the uncertainty principle) quantum Schwarzschild radius i.e. the smallest quantum black hole.
This gravitational quantum “fluctuation” should, according to the prevailing picture,

last for times of the order of Planck’s time.
But since

the Planck fluctuation is energetically stable in the sense that it does not have to decay in Planck times (up to numerical factors of order 1).
The equations written for the Universe at the present time can therefore be rewritten for Planck quantities

etc. with the same considerations.
Thus

When compared to the present quantity

one has

From that we can immediately obtain an expression for Hubble’s parameter at a generic time t and Universe radius R in terms of the present quantities


In general

Thus Hubble’s parameter would have decreased in the course of the expansion by the above 
A hypothetical observer in the past, say 10 billion years ago, would have of course “measured” a younger Universe by roughly a factor ten, which would have reflected in a corresponding bigger Hubble’s parameter(t). These formulas confirm the argument [22] that an observer in the past (


That would answer Perlmutter’s ( [10] ) worry that in the standard picture it appears “a remarkable and implausible coincidence that the mass density, just in the present epoch, is within a factor of 2 of the vacuum energy density because the mass density is supposed to become ever more dilute in the course of the expansion, whereas the vacuum energy density
well of a similar statement [23] “to make things worse, the energy density 
same order of magnitude of the matter density of the Universe 

4. Self Energies: Evolution of Radiation and Matter
Let us inquire how much this parameter free scenario can account for the present 6-parameter cosmological phenomenology in the reconstruction of the past . As regards matter, its total energy in the Universe coming from Hubble’s law is

The present energy density of radiation, coming from the CMB, is

which yields a total energy for the Universe at present

so that

Thus “matter” (by which we mean loosely speaking non radiation) dominates over radiation by such a typical order of magnitude.
The total number of photons is given by

and is of the order of 1087.
Self energy would correct these energies in accord with the black body condition. The relevant point is that the self energy dependence on R is not the same as that of the energy so that this correction does not factorize. Thus self-energy can act as a gauge in the reconstruction of the history of the Universe, undisputedly proving that a creation mechanism must have been constantly at work.
As regards nucleons traditionally from energy conservation of non interacting particles (which amounts to particle number conservation)

one predicts

(this conclusion is somewhat altered when taking into account the temperature and the velocity dependence of baryons. It is however easy to see that the former is totally irrelevant up to a temperature of 

On the contrary the requirement of positivity for the energy coming from the self energy implies that the present black hole condition should hold, if we enforce energy conservation, also going backward in time. Thus as a function of R

(
Again energy conservation of gravitationally interacting particles and particle number conservation are mutually contradictory. Indeed the requirement Equation (44) would make the self energy correction of Equation (45) to turn negative. In other words the fact that less particles were present in the past in the energy conserving case with respect to their constancy of the traditional picture means once more that particles have been created in the expansion.
As regards photons, because of the energy mass equivalence, they are also obviously source of a sizable gravitational field when sufficiently energetic and/or numerous. Their black body treatment at ordinary conditions is absolutely unquestionable. Indeed if we consider e.g. a black body of one cubic meter at room temperature 




For the Universe at present

which is also negligible. And this must have been so for a long time since the energy density of the Planck spectrum which comes to us from the CMB

is remarkably accurate.
So the spectrum has kept its black body shape (which is sort of astonishing in view of the absence of significant later scattering processes) in agreement with scaling properties of the former angular frequency

(where z is the cosmological redshift), provided also the photon temperature 

This is consistent with photon number 

from which the preceding result for the energy density 


follows. Thus

and from the previous estimates, matter and photon energy density would equalize at recombination (rec)

which corresponds to the standard estimate for

at

Thus at

we have, at the same time, equality of matter and photon energy densities and zero total energy for both. This is gratifying since it proves that the self energy mechanism offers an alternative doubly constrained prediction. In former times the self energy mechanism would work both for radiation and for matter thus keeping their ratio constant at the value of recombination.
The different behavior of radiation and matter is then apparent. In the first case, because of the null mass, the wavelength is closely related to the Universe dimensions. This explains why we can reach


To summarize, back to 



Thus typically at a temperature 
Further backward in the reconstruction of the history of the “dark ages”, from the self energy condition for photons

one gets

where the second equality comes from the results of the equations of motion.
The conclusions of this paragraph are therefore a linear connection between matter creation and the dimensions of the Universe throughout, and a linear dependence between the temperature of radiation and radius R back to recombination and quadratic before.
5. Structures
a) CMB and the event horizon
As well known [24] [25] CMB temperature fluctuations 

corresponds to the multipole moment 


where the Universe expansion in the matter dominated era goes, according to the standard treatment, as 

Acoustic oscillations are clearly due to inhomogeneities in the baryon-photon fluid before recombination resulting in “standing waves” connected to the Universe dimensions and hence for us to the event horizon. In the present scenario photons emerging from the last scattering surface at 



Correspondingly that would imply a much bigger z than at recombination.
Notice that in terms of the corresponding quantities at recombination one has

So the acoustic peaks are directly connected to density fluctuations in a much smaller event horizon than that at recombination with corresponding shorter wavelengths. With CMB anisotropies we can “penetrate” the last scattering barrier.
The above prediction would entail a temperature an order of magnitude bigger of the usual 3000 K (i.e. 

These spots which originated well before, when interpreted in terms of the Universe mass at recombination, seem to imply a contribution of the baryonic mass to the total energy

which is one of the parameters entering the angular distribution fits. This is simply due to a theoretical “snapshot” of the Universe disregarding its time dependence and therefore the mass creation mechanism at work. In other words we have invisible matter in a time independent description which disappears when considering its time dependence.
b) supernovae : an accelerated expansion?
In the standard approach far away objects are “measured” through the luminosity distance

which comes from an expansion of the relevant quantities from their present value and where the dots stand for terms involving derivatives of the Hubble parameter. Thus measurements of luminosity distances and redshift parameters z of a number of galaxies have led to the discovery of the accelerated expansion of the Universe. This was once more unexpected since it clashed with our traditional picture of an attractive gravity.
In the present scenario on the other hand no expansion is necessary, since a linear dependence of the Hubble parameter on time has been predicted.
The farther the objects, the older but also within a Universe with a smaller radius


Thus the velocity would be greater than that predicted by 

the distance would consequently appear to be greater for very distant objects, supernovae would look fainter and this might be ascribed, following Riess and Turner [26] , to an acceleration in the past.
c) galaxy clusters
Galaxy clusters involve dimensions of Mpc i.e. factors 

Their distance from us are e.g. 

The gravitational fields are weak; indeed from



The finding that the dynamic mass entering the kinetic energy be much higher than the one determined by luminosity measurements or

has led to speculate on the existence of missing mass or dark matter. These speculations are based on the application of the well known virial theorem which states that

This relation for average values applies for systems remaining within a finite volume, by averaging over “sufficiently” long times. However with the given values, the orbital period of individual galaxies around the common center of mass would be of the order of some billion years. Thus the application of the virial theorem in the preceding form seems at least questionable. More than that, if energy conservation holds true and E is therefore time independent

contradicting the the initial inequality for the energy, which is just a learned way of expressing the simple fact that a system of total positive energy cannot be bound.
Thus it seems plausible that in this domain the formation of gravitationally bound objects out of negative capacity gravitational fluctuations be overcome by the effect of the Universe expansion. As a matter of fact the virial theorem reads in reality

An estimate of the second term, which cannot be averaged over many cycles in this case, yields

i.e. a velocity of the indivual masses

for the present value of the H, which would be increased by an order of magnitude when correctly considering its value some ten times bigger at the formation time thus substantially decreasing the value of the kinetic energy term. This brings velocity and luminosity measurements towards agreement challenging the necessity of invoking a sizable amount of dark matter.
In conclusion the virial theorem in an expanding Universe gets substantial contributions from the expansion questioning the bound state picture [27] [28] .
d) the rotation curves of galaxies
As repeatedly underlined the present scenario concerns the bulk features of the Universe evolution. It is however natural to wonder whether it can account also for the missing mass which seems necessary for the description of galaxies where Hubble’s expansion plays practically no role.
Application of Newton’s law to the rotation curves of masses m (hydrogen atoms emitting the 21 cm line) orbiting a galaxy of total bulge mass M within a radius R reproduces reasonably well experimental data in the inner part i.e. for

whereas in the exterior predicts a decrease of v

contradicted by experimental data which show a roughly constant behavior [29] .
It has been noted that the presence of extra matter (missing mass) in the halo (h) with a density a

which implies

would provide the extra attraction for the rotation curves and an extra deflection for lensing (“This distribution is spacially more extended than that of the visible baryons, demonstrating clearly the existence of dark matter” [30] ), although alternative explanations have been proposed as well as for the bullet cluster [31] .
Indeed that would result in an extra 

The overall situation of the proposed history of the Universe is summarized in Table 1 and Figure 1.
Table 1. Parameters of the Universe evolution. The relevant part of our gravitational history has been spaced.
Figure 1. The Universe evolution.
The three most relevant situations i.e. Planck, total zero energy of radiation and present Universe are represented for a CMB observer, not in scale.
- The Planck “primeval egg” evolves in time, causally connected (c.c.), at the speed of light. No inflation has to be invoked.
- The evolution is accompanied by matter and photons creation which decreases the temperature.
- In all three cases the total energy is zero: we are inside an expanding black hole. This is backed up by the account of inertial forces.
- The evolution of the Universe is determined by the time dependent Hubble’s parameter which measures its age and, within each bubble, the expansion velocity of its constituents.
- The Hubble radius and the event horizon coincide.
6. Conclusions
In the present paper a cosmogonic scenario has been proposed. At variance with respect to the standard matter conservation treatment, energy conservation, with the essential role played by self energy, has been enforced and seen to account for the puzzling non-gravitational collapse due to matter creation balancing gravitational attraction.
In this parameter free phenomenological treatment, the gross features of our Universe evolution from the stable quantum fluctuation at the Planck epoch have been accounted for without any need for the cosmological constant
The stringent connection among a zero total energy Universe, (an extended use of) Hubble’s law, and matter creation in the Universe expansion consistent with the equations of motion for the velocity and the acceleration, has been underlined and emphasized.
We can hence summarize our results as follows:
1) the consideration of self gravitational effects is essential,
2) they play a crucial role both at a classical and at a quantum level and both for matter and for radiation. Indeed the gravitational interaction of photons at cosmic scales necessarily alters the standard black body treatment,
3) the main features of the evolution of our Universe from the Planck to the present scale reasonably follow from energy conservation and (no need for an unbelievably) fine tuning of the cosmological parameters,
4) the evidence for the black hole nature of our Universe coming from the reproduction of inertial forces supports Hubble’s formulation of its expansion. More than that the black hole condition 
5) finally the constancy of the power necessary to create matter in the course of the Universe evolution

where the usual black hole relation has been used (seems to provide a further), piece of support for the consistency of the present approach.
In conclusion, the cosmological term, dark energy and (the bulk of) dark matter seem to be reasonably due only to our use of inadequate equations to account for the gross features of the actual evolution of the Universe.
Acknowledgements
It is a pleasure to thank G. Cicogna for a critical reading of the manuscript and C. Bonati, G. Morchio, P.G. Prada Moroni, S. Degl’Innocenti for useful discussions.
Cite this paper
Paolo Christillin, (2016) Cosmogonic Speculations: Particle Creation from Energy Conservation in the Universe Evolution. Journal of Modern Physics,07,1331-1344. doi: 10.4236/jmp.2016.711119
References
- 1. Hubble, E. (1929) Proceedings of the National Academy of Sciences of the United States of America, 15, 168-173.
http://dx.doi.org/10.1073/pnas.15.3.168 - 2. Penzias, A.A. and Wilson, R.W. (1965) Astrophysical Journal, 142, 419-421.
http://dx.doi.org/10.1086/148307 - 3. Kragh, H. (1999) Cosmology and Controversy: The Historical Development of Two Theories of the Universe. Princeton University Press, Princeton.
- 4. de Bernardis, P., et al. (2000) Nature, 404, 955-959. arXiv:astro-ph/0004404.
http://dx.doi.org/10.1038/35010035 - 5. COBE Mission Design, Spacecraft and Orbit. Goddard Space Flight Center, 18 April 2008.
- 6. Planck Collaboration. ar-Xiv:1502.01582.
- 7. Riess, A.G., et al. (1998) The Astronomical Journal, 116, 1009.
http://dx.doi.org/10.1086/300499 - 8. Perlmutter, S., et al. (1999) The Astrophysical Journal, 517, 565.
http://dx.doi.org/10.1086/307221 - 9. Susskind, L. (2006) The Cosmic Landscape. Hachette Book Group, New York.
- 10. Perlmutter, S. (2003) Physics Today, 56, 53.
http://dx.doi.org/10.1063/1.1580050 - 11. Rubin, V. (1998) Dark Matter in the Universe. Scientific American, Inc., New York, 106.
- 12. Feynman, R.P. (1999) Lectures on Gravitation. Penguin Books, London.
- 13. Hoyle, F. (1948) Monthly Notices of the Royal Astronomical Society, 108, 372-382.
http://dx.doi.org/10.1093/mnras/108.5.372 - 14. Christillin, P. (2011) The European Physical Journal Plus, 126, 88.
http://dx.doi.org/10.1140/epjp/i2011-11088-6 - 15. Sciama, D.W. (1959) The Unity of the Universe. Doubleday, Garden City, NY.
- 16. Berry, M. (1976) Principles of Cosmology and Gravitation. Cambridge University Press, Cambridge.
- 17. Christillin, P. and Barattini, L. (2013) ArXiv:1205.3514v3.
- 18. Christillin, P. (2014) The European Physical Journal Plus, 129, 175.
http://dx.doi.org/10.1140/epjp/i2014-14175-2 - 19. Okun, L.B. (1982) Leptons and Quarks. North Holland, Amsterdam.
- 20. Maoz, D. (2006) Astrophysics in a Nutshell. Princeton University Press, Princeton.
- 21. Lemaître, G. (1927) Annales de la Société Scientifique de Bruxelles, A47, 49-59.
- 22. Barrow, J.D. and Shaw, D.J. (2011) General Relativity and Gravitation, 43, 2555-2560. ArXiv:1105.3105.
- 23. Zee, A. (2003) Physics Letters B, 594, 8-12. ArXiv:hep-th/0309032v1.
- 24. De Bernardis, P. and Bersanelli, M. (2013) Il Nuovo Saggiatore, 29, 25.
- 25. Mennella, A. and Natoli, P. (2015) Il Nuovo Saggiatore, 31, 63.
- 26. Riess, A.G. and Turner, M.S. (2004) Italian edition of Scientific American, 427, 56.
- 27. Ambartsumian, V.A. (1961) Astronomical Journal, 66, 536-540.
http://dx.doi.org/10.1086/108460 - 28. Van den Bergh, S. (2000) ArXiv:astro-ph/0005314v1.
- 29. Roos, M. (2010) ArXiv:1001.0316v1.
- 30. Ellis, R.S. (2010) Philosophical Transactions of the Royal Society A, 368, 967-987.
- 31. Markevitch, M., et al. (2002) The Astrophysical Journal, 567, L27-L31.
- 32. Milgrom, M. (1983) Astro-physical Journal, 270, 365-370.
http://dx.doi.org/10.1086/161130








