Journal of Modern Physics
Vol.3 No.2(2012), Article ID:17693,10 pages DOI:10.4236/jmp.2012.32023
Exact Solution of Dirac Equation with Charged Harmonic Oscillator in Electric Field: Bound States
Physics Department, Near East University, Nicosia, North Cyprus, Turkey
Email: sikhdair@neu.edu.tr
Received October 14, 2011; revised November 25, 2011; accepted December 13, 2011
Keywords: Harmonic Oscillator; Dirac Equation; Spin and Pseudospin Symmetry; Combined Potentials; Nikiforov-Uvarov Method
ABSTRACT
In some quantum chemical applications, the potential models are linear combination of single exactly solvable potentials. This is the case equivalent of the Stark effect for a charged harmonic oscillator (HO) in a uniform electric field 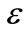 of specific strength (HO in an external dipole field). We obtain the exact s-wave solutions of the Dirac equation for some potential models which are linear combination of single exactly solvable potentials (ESPs). In the framework of the spin and pseudospin symmetric concept, we calculate analytical expressions for the energy spectrum and the corresponding two-component upperand lower-spinors of the two Dirac particles by using the Nikiforov-Uvarov (NU) method, in closed form. The nonrelativistic limit of the solution is also studied and compared with the other works.
of specific strength (HO in an external dipole field). We obtain the exact s-wave solutions of the Dirac equation for some potential models which are linear combination of single exactly solvable potentials (ESPs). In the framework of the spin and pseudospin symmetric concept, we calculate analytical expressions for the energy spectrum and the corresponding two-component upperand lower-spinors of the two Dirac particles by using the Nikiforov-Uvarov (NU) method, in closed form. The nonrelativistic limit of the solution is also studied and compared with the other works.
1. Introduction
The Schrödinger equation provides an insight to the fundamental quantum chemical problems. There are a number of solvable nonrelativistic quantum problems in which all the energy eigenvalues and wave functions are explicitly known from different operator methods [1] and analytical procedures [2] specially developed to solve the desired wave equation. This solution can be done by using the supersymmetry (SUSY) [3,4], the NikiforovUvarov (NU) method [5], the asymptotic iteration method (AIM) [6], the exact quantization rule (EQR) [7] and the tridiagonal J-matrix method (TJM) [8], etc.
The electron confinement in harmonic oscillator (HO) potential exposed to n external electric field is one of the quantum chemical applications. Indeed, this is well known as charged HO in a uniform electric field or an HO in an external dipole field. Moreover, such model could be also used in the measurement of the relative photo ionization cross section of Rb in the presence of various strengths of external electric fields [9]. The model potential also makes specific predictions about the spacing as a function of applied field and used in the calculation of the energy levels of ammonia in strong electric field [10]. The SUSY and shape invariance methods have been used to determine ESPs are extended to obtain the energy eigenvalues and their generalized partner potentials [11]. It demands the existence of the Witten superpotential  [12] associated with the ESPs in order to find the witten superpotential for the combined potential. It is an ansatz used as particular solution of the involved Riccati equation [13]. The generalized eigensolutions of some important ESPs in one-dimension have been studied [11]. Further, the determination of the vibration spectra in some molecular systems is found essential in chemical study. The Morse [14], Hulthén [15,16] and Kratzer [17] potentials are models used to study diatomic molecules. The modifycation on the spectrum energy due to the influence of electric field on a quantum particle of mass
[12] associated with the ESPs in order to find the witten superpotential for the combined potential. It is an ansatz used as particular solution of the involved Riccati equation [13]. The generalized eigensolutions of some important ESPs in one-dimension have been studied [11]. Further, the determination of the vibration spectra in some molecular systems is found essential in chemical study. The Morse [14], Hulthén [15,16] and Kratzer [17] potentials are models used to study diatomic molecules. The modifycation on the spectrum energy due to the influence of electric field on a quantum particle of mass 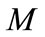 and charge
and charge 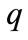 confined by HO potential was studied with a disclination [18,19].
confined by HO potential was studied with a disclination [18,19].
Besides, the spherical relativistic HO with spin symmetry has been studied [20]. The Dirac Hamiltonian with scalar 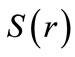 and vector
and vector  potentials quadratic in space coordinates [21] has been used to find an HO like second order equation. This can also be solved analytically for Klein-Gordon (KG) equation with equally mixed scalar and vector potentials
potentials quadratic in space coordinates [21] has been used to find an HO like second order equation. This can also be solved analytically for Klein-Gordon (KG) equation with equally mixed scalar and vector potentials 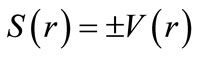 (the sum potential
(the sum potential  and the difference potential
and the difference potential [22]. Recently, the triaxial, axial and spherical HO for the case
[22]. Recently, the triaxial, axial and spherical HO for the case 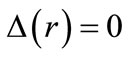 has been solved and applied to the study of antinucleons embedded in nuclei [23-25]. The case
has been solved and applied to the study of antinucleons embedded in nuclei [23-25]. The case 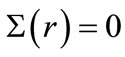 is particularly relevant in nuclear physics since it is a necessary condition for the pseudospin symmetry in nuclei [26,27]. The bound state solution of the spin-1/2 particles in Dirac equation with HO potentials have been obtained by letting either
is particularly relevant in nuclear physics since it is a necessary condition for the pseudospin symmetry in nuclei [26,27]. The bound state solution of the spin-1/2 particles in Dirac equation with HO potentials have been obtained by letting either 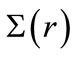 or
or 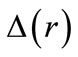 equal to zero [28]. The perturbative breaking of pseudospin symmetry induced by a tensor potential [29] has been studied despite the condition
equal to zero [28]. The perturbative breaking of pseudospin symmetry induced by a tensor potential [29] has been studied despite the condition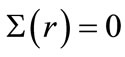 or
or 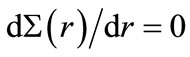 can not be realized in nuclei [30]. The correlation between the pseudospin splitting and the shape of the HO potential, namely the HO frequency and the distance of well-bottom deviation from the center studied in [31]. The relativistic HO in 1 + 1 dimensions, i.e., including a linear potential and quadratic scalar and vector potentials with equal or opposite signs has been solved [32]. The solutions found for zero pseudoscalar potential are related to the spin and pseudospin symmetry of the Dirac equation in 3 + 1 dimensions. The Dirac equation with scalar and vector HO potentials along with the tensor potential as a sum of linear and Coulomb-like potentials has been studied [33]. It was found that the tensor potential preserves the form of the HO potential and generates spin-orbit terms. The bound states of a new ring-shaped equal mixture of vector and scalar HO for spin-1/2 Dirac particles were studied [34]. The bound state solutions of the relativistic pseudoharmonic potential have been studied using the Nikiforov-Uvarov method [35].
can not be realized in nuclei [30]. The correlation between the pseudospin splitting and the shape of the HO potential, namely the HO frequency and the distance of well-bottom deviation from the center studied in [31]. The relativistic HO in 1 + 1 dimensions, i.e., including a linear potential and quadratic scalar and vector potentials with equal or opposite signs has been solved [32]. The solutions found for zero pseudoscalar potential are related to the spin and pseudospin symmetry of the Dirac equation in 3 + 1 dimensions. The Dirac equation with scalar and vector HO potentials along with the tensor potential as a sum of linear and Coulomb-like potentials has been studied [33]. It was found that the tensor potential preserves the form of the HO potential and generates spin-orbit terms. The bound states of a new ring-shaped equal mixture of vector and scalar HO for spin-1/2 Dirac particles were studied [34]. The bound state solutions of the relativistic pseudoharmonic potential have been studied using the Nikiforov-Uvarov method [35].
Our aim is to obtain the exact s-wave Dirac bound state energies and the upperand lower-spinor wave functions in HO potential influenced by a uniform electric field. Further, we investigate the modification on the spectrum energy of a quantum particle influenced by a uniform electric field in the radial direction in the presence of the spin symmetry 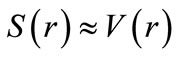 and pseudospin symmetry
and pseudospin symmetry 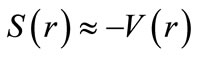 cases in the framework of the NU method [5,14-16,36-39]. These solutions are reduced to the spinless KG and Schrödinger limits when
cases in the framework of the NU method [5,14-16,36-39]. These solutions are reduced to the spinless KG and Schrödinger limits when  and
and  corresponding to exact spin
corresponding to exact spin 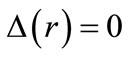 and pseudospin
and pseudospin 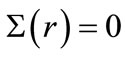 symmetry limitations [23-25,40-47].
symmetry limitations [23-25,40-47].
The performance of any method applied to the Dirac equation depends on the selected representation of this equation and the mathematical structure of the resulting equation, in which there are conditions under which it may be reduced to a Schrödinger equation [48-50].
In this paper, Section 2 briefly introduces Dirac formalisms. The Dirac bound state energies of a particle confined by an ESPs consisting of combined harmonic oscillator-plus-linear (HpL) potential model in the presence of spin and pseudospin symmetry using the NU method. In Section 3, we give our conclusions.
2. Bound State Solutions of the Combined Potential Model
The two radial coupled Dirac equations for the upper 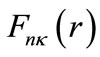 and lower
and lower 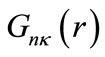 spinor components can be expressed in the form [41]
spinor components can be expressed in the form [41]
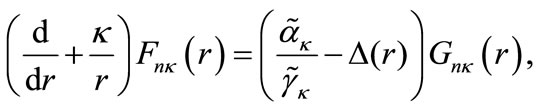 (1a)
(1a)
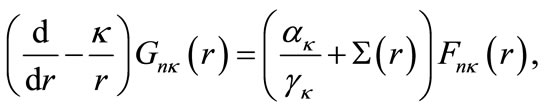 (1b)
(1b)
with
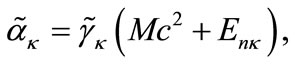 (2a)
(2a)
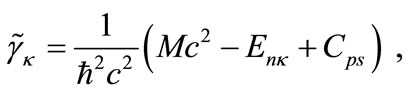 (2b)
(2b)
and
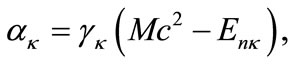 (3a)
(3a)
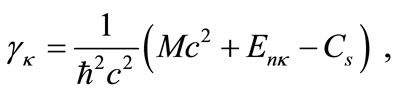 (3b)
(3b)
where 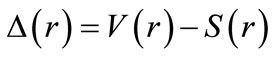 and
and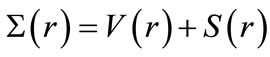 are the difference and sum radial potentials, respectively. Also
are the difference and sum radial potentials, respectively. Also 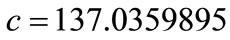 is the velocity of light [35]. In the presence of the spin symmetry (i.e.,
is the velocity of light [35]. In the presence of the spin symmetry (i.e., 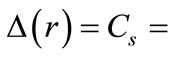 constant), one can eliminate
constant), one can eliminate 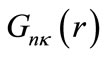 in (1a), with the aid of (1b), to obtain a secondorder differential equation for the upper-spinor component as follows (for details see [41-47]):
in (1a), with the aid of (1b), to obtain a secondorder differential equation for the upper-spinor component as follows (for details see [41-47]):
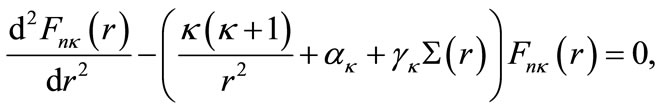 (4)
(4)
and the lower-spinor component can be obtained fd rom (1a) as
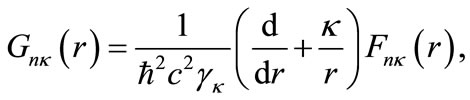 (5)
(5)
where  (only real positive energy states exist) when
(only real positive energy states exist) when 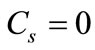 (the exact spin symmetry case). On the other hand, under the pseudospin symmetry (i.e.),
(the exact spin symmetry case). On the other hand, under the pseudospin symmetry (i.e.),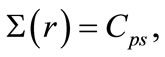 where
where 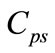 a constant, one can eliminate
a constant, one can eliminate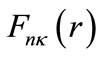 in (1b), with the aid of (1a), to obtain a secondorder differential equation for the lower-spinor component as follows:
in (1b), with the aid of (1a), to obtain a secondorder differential equation for the lower-spinor component as follows:
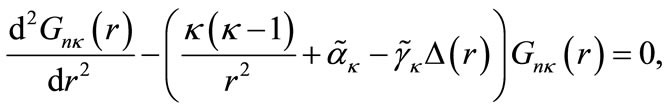 (6)
(6)
and the upper-spinor component 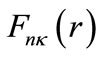 can be obtained from (1b) as
can be obtained from (1b) as
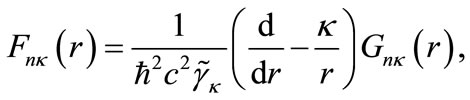 (7)
(7)
where  (only real negative energy states exist) when
(only real negative energy states exist) when 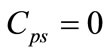 (for exact pseudospin symmetry). Thus, from the above equations, the energy eigenvalues depend on the quantum numbers
(for exact pseudospin symmetry). Thus, from the above equations, the energy eigenvalues depend on the quantum numbers  and
and 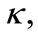 and also the pseudoorbital angular quantum number
and also the pseudoorbital angular quantum number 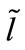 according to
according to 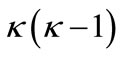
 which implies that
which implies that 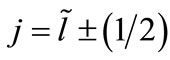 are degenerate for
are degenerate for 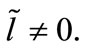 It is worthy to note that the reality and finiteness of our solutions demand that the upper and lower radial components are to satisfy the essential boundary conditions:
It is worthy to note that the reality and finiteness of our solutions demand that the upper and lower radial components are to satisfy the essential boundary conditions: 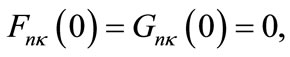 and
and

We shall study the spin and pseudospin symmetric Dirac equation for the charged HO in a uniform electric field of specific strength 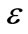 or the HO in an external dipole field. The corresponding scalar and vector components are taken to be the combined potential:
or the HO in an external dipole field. The corresponding scalar and vector components are taken to be the combined potential:
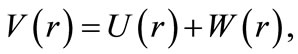 (8)
(8)
where
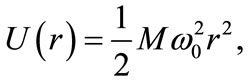 (9)
(9)
is the h.o. potential with the associated force given by
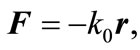 (10)
(10)
and
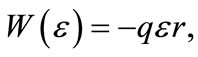 (11)
(11)
is the classical potential energy of a charged particle in a uniform external electric field of specific value 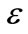 in the radial direction with
in the radial direction with  being the charge of the particle. The combined potential (8) becomes
being the charge of the particle. The combined potential (8) becomes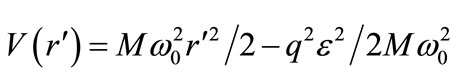 , where
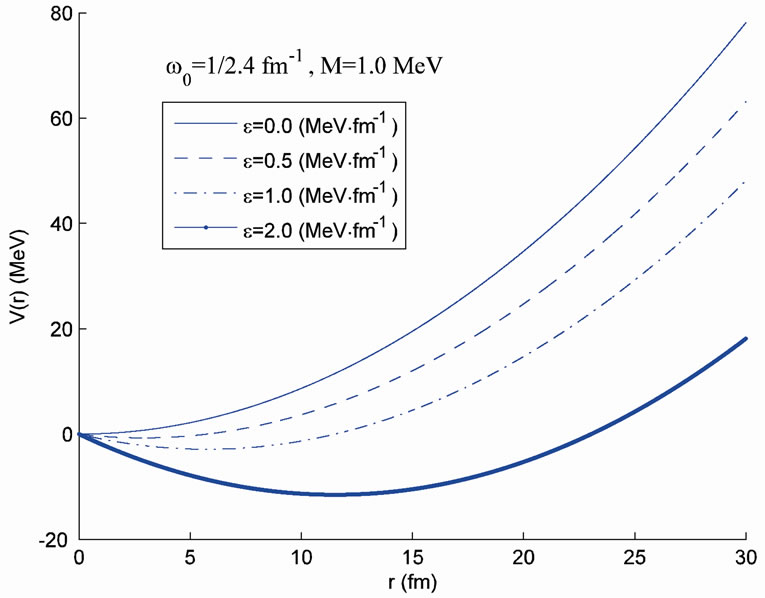
, where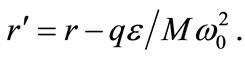 In Figure 1, we plot the ESP
In Figure 1, we plot the ESP 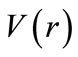 versus distance
versus distance 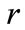 with the choices of parameters (a)
with the choices of parameters (a) 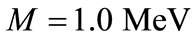 and
and 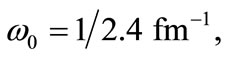 (b)
(b) 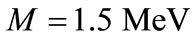 and
and 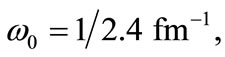 (c)
(c) 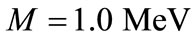 and
and 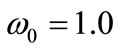
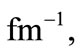 and (d)
and (d)  and
and 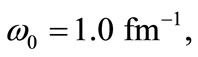 for several values of electric field strength:
for several values of electric field strength: 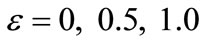 and
and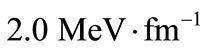 .
.
 (a)
(a)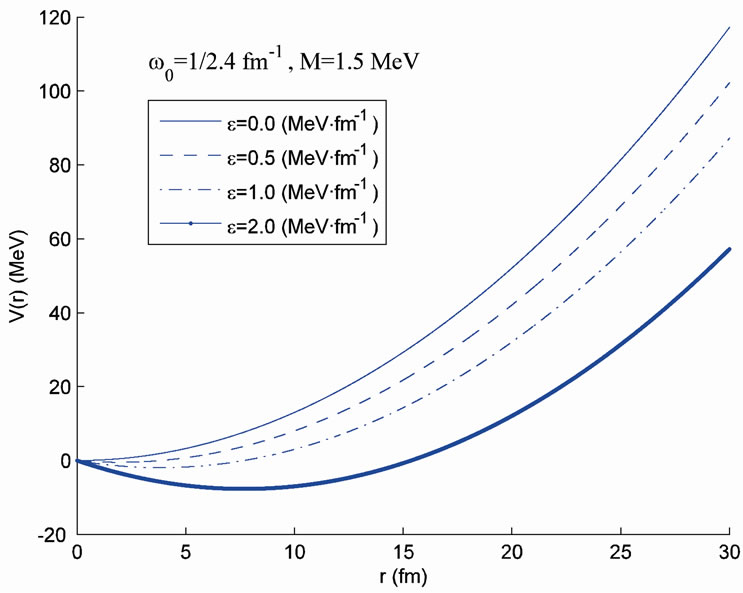 (b)
(b) (c)
(c)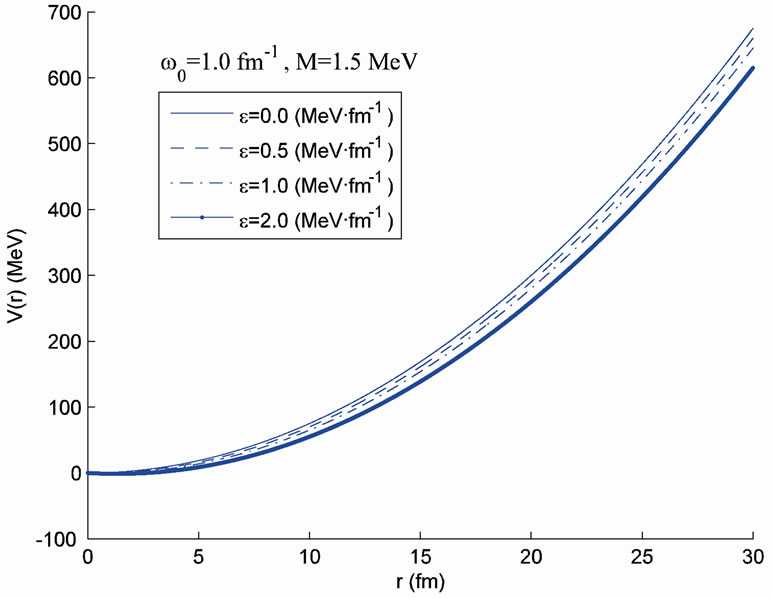 (d)
(d)
Figure 1. Variation of the V(r) with distance  in the presence and absence of electric field for the cases. (a) M = 1.0 MeV and
in the presence and absence of electric field for the cases. (a) M = 1.0 MeV and 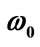 = 1/2.4 fm–1; (b) M = 1.5 MeV and
= 1/2.4 fm–1; (b) M = 1.5 MeV and 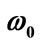 = 1/2.4 fm–1; (c) M = 1.0 MeV and
= 1/2.4 fm–1; (c) M = 1.0 MeV and 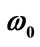 = 1.0 fm–1; and (d) M = 1.5 MeV and
= 1.0 fm–1; and (d) M = 1.5 MeV and 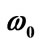 = 1.0 fm–1.
= 1.0 fm–1.
It is clearly seen that the potential 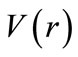 has the harmonic-like behavior with frequency
has the harmonic-like behavior with frequency 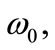 at least in the inner of nuclei, and at a radius
at least in the inner of nuclei, and at a radius 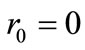 describing the distance of well-bottom deviation from the center. Therefore, the study of spin and pseudospin partners splitting as a function of these parameters is meaningful and realistic enough to be applied to most nuclei at least qualitatively. It is known that, in certain isotope chains, as the mass number
describing the distance of well-bottom deviation from the center. Therefore, the study of spin and pseudospin partners splitting as a function of these parameters is meaningful and realistic enough to be applied to most nuclei at least qualitatively. It is known that, in certain isotope chains, as the mass number 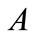 increases, the nuclear harmonic oscillator frequency
increases, the nuclear harmonic oscillator frequency 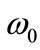 decreases according to the
decreases according to the 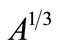 law (
law (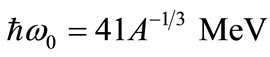 ), which means that it is important to study the role of the parameter
), which means that it is important to study the role of the parameter 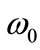 in spin and pseudospin symmetry [31]. In particular, the HO potential can provide fully bound states which are helpful to discuss the symmetry systematically.
in spin and pseudospin symmetry [31]. In particular, the HO potential can provide fully bound states which are helpful to discuss the symmetry systematically.
2.1. The Spin-Symmetry Solutions
Let us now study the potential model (8) in the context of spin symmetric Dirac Equation (4). Therefore, it can be solved exactly for 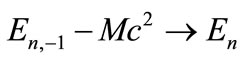 because of the presence of spin-orbit centrifugal term. Under this symmetry, we take the sum potential in (4) as the combined potential, i.e.,
because of the presence of spin-orbit centrifugal term. Under this symmetry, we take the sum potential in (4) as the combined potential, i.e.,
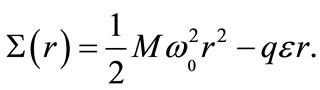 (12)
(12)
We choose 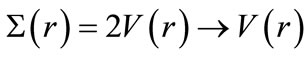 as stated in [41-47]*. The s-wave (
as stated in [41-47]*. The s-wave (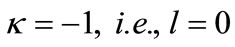 ) case allows to rewrite (4) for the combined potential (12) as
) case allows to rewrite (4) for the combined potential (12) as
 (13)
(13)
where the constants are written as
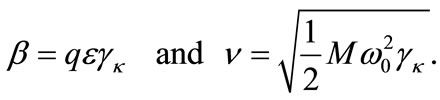 (14)
(14)
To apply the NU method [5,39], we need to compare (13) with (2) of [39] to obtain values for the parameters:
 (15)
(15)
Inserting these values into (11) of [39], the selected forms of  and
and 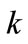 take the following particular values
take the following particular values
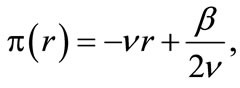 (16)
(16)
and
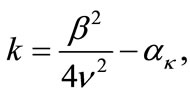 (17)
(17)
for discrete bound state solutions. According to the method, the following polynomial of degree one can be obtained from (6) of [39]:
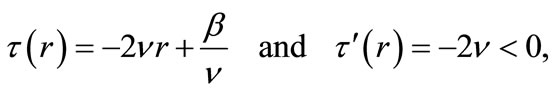 (18)
(18)
with prime denotes the derivative with respect to 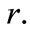 The parameters
The parameters 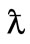 and
and 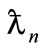 in (7) and (10) of [39] take the simple forms as
in (7) and (10) of [39] take the simple forms as
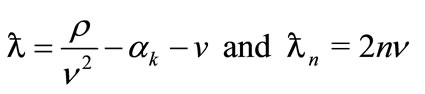 (19)
(19)
Using the condition 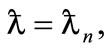 we obtain the transcendental energy equation for the charged particle confined by HO in an electric field of specific strength
we obtain the transcendental energy equation for the charged particle confined by HO in an electric field of specific strength 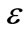 as
as
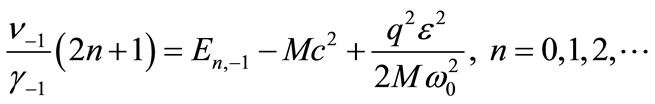 (20)
(20)
where at 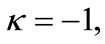 we have defined
we have defined 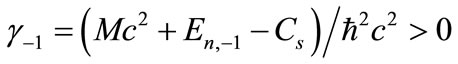 and
and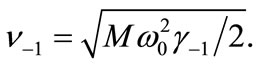 We can compute the energy spectrum by choosing suitable parameters in the symmetric potential. Equation (20) shows the energy spectrum
We can compute the energy spectrum by choosing suitable parameters in the symmetric potential. Equation (20) shows the energy spectrum 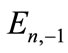 dependence on
dependence on 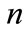 and
and 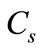 as well as on the parameters
as well as on the parameters 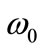 and
and  If we choose
If we choose 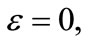 (20) reduces to the one-dimensional energy spectrum of the relativistic HO:
(20) reduces to the one-dimensional energy spectrum of the relativistic HO:
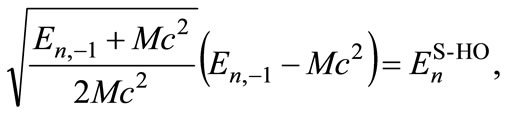
where  is the well-known Schrö- dinger energy spectrum for the HO. The above result resembles the ones given in [22,33]. Hence, Dirac spectrum is composed of two sequences of discrete energy levels separated by the
is the well-known Schrö- dinger energy spectrum for the HO. The above result resembles the ones given in [22,33]. Hence, Dirac spectrum is composed of two sequences of discrete energy levels separated by the 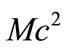 gap. This is Dirac oscillator [22,51-53] based on a construction of the Dirac equation which is ESP and in the NR limit gives the Schrö- dinger HO equation.
gap. This is Dirac oscillator [22,51-53] based on a construction of the Dirac equation which is ESP and in the NR limit gives the Schrö- dinger HO equation.
We use the parameter values of the HO potential  and
and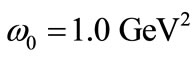 when
when 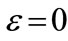 [54]. Hence, the numerical result for the s-wave energy spectrum of the bound state with relativistic corrections for the HO potential is:
[54]. Hence, the numerical result for the s-wave energy spectrum of the bound state with relativistic corrections for the HO potential is: 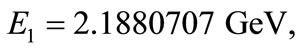
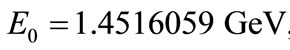
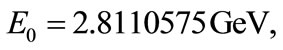 and
and 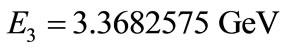 for states
for states 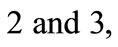
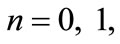 respectively.
respectively.
We use (20) to compute some energy spectrum with relativistic corrections for several values of 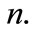 The computed exact spin symmetric (
The computed exact spin symmetric ( ) energy spectrum is displayed in Table 1.
) energy spectrum is displayed in Table 1.
Also, for the combined potential we use the values 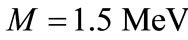 and
and 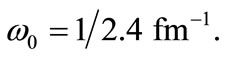 The strength of the electric field is set up at some arbitrary values of
The strength of the electric field is set up at some arbitrary values of 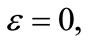
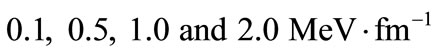 Obviously, the energy levels are only positive under the spin symmetry limit when
Obviously, the energy levels are only positive under the spin symmetry limit when 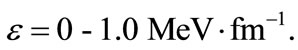 However, as the field strength increases, i.e.,
However, as the field strength increases, i.e., 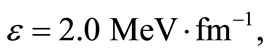 the results are noticed to become negative. The number of states in spec-
the results are noticed to become negative. The number of states in spec-

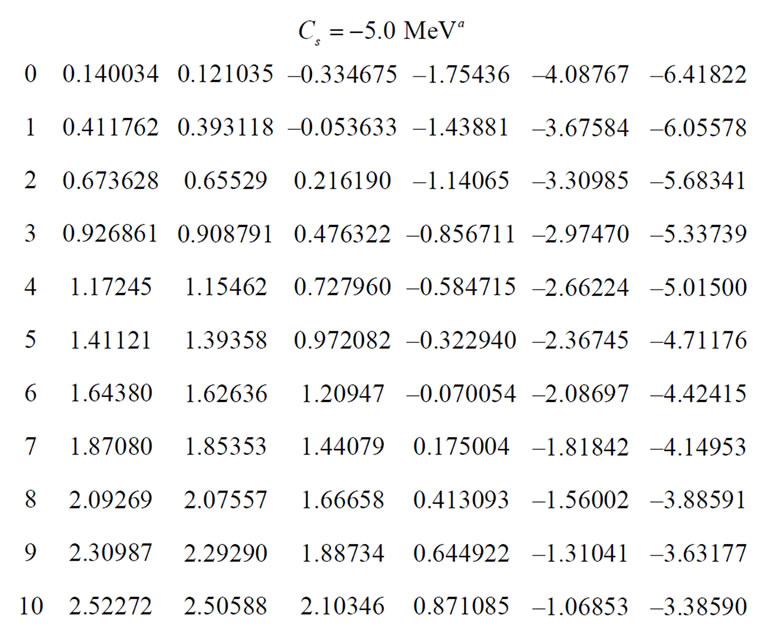
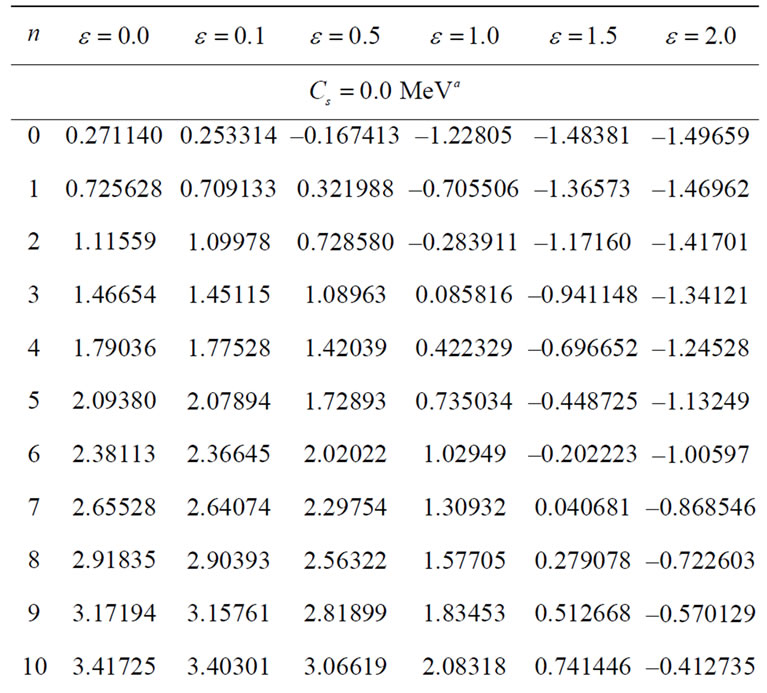
Table 1. Energy levels (in relativistic units) for different quantum numbers.
trum with negative values is finite (as n increases, 
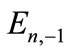 and then energy eigenvalues flip their signs to positive values). In addition, the increase in the field strength,
and then energy eigenvalues flip their signs to positive values). In addition, the increase in the field strength,  , leads to no bound states. We conclude that the strength
, leads to no bound states. We conclude that the strength 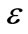 has a maximum limit to provide real spectrum and hence must be adjusted carefully to produce real positive or negative values for the bound states.
has a maximum limit to provide real spectrum and hence must be adjusted carefully to produce real positive or negative values for the bound states.
The NR limit as a special case obtained when 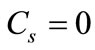 (exact spin symmetry) and employing appropriate parametric transformations:
(exact spin symmetry) and employing appropriate parametric transformations: 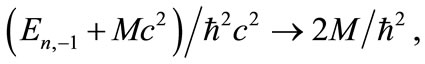 and
and 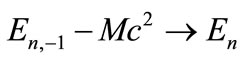 [28,42-47,55]. Therefore, the NR energy solution can be established for an electron confined in HO potential combined with an external electric field [see (8)] is
[28,42-47,55]. Therefore, the NR energy solution can be established for an electron confined in HO potential combined with an external electric field [see (8)] is
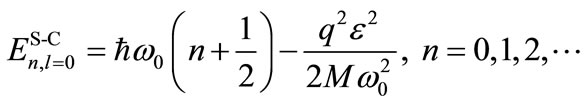 (21)
(21)
leading to the ground-state energy spectrum formula:
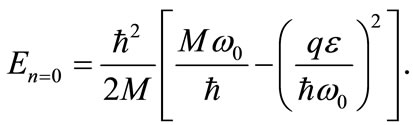
Obviously, we see from (21) that the entire spectrum of the harmonic oscillator (9) is shifted by the quantity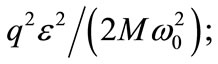 this translation comes from the wellknown fact that the electric field exerts a force on a charged particle. The modification is due only to the electric field. In the NR limit, the above result can be obtained directly from the well-known solution of the shifted HO in the absence of an electric field with change of variable
this translation comes from the wellknown fact that the electric field exerts a force on a charged particle. The modification is due only to the electric field. In the NR limit, the above result can be obtained directly from the well-known solution of the shifted HO in the absence of an electric field with change of variable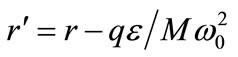 and energy
and energy 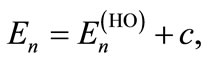 where the shifting energy
where the shifting energy 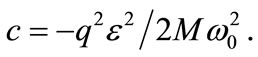 The above results are identical to the ones given in [11,18,19]. Taking
The above results are identical to the ones given in [11,18,19]. Taking 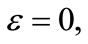 (21) is simply the NR HO solution (cf. e.g., [56]).
(21) is simply the NR HO solution (cf. e.g., [56]).
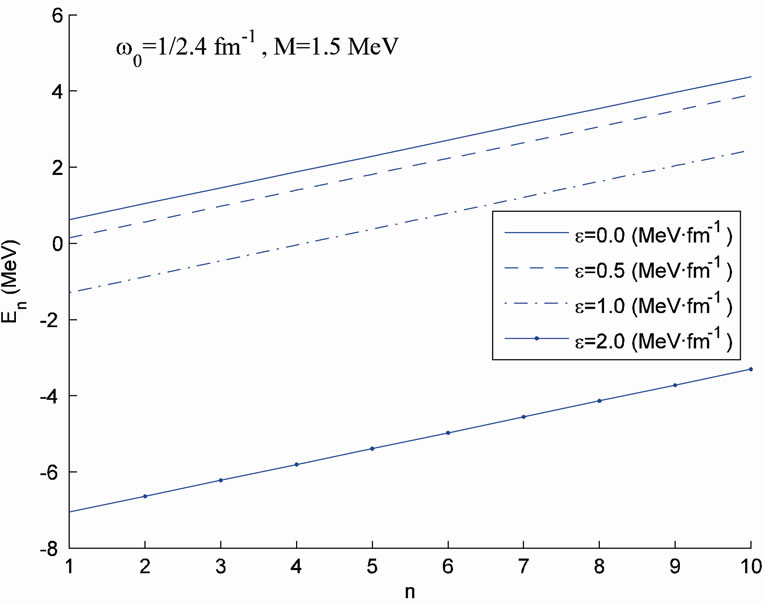
In Figure 2, (in units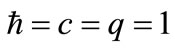 ), we plot the energy spectrum in (21) versus the quantum number n for specific values of
), we plot the energy spectrum in (21) versus the quantum number n for specific values of  with the following choices: (a)
with the following choices: (a) 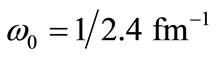
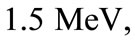
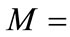 and
and 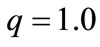 and (b)
and (b)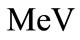
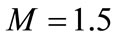 ,
, 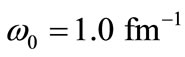 and
and 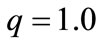 for several values of electrical field strength,
for several values of electrical field strength, . As seen in Figure 2(a) when the frequency is small and in the presence of stronger electrical field, energy states are shifted toward the negative energy part, i.e., for
. As seen in Figure 2(a) when the frequency is small and in the presence of stronger electrical field, energy states are shifted toward the negative energy part, i.e., for 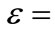
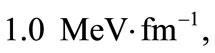 n < 6 are strongly bound, however, when
n < 6 are strongly bound, however, when 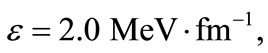 all states become strongly bound by the combined potential.
all states become strongly bound by the combined potential.
On the other hand, in Figure 2(b), as frequency increases, the electrical field has no much effect in shifting energy levels; all states are in the positive energy part.
Next, we start the calculations of the corresponding wave functions. Consequently, both (4) and (9) of [39] give
 (a)
(a)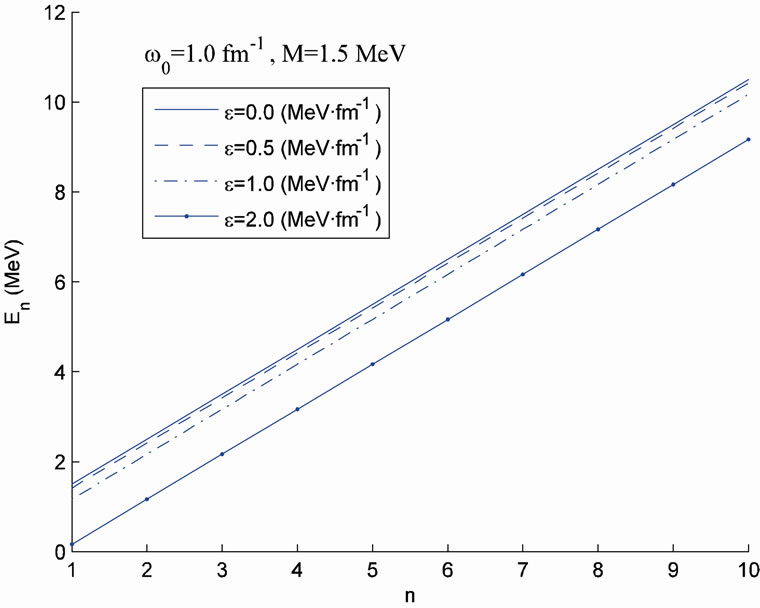 (b)
(b)
Figure 2. Energy spectrum En versus n in the presence and absence of uniform electric field for (a) M = 1.5 MeV and 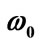 = 1/2.4 fm–1 and (b) M = 1.5 MeV and
= 1/2.4 fm–1 and (b) M = 1.5 MeV and 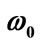 = 1.0 fm–1.
= 1.0 fm–1.
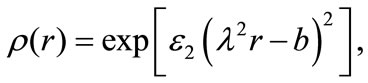 (22)
(22)
 (23)
(23)
where
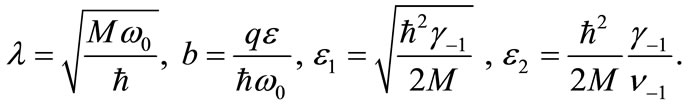 (24)
(24)
Hence, the first part of the wave function is
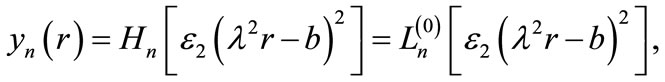 (25)
(25)
where 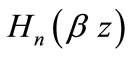 is a nth degree Hermite polynomial, and
is a nth degree Hermite polynomial, and 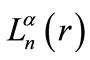 is the associated Laguerre polynomial defined for the argument
is the associated Laguerre polynomial defined for the argument 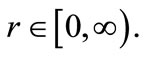 The solution of (2) can be obtained by using (3) of [39] as
The solution of (2) can be obtained by using (3) of [39] as
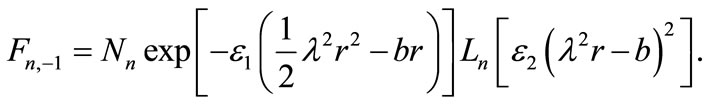 (26)
(26)
In the NR limit, Equation (26) becomes
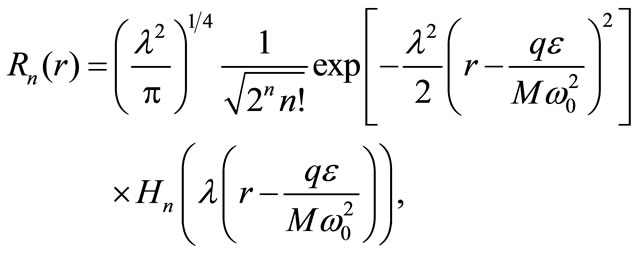 (27)
(27)
where 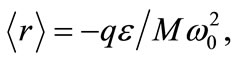 for all eigenstates
for all eigenstates 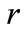 and for the ground state it is given by
and for the ground state it is given by
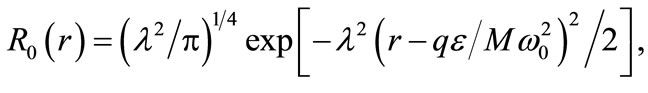
where 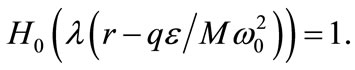
As seen, the modification in (26) is essentially produced from the external electric field. Furthermore, the associated lower-spinor component 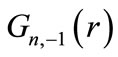 satisfying Equation (5) is taking the form
satisfying Equation (5) is taking the form
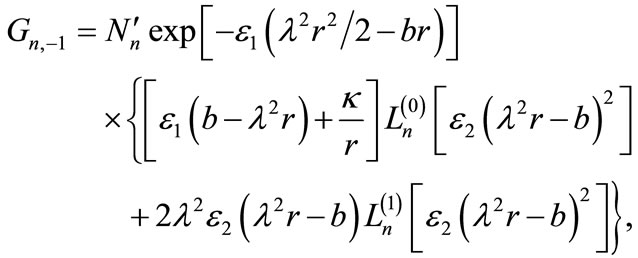 (28)
(28)
where 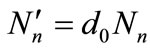 with
with  is counted as a new normalization constant. It is worth to mention that
is counted as a new normalization constant. It is worth to mention that 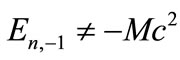 under the exact spin symmetry
under the exact spin symmetry 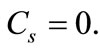
2.2. The Pseudospin Symmetric Solutions
The exact pseudospin symmetry occurs when 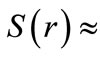
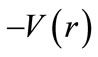 [16,23-25,40] and the quality of the pseudospin approximation in real nuclei is connected with the competition between the pseudo-centrifugal barrier and the pseudospin-orbital potential [31]. Here
[16,23-25,40] and the quality of the pseudospin approximation in real nuclei is connected with the competition between the pseudo-centrifugal barrier and the pseudospin-orbital potential [31]. Here 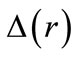 in Equation (6) is taken to be the same as the combined potential (8), that is,
in Equation (6) is taken to be the same as the combined potential (8), that is,
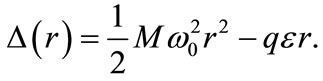 (29)
(29)
Thus, for the s-wave 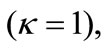 Equation (6) can be rewritten as
Equation (6) can be rewritten as
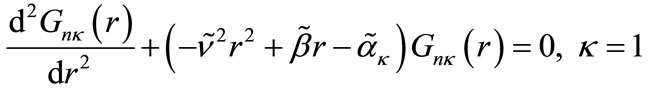 (30)
(30)
where
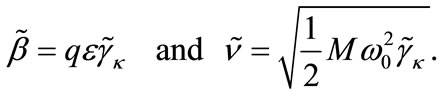 (31)
(31)
To avoid repetition in the solution of Equation (30), a first inspection for the relationship between the present set of parameters 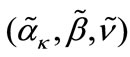 and the previous set
and the previous set 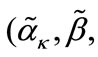
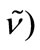 tells us that the energy solution for pseudospin symmetry can be easily obtained directly from the spin symmetry energy solutions by performing the transformation changes [42-47,55,57]:
tells us that the energy solution for pseudospin symmetry can be easily obtained directly from the spin symmetry energy solutions by performing the transformation changes [42-47,55,57]:
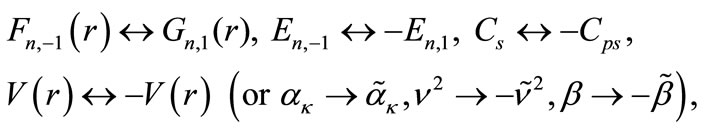 (32)
(32)
or alternatively, the essential parameters given by
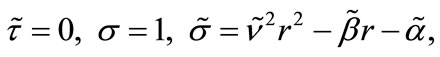
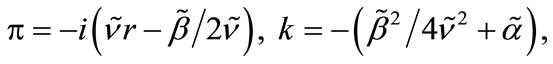
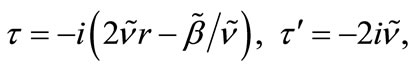
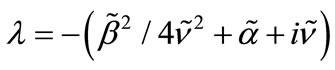 ,
, 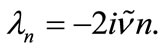
are used to obtain the following transcendental energy equation:
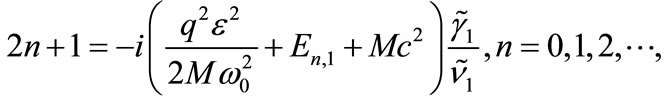 (33)
(33)
with
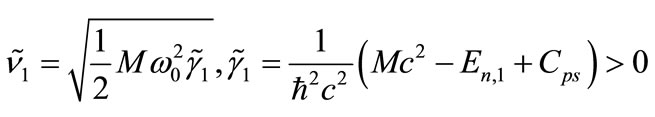 (34)
(34)
where 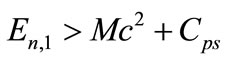 is the restriction condition for the discrete bound states. Hence, Equation (33) is identical to Equation (62) of [23] obtained for the HO potential if the electric field strength
is the restriction condition for the discrete bound states. Hence, Equation (33) is identical to Equation (62) of [23] obtained for the HO potential if the electric field strength  is set to zero.
is set to zero.
The NR limit of Equation (33), when 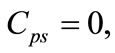 becomes
becomes
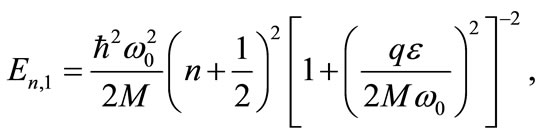 (35)
(35)
where is the classical frequency for small harmonic vibrations [58]. The right hand side of (34) is always positive. Therefore, there are only positive energies in the NR limit for the HO potential [28,35]. Hence, using (33), we can compute the energies by choosing suitable parameters in the pseudo symmetric limit. The energies  are dependent on n and
are dependent on n and  as well as on the parameters
as well as on the parameters 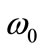 and
and 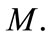 We also compute the energy spectrum of the bound state system with relativistic corrections for several values of n with parameter values of the potential
We also compute the energy spectrum of the bound state system with relativistic corrections for several values of n with parameter values of the potential 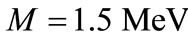 and
and 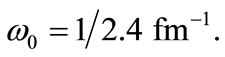 (for two constants
(for two constants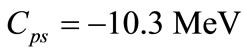 and
and 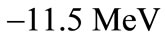 as represented in Table 2. The external electrical field is set up at some values
as represented in Table 2. The external electrical field is set up at some values 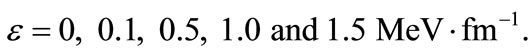
We see that there are only negative energy bound state solutions in the pseudospin symmetry limit when the strength of external electric fields are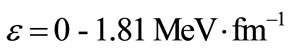 . Nevertheless, as the field strength increases, i.e.,
. Nevertheless, as the field strength increases, i.e., 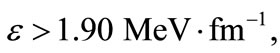 the energies are noticed to become complex for all states. We conclude that when the external
the energies are noticed to become complex for all states. We conclude that when the external
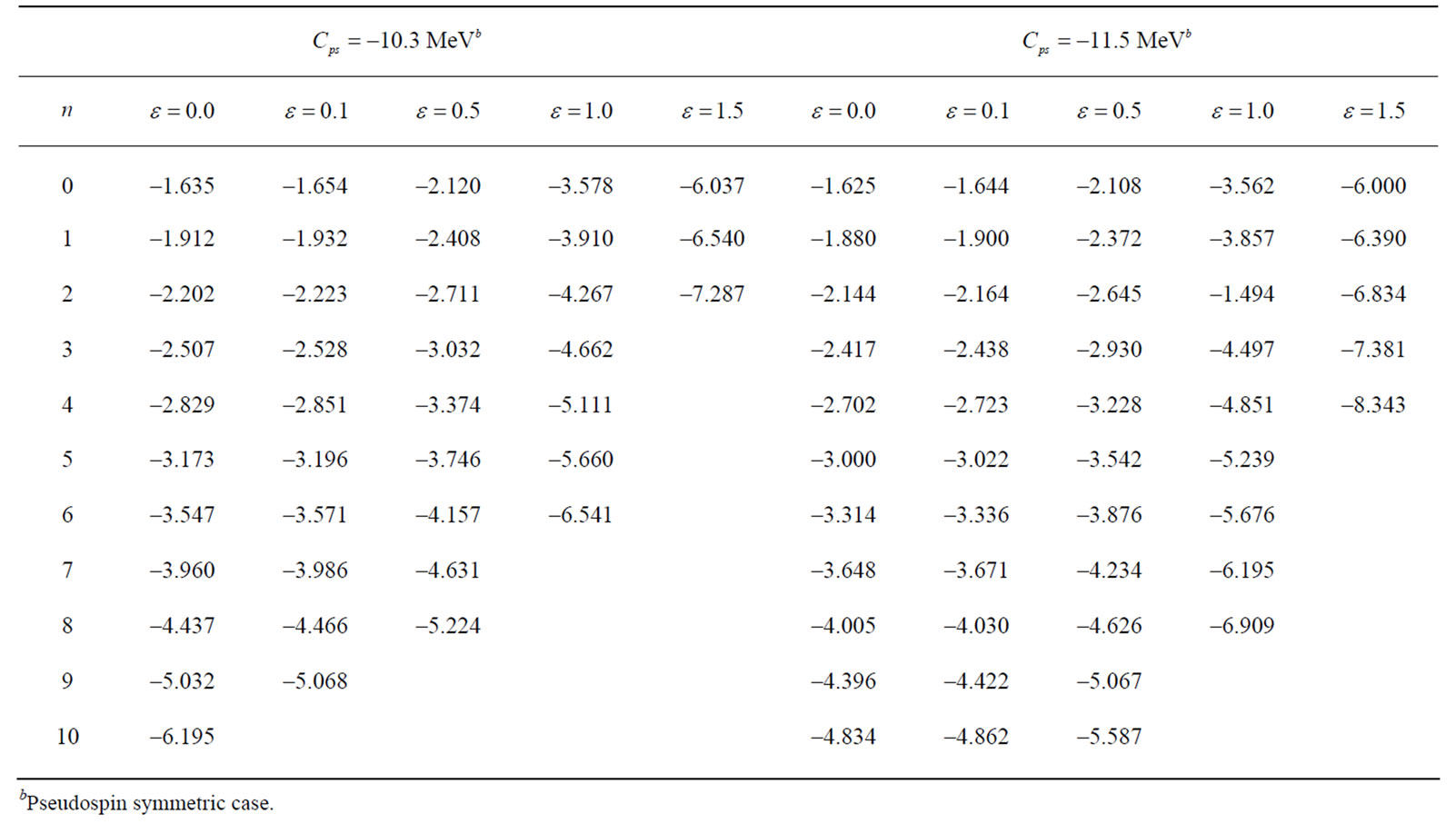
Table 2. Energy levels (in relativistic units) for different quantum numbers.
electric field 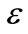 strength exceeds the ionization limit then it provides imaginary spectrum (no bound states). Hence the strength of the electric field must be adjusted carefully to generate real positive/negative bound states. Also, the parameters M and
strength exceeds the ionization limit then it provides imaginary spectrum (no bound states). Hence the strength of the electric field must be adjusted carefully to generate real positive/negative bound states. Also, the parameters M and 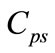 must be adjusted properly for real solutions of the transcendental energy Equation (33).
must be adjusted properly for real solutions of the transcendental energy Equation (33).
Finally, we calculate the lower-spinor wave function which is the solution of (6) as
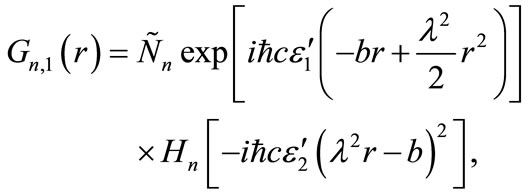 (35)
(35)
where 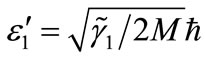 and
and 
3. Conclusion
The exact s-wave Dirac bound states (energy spectra and wave functions) of the potential (8) in the presence of the spin symmetry and pseudospin symmetry are obtained in closed form using the NU method. The wave functions are expressed in terms of the orthogonal Laguerre polynomials. For the exact spin symmetry (i.e.,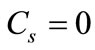 ), the relativistic solution can be readily reduced to the NR one by an appropriate mapping transformations. The presence of an external uniform electric field creates a shift at the energy spectrum and a translation on the wave functions for the HO. In case if the description of diatomic vibration motion is NR, the relativistic model used seems quite justified since it can be easily reduced to the NR limits [18,19]. As numerical example, we take a set of physical parameter values to determine the bound state energy eigenvalues as shown in Tables 1 and 2 for the spin and pseudospin symmetry cases, respectively. It is worth to mention that the strength of the applied electric field
), the relativistic solution can be readily reduced to the NR one by an appropriate mapping transformations. The presence of an external uniform electric field creates a shift at the energy spectrum and a translation on the wave functions for the HO. In case if the description of diatomic vibration motion is NR, the relativistic model used seems quite justified since it can be easily reduced to the NR limits [18,19]. As numerical example, we take a set of physical parameter values to determine the bound state energy eigenvalues as shown in Tables 1 and 2 for the spin and pseudospin symmetry cases, respectively. It is worth to mention that the strength of the applied electric field  needs to be adjusted properly to provide us bound state energy spectrum for certain values of parameters
needs to be adjusted properly to provide us bound state energy spectrum for certain values of parameters 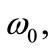

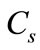 and
and 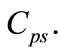
4. Acknowledgements
The author thanks the two kind referees for their enlightening suggestions. This work is dedicated to the memory of my father “Musbah” who passed away in Nablus, Palestine on January, 26, 2012. He taught me a lot to become a Professor. I am really indebted to him. God blesses his soul and may he rests in peace.
REFERENCES
- O. L. de Lange and R. E. Raab, “Operator Methods in Quantum Mechanics,” Clarendon, Oxford, 1991.
- G. Arfken, “Mathematical Methods for Physicists,” Academic Press, San Diego, 1995.
- C.V. Sukumar, “Supersymmetric Quantum Mechanics of One-Dimensional Systems,” Journal of Physics A: Mathematical and General, Vol. 18, No. 6, 1985, pp. 2917-2936. doi:10.1088/0305-4470/18/15/020
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry in Quantum Mechanics,” World Scientific, Singapore, 2001. doi:10.1142/9789812386502
- A. F. Nikiforov and V. B. Uvarov, “Special Functions of Mathematical Physics,” Birkhäuser, Basel, 1988.
- O. Bayrak, I. Boztosun and H. Ciftci, “Exact Analytical Solutions to the Kratzer Potential by the Asymptotic Iteration Method,” International Journal of Quantum Chemistry, Vol. 107, No. 3, 2007, pp. 540-544. doi:10.1002/qua.21141
- W. C. Qiang and S. H. Dong, “Arbitrary l-State Solutions of the Rotating Morse Potential through the Exact Quantization Rule Method,” Physics Letters A, Vol. 363, No. 3, 2007, pp. 169-176. doi:10.1016/j.physleta.2006.10.091
- I. Nasser, M. S. Abdelmonem, H. Bahlouli and A. D. Alhaidari, “The Rotating Morse Potential Model for diatomic Molecules in the Tridiagonal J-Matrix Representation: 1. Bound States,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 40, No. 21, 2007, pp. 4245-4258. doi:10.1088/0953-4075/40/21/011
- R. R. Freeman, N. P. Economou, G. C. Bjorklund and K. T. Lu, “Observation of Electric Field Induced Resonances Above the Ionization Limit in a One Electron Atom,” Physical Review Letters, Vol. 41, No. 21, 1978, pp. 1463- 1467. doi:10.1103/PhysRevLett.41.1463
- J. M. Jauch, “The Hyperfine Structure and the Stark Effect of the Ammonia Inversion Spectrum,” Physical Review, Vol. 72, No. 8, 1947, pp. 715-723. doi:10.1103/PhysRev.72.715
- J. J. Peña, M. A. Romero-Romo, J. Morales and J. L. López-Bonilla, “Exactly Solvable Combined Potentials and their Isospectral Partners from SUSY,” International Journal of Quantum Chemistry, Vol. 105, No. 6, 2005, pp. 731- 739. doi:10.1002/qua.20687
- E. Witten, “Super-Symmetry and Other Scenarios,” International Journal of Modern Physics A, Vol. 19, No. 8, 2004, pp. 1259-1264.
- H. T. Davis, “Introduction to Nonlinear Differential and Integral Equations,” Dover, New York, 1962.
- S. M. Ikhdair, “Rotation and Vibration of Diatomic Molecule in the Spatially Dependent Mass Schrödinger Equation with Generalized q-Deformed Morse Potential,” Chemical Physics, Vol. 361, No. 1-2, 2009, pp. 9-17. doi:10.1016/j.chemphys.2009.04.023
- S. M. Ikhdair, “An Improved Approximation Scheme for the Centrifugal Term and the Hulthen Potential,” European Physical Journal A, Vol. 39, No. 22, 2009, pp. 307- 314. doi:10.1140/epja/i2008-10715-2
- S. M. Ikhdair and R. Sever, “Any l-State Improved QuasiExact Analytical Solutions of the Spatially Dependent Mass Klein—Gordon Equation for the Scalar and Vector Hulthen Potential,” Physica Scripta, Vol. 79, No. 3, 2009, Article ID 035002.
- S. M. Ikhdair and R. Sever, “Exact Quantization Rule to the Kratzer-Type Potentials: An Application to the Diatomic Molecules,” Journal of Mathematical Chemistry, Vol. 45, No. 4, 2009, pp. 1137-1152. doi:10.1007/s10910-008-9438-8
- S. Azevedo, “Harmonic Oscillator in a Space with a Linear Topological Defect,” Physical Letters A, Vol. 288, No. 1, 2001, pp. 33-36. doi:10.1016/S0375-9601(01)00539-4
- S. Azevedo, “Influence of the Electric Field on a Particle in a Space with a Disiclination,” International Journal of Quantum Chemistry, Vol. 101, 2005, pp. 127-130. doi:10.1002/qua.20263
- Q. W. Chao, “Bound States of the Klein-Gordon and Dirac Equations for Scalar and Vector Harmonic Oscillator Potentials,” Chinese Physics, Vol. 11, No. 8, 2002, pp. 757-759. doi:10.1088/1009-1963/11/8/301
- T.-S. Chen, H.-F. Lü, J. Meng, S.-Q. Zhang and S.-G. Zhou, “Pseudospin Symmetry in Relativistic Framework With Harmonic Oscillator Potential and Woods-Saxon Potential,” Chinese Physical Letters, Vol. 20, No. 3, 2003, pp. 358-361. doi:10.1088/0256-307X/20/3/312
- V. I. Kukulin, G. Loyola and M. Moshinsky, “A Dirac Equation with an Oscillator Potential and Spin-Orbit Coupling,” Physical Letters A, Vol. 158, No. 1-2, 1991, pp. 19- 22. doi:10.1016/0375-9601(91)90333-4
- J. N. Ginocchio, “Relativistic Harmonic Oscillator with Spin Symmetry,” Physical Review C, Vol. 69, 2004, Article ID 034318.
- J. N. Ginocchio, “Pseudospin as a Relativistic Symmetry,” Physical Review Letters, Vol. 78, No. 3, 1997, pp. 436-459. doi:10.1103/PhysRevLett.78.436
- J. N. Ginocchio, “Relativistic Symmetries in Nuclei and Hadrons,” Physics Report, Vol. 414, No. 4-5, 2005, pp. 165- 261. doi:10.1016/j.physrep.2005.04.003
- P. Alberto, M. Fiolhais, M. Malheiro, A. Delfino and M. Chiapparini, “Isospin Asymmetry in the Pseudospin Dynamical Symmetry,” Physical Review Letters, Vol. 86, No. 22, 2001, pp. 5015-5018. doi:10.1103/PhysRevLett.86.5015
- P. Alberto, M. Fiolhais, M. Malheiro, A. Delfino and M. Chiapparini, “Pseudospin Symmetry as a Relativistic Dynamical Symmetry in the Nucleus,” Physical Review C, Vol. 65, No. 3, 2002, Article ID 034307. doi:10.1103/PhysRevC.65.034307
- R. Lisboa, M. Malheiro, A. S. de Castro, P. Alberto and M. Fiolhais, “Pseudospin Symmetry and the Relativistic Harmonic Oscillator,” Physical Review C, Vol. 69, 2004, Article ID 024319. doi:10.1103/PhysRevC.69.024319
- R. Lisboa, M. Malheiro, A. S. de Castro, P. Alberto and M. Fiolhais, “Perturbative Breaking of the Pseudospin Symmetry in the Relativistic Harmonic Oscillator,” International Journal of Modern Physics D, Vol. 13, No. 7, 2004, pp. 1447-1451. doi:10.1142/S0218271804005675
- J. N. Ginocchio, “A Relativistic Symmetry in Nuclei,” Physics Reports, Vol. 315, No. 1, 1999, pp. 231-240. doi:10.1016/S0370-1573(99)00021-6
- J.-Y. Guo, X.-Z. Fang and F.-X. Xu, “Pseudospin Symmetry in the Relativistic Harmonic Oscillator,” Nuclear Physics A, Vol. 757, No. 3-4, 2005, pp. 411-421. doi:10.1016/j.nuclphysa.2005.04.017
- A. S. de Castro, P. Alberto, R. Lisboa and M. Malheiro, “Rotating Pseudospin and Spin Symmetries through ChargeConjugation and Chiral Transformations: The Case of the Relativistic Harmonic Oscillator,” Physical Review C, Vol. 73, 2006, Article ID 054309.
- H. Akçay and C. Tezcan, “Exact Solutions of the Dirac Equation with Harmonic Oscillator Potential Including a Coulomb-Like Tensor Potential,” International Journal of Modern Physics D, Vol. 20, No. 6, 2009, pp. 931-940. doi:10.1142/S0129183109014084
- Y. Zhou and J.-Y. Guo, “The Relativistic Bound States for a New Ring-Shaped Harmonic Oscillator,” Chinese Physical B, Vol. 17, No. 2, 2008, pp. 380-384. doi:10.1088/1674-1056/17/2/004
- O. Aydoğdu and R. Sever, “Solution of the Dirac Equation for Pseudoharmonic Potential by Using the Nikiforov-Uvarov Method,” Physica Scripta, Vol. 80, No. 1, 2009, Article ID 015001.
- S. M. Ikhdair and R. Sever, “Improved Analytical Approximation to Arbitrary l-State Solutions of the Schrö- dinger Equation for the Hyperbolical Potentials,” Annals Physics, Vol. 18, 2009, pp. 747-758. doi:10.1002/andp.200910369
- S. M. Ikhdair, “On the Bound-State Solutions of the Manning-Rosen Potential Including an Improved Approximation to the Orbital Centrifugal Term,” Physica Scripta, Vol. 83, No. 1, 2011, Article ID 015010. doi:10.1088/0031-8949/83/01/015010
- S. M. Ikhdair, “Exactly Solvable Effective Mass Dimensional Schrödinger equation for Pseudoharmonic and Modified Kratzer potentials,” International Journal of Modern Physics C, Vol. 20, No. 3, 2009, pp. 361-372. doi:10.1142/S0129183109013674
- S. M. Ikhdair, “Exact Klein-Gordon Equation with Spatially Dependent Masses for Unequal Scalar-Vector Coulomb-Like Potentials,” European Physical Journal A, Vol. 40, No. 2, 2009, pp. 143-149. doi:10.1140/epja/i2009-10758-9
- J. Meng, K. Sugawara-Tanabe, S. Yamaji and A. Arima, “Pseudospin Symmetry in Zr and Sn Isotopes from the Proton Drip Line to the Neutron Drip Line,” Physical Review C, Vol. 59, No. 1, 1999, p. 154.
- W. Greiner, “Relativistic Quantum Mechanics,” Springer, Verlag, Berlin, 1981.
- S. M. Ikhdair, “Approximate Solutions of the Dirac Equation for the Rosen-Morse Potential including SpinOrbit Centrifugal Term,” Journal of Mathematical Physics, Vol. 51, 2010, Article ID 023525. doi:10.1063/1.3293759
- S. M. Ikhdair, “An Approximate
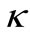 State Solutions of the Dirac Equation for the Generalized Morse Potential under Spin and Pseudospin Symmetry,” Journal of Mathematical Physics, Vol. 52, No. 5, 2011, Article 052303. doi:10.1063/1.3583553
State Solutions of the Dirac Equation for the Generalized Morse Potential under Spin and Pseudospin Symmetry,” Journal of Mathematical Physics, Vol. 52, No. 5, 2011, Article 052303. doi:10.1063/1.3583553 - S. M. Ikhdair and R. Sever, “Approximate Analytical Solutions of the Generalized Woods-Saxon Potential including Spin-Orbit Coupling Term and Spin Symmetry,” Central European Journal of Physics, Vol. 8, No. 4, 2010, pp. 652-666. doi:10.2478/s11534-009-0118-5
- S. M. Ikhdair and R. Sever, “Approximate Bound State Solutions of Dirac Equation with Hulthen Potential Including Coulomb-Like Tensor Potentials,” Applied Mathematical Computation, Vol. 216, No. 3, 2010, pp. 911-923.
- S. M. Ikhdair and R. Sever, “Solutions of the SpatiallyDependent Mass Dirac Equation with the Spin and Pseudospin Symmetry for the Coulomb-Like Potential,” Applied Mathematical Computation, Vol. 216, No. 2, 2010, pp. 545-555.
- S. M. Ikhdair and R. Sever, “Two Approximation Schemes to the Bound-States of the Dirac-Hulthen Problem,” Journal of Physics A: Mathematical and Theoretical, Vol. 44, No. 35, 2011, Article ID 355301. doi:10.1088/1751-8113/44/35/355301
- J. Karwowski, G. Pestka, M. Stanke and F. E. Harris, “Representation of the Dirac Equation and the VariationalPrinciple,” International Journal of Quantum Chemistry, Vol. 106, 2006, pp. 3129-3139. doi:10.1002/qua.21053
- M. Stanke, J. Karwowski and H. Tatewaki, “Kinetically Balanced Dirac Equation: Properties and Application,” Molecular Physics, Vol. 104, No. 13, 2004, pp. 2085-2092. doi:10.1080/00268970600662309
- S. K. Bose, A. Schulze-Halberg and M. Singh, “New Exact Solutions of the Dirac Equation,” Physical Letters A, Vol. 287, No. 5, 2001, pp. 321-324. doi:10.1016/S0375-9601(01)00499-6
- M. Moshinsky, “The Harmonic Oscillator in Modern Physics: From Atoms to Quarks,” Gordon and Breach, New York, 1969, p. 29.
- M. Moshinsky and A. del Sol Mesa, “The Dirac Oscillator of Arbitrary Spin,” Journal of Physical A: Mathematical and General, Vol. 29, No. 1-3, 1996, pp. 4217-4236.
- R. M. Mir-Kasimov, “SUq(1,1) and the Relativistic Oscillator,” Journal of Physical A: Mathematical and General, Vol. 24, No. 18, 1991, pp. 4283-4302.
- W. Lucha, H. Rupprecht and F. F. Schöberl, “Significance of Relativistic Wave Equations for Bound States,” Physical Review D, Vol. 46, No. 5, 1992, pp. 1088-1095. doi:10.1103/PhysRevD.46.1088
- A. D. Alhaidari, H. Bahlouli and A. Al-Hasan, “Dirac and Klein-Gordon Equations with Equal Scalar and Vector Potentials,” Physical Letters A, Vol. 349, No. 1-4, 2006, pp. 87-97. doi:10.1016/j.physleta.2005.09.008
- L. I. Schiff, “Quantum Mechanics,” 3rd Edition, McGrawHill, New York, 1968.
- C. Berkdemir and Y.-F. Cheng, “On the Exact Solutions of the Dirac Equation with a Novel Angle-Dependent Potential,” Physica Scripta, Vol. 79, No. 3, 2009, Article ID 035003. doi:10.1088/0031-8949/79/03/035003
- S. Flügge, “Practical Quantum Mechanics I,” Springer, Berlin, 1971.
Appendix: The Solution of Cubic Energy Equation
Let us solve the general cubic energy equation:
 (A1)
(A1)
where
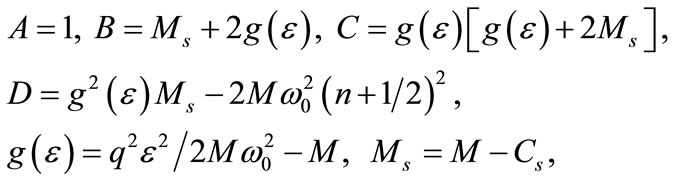 (A2)
(A2)
are real or complex numbers. We want to reduce the cubic equation (A1) to a “depressed” cubic (i.e., the quadratic term disappears) via 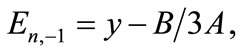 to obtain
to obtain
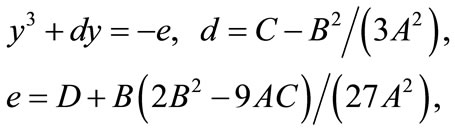 (A3)
(A3)
where
 (A4)
(A4)
Further, the substitution 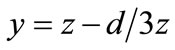 in (A3), we get
in (A3), we get
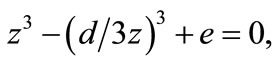 (A5)
(A5)
and multiplying throughout the above equation by 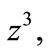 we obtain the quadratic form
we obtain the quadratic form
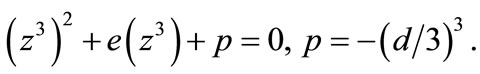 (A6)
(A6)
This equation can be easily solved for real bound states:
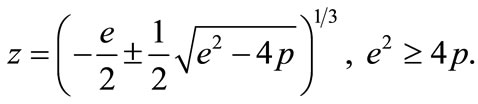 (A7)
(A7)
Thus, the energy in the presence of electric field reads
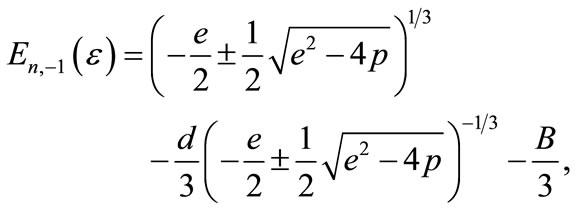 (A8)
(A8)
and also in the absence of electric field,
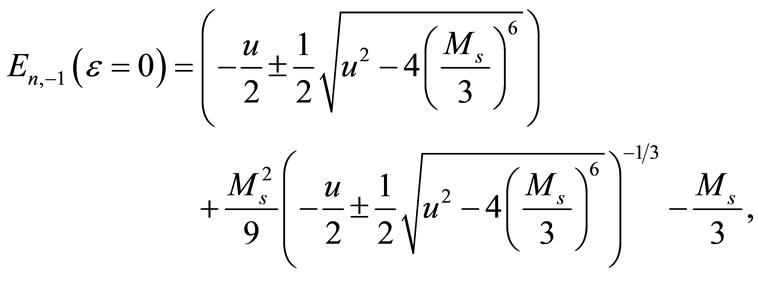 (A9)
(A9)
where