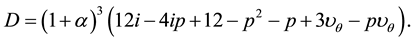Received 6 July 2015; accepted 14 August 2015; published 17 August 2015

ABSTRACT

The effect of Pasternak foundation and non-homogenity on the axisymmetric vibrations of polar orthotropic parabolically varying tapered circular plates has been analyzed on the basis of classical plate theory. Ritz method has been used to find the numerical solution of the specified problem. The efficiency of the Ritz method depends on the choice of basis function based upon deflection of polar orthotropic plates. The effects of different plate parameters viz. elastic foundation, non-homogeneity, taper parameter and that of orthotropy on fundamental, second and third mode of vibration have been studied for clamped and simply-supported boundary conditions. Mode shapes for specified plates have been drawn for both the boundary conditions. Convergence and comparison studies have been carried out for specified plates.

Keywords:

Pasternak Foundation, Parabolically Varying Thickness, Circular Plate, Polar Orthotropy, Non-Homogenity

1. Introduction

The increasing use of composite materials in modern aerospace structures has necessitated studying the vibrational characteristics of plate-type components fabricated by these materials. Orthotropic circular plates are extensively used as structural components for diaphragms and deck plates in launch vehicles. A number of studies dealing with axisymmetric vibrations of plates possessing polar orthotropy (a special case of anisotropic) are available in the literature and few of them are reported in references [1] -[13] . The consideration of the thickness variation together with orthotropy in structural components not only ensures reduction in size and weight whilst maintaining high strength but also meets the desirability of economy [14] - [17] . The use of such plates as structural elements in various technological situations, particularly in high-speed aircrafts, missile technology and space shuttle etc., demands that the material non-homogeneity should be taken into account for the analysis of plate vibrations [18] - [20] .

This work presents an analysis for axisymmetric vibration of polar orthotropic non-homogeneous circular plate of parabolically varying thickness resting on Pasternak foundation. A linear type variation in Young’s moduli and density has been taken into account. This class of orthotropy and non-homogeneity arises during fibre-reinforced plastic structure which uses fibres with different moduli and strength properties. Ritz method has been employed to obtain approximate solution of the problem, where basis functions based upon the static deflection for orthotropic plates have been used. The choice of this method has the advantages of high accuracy and computational efficiency [21] which greatly depend upon the nature of admissible functions. Here, fundamental, second and third modes of frequencies have been obtained for different values of plate parameters viz. taper parameter, density parameter, non-homogeneity parameter, foundation stiffness parameters and rigidity parameter. Normalized transverse displacements of the specified plates for fundamental, second and third modes of vibration for clamped and simply-supported boundary condition have been shown. The comparison results are reported which establish the accuracy of the present method.

2. Mathematical Formulation

Consider a circular plate of radius a, thickness, density 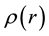and resting on a Pasternak foundation with spring and shear stiffness parameters K_f and G_f, respectively, elastically restrained against rotation by springs of stiffness k_φ, referred to cylindrical polar coordinate, where the axis of the plate is taken as the line r = 0 and its middle surface as the plane z = 0.

The maximum kinetic energy and potential energy of the plate are given by:

(1)

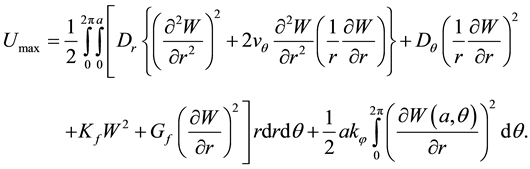(2)

3. Method of Solution: Ritz Method

Ritz method requires that the following functional be minimized.

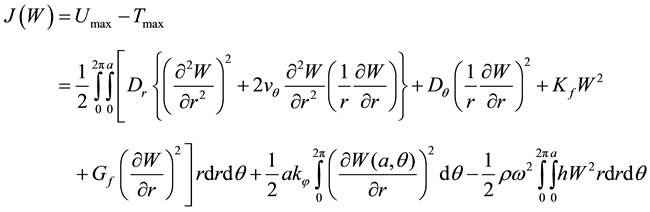(3)

Now, transverse deflection W has been approximated in terms of a set of linearly dependent coordinate functions, which satisfy the boundary conditions of the problem. The choice of function to approximate the deflection using Ritz method has its significance. The deflection function assumed here is based upon the static deflection for polar orthotropic plates.

Introducing the non-dimensional variables 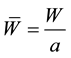and along with relations,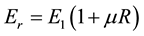

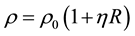, and considering the thickness variation as, where h₀ is thickness of plate at its centre, the functional 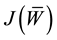given by Equation (3) becomes

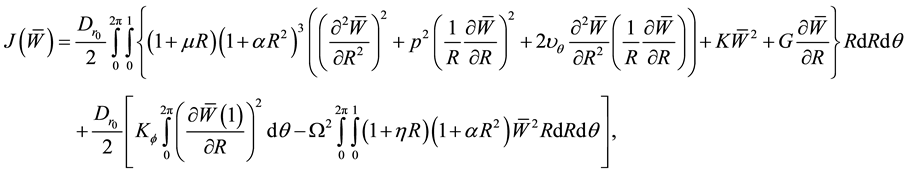(4)

where, , , , ,.

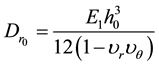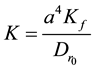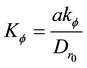
Assume the deflection function as

(5)

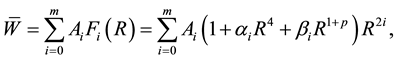
where, A_i are unknown coefficients, and, are unknown constants.

As each coordinate function has to satisfy the elastically restrained against rotation condition at the boundary (i.e. R = 1) [22] , we have the following two boundary conditions (deflection and displacement conditions at boundary)

, (6)

(7)

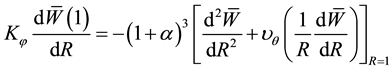
The unknown constants and are determined using these boundary conditions which give

(8)

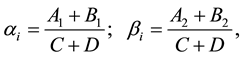
where,

Substituting the value of from Equation (5) into (4), the functional becomes

(9)

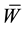
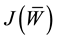
The minimization of the functional given by (9) requires,

(10)

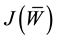
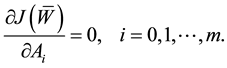
which leads to a system of homogeneous equations in, whose non-trivial solution leads to the frequency equation

(11)

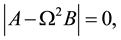
where, and are square matrices of order (m + 1) given by

(12)

(13)

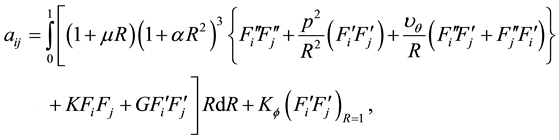
for;.

4. Numerical Results and Discussion

The frequency Equation (11) has been solved to obtain the frequency parameter Ω for non-homogeneous polar orthotropic circular plate of parabolically varying thickness resting on a Pasternak foundation for various values of plate parameters. The first three natural frequencies for clamped and simply-supported boundary conditions have been computed for non-homogeneity parameter µ (= −0.5, 0.0, 1.0); density parameter η (= −0.5, 0.0, 1.0); rigidity ratio p² (= 0.75, 1.0, 2.0, 5.0); taper parameter α (= −0.5(0.2)0.5); spring stiffness parameter K (= 0(100)500) and shear stiffness parameter G (= 0(5)25). The Poisson’s ratio υ_θ has been fixed as 0.3. The value of K_φ has been taken as 10²⁰ and 0.0 for clamped and simply-supported boundary, respectively.

To choose the appropriate number of terms for the evaluation of frequency parameter Ω, a computer program was developed which was run for m = 5(1)20 for different sets of parameters. Figure 1(a), Figure 1(b) present the convergence of normalized frequency parameter Ω/Ω^* for specified plate parameters µ = 1.0, η = 1.0, α = 0.5, K = 500, G = 25, p² = 2.0 for clamped and simply-supported plates, respectively. A consistent improvement is observed in value of Ω with the increase in number of terms. In all the computations, the number of terms m has

been fixed as 13, since further increase in m does not improve the results except in the fourth or fifth place of decimal.

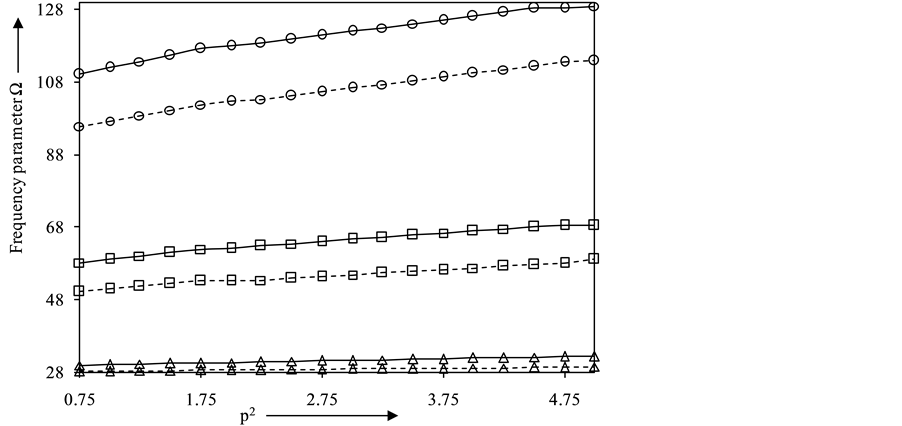
Figure 2 presents the graphs of frequency parameter Ω versus rigidity ratio p² for non-homogeneous circular plate resting on Pasternak foundation i.e., µ = −0.3, η = −0.3, K = 500, G = 25 and α = 0.3. The value of frequency parameter Ω is found to increase with increasing values of p² (i.e. as the plate becomes more and more tangentially stiff). The rate of increase of frequency parameter Ω with p² is higher for clamped plate than that for simply-supported plate, keeping all other plate parameters fixed. This rate of increase gets pronounced as we move towards higher modes.

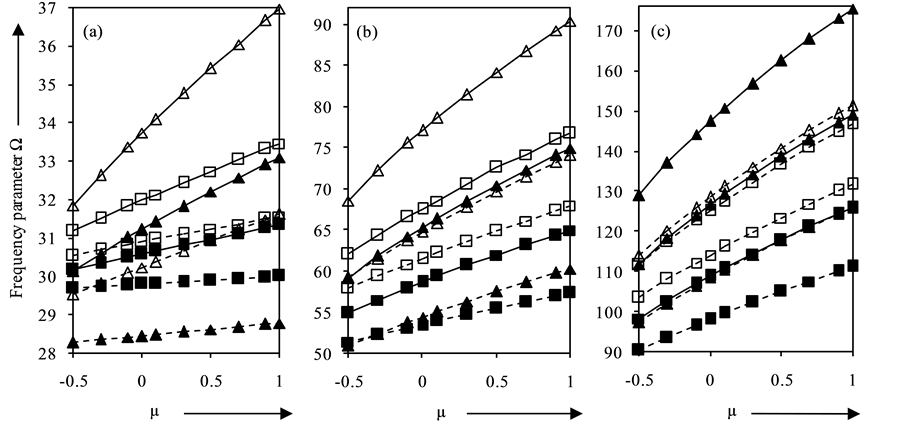
Figures 3(a)-(c) show the effect of non-homogeneity parameter µ on frequency parameter Ω for α = −0.3, 0.3; K = 500, G = 25; η = −0.5 and p² = 1.0, 5.0 for clamped and simply-supported plates for first three modes of vibration, respectively. It is observed that the values of frequency parameter Ω increases linearly with increasing

values of µ. The rate of increase of Ω with µ is higher for clamped plates than that for simply-supported plates. The rate of increase gets pronounced as the plate becomes tangentially stiff. Also, this rate of increase of frequency parameter Ω gets increased by increasing taper parameter α. Furthermore, the rate of increase of Ω with µ increases with increasing number of modes.

Figures 4(a)-(c) depict the variation of frequency parameter Ω versus density parameter η for α = −0.3, 0.3, K = 500, G = 25; µ = −0.5 and p² = 1.0, 5.0 for both clamped and simply-supported plates vibrating in fundamental, second and third modes, respectively. The frequency parameter Ω is found to decrease with increasing values of density parameter η. The rate of decrease of frequency parameter Ω is higher for simply-supported plate than that for clamped plate vibrating in fundamental mode, while for second and third modes the rate of decrease is higher for clamped plate than that for simply-supported plate. It has also been observed that this rate for tangentially stiffened plates (p² = 5) is higher than that for isotropic plates (p² = 1). Also, the rate of decrease of frequency parameter Ω gets increased by increasing taper parameter α, except for isotropic clamped plate vibrating in fundamental mode and isotropic as well as orthotropic simply-supported plate vibrating in second mode.

Figures 5(a)-(c) show the behavior of spring stiffness parameter K for µ = −0.5, η = −0.5, G = 25, α = −0.3, 0.3 and p² = 1.0, 5.0 for clamped and simply-supported plates for first three modes of vibration, respectively. The value of frequency parameter Ω increases by increasing the values of foundation parameter K. The rate of increase of frequency parameter Ω with K increases by decreasing the value of taper parameter α. This rate of increase is higher for isotropic plates than that for tangentially stiffened plates. Also, the rate of increase is higher for simply-supported plate as compared to clamped plate. This rate of increase reduces as we move towards higher modes.

Figures 6(a)-(c) present the plots of frequency parameter Ω versus shear stiffness parameter G for µ = −0.5, η = −0.5, K = 500, α = −0.3, 0.3 and p² = 1.0, 5.0 for clamped and simply-supported plates vibrating in fundamental, second and third mode, respectively. The frequency parameter Ω is found to increase by increasing the shear stiffness parameter G. This rate of increase is higher for α = −0.3 than that for α = 0.3. The rate of increase of frequency parameter Ω is lower for p² = 5.0 than that for p² = 1.0. Also, this rate of increase is higher for simply-supported plate as compared to clamped plate except when plate vibrates in fundamental mode. In this case, the rate of increase is higher for clamped plate as compared to simply-supported plate.

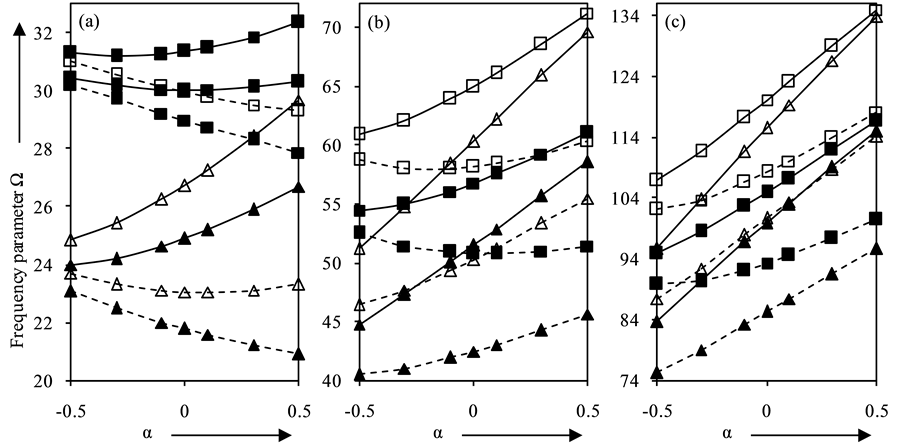
Figure 7(a) shows the effect of taper parameter α on frequency parameter Ω for plates vibrating in fundamental mode. It is found that for clamped plate with µ = η = 1.0, frequency parameter increases while for clamped plate with µ = η = −0.5 frequency parameter first decreases and then increases giving rise to local minima in the vicinity of α = −0.3 for p² = 5.0 and α = 0.0 for p² = 1.0. For orthotropic simply-supported plate with µ = η = −0.5 and isotropic simply-supported plate, the frequency parameter decreases continuously with increasing values of α, while it first decreases and then increases with a minima in the vicinity of α = 0.1 for orthotropic

plate (p² = 5) with µ = η = 1.0. Further, Figure 7(b), Figure 7(c)) show the plots for plates vibrating in second and third mode of vibration, respectively. It is observed that frequency parameter Ω increases by increasing the values of taper parameter α except when simply-supported plate with µ = η = −0.5 vibrates in second mode. In this case, frequency first decreases and then increases with a local minima in the vicinity of α = −0.1 for p² = 5.0 which shifts to α = 0.1 for p² = 1.0.

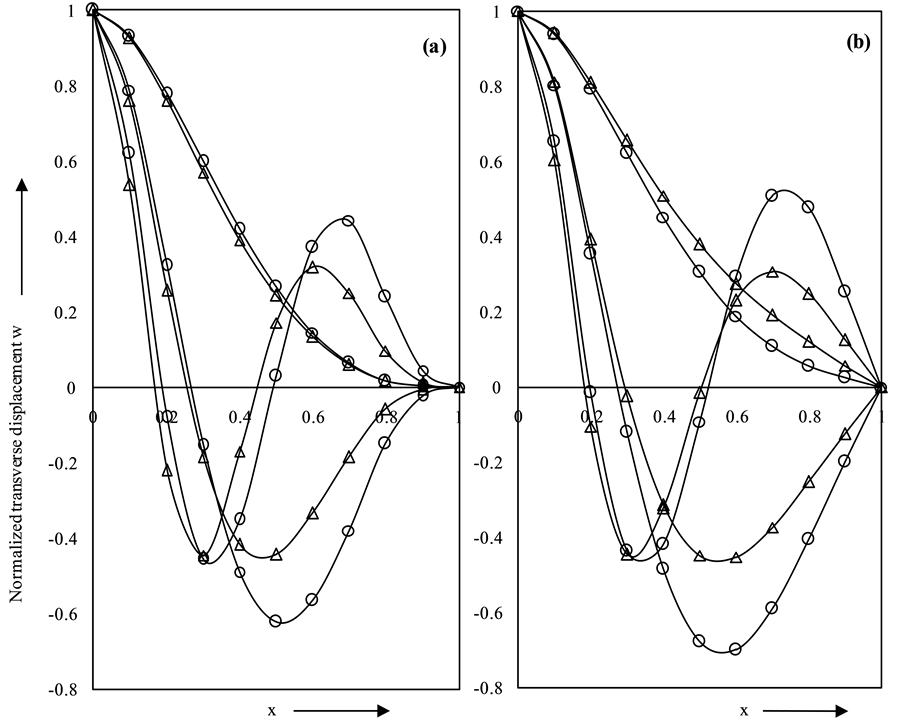
Figure 8(a), Figure 8(b) present the normalized transverse displacement for orthotropic (p² = 0.75) non-ho- mogeneous (µ = 1.0, η = 1.0) clamped and simply-supported plates, respectively, resting on Pasternak foundation (K = 500, G = 25). It has been observed that the radii of nodal circles decrease by decreasing the value of taper parameter α for both the plates.

Table 1 and Table 2 present the comparison of results for polar orthotropic homogeneous parabolically tapered clamped and simply-supported circular plates, respectively, without foundation with those obtained by [10] [23] .

5. Conclusion

It is found that the values of frequency parameter Ω for clamped plate are higher than those of simply-supported

^values taken from [23] , ^*values taken from [10] .

^values taken from [23] , ^*values taken from [10] .

plate, whatever be the values of other plate parameters. The frequency parameter increases with increasing values of non-homogeneity parameter µ, rigidity ratio p², spring stiffness parameter K, and shear stiffness parameter G. A close agreement of our results (Table 1, Table 2) with those available in literature [10] [23] verifies the accuracy of the approach.

Cite this paper

ShivaniSrivastava,SeemaSharma,RoshanLal, (2015) Effect of Foundation and Non-Homogeneity on the Vibrations of Polar Orthotropic Parabolically Tapered Circular Plates. Applied Mathematics,06,1563-1573. doi: 10.4236/am.2015.69139

References