Applied Mathematics
Vol.4 No.10B(2013), Article ID:37459,8 pages DOI:10.4236/am.2013.410A2006
Analysis of a Delayed SIR Model with Exponential Birth and Saturated Incidence Rate
Department of Mathematics, North University of China, Taiyuan, China
Email: *liumaoxing@126.com
Copyright © 2013 Wanwan Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 6, 2013; revised September 6, 2013; accepted September 13, 2013
Keywords: Exponential Birth; SIR Model; Time Delay; Hurwitz Criterion; Hopf Bifurcation
ABSTRACT
In this paper, a delayed SIR model with exponential demographic structure and the saturated incidence rate is formulated. The stability of the equilibria is analyzed with delay: the endemic equilibrium is locally stable without delay; and the endemic equilibrium is stable if the delay is under some condition. Moreover the dynamical behaviors from stability to instability will change with an appropriate critical value. At last, some numerical simulations of the model are given to illustrate the main theoretical results.
1. Introduction
Epidemic models described by ordinary differential equations have become important tools in analyzing the spread and control of infectious diseases. In recent years, more and more delayed models have been investigated during the study of epidemic models [1-8].
When the diseases spread quickly, the population remains constant. Furthermore the population remains constant if the birth is nearly equal to the natural death when the disease we consider it over many years. In fact, in many diseases the birth of the population can not be balanced by the natural death, and then we need to assume that the population is a function of time.
Varying total population has become one of the most important areas in the mathematical theory of epidemicology [3-8]. Anderson and May [1,2] have done a lot of work about varying total population, and Michael Y. Li et al. considered a SEIR model with varying total population in [9]. In this paper the authors incorporated exponential natural birth and death, as well as diseasecaused death into the model, so that the total population size may vary in time, and they analyzed the stability of the model with normalization method. They also present a new method for proving the local stability of the unique endemic equilibrium.
During the study of the dynamical behaviors of the disease, the standard incidence rate  and the bilinear incidence rate
and the bilinear incidence rate 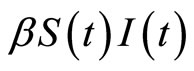 are frequently used [3,5,7-11]. In recent years, more and more researchers are interested in the nonlinear incidence rate; especially the saturate incidence rate has been investigated by many authors in [12-22], in which the recruitment rate of the population is considered as a constant.
are frequently used [3,5,7-11]. In recent years, more and more researchers are interested in the nonlinear incidence rate; especially the saturate incidence rate has been investigated by many authors in [12-22], in which the recruitment rate of the population is considered as a constant.
A class of delayed SIR models has been investigated with nonlinear incidence rate. Capasso and Serio [13] introduced a saturated incidence rate  into epidemic models, where
into epidemic models, where 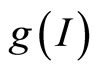 tends to a saturation level when
tends to a saturation level when 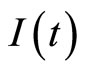 reach the maximum number of effective contacts between infective individuals and susceptible individuals may saturate at high infective levels due to crowding of infective individuals or due to the protection measures by the susceptible individuals[14].
reach the maximum number of effective contacts between infective individuals and susceptible individuals may saturate at high infective levels due to crowding of infective individuals or due to the protection measures by the susceptible individuals[14].
In [15], Rui Xu et al. considered the effect of time delay and nonlinear incidence rate 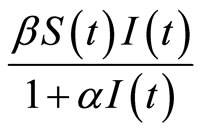 on the dynamics of a SIR epidemic model as follows:
on the dynamics of a SIR epidemic model as follows:
 (1)
(1)
Here parameters 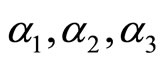 are positive constants representing the death rates of susceptibles, infectives, and recovered, respectively. The parameters
are positive constants representing the death rates of susceptibles, infectives, and recovered, respectively. The parameters 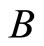 and
and 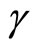 are positive constants representing the birth rate of the population and the recovery rate of infectives, respectively. By analyzing the corresponding characteristic equations, they discussed the local stability of an endemic equilibrium and a disease free equilibrium. By comparison arguments, they analyzed the globally asymptotically stable of the disease free equilibrium, and by means of an iteration technique and Lyapunov functional technique, respectively, sufficient conditions are obtained for the global asymptotic stability of the endemic equilibrium.
are positive constants representing the birth rate of the population and the recovery rate of infectives, respectively. By analyzing the corresponding characteristic equations, they discussed the local stability of an endemic equilibrium and a disease free equilibrium. By comparison arguments, they analyzed the globally asymptotically stable of the disease free equilibrium, and by means of an iteration technique and Lyapunov functional technique, respectively, sufficient conditions are obtained for the global asymptotic stability of the endemic equilibrium.
In [16], Kaddar considered a delayed SIR model with a nonlinear incidence rate  as follows:
as follows:
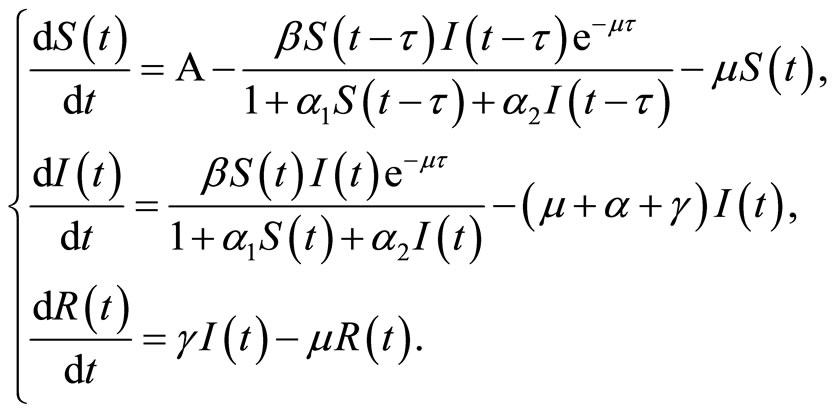 (2)
(2)
The characteristic of this model is: the saturated incidence rate , which includes the three forms:
, which includes the three forms: 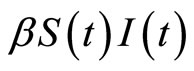 (if
(if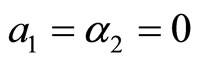 ),
), 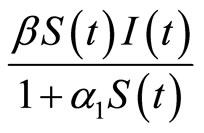 (if
(if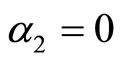 ) and
) and 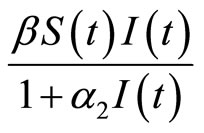 (if
(if ) saturated with the susceptible and the infective individuals. The inclusion of time delay into susceptible and infective individuals in incidence rate, only on the first equation, because susceptible individuals infected at time
) saturated with the susceptible and the infective individuals. The inclusion of time delay into susceptible and infective individuals in incidence rate, only on the first equation, because susceptible individuals infected at time 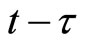 is able to spread the disease at time
is able to spread the disease at time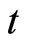 .
.
In the SIR model (2), they consider the period in the evolution of susceptible class, and not in the evolution of infectious class. They discuss the local stability and the existence of Hopf bifurcation. At last some numerical simulations are given to illustrate the theoretical analysis.
In this paper we consider a delayed SIR model with the saturation incidence rate  and exponential birth rate. We also analyze the stability and the existence conditions of Hopf bifurcation. The organization of this paper is as follows: In Section 2, we consider a delayed SIR model with saturation incidence rates and exponential birth rate. Then we also consider an exceptional case. In this case the saturation incidence rate becomes a bilinear incidence rate. Numerical simulations with different values of the delay are given in Section 3.
and exponential birth rate. We also analyze the stability and the existence conditions of Hopf bifurcation. The organization of this paper is as follows: In Section 2, we consider a delayed SIR model with saturation incidence rates and exponential birth rate. Then we also consider an exceptional case. In this case the saturation incidence rate becomes a bilinear incidence rate. Numerical simulations with different values of the delay are given in Section 3.
2. Stability Analysis of the Delayed SIR Model
In Section 2.1, we consider the delayed SIR model with the saturated incidence rate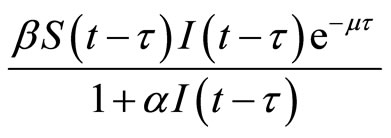 . Then we consider the parameter measure
. Then we consider the parameter measure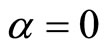 , the saturation incidence rate will become a bilinear incidence rate
, the saturation incidence rate will become a bilinear incidence rate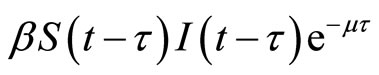 , we consider it in Section 2.2.
, we consider it in Section 2.2.
2.1. The Delayed SIR Model with the Saturated Incidence Rate
In the section, we consider the following SIR model with the saturation incidence rate 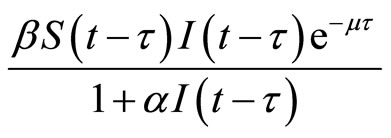 and a time delay describing a latent period. Let
and a time delay describing a latent period. Let 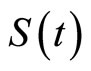 is the number of susceptible individuals,
is the number of susceptible individuals, 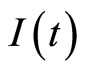 is the number of infective individuals, and
is the number of infective individuals, and  is the number of recovered individuals, then we have the following model:
is the number of recovered individuals, then we have the following model:
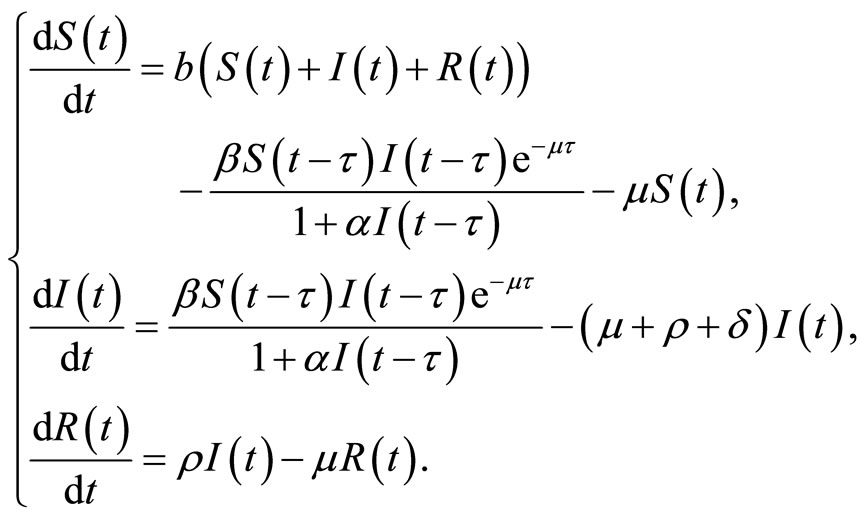 (3)
(3)
The parameter 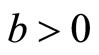 is the rate of natural birth,
is the rate of natural birth,  is the rate of natural death
is the rate of natural death ,
, 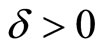 is the rate of disease-related death,
is the rate of disease-related death,  is the rate of recovery,
is the rate of recovery, 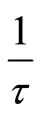 is the incubation period.
is the incubation period. 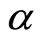 is the parameter that measure in infections with the inhibitory effect. Define the basic reproduction number by
is the parameter that measure in infections with the inhibitory effect. Define the basic reproduction number by
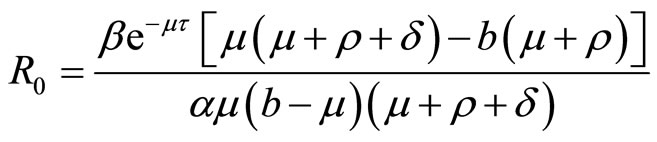
and we have the following theorem.
Theorem 1. If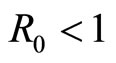 , the solution of system (3) is
, the solution of system (3) is 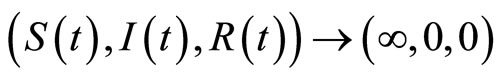 with
with . If
. If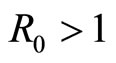 , system (3) has a unique endemic equilibrium
, system (3) has a unique endemic equilibrium 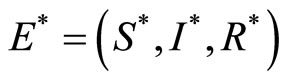 , where:
, where:

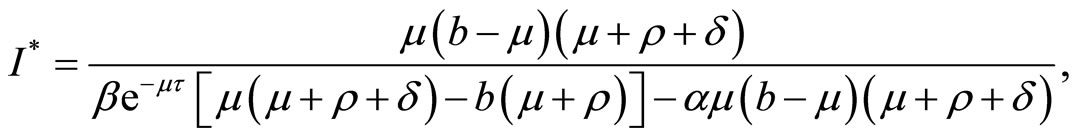
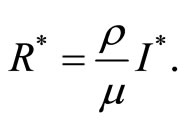
Proof: Considering two case:  and
and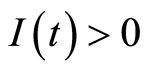 . If
. If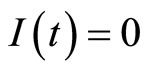 , from the third equation in (3), we get
, from the third equation in (3), we get , then from the first equation in (3), it follows that
, then from the first equation in (3), it follows that
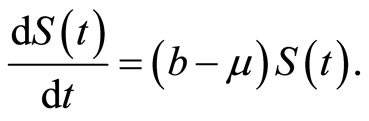
When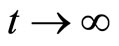 , we have
, we have . Then we can get that the solution of system (3)
. Then we can get that the solution of system (3)
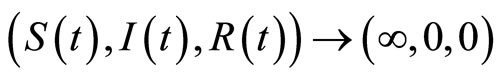 .
.
If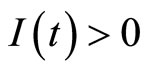 , from the third equation in (3), we get:
, from the third equation in (3), we get:
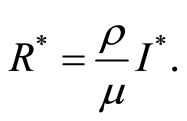
And from the second equation in (3), we can get
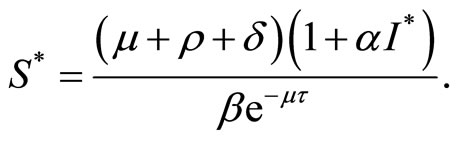
Then substituting the above equations into (2) we get the unique root
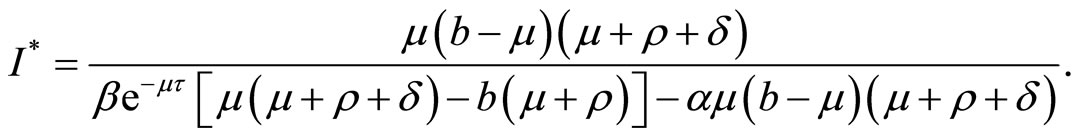
If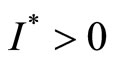 , we must have
, we must have
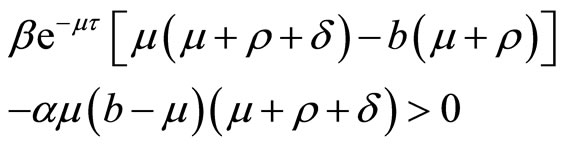
It means that we must make sure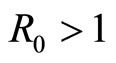 . Thus we get if
. Thus we get if , system (3) has a unique endemic equilibrium.
, system (3) has a unique endemic equilibrium.
In the next, we will analyze the stability of the endemic equilibrium 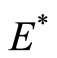 with
with . We analyze the stability by the characteristic equation.
. We analyze the stability by the characteristic equation.
The characteristic equation of system (3) at the endemic equilibrium 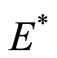 is of the form
is of the form
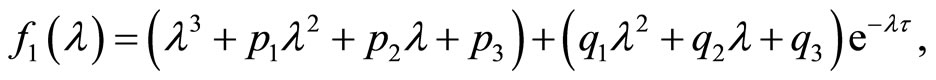 (4)
(4)
where

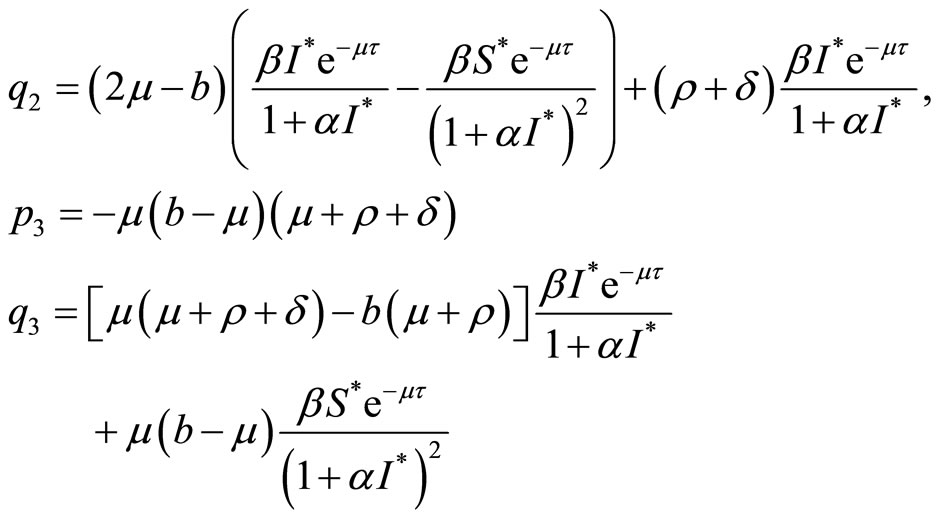
Theorem 2. If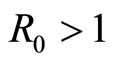 , suppose
, suppose  and when
and when , the endemic equilibrium
, the endemic equilibrium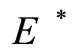 is stable, and when
is stable, and when , it is unstable.
, it is unstable.
Proof. We consider the case without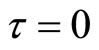 , the characterristic Equation (4) reads as:
, the characterristic Equation (4) reads as:
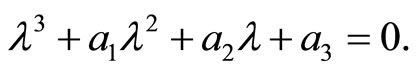
It is easy to show that
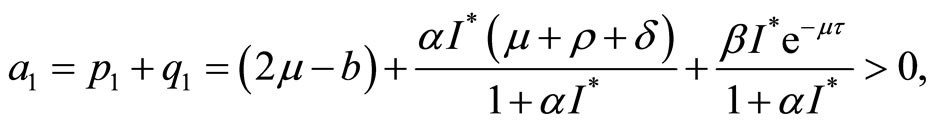

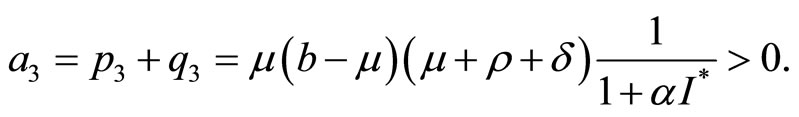
According to the Hurwitz criterion, we can know when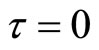 , endemic equilibrium
, endemic equilibrium 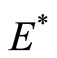 of system (3) is stability.
of system (3) is stability.
When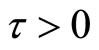 , we suppose system (3) has a purely imaginary root
, we suppose system (3) has a purely imaginary root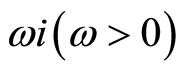 , then separating real and imaginary parts, we have
, then separating real and imaginary parts, we have
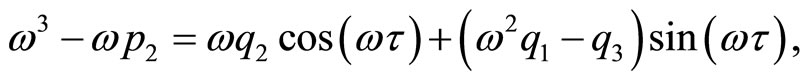 (5)
(5)
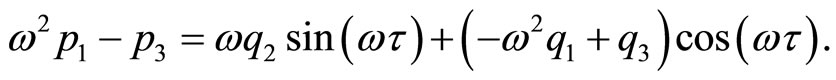 (6)
(6)
Hence,
 (7)
(7)
where

Supposing , let
, let , then
, then
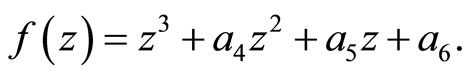 (8)
(8)
It is easy to show that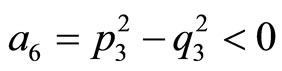 . Then, we have
. Then, we have  and
and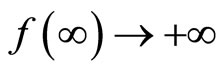 . Thus Equation (8) has at least one positive root
. Thus Equation (8) has at least one positive root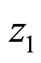 , Equation (7) has at least one positive root, denoted by
, Equation (7) has at least one positive root, denoted by .
.
Now, we turn to the bifurcation analysis. We use the delay  as bifurcation parameter. We view the solutions of Equation (4) as functions of the bifurcation parameter
as bifurcation parameter. We view the solutions of Equation (4) as functions of the bifurcation parameter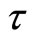 . Let
. Let  be the eigenvalue of Equation (4) such that for some initial value of the bifurcation parameter
be the eigenvalue of Equation (4) such that for some initial value of the bifurcation parameter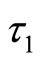 , we have
, we have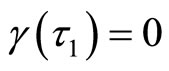 , and
, and 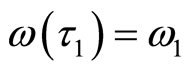 (we assume
(we assume ). From Equations (5) and (6) we have
). From Equations (5) and (6) we have
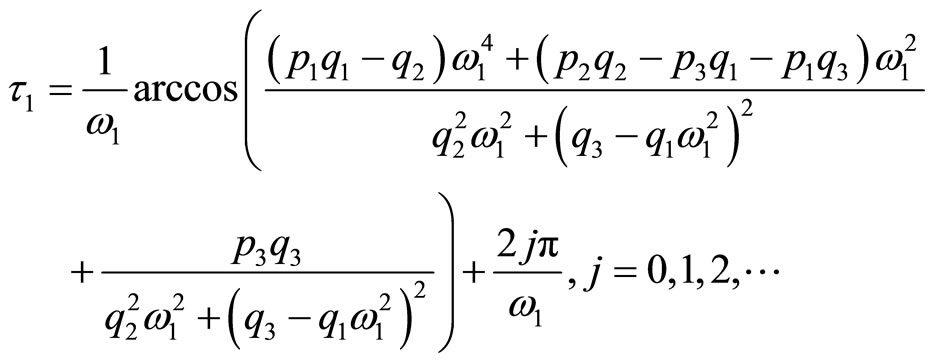
Also, we can have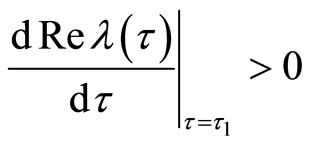 . By continuitythe real part of
. By continuitythe real part of 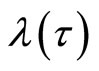 becomes positive when
becomes positive when 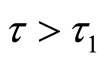 and the steady state becomes unstable. A Hopf bifurcation occurs when
and the steady state becomes unstable. A Hopf bifurcation occurs when 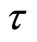 passes through the critical value
passes through the critical value 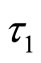 [18].
[18].
2.2. The Delayed SIR Model with the Standard Incidence Rate
When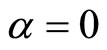 , we have the standard incidence rate
, we have the standard incidence rate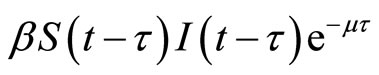 . Then, we can get the following model:
. Then, we can get the following model:
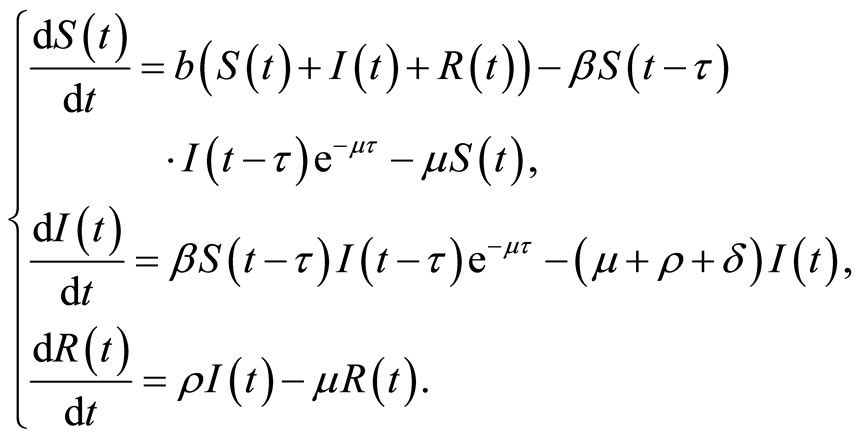 (9)
(9)
Define the basic reproduction number by
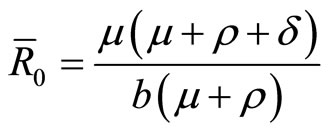
Theorem 3. If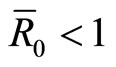 , the solution of system (9) is
, the solution of system (9) is 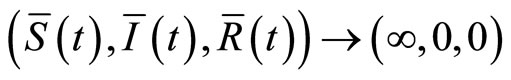 with
with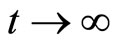 . When
. When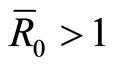 , the system has a unique endemic equilibrium
, the system has a unique endemic equilibrium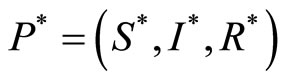 , where:
, where:


Proof: When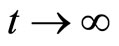 , consider two case:
, consider two case:  and
and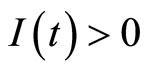 .
.
If , we can get
, we can get  from the third Equation in (9), then we have
from the third Equation in (9), then we have
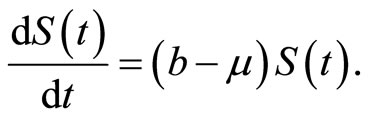
When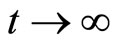 , we have
, we have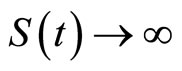 . Then, we can get that system (9) always has
. Then, we can get that system (9) always has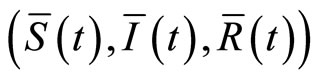
 with
with .
.
If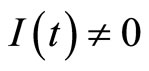 , from the third equation of system (9), we get
, from the third equation of system (9), we get

and from second equation, we have
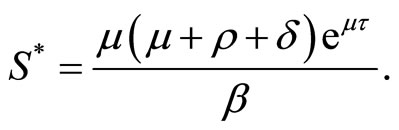
Then, we get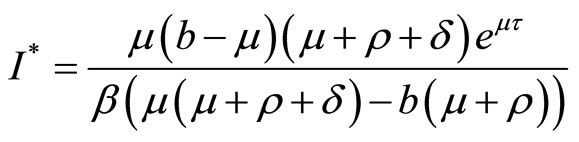 .
.
To make sure 
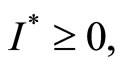
 We must have
We must have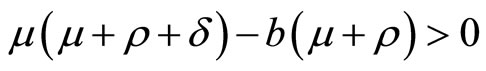 . This implies that there exists the endemic equilibrium with
. This implies that there exists the endemic equilibrium with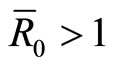 .
.
In the next, we will analyze the stability of the endemic equilibrium 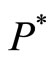 with
with .
.
Theorem 4. If  and when
and when , the endemic equilibrium
, the endemic equilibrium 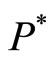 is stable, and when
is stable, and when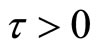 ,
, 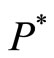 is unstable.
is unstable.
Proof. When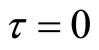 , the characteristic equation of system (9) read as:
, the characteristic equation of system (9) read as:
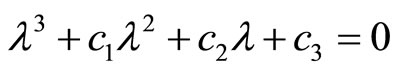
It is easy to show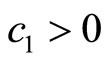 ,
, 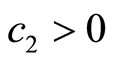 and
and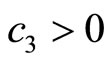 . According to Hurwitz criterion, we can know the system is stable with
. According to Hurwitz criterion, we can know the system is stable with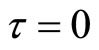 .
.
When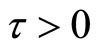 , use the same method as system (3). Suppose it has a purely imaginary root
, use the same method as system (3). Suppose it has a purely imaginary root , then we can get:
, then we can get:
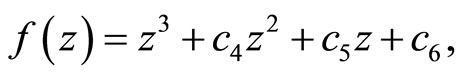 (10)
(10)
where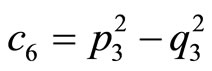 . Then, we have
. Then, we have 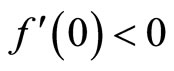 and
and . Thus Eq.(10) has at least one positive root
. Thus Eq.(10) has at least one positive root 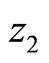 . Also, we can have
. Also, we can have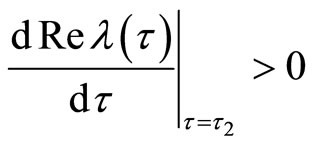 . A Hopf bifurcation occurs when
. A Hopf bifurcation occurs when 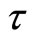 passes through the critical value
passes through the critical value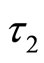 .
.
3. Simulations and Sensitivity Analysis
In this section, we present some numerical results of system (3) and (9) at different values 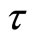 of supporting the theoretical analysis in Section 2.
of supporting the theoretical analysis in Section 2.
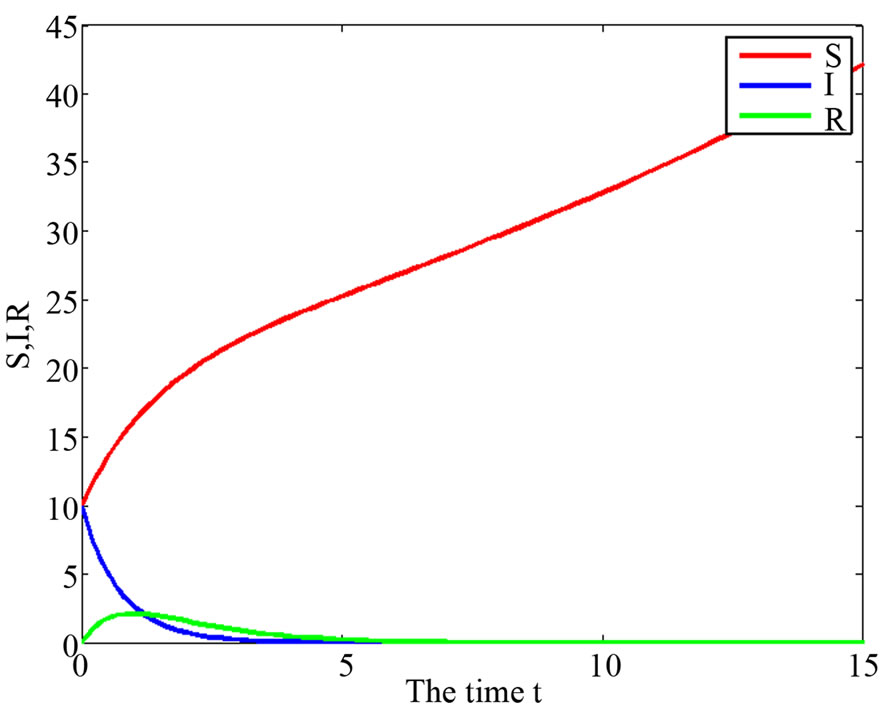
When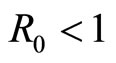 , we know system (3) has
, we know system (3) has 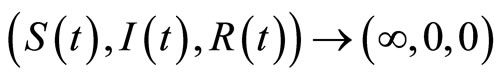 with
with ; and when
; and when 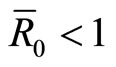 system (9) has
system (9) has . In Figures 1(a) and (b), we give appropriate parameter values of system (3) and system (9) with
. In Figures 1(a) and (b), we give appropriate parameter values of system (3) and system (9) with .
.
From Figure 1, we know system (3) (and system (9)) has 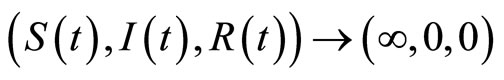 (and
(and 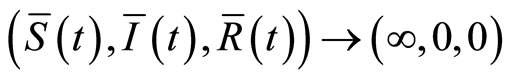 ). The system (3) (or system (9)) exist unique endemic equilibrium with
). The system (3) (or system (9)) exist unique endemic equilibrium with 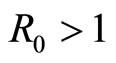 (or
(or ).
).
When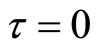 , we give the same parameters for endemic equilibrium in system (3) and (9) as follows:
, we give the same parameters for endemic equilibrium in system (3) and (9) as follows:
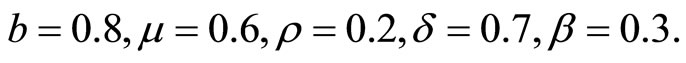
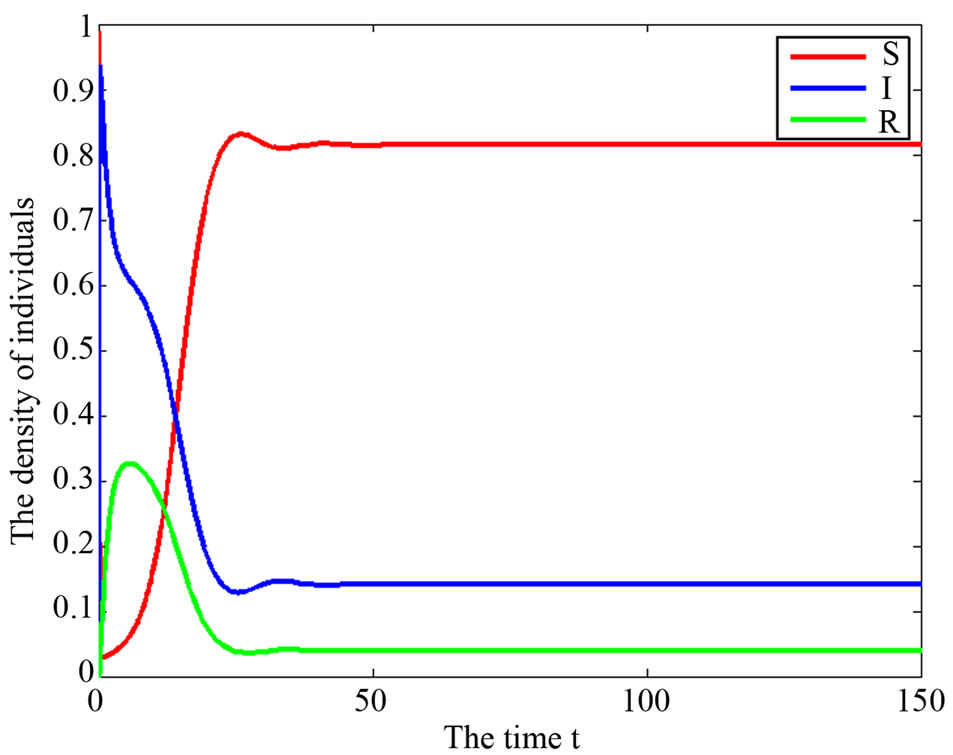
In Figure 2, the numerical simulations support the analysis given in Section 2. The endemic equilibriums of the delayed SIR epidemic model with the saturated incidence rate and the bilinear incidence rate are locally stable without delay.
Compare with system (9), we can know the proportion of  in system (3) is higher, and the proportions of
in system (3) is higher, and the proportions of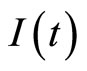 ,
,  are lower.
are lower.
When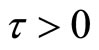 , we give the parameters with different
, we give the parameters with different 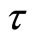 for endemic equilibrium in system (3) as follows:
for endemic equilibrium in system (3) as follows:
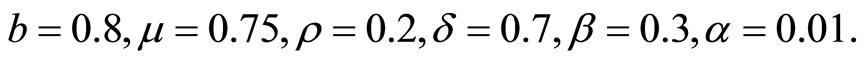
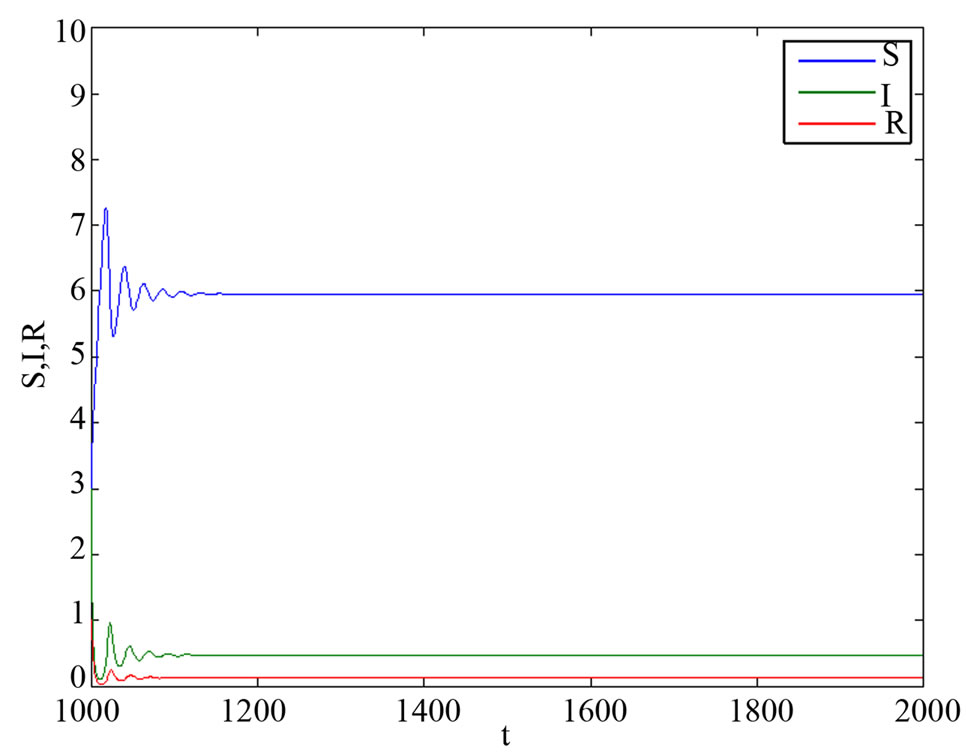
In Figure 3(a), we give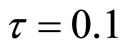 , we find endemic equilibrium in system (3) is stable. When
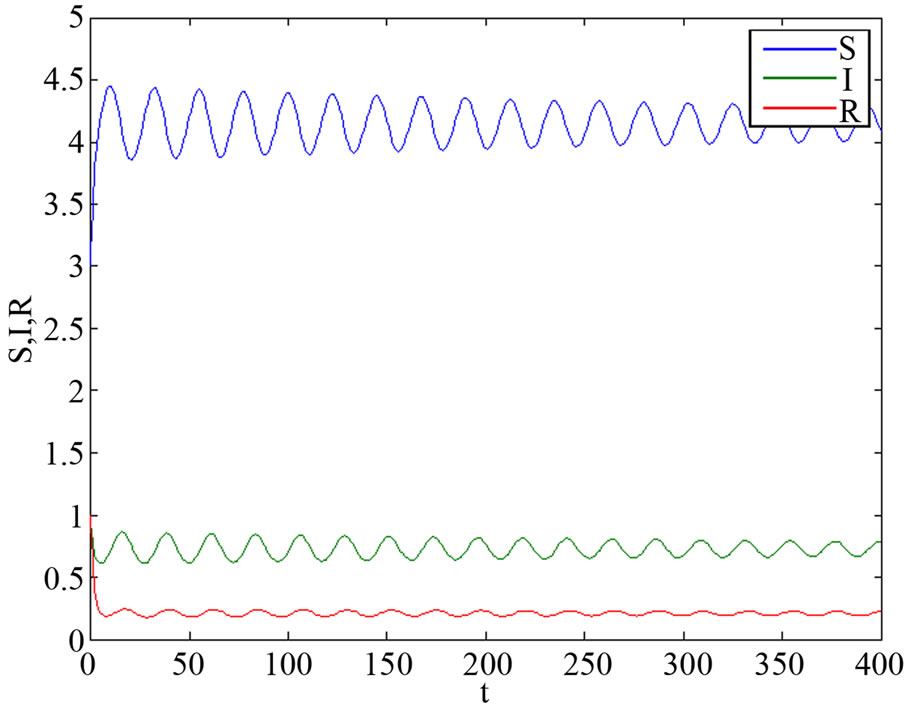
, we find endemic equilibrium in system (3) is stable. When , from Figure 3(b), we find it is unstable; from Figure 3(c), we find endemic equilibrium in system (3) exists a periodic solution.
, from Figure 3(b), we find it is unstable; from Figure 3(c), we find endemic equilibrium in system (3) exists a periodic solution.
If we don’t consider the parameter measure, it means that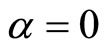 , the incidence rate will become to the standard incidence rate, then we have system (9). We give parameters with different
, the incidence rate will become to the standard incidence rate, then we have system (9). We give parameters with different  for endemic equilibrium in system (9) as follows:
for endemic equilibrium in system (9) as follows:
 (a)
(a)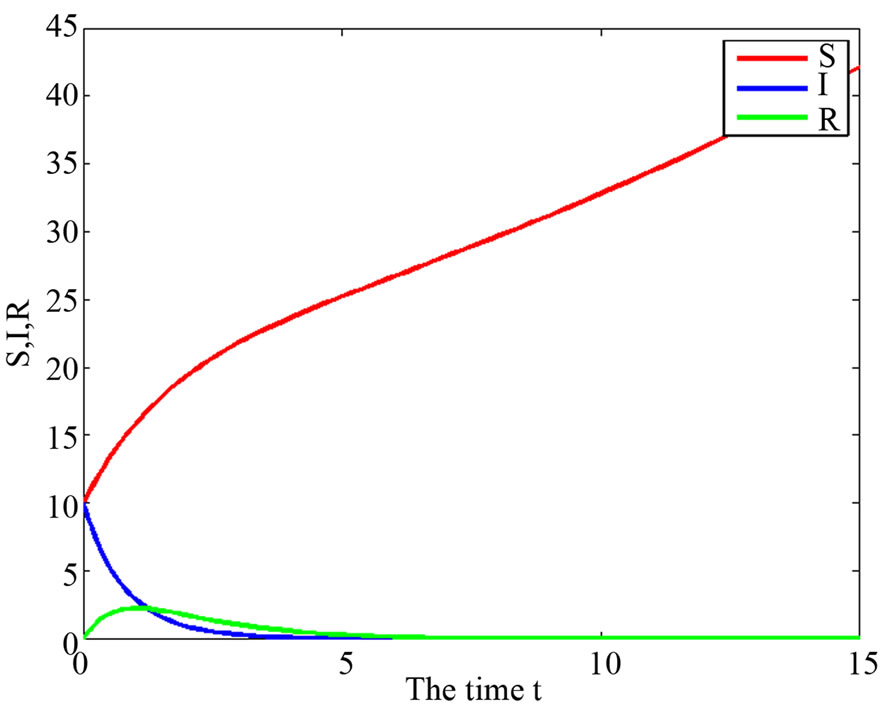 (b)
(b)
Figure 1. (a) System (3) has 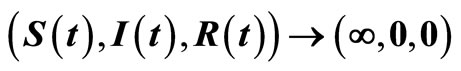 with
with 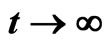 and
and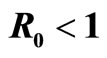 ; (b) System (9) has
; (b) System (9) has 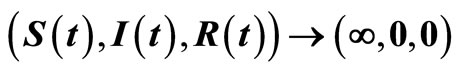 with
with  and
and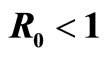 .
.

In Figure 4(a), we give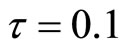 , we find it is stable; from Figure 4(b), we find it is unstable with
, we find it is stable; from Figure 4(b), we find it is unstable with ; and from Figure 4(c), we find the endemic equilibrium in system (9) exists a periodic solution.
; and from Figure 4(c), we find the endemic equilibrium in system (9) exists a periodic solution.
4. Discussions
From the numerical simulations, we show that the endemic equilibrium is locally stable without time delay. In Figure 2, we know it is more effective that taking measures of the inhibition effect from the behavioral change of 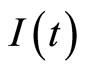 reduce the infective proportion. From Figures 3 and 4, when
reduce the infective proportion. From Figures 3 and 4, when , the endemic equilibrium in system (3) and (9) is locally asymptotically stable; when
, the endemic equilibrium in system (3) and (9) is locally asymptotically stable; when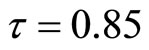 , the endemic equilibrium in system (3) and (9) exists periodic solutions. It showed that endemic equilib-
, the endemic equilibrium in system (3) and (9) exists periodic solutions. It showed that endemic equilib-
 (a)
(a) (b)
(b)
Figure 2. (a) The endemic equilibrium is locally stable with 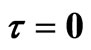 in system (3). (b) The endemic equilibrium is locally stable with
in system (3). (b) The endemic equilibrium is locally stable with  in system (9).
in system (9).
 (a)
(a)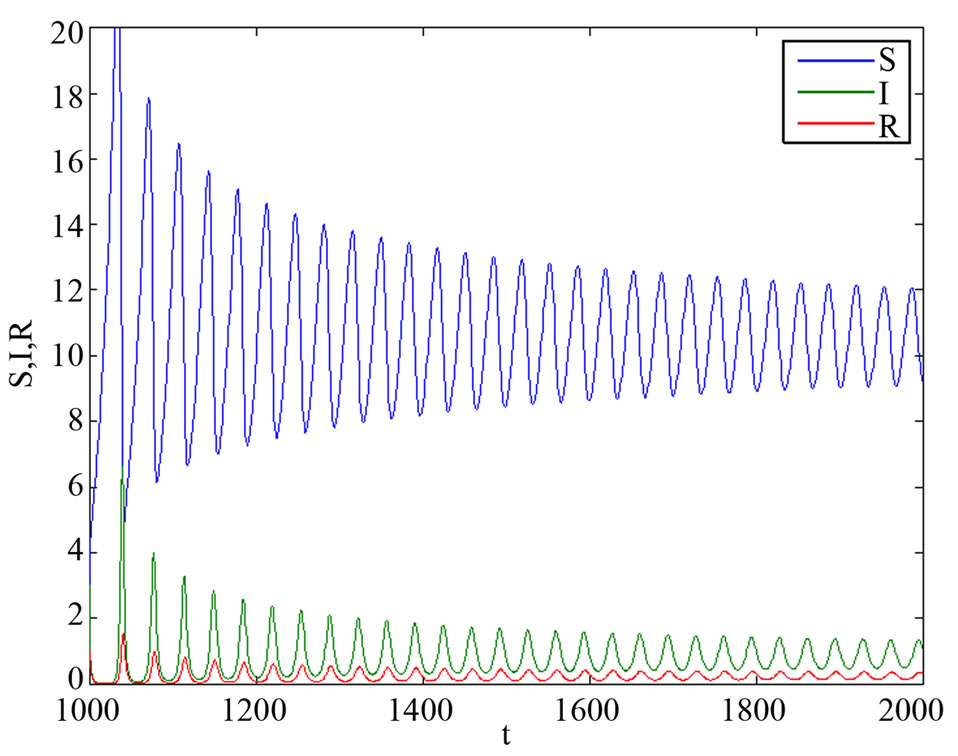 (b)
(b)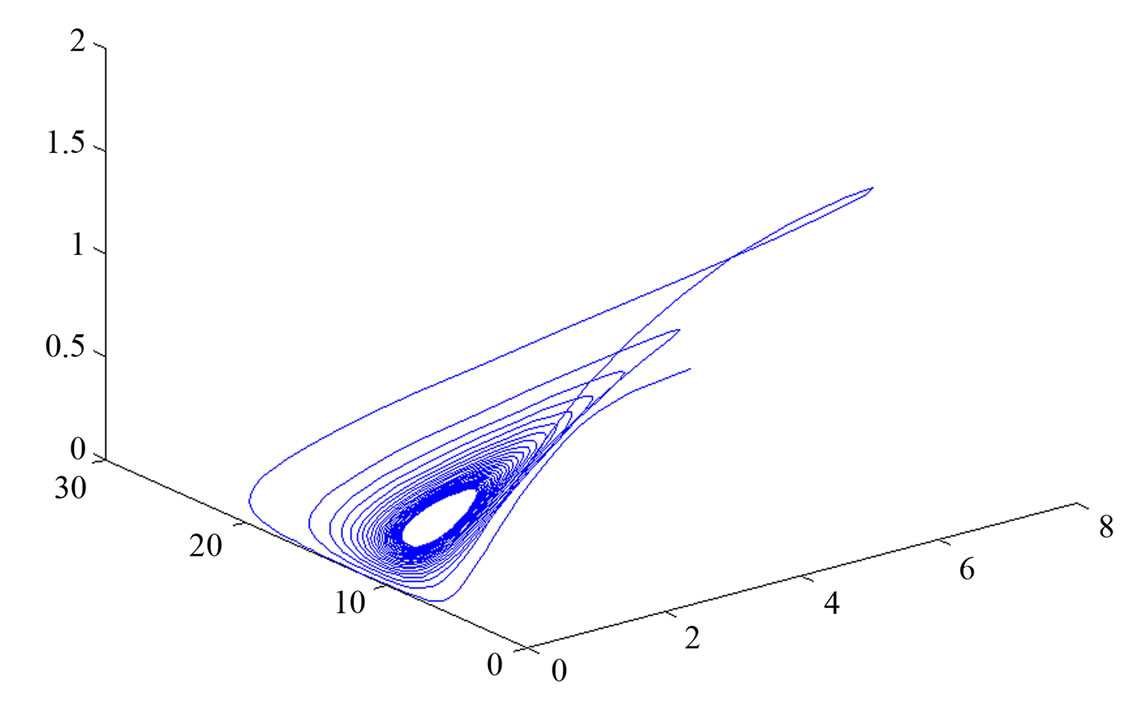 (c)
(c)
Figure 3. (a) The endemic equilibrium is asymptotic stable with 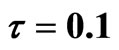 in system (3); (b) The endemic equilibrium is unstable with
in system (3); (b) The endemic equilibrium is unstable with 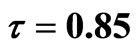 in system (3); (c) The endemic equilibrium exists periodic solution with
in system (3); (c) The endemic equilibrium exists periodic solution with 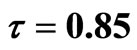 in system (3).
in system (3).
 (a)
(a)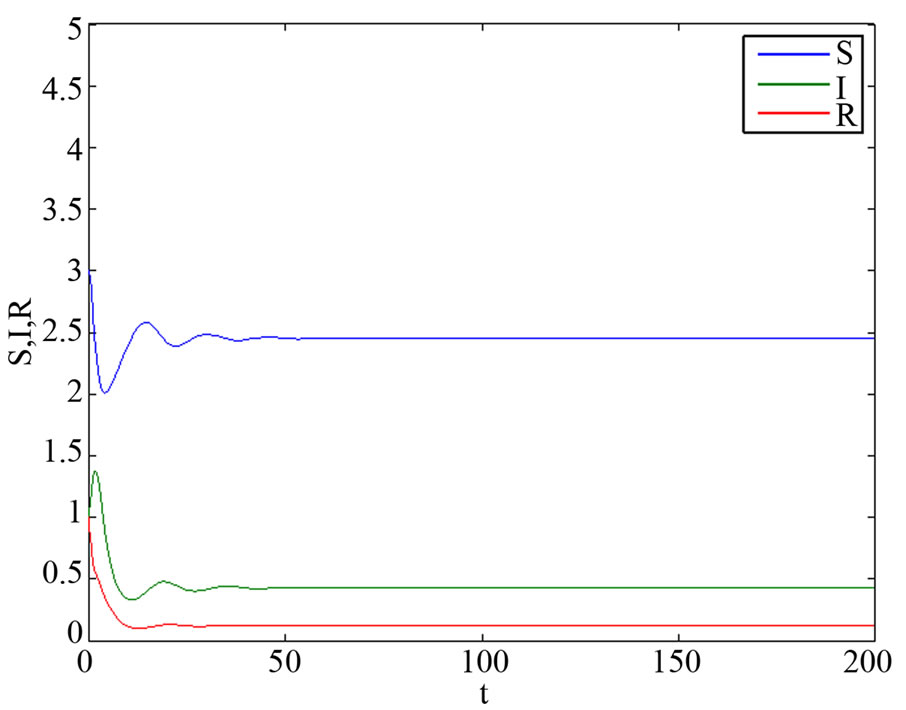 (b)
(b)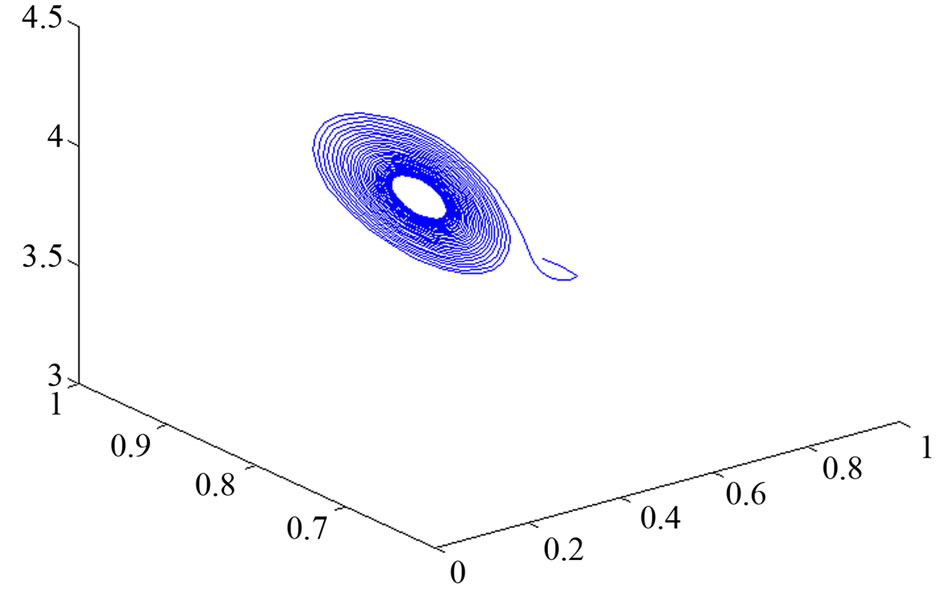 (c)
(c)
Figure 4. (a) The endemic equilibrium is asymptotic stable with 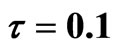 in system (9); (b) The endemic equilibrium is unstable with
in system (9); (b) The endemic equilibrium is unstable with  in system (9); (c) The endemic equilibrium exists periodic solution with
in system (9); (c) The endemic equilibrium exists periodic solution with 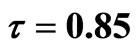 in system (9).
in system (9).
rium of system (3) and (9) is locally stable when 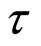 is suitably small. Furthermore, there exist periodic solutions with appropriate
is suitably small. Furthermore, there exist periodic solutions with appropriate  for two models. When
for two models. When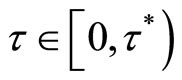 , the endemic equilibriums is locally asymptotically stable; and unstable when
, the endemic equilibriums is locally asymptotically stable; and unstable when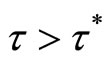 , and there exists a Hopf bifurcation.
, and there exists a Hopf bifurcation.
5. Acknowledgements
This research was supported by the National Science Foundation of China (10901145) and the National Sciences Foundation of Shanxi Province (2012011002-1).
REFERENCES
- R. M. Anderson and R. M. May, “Population Biology of Infectious Diseases I,” Nature, Vol. 280, 1979, pp. 361- 367. http://dx.doi.org/10.1038/280361a0
- R. M. May and R. M. Anderson, “Population Biology of Infectious Diseases II,” Nature, Vol. 280, 1979, pp. 455- 461. http://dx.doi.org/10.1038/280455a0
- H. W. Hethcote and P. van den Driessche, “An SIS EpiDemic Model with Variable Population Size and a Delay,” Journal of Mathematical Biology, Vol. 34, No. 2, 1995, pp. 177-194. http://dx.doi.org/10.1007/BF00178772
- F. Chamchod and N. F. Britton, “Analysis of a VectorBias Model on Malaria Transmission,” Bulletin of Mathematical Biology, Vol. 73, No. 3, 2011, pp. 639-657. http://dx.doi.org/10.1007/s11538-010-9545-0
- K. L. Cooke and P. van den Driessche, “Analysis of an SEIRS Epidemic Model with Two Delays,” Journal of Mathematical Biology, Vol. 35, No. 2, 1996, pp. 240-260. http://dx.doi.org/10.1007/s002850050051
- Y. Takeuchi, W. Ma and E. Beretta, “Global Asymptotic Properties of a Delay SIR Epidemic Model with Finite Incubation Times,” Nonlinear Analysis, Vol. 42, No. 6, 2000, pp. 931-947. http://dx.doi.org/10.1016/S0362-546X(99)00138-8
- J. Mena-Lorca and H. W. Hetheote, “Dynamic Models of Infectious Diseases as Regulators of Population Sizes,” Journal of Mathematical Biology, Vol. 30, No. 7, 1992, pp. 693-716.
- B. K. Mishra and D. K. Saini, “SEIRS Epidemic Model with Delay for Transmission of Malicious Objects in Computer Network,” Applied Mathematics and Computation, Vol. 188, No. 2, 2007, pp. 1476-1482. http://dx.doi.org/10.1016/j.amc.2006.11.012
- M. Y. Li, J. R. Graef, L. Wang and J. Karsai, “Global Dynamics of a SEIR Model with Varying Total Population Size,” Mathematical Biosciences, Vol. 160, No. 2, 1999, pp. 191-213. http://dx.doi.org/10.1016/S0025-5564(99)00030-9
- M. Gabriela, M. Gomes, L. J. White and G. F. Medley, “The Reinfection Threshold,” Journal of Theoretical Biology, Vol. 236, No. 1, 2005, pp. 111-113. http://dx.doi.org/10.1016/j.jtbi.2005.03.001
- Z. Jiang and J. Wei, “Stability and Bifurcation Analysis in a Delayed SIR Model,” Chaos, Solitons & Fractals, Vol. 35, No. 3, 2008, pp. 609-619. http://dx.doi.org/10.1016/j.chaos.2006.05.045
- T. Zhang and Z. Teng, “Global Behavior and Permanence of SIRS Epidemic Model with Time Delay,” Nonlinear Analysis: Real World Applications, Vol. 9, No. 4, 2008, pp. 1409-1424. http://dx.doi.org/10.1016/j.nonrwa.2007.03.010
- V. Capasso and G. Serio, “A Generalization of the Kermack-Mckendrick Deterministic Epidemic Model,” Mathematical Biosciences, Vol. 42, No. 1-2, 1978, pp. 41-61. http://dx.doi.org/10.1016/0025-5564(78)90006-8
- A. Kaddar, “On the Dynamics of a Delayed SIR Epidemic Model with a Modified Saturated Incidence Rate,” Journal of Differential Equations, Vol. 2009, No. 133, 2009, pp. 1-7.
- R. Xu and Z. Ma, “Global Stability of a SIR Epidemic Model with Nonlinear Incidence Rate and Time Delay,” Nonlinear Analysis: Real World Applications, Vol. 10, No. 5, 2009, pp. 3175-3189. http://dx.doi.org/10.1016/j.nonrwa.2008.10.013
- A. Kaddar, A. Abta and H. T. Alaoui, “Stability Analysis in a Delayed SIR Epidemic Model with a Saturated Incidence Rate,” Nonlinear Analysis: Modelling and Control, Vol. 15, No. 3, 2010, pp. 299-306.
- A. Abta, A. Kaddar and H. T. Alaoui, “Global Stability for Delay SIR and SEIR Epidemic Models with Saturated Incidence Rates,” Journal of Differential Equations, Vol. 2012, No. 23, 2012, pp. 1-13.
- H. Wei, X. Li and M. Martcheva, “An Epidemic Model of a Vector-Borne Disease with Direct Transmission and Time Delay,” Journal of Mathematical Analysis and Applications, Vol. 342, No. 2, 2008, pp. 895-908. http://dx.doi.org/10.1016/j.jmaa.2007.12.058
- R. Xu and Z. Ma, “Global Stability of a Delayed SEIRS Epidemic Model with Saturation Incidence Rate,” Nonlinear Dynamics, Vol. 61, No. 1, 2010, pp. 229-239. http://dx.doi.org/10.1007/s11071-009-9644-3
- R. Xu, Z. Ma and Z. Wang, “Global Stability of a Delayed SIRS Epidemic Model with Saturation Incidence Rate and Temporary,” Computers & Mathematics with Applications, Vol. 59, No. 9, 2010, pp. 3211-3221. http://dx.doi.org/10.1016/j.camwa.2010.03.009
- H. Huo and Z. Ma, “Dynamics of a Delayed Epidemic Model with Non-Monotonic Incidence Rate,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 2, 2010, pp. 459-468.
- R. Xu and Z. Ma, “Stability of a Delayed SIRS Epidemic Model with a Nonlinear Incidence Rate,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2319-2325. http://dx.doi.org/10.1016/j.chaos.2008.09.007
NOTES
*Corresponding author.

