Applied Mathematics
Vol.4 No.5(2013), Article ID:31440,7 pages DOI:10.4236/am.2013.45107
Prediction of Wavy Liquid Film Profile for Thin Film on a Falling Film Absorber
Department of Mathematics, College of Sciences and Humanities, Salman Bin Abdulaziz University, Alkharj, KSA
Email: hamza_habib@hotmail.com, essam_zahar2006@yahoo.com, ebady_ahmed @yahoo.com
Copyright © 2013 Hamza M. Habib et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 5, 2013; revised March 5, 2013; accepted March 12, 2013
Keywords: Wavy Film Flow; Gravity-Driven Flow; Analytical Numerical Methods
ABSTRACT
A hydrodynamic model of thin, laminar, gravity-driven, wavy-film flow over a vertical plate was considered. To make advantage of the cyclic boundary conditions and due to the nature of the wavy flow, a solution based on a Fourier series was implemented. Two representative cases of practical importance were studied; Re = 25, Re = 100. This range of Reynolds numbers is of the most practical importance in the process industry. Multiple solutions were obtained. Most of these solutions are mathematically correct but physically are not. It is observed that realistic wave profiles are always obtained once we approach the Froude number corresponding to thin film.
1. Introduction
Thin films flowing down vertical surfaces have been extensively studied because of their common occurrence in a variety of engineering applications. The transport properties typical of thin-film flows are especially suited to applications in industrial process equipment. The efficient heatand mass-transfer characteristics of the film are primarily the result of the thinness of the film and are further enhanced by the presence of waves on the liquidvapor interface.
Gravity is the driving force which creates the film flow and gives rise to the term “falling film”. In addition to the gravity force, the falling film is acted upon by an opposing shear force between the film and the solid surface and by a second shear force caused by the difference in viscosity of the fluid and the gases at the interface. The gravity effect on the falling film is expressed in terms of the Froude number, while the fluid flow rate is expressed in terms of the film Reynolds number.
Casual observation of a thin film on a vertical surface reveals certain important characteristics of the flow. The most obvious feature is the essential unsteadiness of the motion. With disturbances normally present in laboratory situations waves will develop on the liquid-vapor interface. For disturbances with a dominant perturbing frequency and a limited side-band width, a finite-amplitude, wavy-flow state can be observed. In this situation, constant wave amplitude is approached asymptotically with flow length as nonlinear interaction of wave modes results in an equilibrium condition. In other, more common situations, the presence of a wide spectrum of perturbing disturbances precludes the possibility of an observable stable equilibrium state. However, it does appear that developing flow characteristics can be satisfactorily described for much of the flow length by these asymptotic states Hirshburg and Florschuetz [1]. Wavy motion in a falling liquid film has been investigated both experimentally (Emmert and Pigford, [2]; Oliver and Atherinos, [3]; Yih and Seagrave, [4]; Patnaik and Perez-Blanco [5]; Adomeit and Renz [6]; Ambrosini, et al. [7]; Drosos, et al. [8]) and analytically by (Berbente and Ruckenstein, [9]; Javdani, [10]; Beschkov, and Boyadjiev, [11]).
In the literature, several techniques have been attempted to solve the wavy film motion (Dukler, [12]; Nguyen and Balakotaiah, [13]). An approximate solution of wavy film motion was done by Kapitza [14], Shkadov [15] for Re < 100 Hirshburg and Florschuetz [1] attempted to extend Shkadov’s work by including more expansion terms in the solution. However, by truncating the higher harmonic terms, generated by the nonlinear equation, they lost the coefficients of lower harmonic expansion terms of interest. Both Shkadov and Hirshburg employed a periodic wave state assumption which simplified the mathematical derivation substantially. Yang [16] made the same assumption along with constant fluid properties to provide improved solutions via a collocation technique. He has given some details of the growth of finite-amplitude waves.
1) The above brief review suggests that wavy motion in a falling liquid film enhances heat or mass transfer relative to the case of smooth laminar motion and despite progress made in recent years; significant gaps exist in understanding and modeling the falling films.
2) The objective of this work is to predict the wavy film flow profile using a hybrid analytical-numerical method. The solutions are valid for low and moderate Reynolds numbers regimes where the linear stability and the asymptotic finite-amplitude wave analysis of equilibrium flow states are still valid. This range of Reynold’s numbers is of the most practical importance in the process industry.
2. Mathematical Formulation
For two-dimensional laminar flow, the governing equations for constant fluid properties in the coordinate system shown in Figure 1 are
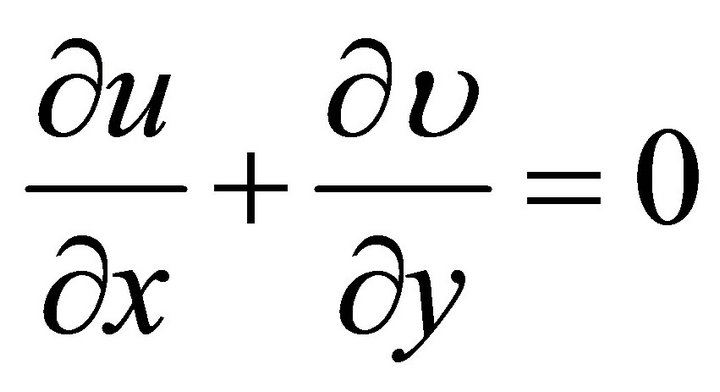 (1)
(1)
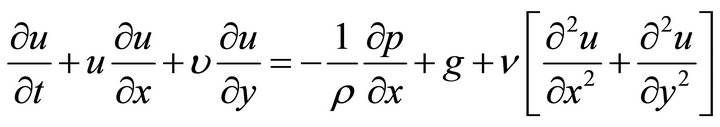 (2)
(2)
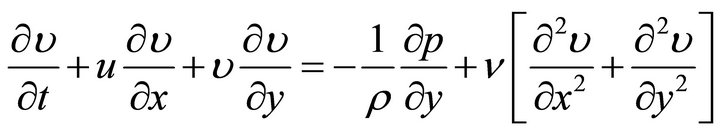 (3)
(3)
The associated boundary conditions are
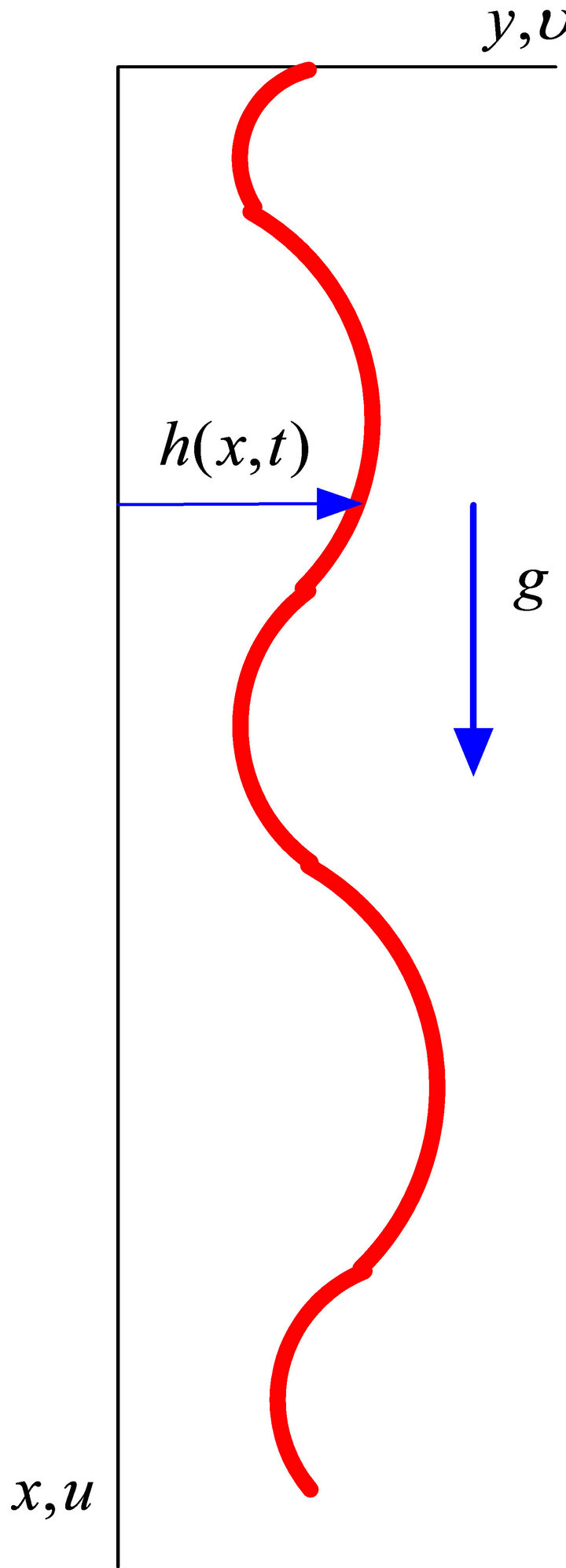
Figure 1. Coordinate system for the falling wavy film.
1) No slip and no penetration on the wall;
2) Negligible shear stress and balanced normal forces on the interface;
3) Specified global mean flow rate;
4) A permanent wave transformation can be employed. This is because we are studying the asymptotic periodic wave state.
The free surface boundary conditions for negligible shear stress and balanced normal forces can be expressed respectively after some manipulations as
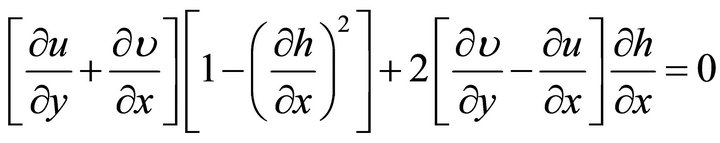 , (4)
, (4)
and
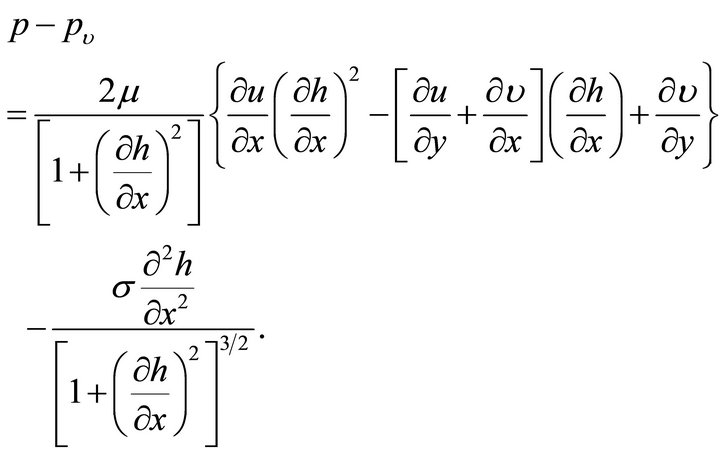 (5)
(5)
From the continuity equation
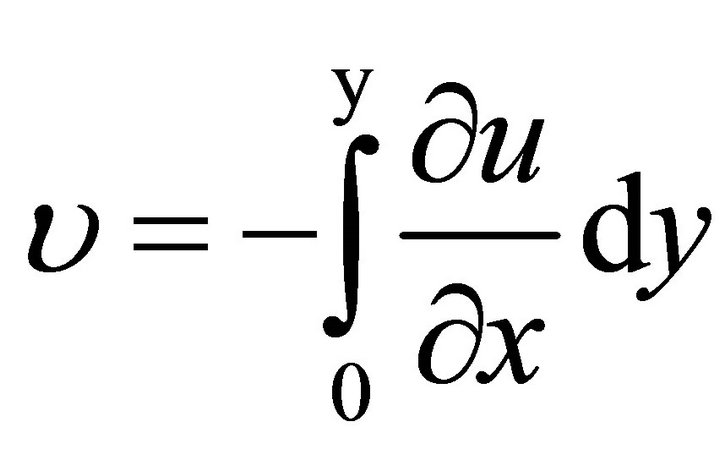 . (6)
. (6)
Since the film thickness 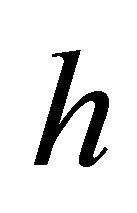 is very small compared to the film length in the x-direction, an order of magnitude analysis combines Equations (1)-(3) and (6) such that:
is very small compared to the film length in the x-direction, an order of magnitude analysis combines Equations (1)-(3) and (6) such that:
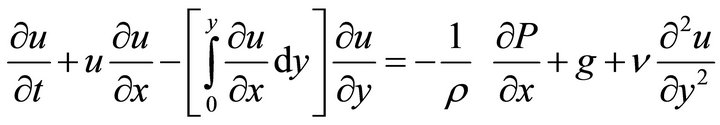 , (7)
, (7)
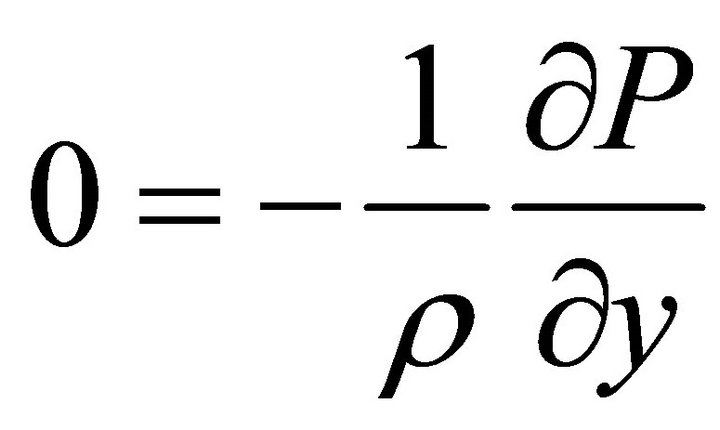 , (8)
, (8)
and the boundary conditions become:
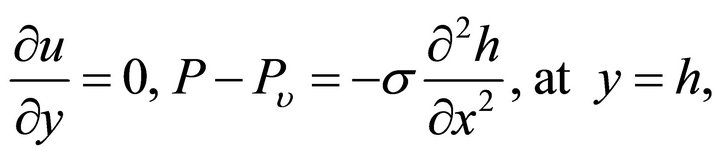 (9)
(9)
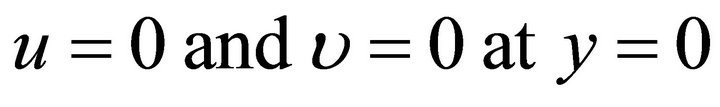 . (10)
. (10)
Udea and Tanaka [17] proved experimentally that parabolic velocity profile is quite accurate for Reynolds numbers flows up to about 150. Therefore the following velocity profile assumption was used.
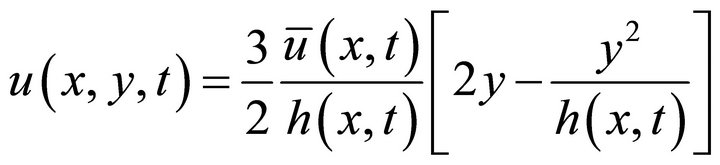 , (11)
, (11)
where 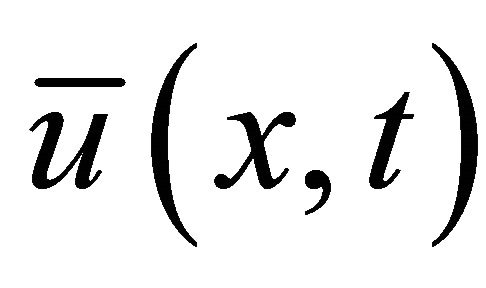 is the cross-sectional mean velocity defined as
is the cross-sectional mean velocity defined as
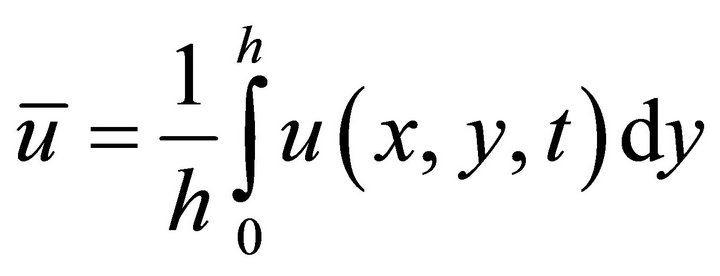 . (12)
. (12)
Plugging Equation (11) and the boundary conditions Equations (9) and (10) into Equation (7) and making all necessary partial derivatives, we obtain
 .(13)
.(13)
For periodic wave states, there exists a permanent wave transformation variable 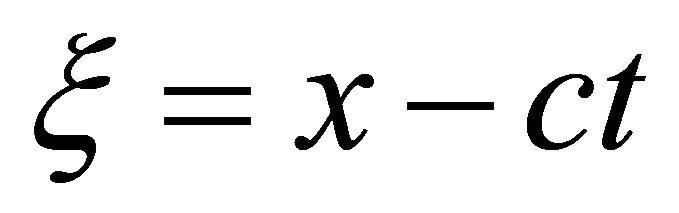 where c is the wave velocity. The wave amplitude can be described by
where c is the wave velocity. The wave amplitude can be described by
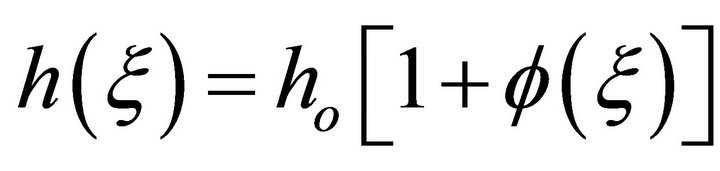 , (14)
, (14)
where, 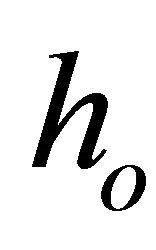 is the mean film thickness over the wavelength and
is the mean film thickness over the wavelength and  is the dimensionless free surface deflection. Substituting Equation (15) into Equation (14) and making all necessary partial derivatives, we obtain
is the dimensionless free surface deflection. Substituting Equation (15) into Equation (14) and making all necessary partial derivatives, we obtain
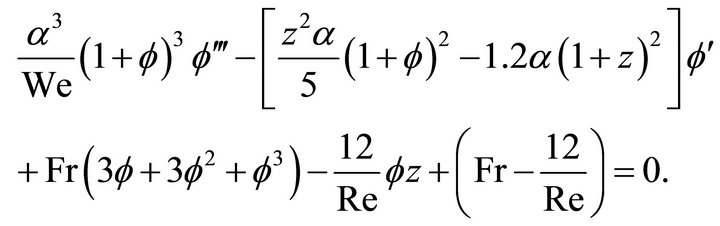 (15)
(15)
The boundary conditions become
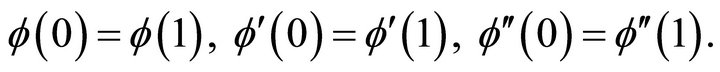 (16)
(16)
Equation (15) is third-order, nonlinear, boundary value problem with the Froude number, Fr, as the eigenvalue. In Equation (15)  is the wave number,
is the wave number, 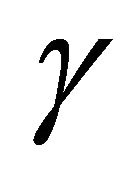 is the capillary-buoyancy coefficient, z is the dimensionless wave velocity, and Re is the film Reynolds number, (flow rate).
is the capillary-buoyancy coefficient, z is the dimensionless wave velocity, and Re is the film Reynolds number, (flow rate).
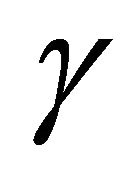 and Fr as
and Fr as 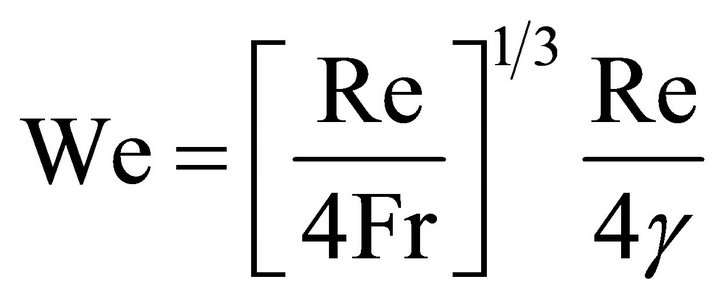 . (17)
. (17)
3. Numerical Method
To make advantage of the cyclic boundary conditions and due to the nature of the wavy flow, a solution in the form of a Fourier series is suggested.
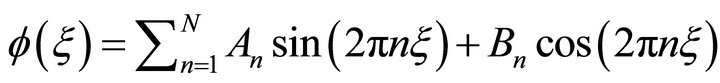 . (18)
. (18)
As seen, this solution satisfies the periodic boundary conditions (16).
Substituting Equation (18) into Equation (15), we get the following algebraic equation.
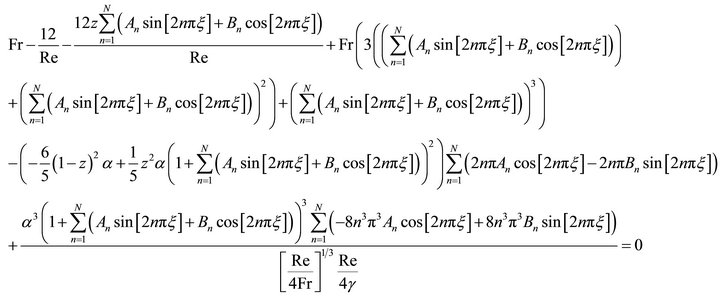 (19)
(19)
Equation (19) involves 2N + 1 unknowns, An, Bn and the Froude number as the eigenvalue. Thus we need 2N + 1 equations. This can be achieved by satisfying Equation (19) at 2N + 1 collocation points. The uniform grid is a good choice for the Fourier series.
4. Results and Discussions
In the physical problem, one need only specify the Reynolds number, Re, (flow rate), and the capillary-buoyancy coefficient, γ. The values for z and  are given by Pierson and Whitaker [18] while the capillary-buoyancy coefficient is:
are given by Pierson and Whitaker [18] while the capillary-buoyancy coefficient is:
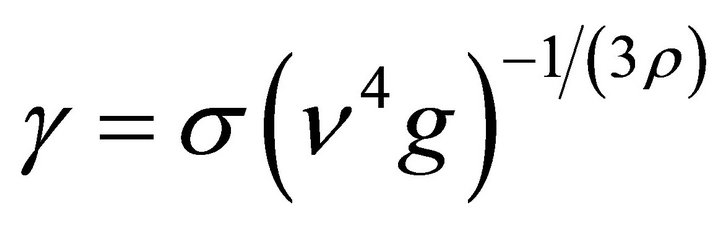 .
.
Since Equation (15) is an eigenvalue problem in Fr, the solution is not unique and we have troubles finding the solutions. Some examples of the solutions obtained for water are shown in Figure 2. While these solutions are mathematically correct they are not physically so.
These wave profiles are unrealistic because the wave amplitude exceeds the boundary at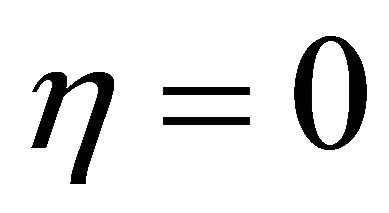 .
.
Figure 3 shows the wave profile for water (γ = 3400 at Reynolds number, Re = 25, z = 2.8, a = 0.009551).
Figures 4 and 5 show the wave profile for water (γ =
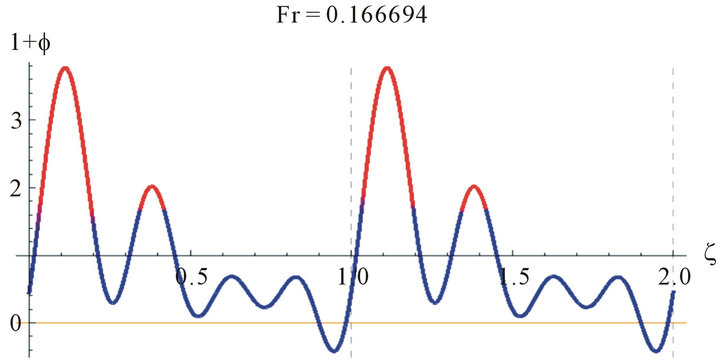
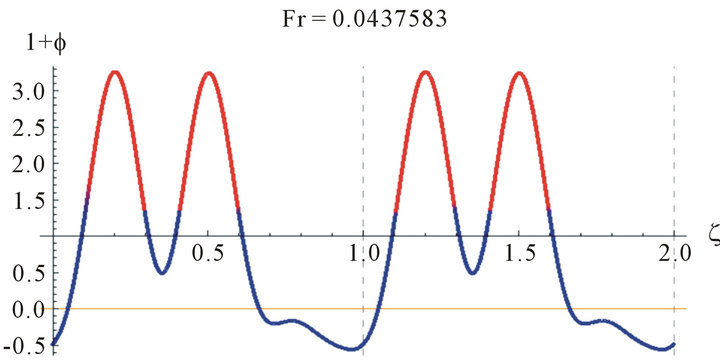
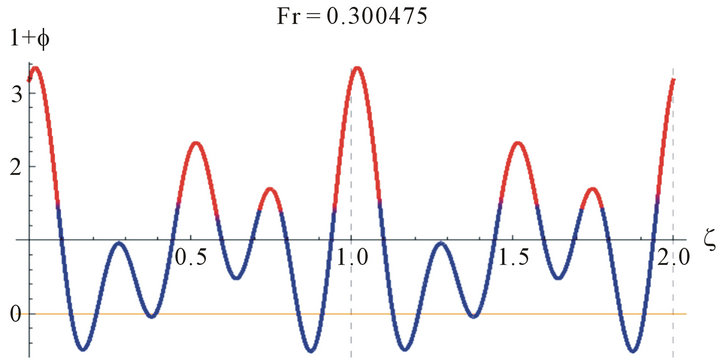
Figure 2. The wave profile for water at Re = 100, and different values of Fr.
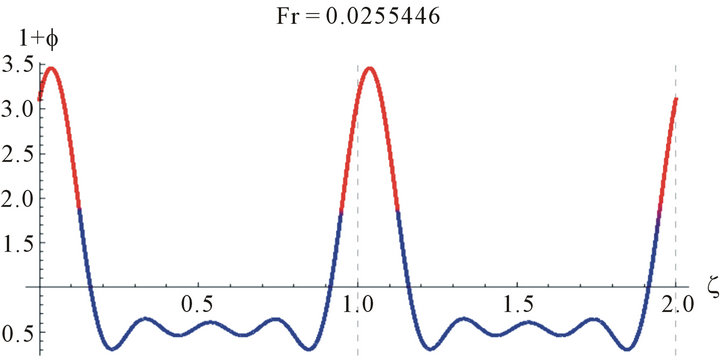
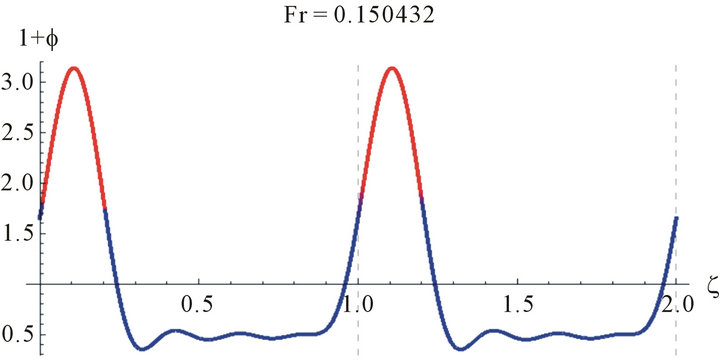
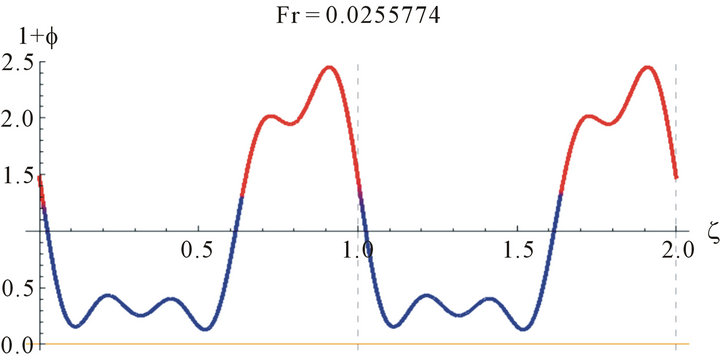
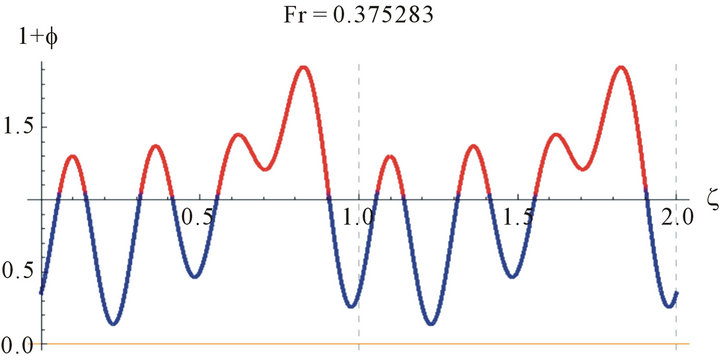
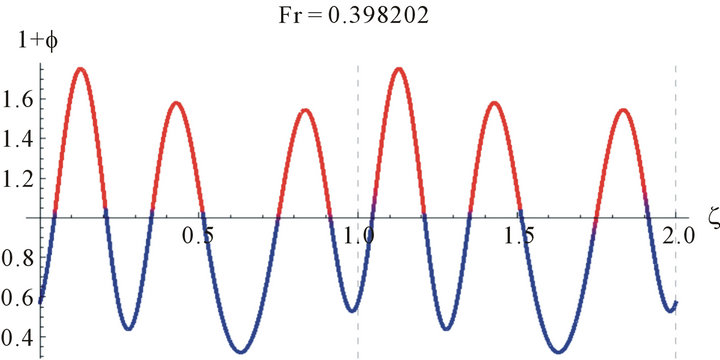
Figure 3. The wave profile for water (γ = 3400 at Reynolds number, Re = 25, z = 2.8, a = 0.009551, and different values of Fr).
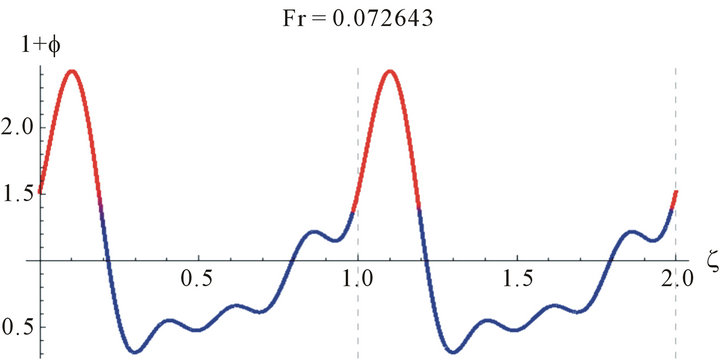
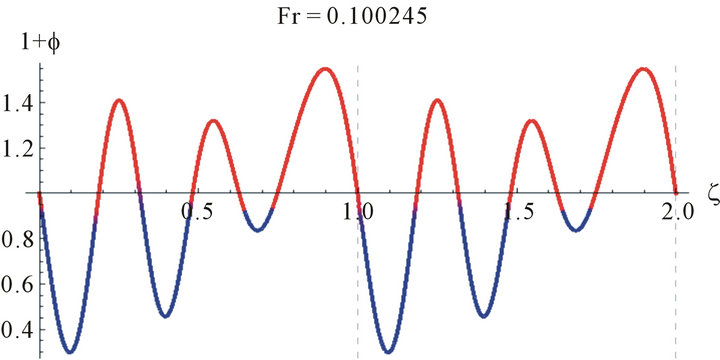
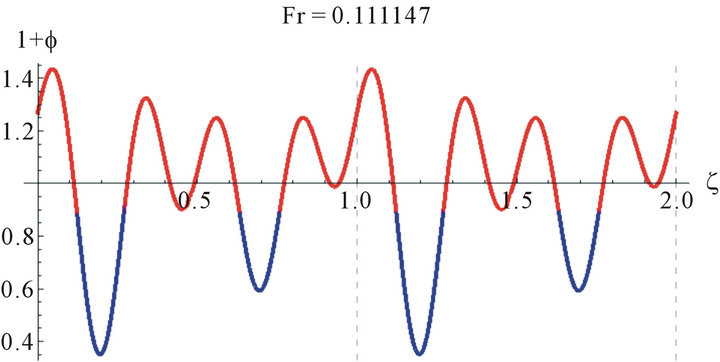
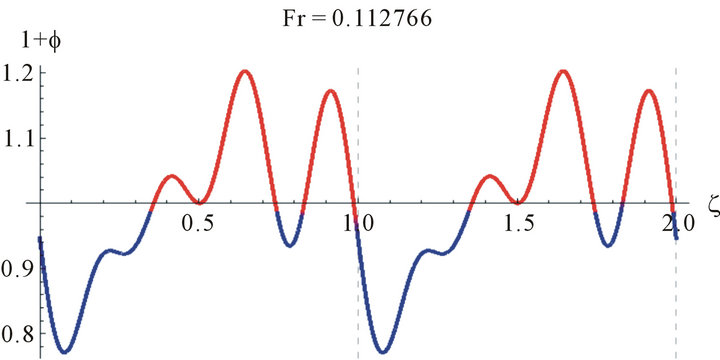
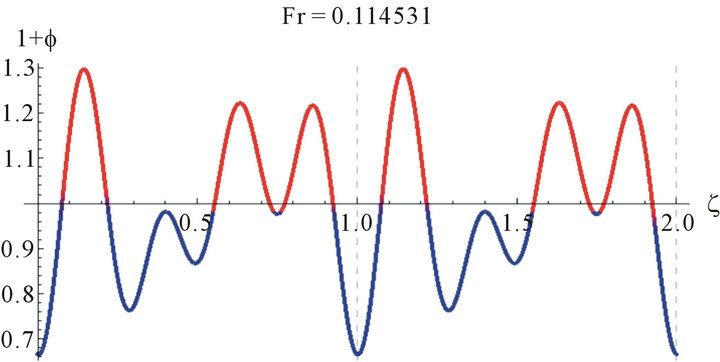
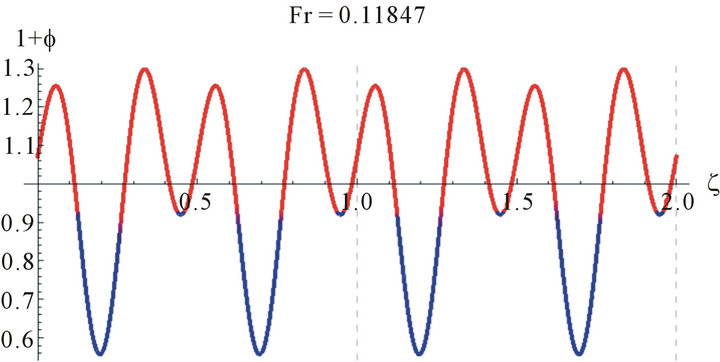
Figure 4. The wave profile for water (γ = 3400 at Reynolds number, Re = 100, z = 2.8, a = 0.021645 and different values of Fr).
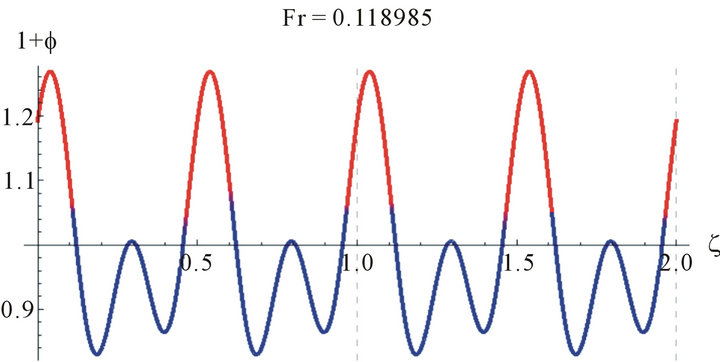
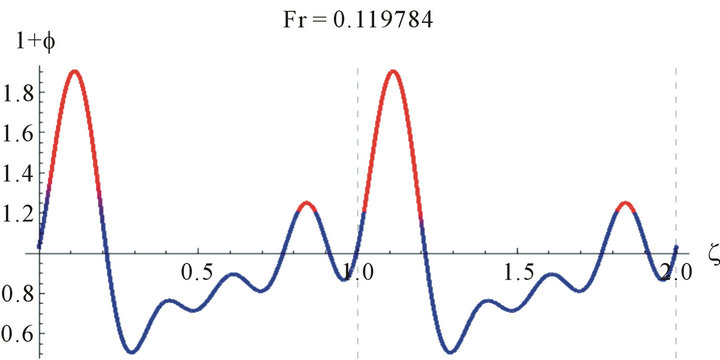
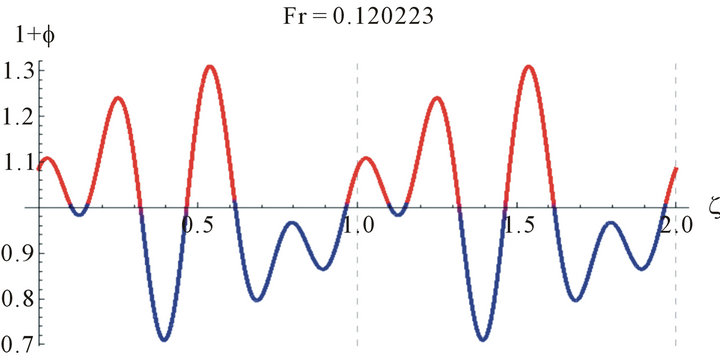
Figure 5. The wave profile for water (γ = 3400 at Reynolds number, Re = 100, z = 2.8, a = 0.021645 and different values of Fr).
3400 at Reynolds number, Re = 100, z = 2.8, a = 0.021645).
Because of the multiplicities of the solutions we need to judge the correct solution by other methods. One way is to compare the values of the Fr with the Nusselt smooth film thickness,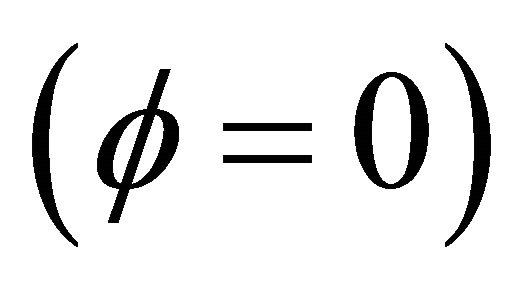 . The Nusselt smooth film corresponds to Fr = 12/Re. A close look at Figures 4 and 5 reveals that the values of the Froude number are centered around Fr = 12/Re, which asserts our hypothesis for comparison with the smooth film.
. The Nusselt smooth film corresponds to Fr = 12/Re. A close look at Figures 4 and 5 reveals that the values of the Froude number are centered around Fr = 12/Re, which asserts our hypothesis for comparison with the smooth film. These realistic sinusoidal-like waves represent the waves appearing at the wave-inception line. This range of Reynolds number studied is of most practical importance in the absorption cooling system. For higher Reynolds number, Pierson and Whitaker’s [18] linear stability analysis is not expected to be reliable due to the increasing importance of nonlinear effects, as they have mentioned as well as the uncertainty in the parabolic velocity profile assumption.
5. Conclusion
The wave profiles for thin, laminar, gravity-driven, flow are obtained for Reynolds numbers Re = 25, Re = 100, this range of Reynolds numbers are of the most practical importance in the absorption cooling absorber. The proposed hybrid analytical-numerical method combining Fourier series and collocation method makes advantage of periodic boundary conditions and the nature of the sinusoidal type waves appearing in such films. We had great troubles in obtaining the solutions. These solutions are much affected by the initial guess. Another problem we faced was the presence of multiple solutions. Most of these solutions are mathematically correct but physically are not that means that they give unrealistic profiles. It is observed that realistic wave profiles are always obtained once we approach the Froude number corresponding to Nusselt smooth film. Deviation from Froude number for smooth film gives an unrealistic wave profile. The results are good for Reynolds number less than 100. For Reynolds number greater than 100, the solutions are obtainable but we are not interested in besides they may not be realistic due to the invalidity of the linear stability theory at this range as well as the uncertainty in the parabolic velocity profile assumption.
6. Acknowledgements
The authors would like to thank the Deanship of Scientific Research, Salaman Bin AbduAlziz University, Kingdom of Saudi Arabia for their support to this research under contract No. 8/h/1432.
REFERENCES
- R. I. Hirshburg and L. W. Florschuetz, “Laminar WavyFilm Flow: Part I, Hydrodynamic Analysis,” Journal of Heat Transfer, Vol. 104, No. 3, 1982, pp. 452-458. doi:10.1115/1.3245114
- R. E. Emmert and R. L. Pigford, “A Study of Gas Absorption in Falling Liquid Films,” Chemical Engineering Progress, Vol. 50, 1954, pp. 87-93.
- D. R. Oliver and T. E. Atherinos, “Mass Transfer to Liquid Films on an Inclined Plane,” Chemical Engineering Science, Vol. 23, No. 6, 1968, pp. 525-536. doi:10.1016/0009-2509(68)89001-3
- S. M. Yih and R. C. Seagrave, “Mass Transfer in Laminar Falling Liquid Films with Accompanying Heat Transfer and Interfacial Shear,” International Journal of Heat and Mass Transfer, Vol. 23, No. 6, 1980, pp. 749-758. doi:10.1016/0017-9310(80)90028-9
- V. Patnaik and H. Perez-Blanco, “Roll Waves in Falling Films: An Approximate Treatment of the Velocity Field,” International Journal of Heat and Fluid Flow, Vol. 17, No. 1, 1996, pp. 63-70. doi:10.1016/0142-727X(95)00075-2
- P. Adomeit and U. Renz, “Hydrodynamics of Three-Dimensional Waves in Laminar Falling Films,” International Journal of Multiphase Flow, Vol. 26, No. 7, 2000, pp. 1183-1208. doi:10.1016/S0301-9322(99)00079-8
- W. Ambrosinr, N. Forgione and F. Oriolo, “Statistical Characteristics of a Water Film Falling down a Flat Plate at Different Inclinations and Temperatures,” International Journal of Multiphase Flow, Vol. 28, No. 3, 2002, pp. 1521-1540. doi:10.1016/S0301-9322(02)00039-3
- E. I. P. Drosos, S. V. Paras and A. J. Karabelas, ”Characteristics of Developing Free Falling Films at Intermediate Reynolds and High Kapitza Numbers,” International Journal of Multiphase Flow, Vol. 30, No. 7, 2004, pp. 853-876. doi:10.1016/j.ijmultiphaseflow.2004.03.003
- C. P. Berbente and E. Ruckenstein, “Hydrodynamics of Wave Flow,” AIChE Journal, Vol. 14, No. 5, 1968, pp. 772-782. doi:10.1002/aic.690140517
- K. Javdani, “Mass Transfer in Wavy Liquid Films,” Chemical Engineering Science, Vol. 29, No. 1, 1974, pp. 61-69. doi:10.1016/0009-2509(74)85030-X
- V. Beschkov and C. Boyadjiev, “ Numerical Investigation of Gas Absorption in a Wavy Film Flow,” Chemical Engineering Communications, Vol. 20, No. 3-4, 1983, pp. 173-182. doi:10.1080/00986448308940588
- A. E. Dukler, “Characteristic Effects and Modeling of the Wavy Gas-Liquid Interface,” Heat and Mass Transfer, Vol. 6, 1972, pp. 207-234.
- L. T. Nguyen and V. Balakotaiah, “Modeling and Experimental Studies of Wave Evolution on Free Falling Films,” Physics of Fluids, Vol. 12, No. 2236, 2000, pp. 2236-2256. doi:10.1063/1.1287612
- P. L. Kapitza, “Wave Flow of Thin Layers of a Viscous Fluid,” Pergamon Press, Oxford, 1965, pp. 261-272.
- V. Ya. Shkadov, “Wave Flow theory for a Thin Viscous Liquid Layer,” Fluid Dynamics, Vol. 3, No. 2, 1968, pp. 20-25.
- R. Yang, “Heat and Mass Transfer in Laminar WavyFilm Absorption with the Presence of Non-Absorbable Gases,” Ph.D. Dissertation, Arizona State University, Tempe, 1987,
- T. Ueda and H. Tanaka, “Measurements of Velocity, Temperature and Velocity Fluctuation Distribution in Falling Liquid Films,” International Journal of Multiphase Flow, Vol. 2, No. 3, 1975, pp. 261-272. doi:10.1016/0301-9322(75)90014-2
- F. W. Pierson and S. Whitaker, “Some Theoretical and Experimental Observations of the Wave Structure of Falling Liquid Films,” Industrial & Engineering Chemistry Fundamentals, Vol. 16, No. 4, 1977, pp. 401-408. doi:10.1021/i160064a002
Nomenclature
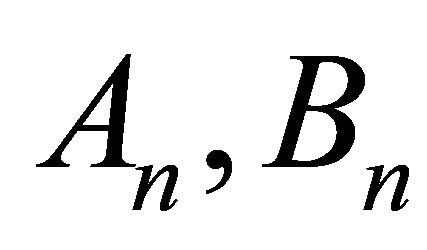 = coefficients of expansion in Equation (18)
= coefficients of expansion in Equation (18)
 = wave velocity (m/s)
= wave velocity (m/s)
 = Froude number
= Froude number 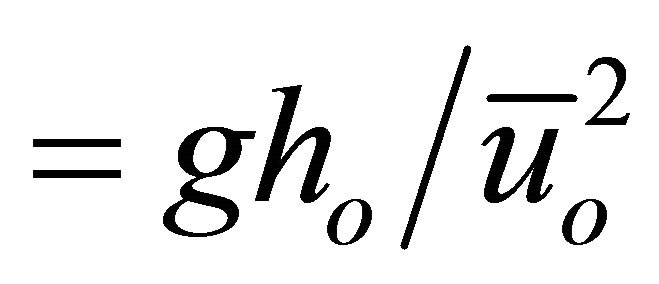
 = gravitational acceleration (m/s2)
= gravitational acceleration (m/s2)
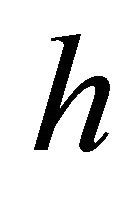 = local film thickness (m)
= local film thickness (m)
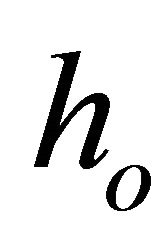 = mean film thickness over a wavelength (m)
= mean film thickness over a wavelength (m)
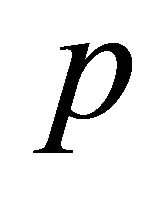 = pressure in liquid (N/m2)
= pressure in liquid (N/m2)
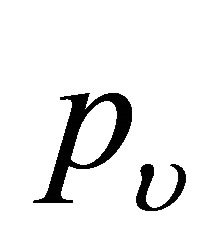 = pressure in gas (N/m2)
= pressure in gas (N/m2)
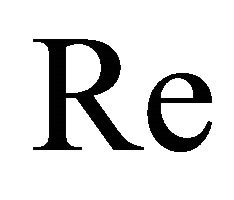 = Reynolds number =
= Reynolds number = 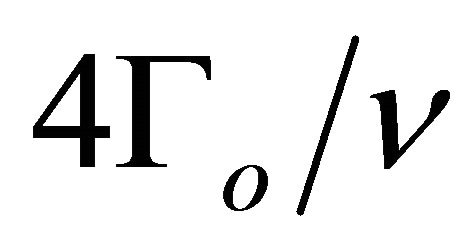
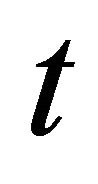 = time(s)
= time(s)
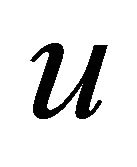 = x-direction velocity (m/s)
= x-direction velocity (m/s)
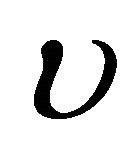 = y-direction velocity (m/s)
= y-direction velocity (m/s)
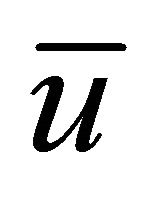 = x-direction mean velocity over film thickness
= x-direction mean velocity over film thickness
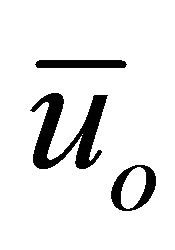 = characteristic velocity
= characteristic velocity 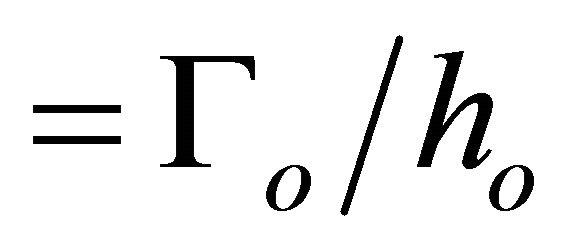 (m/s)
(m/s)
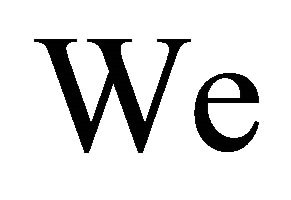 = Weber number
= Weber number 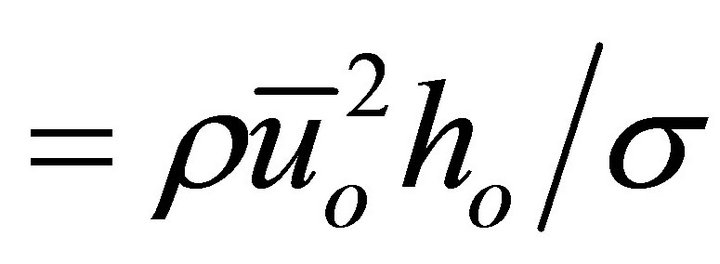
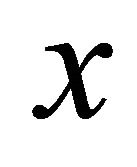 = coordinate parallel to the wall
= coordinate parallel to the wall
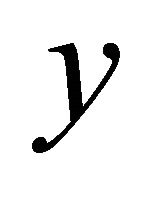 = coordinate normal to the wall
= coordinate normal to the wall
 = dimensionless wave velocity
= dimensionless wave velocity 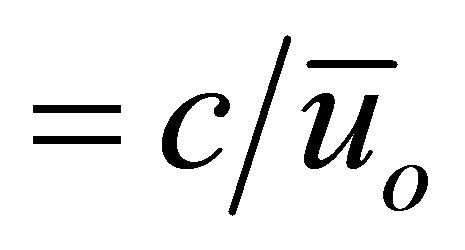
 = wave number
= wave number 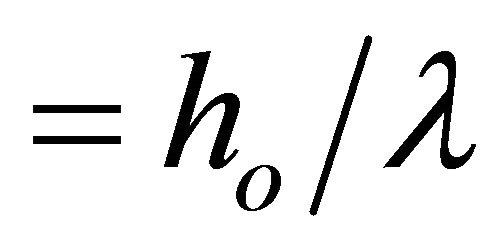
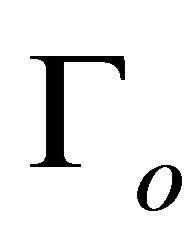 = mean volumetric flow rate over a wavelength (m3/s)
= mean volumetric flow rate over a wavelength (m3/s)
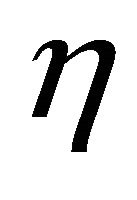 =
= 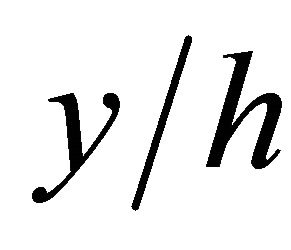
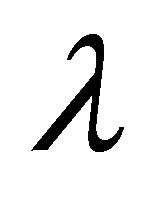 = wavelength (m)
= wavelength (m)
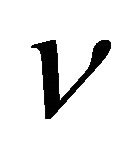 = kinematic viscosity (m2/s)
= kinematic viscosity (m2/s)
 =
= 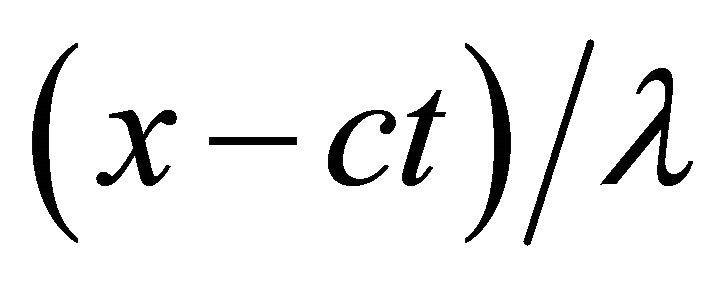
 = liquid density (kg/m3)
= liquid density (kg/m3)
 = surface tension (N/m)
= surface tension (N/m)
 = dimensionless free surface deflection
= dimensionless free surface deflection

