Received 20 August 2014; revised 26 September 2014; accepted 15 October 2014

ABSTRACT

In the realm of Bounded Topology we now consider supernearness spaces as a common generalization of various kinds of topological structures. Among them the so-called Lodato spaces are of significant interest. In one direction they are standing in one-to-one correspondence to some kind of topological extensions. This last statement also holds for contiguity spaces in the sense of Ivanova and Ivanov, respectively and moreover for bunch-determined nearness spaces as Bentley has shown in the past. Further, Doîtchînov proved that the compactly determined Hausdorff extensions of a given topological space are closely connected with a class of supertopologies which he called b-supertopologies. Now, the new class of supernearness spaces—called paranearness spaces—generalize all of them, and moreover its subclass of clan spaces is in one-to-one correspondence to a certain kind of symmetric strict topological extension. This is leading us to one theorem which generalize all former mentioned.

Keywords:

Set-Convergence, Supertopological Space, Lodato Space, Contiguity Space, Nearness, Paranearness

1. Basic Concepts

As usual 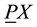denotes the power set of a set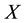, and we use 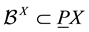to denote a collection of bounded subsets of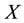, also known as 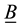-sets, i.e. 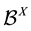has the following properties:

(b₁);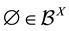

(b₂) imply;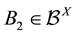

(b₃) 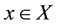implies.

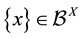Then, for -sets 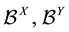a function 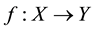is called bounded iff 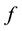satisfies, i.e.

(b).

Definition 1.1 For a set, we call a triple consisting of, -set and an operator a prehypernear space iff the following axioms are satisfied, i.e.

(hn₁) and imply, where iff;

(hn₂) implies;

(hn₃) implies;

(hn₄) implies.

If for some, then we call a -near collection in. For prehypernear spaces, a bounded function is called a hypernear map, shortly hn-map iff it satisfies (hn), i.e.

(hn) and imply; a sected hn-map, shortly shn-map iff it satisfies (shn), i.e.

(shn) and imply with and.

Remark 1.2 Note, that shn-maps between prehypernear spaces are always hn-maps. We denote by PHN^· respectively PHN the corresponding categories.

Examples 1.3 (i) For a prenearness space ([1] ) let be -set. Then we consider the triple where and, otherwise.

(ii) For a -filter space ([2] ) we consider the triple, where for each

is defined by setting:;

(iii) For a set-convergence space ([3] we consider the triple, where for each

is defined by setting:;

(iv) For a generalized convergence space [4] , we consider the triple, where

and

for with; alternately we look at the following triple, where

,

and;

(v) For a ech-closure space ([5] ) let be -set. Then we consider the triple

with for each;

(vi) For a -proximity space ([6] ) we consider the triple, where

for each with;

(vii) For a neighborhood space ([6] ) we consider the triple, where for each.

Remark 1.4 In preparing the next two important examples we give the following definitions.

Definitions 1.5 TEXT denote the category, whose objects are triples—called topological extensions—where are topological spaces (given by closure operators) with -set and is a function satisfying the following conditions:

(tx₁) implies, where denotes the inverse image under;

(tx₂), which means that the image of under is dense in.

Morphisms in TEXT have the form, where are continuous maps such that is bounded, and the following diagram commutes:

If and are TEXT-morphisms, then they can be composed according to the rule:

where “” denotes the composition of maps.

Remark 1.6 Observe, that axiom in this definition is automatically satisfied if is a topological embedding. Moreover we admit an ordinary -set on which need not be necessary coincide with the power. In addition we mention that such an extension is called

(1) strict iff forms a base for the closed subsets of [7] ;

(2) symmetric iff and imply [8] .

Examples 1.7 (i) For a topological extension we consider the triple, where

if and;

(ii) For a symmetric topological extension we consider the triple, where

if and.

2. Fundamental Classes of Prehypernear Spaces

With respect to above examples, first let us focus our attention to some important classes of prehypernear spaces.

Definitions 2.1 A prehypernear space is called

(i) saturated iff;

(ii) discrete iff;

(iii) symmetric iff and imply and

;

(iv) pointed iff implies;

(v) conic iff implies;

(vi) set-defined iff implies.

Theorem 2.2 The category PNEAR of prenearness spaces and related maps is isomorphic to the category SY-PHN^S of saturated symmetric prehypernear spaces and hn-maps.

Proof. According to Example 1.3. (i) we claim that is a symmetric saturated prehypernear space. Conversely, we consider for such proposed space the following prenearness space defined by setting:

.

Hence, the above mentioned connections are functoriell, and thus it remains to prove that the following two statements are valid, i.e.

(i);

(ii).

To (i): “”; and imply, hence, and is valid which shows.

“”: and without restriction. Choose, hence by hypothesis,

and follows.

Since we claim.

To (ii): “”: Without restriction let be.

For we have to verify. So, let be, hence since is symmetric and saturated by hypothesis. Consequently, is valid.

“” Conversely, let be, hence. Choose (according to re- spectively). Thus holds, and follows by hypothesis. But, hence is valid.

Remark 2.3 In this context we point out that each prehypernear space induces in general the following ech-closure operators by setting:

(1);

(2),

where the following inclusion is valid: implies. In the symmetric case these two operators coincide, moreover we have iff, and finally defines a symmetric ech-closure space.

Definition 2.4 A prehypernear space is called a pseudohypernear space iff is isoton, i.e. satisfies (is) imply. We denote by PSHN the corresponding full subcate- gory of PHN.

Remark 2.5 In this context we refer to Examples 1.3. (i), (iv), (v), (vi), (vii), respectively Examples 1.7. (i), (ii).

Theorem 2.6 The category Č-CLO of Čech-closure spaces and continuous maps is isomorphic to a full subcategory of PSHN.

Remark 2.7 Now, before showing the above mentioned theorem we give the following definition.

Definition 2.8 A prehypernear space is called sected iff satisfies (), i.e.

(sec) and imply.

Remark 2.9 In this connexion we point out that each pointed prehypernear space (see Remark 3.6) is always sected.

Moreover, sected prehypernear spaces are already pseudohypernear spaces.

Definition 2.10 A sected conic saturated prehypernear space is called closed, and we denote by CL-PHSN the full subcategory of PSHN, whose objects are closed pseudohypernear spaces.

Proof of Theorem 2.6.

According to Example 1.3. (v) we claim that is a closed pseudohypernear space. Conversely, we consider for such proposed space the ech-closure space. Hence, the above mentioned connections are functoriell, and thus it remains to prove that the following two statements are valid, i.e.:

(i);

(ii).

To (i): Now let be, we have to verify. Firstly, implies, hence, and results.

Secondly, implies, hence, and follows.

To (ii): Now, let be without restriction. and imply according to, hence by hypothesis, and results.

Conversely, implies.

Now, we will show that. implies by hypothesis.

Choose with, hence, since satisfies (is). But then

is valid which implies, hence concluding the proof.

Remark 2.11 Now, in the following another important class of prehypernear spaces will be examined, being fruitful in considering convergence problems and having those properties, which are characterizing topological universes.

3. Grill-Spaces

Definitions 3.1 A prehypernear space is called a prehypergrill space iff N satisfies (gri), i.e.

(gri) and imply there exists,

where, and is called grill (Choquet [9] ) iff it satisfies

(gri₁);

(gri₂) iff or.

We denote by G-PHN the category, whose objects are the prehypergrill spaces with hn-maps between them and by G-PHN the category, whose objects are the prehypergrill spaces with shn-maps between them.

Remark 3.2 We refer to Examples 1.3. (ii), (iii), (iv), (vi), (vii) respectively and to Examples 1.7. (i), (ii).

Theorem 3.3 The category GRILL of grill-determined prenearness spaces and nearness preserving maps is isomorphic to a full subcategory of G-PHN.

Proof. According to Theorem 2.2 we already know that is a symmetric saturated prehypernear space, hence additionally it is a prehypergrill space by hypothesis. Conversely, is grill-determined by supposition.

Theorem 3.4 The category SETCONV ([3] ) of set-convergence spaces and related maps is isomorphic to a full subcategory of G-PHN.

Proof. According to Example 1.3. (iii) we claim that the triple is a set-defined prehypergrill space. Conversely, we consider for such proposed space the following set-convergence space defined by setting: iff for each. Hence, the above mentioned connections are functoriell with respect to shn-maps. Thus, it remains to prove that the following two statements are valid, i.e.

(i);

(ii).

To (i) “”implies, evidently.

“”: implies, hence there exists and. Since we conclude with.

To (ii): “”: implies the existence of with. Consequently, and results, hence is valid.

“”: implies that and hold. Hence, and re- sults.

Corollary 3.5 The category GCONV of generalized convergence spaces and related maps is isomorphic to the category DISG-PHN^·, whose objects are the discrete prehypergrill soaces and whose morphisms are the sected hn-maps.

Remark 3.6 Now, in this connextion it is interesting to note that there exists and alternate description of generalized convergence spaces in the realm of prehypergrill spaces. Analogously, how to describing set convergence on arbitrary B-sets we offer now a corresponding one for the point convergence as follows: Let be given a point-convergence space, where is satisfying some natural conditions. Then we consider the following pointed prehyergrill space by setting and

if.

Conversely let be given a pointed saturated prehypergrill space then we naturally define a point- convergence space by setting iff. As a consequence we obtain the result that point convergence can be essentially expressed by means of its corresponding pointed saturated prehypergrill spaces and sected hn-maps.

Hence, the last mentioned category also is isomorphic to DISG-PHN^·.

Remark 3.7 Another interesting fact is the following one. As Wyler has shown in [3] supertopological spaces in the sense of Doîtchînov can be regarded as special set-convergence spaces. Hence it is also possible for describing them in the realm of prehypergrill spaces. Concretely let be given a supertopological space (see [10] ) or more generally a neighborhood space in the sense of [6] , in the following referred as to presupertopological space. Then we consider the triple, where for each. Hence the triple is a conic pseudohypergrill space. Hereby, a prehypergrill space is called pseudohypergrill space iff N satisfies (is) (see also Definition 2.4). By CG-PSHN respectively CG-PSHN^· we denote the corresponding categories. At last we point out that conic pseudohypernear spaces are even set-defined.

Theorem 3.8 The category PRESTOP of presupertopological spaces and continuous maps is isomorphic to the category CG-PSHN^·.

Proof. According to Remark 3.7 we consider conversely for a conic pseudohypergrill space the space, where for each is defined by setting:

for each. Then is a presupertopological space. Hence, the above mentioned connections are functoriell with respect to shn-maps. Thus, it remains to prove that the following two statements are valid, i.e.

(i);

(ii).

To (i): “”: For let be. implies the existence of with, hence follows. Consequently is valid, showing that.

“”: Since is grill we get, hence

is valid.

To (ii): “”implies the existence of with by hypothesis, hence.

“”implies, hence according to.

Remark 3.9 -proximities (see [6] ) are of significant importance when considering topological extensions. Here we will give two interesting examples in that direction as follows:

(1) For a symmetric topological space (given by a closure operator t) let be a -set with, then we define a -proximity by setting: iff for each and. Now, it is easy to verify that is -compatible, which means the equality holds by restricting on, where denotes the closure-operator induced by.

(2) Let being the same hypothesis as in (1). We set and define a near-

ness relation by setting: iff. Then defines a b-proximity with the same properties as mentioned above. Now, we recall the definition of a b-proximity respectively b-proximity space as follows:

Definition 3.10 A -proximity space consists of a triple, where is set, -set and satisfying the following conditions:

(bp₁) and (i.e. is not in relation to, and analogously this is also holding for);

(bp₂) iff or;

(bp₃) implies;

(bp₄) and imply.

Remark 3.11 Here we point out that b-proximities are in one-to-one correspondence with presupertopologies. In the symmetric case, if additionally satisfies (sbp), i.e.

(sbp) and imply and moreover equals, then symmetric b-proximities coincide with the Čech-proximities mentioned by Deák ([11] ).

Definition 3.12 For -proximity spaces, a bounded function is called p-map iff satisfies (p), i.e.

(p) and imply. By b-PROX we denote the corresponding category.

Theorem 3.13 The category b-PROX and CG-PSHN are isomorphic.

Proof. For a b-proximity space we consider the triple, where

for each with. Then is a conic pseudohypergrill space. Con-

versely let be given such a space, then we consider the triple, where

is defined by setting iff for each and. Hence, is a b-pro- ximity space. The above mentioned connections are functoriell, and thus it remains to prove that the following two statements are valid, i.e.

(i);

(ii).

To (i): “”: implies, hence.

“”: implies, hence follows.

To (ii): “”: and imply, hence, and results.

“”implies. We will show that.

implies by hypothesis, hence, and results which concludes the proof.

Résumé 3.14 Respecting to former advisements we note that we have established only some topological concept in which some important classical ones can be now expressed and studied in a very natural way. Moreover, the fundamental categories how as GRILL, b-PROX, PRESTOP, GCONV and SETCONV can be regarded as special subcategories of G-PHN. (see also the Theorem 3.3, 3.4, 3.8 and 3.13 respectively).

4. Bonding in Prehypernear Spaces

A slight modification of the definition for being a prehypergrill space leads us to the following notation.

Definition 4.1 A prehypernear space is called bonded iff satisfies (b), i.e.

(b) and imply or, where

.

Remark 4.2 Each prehypergrill space is bonded.

Proof. evident.

Definition 4.3 Now, we call a bonded pseudohypernear space a semihypernear space and denote by SHN the full subcategory of PSHN.

Theorem 4.4 The category PrTOP of pretopological spaces and continuous maps is isomorphic to a full subcategory of SHN.

Proof. According to Theorem 2.6 respectively Definition 2.10 it is evident that additionally satisfies, hence being a pretopology on its underlying set. On the other hand is

bonded, because implies. We suppose that,

hence there exist, such that. Consequently,

.

But leads us to a contradiction.

Theorem 4.5 The category SNEAR of seminearness spaces and related maps is isomorphic to a full sub- category of SHN.

Proof. According to Theorem 2.2 we firstly show that is bonded. Without restriction bet be

and, hence. Since we ob-

tain. Thus or results, showing that is satisfying (b). On the other hand let be and without restriction. We suppose, hence there exist, with and. Consequently follows. Then we get by hypothesis. Since M is bounded we have, or. By symmetry of we obtain the statement or . Consequently, or leads us to a contradiction.

Remark 4.6 A pseudohypernear space induces two underlying psb-hull operators by setting for each:

whereby the inclusion is valid for each. If is symmetric then the two operators coincide, and moreover we claim the following equalities for each, i.e.. Hereby, a function is called a psb-hull operator, and the triple is called a psb-hull space iff satisfies the following conditions:

(bh₁);

(bh₂) implies;

(bh₃) imply.

For psb-hull spaces, let be a bounded function, then is called b- continuous iff implies. We denote by Psb-HULL the corresponding category.

Definition 4.7 Now, we call a conic pseudohypernear space a pseudohull space iff satisfies (h), i.e.

(h) and imply. We denote by PSHU the full subcategory of PSHN, whose objects are the pseudohull spaces.

Theorem 4.8 The categories Psb-HULL and PSHU are isomorphic.

Proof. According to Remark 4.6 we already know that is a psb-hull space. Conversely, for a

psb-hull space we consider the triple by setting for each

.

Then is a pseudohull space. Hence, the above mentioned connections are functoriell. Thus it re- mains to prove that the following two statements are valid, i.e.

(i);

(ii).

To (i): “”: For let be, hence. Consequently, follows, showing that is valid.

“”: evident.

To (ii): “”: and imply by hypothesis, hence is valid.

“”:; we will show that is valid. implies

by hypothesis. Choose with, hence according to (hn₁). Consequently, the above mentioned inclusion is valid, showing that.

Corollary 4.9 In the saturated case CL-PSHN and PSHU are isomorphic categories.

Proof. We refer to Theorem 2.6, Definition 2.10 and Theorem 4.8 respectively.

Definition 4.10 A prehypernear space is called connected if satisfies (cnc), i.e.

(cnc) and imply.

Remark 4.11 We note that each pointed prehypernear space is connected, moreover this also is holding for any symmetric semihypernear space. Consequently, the underlying psb-hull operator additionally satisfying (ad), i.e.

(ad). Now, let us call such an operator b-hull operator, and we denote by b-HULL the corresponding full subcategory of Psb-HULL with related objects. In the saturated case we claim that b-HULL and CL-SHN are isomorphic categories. Hereby CL-SHN denotes the full subcategory of SHN, whose objects are the closed semihypernear spaces.

5. Hypernear Spaces

As already observed, hypertopologies appear in connexion with certain interior operators studied by Kent and Min ([12] ). Hereby a function is called a hypertopology on, and the pair is called a hypertopological space iff “−” satisfies the following conditions:

(hyt₁);

(hyt₂) implies;

(hyt₃) imply;

(hyt₄) implies.

For hypertopological spaces, let be a function, then is called continuous

iff implies. By HYTOP we denote the corresponding subcategory of -CLO.

Evidenly, the category TOP of topological spaces and continuous maps can be now regarded as a special case of HYTOP. On the other hand certain nearnesses play an important role in the realm of unifications and extensions, respectively. This is holding for distinguished nearness spaces and b-proximity spaces in fact. Moreover, certain supertopologies are involved, too. Now, in the following we will give a common description of them all by introducing the so called concept of a hypernear space.

Definition 5.1 A pseudohypernear space is called a hypernear space iff satisfies (hn), i.e.

(hn) and imply.

We denote by HN the corresponding full subcategory of PSHN. Note, that in this case is a hypertopology on.

Theorem 5.2 CL-HN denotes the full subcategory of CL-PSHN, whose objects are the closed hypernear spaces, then CL-HN and HYTOP are isomorphic.

Proof. The reader is referred to Theorem 2.6 and Definition 2.10, respectively.

Remark 5.3 As pointed out in Remark 3.6, point convergence can be described by certain pointed prehypernear spaces. To obtain a result more closer related to hypertopologies we will give the following definition.

Definition 5.4 A prehypernear space is called surrounded, iff satisfies (sr), i.e.

(sr) and imply there exists .

Remark 5.5 Here we claim that each pointed prehypernear space is surrounded, hence sected, too. (See also Definition 2.8).

Lemma 5.6 For a hypernear space the following statements are equivalent:

(i) is pointed;

(ii) is surrounded.

Proof. The only remaining implication “(ii) (i)” will be shown now: and imply the existence of with. Consequently,

,

hence follows, and results according to (hn).

Remark 5.7 Now, if we consider a bounded hypertopology, this is a psb-hull operator on a B-set, which additionally satisfies (bh₄), i.e.

(bh₄) and imply, then the corresponding category is isomorphic to the full subcategory SR-HN of HN, whose objects are the surrounded hypernear spaces. In this connexion we consider the restriction of on the B-set. Conversely, for a bounded hypertopological space we define the corresponding sourrounded hypernear space by setting; and, otherwise. In the saturated case then we can recover all hy- pertopological spaces. So, in general it is now possible to study those closure operators not only on, but also on arbitrary B-sets even in the realm of the broader concept of hypernear spaces.

Remark 5.8 In this connexion another concept of closure operators seems to be of interest, and it is playing an important rule when considering classical nearness structures. In the following we will give some notes in this direction.

Definition 5.9 We call a prehypernear space neartopological iff is satisfying (nt), i.e.

(nt) and imply.

Remark 5.10 We note that each surrounded prehypernear space is neartopological. On the other hand let be given a symmetric bounded hypertopological space, where in addition is satisfying (sym), i.e.

(sym) and imply,

then we define the corresponding neartopological hypernear space by setting: and, otherwise. By definition is automatically symmetric (see Definition 2.1. (iii)). At this point we mention the fact that symmetric hypernear spaces are always dense, which means is satisfying (d), i.e.

(d) and imply.

This can be seen as follows: Without restriction let be, implies

by hypothesis.

,

hence follows, and is valid according to (hn). But then

results, since is symmetric. Consequently, can be deduced according to (hn). Now, we point out that in some cases is round which means additionally satisfies (ron), i.e.

(ron) implies. (see also Remark 3.9.(2)).

A detailed description of this fact will be given in some forthcoming papers. Then evidently saturated spaces are round. Analogously, we can consider roundbounded symmetric hypertopological spaces, i.e. spaces, where is satisfying (rb), i.e.

(rd) implies.

Then the corresponding category is isomorphic to the full subcategory RNT-HN of HN, whose objects are the round neartopological hypernear spaces. As above defined we only verify the following two statements:

(i);

(ii).

To (i): Let be and, then by definition. Hence there exists with. Since is symmetric we get, and results.

To (ii): Without restriction let be. implies the existence of such

that. Consequently, , and

results.

In the saturated case then we can recover all symmetric hypertopological spaces.

6. Supernear and Paranear Spaces

Now, based on former advisements we are going to consider two special classes of hypernear spaces, which are being fundamental in the theory of topological extensions.

Definition 6.1 We call a bonded hypernear space a supernear space and denote by SN the corresponding full subcategory of HN.

Corollary 6.2 The category TOP of topological spaces and continuous maps is isomorphic to a full sub- category of SN.

Proof. According to Example 1.3. (v), Theorem 2.6, Theorem 4.4 and Definition 5.1 we only have to verify that is satisfying (hn). Now, let be, with, hence

.

For we have. But is valid. Since “−” is a topological closure oper-

ator we get, and consequently results.

Corollary 6.3 The category STOP of supertopological spaces and continuous maps is isomorphic to a sub- category of SN.

Proof. The reader is referred to Remark 3.7, Theorem 3.8 and Remark 4.2 respectively.

Remark 6.4 b-proximities (see Definition 3.10) are playing an important rule when considering topological extensions (see Remark 3.9). In this connexion we are now giving two special cases of them. First of all we call a b-proximity space a preLEADER space iff in addition satisfies (bp₅), i.e.

(bp₅) and with imply, where.

By pLESP we denote the corresponding full subcategory of b-PROX.

In the saturated case (if) LEADER proximity spaces then can be recovered as special objects.

Corollary 6.5 The category pLESP is isomorphic to a full subcategory of SN.

Proof. According to Example 1.3. (vi), Remark 3.11 and Theorem 3.13 respectively it remains to verify that satisfies (hn) and (bp₅) respectively.

To (hn):, and imply. We have to verify that

. So let be, hence, and consequently is valid. The inclusion

holds, because implies, hence, and

results, showing that is valid. According to (bp₅) we get, and the proposed inclusion holds.

To (bp₅): Conversely, let be and with, we have to verify.

By hypothesis is valid., since. Because

implies, leads us to the statement. According to (hn₁) we obtain

, and results by axiom (hn). Consequently is valid.

Remark 6.6 At this point we note that certain supernear spaces are in one-to-one correspondence to strict topological extensions which we study in a forthcoming paper. Here, we will examine the case if a symmetric topological extension is presumed (see Example 1.7. (ii)). In this connexion bunch-determined nearness and certain preLODATO spaces are playing an important role. Now, we will give the definition of a preLODATO space:

Definition 6.7 A preLEADER space is called a preLODATO space iff in addition satisfies the following axioms, i.e.

(bp₆) and imply or;

(bp₆) and imply;

(bp₆) and imply.

By pLOSP we denote the corresponding full subcategory of pLESP.

Remark 6.8 In the saturated case LODATO proximity spaces then can be recovered as special objects. More- over, we note that each b-supertopological space then can be regarded as special preLODATO space. A slight specialization lead us to the so-called LODATO space by adding the axiom (bp₉), i.e.

(bp₉) implies.

Once again, in the saturated case the two definitions coincide, and LODATO proximity spaces then can be recovered as special objects.

But in general the two definitions differ, and the reader is referred to Remark 3.9 in connexion with Remark 5.10. In a forthcoming paper we will show that the corresponding category LOSP of LODATO spaces can be re- garded as a full subcategory of SN, whose objects are symmetric. On the other hand nearness also leads us to a certain symmetric supernear space, hence we give the following definition.

Definition 6.9. A symmetric supernear space is called a paranear space and we denote by PN the corresponding full subcategory of SN.

Theorem 6.10. The category NEAR of nearness spaces and related maps is isomorphic to a full subcategory of PN.

Proof. According to Example 1.3. (ii) and Theorem 4.5 respectively it remains to verify that satisfies (hn) and the nearness axiom.

To (hn): Without restriction let be, and, hence

.

But, because for and we have, hence

is valid. Consequently results which shows. Since satisfies the

nearness axiom: we get, and results. Conversely, let be for. We have to verify. So let be, our goal is to show. By hypothesis we get

. But, since implies, hence

follows, and is valid, which shows. Consequently,

with is valid according to (is) of Definition 2.4.

Since M is dense (see Remark 5.10) we get according to (hn₁). But then follows by (hn), which concludes the proof.

Corollary 6.11. For a saturated paranear space the following statements are equivalent:

(i) is topological nearness;

(ii) is neartopological.

Proof. evident according to Remark 5.10.

“Relationship between important categories”

7. Topological Extensions and Their Corresponding Paranear Spaces

Taking into account Example 1.7.(ii), Remark 3.9, 6.6 and 6.8 respectively we will now consider the problem for finding a one-to-one correspondence between certain topological extensions and their related paranear spaces. In this connexion we point out that certain grill-spaces come into play.

Definition 7.1 Let be given a supernear space. For, is called a B-clan in iff it satisfies

(cla₁);

(cla₂) and imply.

Remark 7.2 For a supernear space and each with is a B-clan in.

Definitions 7.3 A supernear space respectively paranear space is called superclan space respectively paraclan space iff satisfies (cla), i.e.

(cla) and imply the existence of a B-clan in with.

Remark 7.4 In giving some examples we note that each surrounded supernear space is a superclan space, and each neartopological paranear space is a paraclan space. This is analogical valid for the spaces considered in 1.7.

Proof of Example 1.7. (ii)

First, we prove the equality of the corresponding closure operators. So, let be and, then by (tx₁) with, hence follows, which shows. Conversely, let, hence follows, which implies the existence of

with. But now, holds, because the presumed extension is sym-

metric. Consequently, follows, which shows that according to (tx₁). Alltogether, the equality now results. Secondly, it is easy to verify that fulfills the axioms for being a semihypernear space. N^e is symmetric, since for implies the existence of with

, hence follows. Now, implies,

since by supposition, hence symmetric. is a supernear space,

because and imply the existence of with

. implies, hence

,

consequently follows, which shows that is a paranearness space. It remains to prove N^e satisfies the axiom (cla). For let be, hence for some

. We set, consequently is the desired -clan in proving

that is a paraclan space.

Convention 7.5 We denote by SY-TEXT the full subcategory of TEXT, whose objects are the symmetric topological extensions and by CLA-PN the full subcategory of PN, whose objects are the paraclan spaces.

Theorem 7.6 Let SY-TEXT CLA-PN be defined by:

(a) For a SY-TEXT-object we put;

(b) for a TEXT-morphism we put.

Then: SY-TEXT CLA-PN is a functor.

Proof. We already know that the image of lies in CLA-PN. Now, let be a TEXT-morphism; it has to be shown that preserves B-near collections for each. Without restric-

tion let and, hence we can choose with.

Our goal is to verify the existence of such that. By hypothesis

we have, consequently results, since (f, g) is a TEXT-morphism

by assumption. Now, consider some, because, we have, which results in.

8. Strict Topological Extensions

Remark 8.1 In the previous section we have found a functor from SY-TEXT to CLA-PN. Now, we are going to introduce a related one in the opposite direction.

Lemma 8.2 Let be a paranear space. We set is a B-clan in for some, and for each we put:

where. (By convention if). Then is a topological closure operator.

Proof. We first note that, since for each. Let be a subset of and consider. Then implies, hence. Now, let be.

Then, , which implies. For arbitrary subsets we consider

an element such that. Then we have and. Choose

with and with. Because we get. On the

other hand, implies. At last, let be an element

of and suppose. Choose with. By assumption we have

, hence. Consequently there exists with But this im-

plies, and results, which leads us to a contradiction.

Theorem 8.3 For paranear spaces, let be a hn-map. Define a func- tion by setting for each:

Then the following statements are valid:

(1) is a continuous map from to;

(2) The composites and coincide, where denotes the function which assigns the -clan to each.

Proof. First, let be a -clan in. We will show that is a -clan in. It is easy to verify that, which satisfies (cla) in Definition 7.1. In order to establish (cla₁) we observe that by hypothesis. We will now verify that

(Note, that is a hn-map by assumption.) For any we have, hence

.

Since and we get, and all together we con-

clude that defines a -clan in. Consequently, results.

To (1): Let, and suppose. Then,

hence for some, which means. Since, we get

for some. Consequently results, which leads us to a contradiction, because is valid.

To (2): Let be an element of. We will prove the validity of. To this end, let

. Then, , hence, and consequently.

Thus, proving the inclusion. Since is maximal with re-

spect to and moreover, since by hypothesis

is a hn-map, we obtain the desired equality.

Theorem 8.4 We obtain a functor: CLA-PN toSY-TEXT by setting:

(a) for any paraclan space with and

;

(b) for any hn-map.

Proof. With respect to Corollary 6.2 it is straight forward to verify that is a topological closure operator on. We also have the topological closure operator on. Therefore we obtain topological spaces with -set, and is a continuous map, which can be seen as follows: Let for, we have to verify that. implies and for some by supposition. Consequently, follows which shows. To establish (tx₁), let be a subset of and suppose. Then we get, hence

which means that. Conversely, let be an element of

. Then by definition we have, and consequently. This implies, which means. To establish (tx₂), let be and suppose

. By definition we get, so that there exists a set with. But

follows. Since for some, we get, hence, because

satisfies (cla₂). But this is a contradiction, and thus is valid. In showing is

symmetric let x be an element of such that. We have to prove. By

hypothesis we have and moreover for some. Since

and N is symmetric we get with, hence follows according to (hn₁).

But is maximal with respect to, which means that coincides with. By

hypothesis is a hn-map, so that is continuous and bounded with respect to the given -sets and corresponding closure operators. It remains to prove that the following diagram commutes:

To this end let be an element of. We must show.

“”implies, which means, hence

.

Since is continuous we have and follows.

“”implies, hence follows and consequently

. Thus, , which means.

Finally, this establishes that the composition of hn-maps is preserved by G. At last we will show that the image of G also is contained in STR-TEXT, whose objects are the strict topological extensions. Consider and let be closed in with. Then, hence. We can find some such that. Now, for each we have, which implies, and therefore we conclude. On the other hand since, we have, hence, which put an end of this.

Theorem 8.5 Let: SY-TEXT CLA-PN and: CLA-PN SY-TEXT be the above defined func- tors. For each object of CLA-PN let denote the identity map

Then is natural equivalence from to the identity functor, i.e.

is a hn-map in both directions for each object, and the following diagram commutes for each hn-map:

Proof. The commutativity of the diagram is obvious, because of. It remains to prove that

is a hn-map in both directions. To fix the notation let be such that

.

It suffices to show that for each we have. To this end assume

, then there exists such that, hence. We

get and for some. Since N is symmetric, we obtain with

, hence. But implies, hence with.

Now results, which shows. Conversely, let. Since is a paraclan space we can choose a -clan in such that. In order to show we need to verify

(1);

(2) implies.

To (1): By definition of it suffices to establish. So let be an element of, hence follows which implies. But is B-clan in N, consequently we get.

To (2): Let A be an element of and D be an element of, hence. Since by hypothesis, we get and analogously as above we infer, which concludes the proof.

Remark 8.6 Making the theorem more transparent we claim that a paranear space is a paraclan space if it can be embedded in a topological space such that the B-near collections are characterized by the fact that the closures of its members meet in. Therefore this theorem generalize in one direction the Bentley- characterization of bunch-determined nearness spaces, in another the description of Doitchinov’s b-superto- pologies by compactly determined topological extensions and moreover the analogous existing correspondence respected to LODATO spaces involving the famous theorem of LODATO.

Corollary 8.7 If is separated that means satisfies (sep), i.e.

(sep) and imply, then is injective. Conversely, for a extension, where is a topological embedding and a -space, then is separated.

References