World Journal of Mechanics
Vol.2 No.3(2012), Article ID:20009,4 pages DOI:10.4236/wjm.2012.23020
An Analytical Approach for Degree Correlations in Complex Network
Uwado-shinmachi 5-4, Kawagoe-shi, Saitamaken 3500817, Japan
Email: coutakagi@mse.biglobe.ne.jp
Received April 10, 2012; revised May 15, 2012; accepted May 25, 2012
Keywords: Scale-Free Network; Degree Distribution; Degree Correlations; Power Law
ABSTRACT
We investigate correlations between neighbor degrees in the scale-free network. According to the empirical studies, it is known that the degree correlations exhibit nontrivial statistical behaviors. With an analytical approach, we show that the scale-freeness and one of statistical laws for degree correlations can be reproduced consistently in a unified framework. Our result would have its importance in understanding the mechanisms which generate the complex network.
1. Introduction
It is known that a diversity of complex networks includeing sociological, technological, and biological ones exhibit the scale-freeness [1-13]. These results pose us a problem about the origin of this feature and about mechanisms which produce such organized behavior in complex networks. Naturally it is considered that the complex networks are generated through processes in which nodes are correlated to each other. The experimental data which exhibits the organized and hierarchical structures enhances the importance of the node correlations in the complex networks [14-18]. Indeed the model based studies have shown that, in order to reproduce the network structure in the real world, additional ingredients other than the simple rule such as the preferential attachment are required in the simulation [11-18].
Recent empirical studies have revealed that there exist ordered structures of node correlations in real world complex networks. One example of these structures would be given by fractality which characterize geometrical structures of various complex systems, in which they show the self-similarity on all length scales [14,15]. On the other hand, more primitive relation between nodes would be represented by a joint probability  for two neighbor nodes of degree
for two neighbor nodes of degree 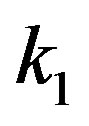 and
and 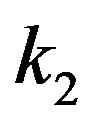 connected by an edge. In this paper, we investigate this basic statistics, the degree-degree correlation in the complex network. One characteristic feature of
connected by an edge. In this paper, we investigate this basic statistics, the degree-degree correlation in the complex network. One characteristic feature of 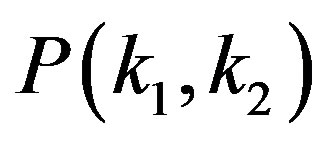 can be quantified by
can be quantified by 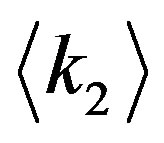 for each fixed
for each fixed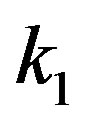 , the average of the neighbor degrees for a given value of
, the average of the neighbor degrees for a given value of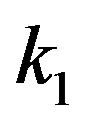 . It has been reported that the
. It has been reported that the 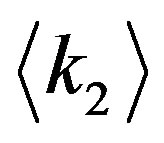 profile is fitted with a power law
profile is fitted with a power law
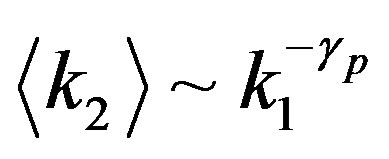 (1)
(1)
with a constant 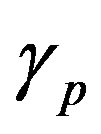 for the interaction and regulatory networks of proteins [16]. The same tendency is also confirmed with the Internet, another typical example of the complex networks [17].
for the interaction and regulatory networks of proteins [16]. The same tendency is also confirmed with the Internet, another typical example of the complex networks [17].
The ubiquity of scale-free networks in the real world is one of the fundamental issues in the complex network studies. It would suggest that there exist common mechanisms which underlie complex networks. Then one of our final goals is to obtain a theory which can describe various complex networks and their statistical behaviors in a unified framework. For this aim, we have introduced in the recent study an analytical approach in which conditions required for the scale-free degree distribution are considered [19]. Due to the ubiquity of the scale-freeness, it is expected that the analytical conditions are given by those which are independent to specific systems and common to a wide variety of networks. Indeed, it has been shown that the power law distribution can be obtained without introducing conditions except for general ones. In this paper we extend the framework given in this previous study and show that it gives the degree correlation which corresponds to the experimental measurement represented by Equation (1).
2. Framework for P(k1, k2)
By using a framework introduced in the recent study [19], we investigate the degree correlation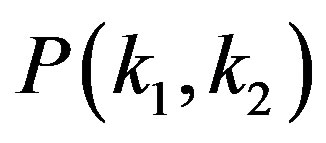 . At first we normalize the pair of degrees
. At first we normalize the pair of degrees 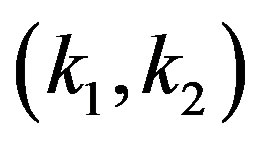 and introduce variables
and introduce variables  which take their values respectively on the finite interval
which take their values respectively on the finite interval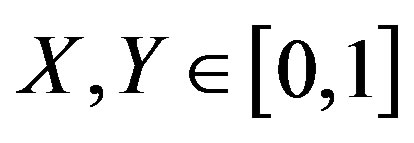 . For example, relations between
. For example, relations between 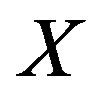 and
and 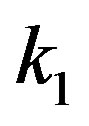 are given by
are given by
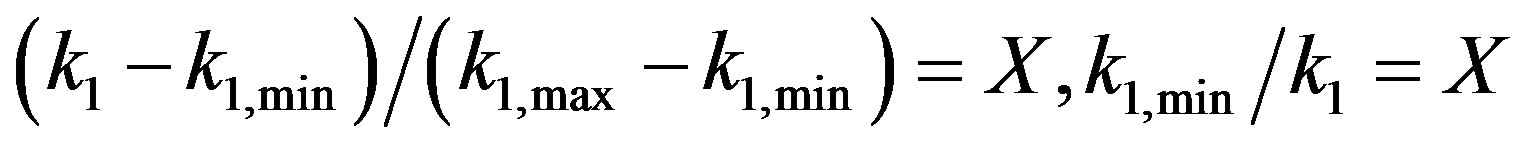 (2)
(2)
where the former example is taken for cases such as 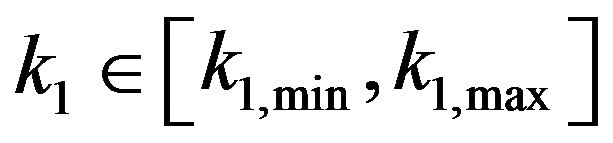 and the latter for
and the latter for . These normalizations are summarized by the expression
. These normalizations are summarized by the expression
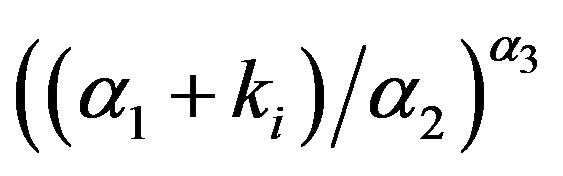 (3)
(3)
with constants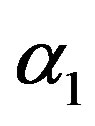 ,
,  , and
, and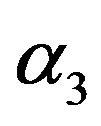 . Under the transforms between
. Under the transforms between 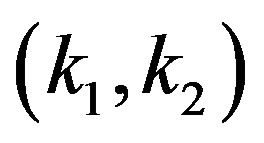 and (X, Y) given by the expression (3), the probability
and (X, Y) given by the expression (3), the probability  is represented by
is represented by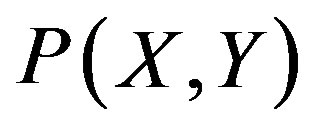 .
.
In this approach we take an analytical expression of  in the expanded form and consider the condition required for this function. Then, for variables (X, Y) and the probability
in the expanded form and consider the condition required for this function. Then, for variables (X, Y) and the probability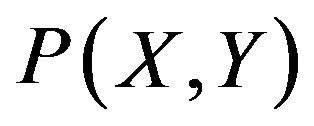 , we require conditions that
, we require conditions that  and
and  are continuous and that
are continuous and that 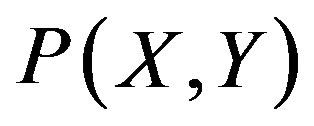 is given by the smooth function with respect to
is given by the smooth function with respect to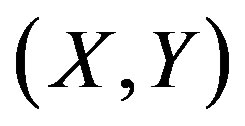 . Also in order to investigate the scaling behavior of
. Also in order to investigate the scaling behavior of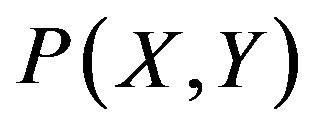 , we take
, we take 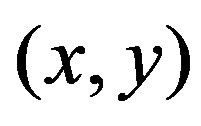
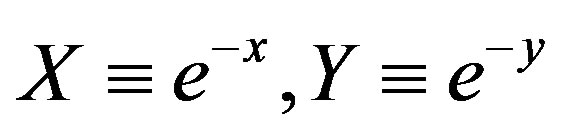 (4)
(4)
where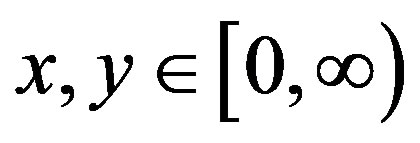 . Because
. Because 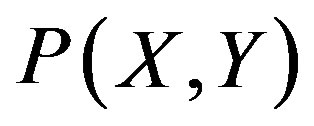 is a positive function which takes its value in the finite interval
is a positive function which takes its value in the finite interval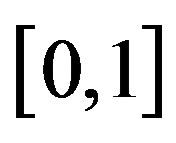 , the analytical representation of
, the analytical representation of  as the function of
as the function of  is given in the form
is given in the form
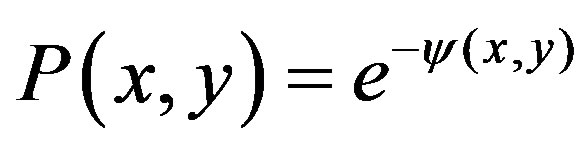 (5)
(5)
with the scaling function 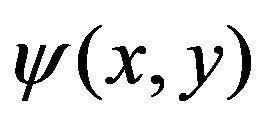
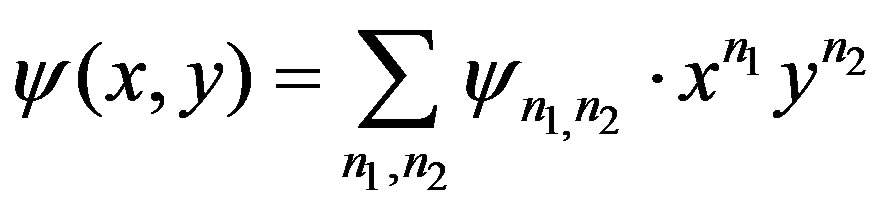 (6)
(6)
where  are constant coefficients and
are constant coefficients and 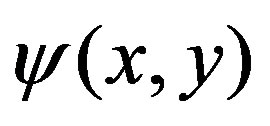 is taken to satisfy the normalization
is taken to satisfy the normalization
 (7)
(7)
For the single variable case, 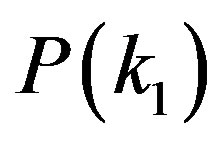 is transformed to
is transformed to 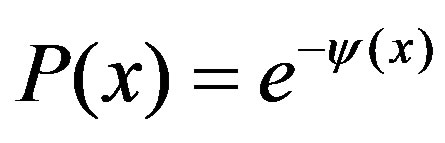 with
with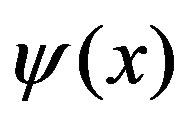 , the expansion of x. If
, the expansion of x. If 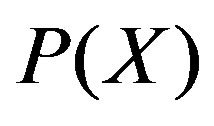 is scale-free and given in the power law
is scale-free and given in the power law 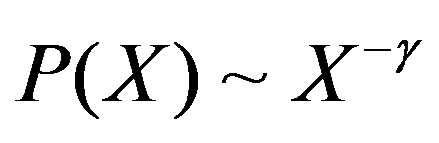 with a constant
with a constant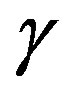 ,
, 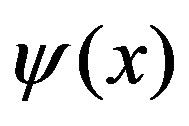 is given by the first order expansion which satisfies
is given by the first order expansion which satisfies
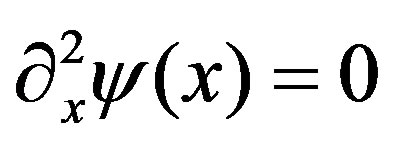 (8)
(8)
Although, according to the result given in the recent study [19], the converse fact has been shown that the condition (8) is derived without introducing special conditions except for the continuous conditions for 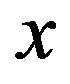 and
and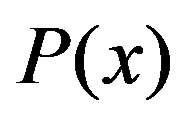 . The point of this result is that this condition (8) is obtained with using the identical relations which the continuous distribution function satisfies generally. Then this condition is required for arbitrary variables such as
. The point of this result is that this condition (8) is obtained with using the identical relations which the continuous distribution function satisfies generally. Then this condition is required for arbitrary variables such as 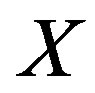 and
and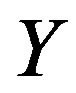 .
.
3. The Representation of P(k1, k2)
Extending the analysis with the single variable given in the reference [19], we can show that 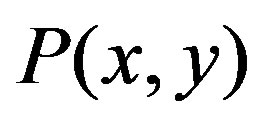 representation is uniquely determined in our framework. At first we take a conditional probability
representation is uniquely determined in our framework. At first we take a conditional probability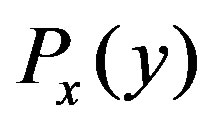 , the function with respect to
, the function with respect to 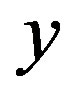 for each fixed value of
for each fixed value of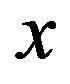 , defined as
, defined as
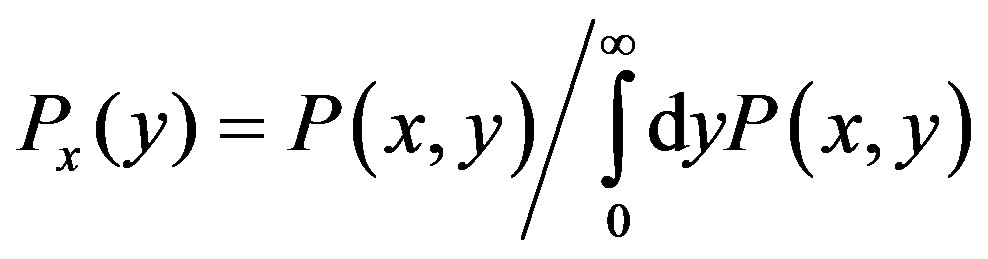 (9)
(9)
It apparently satisfies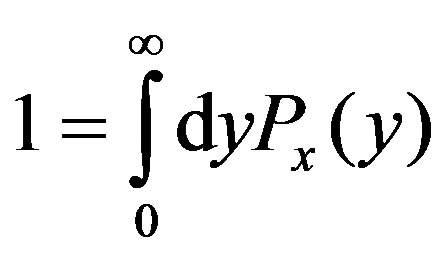 .
.
For convenience of calculation, we introduce the cumulative distribution of 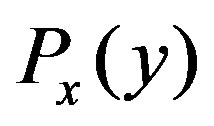 by
by
 (10)
(10)
Then we can represent it as
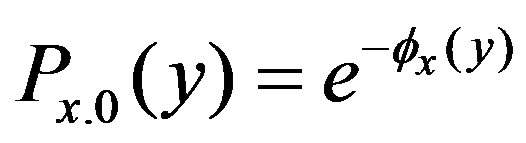 (11)
(11)
with an expansion
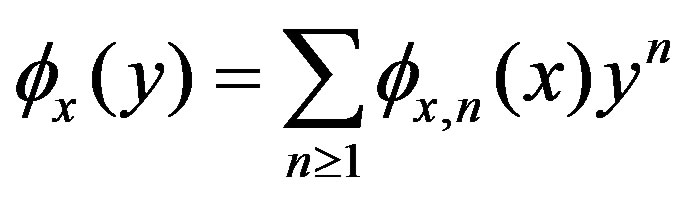 (12)
(12)
where 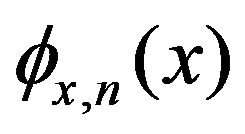 is given by the other expansion of
is given by the other expansion of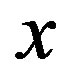 . According to these definitions,
. According to these definitions, 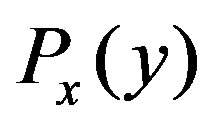 is given by
is given by
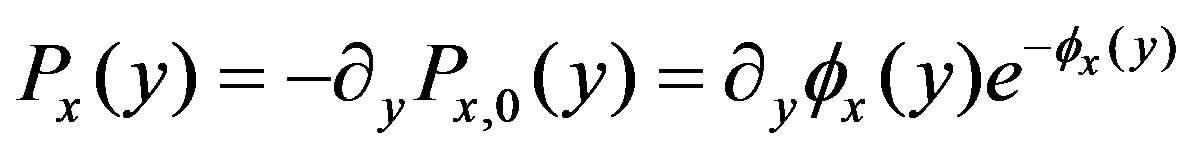 (13)
(13)
Applying the condition (8), it is required that
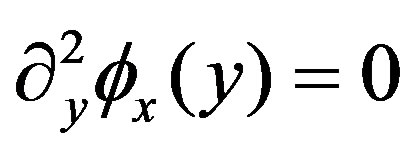 (14)
(14)
and
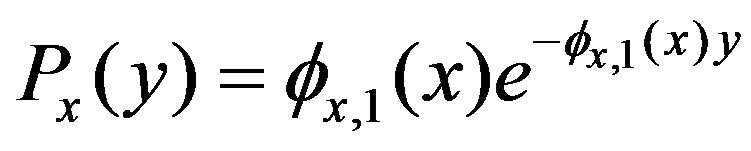 (15)
(15)
For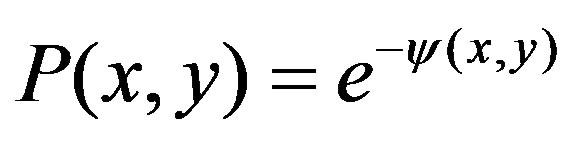 , we can show that the same condition (11) requires that
, we can show that the same condition (11) requires that
 (16)
(16)
If we take the conditional probability  with respect to x, then from the condition (11) it is required to have the form
with respect to x, then from the condition (11) it is required to have the form
 (17)
(17)
Introducing  and
and 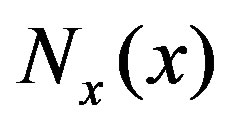 by
by
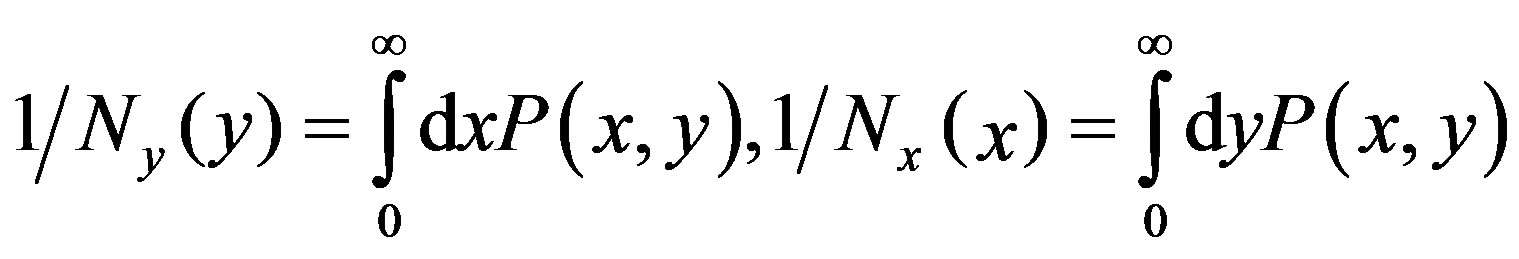 (18)
(18)
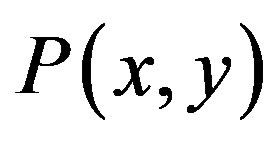 is represented by the equivalent two forms
is represented by the equivalent two forms
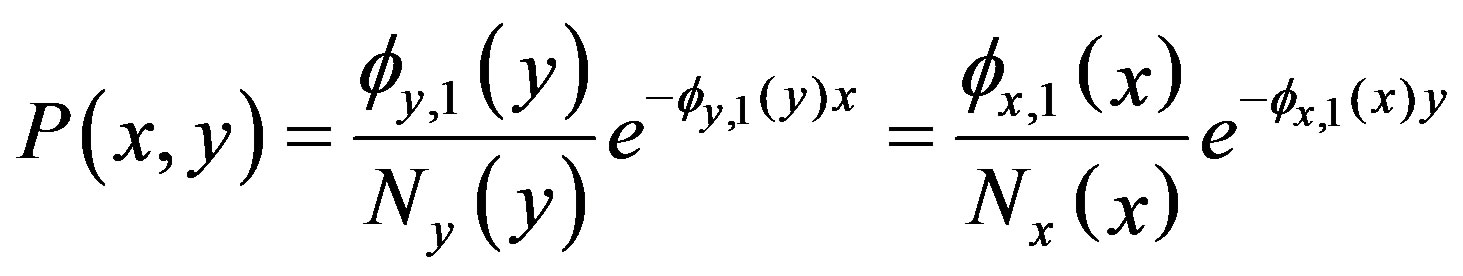 (19)
(19)
and we obtain the identical relation
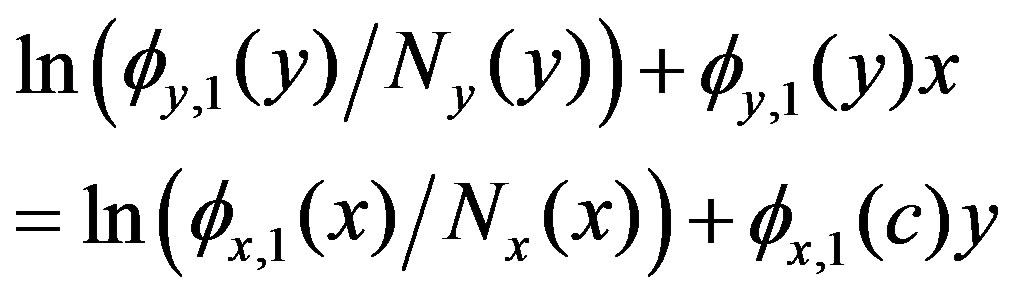 (20)
(20)
Because 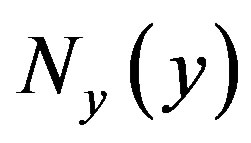 and
and  are independent to x and y respectively, the condition (16) for
are independent to x and y respectively, the condition (16) for  is given by comparing each side of Equation (20). Thus we obtain the
is given by comparing each side of Equation (20). Thus we obtain the 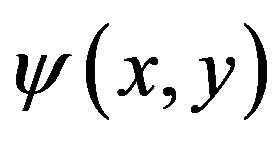 representation
representation
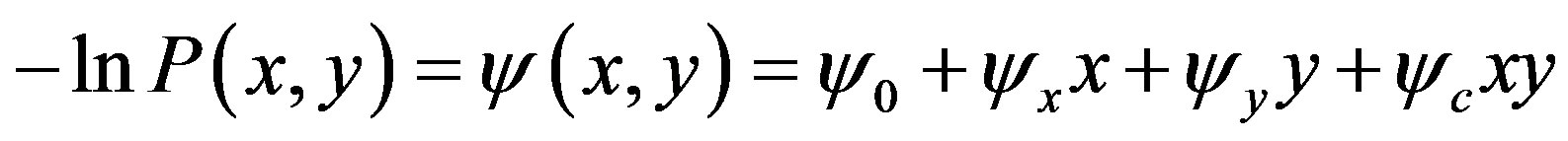 (21)
(21)
with constants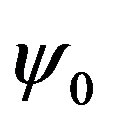 ,
, 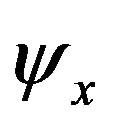 ,
, 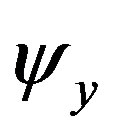 and
and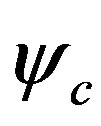 .
.
4. Degree Correlations in Real World Networks
In order to confirm our result in the previous section, we give a comparison to the experimental measurement of the real world networks. For the degree-degree correlations 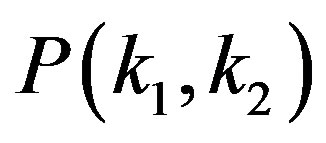 given from Equation (21), we calculate
given from Equation (21), we calculate 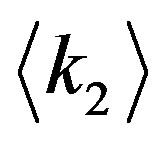 for each fixed value of
for each fixed value of 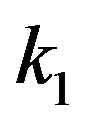 and compare it to the experimental representation (1).
and compare it to the experimental representation (1).
At first, with using the expression (3) for the normalization of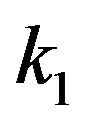 , the correspondence between
, the correspondence between  and
and 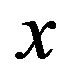 is given by
is given by
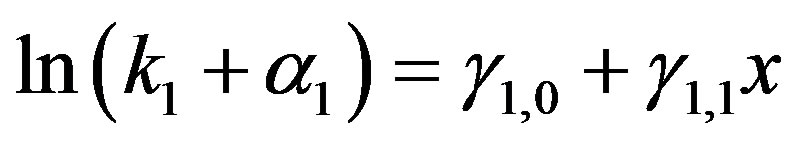 (22)
(22)
with constants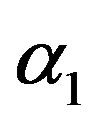 ,
, 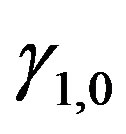 , and
, and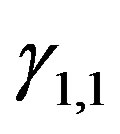 . While, from the representation (21), the transform between
. While, from the representation (21), the transform between 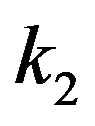 and
and 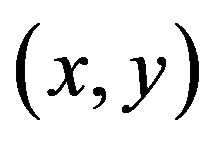 is generally given by
is generally given by
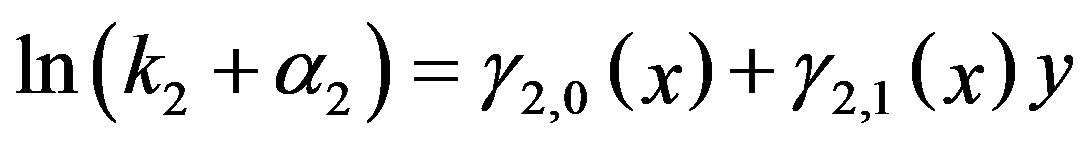 (23)
(23)
where 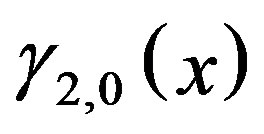 and
and 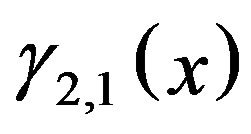 are given by linear equations of
are given by linear equations of 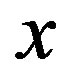 and
and  is a constant.
is a constant.
Then 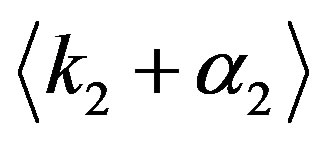 is given by
is given by
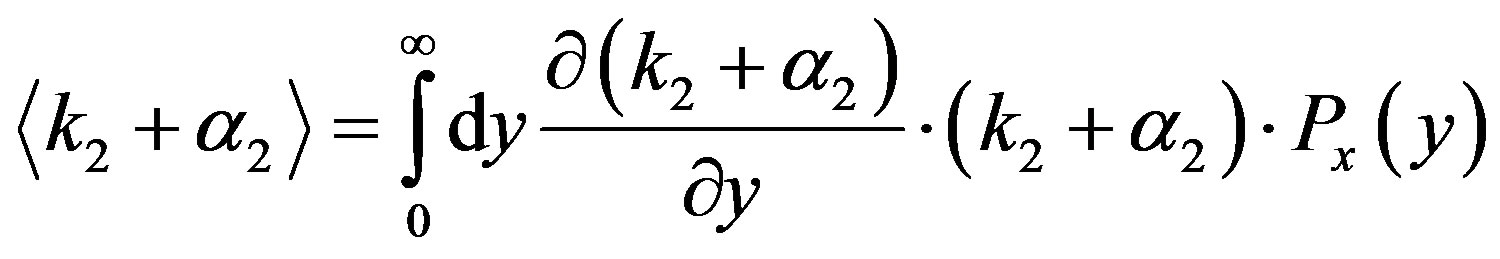 (24)
(24)
Using the representation of 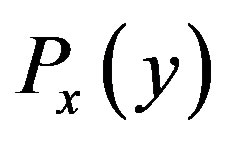 given by Equation (9) and Equation (21), the average is given by
given by Equation (9) and Equation (21), the average is given by
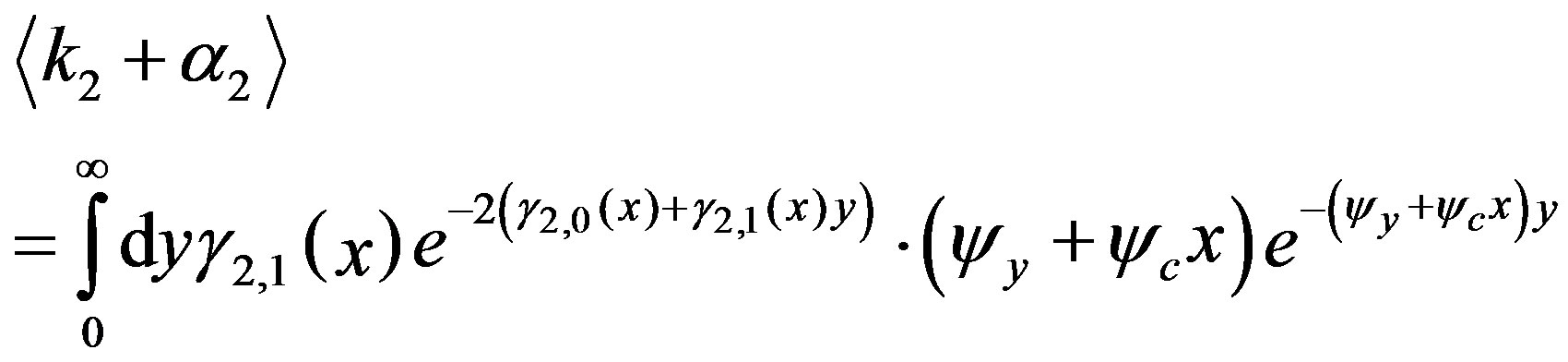 (25)
(25)
with constants 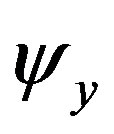 and
and 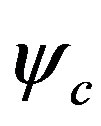 and this is calculated as
and this is calculated as
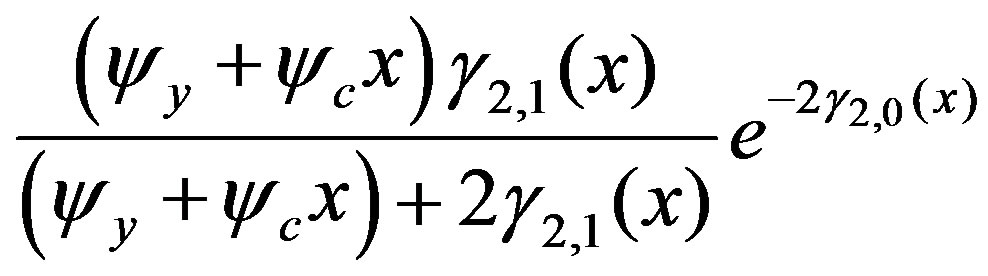
 (26)
(26)
Because 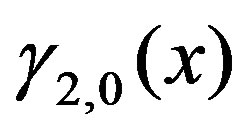 and
and 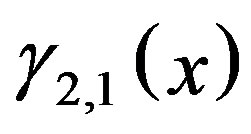 are represented by the linear equations of
are represented by the linear equations of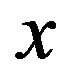 , the first term in the above equation is estimated as
, the first term in the above equation is estimated as
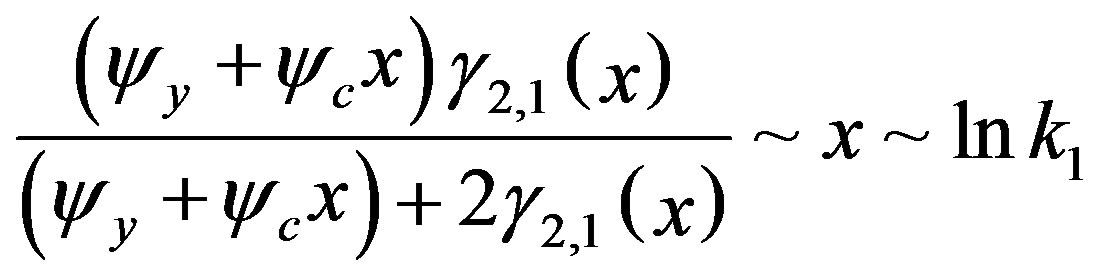 (27)
(27)
for . Furthermore, using the approximation
. Furthermore, using the approximation 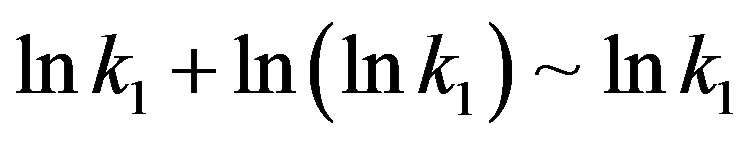 , Equation (26) is approximated by a power law
, Equation (26) is approximated by a power law
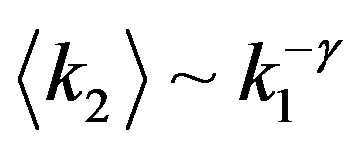 (28)
(28)
with a constant 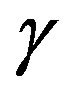 for a large
for a large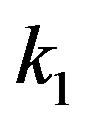 . Then behavior of
. Then behavior of 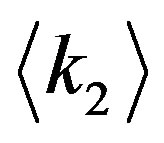 tail for a large
tail for a large 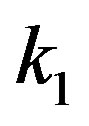 agrees to the experimental representation (1).
agrees to the experimental representation (1).
5. Discussions
As we have mentioned in the introduction, our final goal is to give a description of the complex network in a unified framework. For this aim, it is required to obtain a theory which explains the organized structure of the complex network and allows to deal with different networks. In this final section, we discuss this issue.
In this paper we have shown that the extension of the framework introduced in the recent study [19] consistently produces the degree correlation in the form which corresponds to the experimental data. Applying the analytical condition (8) for the single variable distribution to the joint probability, we obtain a unique representation for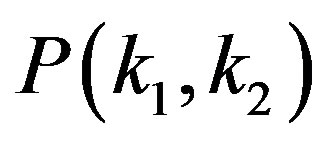 , the distribution of the neighbor degrees. We should notice that some properties of the complex network, the scale-free distribution and the degree correlation represented by Equation (1), can be derived from the same condition (8). It would suggest that the rules which generate scale-free networks and their correlated structures can be described in a unified framework.
, the distribution of the neighbor degrees. We should notice that some properties of the complex network, the scale-free distribution and the degree correlation represented by Equation (1), can be derived from the same condition (8). It would suggest that the rules which generate scale-free networks and their correlated structures can be described in a unified framework.
Also we should notice that our framework which gives the condition (8) does not depend on the specific system. Then we can apply our results straightforwardly to various complex networks such as the protein networks and the Internet. Then our result would provide a clue to understand the mechanism which underlies various types of complex networks.
Although, for our final goal, further investigations should be required. At first we should take into account some exceptional cases for which we can not apply our representation. An example is given by a random network, in which distributions take forms such as the Gaussian or the Poisson distributions. Then it would be required for us to describe explicitly the difference between our framework and these random systems. Also we should notice that the condition (8) is derived under the assumption that the variable is continuous. However some variables such as the degree take only the discrete number. We will deal with issues such as above in the future works.
REFERENCES
- A.-L. Barabási and R. Albert, “Emergence of Scaling in Random Networks,” Science, Vol. 286, No. 5439, 1999, pp. 509-512. doi:10.1126/science.286.5439.509
- A. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, R. Stata, A. Tomkins and J. Wiener, “Graph Structure in the Web,” Computer Networks, Vol. 33, No. 1-6, 2000, pp. 309-320. doi:10.1016/S1389-1286(00)00083-9
- M. Faloutsos, P. Faloutsos and C. Faloutsos, “On PowerLaw Relationships of the Internet Topology,” ACM SIGCOMM Computer Communication Review, Vol. 29, No. 4, 1999, pp. 251-262. doi:10.1145/316194.316229
- S. N. Dorogovtsev and J. F. F. Mendes, “Evolution of Networks,” Advances in Physics, Vol. 51 No. 4, 2002, pp. 1079-1187. doi:10.1080/00018730110112519
- R. Albert and A.-L. Barabási, “Statistical Mechanics of Complex Networks,” Reviews of Modern Physics, Vol. 74, No. 1, 2002, pp. 47-97. doi:10.1103/RevModPhys.74.47
- M. E. J. Newman, “The Structure and Function of Complex Networks,” SIAM Review, Vol. 45, No. 2, 2003, pp. 167-256 doi:10.1137/S003614450342480
- R. Albert, H. Jeong and A.-L. Barabási, “Internet: Diameter of the World-Wide Web,” Nature, Vol. 401, No. 6749, 1999, pp. 130-131. doi:10.1038/43601
- M. E. J. Newman, “Scientific Collaboration Networks. I. Network Construction and Fundamental Results,” Physical Review E, Vol. 64, No. 1, 2001, pp. 1-8. doi:10.1103/PhysRevE.64.016131
- H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai and A.-L. Barabási, “The Large-Scale Organization of Metabolic Networks,” Nature, Vol. 407, No. 6804, 2000, pp. 651- 654. doi:10.1038/35036627
- H. Jeong, S. Mason, A.-L. Barabási and Z. N. Oltvai, “Lethality and Centrality in Protein Networks,” Nature, Vol. 411, No. 6833, 2001, pp. 41-42. doi:10.1038/35075138
- A.-L. Barabási, R. Albert and H. Jeong, “Mean-Field Theory for Scale-Free Random Networks,” Physica A, Vol. 272, No. 1-2, 1999, pp. 173-187. doi:10.1016/S0378-4371(99)00291-5
- P. L. Krapivsky, S. Redner and F. Leyvraz, “Connectivity of Growing Random Networks,” Physical Review Letters, Vol. 85, No. 21, 2000, pp. 4629-4632. doi:10.1103/PhysRevLett.85.4629
- S. N. Dorogovtsev, J. F. F. Mendes and A. N. Samukhin, “Structure of Growing Networks with Preferential Linking,” Physical Review Letters, Vol. 85, No. 21, 2000, pp. 4633-4636. doi:10.1103/PhysRevLett.85.4633
- C. Song, S. Havlin and H. A. Makse, “Self-Similarity of Complex Networks,” Nature, Vol. 433, No. 7024, 2005, pp. 392-395. doi:10.1038/nature03248
- C. Song, S. Havlin and H. A. Makse, “Origins of Fractality in the Growth of Complex Networks,” Nature Physics, Vol. 2, 2006, pp. 275-281. doi:10.1038/nphys266
- S. Maslov and K. Sneppen, “Specificity and Stability in Topology of Protein Networks,” Science, Vol. 296 no. 5569 2002, pp. 910-913. doi:10.1126/science.1065103
- R. Pastor-Satorras A. Vázquez and A. Vespignani, “Dynamical and Correlation Properties of the Internet,” Physical Review Letters, Vol. 87, No. 25, 2001, p. 258701. doi:10.1103/PhysRevLett.87.258701
- M. E. J. Newman, “Assortative Mixing in Networks,” Physical Review Letters, Vol. 89, No. 20, 2002, p. 208701. doi:10.1103/PhysRevLett.89.208701
- K. Takagi, “Scale Free Distribution in an Analytical Approach,” Physica A, Vol. 389, No. 10, 2010, pp. 2143- 2146. doi:10.1016/j.physa.2010.01.034

