World Journal of Condensed Matter Physics
Vol.4 No.1(2014), Article ID:42850,9 pages DOI:10.4236/wjcmp.2014.41006
Thermal Conductivity of Superconducting MgB2
![]()
1Theory Group, School of Environmental Sciences, Jawaharlal Nehru University, New Delhi, India; 2Present Address: B-208 Sushant Lok I, Gurgaon, Haryana, India; 3Physics Department, Miranda House, University of Delhi, Delhi, India.
Email: gulshanpmalik@yahoo.com, malik@mail.jnu.ac.in, malik_usha@hotmail.com
Copyright © 2014 G. P. Malik, Usha Malik. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property G. P. Malik, Usha Malik. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 15th, 2013; revised December 24th, 2013; accepted January 9th, 2014
KEYWORDS
MgB2; Thermal Conductivity; Multiple Gaps; Generalized-BCS, Geilikman, and Geilikman-Kresin Equations; Two-Phonon Exchange Mechanism; Cooper Pairs with Different Binding Energies
ABSTRACT
Employing the Geilikman-Kresin (GK) theory, we address the experimental data obtained by Bauer et al., and by Schneider et al., on the thermal conductivity (κ) of superconducting MgB2. The two gaps of this compound have qualitatively been understood via the well-known Suhl, Matthias, and Walker’s (SMW) approach to multigap superconductivity. Since this approach is based on one-phonon exchange mechanism for the formation of Cooper pairs, it cannot give a quantitative account of the values of Tc and the multiple gaps that characterize MgB2 and other high-Tc superconductors (SCs). Despite this fact and some rather ambiguous features, it has been pointed out in a recent critical review by Malik and Llano (ML) that the SMW approach provides an important clue to deal with an SC the two gaps of which close at the same Tc: consider the possibility of the interaction parameters in the theory to be temperature-dependent. Guided by this clue, ML gave a complete summary of parameters that quantitatively account for the Tc and the gaps of MgB2 via the generalized BCS equations (GBCSEs). GBCSEs which we recall, invoke multi-phonon exchange mechanism for the formation of Cooper pairs and multiple Debye temperatures to deal with composite SCs. The parameter-values given in ML are used here to calculate the temperature-dependent gaps, which are an essential input for the GK theory. Notable features of this work are: 1)  is calculated for both—the scenario in which the two gaps of MgB2 close/do not close at the same temperature whence it is found that 2) the latter scenario yields results in better agreement with experiment.
is calculated for both—the scenario in which the two gaps of MgB2 close/do not close at the same temperature whence it is found that 2) the latter scenario yields results in better agreement with experiment.
1. Introduction
Thermal conductivity (κ) of a superconductor (SC) is an important parameter from the point of view of applications; additionally, it helps in the theoretical understanding of the superconducting state [1]. An appreciation of the latter follows by recalling that: 1) in the kinetic theory, κ is proportional to the following properties of the heat carriers: a) number density, b) specific heat and c) mean free path (MFP); this is so regardless of whether the system is in the normal or the superconducting state. A nontrivial statement about MFP in any system at any temperature T is that it has the same value for both the normal and the superconducting states [2]. This, indeed, is not so for the other two properties. 2) The feature that distinguishes the superconducting state from the normal state is that the former is characterized by the existence of a temperature-dependent gap ∆(T) which is zero for the latter state. 3) The increase in ∆(T)—from zero at T = Tc to its maximum value at T = 0—is synonymous with a similar increase in the number of density of Cooper pairs (CPs) and hence with a decrease in the number density of heat carriers because CPs have zero entropy.
The existence of a gap in an SC at any T thus profoundly affects (lowers) both, the number density of the heat carriers (the unpaired electrons) and their specific heat. If κ of an SC at any T does not have a value as low as one might expect on these grounds, it is so because the lower the T is, the greater the MFP is. There is another feature that affects κ: heat is transported not only by electrons, but also by phonons—the quanta of lattice vibrations. The determination of κ due to any of these carriers requires the solution of a Boltzmann equation taking into account the nature of the dominant scattering processes appropriate for a given sample. If one is dealing with a composite superconductor (CS), there are additional complicating factors. Calculation of κ(T) of a CS is thus a rather formidable problem; we refer the reader to the lucid review by Uher [1] for its further elaboration.
The basic equations that yield the thermal conductivity of an SC based on the BCS theory [3] were given by Geilikman (G) [4], and by Geilikman and Kresin (GK) [5]. While the equation given by G determines κes, the electronic thermal conductivity of a simple superconductor when the scattering of electrons by impurities is the dominant process, the equation given by GK determines κgs, the thermal conductivity due to phonons when phononelectron scattering dominates. Not surprisingly, one finds that an application of these equations requires knowledge of ∆(T) of the SC for all T ≤ Tc. We note that equations similar to the G and the GK equations were also derived by Bardeen, Rickayzen and Tewordt (BRT) [6].
In this paper, we address the experimental data on the thermal conductivity of MgB2 obtained by Bauer (B) et al. [7], and by Schneider (S) et al. [8], in an approach that supplements the G [4] and the GK [5] equations by the recently derived generalized BCS equations (GBCSEs) [9]. Indeed, each of the groups [7,8] that obtained the said data also carried out a similar study based on the G and GK/BRT equations. Analyses of the data in these papers, however, were carried out without a detailed knowledge of the T-variation of the two gaps that characterize MgB2. Employing GBCSEs to calculate the values of these gaps for , we attempt here to shed light on their role, individually and collectively, in determining the total thermal conductivity of the compound. We note that in the earlier work [10-12] in which GBCSEs were used for a variety of high-temperature superconductors (HTSCs), the gap-values were calculated only at T = 0.
, we attempt here to shed light on their role, individually and collectively, in determining the total thermal conductivity of the compound. We note that in the earlier work [10-12] in which GBCSEs were used for a variety of high-temperature superconductors (HTSCs), the gap-values were calculated only at T = 0.
An experimental feature of MgB2 as reported by, e.g., Iavarone et al. [13] is that its two gaps close at the same temperature (~40 K). This is a situation that was envisaged by Suhl, Matthias, and Walker (SMW) [14] in a seminal paper. Partly for this reason and partly because of a lack of an alternative framework, multi-gap superconductivity has been understood solely via the SMW approach for about five decades now. It is therefore natural to ask: why can’t one use it to address the Tc and the gap-values of the high-Tc SC (HTSC) MgB2? Since the approach was originally given in the context of transition elements, it can only be adapted for composite SCs such as MgB2 which has no d-electrons. Such attempts have of course been made. Thus, making out a case for going beyond even the Eliashberg superconductivity, Liu et al. [15] were led to attribute the existence of the two gaps in MgB2 to the multiple band structure of its Fermi surface that brings into play different phonon modes; in particular, based on density-functional calculations invoking twophonon exchange mechanism they arrived at the value of  (clean limit) for the effective electron-phonon coupling constant which, they concluded, “is arguably consistent with the measured Tc of nearly 40 K.” In another appeal to the SMW approach in the context of MgB2, Choi et al. [16] invoked a qualitative picture similar to that of [15]. In this paper [16] the multiple gaps and Tc of MgB2 were attributed to the existence of two separate populations of electrons—nicknamed “red” and “blue,” leading them to note: “Stated differently, electrons on different parts of the Fermi surface form pairs with different binding energies.”
(clean limit) for the effective electron-phonon coupling constant which, they concluded, “is arguably consistent with the measured Tc of nearly 40 K.” In another appeal to the SMW approach in the context of MgB2, Choi et al. [16] invoked a qualitative picture similar to that of [15]. In this paper [16] the multiple gaps and Tc of MgB2 were attributed to the existence of two separate populations of electrons—nicknamed “red” and “blue,” leading them to note: “Stated differently, electrons on different parts of the Fermi surface form pairs with different binding energies.”
Notwithstanding the above developments, the SMW approach has till now not led to a framework in which the T-dependent gaps and Tc of an HTSC may be calculated. However, it seems interesting that it should have led to such concepts as two-phonon exchange mechanism [15] and CPs with different binding energies [16]. Further, in a recent critical review [17] of the SMW approach, it has been pointed out that it gives yet another clue to deal with an SC the two gaps of which close at the same Tc, the clue being: consider also the possibility of the interaction parameters in the theory to be T-dependent. These are precisely the concepts that are manifestly incorporated in the Bethe-Salpeter equation (BSE)-based approach that led to GBCSEs (Approach 2 hereafter); this approach has already been shown to deal quantitatively with the multiple gaps and Tcs of a variety of HTSCs with a measure of success [10-12]. It is worth noting that each interaction parameter in Approach 2 satisfies the Bogoliubov constraint for the BCS theory given by
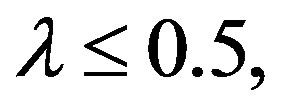 (1)
(1)
as discussed in [18].
The paper is organized as follows. In the next section, we give an account of GBCSEs and the G and the GK equations which form our framework. Since it was reported in [13] that both the gaps of MgB2 close at about 40 K, we consider in Section 3 the experimental data of both the B [7] and the S [8] groups in this scenario (Scenario 1). Additionally, for reasons spelled out below, we use as input the T-dependent gap values for the G and GK equations when the two gaps of MgB2 close at different temperatures (Scenario 2). Interestingly, it is found that whereas both the scenarios lead to almost indistinguishable results for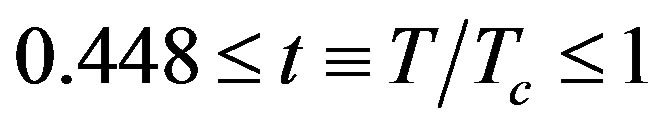 , the latter scenario yields results in better agreement with experiment for t < 0.448. To avoid repetition, we present here the results of our calculations pertaining to the data of only B’s group. Our findings pertaining to the data of the other group are of course summarized. The final section sums up our findings.
, the latter scenario yields results in better agreement with experiment for t < 0.448. To avoid repetition, we present here the results of our calculations pertaining to the data of only B’s group. Our findings pertaining to the data of the other group are of course summarized. The final section sums up our findings.
2. Framework
Our framework has three constituents. The first of these is concerned with calculating the values of ∆1(T) and ∆2(T) of MgB2 for all 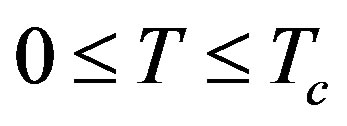 via GBCSEs in both the scenarios mentioned above. We first deal with Scenario 2 in which the interaction parameters are T-independent and recall that the BCS equation for ∆(T) for a simple SC is:
via GBCSEs in both the scenarios mentioned above. We first deal with Scenario 2 in which the interaction parameters are T-independent and recall that the BCS equation for ∆(T) for a simple SC is:
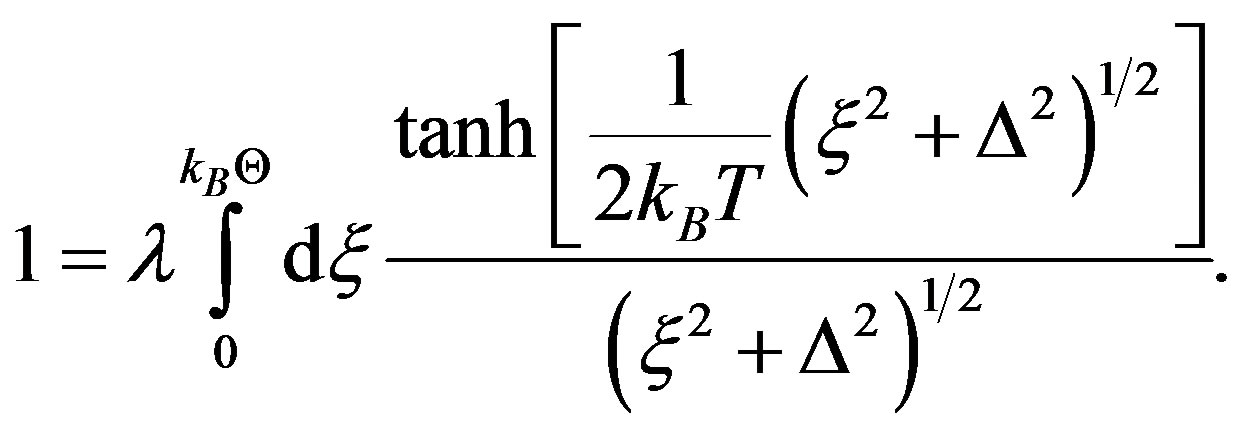 (2)
(2)
The GBCSE equivalent to (2) is [9,19]:
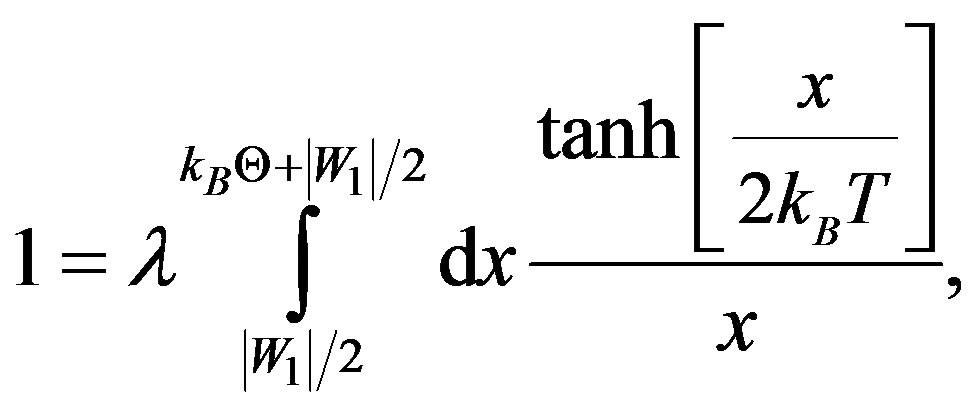 (3)
(3)
or
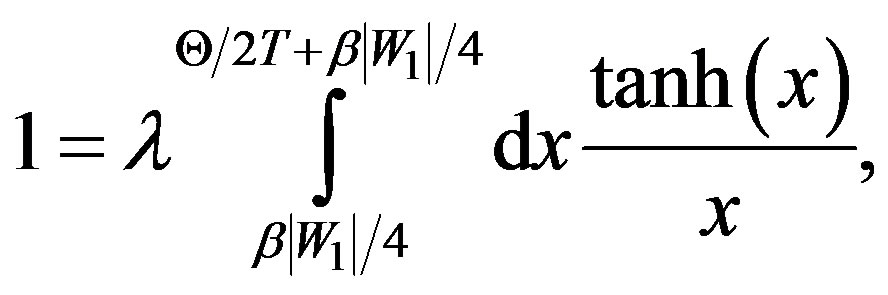 (3a)
(3a)
where β = 1/kBT, kB being the Boltzmann constant, Θ the Debye temperature, and 2|W1| is the binding energy of a CP that is bound via one-phonon exchanges (recall that the energy required to break a CP is 2∆). Note that putting W1 = 0 in (3) or ∆ = 0 in (2) yields the familiar BCS equation for Tc of the SC. This already suggests a connection between W and ∆. Further, it is readily seen that when T = 0 (tanh = 1) and λ→0, both (2) and (3) yield: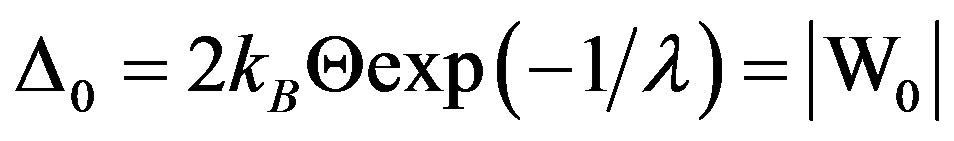 .
.
The generalized version of (3) when CPs in a CS are bound via two-phonon exchanges is [9]:
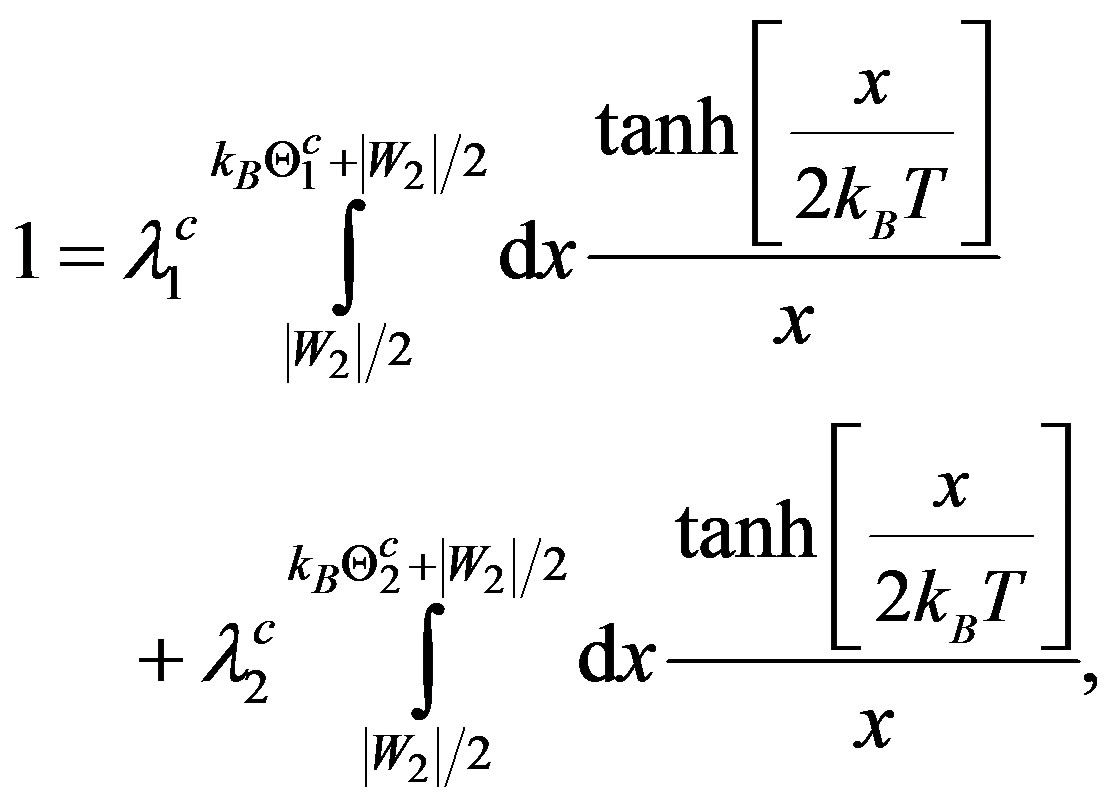 (4)
(4)
or
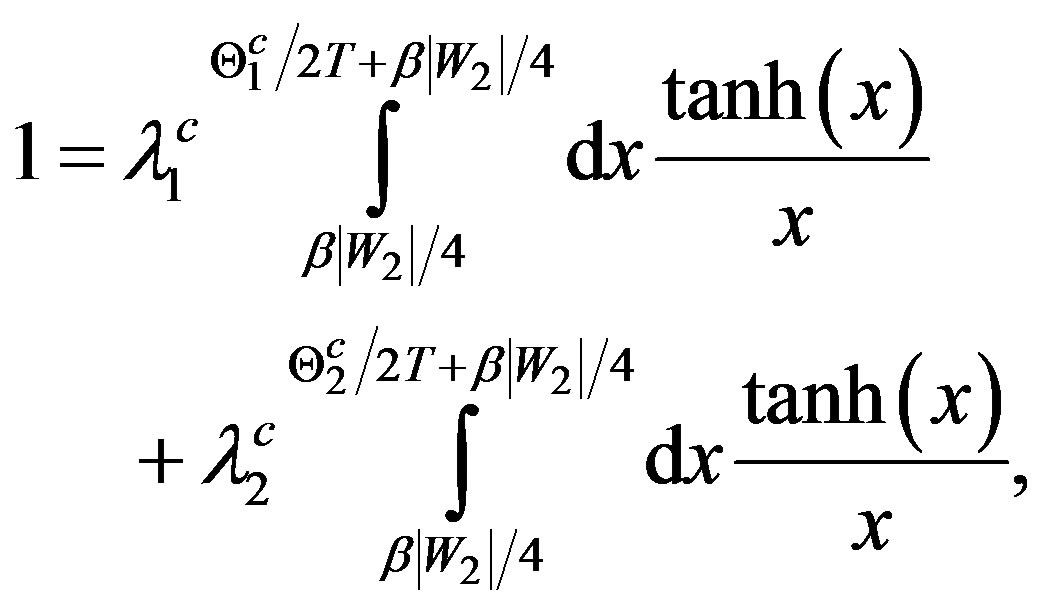 (4a)
(4a)
where 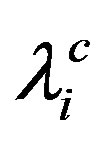 is the interaction parameter due to the ith species of ions in the CS, to be distinguished from λi, which denotes the interaction parameter of the same species in its free state; a similar distinction applies to
is the interaction parameter due to the ith species of ions in the CS, to be distinguished from λi, which denotes the interaction parameter of the same species in its free state; a similar distinction applies to  and Θi; 2|W2| is the binding energy of a CP bound via two phonon exchanges. The equation for Tc of the CS in this case follows by putting W2 = 0 in (4a):
and Θi; 2|W2| is the binding energy of a CP bound via two phonon exchanges. The equation for Tc of the CS in this case follows by putting W2 = 0 in (4a):
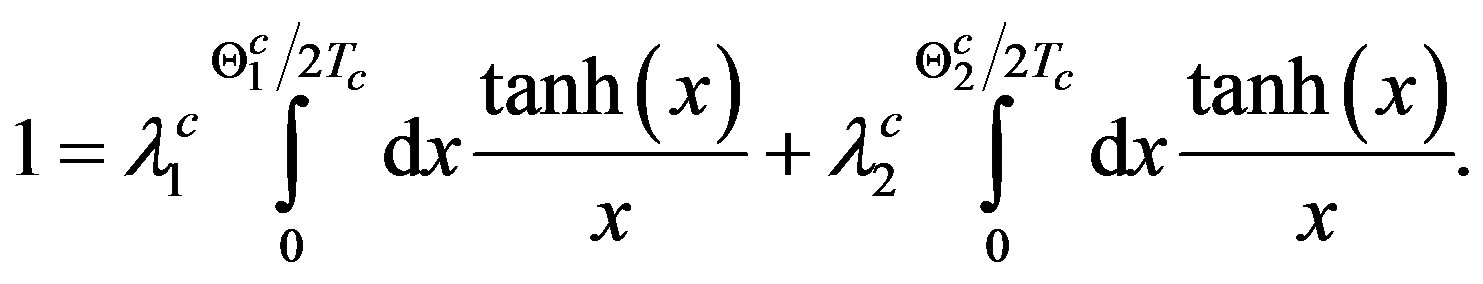 (5)
(5)
The two Debye temperatures in the problem cater to the anisotropy of the CS [9]. The physical significance of CPs bound via oneand two-phonon exchange mechanisms is that there are two kinds of “glues” or “springs” that bind them, leading to two binding energies in the problem.
The framework of GBCSEs [9] has been applied to a variety of CSs [10-12]; the set of parameters thus arrived at for MgB2 is [10]:
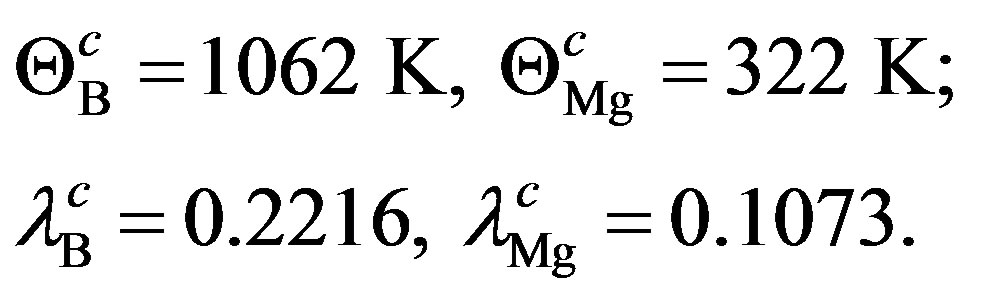 (6)
(6)
These lead via (4a) and (5) to
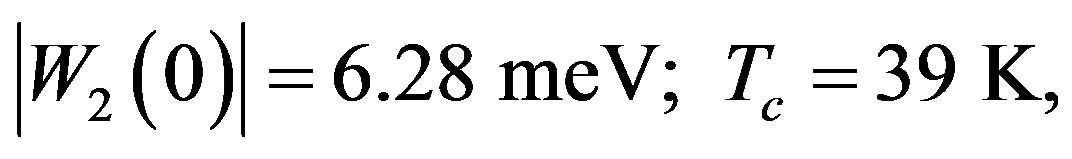 (7)
(7)
The parameters corresponding to B alone in (6) lead via (3a) and the BCS equation for Tc (Equation (5) with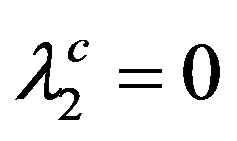 ) to
) to
 (7a)
(7a)
Hence we use |W1,2| and |∆1,2| interchangeably from now on; the T-dependent values of these can be calculated via (3a) and (4a). Note that both the λs in (6) satisfy the Bogoliubov constraint given in (1) above.
If experiment dictates that the smaller gap of MgB2 also closes at about 39 K (and not at about 13 K)—as has been reported in [13], then to address Scenario 1 one must invoke T-dependence of the interaction parameters in the theory. It has recently been shown that [19], even in the BCS theory for elemental superconductors, such dependence has a bearing on the violation of the alleged universality of the relation 2∆/kBTc = 3.53. For a detailed discussion of how the SMW approach also implies such dependence of the interaction parameters, we refer the reader to [17], where it is noted that the requirement of closure of both the gaps in MgB2 is met by replacing 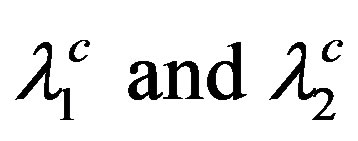 above as follows:
above as follows:
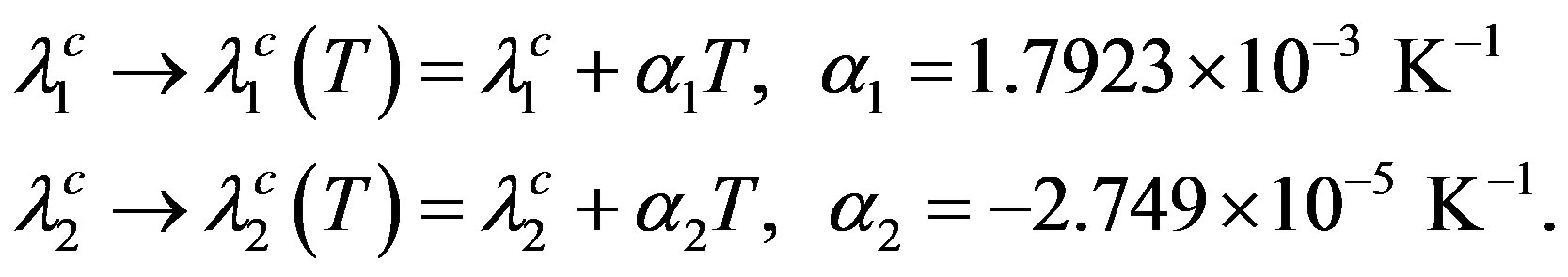 (8)
(8)
Figure 1 shows how these replacements in (3a) and (4a) lead to closure of both the gaps at the 39 K.
We now turn to the second constituent of our framework: the G equation for κes(T) when electrons are scattered predominantly by impurities. This equation is [4]:
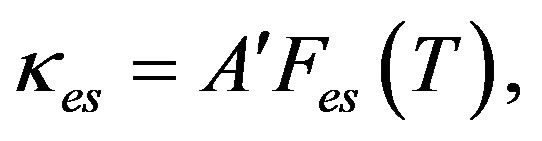 (9)
(9)
where 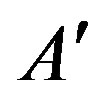 is independent of T,
is independent of T,
 (10)
(10)
and
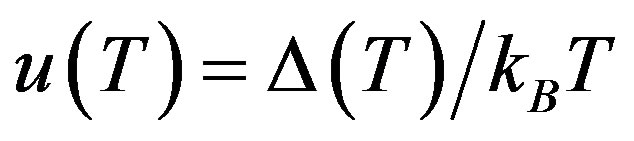 .
.
We note that [4] also gives an alternative expression for the integral in (10) as a sum of three terms (one of which is a sum of an infinite number of terms). Having checked our results obtained directly via (10) with those obtained via the alternative form, we have not reproduced the latter here.
The final constituent of our framework is the GK equation for κgs when the phonons are scattered predominantly by electrons. This equation is [5]:
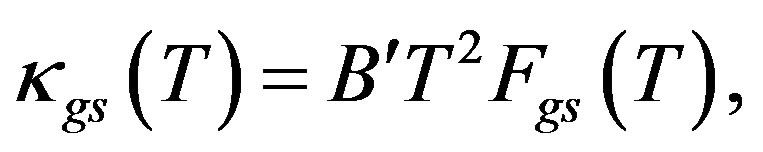 (11)
(11)
where 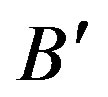 is independent of temperature, and
is independent of temperature, and
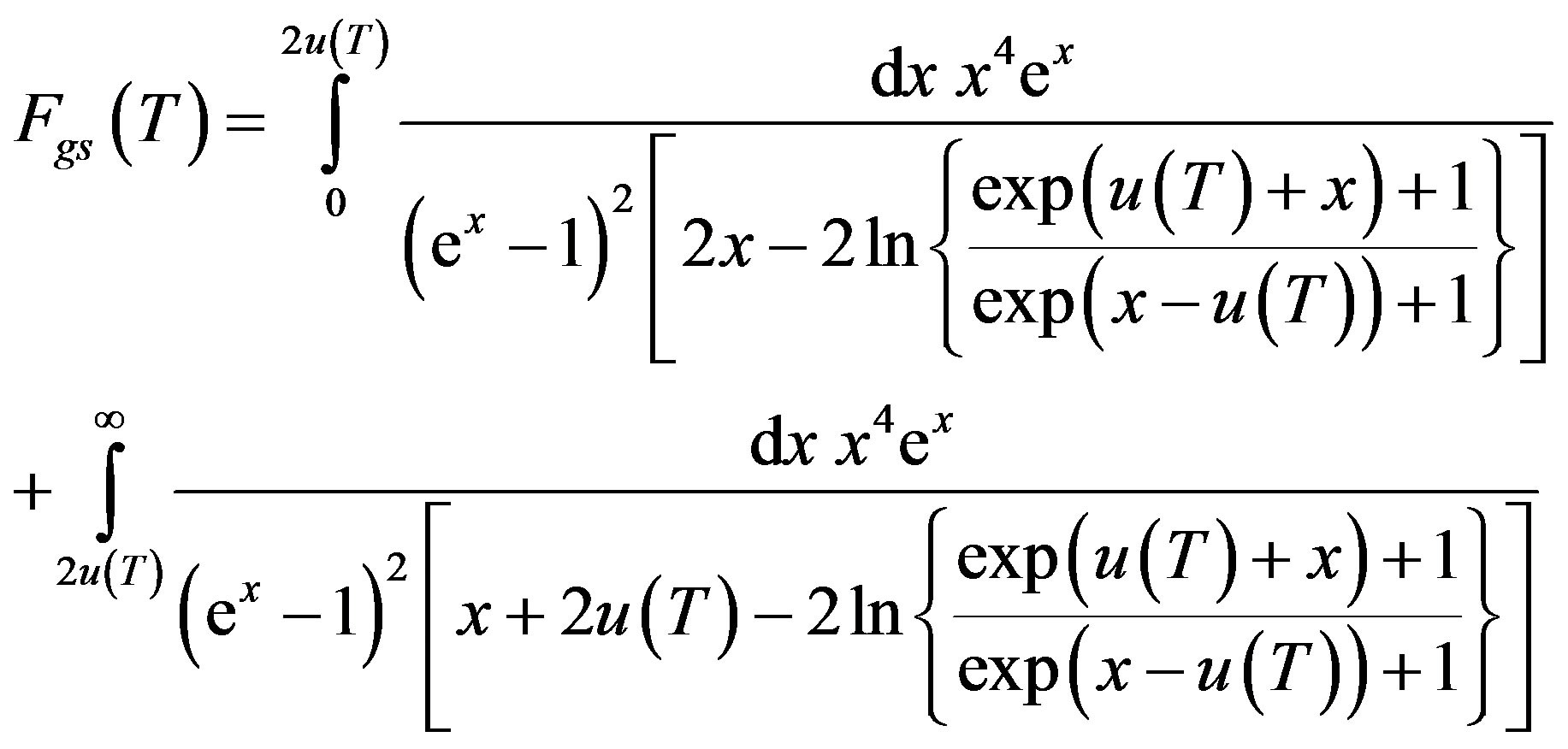 (12)
(12)
As was the case for (11), [5] also gives an alternative expression for the RHS of (12) which now comprises many terms some of which are sums of infinite number of terms. Again, having checked our results obtained directly via (12) with those obtained via the alternative form, we have not quoted the latter here.
3. Total Thermal Conductivity κs of MgB2 in the Superconducting State
We first address the data under consideration in Scenario 1, i.e., when both the gaps close at the same Tc. To this end we solve (3a) and (4a) for ∆1(T) and ∆2(T) with  - values taken from (6) and expressions for λ(T) as given in (8); the results are given in Table 1. With ∆(T)s known, we are enabled to calculate, for each of the gap-values, Fes(T, ∆) and Fgs(T, ∆) via (10) and (12), respectively. This exercise is carried out at each of the 38 temperatures below Tc for which the experimental values of the total thermal conductivity κs are given in the data of B et al.
- values taken from (6) and expressions for λ(T) as given in (8); the results are given in Table 1. With ∆(T)s known, we are enabled to calculate, for each of the gap-values, Fes(T, ∆) and Fgs(T, ∆) via (10) and (12), respectively. This exercise is carried out at each of the 38 temperatures below Tc for which the experimental values of the total thermal conductivity κs are given in the data of B et al.

Figure 1. Variation of the reduced gaps of MgB2 with t for 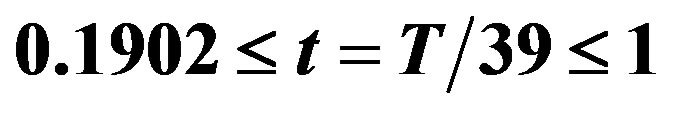 obtained via solutions of (3a) and (4a) with inputs from (6) and (8).
obtained via solutions of (3a) and (4a) with inputs from (6) and (8).
[7]. The results of these calculations are also given in Table 1.
Using (9) and (11), we now write
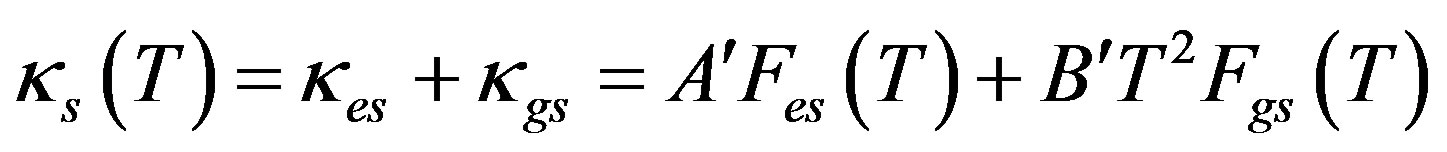 (13)
(13)
as
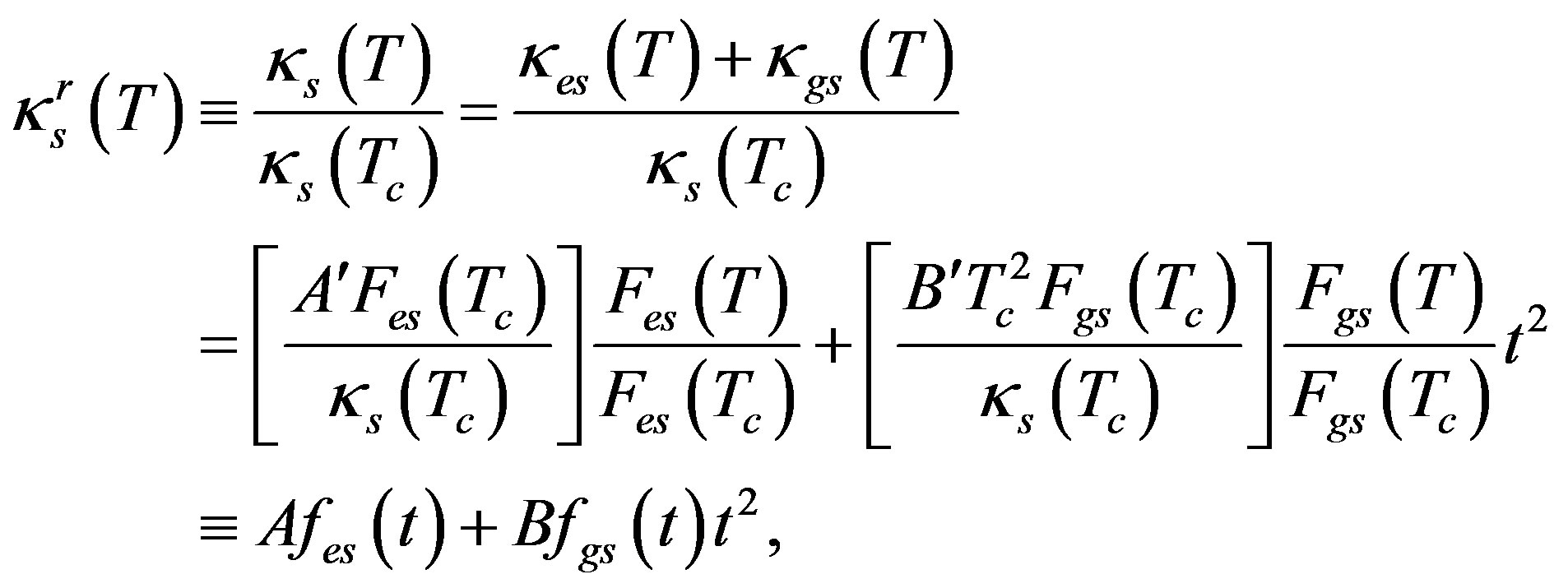 (14)
(14)
where 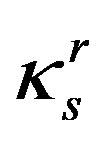 denotes reduced thermal conductivity, t = T/Tc, and A, B, fes and fgs are dimensionless.
denotes reduced thermal conductivity, t = T/Tc, and A, B, fes and fgs are dimensionless.
Equation (14) pertains to the situation when the SC is characterized by one gap; when there are two gaps, we have
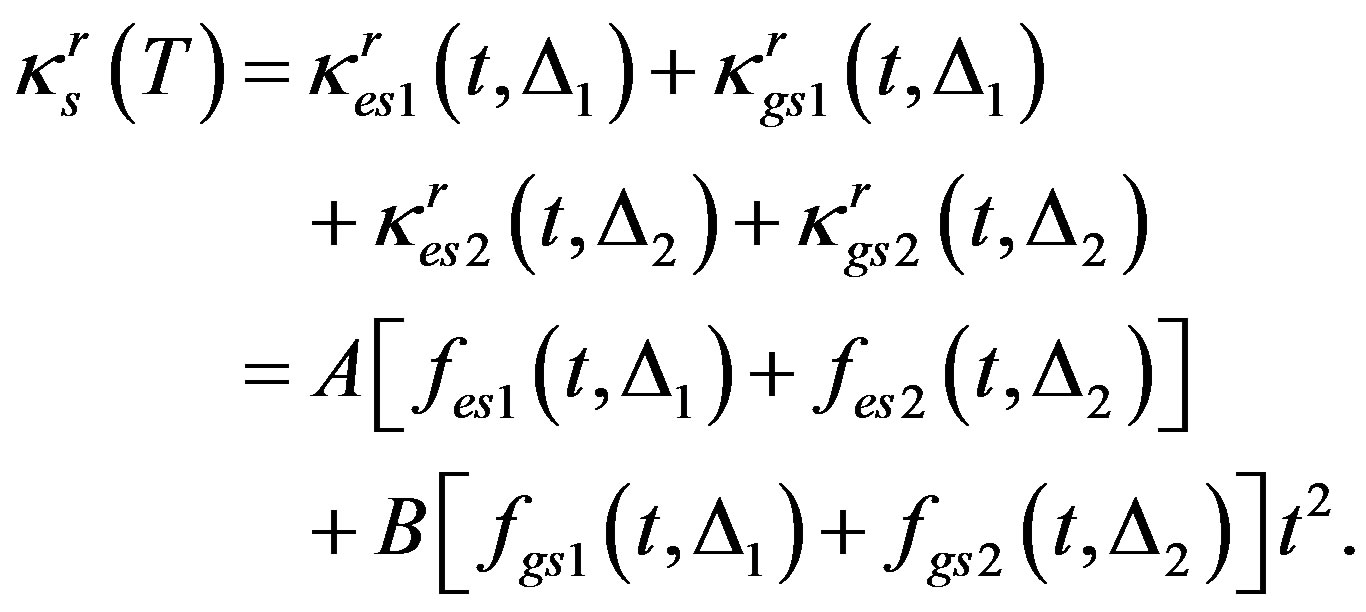 (15)
(15)
We now need to reduce the four F’s in Table 1; this is done by using the set of values given in the last row of the table:
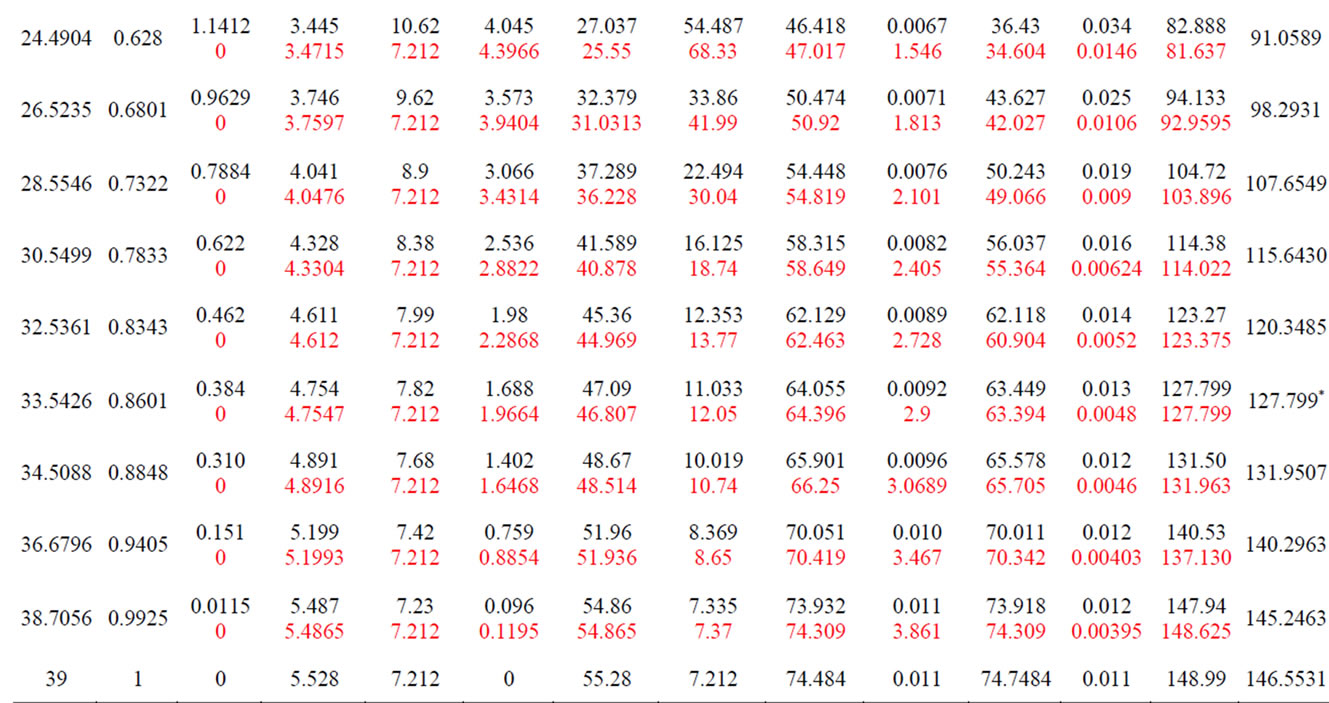
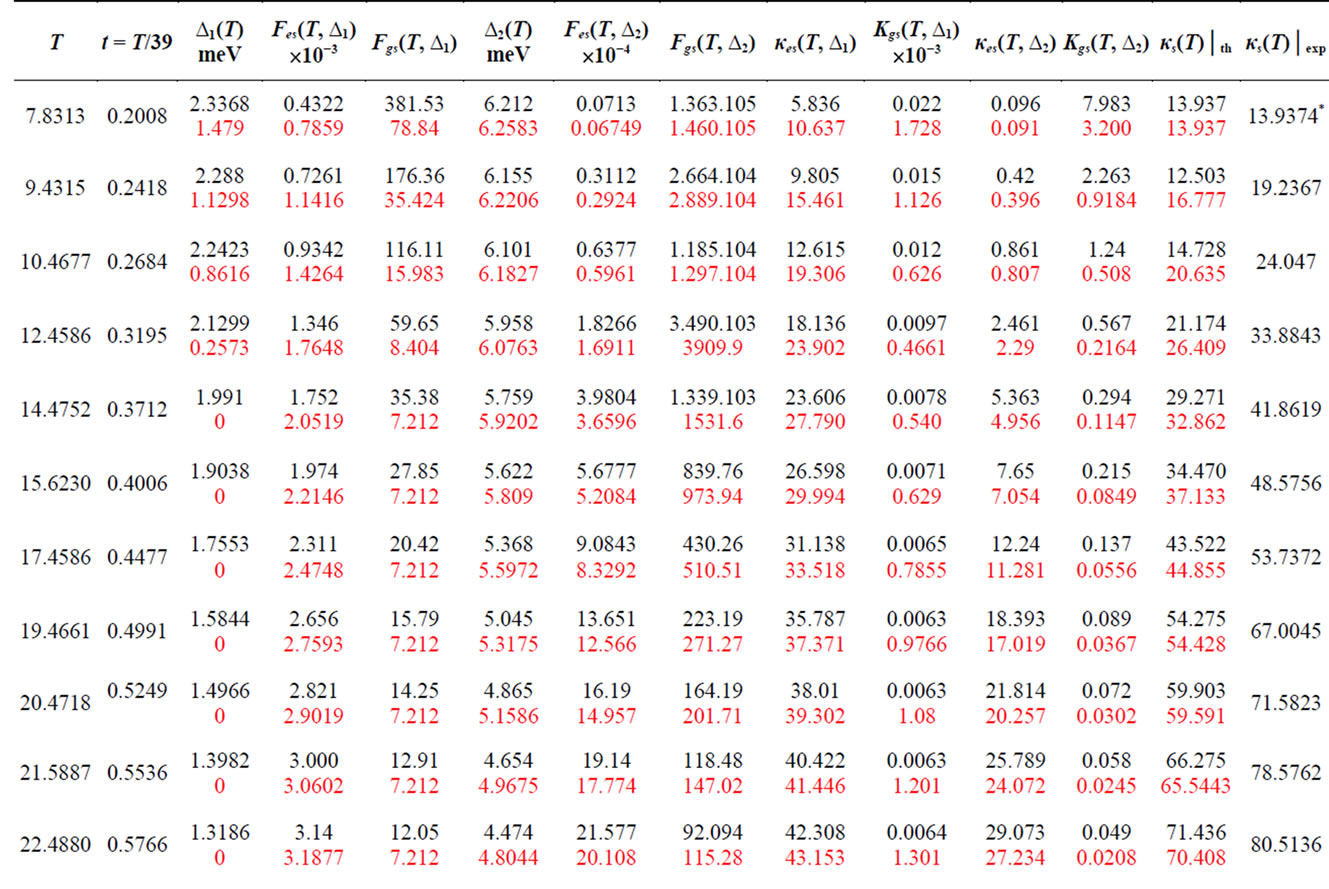
Table 1. Values of ∆1(T), Fes(T, ∆1), Fgs(T, ∆1) and ∆2(T), Fes(T, ∆2) and Fgs(T, ∆2) for all T ≤ Tc in the data of B et al. [7] in the scenarios: a) both the gaps close at 39 K and b) ∆1 closes at 13.2 K while ∆2 closes at 39 K. Entries corresponding to b) are marked in red. In both the scenarios Θ’s are as given in (6). In the former scenario ∆1(T) is calculated via (3a) with 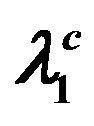 given by (9), and ∆2(T) via (4a) with λs given by (9) and (11). In the latter scenario, ∆1(T) and ∆2(T) are calculated with λs as in (6). Fes(T) and Fgs(T) corresponding to each ∆(T) are calculated via (14a) and (16a), respectively. κs(T) is calculated via (19). Entries marked with (*) are used as input to fix A and B.
given by (9), and ∆2(T) via (4a) with λs given by (9) and (11). In the latter scenario, ∆1(T) and ∆2(T) are calculated with λs as in (6). Fes(T) and Fgs(T) corresponding to each ∆(T) are calculated via (14a) and (16a), respectively. κs(T) is calculated via (19). Entries marked with (*) are used as input to fix A and B.
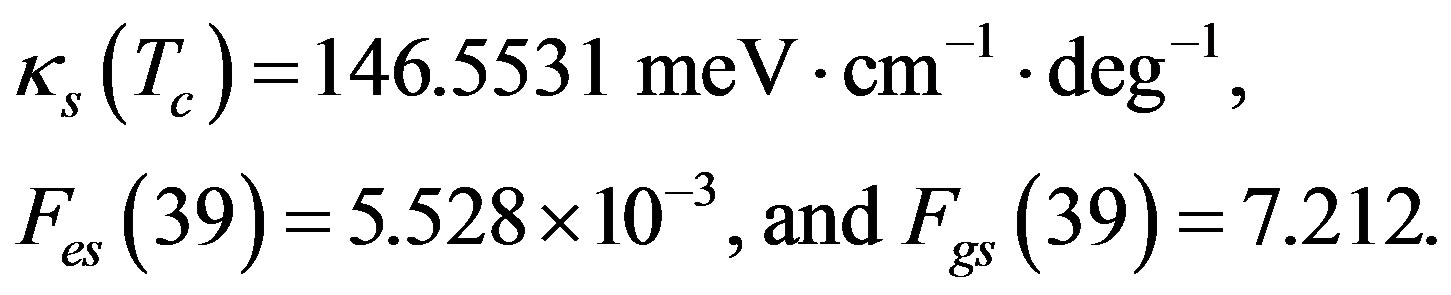
To proceed further we need to fix A and B. We do so by appealing to the experimental values of κs at two temperatures. This enables us to calculate κs at the remaining 36 temperatures.
The above calculations are repeated for Scenario 2. Given below are the values for A and B found at different combinations of temperatures in the two scenarios (the values in the parentheses correspond to Scenario 2):
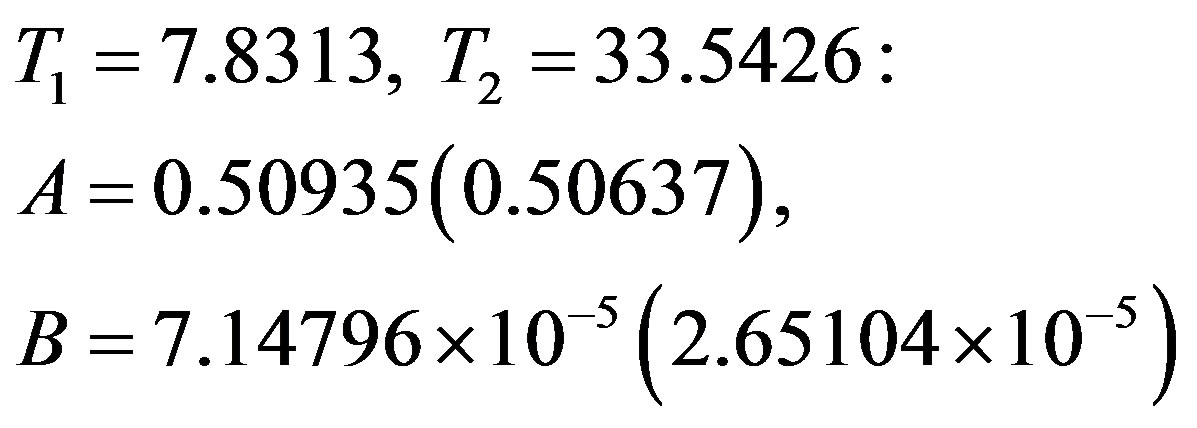
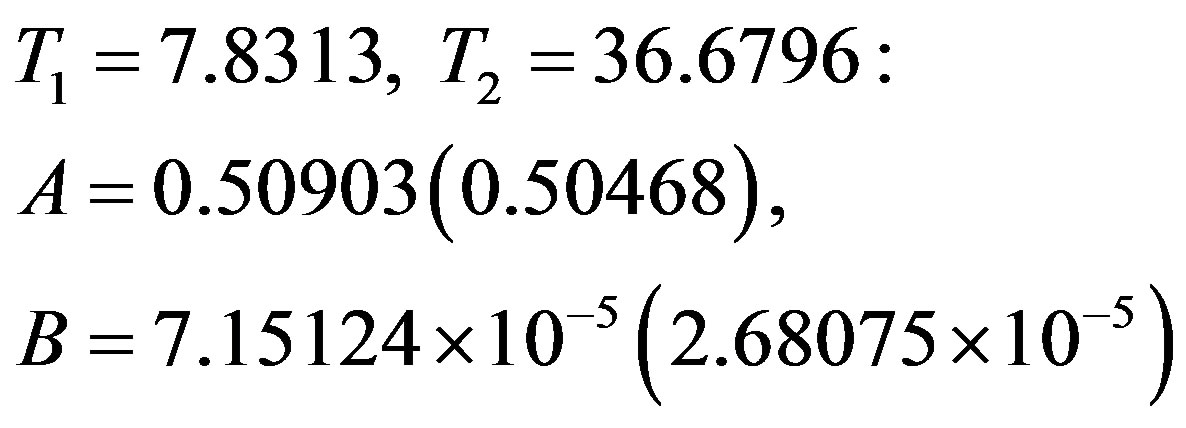
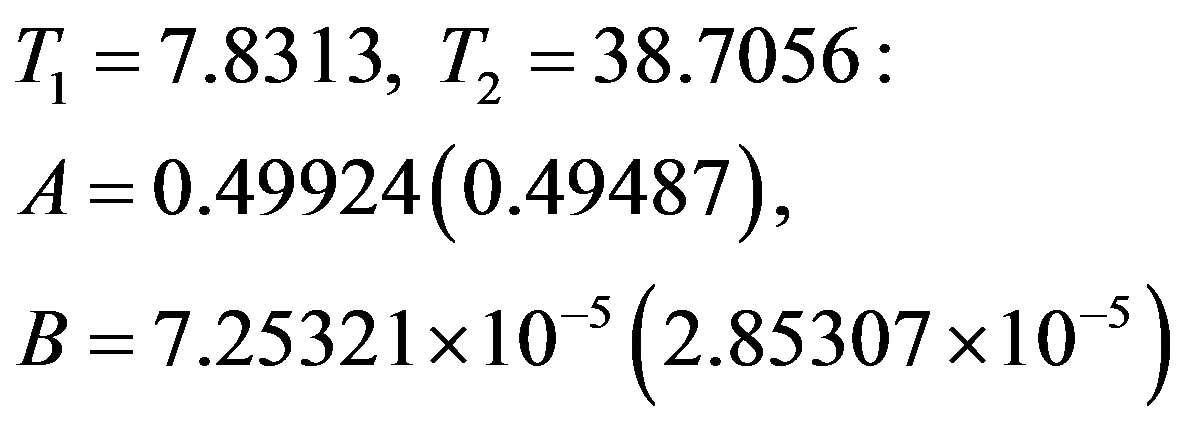
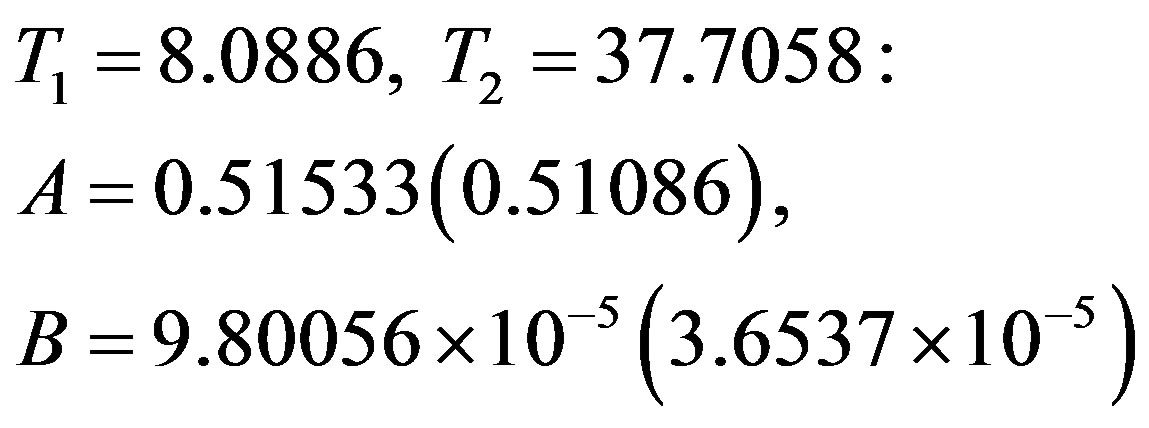
In each scenario, the results for κs(T) yielded by all of the above pairs of A, B values are similar. The values adopted by us are those given in the top set. While we have thus calculated κs(T)s at each of the remaining 36 temperatures in the data under consideration, we have given in Table 1—for both the scenarios—the results at 20 temperatures to save space. Also given in this table are, separately, the contributions of the electronic and the lattice parts of the thermal conductivity due to each gap. Figure 2 gives plots of κs(T)│theory (and its constituents) in the two scenarios—together with the plot of κs(T)│exp— plotted against the reduced temperature.

Figure 2. Clockwise, plots of: a) the experimental values of the total thermal conductivity κt (meV×cm‒1×deg‒1) against t = T/Tc (blue) for all T ≤ Tc in the data of B et al. [7]; b) the theoretical values of κs in Scenario 2 (green); c) the theoretical values of κs in Scenario 1 (black). The remaining four plots correspond to Scenario 2: uppermost of these is for the electronic part of κt due to the smaller gap, followed by the similar part due to the larger gap. The two coincident plots at the bottom of the figure are the lattice parts of the total thermal conductivity due to the two gaps.
We have also analyzed the data of S et al. [8] by following the same approach. Typically, both A and B now have somewhat lower values than was the case for the data of B et al. An example: with T1 = 0.452423 K and T2 = 25.84772 K, we obtain: 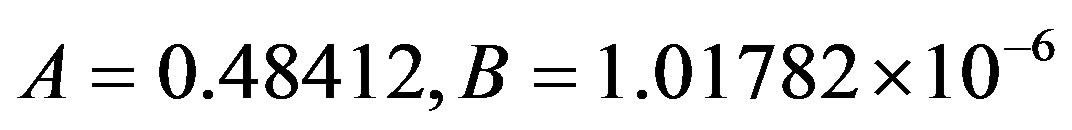 . Figure 3 gives plots of κs(T)│exp and κs(T)│theory against some selected reduced temperatures for this case.
. Figure 3 gives plots of κs(T)│exp and κs(T)│theory against some selected reduced temperatures for this case.
4. Discussion
1) While it has been reported [13] that the two gaps of MgB2 close at the same Tc (Scenario 1), this result does not pertain to the conditions under which thermal conductivity is determined. For this reason we chose here to also address the experimental data in the additional scenario in which the gaps close at different Tcs (Scenario 2). In both cases, as can be seen from Table 1, the total thermal conductivity is constituted predominantly by the electronic part. While both κes(T, ∆1) and κes(T, ∆2) decrease with T, near Tc,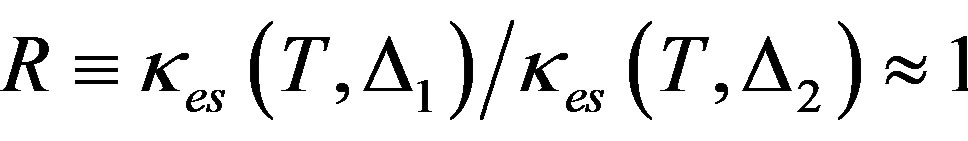 . Further, at the lowest temperature in the table, R ≈ 60 (Scenario 1) and R ≈ 115 (Scenario 2). Thus: a) in the entire range of temperature to which the experimental data of B et al. [7] pertain, i.e.,
. Further, at the lowest temperature in the table, R ≈ 60 (Scenario 1) and R ≈ 115 (Scenario 2). Thus: a) in the entire range of temperature to which the experimental data of B et al. [7] pertain, i.e., 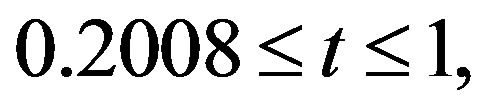 κgs(t) makes negligible contribution to κs(t) in both the scenarios, b) in the range
κgs(t) makes negligible contribution to κs(t) in both the scenarios, b) in the range 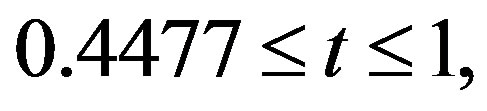 the results in the two scenarios differ by no more than 3%, and c) for t < 0.4477, κs(t)-values in Scenario 1 are lower than in Scenario 2—by about 40% at t = 0.2684, for example. Overall, the latter scenario is thus found to be in better agreement with experiment 2) In order to shed light on the above findings, we draw attention to the following relations obtained via the Gorter-Casimir two-fluid theory of superconductivity, as in, e.g., [20]:
the results in the two scenarios differ by no more than 3%, and c) for t < 0.4477, κs(t)-values in Scenario 1 are lower than in Scenario 2—by about 40% at t = 0.2684, for example. Overall, the latter scenario is thus found to be in better agreement with experiment 2) In order to shed light on the above findings, we draw attention to the following relations obtained via the Gorter-Casimir two-fluid theory of superconductivity, as in, e.g., [20]:
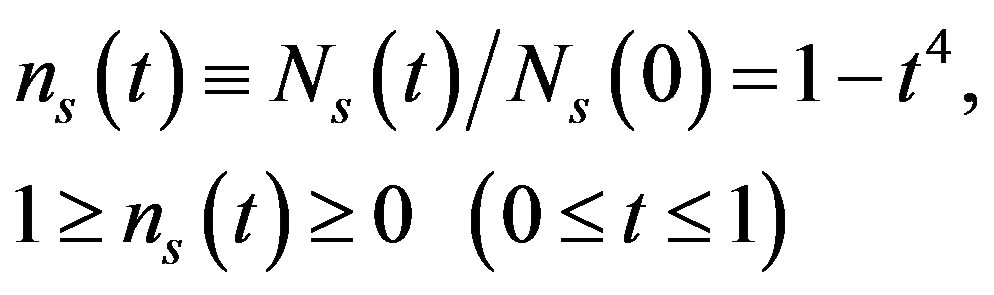 (16)
(16)
where Ns is the density of superconducting electrons. So far as the temperature dependence in (16) is concerned, it has been noted that “some authors report other exponent values or related expressions” [20], but that does not concern us here.
The second relation in (16) is strikingly similar to
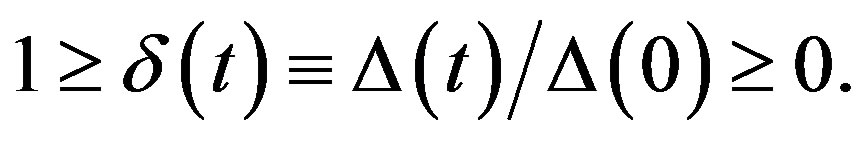 (17)
(17)
We thus infer that greater the value of δ(t)  greater is the fraction of superconducting electrons (or CPs) and therefore smaller the fraction of available electrons as heat-carriers. It is only under this circumstance that heat is predominantly carried by phonons, i.e., when t is close to 0 K. This explains the result in para 1 (a) in this section: the contribution of κgs(t) to κs(t) is negligible be-
greater is the fraction of superconducting electrons (or CPs) and therefore smaller the fraction of available electrons as heat-carriers. It is only under this circumstance that heat is predominantly carried by phonons, i.e., when t is close to 0 K. This explains the result in para 1 (a) in this section: the contribution of κgs(t) to κs(t) is negligible be-
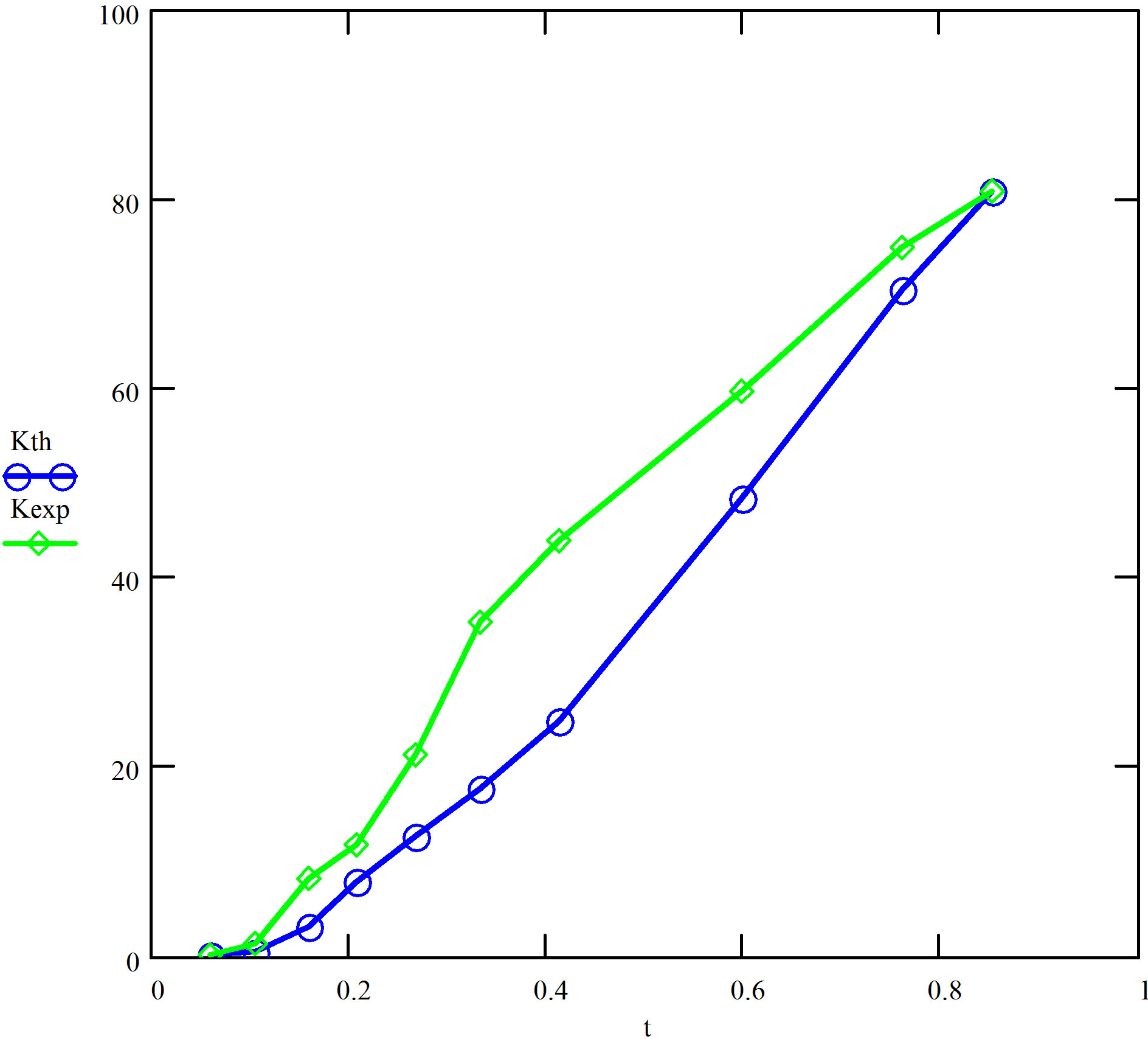
Figure 3. Plots of the experimental values (green) of total thermal conductivity (meV×cm−1×deg−1) in the data of S et al. [8] against t = T/Tc at some selected temperatures below Tc and their theoretical counterparts (blue) in Scenario 2.
cause bulk of the data under consideration pertains to values of t not close enough to 0 K. Note that in both the scenarios the Sp. Ht. and the MFP of electrons have the same values at any T. The result in para 1 (c) is explicable if the sum of the gap-values at any t is naively regarded as proportional to the number of superconducting electrons (or CPs) at that t. An example: at t = 0.3195 the sum of the two gap values is 8.0879 in Scenario 1 and 6.3336 meV in Scenario 2. This implies that there are fewer CPs in the latter scenario (and therefore more left over electrons as carriers of heat) than in the former. This is reflected in the κs values: 21.174 (Scenario 1), 26.409 W∙cm−1∙deg−1 (Scenario 2).
3) The result in para 1 (b) implies that number of carriers in the stated range is more or less the same in both the scenarios; this however is not seen as convincingly as in the preceding case.
4) A feature of our approach is that we have not relied upon the Wiedemann-Franz law to separate out the lattice part of the total thermal conductivity. There is a difference of opinion about the utility of this law for the problem addressed here: while B et al. [7] have found it useful for the analysis of their data, Sologubenko et al. [21] have questioned its applicability for MgB2 at low temperatures.
5) We now report our findings about the data of S et al. [8], the values of A and B for which were given above. We note that at around the same temperatures below 39 K, the values of κs(T) reported by S et al. are lower than the values reported by B et al. [7]. At the highest temperature below 39 K, for example, they quote κ (38.86986 K) = 80.4 mW∙cm−1deg−1 as against κ (38.7056) = 145.2463 mWcm−1deg−1 quoted by B et al. We also note that B et al. have reported their data up to T = 7.4187 K, whereas S et al. have done so up to T = 1.8752 K. The differences in the values of κs(T) of the two groups can be ascribed to the compositional differences of the samples and the manners of their preparation since these can cause the scattering mechanism in the two samples to differ. This is an observation about which S has remarked [22]: “Concerning the MgB2 sample quality, I fully agree with you. It was the early time of superconducting MgB2. Thus, sample composition, granularity etc. may differ significantly from group to group. This assumption is also supported by varying reported values of, e.g., the thermoelectric power.”
6) It seems interesting to point out that the approach followed in this paper is remarkably similar to the qualitative approach of Sologubenko et al. [21], who have noted: “Thus, we consider two subsystems of quasiparticles with gaps ∆1 and ∆2, different parameters E1 and E2 of phonon-electron scattering, and separate contributions κe1 and κe2 to the heat transport.” In this manner—in the early days of MgB2—they were able to give good estimates of the zero-temperature values of the two gaps.
5. Conclusions
1) We have presented here a detailed study of the thermal conductivity of MgB2 in the superconducting state via GBCSEs that were derived from a BSE by appealing to the twin concepts of a superpropagator and multiple Debye temperatures. This approach manifestly gives the ideas of Liu et al. [15], Choi et al. [16], and Sologubenko et al. [21] a concrete form.
2) A remarkable result of this paper is: while over a substantial range of temperatures below Tc the results in Scenario 1 are indistinguishable from those of Scenario 2, the latter scenario yields results in progressively better agreement with experiment when T ≤ 15 K. As is well known, thermal conductivity is a non-equilibrium phenomenon; it is measured under conditions of no electric current. Since a thermal current tends to drag a small electric current with it, this current must be balanced by an equal and opposite current. In an SC, it is balanced by a supercurrent. For these reasons, measurement of thermal conductivity requires a rather elaborate experimental setting up. It is not inconceivable therefore that cumulative effect of the stresses caused by this setting up lifts the “degeneracy” of the two gaps closing at the same T.
3) We finally note that the approach followed here may also shed light on whether or not the Tland the Bi-based HTSCs are characterized by three gaps—the possibility of which was suggested in [11].
6. Acknowledgements
G. P. M. thanks Prof. V. Z. Kresin for clarifying some points related to the original literature [4,5] on the subject matter of this paper. He also thanks Prof. D. C. Mattis for advice whenever approached. The authors are grateful to Prof. E. Bauer and Prof. M. Schneider for making their detailed experimental data available to them.
REFERENCES
- C. Uher, “Thermal Conductivity of High-Tc Super Conductors,” Journal of Superconductivity, Vol. 3, No. 4, 1990, pp. 337-389. http://dx.doi.org/10.1007/BF00617463
- P. Wyder, “Frier Wegländen in Supraleitenden Zustand, in Normalen Zustand und in Zwischenz ustan,” Phys Konden Materie, Vol. 3, 1965, pp. 292-304.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, “Theory of Superconductivity,” Physical Review, Vol. 108, No. 5, 1957, pp. 1175-1204. http://dx.doi.org/10.1103/PhysRev.108.1175
- B. T. Geilikman, “Thermal Conductivity of Super Conductors,” Soviet Physics, JETP, Vol. 7, 1958, pp. 721- 722.
- B. T. Geilikman and V. Z. Kresin, “Phonon Thermal Conductivity of Superconductors,” Soviet Physics Doklady, Vol. 3, 1958, pp. 1161-1163.
- J. Bardeen, G. Rickayzen and L. Tewordt, “Theory of Thermal Conductivity of Superconductors,” Physical Review, Vol. 113, No. 4, 1959, pp. 982-994. http://dx.doi.org/10.1103/PhysRev.113.982
- E. Bauer, et al., “Thermal Conductivity of MgB2,” Journal of Physics: Condensed Matter, Vol. 13, No. 22, 2001, pp. L487-L493. http://dx.doi.org/10.1088/0953-8984/13/22/107
- M. Schneider, et al., “Heat and Charge Transport Properties of MgB2,” Physica C, Vol. 363, No. 1, 2001, pp. 6- 12. http://dx.doi.org/10.1016/S0921-4534(01)00947-9
- G. P. Malik, “On the Equivalence of the Binding Energy of a Cooper Pair and the BCS Energy Gap: A Framework for Dealing with Composite Super Conductors,” International Journal of Modern Physics B, Vol. 24, No. 9, 2010, pp. 1159-1172. http://dx.doi.org/10.1142/S0217979210055408
- G. P. Malik, “Generalized BCS Equations: Applications,” International Journal of Modern Physics B, Vol. 24, No. 19, 2010, pp. 3701-3712. http://dx.doi.org/10.1142/S0217979210055858
- G. P. Malik and U. Malik, “A Study of the Thalliumand Bismuth-Based High-Temperature Superconductors in the Framework of the Generalized BCS Equations,” Journal of Superconductivity and Novel Magnetism, Vol. 24, No. 1-2, 2011, pp. 255-260. http://dx.doi.org/10.1007/s10948-010-1009-0
- G. P. Malik, I. Chávez and M. de Llano, “Generalized BCS Equations and Iron-Pnictide Superconductors,” Journal of Modern Physics, Vol. 4, 2013, pp. 474-480. http://dx.doi.org/10.4236/jmp.2013.44067
- M. Iavarone, et al., “Two-Band Superconductivity in MgB2,” Physical Review Letters, Vol. 89, No. 18, 2002, 4 p. http://dx.doi.org/10.1103/PhysRevLett.89.187002
- H. Suhl, B. T. Matthias and L. R. Walker, “Bardeen-Cooper-Schrieffer Theory of Superconductivity in the Case of Overlapping Bands,” Physical Review Letters, Vol. 3, No. 12, 1959, pp. 552-554. http://dx.doi.org/10.1103/PhysRevLett.3.552
- A. Y. Liu, I. I. Mazin and J. Kortus, “Beyond Eliashberg Superconductivity in MgB2: Anharmonicity, Two-Phonon Scattering, and Multiple Gaps,” Physical Review Letters, Vol. 87, No. 8, 2001, 4 p. http://dx.doi.org/10.1103/PhysRevLett.87.087005
- H. J. Choi, D. Roundy, H. Sun, M. L. Cohen and S. G. Louie, “The Origin of the Anomalous Superconducting Properties of MgB2,” Nature, Vol. 418, 2002, pp. 758- 760. http://dx.doi.org/10.1038/nature00898
- G. P. Malik and M. de Llano, “An Alternative Approach to Multi-Gap Superconductivity,” International Journal of Modern Physics B, Vol. 27, No. 29, 2013, 9 p. http://dx.doi.org/10.1142/S0217979213470085
- J. M. Blatt, “Theory of Superconductivity,” Academic Press, New York, 1964.
- G. P. Malik and M. de Llano, “Some Implications of an Alternate Equation for the BCS Energy Gap,” Journal of Modern Physics, Vol. 4A, 2013, pp. 6-12. http://dx.doi.org/10.4236/jmp.2013.44A002
- C. P. Poole, “Handbook of Superconductivity,” Academic Press, San Diego, 2000.
- A. V. Sologubenko, J. Jun, S. M. Kazakov, J. Karpinski and H. R. Ott, “Thermal Conductivity of Single Crystalline MgB2,” Physical Review B, Vol. 66, No. 1, 2002, 8 p. http://dx.doi.org/10.1103/PhysRevB.66.014504
- M. Schneider, “Private Communication.”

