Received 3 February 2016; accepted 26 February 2016; published 29 February 2016

ABSTRACT

The use of frames is analyzed in Compressed Sensing (CS) through proofs and experiments. First, a new generalized Dictionary-Restricted Isometry Property (D-RIP) sparsity bound constant for CS is established. Second, experiments with a tight frame to analyze sparsity and reconstruction quality using several signal and image types are shown. The constant 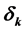is used in fulfilling the definition of D-RIP. It is proved that k-sparse signals can be reconstructed if by using a concise and transparent argument¹. The approach could be extended to obtain other D-RIP bounds (i.e.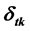). Experiments contrast results of a Gabor tight frame with Total Variation minimization. In cases of practical interest, the use of a Gabor dictionary performs well when achieving a highly sparse representation and poorly when this sparsity is not achieved.

Keywords:

Compressed Sensing, Total Variation Minimization, l₁-Analysis, D-Restricted Isometry Property, Tight Frames

1. Introduction

Let and 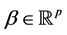be a signal such that

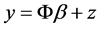(1)

with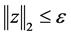. In compressed sensing, one can find a good stable approximation (in terms of 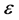and the tail of 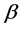consisting of smallest entries) of 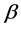from the measurement matrix 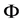and the measurement y through solving an 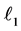-minimization, provided that 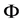belongs to a family of well behaved matrices. A subclass of this family of matrices can be characterized by the well known Restrictive Isometry Property (RIP) of Candès, Romberg, and Tao, [3] [4] . This property requires the following relation for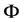

(2)

for every k-sparse vector c (namely, c has at most k non-zero components), for some small constant. Some bounds on have been determined in previous publications [3] -[6] . Notably, Cai and Zhang have established

several sharp RIP bounds that cover the most interesting cases of δ_k and [7] [8] showing.

A key requirement in this setting is a signal being sparse or approximately sparse. Indeed, Many families of integrating signals have sparse representations under suitable bases. Recently, an interesting sparsifying scheme was proposed by Candès et al. [9] . In their scheme, instead of bases, tight frames are used to sparsify signals.

Let () be a tight frame and. Candès et al. [9] suggests that one use the following optimization to approximate the signal:

(3)

The traditional RIP is no longer effective in the generalized setting. Candès et al. defined the D-restricted isometry property which extends RIP [9] . Here the formulation of D-RIP is used as in Lin et al. [10] .

Definition 1. The measurement matrix obeys the D-RIP with constant if

(4)

holds for all k-sparse vectors.

The RIP is now a special case of D-RIP (when the dictionary D is the identity matrix). For D being a tight frame, Candès et al. [9] , proved that if, then if is approximately k-sparse, the solution to (3) is a good approximation of. Lin et al. [10] , improved this result to by using some techniques developed by Candès et al. [3] .

Contribution

The proof in Section 2 establishes an improved D-RIP bound which states that. This result was

previously available [1] and it has been improved on by Wu and Li [2] . The main ingredient of the proof in Section 2 is a tool developed by Xu et al. [11] . This approach takes its inspiration from the clever ideas of Cai and Zhang [7] [8] .

The practical application of this proof consists of experiments targeting the theory of using tight frames in this CS setting satisfying D-RIP. Similar experimental methods to those used by Candès et al. are followed [9] [12] . However, an expanded variety of relevant sparse and non-sparse signals are used to test the robustness of the Gabor transform. Additionally, these experiments analyze sparsity in the coefficient domain and show that a highly sparse representation is a good indicator of reconstruction quality. These results are contrasted with a commonly used CS approach of Total Variation (TV) minimization.

This paper is organized into four main sections. Background information is presented in Section 1. Section 2 describes a proof of an improved D-RIP sparsity bound by using a concise and transparent approach. Section 3 details the methods of experimentation used to apply the tight frame in practical applications of signals and image recovery. Section 4 shows and discusses the reconstruction simulation results with an analysis of the robustness and shortcomings of using tight frames in CS.

2. New D-RIP Bounds

Theorem 2. Let D be an arbitrary tight frame and let be a measurement matrix satisfying D-RIP with

. Then the solution to (3) satisfies

(5)

where the constants and depend on, is the vector with all but the k largest

components (in magnitude) set to zero.

Before proving this theorem, some remarks are helpful. Firstly, Cai and Zhang have obtained a sharp bound

for the case [8] . Their work inspired pursuit of the bound in this proof. Secondly, following

the ideas of Cai and Zhang [7] [8] , more general results (other D-RIP bounds) can be obtained in parallel.

In order to prove Theorem 2, the following -norm invariant convex k-sparse decomposition by Xu and Xu [11] , and Cai and Zhang [8] are needed.

The following description is taken from Xu et al. [11] .

Lemma 1. For positive integers, and positive constant C, let be a vector with and

. Then there are k-sparse vectors with

(6)

such that

(7)

for some nonnegative real numbers with.

Now Theorem 2 is proven.

Proof. This proof follows some ideas in the proofs of Theorems 1.1 and 2.1 by Cai et al. [8] , incorporating some simplified steps. Some strategies from Cai et al. [5] [13] are also used. This proof deals only with the case so that the key ideas can be conveyed clearly.

Let.

For a subset, denoted by the matrix D is restricted to the columns indexed by S (and replacing other columns by zero vectors). Let denote the index set of the largest k components of (in

magnitude), i.e.,. With this notation there is. As in Candès et al.

[9] , one can easily verify the following:

(8)

(9)

Denote for, where is the i-th column of D, then

(10)

By rearranging the columns of D if necessary, assume. Let. In this case, have

(11)

Assume that the tight frame D is normalized, i.e., , and for all. Thus there is the following useful relation:

(12)

From the facts and, the relation

yields

(13)

Since, use Lemma 1 to get the following -invariant convex

k-sparse decomposition of:

(14)

with each being k-sparse, and. From this and the

Cauchy-Schwartz inequality, there is

(15)

By the triangle inequality, holds and thus

(16)

Note that and. In order to prove

the theorem, it suffices to show that there are constants such that

(17)

In fact, assuming (17) there is

(18)

(19)

(20)

(21)

Now moving to the proof of (17). Denote

(22)

First, as is k sparse, hence 2k sparse. There is

(23)

On the other hand, as each is 2k sparse, there is

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

Combining this with (23) shows

(34)

By making a perfect square, there is

(35)

which implies that

(36)

and finally have (17):

(37)

This demonstrates the use of Lemma 1 to get a good result. This could be pursued further to general cases for an even better bound. Indeed, this has been done recently by Wu and Li [2] to improve the result of this proof which has been available previously [1] .

3. Experiments

The focus in these experiments is to show practical applications of a sparsifying frame that satisfies the new lower bound proven in the previous section. A time-frequency Gabor dictionary is used as a sparsifying trans- form in re-weighted minimization [12] . The Gabor dictionary fulfills the requirements of D-RIP because it is a tight frame.

One of the advantages of a Gabor dictionary is its characteristic of translational invariance both in time and frequency. In a similar context, a translational invariant wavelet transform was used with good results in MRI reconstruction [14] . Invariance in the minimization penalty term is advantageous for its ability to represent different signals sparsely.

Here comparison measurements of sparsity in Gabor and TV Coefficients of various signals are used to verify if good and robust results can be achieved. A selection of 5 different real valued signals and/or images with variants are used to simulate the complexity of practical signals.

・ Sinusoidal pulses (GHz range)

・ Shepp-Logan phantom image

・ Penguin image

・ T1 weighted MRI image

・ Time of Flight (TOF) Maximum Intensity Projection (MIP) MRI image

The original images and signals are sized to be a total length of 16k values-for images, this is a 128 × 128 gray-scale image, shown in part (a) of each figure. These signals are not sparse in their native domain, but can become sparse when a transform is applied.

The use of the Gabor dictionary to reconstruct these signals utilizes a core optimization algorithm solver for the primal-dual interior point method provided by -Magic [15] . The redundancy of the Gabor transform coefficients compared to the original signal is about 43 times. These results are compared to reconstructions of the same input signal using another CS optimization algorithm solver, TV minimization with quadratic con- straint, which is also provided by -Magic. These algorithms operate on the full sized image (or signal) without breaking up the data into segments. In both settings, the same under-sampling is performed by using a pseudo-random Gaussian measurement matrix with a factor of 2.

In Table 1, there is a comparison of two measures for this analysis, the Mean Square Error (MSE) and

Sparsity. Measurements of normalized MSE are taken, where and are the original and reconstructed image.

(38)

A Linear (L) MSE of the reconstruction is used as a reference, shown as (b) in each figure. This is calculated by the transpose of the measurement matrix as the pseudo inverse. Gabor (G) MSE identifies the error in the use of that dictionary in the CS reconstruction, shown in parts (c) of the figures. TV MSE is a measure of the error when TV weighted minimization is performed and is shown in part (d) of each figure.

Sparsity measurements taken in the coefficient domain are based on a ratio of the count of values that are less than 1/256 of the maximum coefficient, divided by the total number of the coefficients. This ratio then is a percentage of sparsity. Two sparsity measures are taken:

・ % G Sparse-Sparsity of the Gabor transform coefficients of the fully sampled signal

・ % TV Sparse-Sparsity of the TV calculation of the fully sampled signal

4. Results and Discussion

The goal is to show how well a sparse tight frame representation of various signals performs in CS recon- struction. Analysis is done of the Gabor dictionary as a sparsifying transform on non-sparse signals and images. A large range of reconstruction errors and sparsity levels are observed for different image types and signals. The use of the Gabor frame with a reference of TV weighted minimization in compressed sensing reconstruction is compared. Table 1 quantifies MSE and sparsity for each reconstruction test. Figures 1-8 are the corres- ponding image and signal reconstructions.

According to these measurements, sparsity in the coefficient domain will correlate to image reconstruction

success. For example, test 1 measures a Gabor coefficient sparsity of over 99% and a reconstruction success which reduces the MSE by 36 times compared to the linear reconstruction. Whereas, with the same signal, which is not sparse at all in the TV domain, TV minimization actually increases the MSE when compared with the linear reconstruction, see Figure 1. It is important to note that the sparsity calculated on the Gabor coefficient set is on a much larger set of redundant coefficients than the non-redundant TV coefficients.

In test 2, the complexity and sparsity are adjusted by adding additional sinusoidal pulses which may overlap. The complexity of the pulses significantly increases to 20 pulses and the Gabor dictionary is able to sparsely represent the signal very well compared to TV minimization, see Figure 2. Similar to the results in test 1, the reconstruction MSE is reduced by 36 times.

In tests 3 and 4, images are chosen which are sparse in the TV domain but not in the Gabor domain. The TV reconstruction reduces the MSE to zero compared to the Gabor reconstruction reducing by only a factor of 2.6 and 2.4 respectively. The penguin image is an example with a different background magnitude from the Shepp-Logan phantom, see Figure 3 and Figure 4.

The signal in test 5 is a combination of a pulse from test 1 with the Shepp-Logan image from test 3. The same signal is plotted in the time domain for Figure 5 and in the image domain for Figure 6. Although both Gabor and TV CS reconstructions improve the result over the linear calculation, the error still remains quite large. It is noteworthy that the sparsity percentages are much lower for this case in both the TV and Gabor domains. This underscores the important connection between having a sparse representation and making a good reconstruction.

In the last experiments, tests 6 and 7, MRI images of the brain as either T1 weighted or TOF MIP are used. They appear not to be sparsely represented in either the Gabor domain or in TV. The MSE result is poor in both reconstruction algorithms, see Figure 7 and Figure 8. It is important to note that under-sampling is in the image domain and not in the native MRI signal domain of k-space. However, this is still an equivalent comparison for cases when the under-sampled k-space produces artifacts that are incoherent as in this experiment. A require- ment of CS reconstruction is that artifacts due to sampling are similar to uniform noise with an even distribution across the image.

It is also important to point out that the linear reconstructions, calculated with a pseudo-inverse, have a consistent MSE for all experiments, see L MSE in Table 1. This is not the case for this tight frame. These findings show remarkably good results for some periodic signals. However, the Gabor tight frame does not appear to be advantageous for the images investigated here. The ability of the sparsifying transform to produce a high percentage of sparsity contributes greatly to the reduction of reconstruction error. When using CS in these cases, it is vital to pick a dictionary which will effectively and sparsely represent the signal of interest.

5. Conclusion

The use of a new D-RIP sparsity bound constant for compressed sensing is proven using a transparent and concise approach. Practical numerical experiments for this setting are performed. The use of a Gabor tight frame in CS is contrasted with TV weighted minimization by simulation. Measurements of reconstruction error and coefficient sparsity in each domain are presented and analyzed. Sparse representation by frames does provide good results when the dictionary is chosen appropriately. Care must be taken to assure high levels of sparsity are achieved in the coefficient domain. Otherwise, poor fidelity in reconstruction may occur.

Acknowledgements

The author wishes to thank several people: Academic supervisor, Professor Guangwu Xu, for his assistance in the proofs of the results in Section 2, suggestions in setting up experiments, and help with analysis. Bing Gao, for pointing out an error in the earlier version of the proof [1] . Dr. Kevin King, from GE Healthcare for providing the MRI images and suggestions for improvement. Dr. Michael Wakin [12] , who provided some code useful for experiment comparison.

Cite this paper

ChristopherBaker, (2016) Sparse Representation by Frames with Signal Analysis. Journal of Signal and Information Processing,07,39-48. doi: 10.4236/jsip.2016.71006

References

NOTES

¹This was proven in 2014 [1] . This result is improved upon [2] .