International Journal of Modern Nonlinear Theory and Application
Vol.2 No.4(2013), Article ID:40322,4 pages DOI:10.4236/ijmnta.2013.24032
On Dislocated Metric Topology
Department of Mathematics, Faculty of Science, Assiut University, Qesm Than Asyut, Egypt
Email: mahmed68@yahoo.com, zeyada1@hotmail.com
Copyright © 2013 Mohamed A. Ahmed et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 4, 2013; revised May 18, 2013; accepted June 10, 2013
Keywords: Generalized Topology; Dislocated Neighbourhood Systems; Dislocated Metric
ABSTRACT
In this paper, we give a comment on the dislocated-neighbourhood systems due to Hitzler and Seda [1]. Also, we recover the open sets of the dislocated topology.
1. Introduction
In recent years, the role of topology is of fundamental importance in quantum particle physics and in logic programming semantics (see, e.g. [2-6]). Dislocated metrics were studied under the name of metric domains in the context of domain theory (see, [7]). Dislocated topologies were introduced and studied by Hitzler and Seda [1].
Now, we recall some definitions and a proposition due to Hitzler and Seda [1] as follows.
Definition 1.1. Let 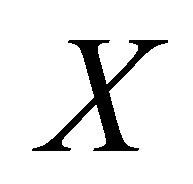 be a set.
be a set. 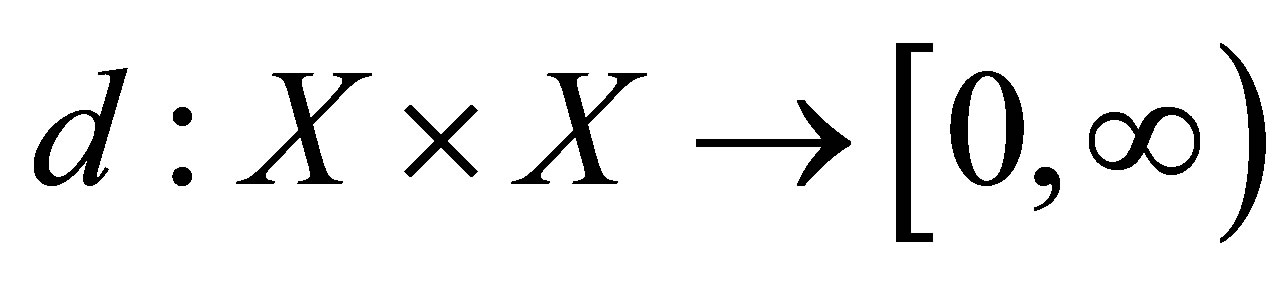 is called a distance function. Consider the following conditions, for all
is called a distance function. Consider the following conditions, for all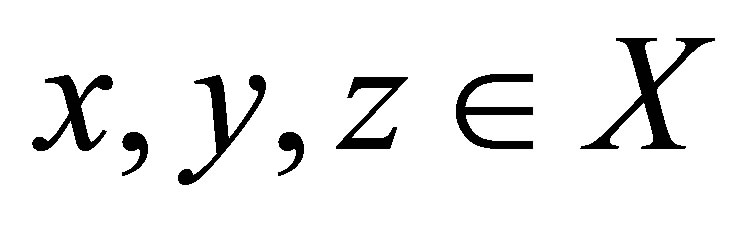 ,
,
(d1)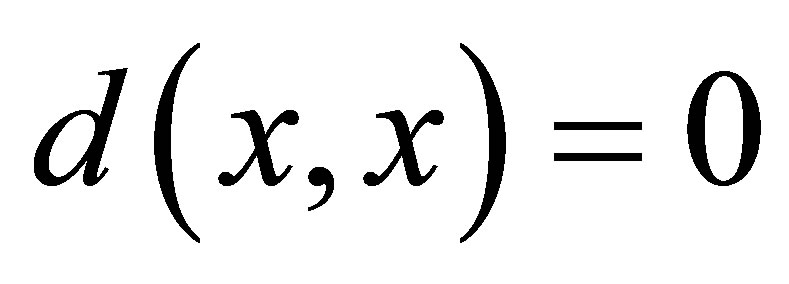 ;
;
(d2) if , then
, then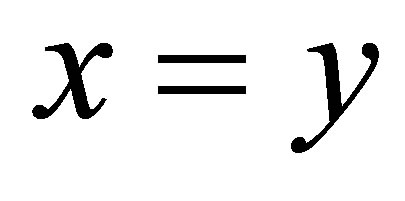 ;
;
(d3)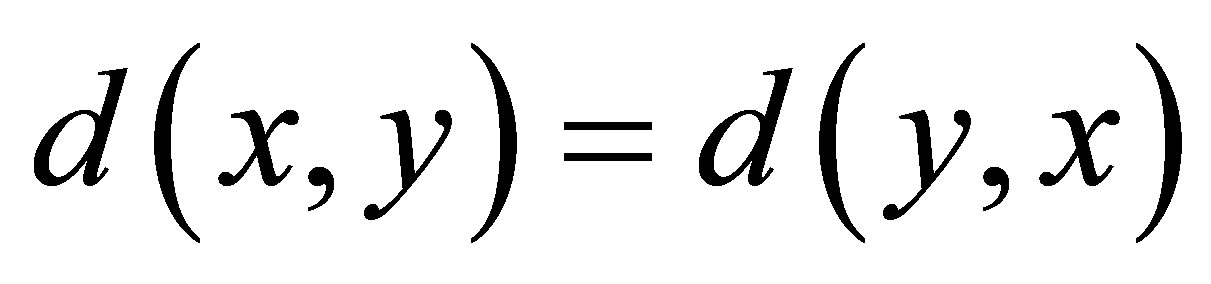 ;
;
(d4)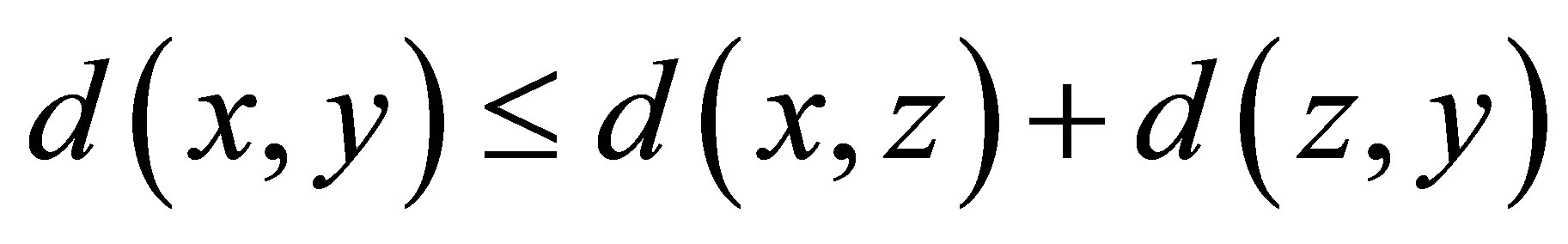 .
.
If  satisfies conditions (d1) - (d4), then it is called a metric on
satisfies conditions (d1) - (d4), then it is called a metric on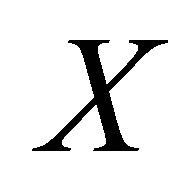 . If it satisfies conditions (d2) - (d4), then it is called a dislocated metric (or simply d-metric) on
. If it satisfies conditions (d2) - (d4), then it is called a dislocated metric (or simply d-metric) on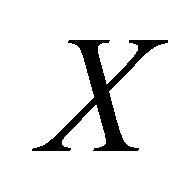 .
.
Definition 1.2. Let 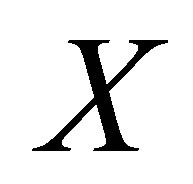 be a set. A distance function
be a set. A distance function  is called a partial metric on
is called a partial metric on 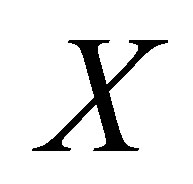 if it satisfies (d3) and the conditions:
if it satisfies (d3) and the conditions:
(d5)  if and only if
if and only if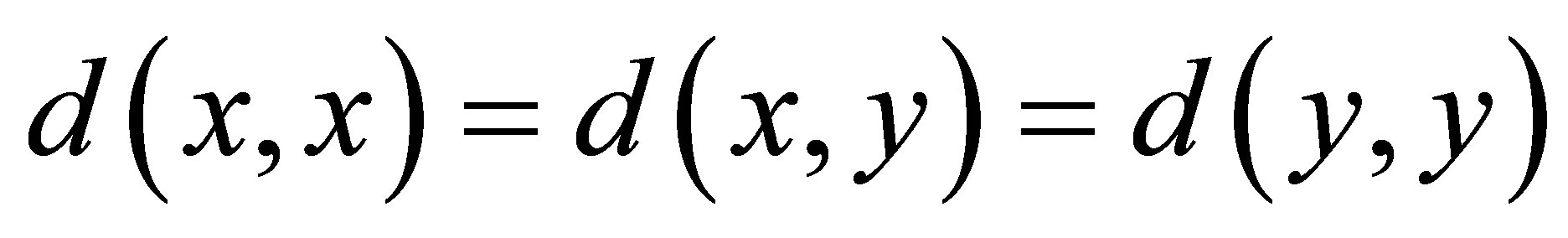 ;
;
(d6)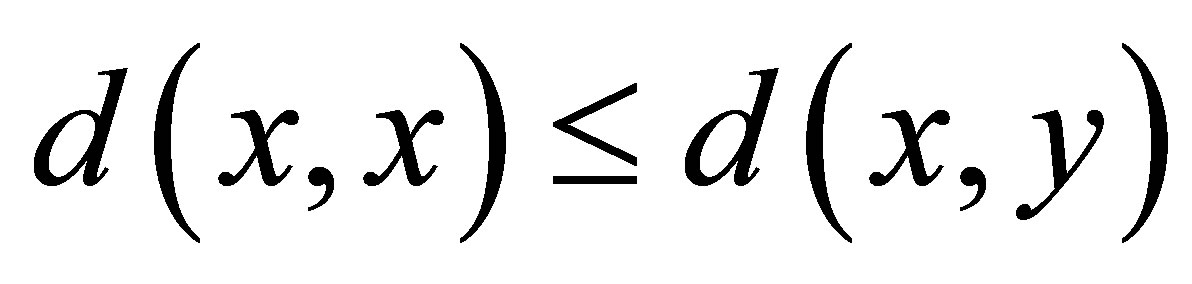 ;
;
(d7)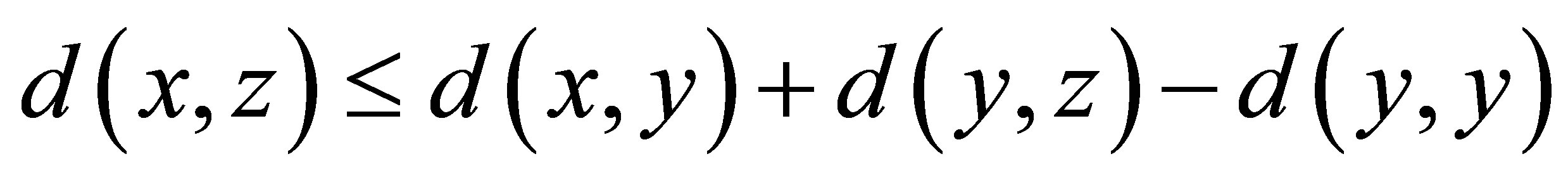 for each
for each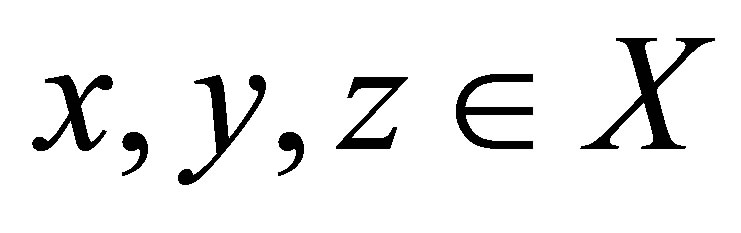 .
.
It is obvious that any partial metric is a d-metric.
Definition 1.3. An (open ) ball in a d-metric space
) ball in a d-metric space 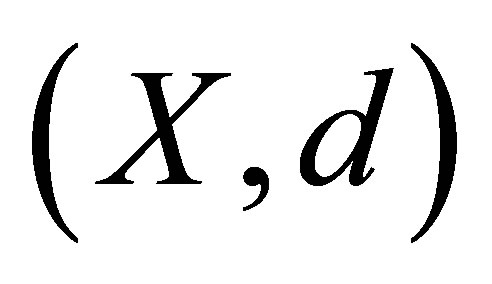 with centre
with centre 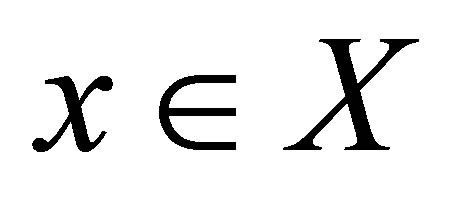 is a set of the form
is a set of the form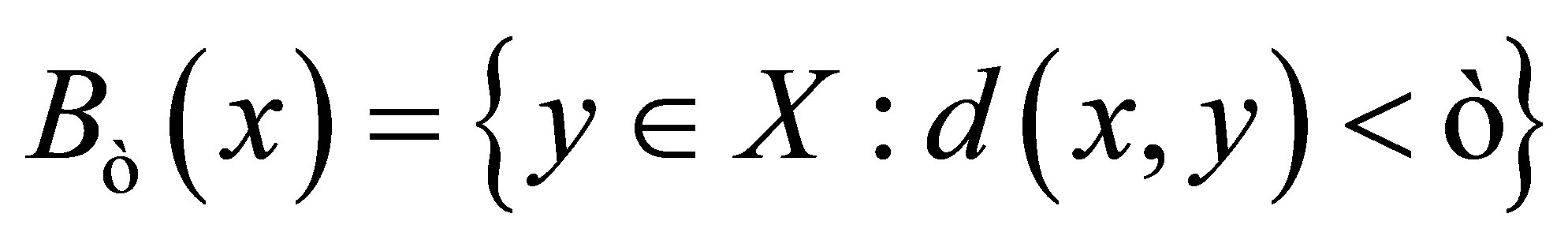 , where
, where .
.
It is clear that 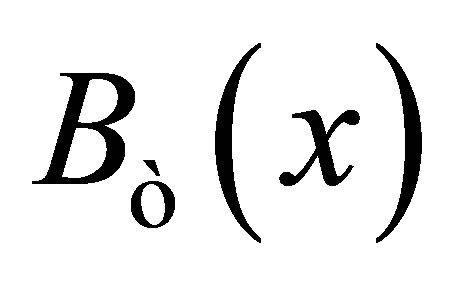 may be empty in a d-metric space
may be empty in a d-metric space 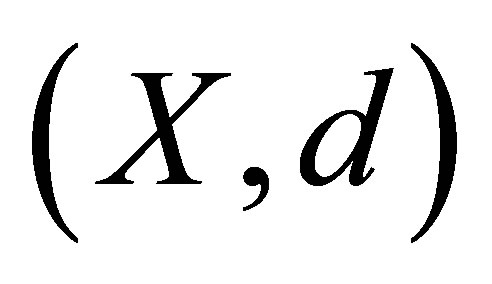 because the centre
because the centre 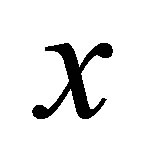 of the ball
of the ball  doesn’t belong to
doesn’t belong to .
.
Definition 1.4. Let 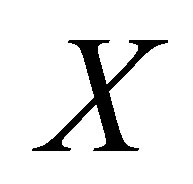 be set. A relation
be set. A relation  is called a d-membership relation(on
is called a d-membership relation(on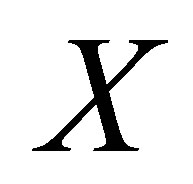 ) if it satisfies the following property for all
) if it satisfies the following property for all 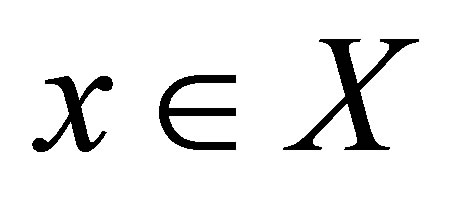 and
and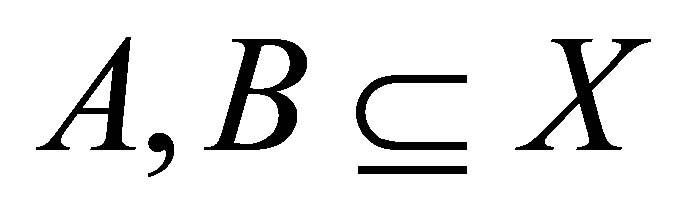 :
: 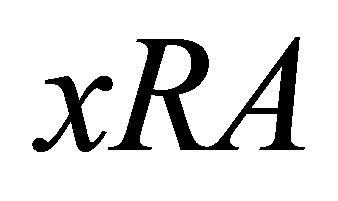 and
and 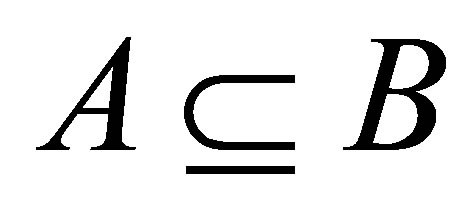 implies
implies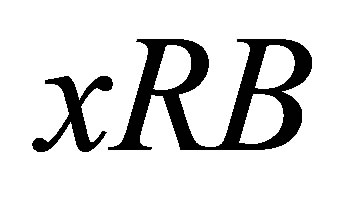 .
.
It is noted that the “d-membership”-relation is a generalization of the membership relation from the set theory.
In the sequel, any concept due to Hitzler and Seda will be denoted by “HS”.
Definition 1.5.Let 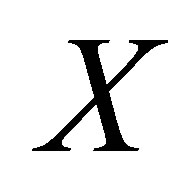 be a nonempty set. Suppose that
be a nonempty set. Suppose that 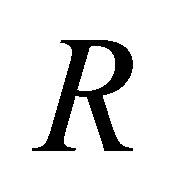 is a d-membership relation on
is a d-membership relation on 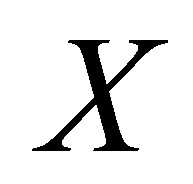 and
and 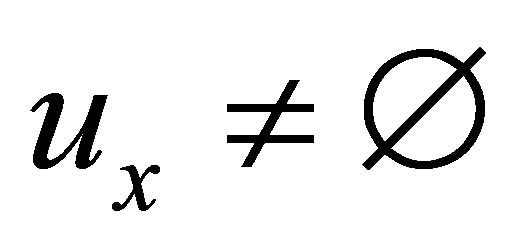 is a collection of subsets of
is a collection of subsets of  for each
for each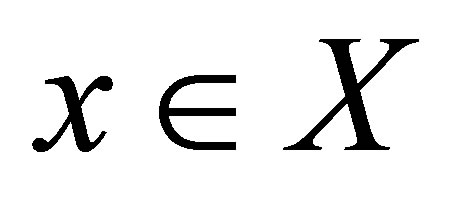 . We call
. We call 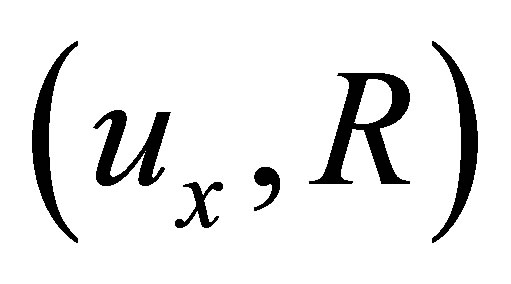 a d-neighbourhood system (d-nbhood system) for
a d-neighbourhood system (d-nbhood system) for 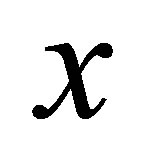 if it satisfies the following conditions:
if it satisfies the following conditions:
(Ni) if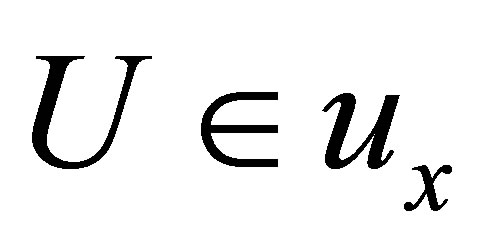 , then
, then ;
;
(Nii) if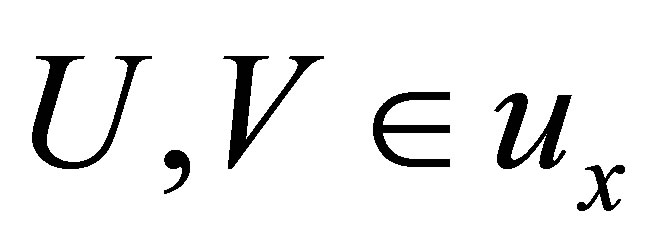 , then
, then ;
;
(Niii) if , then there is a
, then there is a 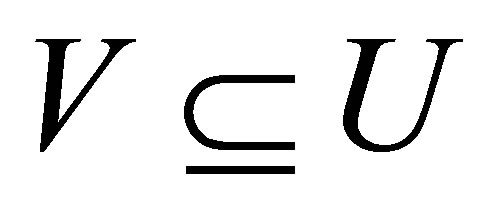 with
with 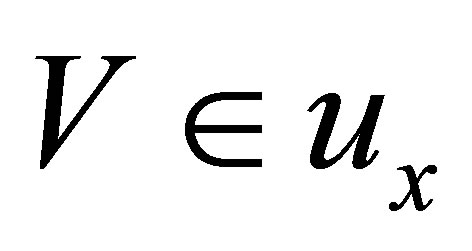 such that for all
such that for all 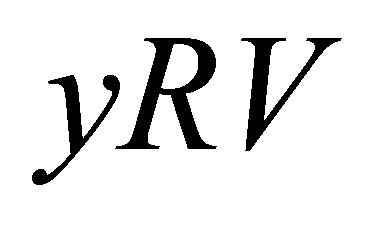 we have
we have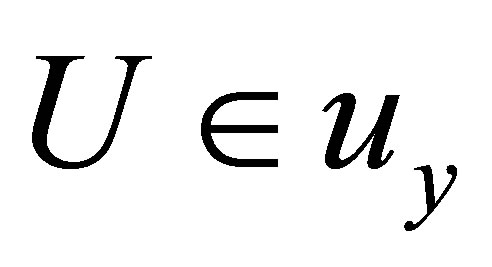 ;
;
(Niv) if 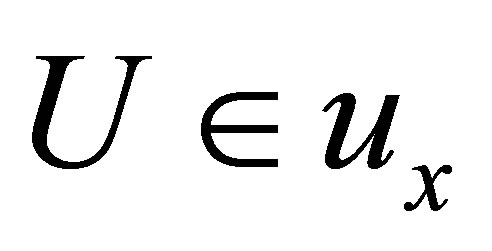 and
and 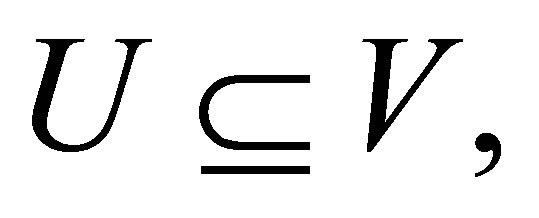 then
then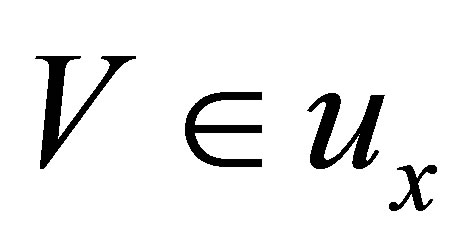 .
.
Each 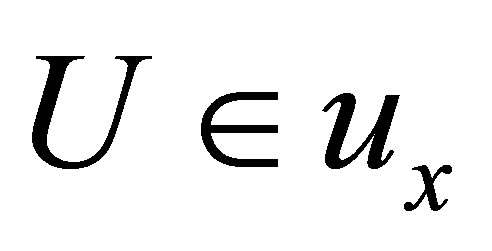 is called an HS-d-neighborhood (HS d-nbhood) of
is called an HS-d-neighborhood (HS d-nbhood) of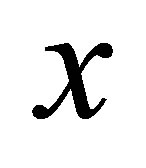 . The ordered triple
. The ordered triple 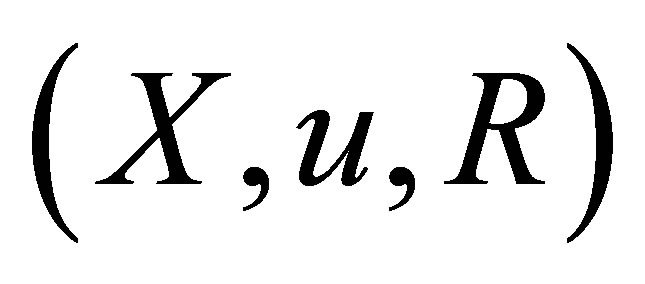 is called an HS-d-topological space where
is called an HS-d-topological space where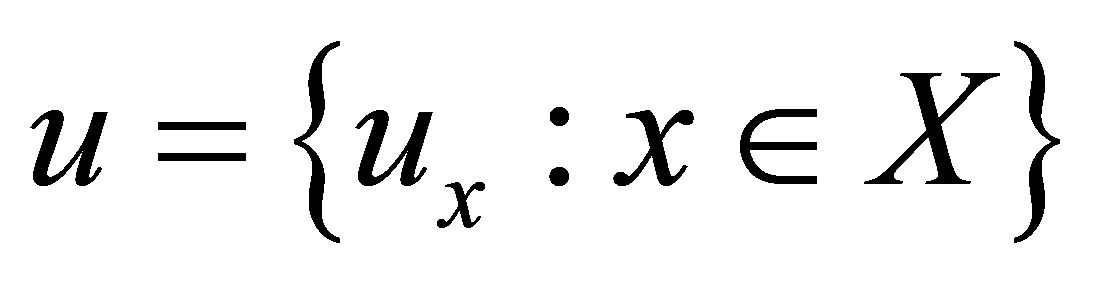 .
.
Proposition 1.1. Let 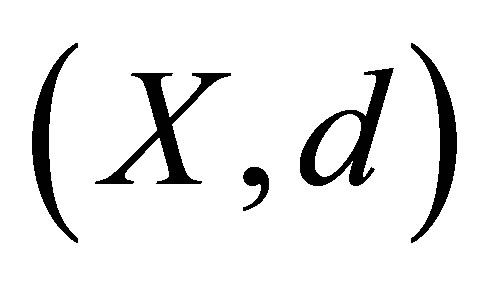 be a d-metric space. Define the d-membership relation
be a d-metric space. Define the d-membership relation 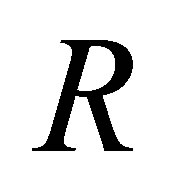 as the relation
as the relation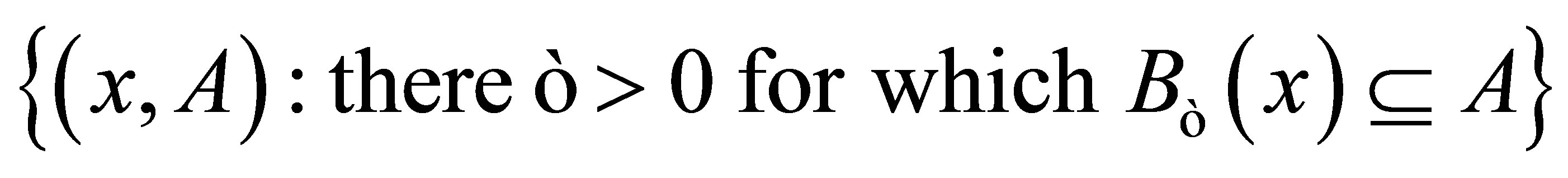 . For each
. For each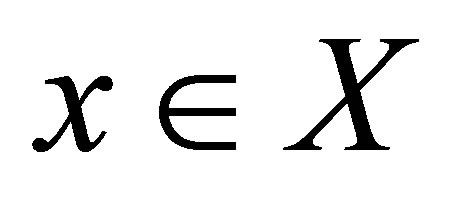 , let
, let 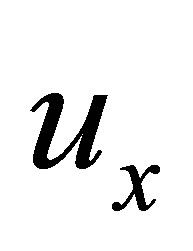 be the collection of all subsets
be the collection of all subsets  of
of 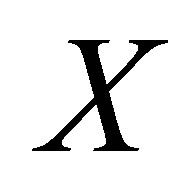 such that
such that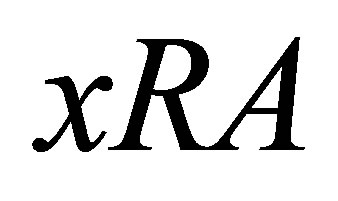 . Then
. Then 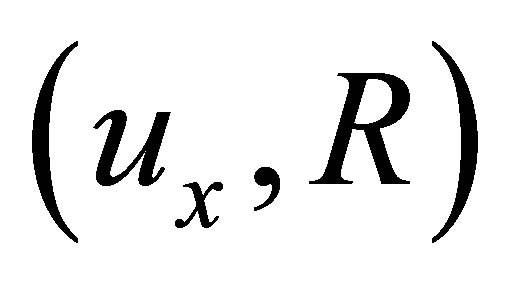 is an HS d-nbhood system for
is an HS d-nbhood system for  for each
for each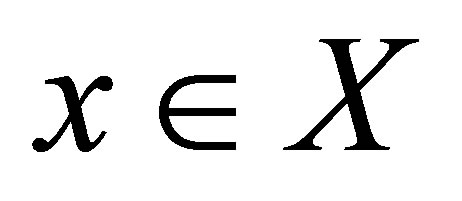 , i.e.,
, i.e., 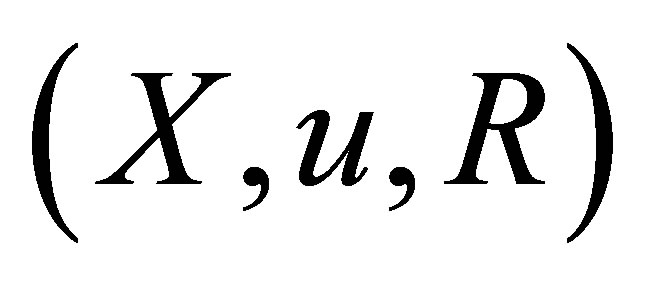 is an HS d-topological neighbourhood space.
is an HS d-topological neighbourhood space.
The present paper is organized as follows. In Section 2, we redefine the dislocated neighbourhood systems given due to Hitzler and Seda [1]. Section 3 is devoted to define the concept of dislocated topological space by open sets. In Section 4, we study topological properties of dislocated closure and dislocated interior operation of a set using the concept of open sets. Finally, in Section 5, we study some further properties of the well-known notions of dislocated continuous functions and dislocated convergence sequence via d-topologies.
2. Redefinition of Definition 1.5.
In Proposition 1.1, it is proved that 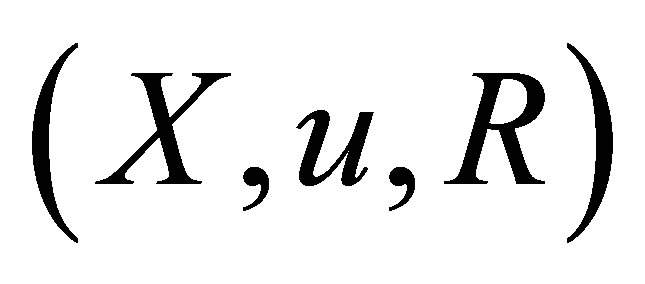 is an HS d-topological neighbourhood space. We remark that Property (Niii) can be replaced by the following condition:
is an HS d-topological neighbourhood space. We remark that Property (Niii) can be replaced by the following condition:
(Niii) * If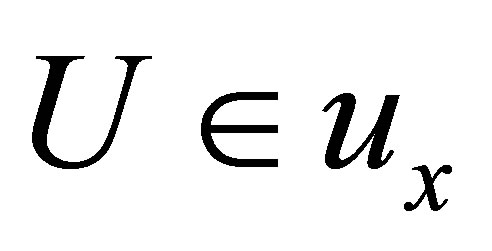 , then for each
, then for each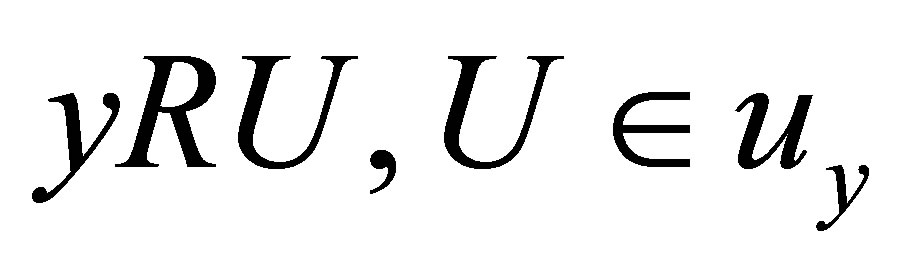 .
.
One can easily verifies that 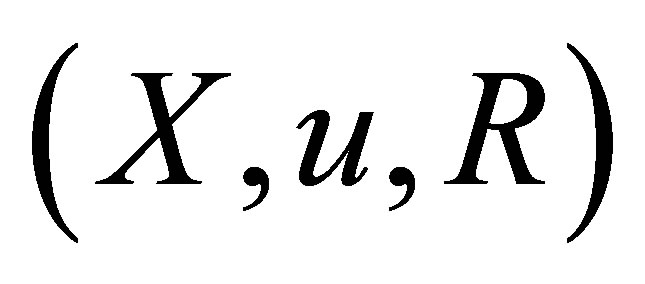 satisfies (Niii) *.
satisfies (Niii) *.
According to the above comment, we introduce a redefinition of the concept of the dislocated-neighbourhood systems due to Hitzler and Seda [1] as follows.
Definition 2.1. Let 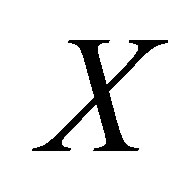 be a nonempty set. Suppose that
be a nonempty set. Suppose that 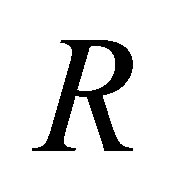 is a d-membership relation on
is a d-membership relation on  and
and  be a collection of subsets of
be a collection of subsets of  for each
for each . We call
. We call 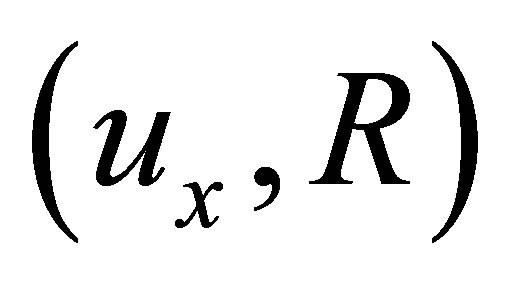 a d*-neighbourhood system (d*-nbhood system) for
a d*-neighbourhood system (d*-nbhood system) for 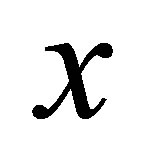 if it satisfies the following conditions:
if it satisfies the following conditions:
(Ni) if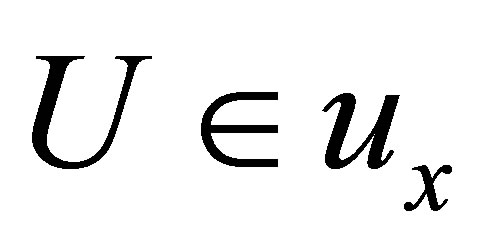 , then
, then ;
;
(Nii) if , then
, then ;
;
(Niii)* if  and
and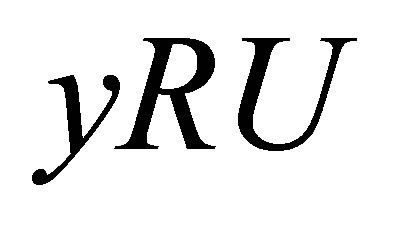 , then
, then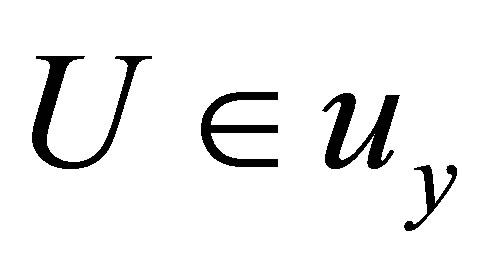 ;
;
(Niv) if 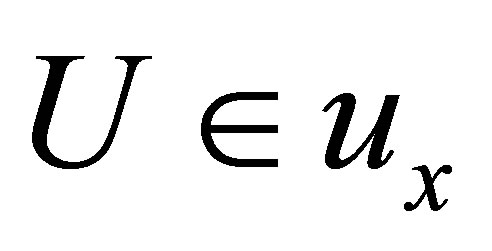 and
and , then
, then .
.
Each 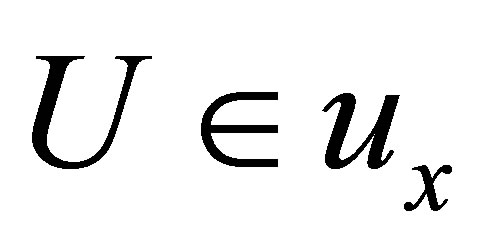 is called a d*-neighborhood of
is called a d*-neighborhood of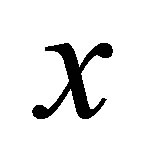 . If
. If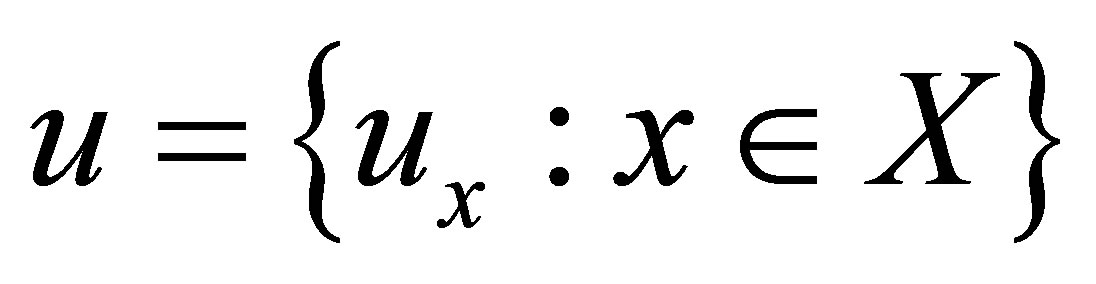 , then
, then 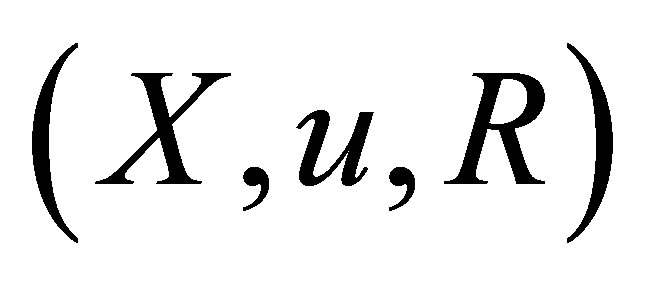 is called a d*-topological neighborhood space.
is called a d*-topological neighborhood space.
Now, we state the following theorem without proof.
Theorem 2.1. Let 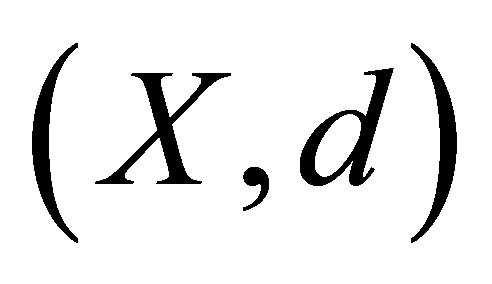 be a d-metric space. Define the d-membership relation
be a d-metric space. Define the d-membership relation 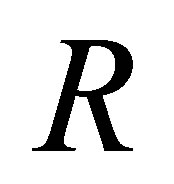 as the relation
as the relation 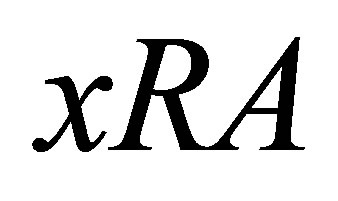 iff there exists
iff there exists 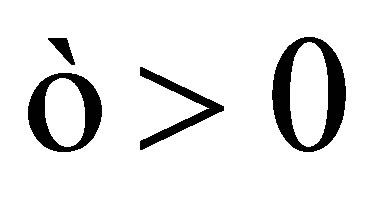 for which
for which . Assume that
. Assume that  and
and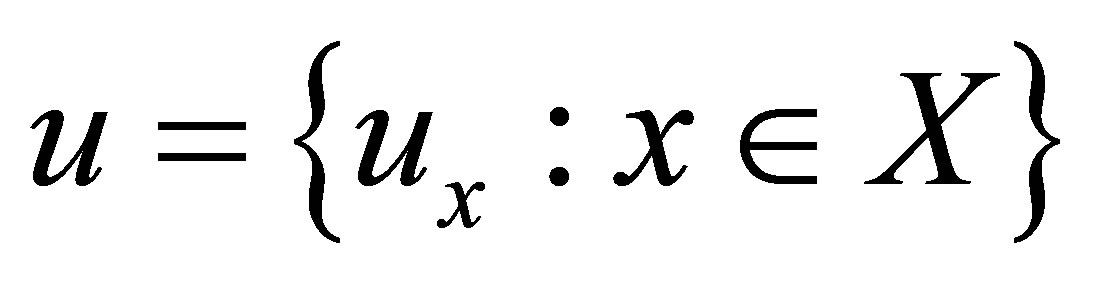 . Then
. Then 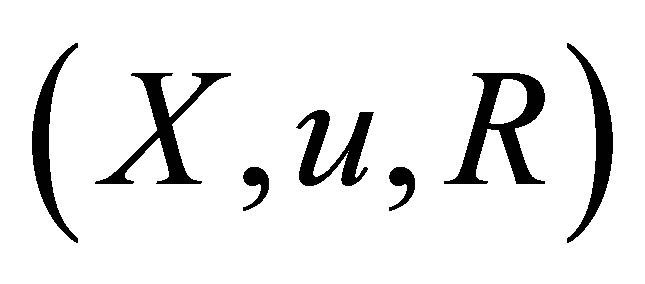 is a d*-topological neighborhood space.
is a d*-topological neighborhood space.
3. Dislocated-Topological Space
In what follows we define the concept of dislocatedtopological space (for short, d-topological space) by the open sets and prove that this concept and the concept of d*-topological neighborhood space are the same.
Definition 3.1. Let 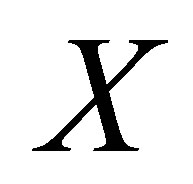 be a nonempty set. Suppose that
be a nonempty set. Suppose that  is a d-membership relation and
is a d-membership relation and 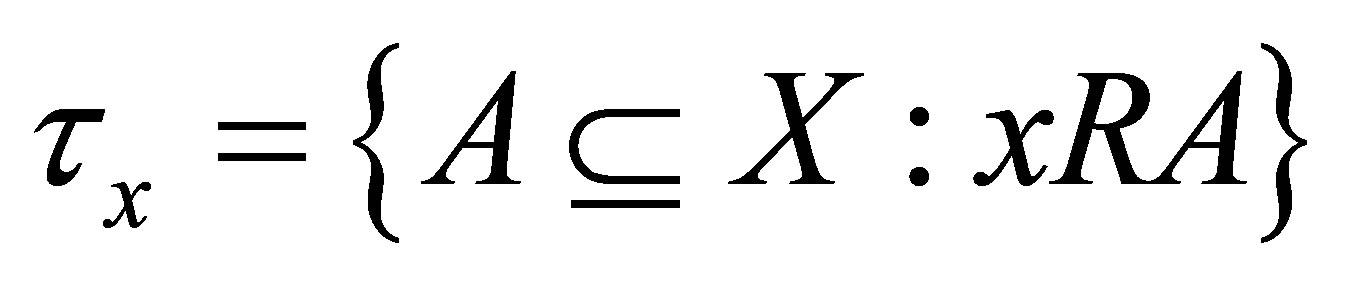 for each
for each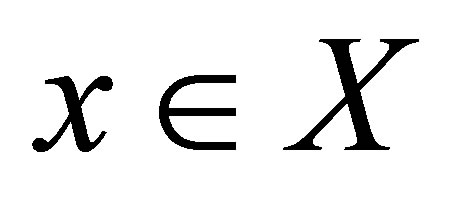 . We call
. We call 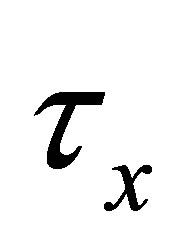 an
an 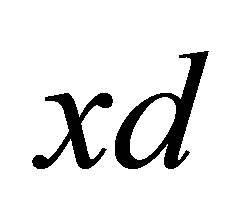 -topology on
-topology on 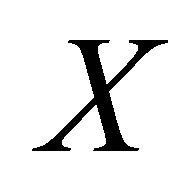 iff it satisfies the following conditions:
iff it satisfies the following conditions:
(dτx1) 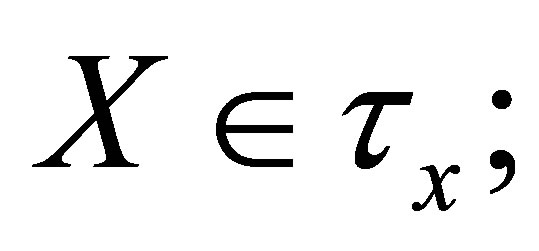
(dτx2) 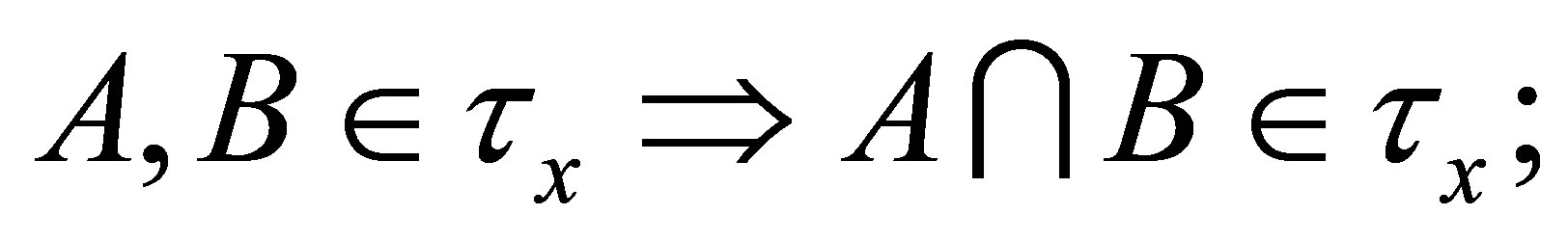
(dτx3) 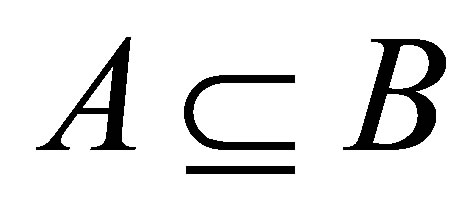 and
and .
.
Each 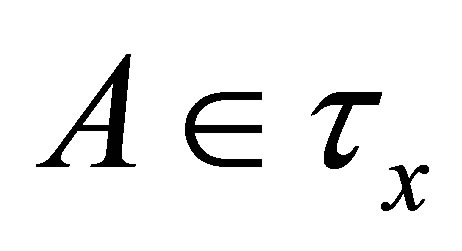 is called a
is called a 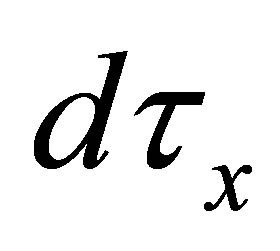 -open set. If
-open set. If 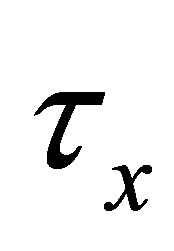 is an
is an  -topology on
-topology on  for each
for each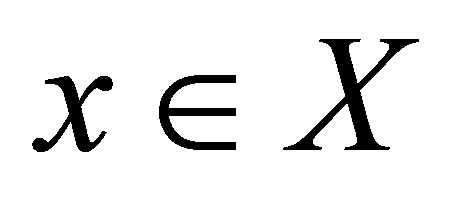 , then
, then 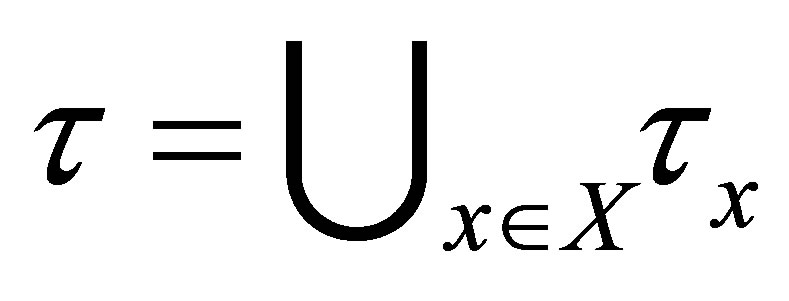 is called a d-topology on
is called a d-topology on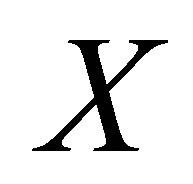 . The triple
. The triple  is called an
is called an 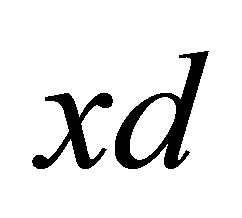 -topological space and the triple
-topological space and the triple 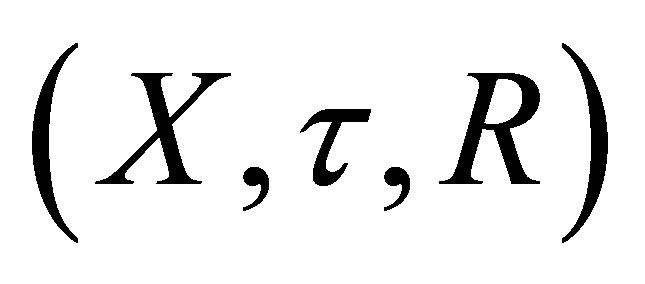 is called a d-topological space.
is called a d-topological space.
Definition 3.2. Let 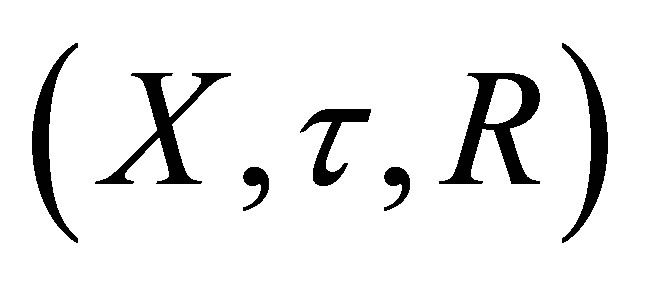 be an
be an 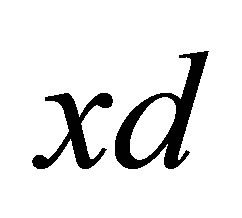 -topological space.
-topological space.  is called a
is called a 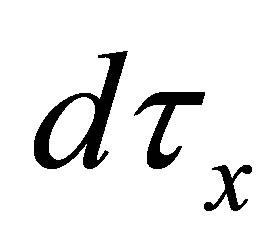 -closed iff
-closed iff 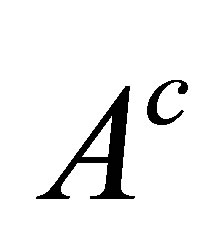 is a
is a 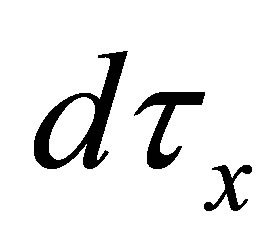 - open..
- open..
Theorem 3.1. The concepts of d*-topological neighborhood space and d-topological space are the same.
Proof. Let 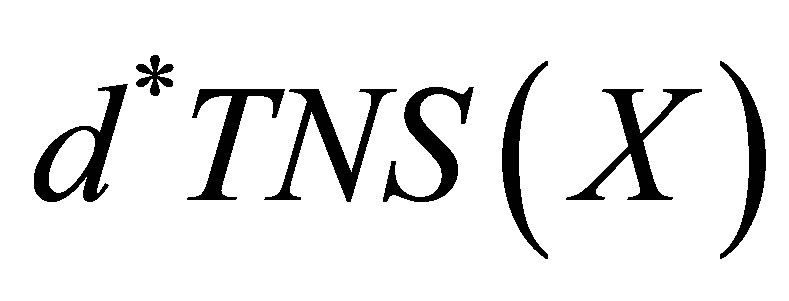 be the family of all d*- topological neighbourhood systems on
be the family of all d*- topological neighbourhood systems on 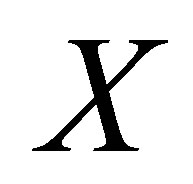 and let
and let 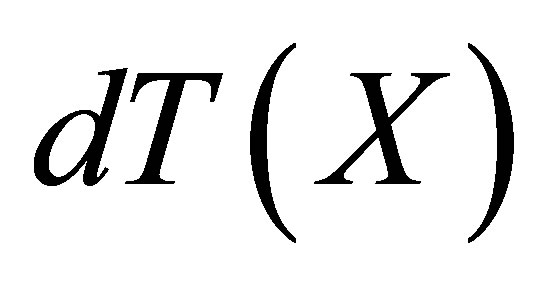 be the family of all d-topologies on
be the family of all d-topologies on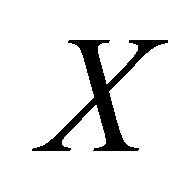 . The proof is complete if we point out a bijection between
. The proof is complete if we point out a bijection between 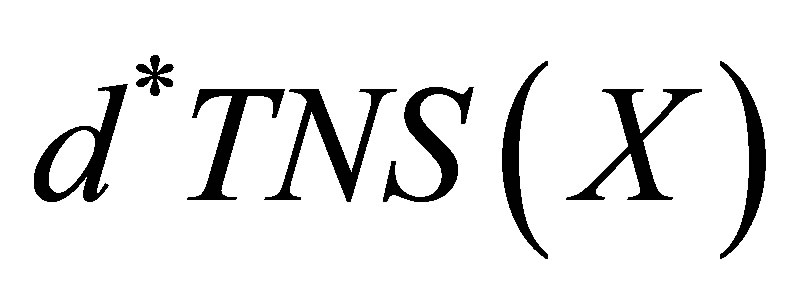 and
and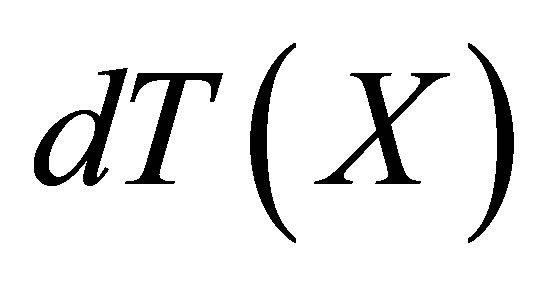 . Let
. Let 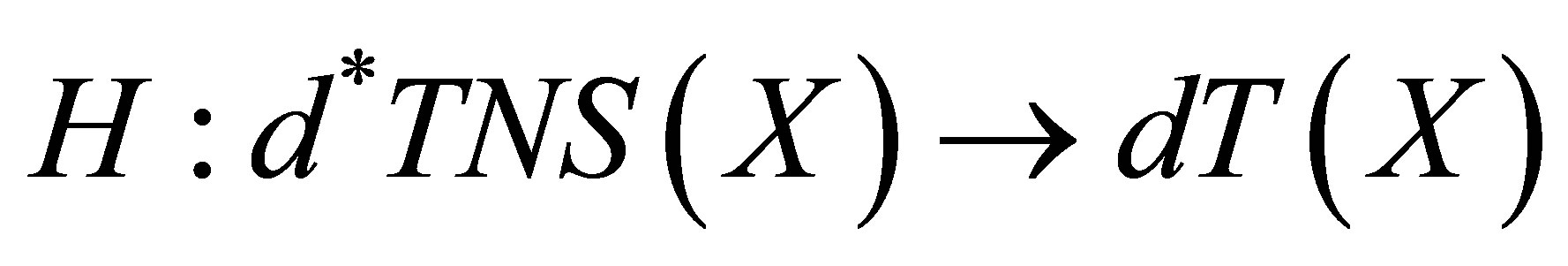 and
and 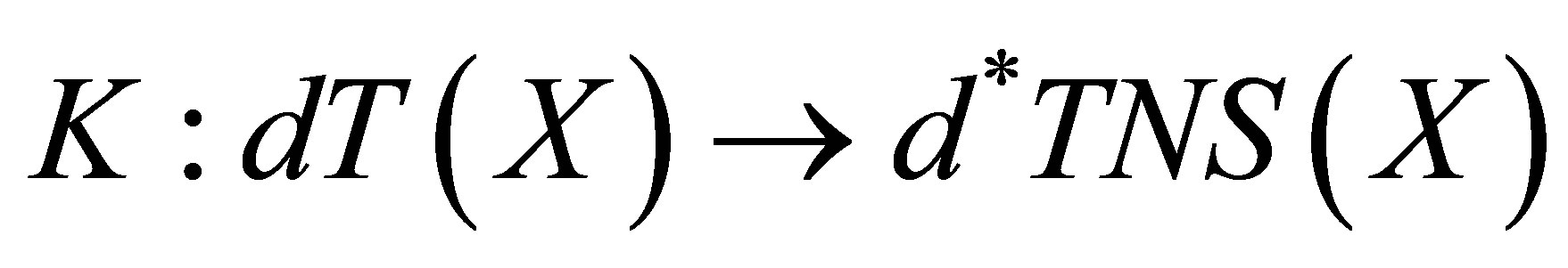 be functions defined as follows:
be functions defined as follows: , where
, where 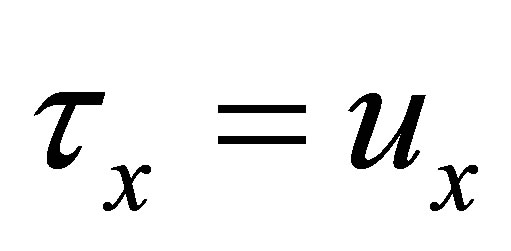 for each
for each 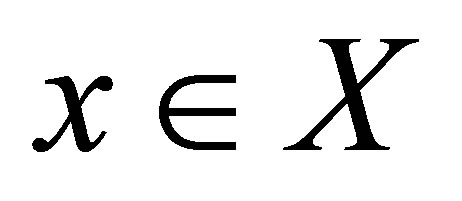 and
and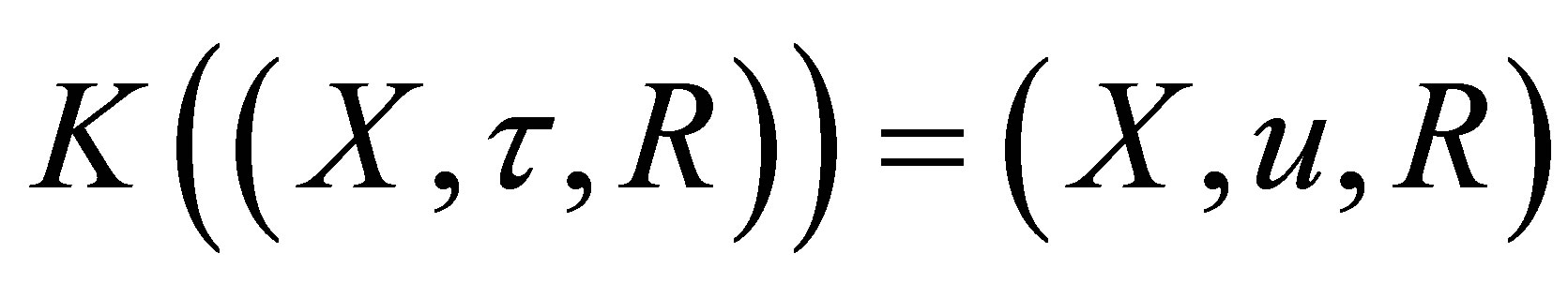 , where
, where 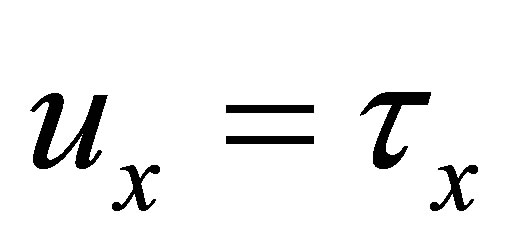 for each
for each . One can easily verifies that these functions are well defined,
. One can easily verifies that these functions are well defined,  and
and .
.
The following counterexample illustrates that the statement: 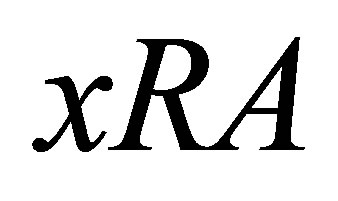 iff
iff 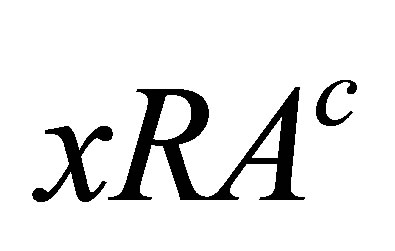 may not be true.
may not be true.
Counterexample 3.1. Let 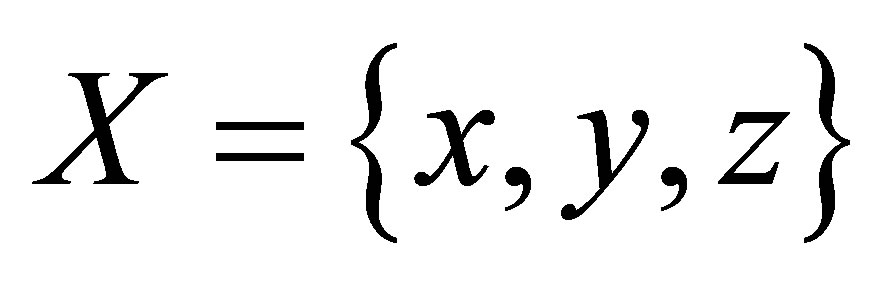 and
and
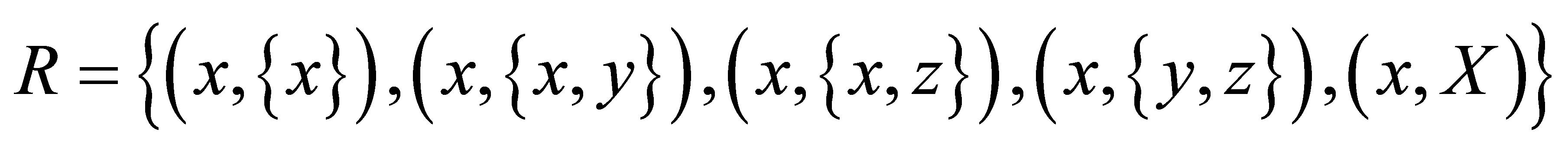 .
.
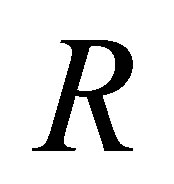 is a d-membership relation. Since
is a d-membership relation. Since 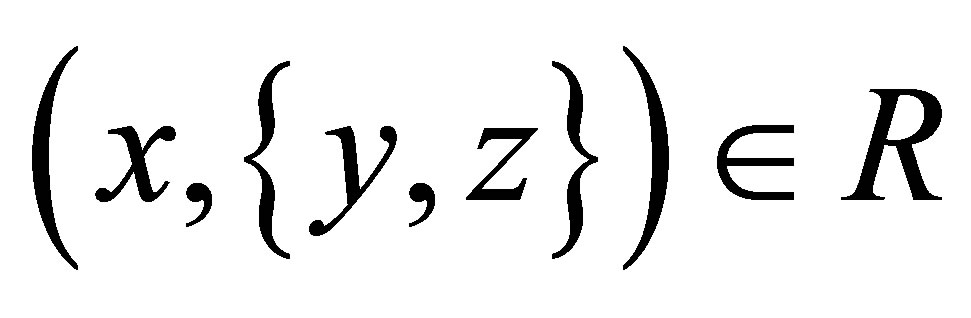 , then
, then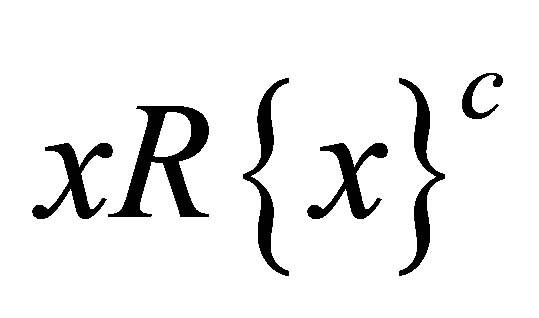 , i.e.
, i.e. 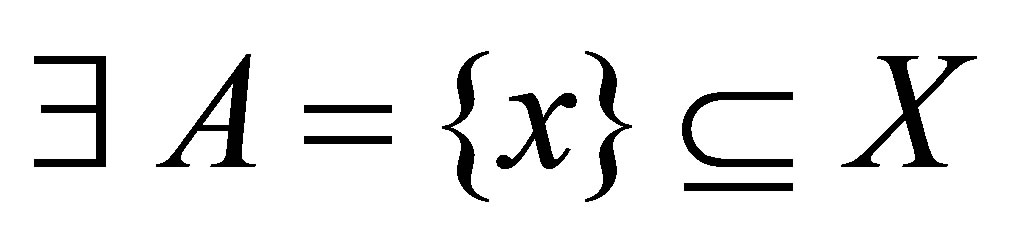 such that
such that 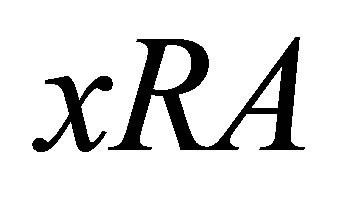 and
and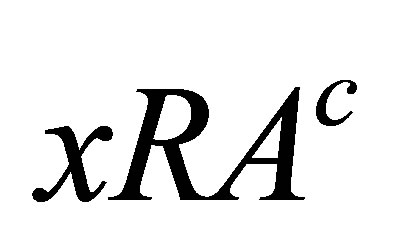 .
.
We get the following theorem without proof.
Theorem 3.2. Let 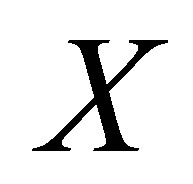 be a nonempty set. Suppose that
be a nonempty set. Suppose that  is a d-membership relation and
is a d-membership relation and 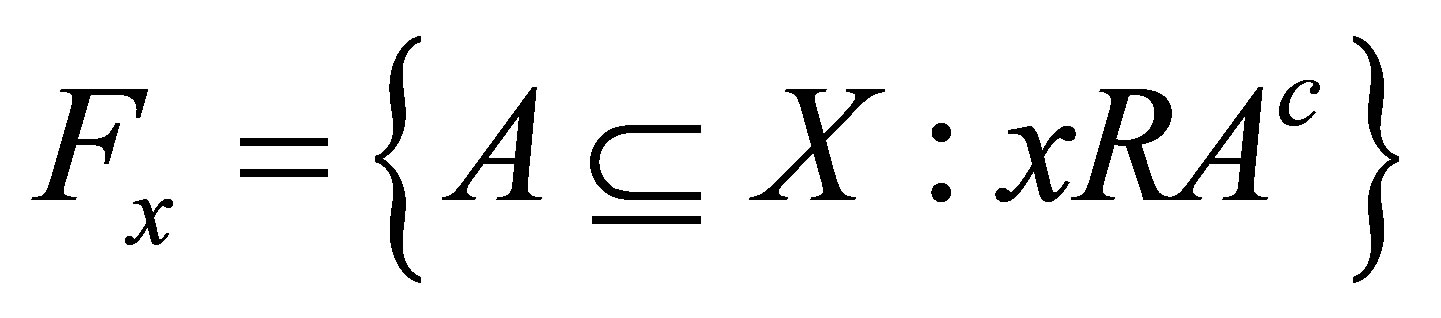 for each
for each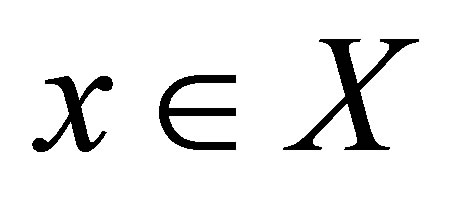 . Assume that
. Assume that 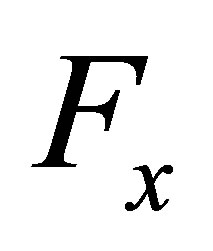 satisfies the following conditions:
satisfies the following conditions:
(dFx1)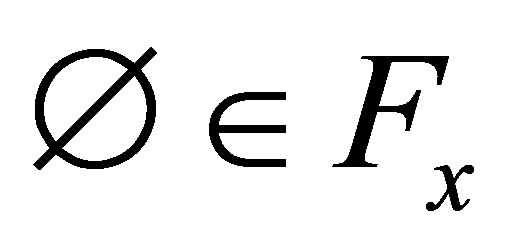 ;
;
(dFx2)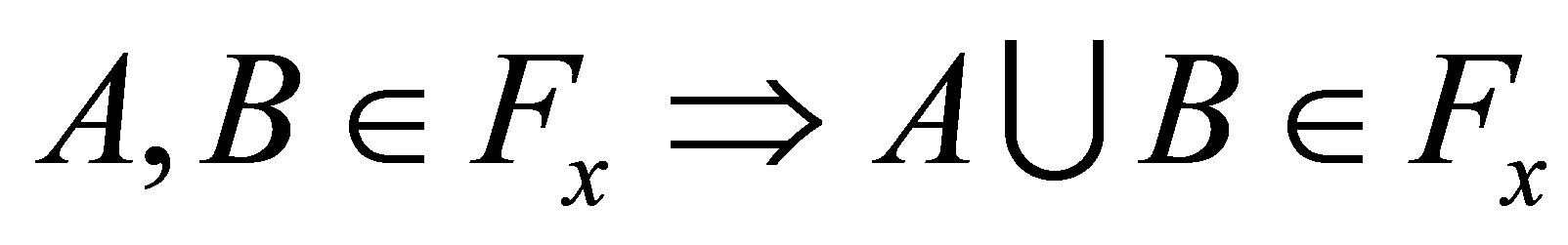 ;
;
(dFx3) 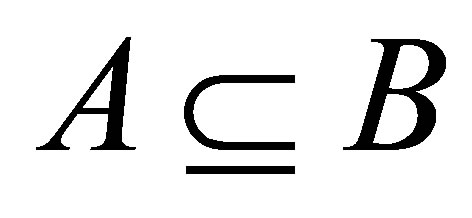 and
and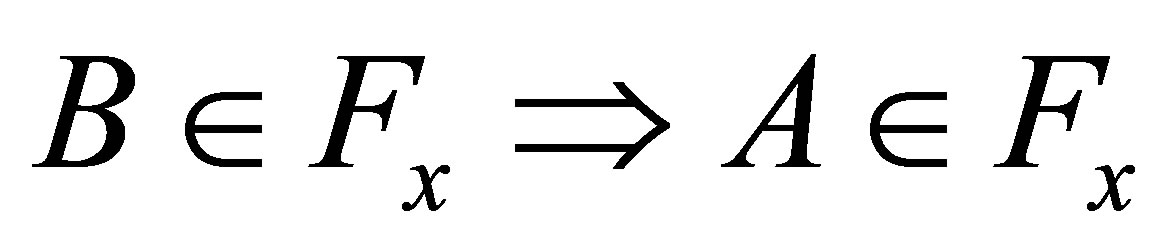 .
.
Then  is a d-topology on
is a d-topology on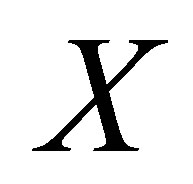 , where
, where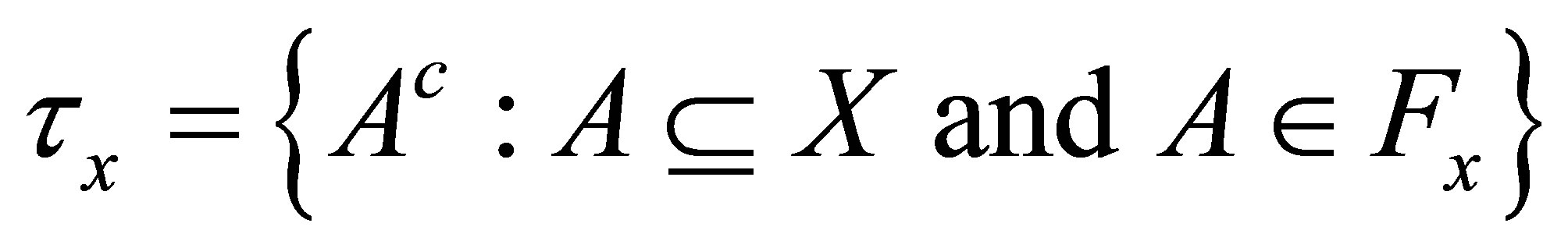 . If
. If  is a dtopological space, then for each
is a dtopological space, then for each 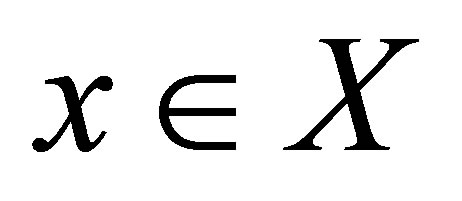 the family
the family  of all
of all 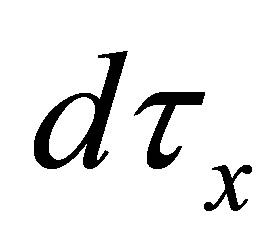 -closed sets satisfies the conditions (dFx1)- (dFx3).
-closed sets satisfies the conditions (dFx1)- (dFx3).
4. Dislocated Closure and Dislocated Interior Operations
In the sequel we define the dislocated closure and dislocated interior operations of a set and study some topological properties of dislocated closure and dislocated interior operation.
Definition 4.1. Let 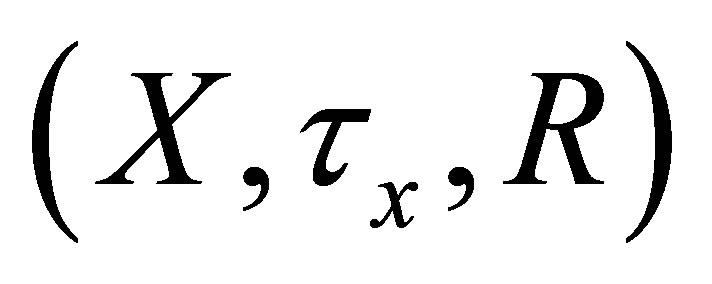 be an
be an 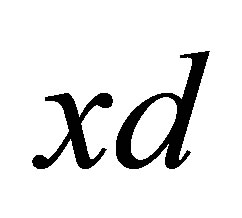 -topological space. The
-topological space. The 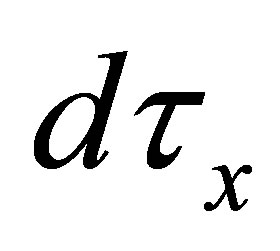 -interior of a subset
-interior of a subset  of
of 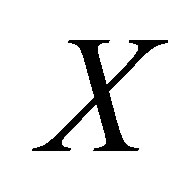 is denoted and defined by:
is denoted and defined by: .
.
Remark 4.1. From Definition 4.1, if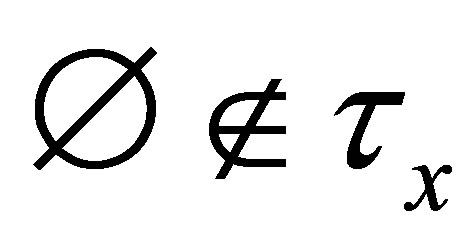 , then
, then 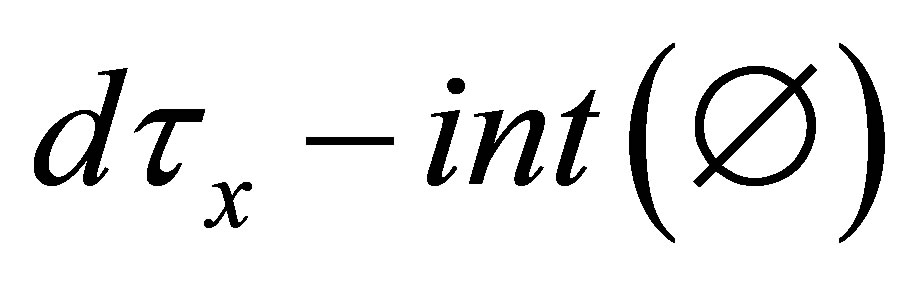 is undefined. If
is undefined. If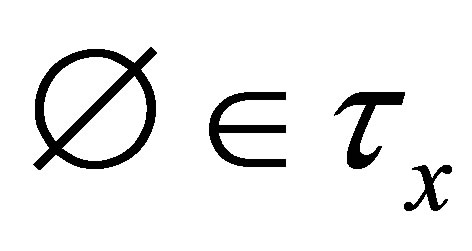 , then
, then 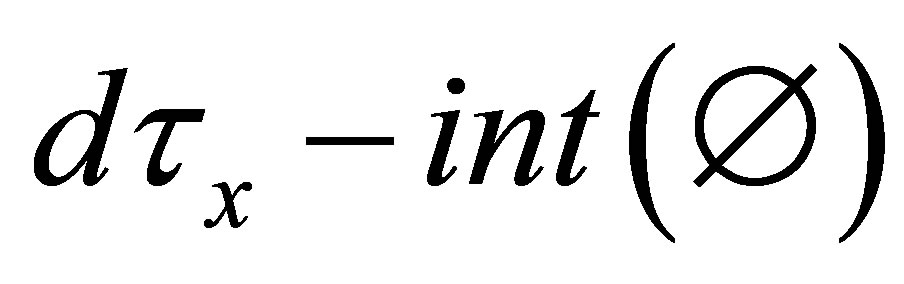 is defined.
is defined.
Theorem 4.1. Let 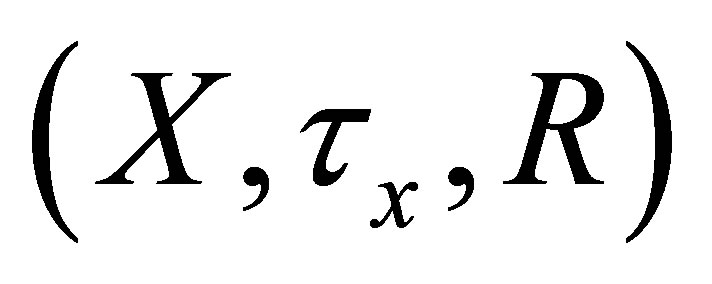 be an
be an  -topological space.
-topological space.
(A) If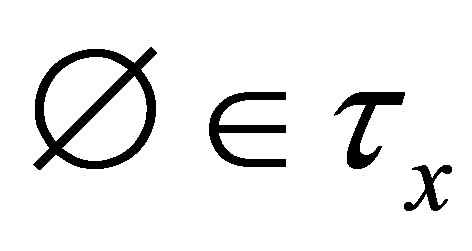 , then
, then  for each
for each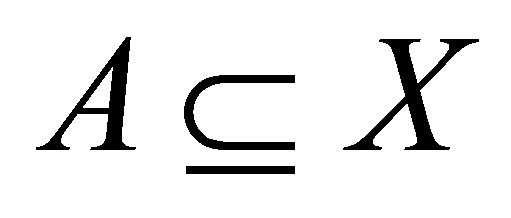 .
.
(B) If , then
, then
(i)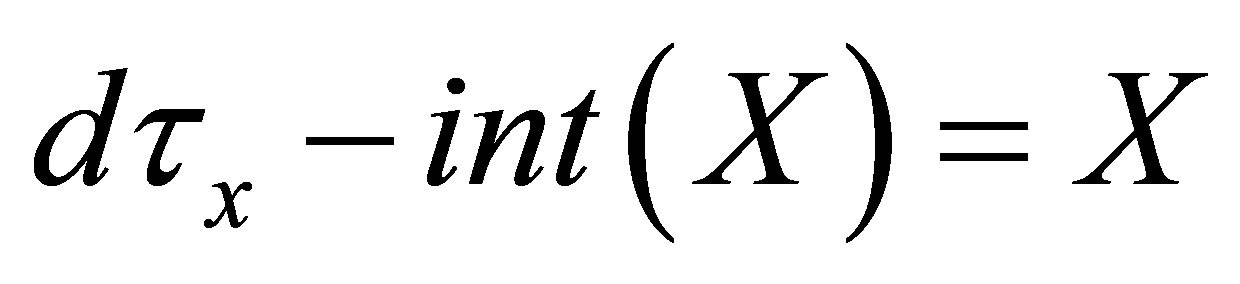 ;
;
(ii)  for each
for each ;
;
(iii) 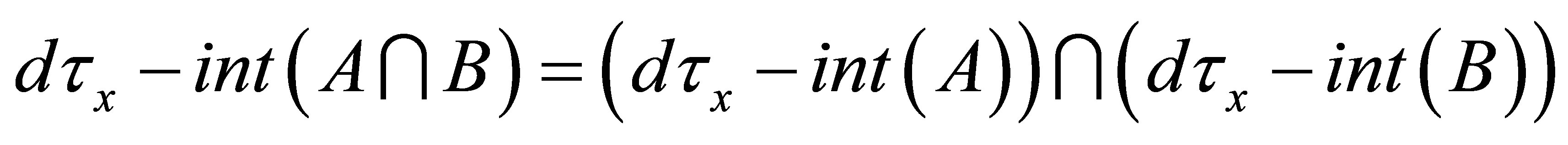 for each
for each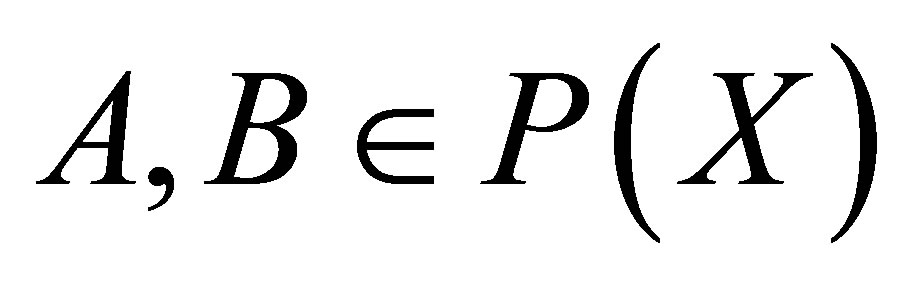 ;
;
(iv) 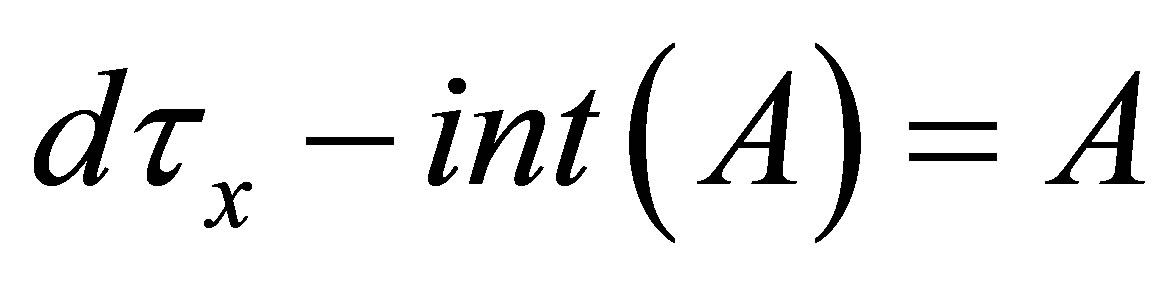 or
or  for each
for each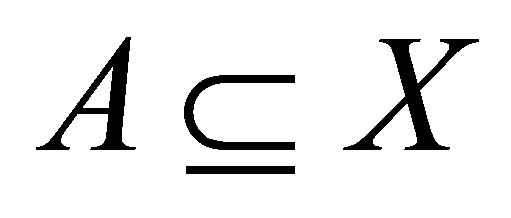 .
.
(v)  if
if 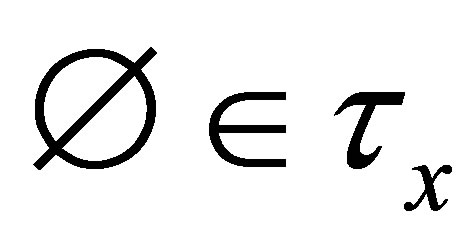 or
or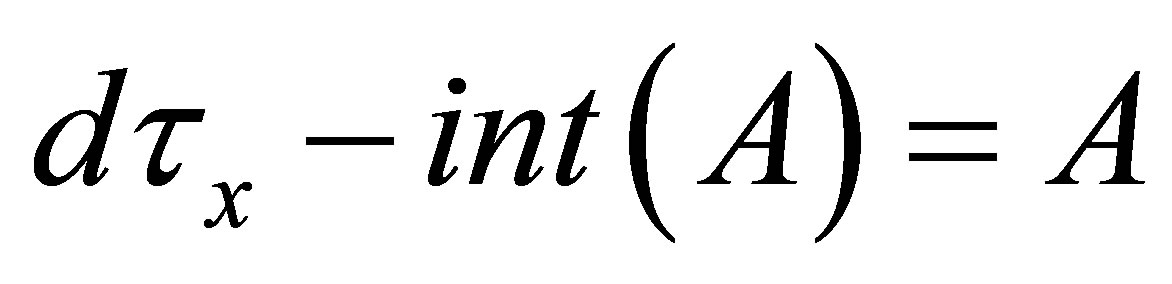 .
.
Corollary 4.1. (1) If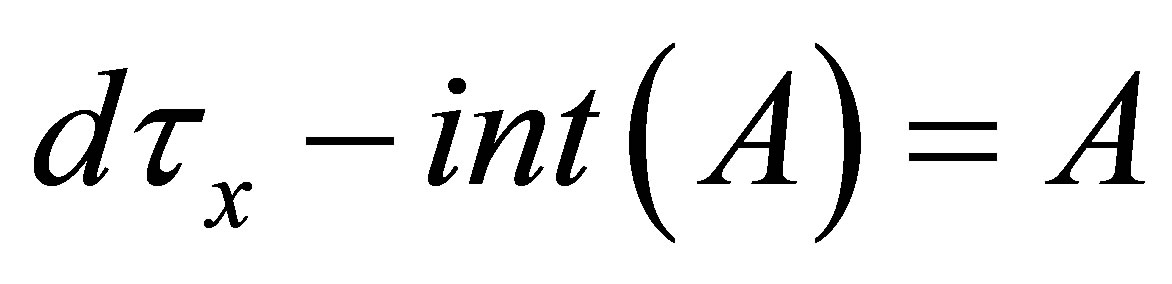 , then
, then 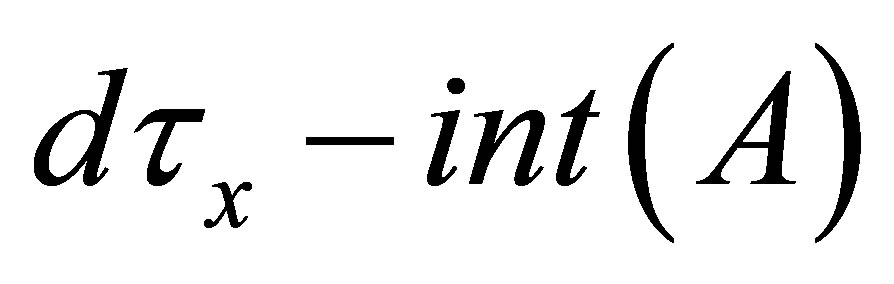 is a
is a 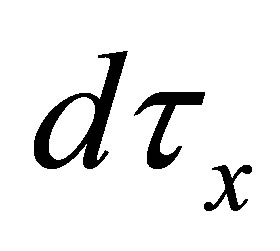 -open.
-open.
(2) If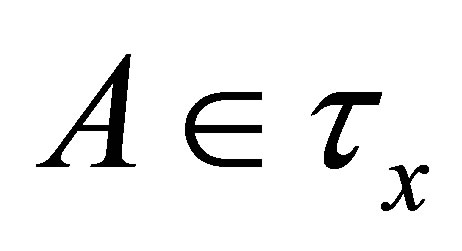 , then
, then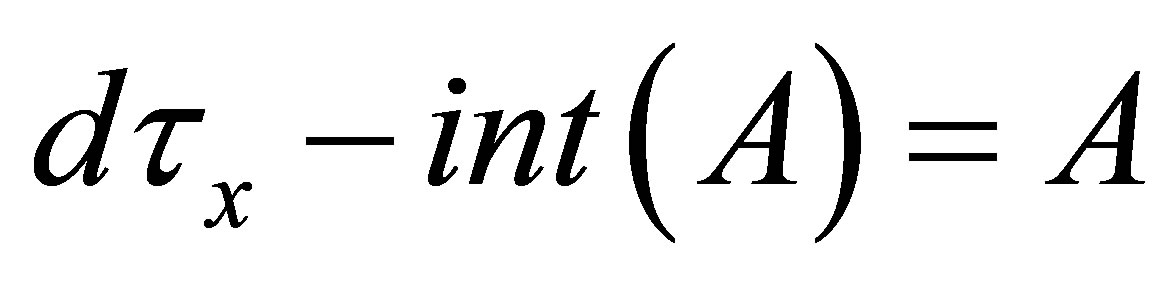 .
.
Theorem 4.2. If 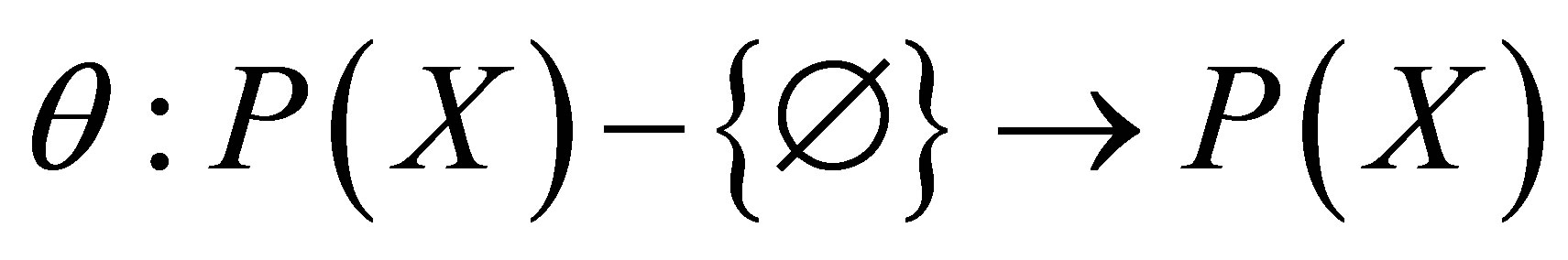 such that the conditions B(i), B(iii) and B(iv) are satisfied then
such that the conditions B(i), B(iii) and B(iv) are satisfied then
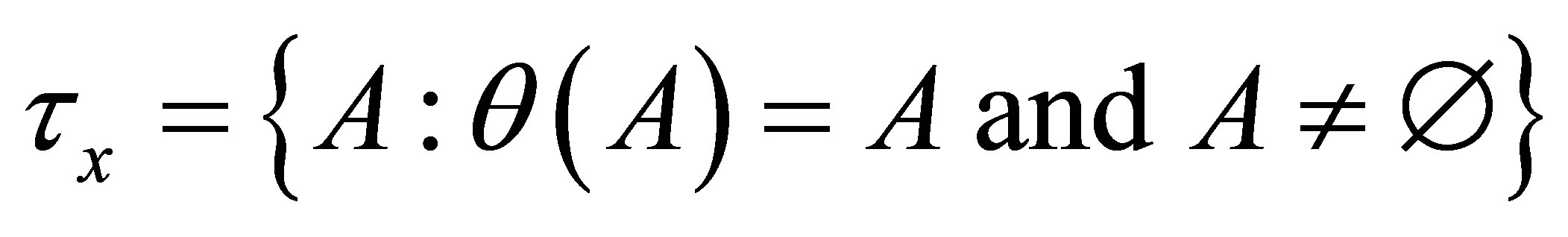 is an
is an 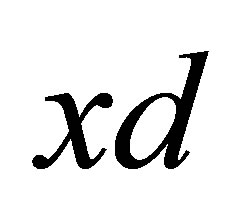 -topology on
-topology on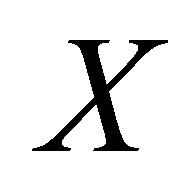 . The
. The 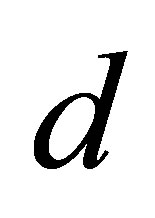 -membership relation is defined as
-membership relation is defined as 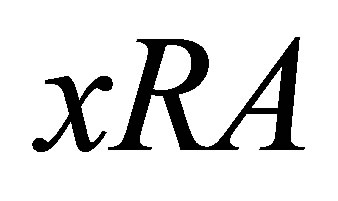 iff
iff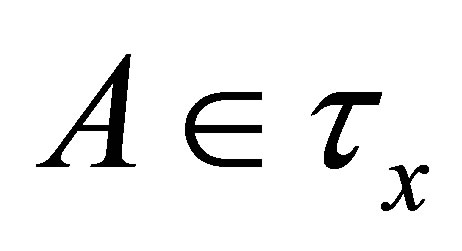 .
.
Proof. The desired result is obtained from the following:
(I) (dτx1) 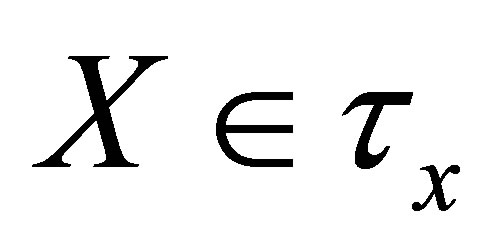 since
since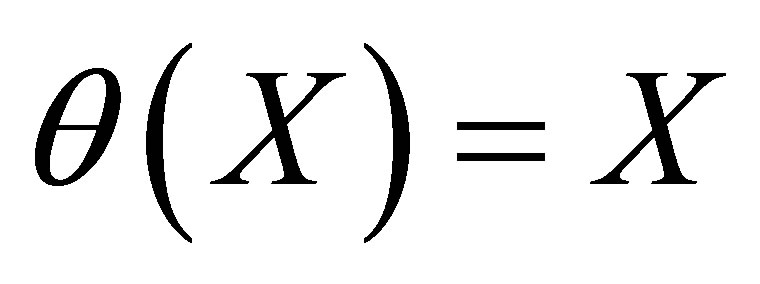 ;
;
(dτx2)  and
and
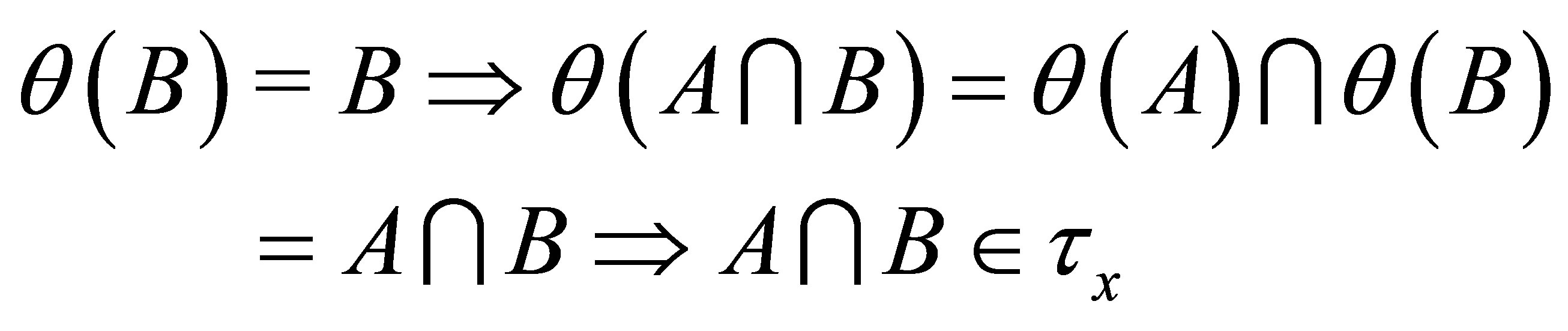 ;
;
(dτx3) 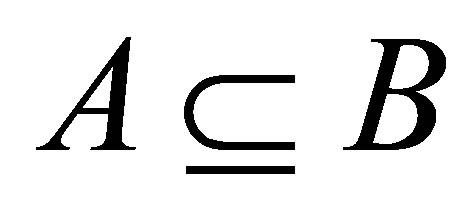 and
and ,
, 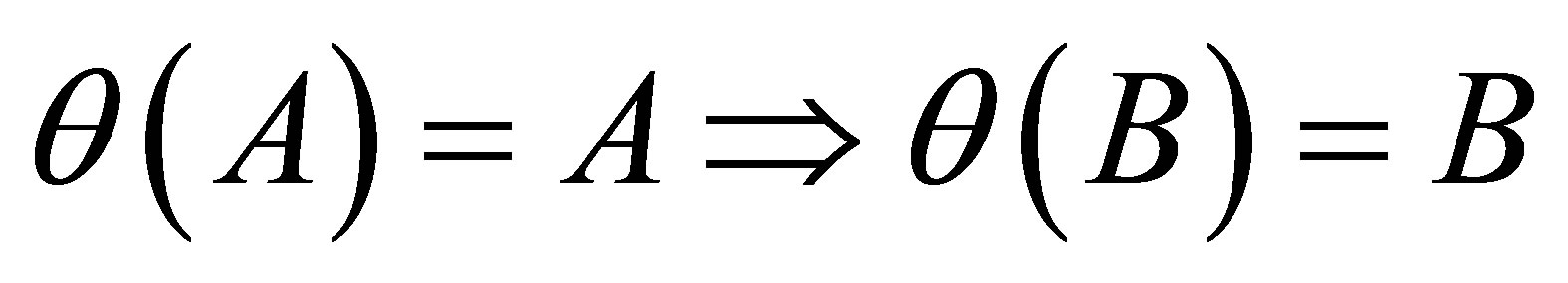 (from B(iii)-(iv)).
(from B(iii)-(iv)).
(II)  and
and  and
and  (from I
(from I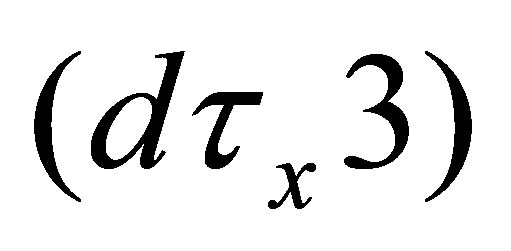 ).
).
Definition 4.2. Let 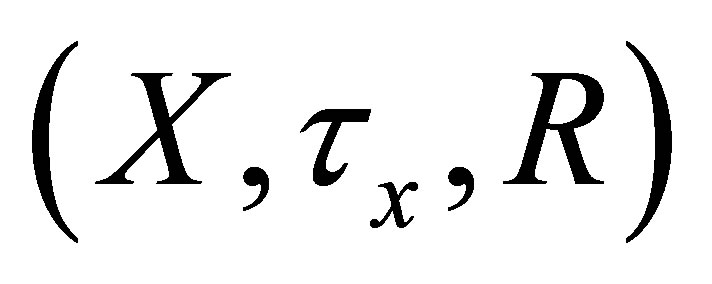 be an
be an 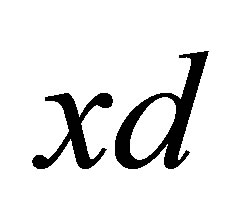 -topological space. The
-topological space. The 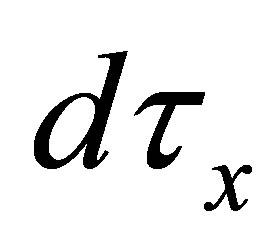 -closure of a subset
-closure of a subset  of
of 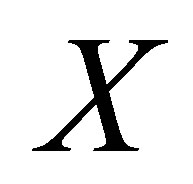 is denoted and defined by:
is denoted and defined by: .
.
If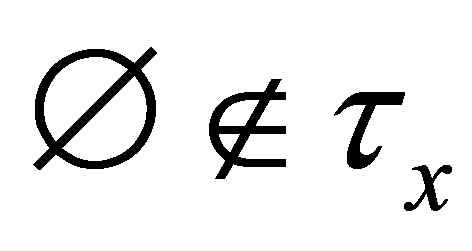 , then
, then 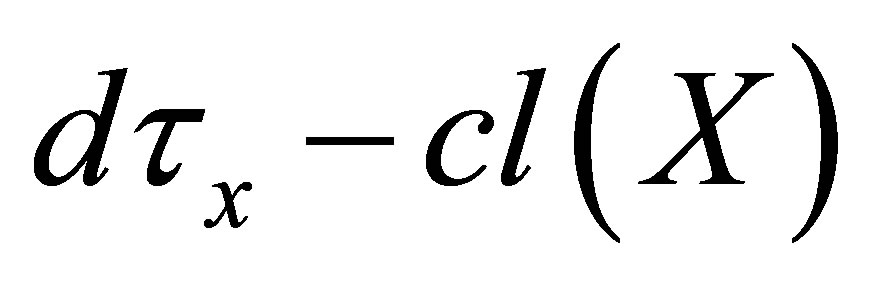 is undefined but if
is undefined but if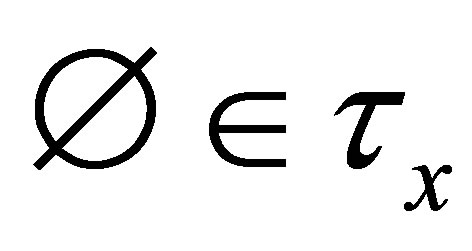 , then
, then 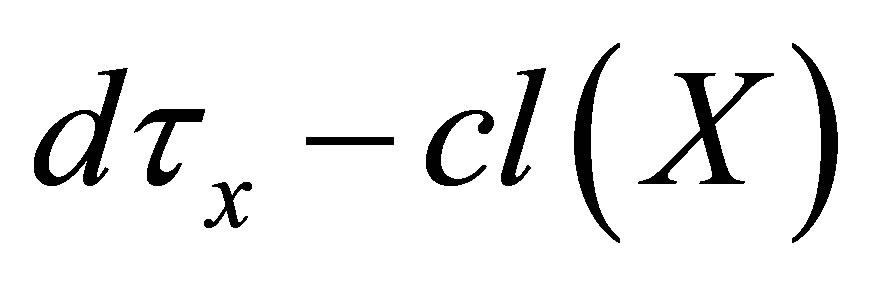 is defined.
is defined.
Theorem 4.3. Let 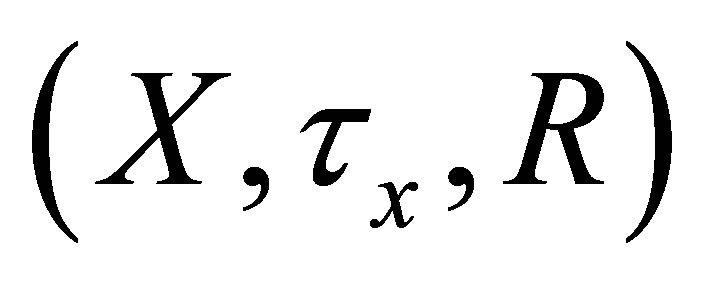 be an
be an  -topological space. Then for each
-topological space. Then for each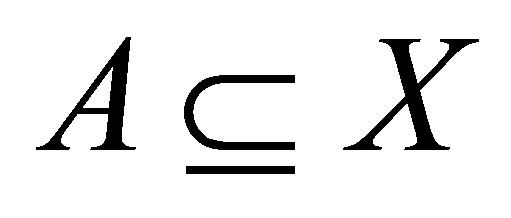 ,
,
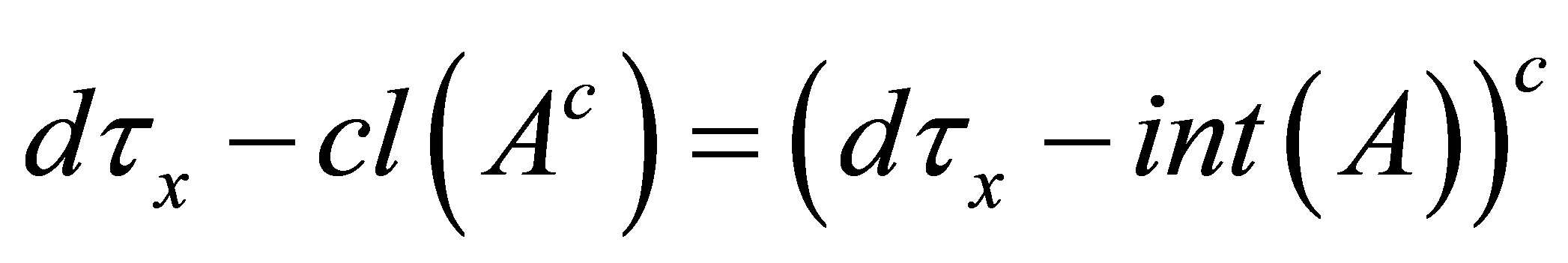 .
.
Proof.

From Theorems 4.1 and 4.3, we obtain the following theorem without proof.
Theorem 4.4. Let 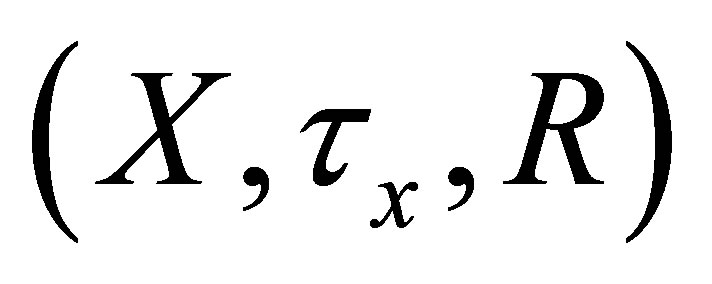 be an
be an 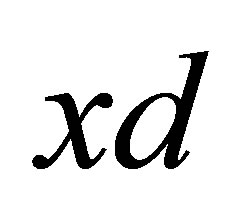 -topological space.
-topological space.
(A) If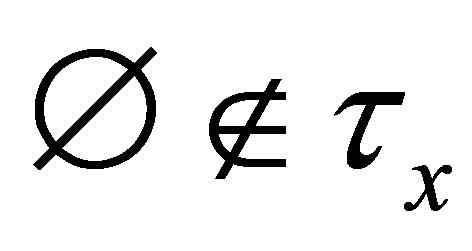 , then
, then 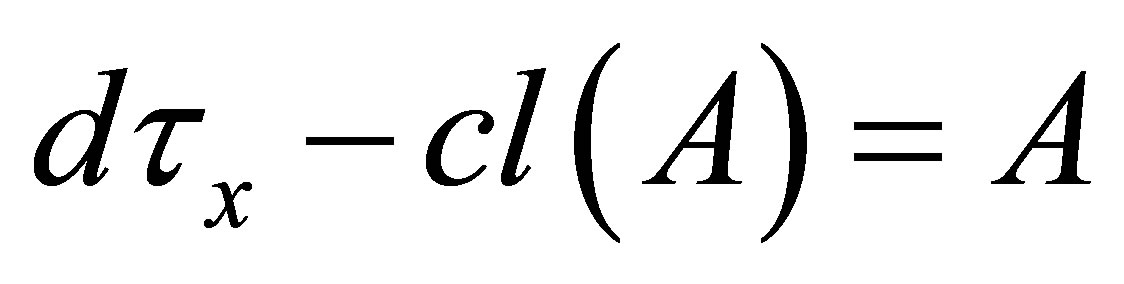 for each
for each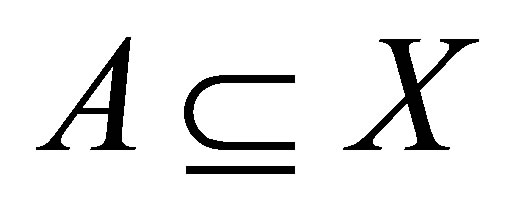 .
.
(B) If , then
, then
(i)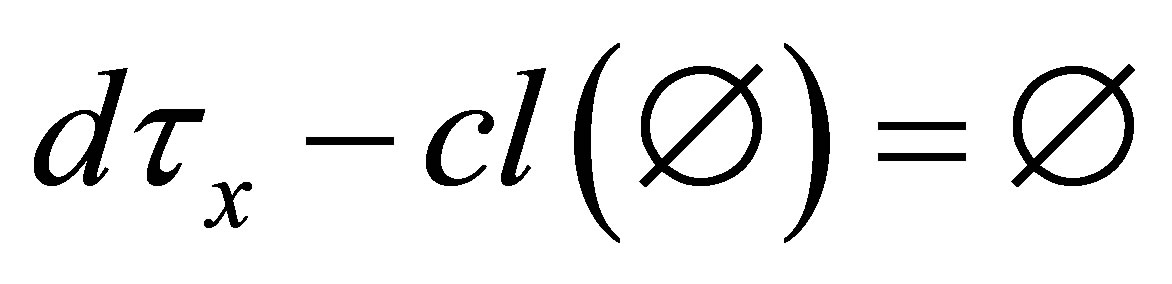 ;
;
(ii) 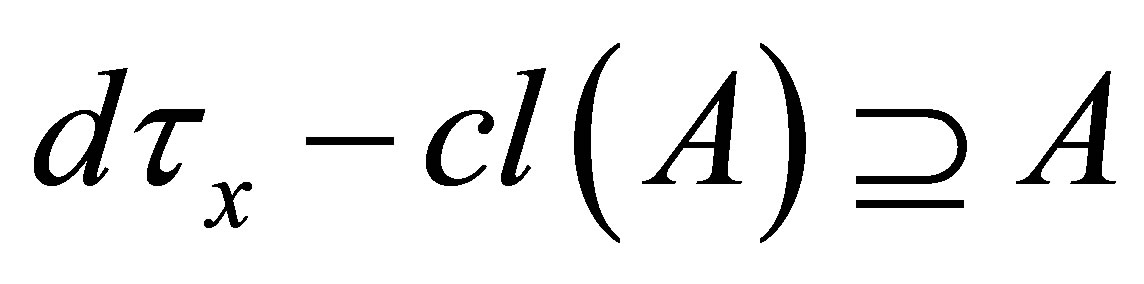 for each
for each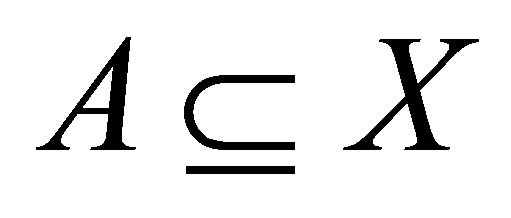 ;
;
(iii)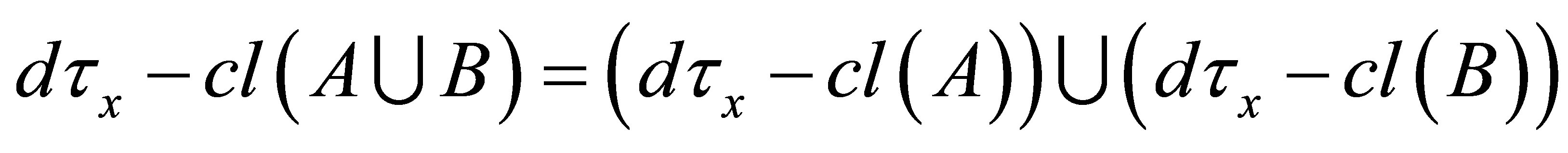 ;
;
(iv) 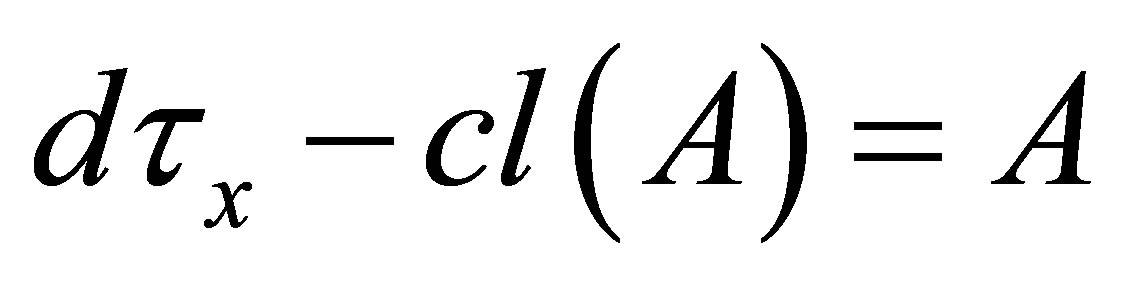 or
or  for each
for each ;
;
(v) 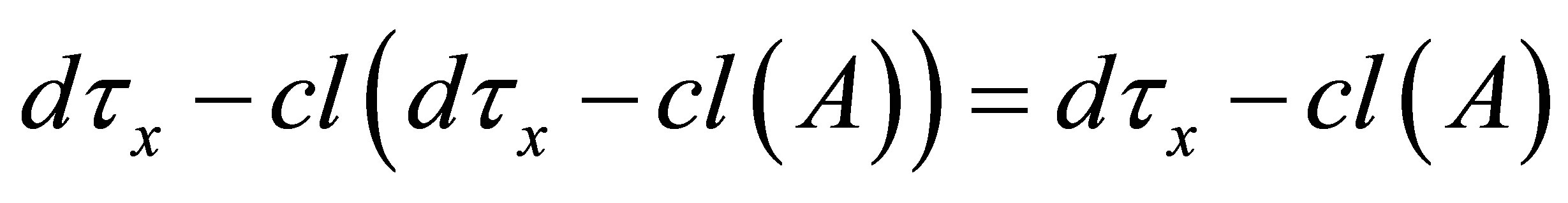 if
if 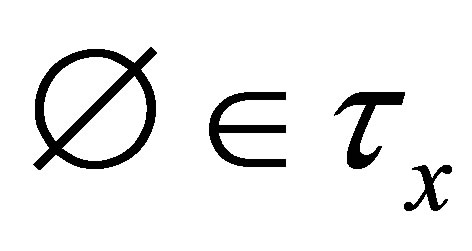 or
or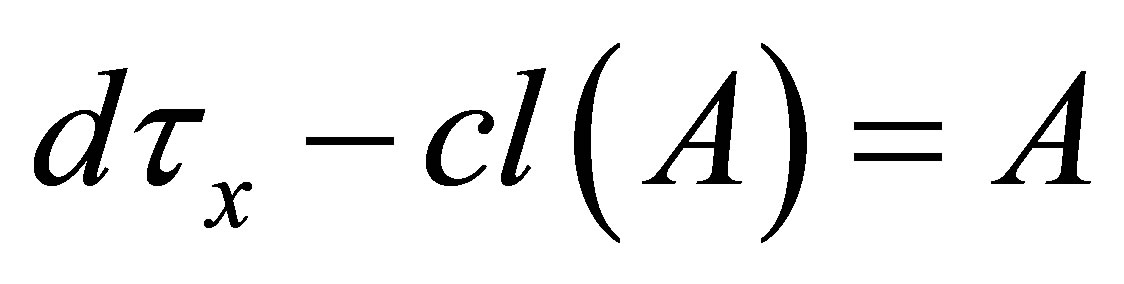 .
.
Corollary 4.2. (1) If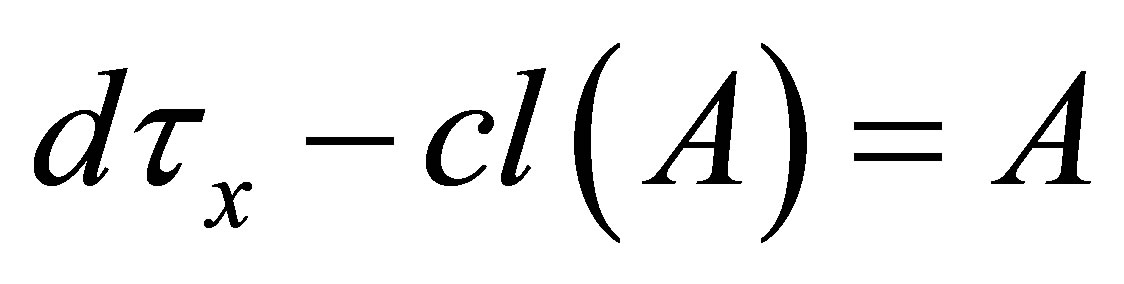 , then
, then 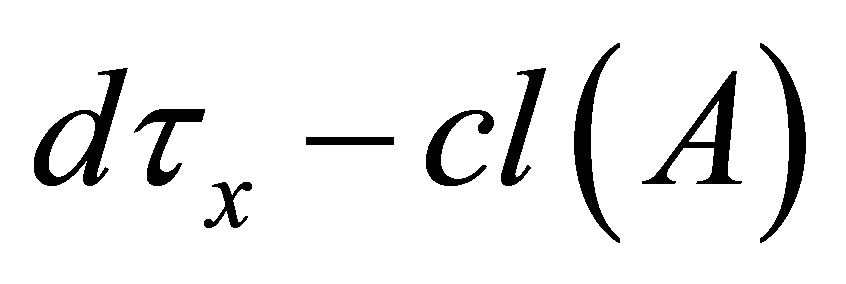 is a
is a 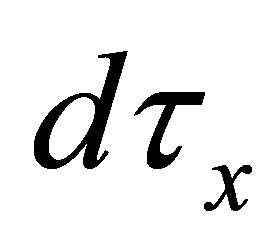 -closed.
-closed.
(2) If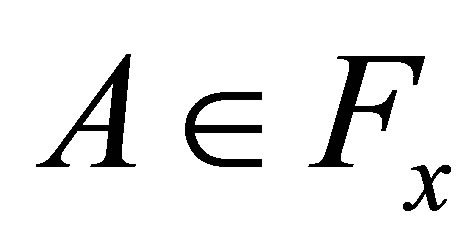 , then
, then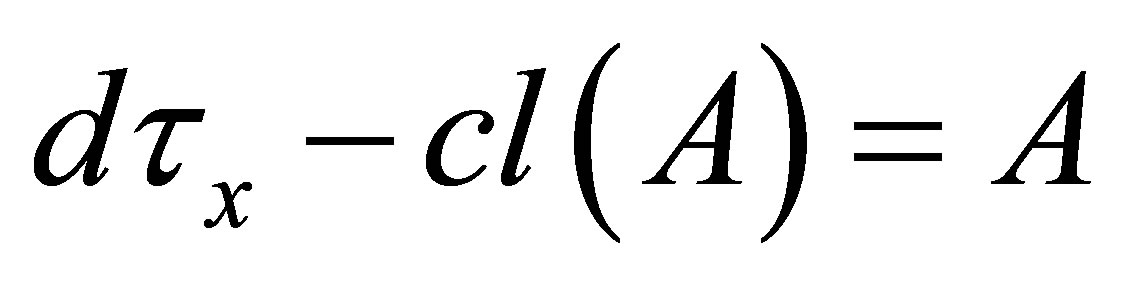 .
.
5. Dislocated Continuous Functions and Dislocated Convergence Sequences via d-Topologies
Now, we define the dislocated continuous functions and dislocated convergence sequences. We also obtain a decomposition of dislocated continuous function and dislocated convergence sequences.
Definition 5.1. Let  and
and  be dislocated-metric spaces. A function
be dislocated-metric spaces. A function  is called d-continuous at
is called d-continuous at 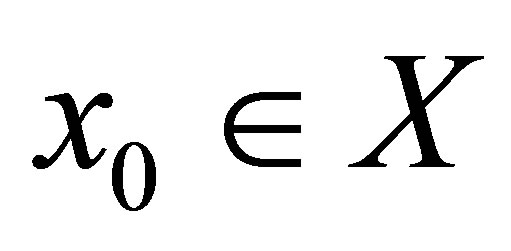 iff
iff 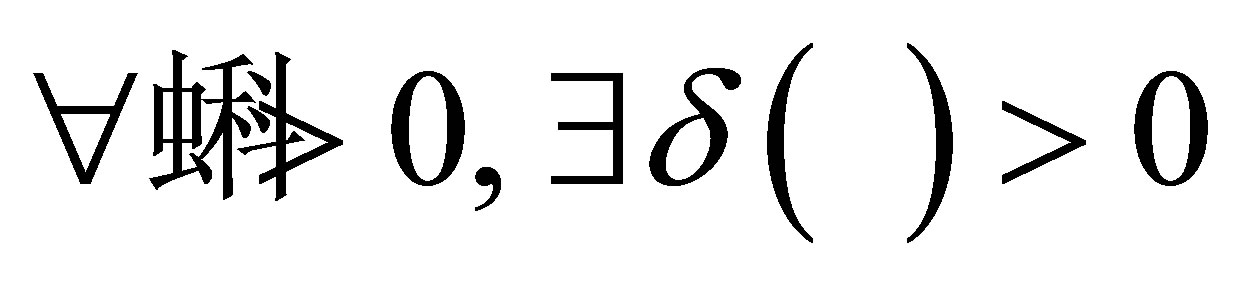 such that
such that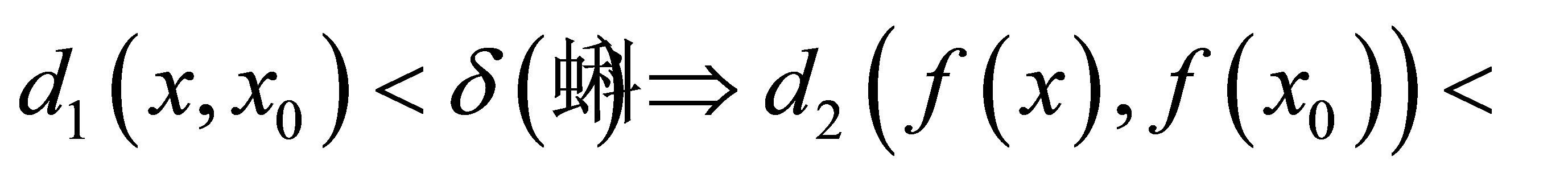 . We say
. We say 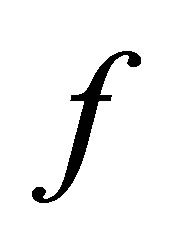 is d-continuous iff
is d-continuous iff 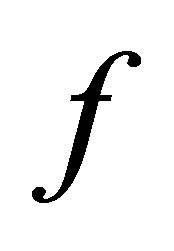 is d-continuous at each
is d-continuous at each 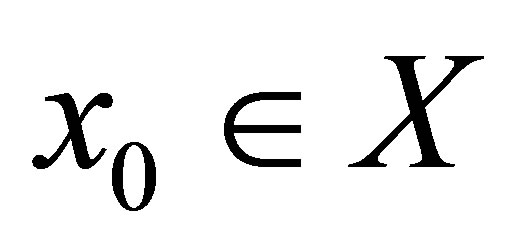
Theorem 5.1. Let 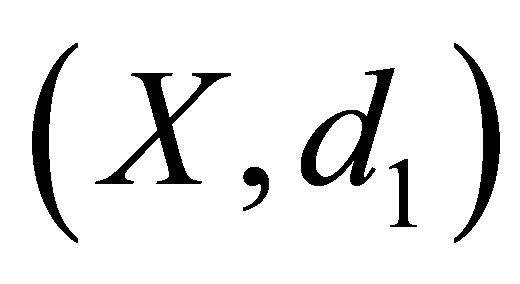 and
and  be dislocated-metric spaces and
be dislocated-metric spaces and 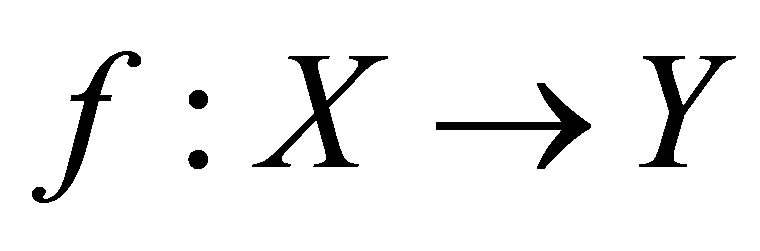 be any function. Assume that
be any function. Assume that 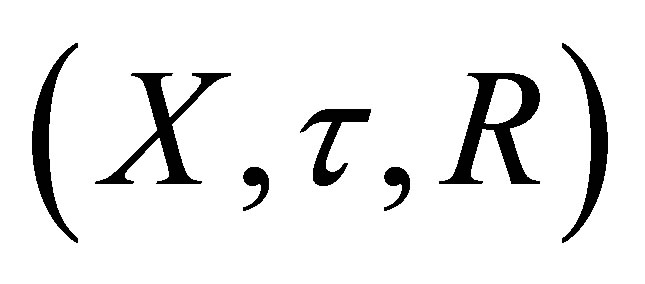 (resp.
(resp. ) be the d-topological space obtained from
) be the d-topological space obtained from 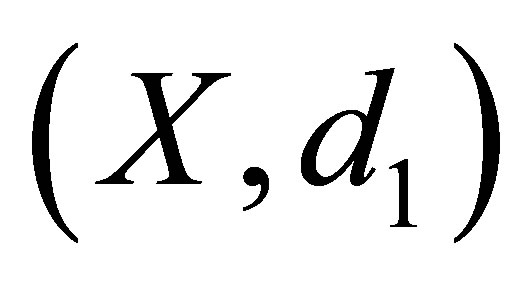 (resp.
(resp.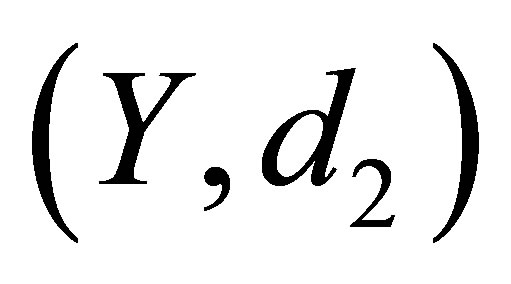 ). Then the following statements are equivalent:
). Then the following statements are equivalent:
(1) 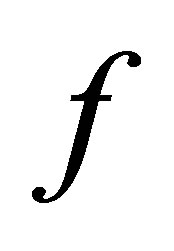 is d-continuous at
is d-continuous at .
.
(2) 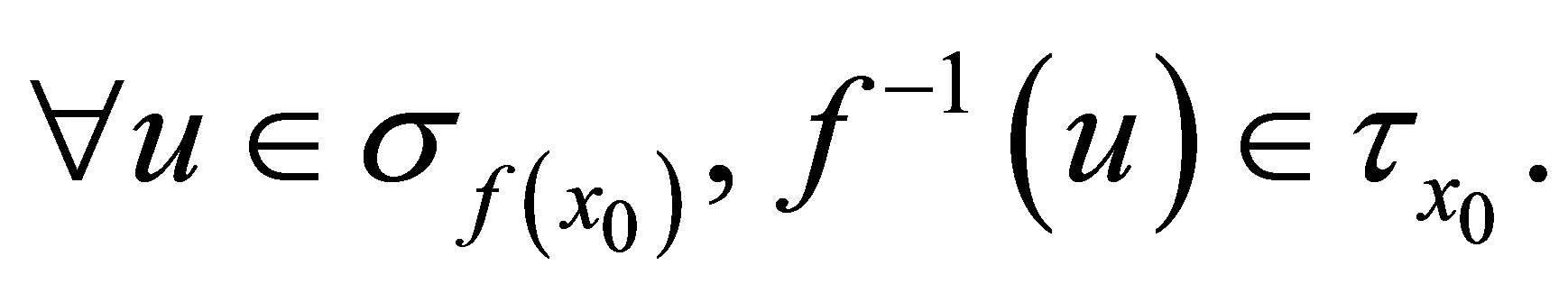
(3) 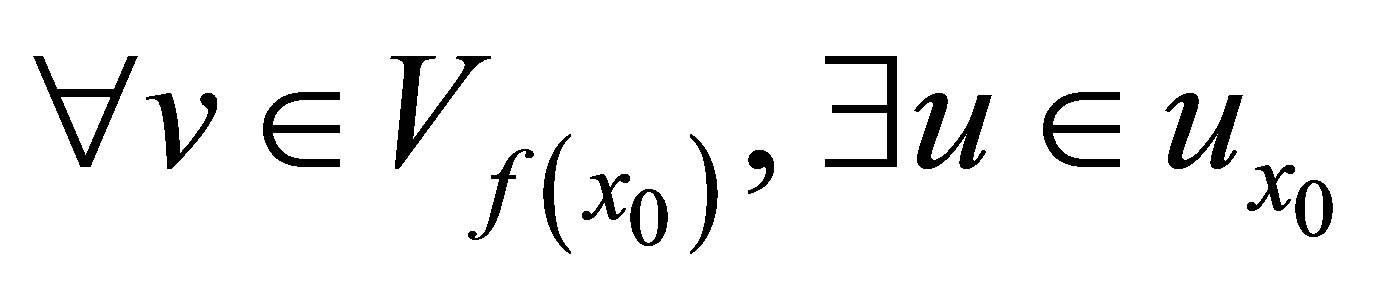 such that
such that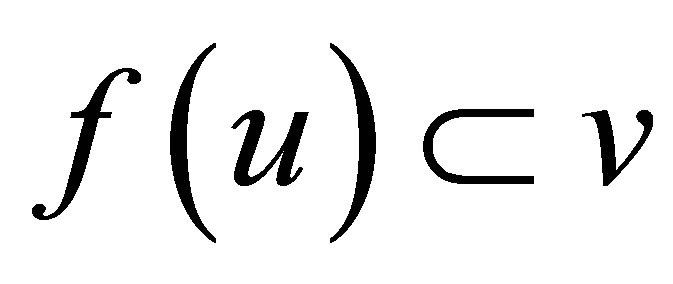 , where
, where 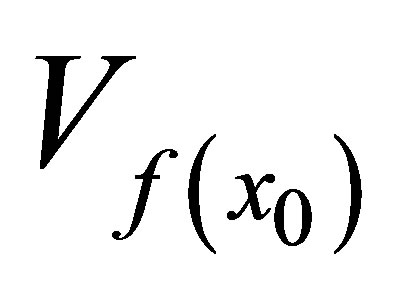 and
and 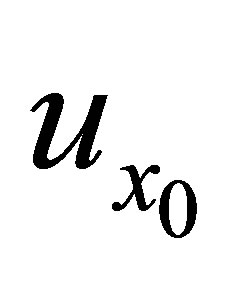 are the d*-topological neighborhood systems obtained from
are the d*-topological neighborhood systems obtained from 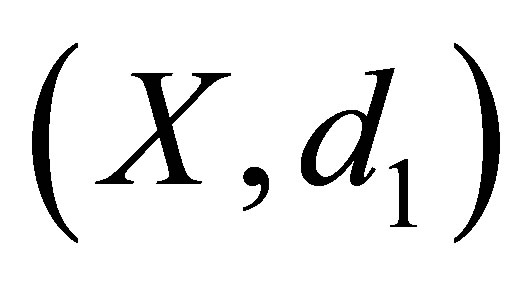 and
and 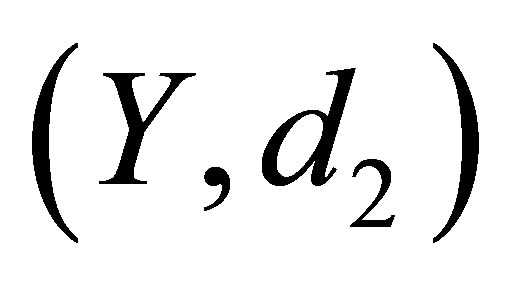 respectively.
respectively.
(4) 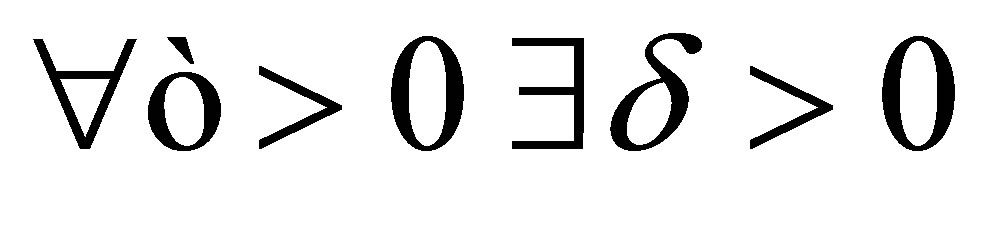 such that
such that .
.
Proof. ((1)Þ(2)): Let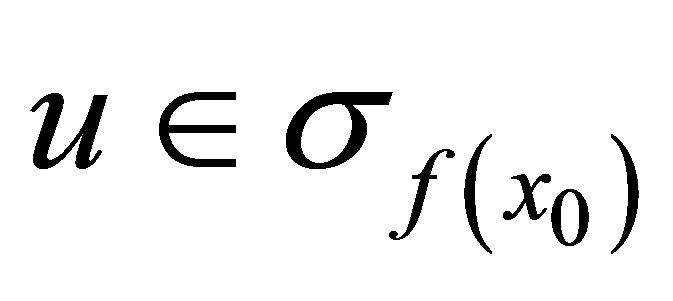 . Then
. Then 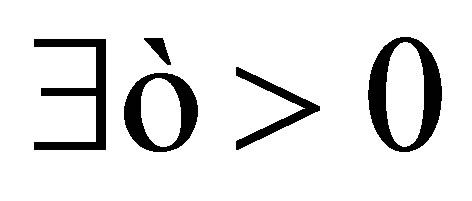 such that
such that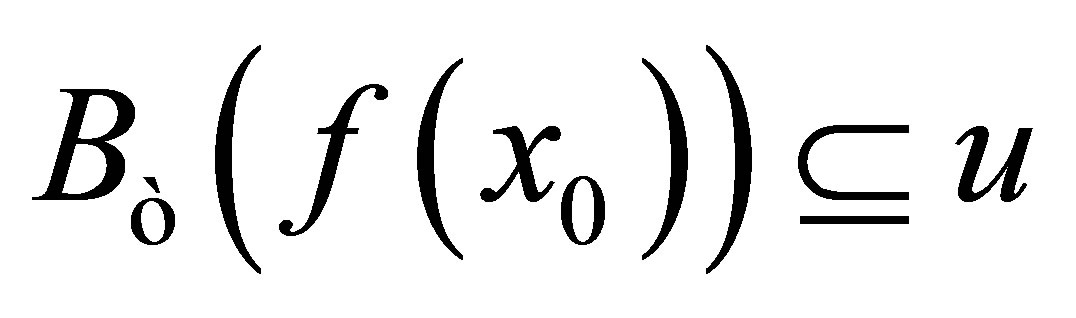 . Thus
. Thus 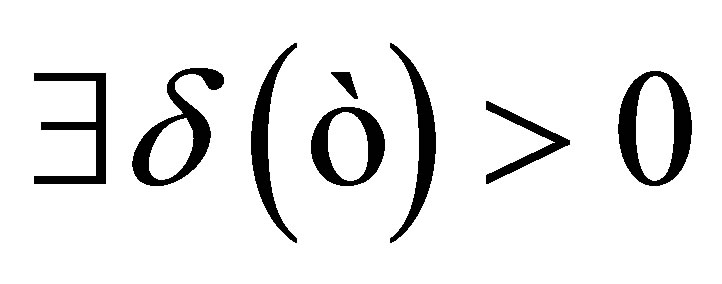 such that
such that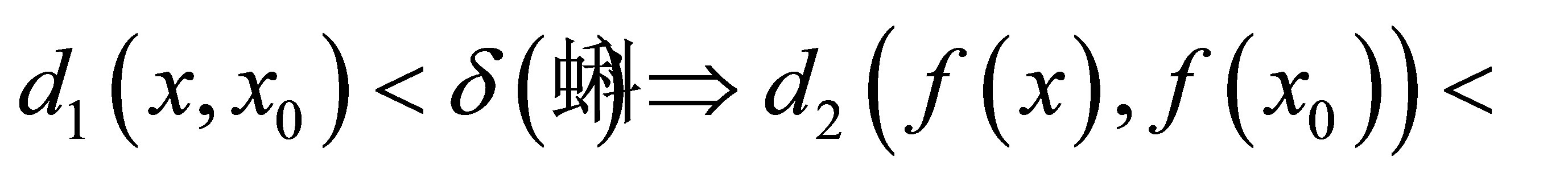 , i.e.,
, i.e.,  ,
, 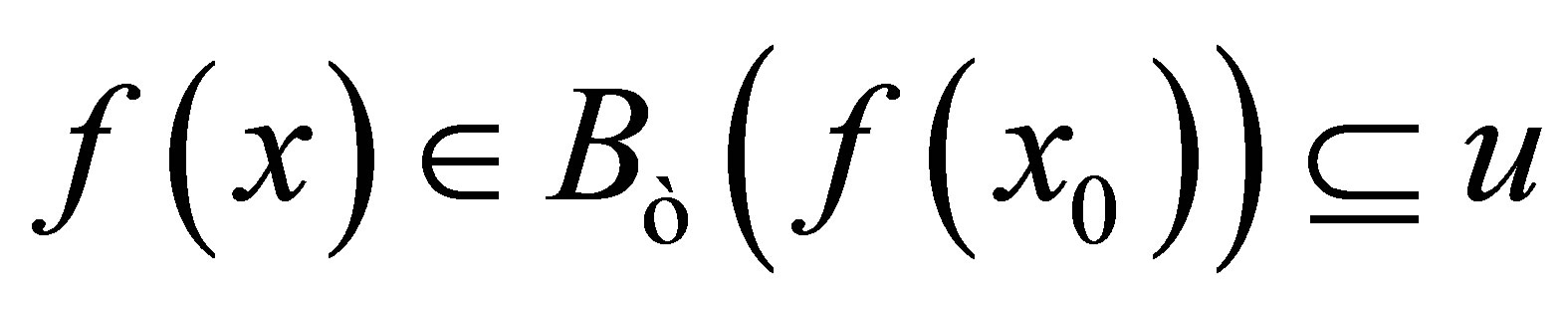 , then
, then . Hence
. Hence .
.
((2)Þ(1)): Let . Suppose that for each
. Suppose that for each ,
,  such that
such that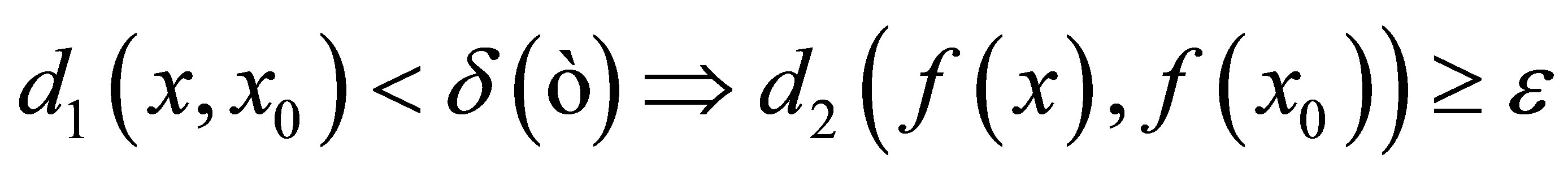 . Now,
. Now,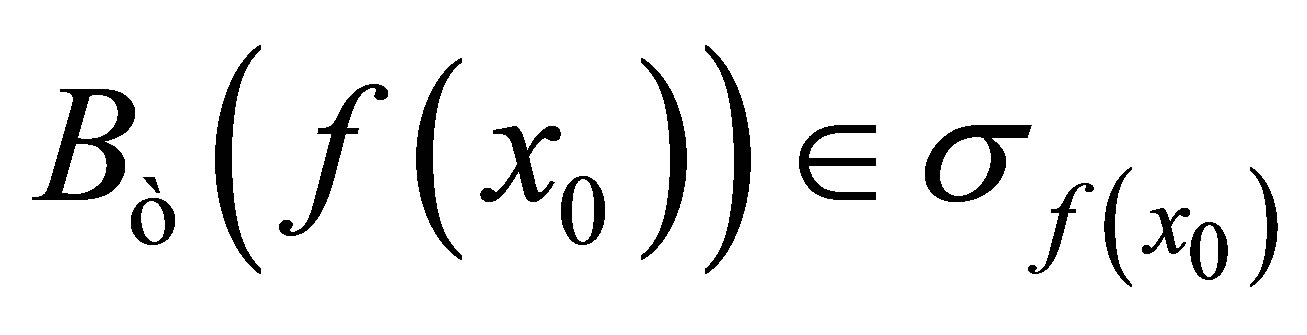 . From the assumption
. From the assumption , i.e.,
, i.e., 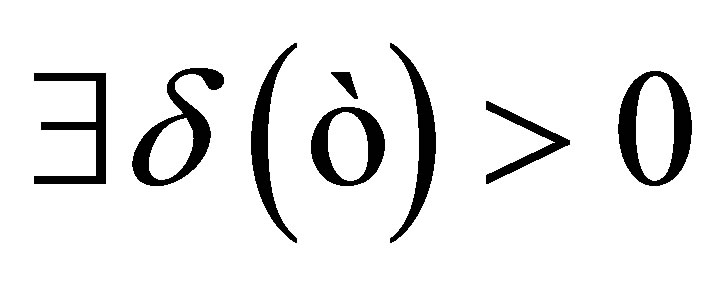 such that
such that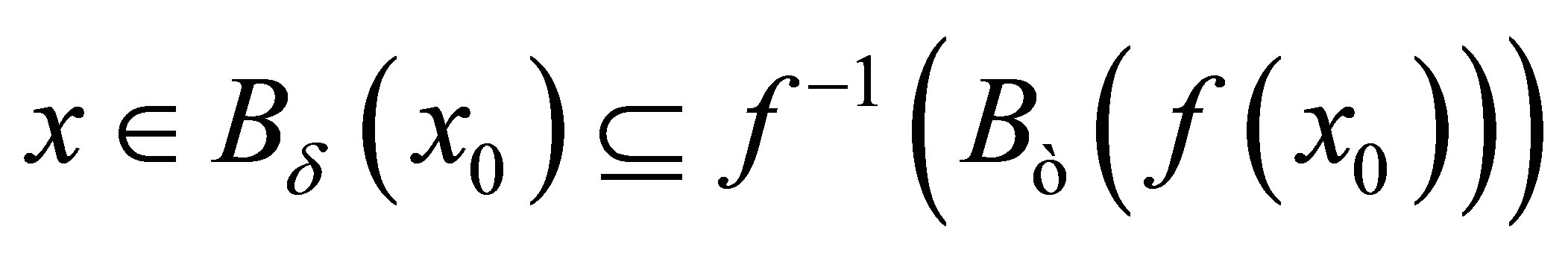 . Then
. Then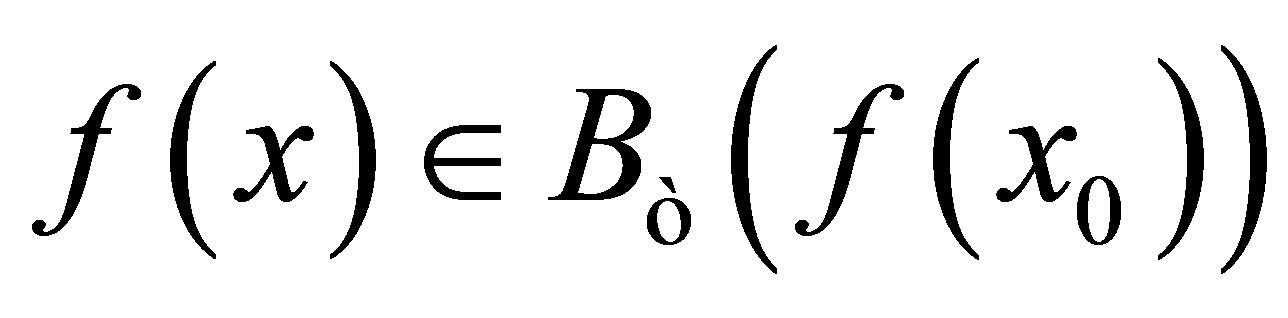 . The contradiction demands that
. The contradiction demands that 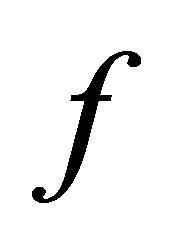 is d-continuous at
is d-continuous at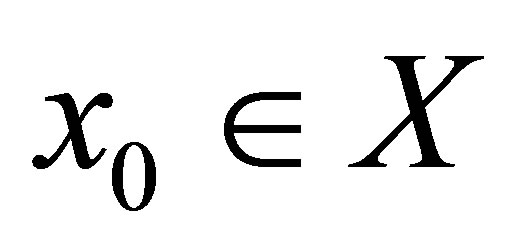 .
.
(1) Û (4) and (2) Û (3) are immediate.
Definition 5.2. Let  be a d-metric space. A sequence
be a d-metric space. A sequence 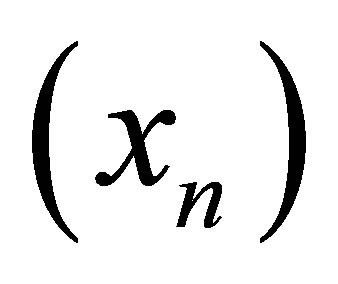 d-converges to
d-converges to 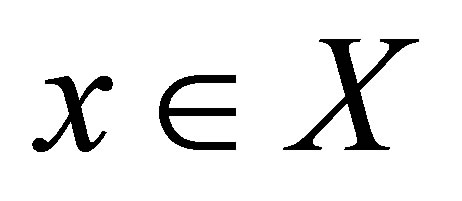 if
if 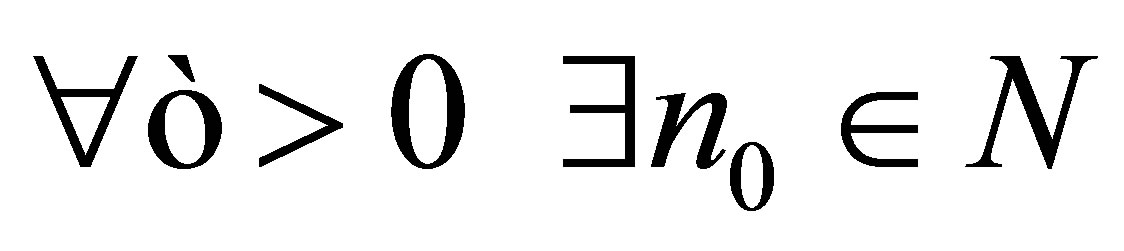 such that
such that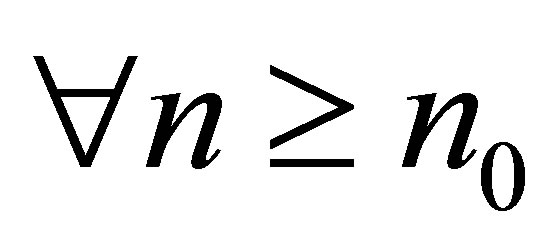 ,
,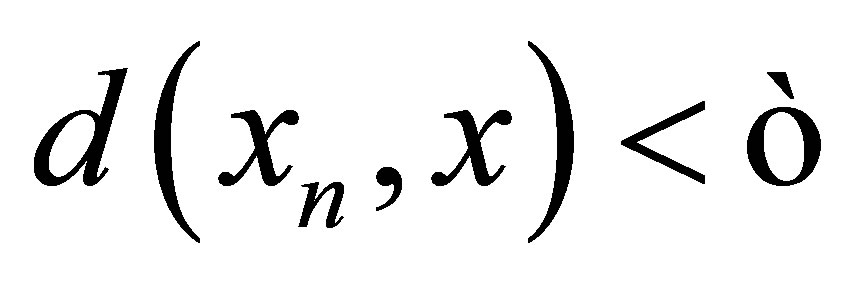 .
.
Theorem 5.2. Let 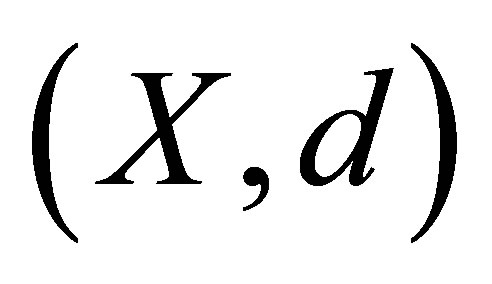 be a d-metric space and
be a d-metric space and 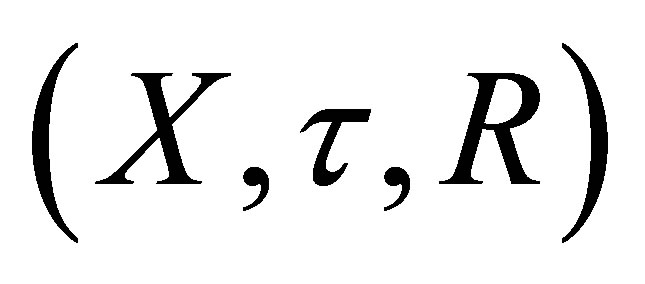 be the d-topological space obtained from it. Then the sequence
be the d-topological space obtained from it. Then the sequence 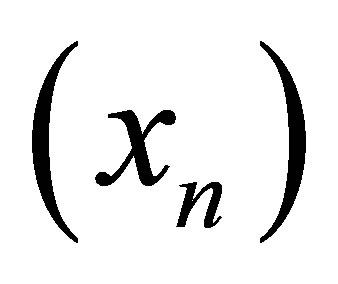 d-converges to
d-converges to  iff
iff 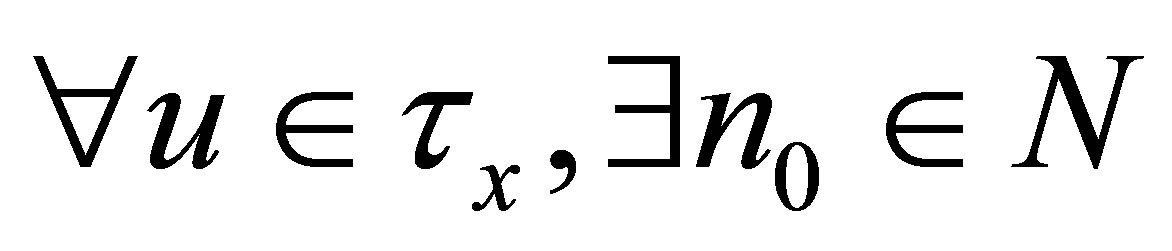 such that for each
such that for each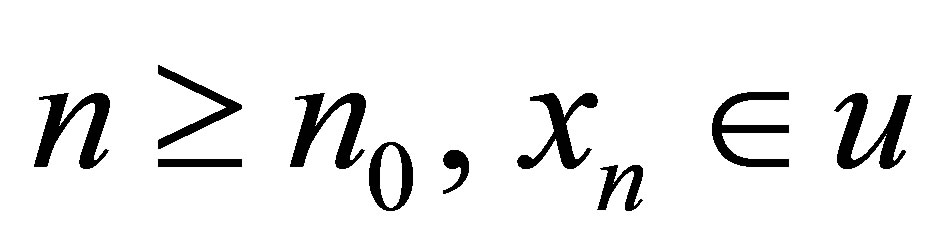 .
.
Proof. (Þ:) Let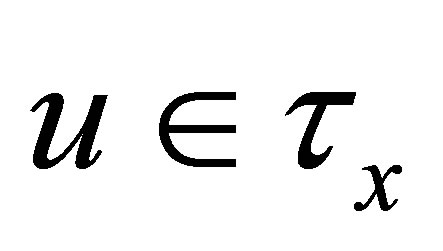 . Then there exists
. Then there exists 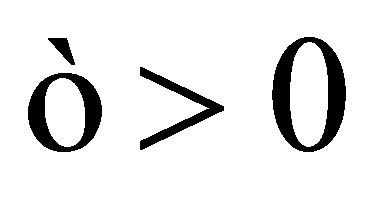 such that
such that . From the assumption
. From the assumption 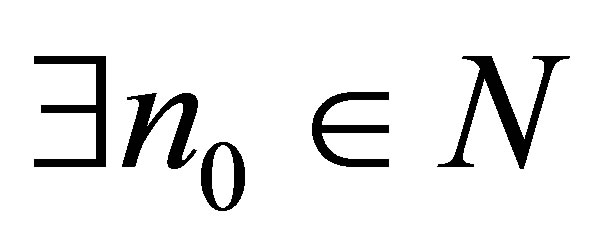 such that
such that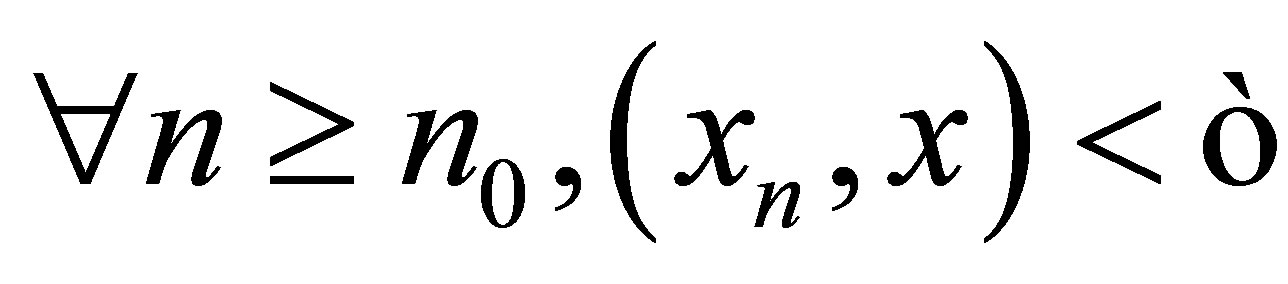 . Thus
. Thus 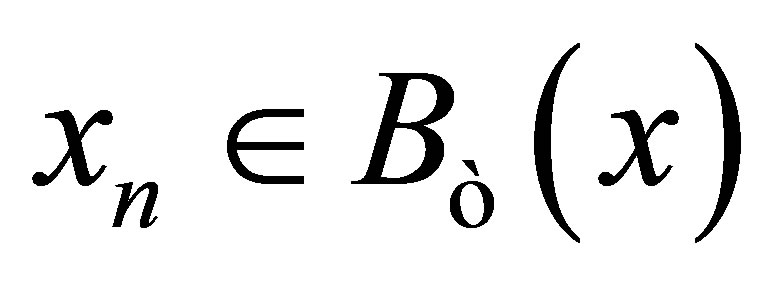 for each
for each . So
. So 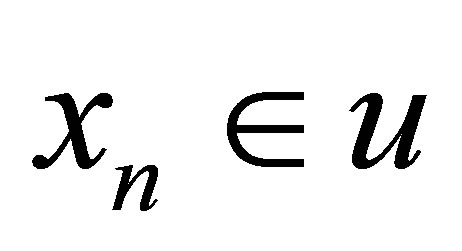 for each
for each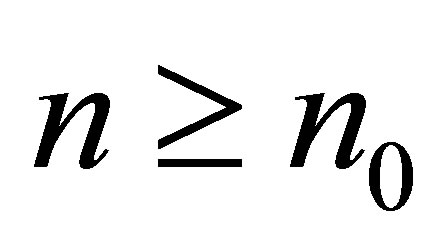 .
.
(Ü:) Let . Since
. Since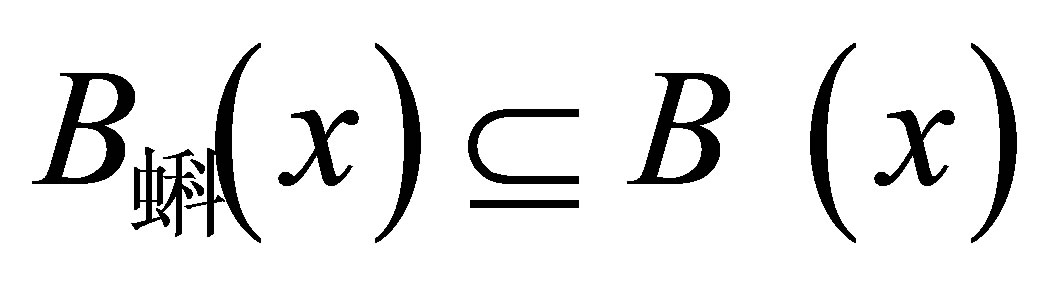 , then
, then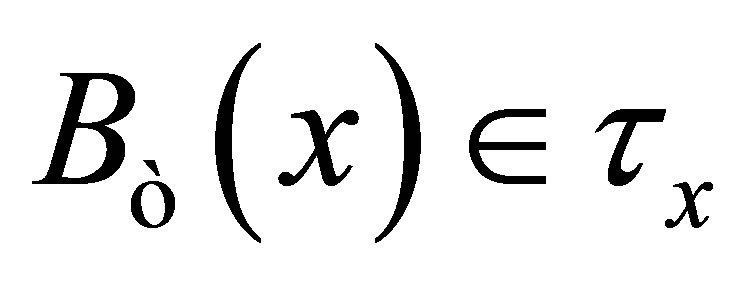 . Thus
. Thus 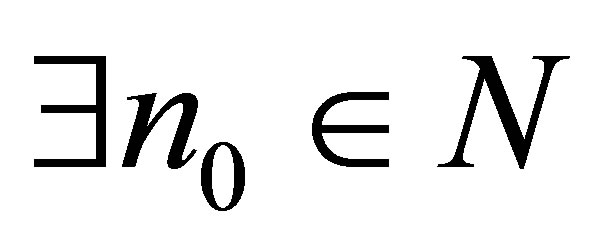 such that for each
such that for each 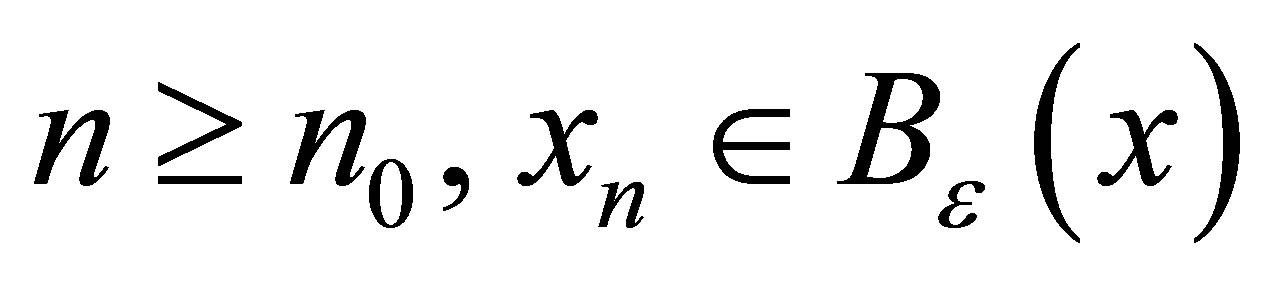 ,i.e.,
,i.e.,  for each
for each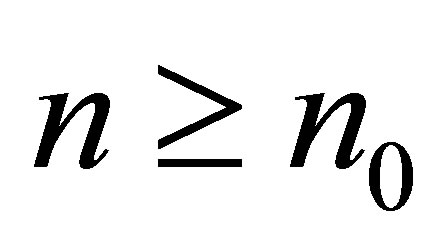 . Hence
. Hence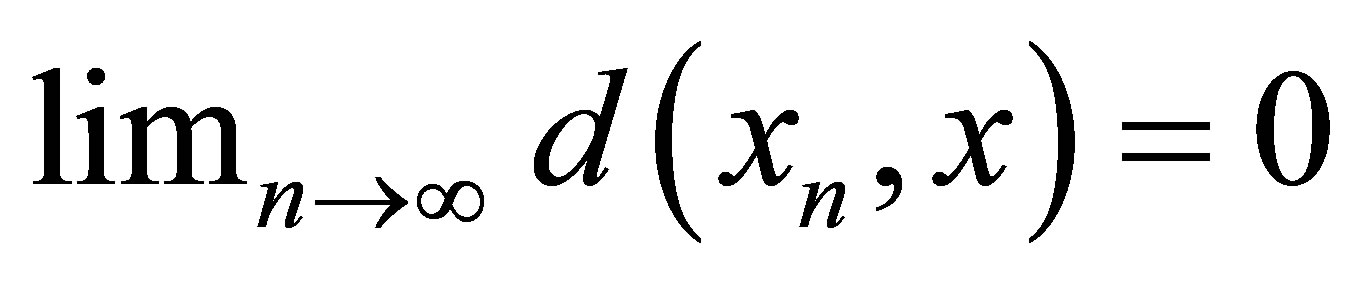 .
.
REFERENCES
- P. Hitzler and A. K. Seda, “Dislocated Topologies,” Journal of Electrical Engineering, Vol. 51, No. 12, 2000, pp. 3-7.
- A. Batarekh and V. S. Subrahmanian, “Topological Model Set Deformations in Logic Programming,” Fundamenta Informaticae, Vol. 12, No. 3, 1998, pp. 357-400.
- M. S. El Naschie, “A Review of E-Infinity Theory and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons and Fractals, Vol. 19, No. 1, 2004, pp. 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- M. S. El Naschie, “The Idealized Quantum Two-Slit Gedanken Experiment Revisted-Criticism and Reinterpretation,” Chaos, Solitons and Fractals, Vol. 27, No. 1, 2006, pp. 9-13. http://dx.doi.org/10.1016/j.chaos.2005.05.010
- P. Hitzler, “Generalized Metrics and Topology in Logic Programming Semantics,” Ph.D. Thesis, National University of Ireland, University College, Cork, 2001.
- A. K. Seda, ‘Topology and the Semantics of Logic Programs,” Fundamenta Informaticae, Vol. 24, No. 4, 1995, pp. 359-386.
- S. G. Matthews, “Metric Domains for Completeness,” Ph.D. Thesis, University of Warwick, Warwick, 1986.
NOTES
*Current address: Department of Mathematics, Faculty of Science, Northern Boarders University, Arar, KSA.

