International Journal of Modern Nonlinear Theory and Application
Vol.2 No.2(2013), Article ID:33414,2 pages DOI:10.4236/ijmnta.2013.22019
Some Notes on the Paper “New Common Fixed Point Theorems for Maps on Cone Metric Spaces”
Department of Mathematics, Faculty of Science, Assiut University, Assiut, Egypt
Email: mahmed68@yahoo.com
Copyright © 2013 Mohamed Abd El-Rahman Ahmed. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 17, 2013; revised February 21, 2013; accepted March 19, 2013
Keywords: Cone Metric; Weakly Compatible; Fixed Point
ABSTRACT
In this paper, we show that Theorem 2.1 [1] (resp. Theorem 2.2 [1]) is a consequence of Corollary 2.1 [1] ( resp. Corollary 2.2 [1]).
1. Introduction
In 2007, Huang and Zhang [2] initiated fixed point theory in cone metric spaces. On the other hand, in 2011, Haghi, Rezapour and Shahzad [3] gave a lemma and showed that some fixed point generalizations are not real generalizations. In this note, we show that Theorem 2.1 [1] and Theorem 2.2 [1] are so.
Following [2], let  be a real Banach space and
be a real Banach space and  be the zero vector in
be the zero vector in , and
, and .
.  is called cone iff 1)
is called cone iff 1) 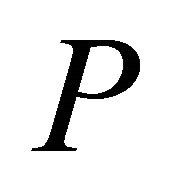 is closed, nonempty and
is closed, nonempty and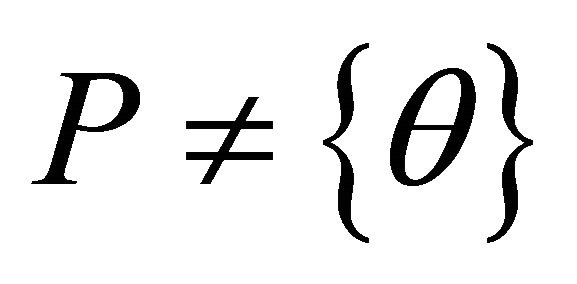 2)
2)  for all
for all  and nonnegative real numbers
and nonnegative real numbers 3)
3) .
.
For a given cone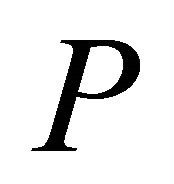 , we define a partial ordering
, we define a partial ordering  with respect to
with respect to 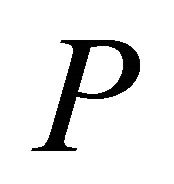 by
by  iff
iff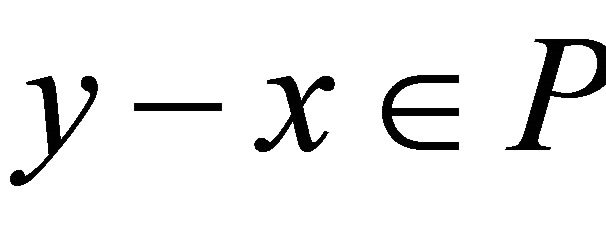 .
. 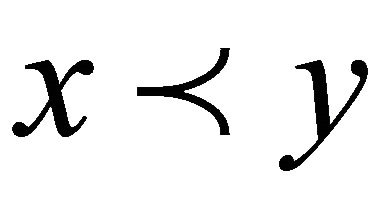 (resp.
(resp. ) stands for
) stands for 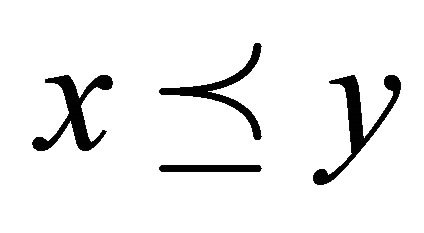 and
and 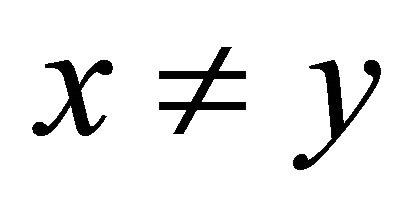 (resp.
(resp.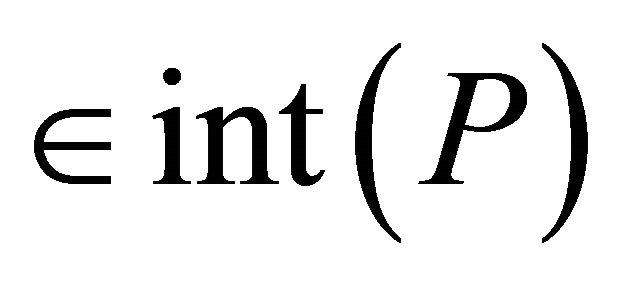
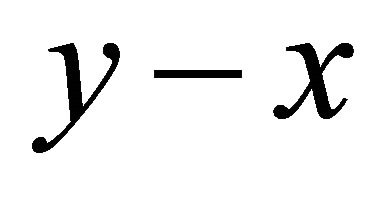 ), where
), where  denotes the interior of
denotes the interior of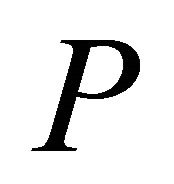 . In the paper we always assume that
. In the paper we always assume that 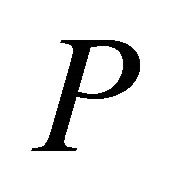 is solid, i.e.,
is solid, i.e.,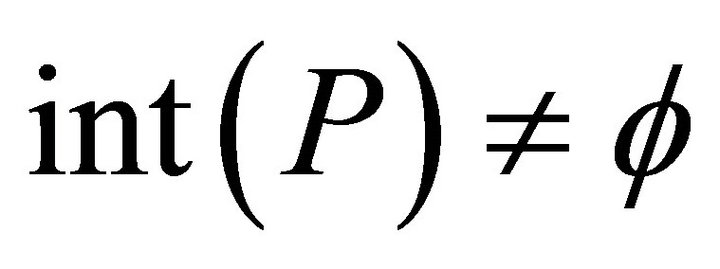 . It is clear that
. It is clear that  leads to
leads to 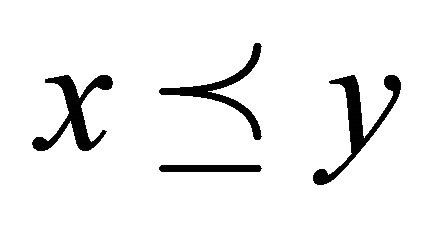 but the reverse need not to be true.
but the reverse need not to be true.
The cone  is called normal if there exists a number
is called normal if there exists a number 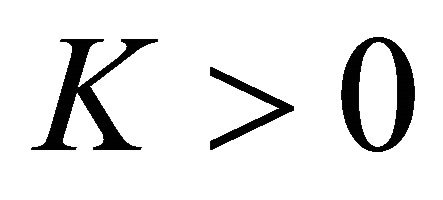 such that for all
such that for all ,
,  implies
implies .
.
The least positive number satisfying above is called the normal constant of .
.
Definition 1.1 [2]. Let 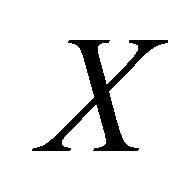 be a nonempty set. A function
be a nonempty set. A function 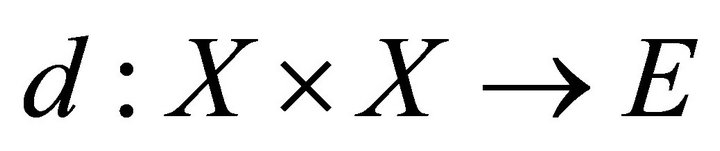 is called cone metric iff
is called cone metric iff
(M1)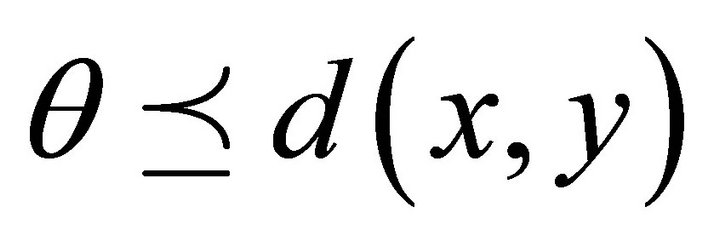 (M2)
(M2) 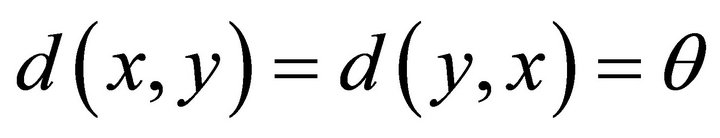 iff
iff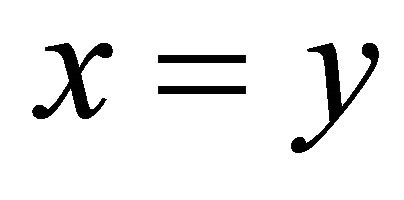 ,
,
(M3)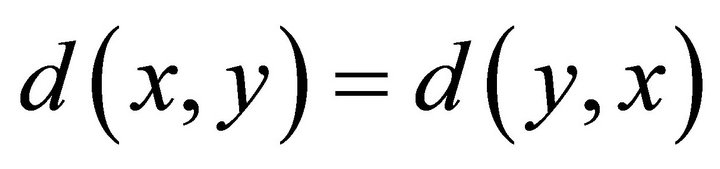 ,
,
(M4) for all
for all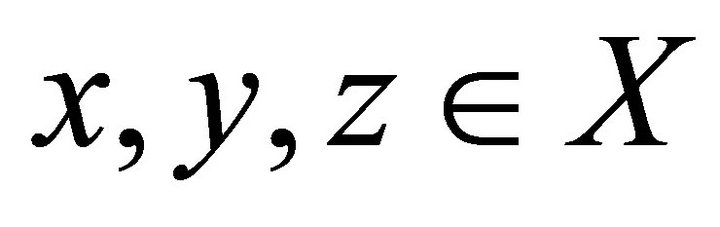 .
. 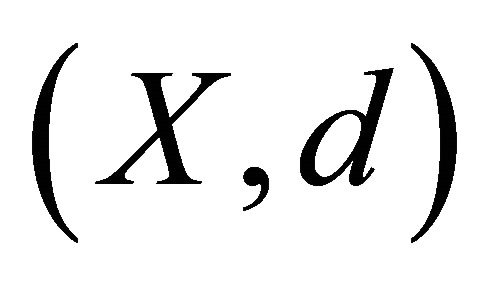 is said to be a cone metric space.
is said to be a cone metric space.
Lemma 1.1 [3]. Let 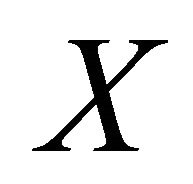 be a nonempty and
be a nonempty and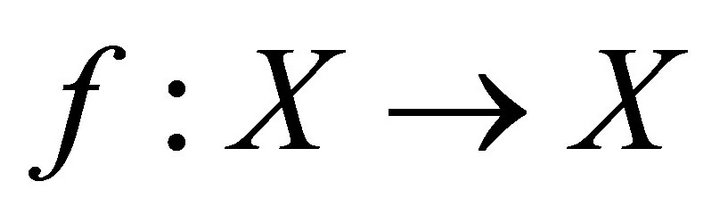 . Then there exists a subset
. Then there exists a subset 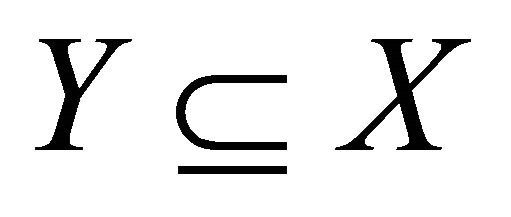 such that
such that 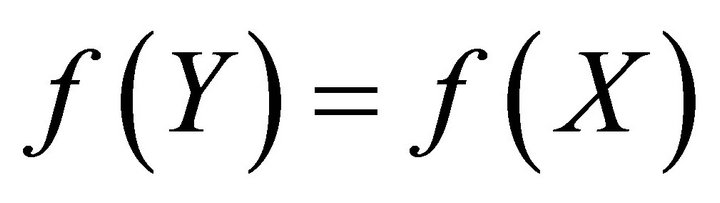 and
and 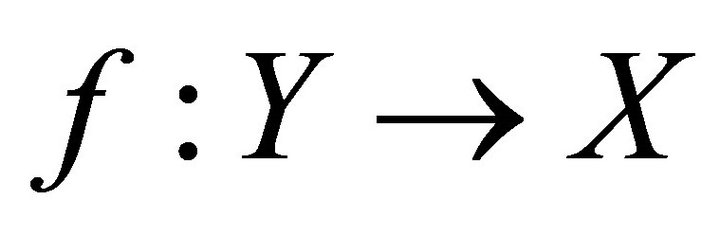 is one-to-one.
is one-to-one.
Definition 1.2 [4]. Let  be a cone metric space and
be a cone metric space and  be mappings. Then,
be mappings. Then, 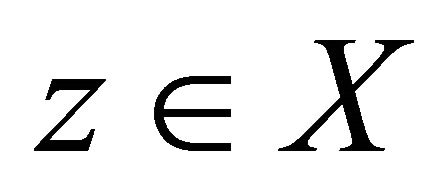 is called a coincidence point of
is called a coincidence point of 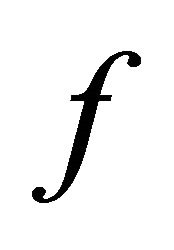 and
and 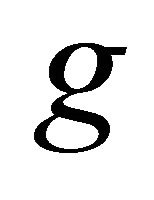 iff
iff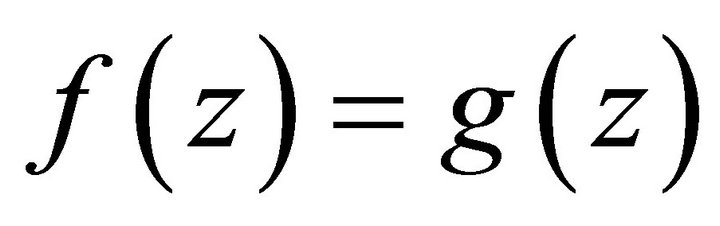 .
.
Definition 1.3 [4]. Let 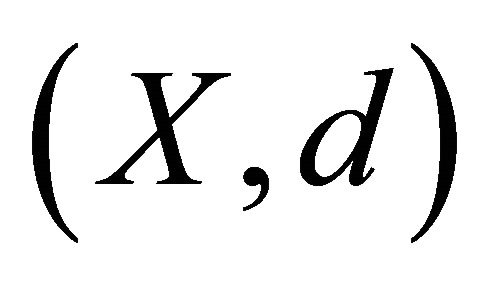 be a cone metric space. The mappings
be a cone metric space. The mappings 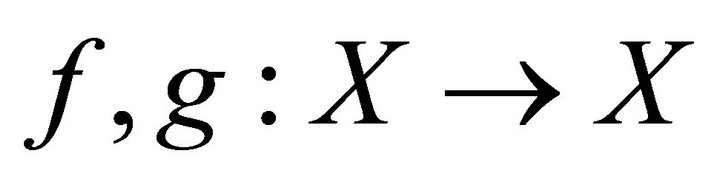 are weakly compatible iff for every coincidence point
are weakly compatible iff for every coincidence point  of
of 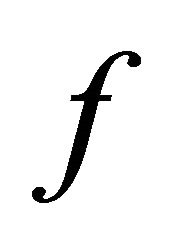 and
and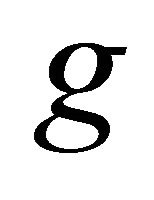 ,
, .
.
Theorem 1.1 (Theorem 2.1 [1]). Let 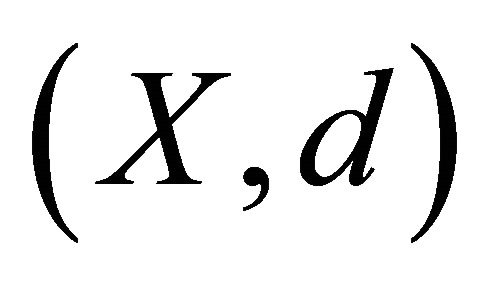 be a cone metric space and let
be a cone metric space and let 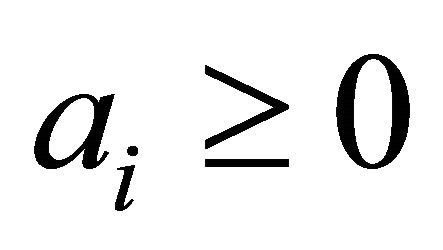
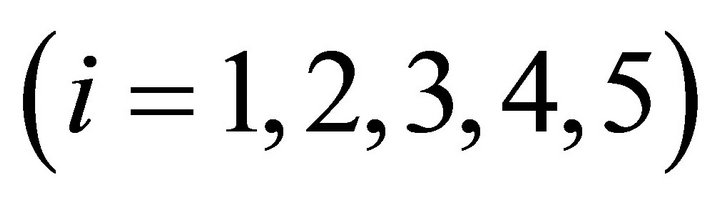 be constants with
be constants with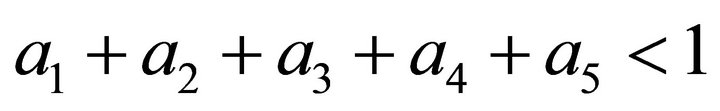 . Suppose that the mappings
. Suppose that the mappings 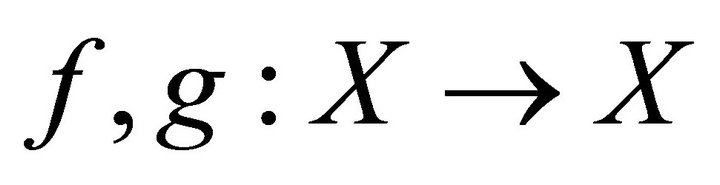 satisfy the condition
satisfy the condition
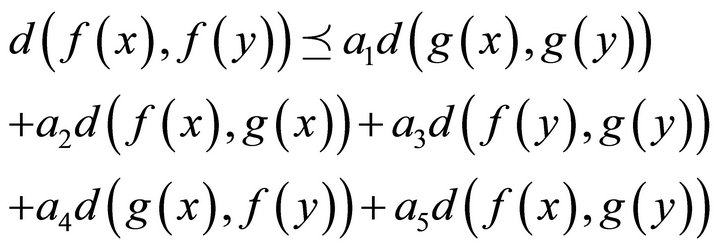
for all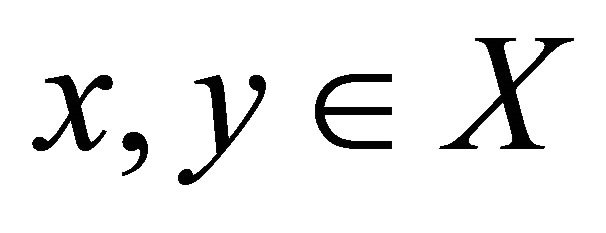 .
.
If the range of 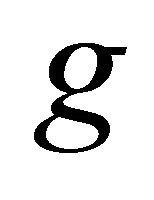 contains the range of
contains the range of 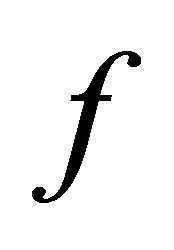 and
and 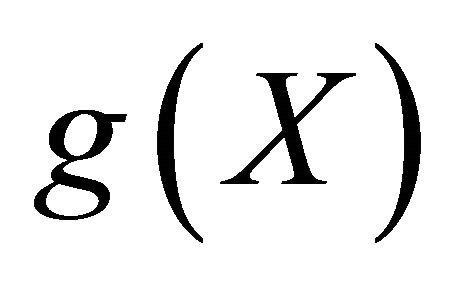 is a complete subspace, then
is a complete subspace, then 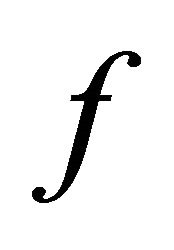 and
and 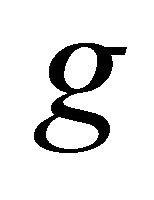 have a unique point of coincidence in
have a unique point of coincidence in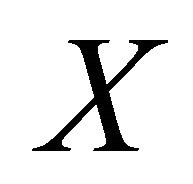 . Moreover, if
. Moreover, if 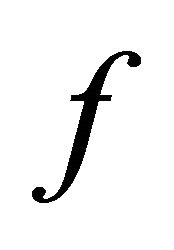 and
and 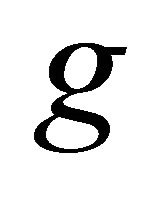 are weakly compatible, then
are weakly compatible, then 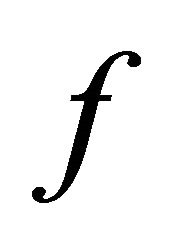 and
and 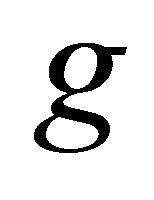 have a unique fixed point.
have a unique fixed point.
Theorem 1.2 (Corollary 2.1 [1]). Let  be a complete cone metric space and let
be a complete cone metric space and let  i = (1,2,3,4,5) be constants with
i = (1,2,3,4,5) be constants with . Suppose that the mapping
. Suppose that the mapping  satisfies the condition
satisfies the condition
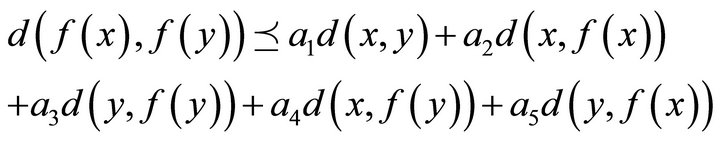
for all .
.
Then 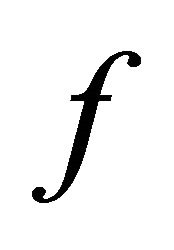 has a unique fixed point
has a unique fixed point 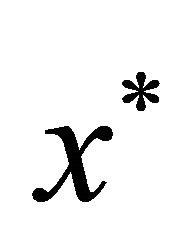 in
in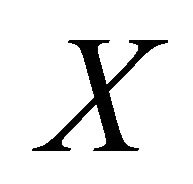 .
.
Theorem 1.3 (Theorem 2.2 [1]). Let 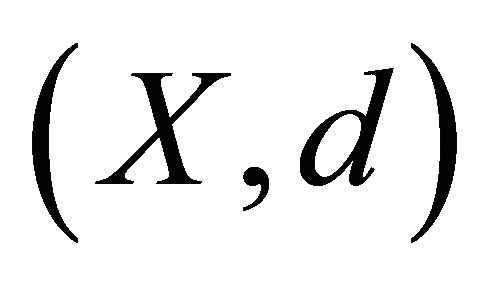 be a cone metric space and let the mappings
be a cone metric space and let the mappings  satisfy the condition
satisfy the condition
 , for all
, for all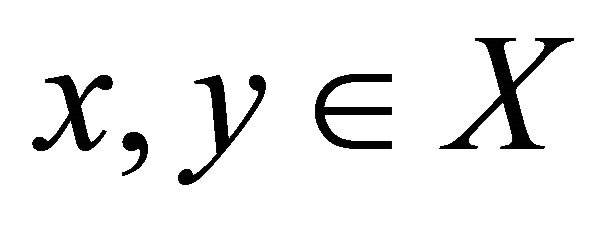 where
where
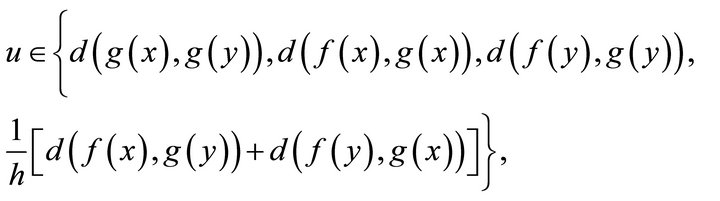
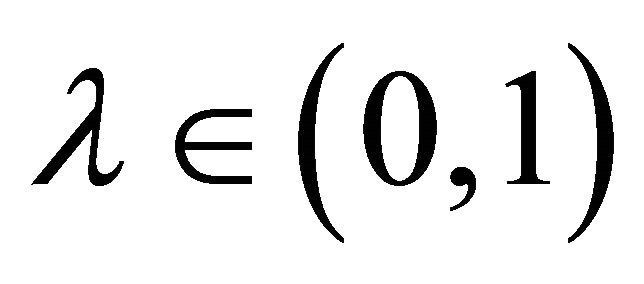 ,
, .
.
If the range of  contains the range of
contains the range of  and
and 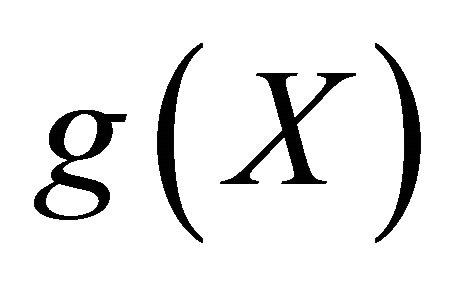 is a complete subspace, then
is a complete subspace, then  and
and 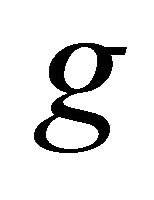 have a unique point of coincidence in
have a unique point of coincidence in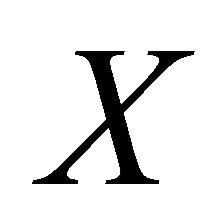 . Moreover, if
. Moreover, if 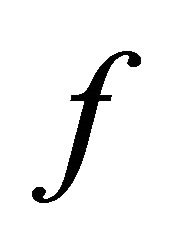 and
and  are weakly compatible, then
are weakly compatible, then  and
and 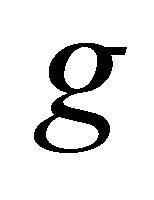 have a unique fixed point.
have a unique fixed point.
Theorem 1.4 (Corollary 2.2 [1]). Let 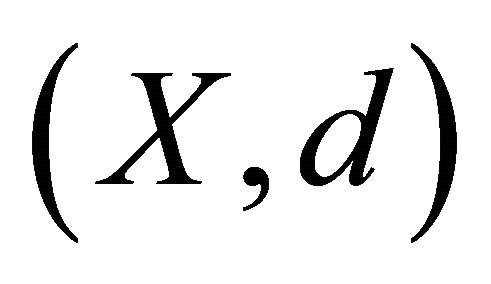 be a complete cone metric space and let the mapping
be a complete cone metric space and let the mapping  satisfies the condition
satisfies the condition
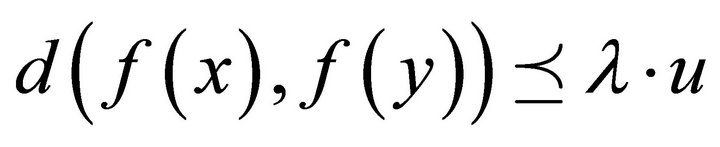 , for all
, for all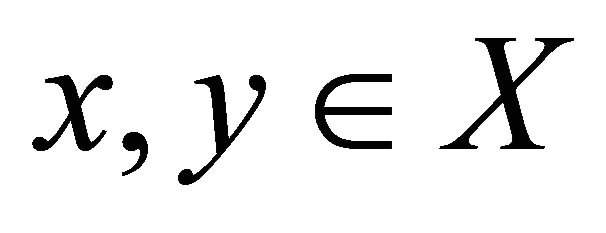 where
where
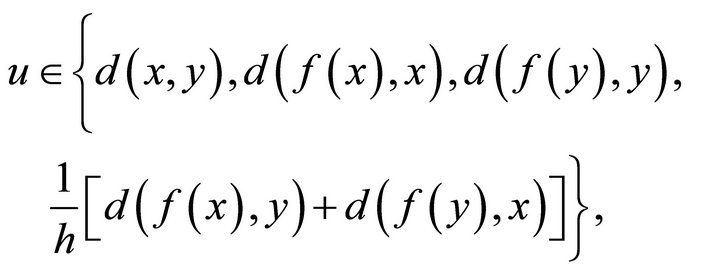
 ,
, .
.
Then  has a unique fixed point
has a unique fixed point 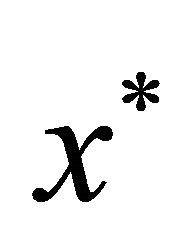 in
in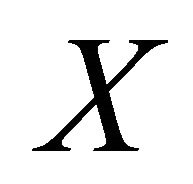 .
.
2. Main Result
In this section, we show that that Theorem 1.1 (resp. Theorem 1.3) is a consequence of Theorem 1.2 (resp. Theorem 1.4).
Theorem 2.1. Theorem 1.1 is a consequence of Theorem 1.2.
Proof. By Lemma 1.1, there exists 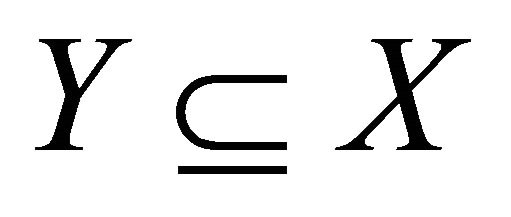 such that
such that 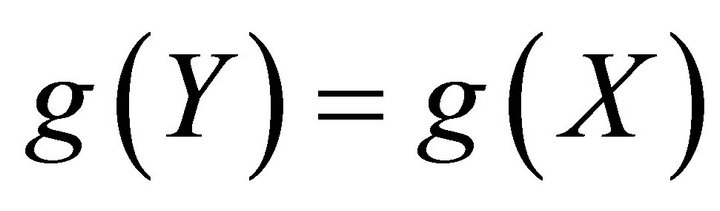 and
and 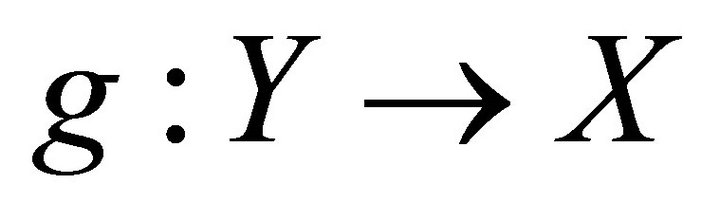 is one-to-one. Define a map
is one-to-one. Define a map 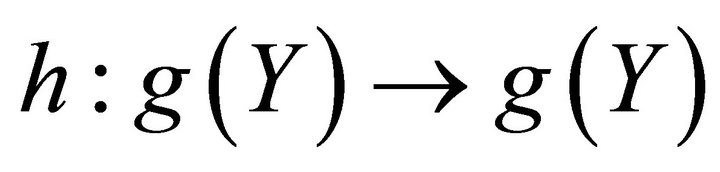 by
by  for each
for each . Since
. Since 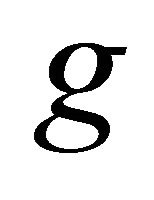 is one-to-one on
is one-to-one on , then
, then 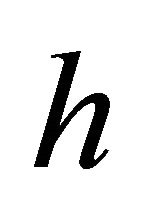 is well-defined. Also, for arbitrary
is well-defined. Also, for arbitrary ,
,

where 
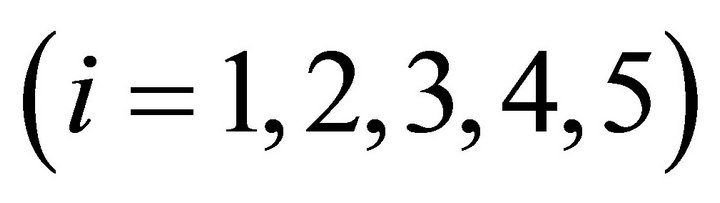 are constants with
are constants with
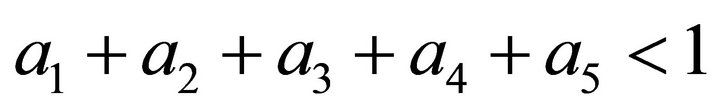 .
.
From the completeness of , there exists
, there exists 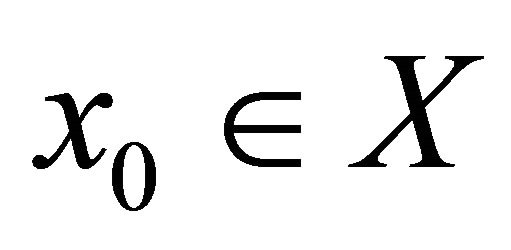 such that
such that

by Theorem 1.2. Hence,  and
and 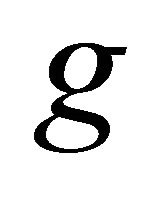 have a point of coincidence which is also unique. Since
have a point of coincidence which is also unique. Since 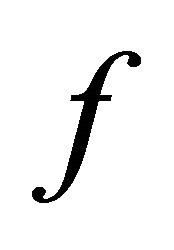 and
and 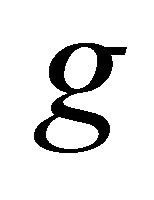 are weakly compatible, then
are weakly compatible, then 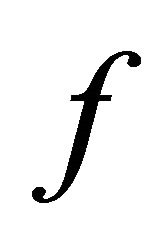 and
and  have a unique common fixed point.
have a unique common fixed point.
Theorem 2.2. Theorem 1.3 is a consequence of Theorem 1.4.
REFERENCES
- G. Song, X. Sun, Y. Zhao and G. Wang, “New Common Fixed Point Theorems for Maps on Cone Metric Spaces,” Applied Mathematics Letters, Vol. 23, No. 9, 2010, pp. 1033-1037. doi:10.1016/j.aml.2010.04.032
- L.-G. Huang and X. Zhang, “Cone Metric Spaces and Fixed Point Theorems of Contractive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 332, No. 2, 2007, pp. 1468-1476. doi:10.1016/j.jmaa.2005.03.087
- R. H. Haghi, Sh. Rezapour and N. Shahzad, “Some Fixed Point Generalizations Are Not Real Generalizations,” Nonlinear Analysis, Theory, Methods and Applications, Vol. 74, 2011, pp. 1799-1803.
- C. Di Bari and P. Vetro, “ϕ-Pairs and Common Fixed Points in Cone Metric Spaces,” Rendiconti del Circolo Matematico di Palermo, Vol. 57, No. 2, 2008, pp. 279- 285. doi:10.1007/s12215-008-0020-9

