International Journal of Intelligence Science
Vol.2 No.4(2012), Article ID:23704,9 pages DOI:10.4236/ijis.2012.24015
To Comma or Not to Comma: The Mathematics of the Relative Clause, All Types, via Boole and Venn
1Department of Egyptology and Ancient Western Asian Studies, Brown University, Providence, USA
2Department of the Classics, Harvard University, Cambridge, USA
Email: leo_depuydt@brown.edu
Received March 8, 2012; revised July 8, 2012; accepted July 21, 2012
Keywords: Boolean Algebra; Brain Science; Digital Structure; Electrical Engineering; Language; Linguistics; Logic; Mathematics; Neuroscience; Rational Thought
ABSTRACT
The present paper is part of a large scale project in Intelligence Science. The near-term aim of this project is the increased digitalization of the analysis of human intelligence in as far as intelligence is rational. The ultimate aim is to draw up a complete and definitive map of the totality of rational human intelligence or rational thought and language. As far as the mathematical component of this project is concerned, two contributions have appeared so far, the following: 1) “The Monty Hall Problem and beyond: Digital-Mathematical and Cognitive Analysis in Boole’s Algebra, Including an Extension and Generalization to Related Cases”, in Advances in Pure Mathematics (www.scirp.org/journal/apm), Vol. 1, No. 4 (July 2011), pp. 136-154; 2) “Higher Variations of the Monty Hall Problem (3.0, 4.0) and Empirical Definition of the Phenomenon of Mathematics, in Boole’s Footsteps, as Something the brain does”, in Advances in Pure Mathematics (www.scirp.org/journal/apm), Vol. 2, No. 4 (July 2012), pp. 243-273, including an appendix by Richard D. Gill. The present paper pertains to the linguistics branch of the project. It is concerned with linguistic cognition. The focus of this paper is on a single phenomenon, the relative clause and all its possible types. The method of analyzing the structure of rational thought and language that is advanced in this paper and applied to the relative clause claims validity on the following three grounds. First, it is mathematical and digital in the strictest possible sense. Second, the empirical data to which this mathematical method is applied are fully accessible in language. After all, all that is essential to that structure must be exteriorized in sounds or written symbols for the structure to be transported from one brain to another and understood. The structure must somehow be encoded in its entirety in the airwaves or light beams that travel to a hearer’s ear or a reader’s eye. And these airwaves and light beams are accessible to observation. Third, general inspiration and encouragement can be drawn from the fact that it has already been long established that the brain teems with digital activity, including in the prefrontal cortex. In sum, there is every incentive for dissecting language in search of the digital structure of rational thought and its expression in language. The design of the present paper is to demonstrate that the structure can be found.
1. The Relative Clause and All Its Types: A Digital Analysis and Deductive Approach
The aim of what follows is to present a mathematical model that accounts for exactly how many basic types of relative clauses can exist in any language and how exactly they relate to one other. I have applied the present mode of inquiry in other publications [1-6]. But it would seem that the relative clause more transparently illustrates this mode than many other phenomena of language.
There is no need for examining large numbers of relative clauses to construct the model. Because the model claims to be all-comprehensive, the question arises: How can the model be constructed without studying as many relative clauses as possible? The reason that it can be constructed is that it is mathematical and deductive and not inductive. In the deductive thinking of mathematics, the particular can shed light on the general in its entirety. In this connection, Boole writes as follows about the axioms of digital mathematics, which he calls “the laws of thought” or “the laws of the mind” [7]:
The knowledge of the laws of the mind does not require as its basis any extensive collection of observations. The general truth is seen in the particular instance, and it is not confirmed by the repetition of instances… A truth is made manifest in all its generality by reflection upon a single instance of its application.
Evidently, in Euclid’s Elements, theorems are not derived from repeated experimentation in a laboratory that leads to inductive observations. It suffices to consider just one triangle or one circle to deduce what the properties of all triangles or all circles are. Likewise, in constructing a deductive model, the examination of just a handful of relative clauses can shed light on all relative clauses.
Moreover, relative clauses can shed light on more than just relative clauses. If the structure of relative clauses is fundamentally mathematical and digital, it is likely that everything that contracts relationships with relative clauses in language is also mathematical and digital.
2. Coptic and English as Case Languages
In dealing with language, a choice of specific languages imposes itself. The present choice is Egyptian, which has the longest attested history of all languages, and more specifically Coptic Egyptian, its latest stage. As opposed to earlier Egyptian, Coptic is not written with the hieroglyphic script, but with Greek letters supplemented with a few additional characters.
There will also be much reference to English as the language of this paper and therefore the language in which the Coptic examples are translated. But what is said below should also apply to all other languages.
The main focus will be on Coptic, the latest stage of Egyptian, because the three types of relative clauses are empirically fully distinct in Coptic. One would expect to find these three types also in other languages. Importantly, one would expect to find nowhere more than three. Then again, one might find fewer, so apparently in earlier Egyptian. The reason is as follows. Egyptian has the longest attested history of any language. As far as I can see, in the course of the long history of Egyptian, the articulation between the three types of relative clauses came into being only gradually. Accordingly, one might expect a certain lack of articulation of the three types in the earlier histories of other languages as well. The way in which the brain operates with relative clauses presumably had to mature over many centuries.
3. To Comma or Not to Comma
The key issue pertaining to writing out a relative clause as far as English is concerned is whether or not to separate it from what comes before by means of a comma. Consider the expression “The diplomat, [comma!] who spoke on condition of anonymity” [8]. Omitting the comma in front of this relative clause would produce a different purport. Without comma, “The diplomat who spoke on condition of anonymity” would imply that there was another diplomat who did not speak on condition of anonymity. A related distinction is the distinction between “that” and “which”. An overall correlation applies between “that” and absence of a comma, on the one hand, and “which” and presence of a comma, on the other hand. I assume that some version of this distinction is taught in high school and college composition classes.
4. The First Two of the Three Types of Relative Clauses: “Restrictive” and “Explicative”
The distinction between absence and presence of a comma leads to a distinction between two types of relative clauses. Many names have been proposed for the two types. One type has been called “restrictive”, “determinative”, and “specifying”. The other type has been called “explicative” and “appositive”.
Restringere, determinare, specificare, explicare, and apponere are respectable Latin verbs. But what do these verbs tell us about the two types of relative clauses? In this connection, Polotsky writes as follows [9]:
The terms “restrictive” vs. “non-restrictive” or “defining” vs. “non-defining,” and similar terms, are deficient in that a contradictory expression is deemed sufficient to denote the second type.
It is not entirely clear to me how “non-restrictive” or “non-defining” are “contradictory”. Presumably, what is meant is that the terms describe what the type is not.
Before proceeding with a digital definition, it will be useful to have a look at specific Coptic examples of the two types (see §6).
The present focus is uniquely on the digital structure of relative clauses. Comprehensive descriptions of all manner of other properties of Coptic relative clauses are found in recent accounts by Polotsky [10] and Layton [11]. Polotsky believed his own account to be incomplete, noting that “analyzing the semantics of the explicative (parathetical) relative clause must be left to a special investigation” [12].
A principal aim of the present paper is to demonstrate that the meaning of the explicative relative clause is digital and that its exact relations to all the other types of relative clauses can be expressed digitally.
5. Boolean Algebra
The descriptions of examples below will include symbols of digital mathematics or Boolean algebra. Within the confines of the present article, Boolean algebra will be kept to a minimum. The symbols that will be used in this paper are listed with a definition in Table 1.
In describing digital models, a minimum of mathematical notation is in my experience unavoidable. In a note penciled on the back of the last page of a posthumously published manuscript deposited at the Royal Society in London [13], Boole’s wife Mary writes as follows [14]:
Mr. Macmillan wished G.B. to write a work [putting the principles of the Laws of Thought into non-mathematical language] and he often attempted it; but always failed.
a work [putting the principles of the Laws of Thought into non-mathematical language] and he often attempted it; but always failed.
And she identifies the manuscript in question as the beginning of such an attempt.
6. Examples of “Restrictive” and “Explicative” Relative Clauses in Coptic and in English
6.1. The “Restrictive” Relative Clause
A generic English example of the “restrictive” type of relative clause is “French who are doctors”. In this case, the Coptic equivalent is unmarked. Coptic examples of this type are found in Table 2.
6.2. The “Explicative” Relative Clause
A generic English example of the “appositive” type of relative clause is “French, who are Europeans.” In this case, the Coptic equivalent is augmented with a distinctive marker, marked here in bold. The Coptic equivalent is described in more detail by Polotsky [15] and Layton [16]. Examples are found in Table 3.
In the first example, the extra element not found in the “restrictive” relative clause is p. In the second example, the extra element is pai. Pai is the near demonstrative pronoun meaning “this.” But as a comparison with the Greek from which the passage is translated reveals, pai does not have demonstrative meaning when it serves as the marker of the “explicitative” type of relative clause. There is no demonstrative pronoun in the original Greek.
7. The Third Type of Relative Clause
There is a third type of relative clause. It may be called “hermeneutical” or “explanatory”. One might also call it the “i.e.” type. A generic example is “Paris, which is (i.e.) the capital of France”. The essential characteristic of this type is that the two entities that are associated with one another completely overlap. There is no Paris outside the capital of France and no capital of France outside of Paris. The Coptic equivalent is described in more detail by Polotsky [17] and Layton [18]. An example can be found in Table 4.
This third type is rare. But its inclusion in the present analysis of the relative clause is absolutely essential. It makes the mathematical model pertaining to the structure of the relative clause proposed in the present paper complete. Mathematical models need to be comprehensive and account for all cases. In that regard, it is proposed that there can be no more than three types of relative clauses.

Table 1. List of Boolean symbols used in this paper, with definitions.

Table 2. Coptic examples of the relative clause of type 1.

Table 3. Coptic examples of the relative clause of type 2.

Table 4. Coptic example of the relative clause of type 3.
8. The Digital Definition of All Three Types of Relative Clauses
8.1. Levels in the Digital Definition
This is not the place for an all-encompassing digital definition of all the types of relative clauses. Such a definition would include at least five levels, to wit: 1) Boolean algebra; 2) Venn diagrams; 3) The linguistic level; 4) The electromechanical level; and 5) The biochemical level.
I believe that Boolean algebra, in constituting the mathematical level, provides the sharpest answers. The final understanding of physical reality is mathematical. Rational thought and language are no exception. Venn diagrams optimally visualize Boolean equations. But they exhibit limitations. On the linguistic level, the exact elements of language are identified that exteriorize the differences between the types of relative clauses in sound and writing. A description on the electromechanical level is inspired by the belief that everything biochemical in language can be mimicked by an equivalent electromechanical model. The fifth level, the biochemical level, is the source of everything. But comparatively little can be said about it at this time.
8.2. Properties of the Digital Definition
The three types of relative clauses transmit different kinds of information. A digital definition of the three kinds of information that are communicated by relative clauses ought to exhibit three properties.
First, it ought to be entirely binary in being cast completely in terms of On-or-Off, or 1/0, to satisfy the electrical engineers among us. Second, it ought to state the exact number of On-or-Off toggles. Third, it ought to define exactly what is On (1) and what is Off (0).
Aristotelian logic and scholastic logic are mostly concerned with Ons, hardly with Offs. These types of logic revolve mostly around the syllogism, of which an example is as follows.
Human beings are mortal.
Socrates is a human being.
Therefore Socrates is mortal.
Since De Morgan and Boole, it has become abundantly clear that the Offs are as important as the Ons. It is not so much that Aristotle’s logic and scholastic logic are wrong. Rather, they are incomplete. In reference to the example just cited, the Offs are “non-human”, “nonmortal”, and “non-Socrates”, or “the set of all that is not human”, and so on.
No one more than Venn has emphasized that a precise calibration of what an item of information communicates requires establishing exactly which sets are available and which sets are non-available, or which sets are full and which sets are empty [19]. It is then a small step—one that Venn did not take—towards interpreting a full set as a switch that is On and an empty set as a switch that is Off.
8.3. Transparency of the Digital Definition
The three types of relative clauses convey different types of information. The difference between these types of information is not of the same kind as the difference between “This is a house” and “This is a car” or between “This wall is red” and “This wall is green”. The difference in meaning between the types of relative clauses seems more abstract. Concepts such as “restrictive” and “explicative” are in danger of appearing detached from reality as it manifests itself to us in a readily transparent manner.
The digital definition of the types of relative clauses proposed in this paper has no chance of success if the differences in information between the types of relative clauses cannot be formulated in terms that are as immediately transparent as the difference between “This is a house” and “This is a car”. The aim of §9 and §10 is to render the digital definition at hand more accessible by specifying to which obvious feature of reality it refers.
9. Metaphor Illustrating the Differences in Information Conveyed by the Three Types of Relative Clauses: Three Bars and Two Wines
One way of showing that the differences in information conveyed by the three types of relative clauses are real and tangible is a metaphor, even if metaphors come with limitations.
The metaphor I propose involves a person who almost always drinks either Pinot Grigio or Chardonnay when going to a bar, rarely other wines. The three types of relative clauses are like what happens in three bars. In each of the three bars, the man drinks a glass of Chardonnay. At the surface, the same thing happens three times. In the same way, the three types of relative clauses basically all convey the same information. A clause is subordinated to an antecedent. So what is the difference? The difference concerns what other exact information is known about the three bars.
The first bar corresponds to the so-called “restrictive” relative clause, the one without the comma in English. The crucial piece of information regarding the first bar is that both Pinot Grigio and Chardonnay are available. The man therefore selects Chardonnay.
The second bar corresponds to the so-called “explicative” relative clause. The crucial piece of information regarding the second bar is that there is no Pinot Grigio available. The man is therefore compelled to drink what is available, namely Chardonnay.
The “restrictive” relative clause and the “explicative” relative clause are equally informative. But the quality of the information differs. And this difference can be described in the sharpest and most rigorous way, namely digitally. In the “restrictive” type, there is elimination of an option that is On. In other words, a switch is turned from On to Off. In the “explicative type”, there is a nonavailability of an option because the option is Off. In other words, the same switch is in an Off-position. The contrast between the two types of relative clause is exactly the same as between elimination or turning On into Off and non-availability or being Off. It is the difference between a switch being turned Off and that same switch being Off.
Elimination and non-availability are a kind of negated information. They pertain more to the Offs than to the Ons of a digital structure. Again, in calibrating information in digital fashion, the Offs are as important as the Ons.
As regards the importance of negated information, one is reminded of the curious incident of the dog in the night-time. The incident plays a key role in one of the most popular of Arthur Conan Doyle’s 56 Sherlock Holmes stories, Silver Blaze (1892). Someone has been murdered and at the same time a horse named Silver Blaze has vanished. Mr. Gregory, an inspector with Scotland Yard, is asked to investigate. After gathering all the pertinent evidence, the inspector asks Holmes whether there is any point to which he would wish to draw attention. “To the curious incident of the dog in the night-time”, Holmes replies. “The dog did nothing in the night-time”, the inspector counters. “That was the curious incident”, declares Holmes. That explained what happened.
Likewise, upon learning that the man drank Chardonnay in the second bar, one might be puzzled because he seemed to be in the mood for Pinot Grigio or it is Saturday and he always drinks Pinot Grigio on Saturday. In this case, the “curious incident” is that there was no Pinot Grigio. That explains what happened.
In the same way, upon hearing “French, who are Europeans”, behave in a certain way, someone geographically challenged who has not heard the pause expressed by the comma in writing might ask how French who are not Europeans behave. In this case, the “curious incident” is that there are no non-European French. All French are Europeans.
But what about the third bar? The fundamental difference with the other two bars is as follows. In the first and second bars, there were other wines except Pinot Grigio and Chardonnay. But in the third, Chardonnay is the only wine available. In this case, a double nonavailability explains why the man drinks Chardonnay. Digitally speaking, this double non-availability corresponds to not one but two switches being Off (as opposed to being turned Off). In other words, even if the man had fancied another wine but Chardonnay, the nonavailability of any other wines would have excluded the option.
10. Diagrams Denoting the Differences in Information Content Conveyed by the Three Types of Relative Clauses
Venn diagrams are an eminently useful tool for representing differences in information content in a manner that is both digital and transparent. They can easily be interpreted as magnetic coils and switches or transistors or memristors functioning in a digital circuit.
In the digital realm, in which all is either On or Off, or either 1 or 0, any set in fact involves two sets, itself and all that it is not. For example, the set “sheep” (s) generates the two sets “sheep” (s) and all that is not sheep (1 − s, that is, the universe [1] or all that one could think about minus [−] sheep [s]). Two sets that are associated with one another generate four combination sets. Consider the two sets “French” and “doctor”. Relating the two sets to one another generates the following four combination sets: 1) “French doctors”; 2) “non-French doctors”; 3) “all that is French but not a doctor”; and 4) “anything that is neither French nor a doctor”.
Two sets can be represented by two circles. The relation between the two sets can be depicted by a Venn diagram in which the two circles overlap. The overlap generates four compartments. Each compartment corresponds to one of the four combination sets generated by relating the two sets with one another.
The step from representation by means of Venn diagrams to representation by means of a digital circuit consisting of either magnetic coils and mechanical switches or transistors or memristors is small and easily accomplished. The combination sets of Venn diagrams are either occupied or empty. An occupied or full combination set corresponds to the On-position of a mechanical switch or its equivalent in a transistor or a memristor. An empty set corresponds to the Off-position of a switch or its equivalent.
A relative clause and its antecedent both represent a set or class. For example, “French who are doctors” features the two sets “French” and “all those who are doctors”. “French, who are Europeans” likewise features two sets, namely “French” and “all that is European”.
In the first type of the total of three types of relative clause, “the restrictive” type, none of the four combination sets that are generated by relating two sets to one another as antecedent and relative clause are empty, as in the Venn diagram depicted in Figure 1.
As one progresses from the first type of relative clause to the second type and then to the third, what happens digitally speaking is that compartments get scratched out or blotted out, or destroyed as Venn would say. In an electronic circuit, switches are flipped to an Off-position.
In an “explicative” relative clause such as “French, who are Europeans”, one switch is flipped, as it were, as can be seen in the Venn diagram in Figure 2.
The digital configuration of the “explicative” type of relative clause is characterized or marked by the nexus f = fe “French are Europeans”, whose digital purport is depicted in Figure 3 by the same Venn diagram as in Figure 2 as well as by a corresponding Euler diagram. Euler diagrams are inferior to Venn diagrams because they do not depict empty combination sets, which are the Offs of digital purport.
In a “hermeneutical” relative clause such as “Paris, which is the capital of France”, two combination sets of the Venn diagram are empty, as can be seen in the Venn diagram depicted in Figure 4. Two empty combination sets correspond digitally to two switches that are turned Off.
The digital configuration of the “hermeneutical” type of relative clause is characterized or marked by the nexus p = c “Paris is France’s capital”, which may be represented by the same Venn diagram as in Figure 4 as well as by the Euler diagram in Figure 5.
Flipping a third switch could mean that the universe of thought, everything that one could possibly think about, consists of what is both Paris and the capital of France, in addition to what else it might be. While this may be a pleasant thought to anyone who likes Paris, it is easy to see why this last possibility is not exploited in language. Flipping a third switch could also mean that nothing is either Paris or the capital of France.
11. Distinctive Linguistic Markers of the Three Types
How is the distinction between the three types achieved linguistically? Relative clauses are after also sound patterns that can be sent from the mouth of a speaker to the ear of a hearer. Some distinctive empirical part of that sound pattern needs to communicate or signal or mark
“RESTRICTIVE” RELATIVE CLAUSE Boolean set fd (f × d) = “French who are doctors” (“French doctors”)
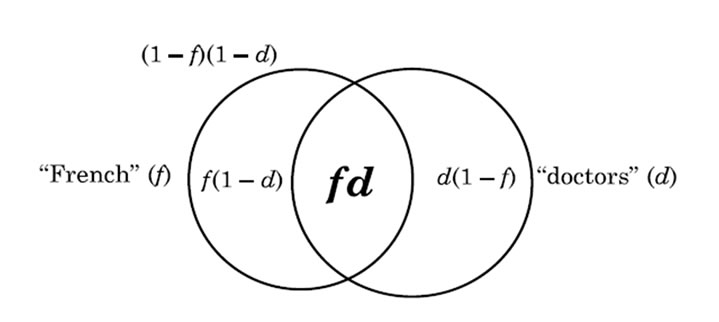
Figure 1. Venn diagram depicting the relative clause of type 1.
“EXPLICATIVE” RELATIVE CLAUSE Boolean set fe (f × e) = “French, [comma!] who are Europeans”
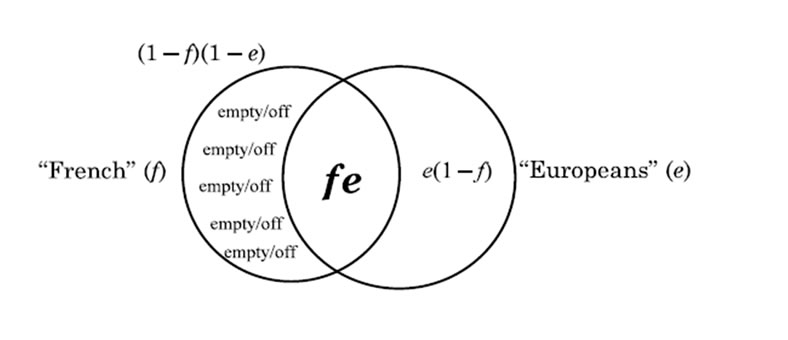
Figure 2. Venn diagram depicting the relative clause of type 2.
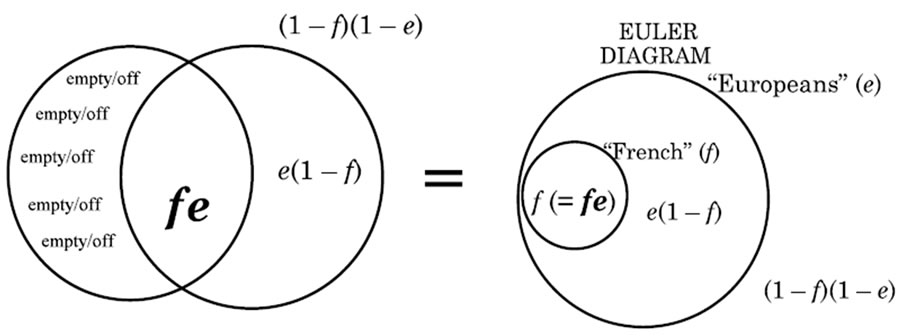
Figure 3. Venn and Euler diagrams depicting the purport of “French are Europeans”.
“HERMENEUTICAL” RELATIVE CLAUSE Boolean set pc (p × c) = “Paris, which is (i.e.) France’s capital”
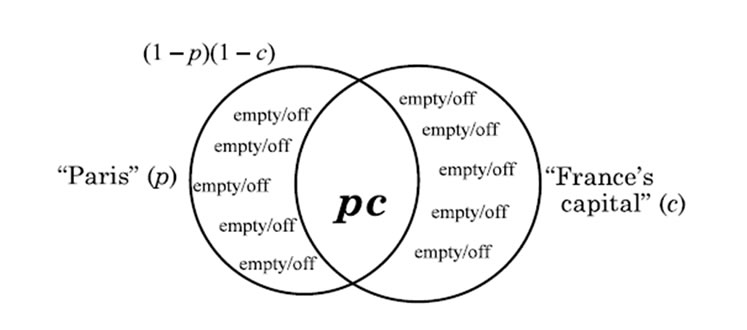
Figure 4. Venn diagram depicting the relative clause of type 3.
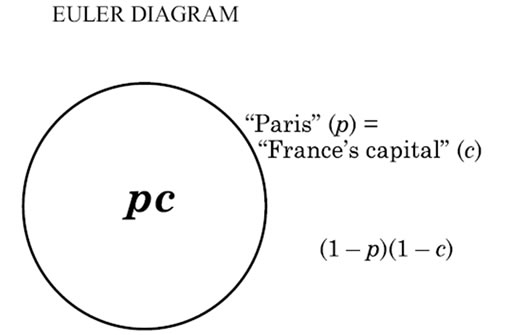
Figure 5. Euler diagram depicting the purport of “Paris is France’s capital”.
that a relative clause belongs to one of the three types and not to the two others. What does one need to look for in all kinds of languages to identify the three types, to the extent that the three types are articulated?
According to the theoretical model proposed above, the second and third types are in a sense marked. One or two of a total of four combination sets are empty. One or two switches are in an Off-position. For example, in the transition from the first to the second type, a compartment is declared non-available on the level of logical purport. But how is this conveyed on the linguistic level? Which morphemes mark non-availability, and how? Consider the generic example “French, who are Europeans”. Clearly, the information “French are Europeans” is implied. Or, if one refers to the French by a pronominal representative, this information may be described as “They are Europeans”. Chances are that some kind of pronominal representative such as “they” or “those” marks the relative clause of the second type as a distinct type.
I believe that exactly such pronominal reference is the function of the extra pai or pin the “explicative” type of relative clause in Coptic. Accordingly, as was noted above, pai does not have demonstrative function, as it otherwise always has. In the example Deuteronomy 1:32-33 cited in §6.6.2, the expression p-et-mooše “the one who is walking, the one who walks” is a conversion of the nexus f-mooše “He is walking, He walks”, whose logical purport is “He is a member of the set of those that are walking”, as Boole points out by means of a different example [20].
The information conveyed by the nexus is fully preserved in the shift from “He is walking” to “the one who is walking”. This conversion is the subject of H.J. Polotsky’s last article, an abstract submitted for the international conference on Egyptian grammar “Crossroads II” held at UCLA in 1990, which in the end he was not able to attend [21].
The elements p- “the one” and f- “he” convey the same information, that is, a reference to an entity involved in the event. It is this information that is needed to declare one of the four combination sets non-available so that it is switched off.
In English, the linguistic marker can be a slight pause, as marked by a comma in writing. A pause appears to have to the same effect as a pronominal element referring back to something previously mentioned. Therefore, two sentences such as “He arrived there, and that late” and “He arrived there—late”, the pronominal element “that”, which refers back to something stated before, and the pause expressed by the Em-dash have roughly the same purport.
In Coptic, the linguistic marker of the third type of relative clause is the expression ete pai pe p- “which is” or “i.e.” (literally: “about which one can say: that is the [or another definite expression]”). Clearly, an expression such as “i.e.” links two classes that completely overlap, which is the digital hallmark of the third type.
12. Other Aspects of Relative Clauses
A more comprehensive study of the relative clause would also need to address matters not discussed in this paper. Among them are the following two phenomena.
First, students of Egyptian and of Semitic languages such as Arabic are acquainted with the contrastive behavior involving indefinite and definite antecedents. From the perspective of modern European languages, this contrastive behavior may be described as follows. In both classical Arabic and later Egyptian, one says something like “the man who” but “a man while” or “a man when”. There are two basic questions. First, does this so-called virtual relative clause, named Hāl in Arabic, point to the common Afrasian origin of Egyptian and Arabic? I believe the answer is “No”. The second question is: What do indefinite expressions share with circumstantial clauses? I believe an answer is possible to this question as well. And the answer differs, as far as I can see, for Egyptian and for Arabic. I would hope to clarify my answers to both questions elsewhere.
A second phenomenon involving relative clauses is a peculiar association between relative clause and conditional clause, first extensively documented for Coptic by Polotsky [22].
For example, the Greek of John 7:37 is ean tis dipsai erkhesthÇ pros me “When someone is thirsty, let him come to me”, which contains a conditional clause. The Coptic translation is petobe marefei šaroi “Whoever is thirsty, let him come to me”, which contains a relative clause. As I hope to show elsewhere, the association can be explained effortlessly in Boolean terms.
13. The Role of Negation in Rational Thought and Language
Negation has been a difficult concept to tame. Ernst Schröder, who taught at the Technische Hochschule in Karlsruhe and was once its director, evokes the tortured path of the study of negation from the time of Aristotle and even before as [23]
a field of investigation in which great caution is warranted, since the most renowned philosophers of all time—I mention in first place Aristotle and Kant— widely diverge from one another in this regard, a field also in which even in most recent times authoritative voices have constructed untenable theories, theories that have entangled their creators in the greatest contradictions with themselves.
It was Boole who finally tamed the beast. Augustus De Morgan was an important precursor and Venn did much to make Boole’s ideas more accessible. One of Venn’s great merits, in my opinion, is to have emphasized again and again how hardly anything more than the elimination or negation of classes among all possible combination classes gives the mind the power to engage reality and reason about it.
The single most important step in domesticating negation, and also a main point of this paper, is that negation plays as important a role in affirmative statements as it does in negated statements. I believe that, without heeding this point, the analysis of language will never be pushed back to its final frontier.
14. How the Mind Seizes Control of Reality in Digital Fashion
Already from the mere contemplation of the relative clause, a partial picture emerges of how the mind seizes hold of reality and molds it into information and reasons about it. This procedure is recognizable in all facets of rational thought and language. Only an outline is presented here. I would hope to present a more detailed account in a paper entitled “How the Biological Brain Reasons: The Four Digital Operations Underlying All Rational Thought and Its Expression in Language”. The main steps are as follows.
1) Reality presents itself to the senses as discrete elements.
2) These discrete elements are stored in the mind for what they are, discrete elements.
3) Knowledge seriously takes off when two elements are related to one another.
4) In relating two elements to one another, the mind produces the four combination sets involving the two elements and their supplement sets. The set itself corresponds to an On-position (1). Its supplement corresponds to an Off-position (0). The four combination sets can therefore be characterized as On/On, On/Off, Off/On, and Off/Off. Importantly, the four combination sets encompass all that is thinkable.
5) Knowledge derives its principal strength from the shutting down, or the switching off, of one or two of the four combination sets. But switching off three or four is hardly informative.
The case of the relative clause has been described in detail above. But the exact same switching off as a way of achieving knowledge is also found throughout rational thought and language. It shows rational thought and language to be profoundly digital. Two additional examples of this digital imprint are as follows.
First is a sentence such as “Aristoteles is a philosopher”, which would correspond to a nominal sentence in Coptic. The relation between the two sets “Aristotle” and “philosophers” generates four combination sets. One of these four combination sets is switched off, namely On/ Off, or all that is both Aristotle and not a philosopher.
Second is a conditional sentence such as “When it rains, I stay inside”. Again, one of four combination sets is switched off, and it is again On/Off, that is, all instances in which it rains and I do not stay inside. The three other combination sets are occupied and therefore correspond to an On-position: 1) all instances when it rains and I stay inside; 2) all instances when it does not rain and I stay inside; and 3) all instances when it does not rain and I do not stay inside.
15. Scope of the Present Paper: A Single Mathematical Theorem
In mathematics, which is deductive, one focuses narrowly on an individual phenomenon, a certain property of triangles or a certain type of equation, in an attempt to determine the single valid way of analyzing it. There is no need to observe countless instances of a phenomenon as is necessary in the many inductive endeavors of the sciences. The careful contemplation of just one instance of the phenomenon suffices. The desired outcome is a theorem, such as the theorem in Proposition 32 of the first book of Euclid’s Elements that the three interior angles of the triangle are equal to two right angles. Similarly, the present article exhibits the scope of one theorem as expanded by preliminary remarks on method. The theorem holds that all the possible types of relative clauses relate to one another in a way that may be called digital. Implied is the distinct possibility, to be confirmed or rejected by further investigation, that much if not most else in rational thought and languages is also digital. In general, it is preferable to firmly secure one theorem before moving on to another. The firmer a theorem, even if it is just one, the more promise it holds for what is yet to come.
16. Acknowledgements
I am grateful for two opportunities to present versions of this paper to audiences, first in the form of a lecture addressed on Mar. 20, 2008 to the members of the Semitic Philology Workshop of Harvard University’s Department of Near Eastern Languages and Civilizations, at the invitation of event organizer Na’ama Pat-El, and second as part of a paper read at the international conference on “Language Typology and Egyptian-Coptic Linguistics” held at the Max Planck Institute for Evolutionary Anthropology in Leipzig on Oct. 2-5, 2008 and organized by Sebastian Richter and Martin Haspelmath. I also thank the founders of www.BestThinking.com for having hosted a provisional version of the present paper on their website until it was accepted for publication.
I am also grateful for comments provided by referees of the version of this paper initially submitted to this journal. They have done much to improve the paper.
REFERENCES
- L. Depuydt, “Questions and Related Phenomena in Coptic and in General: Final Definitions Based on Boole’s Laws of Thought,” In: D. W. Johnson, J. E. Goehring and J. E. Timbie, Eds., The World of Early Egyptian Christianity, The Catholic University of America Press, Washington DC, 2007, pp. 72-94.
- L. Depuydt, “The Other Mathematics,” Gorgias Press, Piscataway, 2008, pp. 307-321.
- L. Depuydt, “The Conjunctive in Egyptian and Coptic: Towards a Final Definition in Boolean Terms,” In: Ch. G. Häberl, Ed., Afroasiatic Studies in Memory of Robert Hetzron: Proceedings of the 35th Annual Meeting of the North American Conference on Afroasiatic Linguistics (NACAL 35), Cambridge Scholars Publishing, Newcastle upon Tyne, 2009, pp. 12-30.
- L. Depuydt, “Towards the Full Digitalization of Grammar: The Case of the Egyptian and Coptic Nominal Sentence,” Lingua Aegyptia, Vol. 17, 2010, pp. 27-50.
- L. Depuydt, “From ‘My Body’ to ‘Myself’ to ‘As for Me’ to ‘Me Too’: Philological and Digital Analysis of a Triple Shift in Egyptian,” Journal of the American Research Center in Egypt, Vol. 45, 2009, pp. 247-290.
- L. Depuydt, “Zur Unausweichlichen Digitalisierung der Sprachbetrachtung: ‘Allein’, ‘Anderer’, ‘Auch’, ‘Einziger’, ‘(Seiner)seits’, und ‘Selbst’ als Digitales Wortfeld im Ägyptisch-Koptischen und im Allgemeinen,” In: A. I. Blöbaum, K. Butt and I. Köhler, Eds., Lexical Fields, Semantics and Lexicography, Aegyptiaca Monasteriensia, Vol. 7, Shaker Verlag, Aachen, 2011, pp. 5-38.
- G. Boole, “An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities,” Walton and Maberly, London, 1854, p. 4.
- C. J. Chivers, “Political Heir Is Less Rosy than Putin on the State of Russia,” The New York Times, 2008. www.nytimes.com/2008/02/16/world/europe/16russia.html
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” 2 Vols., American Studies in Papyrology 27 and 29, Scholars Press, Decatur (Vol. 1) and Atlanta (Vol. 2), 1987 and 1990, p. 51.
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” Scholars Press, Decatur and Atlanta, 1987 and 1990, pp. 45-127.
- B. Layton, “A Coptic Grammar,” 2nd Edition, Otto Harrassowitz Verlag, Wiesbaden, 2004, pp. 324-335.
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” Scholars Press, Decatur and Atlanta, 1987 and 1990, p. 93.
- G. Boole, “Studies in Logic and Probability,” Edited by R. Rhees, Watts & Co., London, 1952, pp. 211-229.
- G. Boole, “Studies in Logic and Probability,” Edited by R. Rhees, Watts & Co., London, 1952, p. 211.
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” Scholars Press, Decatur and Atlanta, 1987 and 1990, pp. 89-93.
- B. Layton, “A Coptic Grammar,” Otto Harrassowitz Verlag, Wiesbaden, 2004, pp. 329-331.
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” Scholars Press, Decatur and Atlanta, 1987 and 1990, pp. 104-105.
- B. Layton, “A Coptic Grammar,” Otto Harrassowitz Verlag, Wiesbaden, 2004, pp. 331-332.
- J. Venn, “Symbolic Logic,” 2nd Edition, Macmillan and Co., London and New York, 1894.
- G. Boole, “Investigation,” Walton and Maberly, London, 1854, p. 35.
- H. J. Polotsky, “‘Article’ and ‘Determinative Pronoun’ in Coptic,” Lingua Aegyptia, Vol. 1, 1991, pp. 241-242.
- H. J. Polotsky, “Grundlagen des koptischen Satzbaus,” Scholars Press, Decatur and Atlanta, 1987 and 1990, pp. 81-84.
- E. Schröder, “Vorlesungen über die Algebra der Logik (Exakte Logik),” Vol. 1, B.G. Teubner, Leipzig, 1895, p. 319.

