ABSTRACT

It is possible to construct an arbitrage-free interest rate model in which the LIBOR rates follow a log-normal process leading to Black-type pricing formulae for caps and floors. The key to their approach is to start directly with modeling observed market rates, LIBOR rates in this case, instead of instantaneous spot rates or forward rates. This model is known as the LIBOR Market Model. We formulate the SAFEX-JIBAR market model based on the fact that the forward JIBAR rates follow a log-normal process. Formulae of the Black-type are deduced.

1. Introduction

Instantaneous rate models, although theoretically satisfying, are less so in practice. Instantaneous rates are not observable and calibration to market data is complicated. Hence, the need for a market model where one models LIBOR rates seems imperative. In this modeling process, we aim at regaining the Black-76 formula [1] for pricing caps and floors since these are the ones used in the market. To regain the Black-76 formula we have to model the LIBOR rates as log-normal processes. The whole construction method means calibration by using market data for caps, floors and swaptions is straight-forward. Brace, Gatarek and Musiela [2] and, Miltersen, Sandmann and Sondermann [3] showed that it is possible to construct an arbitrage-free interest rate model in which the LIBOR rates follow a log-normal process leading to Black-type pricing formulae for caps and floors. The key to their approach is to start directly with modeling observed market rates, LIBOR rates in this case, instead of instantaneous spot rates or forward rates. Thereafter, the market models, which are consistent and arbitrage-free [2,4,5], can be used to price more exotic instruments. The resulting model is known as the LIBOR Market Model.

Some of the advantages of market models as compared to other traditional models are that market models imply pricing formulae for caplets, floorlets or swaptions that correspond to market practice. Consequently, calibration of such models is relatively simple.

The plan of this work is as follows. Based on an improved version of the standard risk-neutral valuation approach, the forward risk-adjusted valuation approach, and on an elaborate process of computing forward riskadjusted measures, a proposition is made to apply the technique to the pricing of South African caps and floors. Secondly, based on general interest rate modeling [6-25] and the formulation of the LIBOR, the technique used will enable us to formulate and name a new model for the South African market, the SAFEX-JIBAR model.

2. The JIBAR

Each day at 10:30 am, each of the 14 South African and South African-based foreign banks are asked to provide the midpoint between Bid and Offer of their 1, 3, 6, 9 and 12 month deposit National (Negotiable) Certificate of Deposit (NCD) rates quoted as yield. In each category, e.g., in the 1 month category, the 14 rates are arranged in order. The top two and the bottom two are eliminated and the remaining 10 are averaged and rounded to 3 decimal places. The resulting rate is termed a k-month JIBAR rate where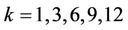. JIBAR stands for Johannesburg Inter Bank Agreed Rate. It is the rate at which banks buy and sell short-term money among themselves and is traditionally a wholesale and not a retail rate. It is reset every quarter and is fixed for the duration of the quarter. Let represent the -month SAFEX-JIBAR rate. Let represent the -month SAFEX-JIBAR rate. Then

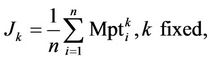
where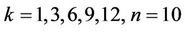, 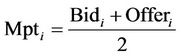is the midpoint corresponding to bank.

3. Background to Interest Rate Caps and Floors: The South African Context

In many circumstances, corporate treasurers in South Africa are hesitant to enter into interest rate derivative agreements which involve an element of optionality. The main deterrent factor is that many of them do not necessarily have access to sophisticated pricing models to accurately price these derivatives. However, for many corporate treasurers, caps and floors have been the preferred method of achieving disaster insurance against incidents like the 1998 emerging markets crisis. This sterms from the fact that caps and floors are highly adaptable to the particular needs and requirements of companies wishing to manage and hedge against interest rate reset risk on interest-sensitive assets and liabilities. On the exercise date of the cap or floor agreement, the prespecified strike rate is compared to the standard reference floating rate, that is the 3-month SAFEX-JIBAR rate. The interest differential is then applied to the contractually specified notional principal amount (amount to be borrowed/lent) in order to calculate the amount to be paid by the writer/seller to the holder/buyer (the settlement). The notional principal amount is normally at least R1 million.

Settlement of a single period cap/caplet is done in the following manner. The seller of a cap agrees to pay the buyer the difference between the fixed strike rate and the reference floating rate (JIBAR), based on the notional principal amount, when the JIBAR reset exceeds the fixed strike rate. Settlement occurs on each reset date according to the formula:

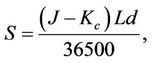
where 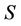is the settlement amount in Rands, 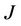is the JIBAR rate for that period/quarter, 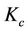is the cap strike rate, 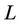is the notional principal amount, and 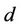is the exposure period in days (usually 91 or 92).

In the majority of cases, settlement takes place in arrears, in which case the settlement amount is then present-valued to the exercise date.

In a similar fashion, the settlement amount of a single period floor/floorlet is given by the formula:

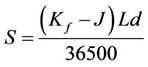
where 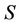is the settlement amount in Rands, 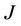is the JIBAR rate for that period, 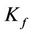is the floor strike rate, 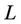is the notional principal amount, and 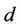is the exposure period in days.

In this case, the seller of a floor agrees to pay the buyer the difference between the fixed strike rate and the SAFEX-JIBAR, based on the notional principal amount, when the SAFEX-JIBAR rate resets below the fixed strike rate. Settlement also takes place on each reset date. To get a better feeling of this, take a company that expects a surplus cash receipt of R1 million in a month’s time which it will wish to invest. The company fears rates will be lower in future and therefore decides to buy a T1m-T4m at-the-money floorlet with a maturity of 3 months, to hedge against the risk of losing money.

4. Pricing Caps, Floors and Collars

Each caplet/floorlet is priced from the implied 3-month forward rate for that period, from the yield curve. Hence, the at-the-money price of a caplet/floorlet is just the forward rate for that period. A strike price lower than that implied by the forward rate will result in an in-the-money caplet with both intrisic and time values, whereas a strike price above the forward rate will result in an out-themoney caplet. Similarly as with most option-styled derivative instruments, the more time to expiry, the greater the time value inherent in the option. This means that a T3m-T6m period caplet has time value of 3 months while a T21m-T24m period caplet has time value of 21 months. Volatility (annualized) is another factor that affects the value of a cap/floor. There is a positive correlation between volatility and the price of both caps and floors. The more volatile the price or rate of an asset, the more likely it is to reach the option strike price, and so the more valuable the option. In brief, higher volatility implies higher option value. Standard option pricing theory postulates that the spot price or rate of the underlying follows a lognormal random walk. The fact that there are so many factors impacting on the price of a cap/floor makes it practically impossible for market-makers to hedge caps and floors. Cap and floor values also change as the shape of the yield curve changes, something which is not a factor in equity derivatives. Basically, the pricing of caps and floors in the South African market follows an extension of the Black-Scholes option valuation formula and is done in the following manner.

Suppose we have an interest rate cap with strike rate 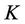and reset at times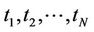, with a final payment to be made at time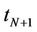. If we let 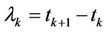and 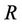be the 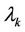maturity forward rate observed at time 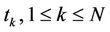, then the time-t of the kth caplet 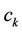is given by

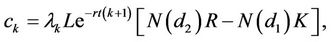(1)

where 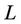is the nominal amount.

Similarly for a floor, the price of the kth floorlet 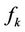with strike 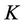is given by

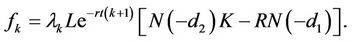(2)

In both cases,

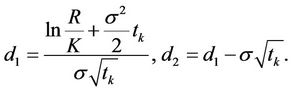
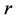is the continuously compounded rate at the caplet/ floorlet payment time 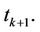The cap/floor price is the sum of the prices of the caplets/fllorlets.

5. The SAFEX-JIBAR Market Models

Consider a fixed set of increasing maturities

such that 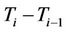= exposure period in days. Define 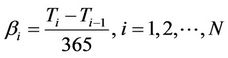as the daycount factor (usually 91/365 or 92/365). Denote by 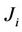the 3-month SAFEX-JIBAR rate corresponding to the period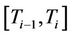. We can therefore define a caplet with strike 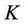and resettlement dates 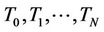as a contract which at time 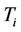gives the holder a pay-off or settlement amount of

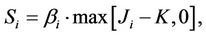(3)

where 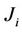is the reference floating SAFEX-JIBAR rate for the period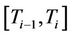; 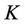is the caplet strike. 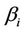is normally termed the tenor. Both the floating and strike rates are in decimal form.

Thus, for a portfolio of 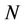caplets we would have the following settlements:

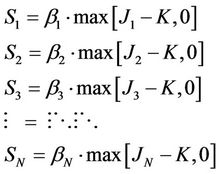
Since by definition, 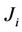is an average, for every

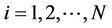, the JIBAR-SAFEX process 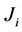is a martingale under the corresponding forward measure 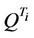on the interval 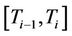[6]. Standard option pricing theory postulates that the spot price or the rate of the underlying follows a log-normal random walk. If for each 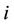the SAFEX-JIBAR rate 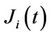is log-normal under its measure, we assume 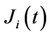is a Geometric Brownian Motion, then we have

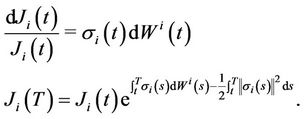(4)

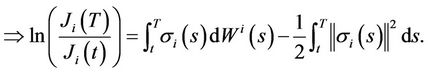(5)

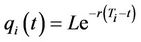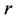Define where is the continuously compounded forward rate for the period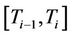. We propose the following new results.

Proposition 5.1 In the SAFEX-JIBAR market, the time-t price of a caplet with strike 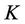is given by

(6)

where

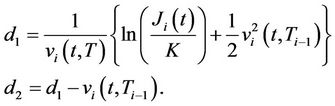
Here,

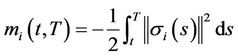
and

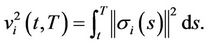
Proof: Since

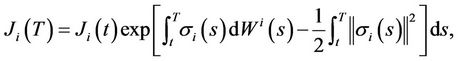(7)

the value of caplet 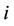is given by

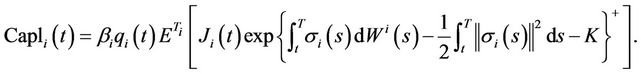(8)

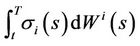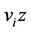Write as where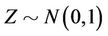. Thus

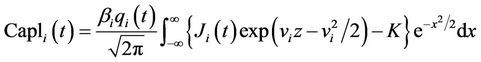
and

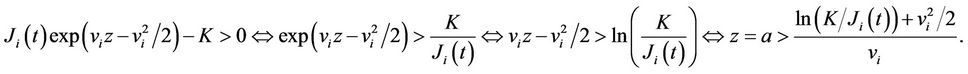
Hence

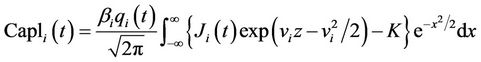
becomes

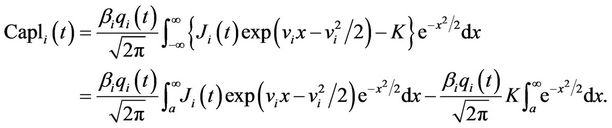
Let

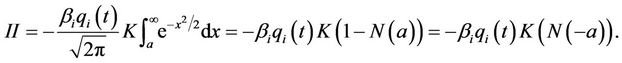
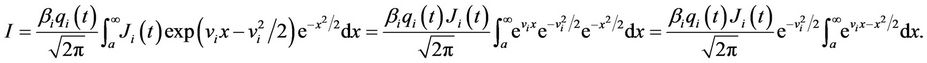
Now completing the square,

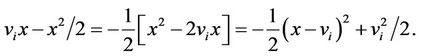
Thus

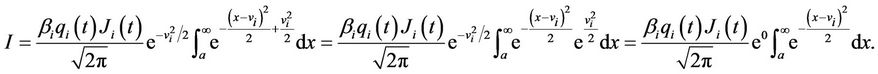
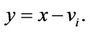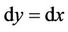Let Then and

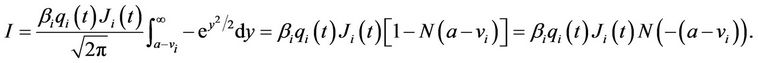
Hence

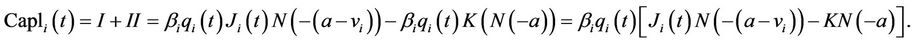(9)

Since

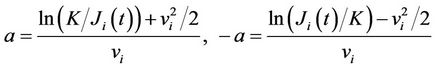
and

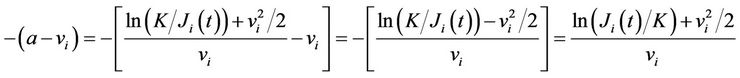
Now letting 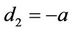and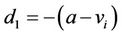, we have, as required that

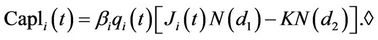(10)

Definition 5.2 A floorlet with strike 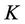and resettlement dates 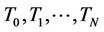is a contract which at time 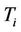gives the holder a settlement amount of

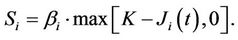(11)

Proposition 5.3 In the SAFEX-JIBAR market, the price of a floorlet whose settlement amount is given by

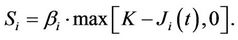(12)

is given by the formula

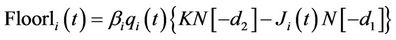(13)

where

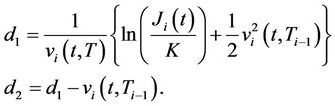
where 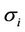is the volatility of the interest rate of the period.

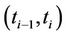Proposition 5.4 The time-t price of a SAFEX-JIBAR collar with resettlement dates 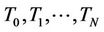is given by

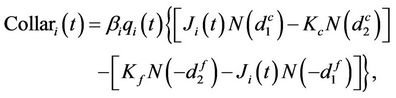
where 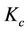and 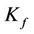are the cap and floor strike rates respectively,

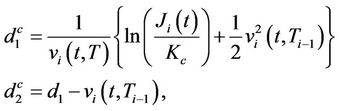
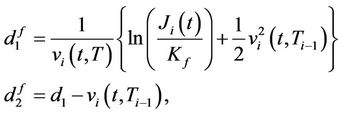
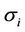is the volatility of the interest rate of the period.

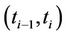Equations (6) and (9) show that the numeraire for the pricing of caps and floors in the JIBAR market is.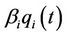

6. The Greeks

In this section, we intend to derive formulae for some hedging measures for our model. Most traders employ sophisticated hedging schemes which involve the calculation of such measures as delta, gamma and vega. The delta of an option measures the rate at which the option price changes with respect to the price of the underlying forward rate. Gamma is the rate of change of the option’s delta with respect to the forward rate. Vega is the rate of change of option price with respect to the volatility of the underlying. If vega is high in absolute terms, then the option value is sensitive to small changes in volatility. In contrast, if vega is small in absolute terms, volatility changes have relatively little impact on the value of the option. We will recall that

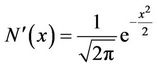
and that

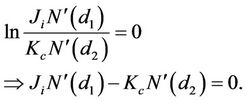
This fact will help us deduce our measures in the following manner. For a caplet,

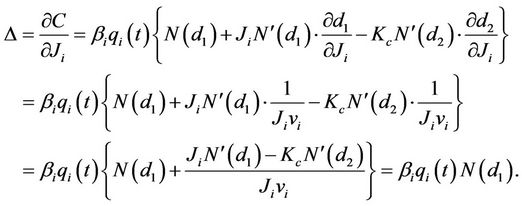
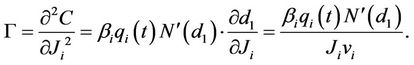
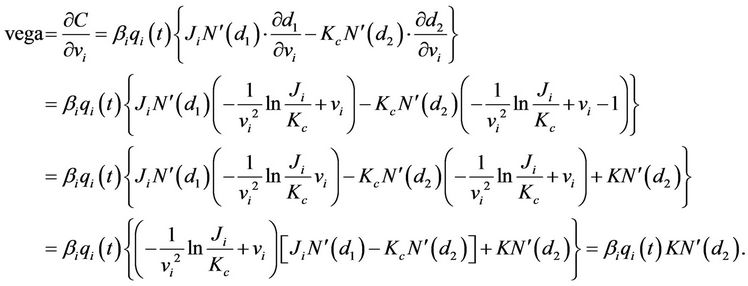
Similarly, it can be shown that for floorlets,

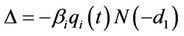
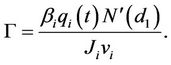
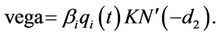
Note that the delta, gamma and vega of a cap/floor is simply the arithmetic sum of the respective delta, gamma and vega for the caplets involved.

7. Conclusion

The present work has made some notable contribution in the interest rate modeling arena. A clear understanding of the LIBOR theory enabled an easy extension of the same ideas to the construction of the SAFEX-JIBAR market model which gives prices consistent with both economic practicality and with other Black-type models.

REFERENCES