Received 13 June 2014; revised 15 July 2014; accepted 21 July 2014

ABSTRACT

A tractable nonparametric prior over densities is introduced which is closed under sampling and exhibits proper posterior asymptotics.

Keywords:

Bayesian Nonparametrics, Bayesian Density Estimation, Random Densities, Random Partitions, Stochastic Simulations, Smoothing

1. Introduction

The early 1970’s witnessed Bayesian inference going nonparametric with the introduction of statistical models with infinite dimensional parameter spaces. The most conspicuous of these models is the Dirichlet process [1] , which is a prior on the class of all probability measures over a given sample space that trades great analytical tractability for a reduced support: as shown by Blackwell [2] , its realizations are, almost surely, discrete probability measures. The posterior expectation of a Dirichlet process is a probability measure that gives positive mass to each observed value in the sample, making the plain Dirichlet process unsuitable to handle inferential problems such as density estimation. Many extensions and alternatives to the Dirichlet process have been proposed [3] .

In this paper we construct a prior distribution over the class of densities with respect to Lebesgue measure. Given a partition in subintervals of a bounded interval of the real line, we define a random density whose realizations have a constant value on each subinterval of the partition. The distribution of the values of the random density on each subinterval is specified by transforming and conditioning a multivariate normal distribution.

Our simple random density is the finite dimensional analogue of the stochastic processes introduced by Thorburn [4] and Lenk [5] . Computations with these stochastic processes involve an intractable normalization constant, and are restricted to values of the random density on a finite number of arbitrarily chosen domain points, demanding some kind of interpolation of the results. The finite dimensionality of our random density makes our computations more direct and transparent and gives us simpler statements and proofs.

An outline of the paper is as follows. In Section 2, we give the formal definition of a simple random density. In Section 3, we prove that the distribution of a simple random density is closed under sampling. The results of the simulations in Section 4 depict the asymptotic behavior of the posterior distribution. We extend the model hierarchically in Section 5 to deal with random partitions. Although the usual Bayes estimate of a simple random density is a discontinuous density, in Section 6 we compute smooth estimates solving a decision problem in which the states of nature are realizations of the simple random density and the actions are smooth densities of a suitable class. Additional propositions and proofs of all the results in the paper are given in Section 7.

2. Simple Random Densities

Let be the probability space from which we induce the distributions of all random objects considered in the paper. For some integer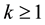, let 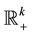be the subset of vectors of 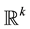with positive components. Write 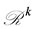for the Borel sigma-field of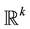. Let 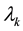denote Lebesgue measure over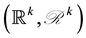. We omit the indexes when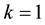. The components of a vector 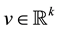are written as.

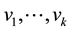Suppose that we have been given an interval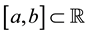, and a set of real numbers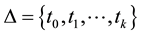, such that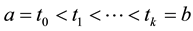, inducing a partition of 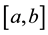into the 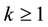subintervals

The class of simple densities with respect to this partition consists of the nonnegative simple functions which have a constant value on each subinterval and integrate to one. Let, for, and define the map by. Each simple density within this class can be represented as

in which is such that each, and. The’s are the heights of the steps of the simple density f.

From now on, let, for. Note that, by the definition of the’s given above, it follows that if. Moreover, define the projection on the first coordinates by. For a normal random vector with mean and covariance matrix, denote by the distribution of the lognormal random vector. If is nonsingular, it is easy to show that U has a density

in which is the determinant of, and we have introduced the notations and.

We define a random density whose realizations are simple densities with respect to the partition induced by specifying the distribution of the random vector of its steps heights. Informally, the steps heights will have the distribution of a lognormal random vector U given that. The formal definition of the random density is given in terms of a version of the conditional distribution of U given and the expression of its conditional density with respect to a dominating measure. However, we are outside the elementary case in which the joint distribution is dominated by a product measure. In fact, we have in Proposition 7.1 a simple proof that Lebesgue measure and the joint distribution of U and are mutually singular.

A suitable family of measures that dominate the conditional distribution of U given, for each value of, is described in the following lemma.

Lemma 2.1. Let be defined by, for. Then, each is a measure over.

The proof of Lemma 2.1 is given in Section 7. Figure 1 gives a simple geometric interpretation of the measures when the underlying partition is formed by three subintervals.

The following result is the basis for the formal definition of the random density.

Theorem 2.2. Let, with nonsingular, and let be the family of measures over defined on Lemma 2.1. Then, we have that defined by

is a regular version of the conditional distribution of given, in which

Moreover, , for each.

The necessary lemmata and the proof of Theorem 2.2 are given in Section 7. The following definition of the random density uses the specific version of the conditional distribution constructed in Theorem 2.2.

Definition 2.3. Let, with nonsingular. We say that the map defined by

is a simple random density, in which are the random heights of the steps of, with distribution given by, for, and is the regular version of the conditional distribution of U given obtained in Theorem 2.2. Hence, for every, we have

in which and it holds that. We use the notation.

3. Conditional Model

Now, we model a set of absolutely continuous observables conditionally, given the value of a simple random density. The following lemma, proved in Section 7, describes the conditional model and determines the form of the likelihood.

Lemma 3.1. Consider represented as

and let the random variables be conditionally independent and identically distributed, given that, with distribution

in which we have defined. Define and let.

Then, , almost surely, with Radon-Nikodym derivative

in which, for.

The factorization criterion implies that is a sufficient statistic for. That is, in this conditional model, as one should expect, all the sample information is contained in the countings of how many sample points belong to each subinterval of the partition induced by.

Using the notation of Lemma 3.1, and defining, we can prove that the prior distribution of is closed under sampling.

Theorem 3.2. If, then, in which.

This result, proved in Section 7, makes the simulations of the prior and posterior distributions essentially the same, the only difference being the computation of.

4. Stochastic Simulations

We summarize the distribution of a simple random density, represented as , in two ways. First, motivated by the fact, proved in Proposition 7.5, that the prior and posterior expectations are predictive densities, we take as an estimate the expectation of the steps heights. Second, the uncertainty of this estimate is assessed defining

for, and taking as a credible set the with the smallest such that, in which is the credibility level.

The Random Walk Metropolis algorithm [6] is used to draw dependent realizations of the steps of as

values of a Markov chain. The two summaries are computed through ergodic means of this chain. For

example, the credible set is determined with the help of the almost sure convergence of

As for the parameters appearing in Definition 2.3, we take in our experiments all the’s equal to one, and the covariance matrix is chosen in the following way. Given some positive definite covariance function, we induce from C defining

for. In our examples we study the family of Gaussian covariance functions defined by , with dispersion parameter and scale parameter.

Example 4.1. Let and consider the sample space with. For the sake of generality, we induce from the family of Gaussian covariance functions with fixed dispersion parameter but with random scale parameter, in which. These choices guarantee that computations with are numerically stable. In Figure 2, the summaries of the prior distribution of show that the value of controls the concentration of the prior. Fixing and generating data from the mixture

we have in Figure 3 the posterior summaries for different sample sizes. Note the concentration of the posterior as we increase the size of the samples.

We observe the same asymptotic behavior of the posterior distribution with data coming from a triangular distribution and a mixture of normals (with appropriate truncation of the sample space).

5. Random Partitions

Inferentially, we have a richer construction when the definition of the simple random density involves a random partition. Informally, we want a model for the random density in which the underlying partition adapts itself according to the information contained in the data.

We consider a family of uniform partitions of a given interval. Each partition of this family will be described by a positive integer random variable K, which determines the number of subintervals in the partition. Since the parameter of the family of Gaussian covariance functions used to induce may have different meanings for different partitions, we treat it as a positive random variable R.

Explicitly, we are considering the following hierarchical model: K and R are independent. Given that and, we choose the uniform partition of the interval induced by

induce from the family of Gaussian covariance functions, and take the simple random density . Finally, the observables are modeled as in Lemma 3.1. This hierarchy is summarized in the following graph.

In the following example, instead of specifying priors for K and R, we define the likelihood of K and R by, whose form is obtained in Proposition 7.6, find the maximum

, and use these values in the definitions of the prior, determining the posterior summaries as we did in Section 4.

Example 5.1. With a sample of size 2000 generated from a distribution, we find the maximum of the likelihood of K and R at. In Figure 4 we have the posterior summaries obtained using these values in the definition of the prior. Moreover, in the left graph of Figure 5 we have the distribution function corresponding to the estimated posterior density. For the sake of comparison, we plot in the right graph of Figure 5 some quantiles of this distribution against the quantiles of the distribution from which we generated the data.

6. Smooth Estimates

It is possible to go beyond the discontinuous densities obtained as estimates in the last two sections and get smooth estimates of a simple random density solving a Bayesian decision problem in which the states of nature are the realizations of and the actions are smooth densities of a suitable class.

In view of Theorem 3.2, it is enough to consider the problem without data. As before, the sample space is the interval, which is partitioned according to some. For a density f with respect to Lebesgue measure, we

denote its norm by.

Proposition 6.1. For, let be densities with respect to Lebesgue measure, with support, such that, and let be the class of densities of the form, with, for

, and. Let and define as the class of densities which are realizations of. Define the loss function by

Then, the Bayes decision is, in which minimize globally the quadratic form

subject to the constraints, for, and, with the definitions

We use the result of Proposition 6.1, proved in Section 7, choosing the’s inside a class of smooth densities that serve approximately as a basis to represent any continuous density with the specified support.

For the next example, suppose that the support of the densities is the interval. Bernstein’s Theorem (see [7] , Theorem 6.2) states that the polynomial

approximates uniformly any continuous function f defined on, when. Suppose that f is a density. If we define, for,

we can rewrite the approximating polynomial as, in which is a density of a random variable. Hence, if we take a sufficiently large N, we expect that any continuous density with support will be reasonably approximated by a mixture of these’s.

Example 6.2. Suppose that we have a sample of 5000 data points simulated from a truncated exponential distribution, whose density is

Repeating the analysis made in Example 5.1, we find the maximum of the likelihood of K and R at . The left graph of Figure 6 presents the posterior summaries. After that, we solved the problem of constrained optimization in Proposition 6.1 and found the results shown in the right graph of Figure 6.

7. Additional Results and Proofs

In this section we present some subsidiary propositions and give proofs to all the results stated in the paper.

Proposition 7.1. Let and denote by the joint distribution of and. Then,.

Proof. Define the set. Then,

by definition of. On the other hand, note that, since this is the -volume of the k-di-

mensional hyperplane defined by the set A. Since, the result follows.

Proof of Lemma 2.1. When, the result is trivial, since in this case, making a null measure. Suppose that and let be the function defined by

Define by. We will show that, for every. Suppose that. Then, there is a such that and

Since, we have that, implying that. Since, it follows from

the definition of the inverse image of that and, therefore, we conclude that . To prove the other inclusion, suppose that and define. Hence, and by the definition of we have that

implying that, because. Since and, it follows that . Therefore,. Hence, we have that and the properties of the inverse image of and the Lebesgue measure entail that each is a measure over.

Lemma 7.2. Let. Let, defined by

be a measure over. Denote by the joint distribution of and. Then, we have that, with Radon-Nikodym derivative given by

in which and.

Proof. Define the function by. Note that. Define the function by, with and. The diagram

commutes, since, for every. For every, we have that

in which the fifth equality is obtained transforming by T, and. It follows that, and the Radon-Nikodym derivative has the desired expression.

Lemma 7.3. Let be the measure defined on Lemma 7.2 and let be the family of measures defined on Lemma 2.1. Then, for every measurable nonnegative, we have that

in which and.

Proof. Define by. Hence, f is a differentiable function whose inverse is the differentiable function g defined on Lemma 2.1. The value of the Jacobian on the point is. Let, , , and define as in Lemma 2.1. When, we have already shown in the course of the proof of Lemma 2.1 that, for every. Remembering

that, by definition, , it follows that and we conclude that

. Now suppose that. In this case, since, we have that. As for the value of, consider two subcases: since

if any of the, then, otherwise, we have

and again it happens that. Therefore, we conclude that in this case also

. Hence, for and, we have that

in which and, the third equality is obtained transforming by f, and the penultimate equality is a consequence of Tonelli’s Theorem. The result follows from the Product Measure Theorem and Fubini’s Theorem (see [8] , Theorems 2.6.2 and 2.6.4).

Lemma 7.4. Let. Let be the family of measures defined on Lemma 2.1. Let be the distribution of. Then, with Radon-Nikodym derivative given by

Proof. Let, , and. Let be the measure defined on Lemma 7.2. We have that

in which the penultimate equality follows from Lemma 7.2, and the last equality follows from Lemma 7.3. Hence, and the Radon-Nikodym derivative has the desired expression.

Proof of Theorem 2.2. Let be the joint distribution of and, and let be the distribution of. For and, by the definition of conditional distribution, we have that

in which we have used the Leibniz rule for the Radon-Nikodym derivatives. On the other hand, by Lemmas 7.2 and 7.3, we have that

with and. Both expressions for are compatible if

for almost every r. Therefore, we have that, for almost every , with Radon- Nikodym derivative given by

as desired. The fact that follows immediately.

Proof of Lemma 3.1. Let be the measures over defined by, for

each. Let, with, for. By the hypothesis of conditional independence and Tonelli’s Theorem, we have that

Hence, and agree on the -system of product sets that generate. Therefore, by Theorem A.26 of [9] , both measures agree on the whole sigma-field. It follows that, almost surely, and the Radon-Nikodym derivative has the desired expression.

Proof of Theorem 3.2. By Bayes Theorem, for each, we have that

in which we have used the expression of the likelihood obtained in Lemma 3.1, the Leibniz rule for the Radon-Nikodym derivatives, the expression of in Definition 2.3, and the constant is such that. The remainder of the proof relies on some matrix algebra. Let I be the identity matrix. Since,

by definition, is symmetric , we have that. Therefore, we have that

. Write. Since the scalar is equal to its transpose, we have that

Defining, we have

with. Define. Since the scalar

, we have that. Hence, we obtain

Using this result in the expression of together with the expression of, we have

in which and is a density of the random vector. We conclude that, given that, the vector H has the distribution of the heights of the steps of, as desired.

Proposition 7.5. Suppose that the random variables are modeled according to Lemma 3.1. Denote by the distribution of, for. For convenience, use the notations and. Then, for every, we have

1), for;

2), a.s..

Proof. By Definition 2.3, we have

in which and, for. In an analogous manner, we have

For item 1), note that

in which the fourth equality follows from Tonelli’s Theorem. For item 2), for each, we have

On the other hand, we have

in which the third equality follows from the hypothesis of conditional independence and Theorem B.61 of [9] , the fourth equality is a consequence of Theorem 2.6.4 of [8] , and the sixth equality is due to Tonelli’s Theorem. Comparing both expressions for, we get the desired result.

Proposition 7.6. Let over be the distribution of K and let over be the distribution of R. Denote by the joint distribution of K and R, which by the independence of K and R is equal to the product measure, and let be the joint distribution of K, R and H. In the hierarchical model described in Section 5, we have that, almost surely, with Radon-Nikodym derivative

for the defined on Lemma 3.1.

Proof. Let and. By the definition of conditional distribution, we have

On the other hand, by arguments similar to those used in the proof of Proposition 7.5, we have

Comparing both expressions for, we have

almost surely, and the result follows.

Proof of Proposition 6.1. By Tonelli’s Theorem, the expected loss is

in which we have defined the positive constant. By hypothesis, each has the form, leading us to

in which we have used the linearity of the integral. Therefore, minimizing the expected loss is the same as solving the problem of constrained minimization of the quadratic form Q. For the matrix, note that, for every non null, we have

in which we have used the linearity of the integral. Therefore, the matrix M is positive definite, yielding (see [10] ) that the quadratic form Q is convex and the problem of constrained minimization of Q has a single global solution. Since the Bayes decision is the f that minimizes the expected loss, the result follows.

8. Conclusion

The random density considered in the paper can be extended to multivariate problems introducing analogous partitions of d-dimensional Euclidean space. Also, as an alternative to the empirical approach used in Section 5, we can specify full priors for the hyperparameters. Although more computationally challenging, this choice defines a more flexible model with random dimension for which the density estimates are no longer simple densities. More general random partitions can also be considered.

References