Open Journal of Statistics
Vol.4 No.3(2014), Article ID:45276,10 pages DOI:10.4236/ojs.2014.43021
Extracting the Influential Commodities in Stochastic Model of Simple Laspeyre Price Index Numbers with AR(2) Errors
Arfa Maqsood1, Syed Mohammad Aqil Burney2
1Department of Statistics, University of Karachi, Karachi, Pakistan
2Department of Actuarial Science and Risk Management, College of Computer Science and Information Systems, Institute of Business Management Karachi, Karachi, Pakistan
Email: amaqsood@uok.edu.pk, aqil.burney@iobm.edu.pk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 24 March 2014; revised 24 April 2014; accepted 30 April 2014
Abstract
This paper, on the first hand, deals with the problem of estimation of Laspeyre price index number when the errors are assumed to be generated from AR(2) process. The general expression of hat matrix and DFBETA measure to find the influential consumer commodities in stochastic Laspeyre price model with AR(2) errors are developed on the other. The hat values show the noteworthy findings that the corresponding weights of consumer items have large influence on the parameter estimates for simple Laspeyre price index number and are not affected by the parameter of autoregressive process of order two. While, DFBETA measures are the functions of both weights and autocorrelation parameters. Lastly, an example is presented with reference to price data of Pakistan, and shows its practical importance in financial time series.
Keywords
Hat Matrix; DFBETA; Laspeyre Price Index Number; Influential Observation; Autoregressive Process

1. Introduction
For many decades, the problem of measuring index numbers or inflation rate and detecting its major determinants remained one of the most attention grabbing and debatable issues that had been discussed and worked on by many economists and researchers throughout the world. In 1980’s and 1990’s, due concern was given to the area of estimation and prediction of inflation rates by establishing the stochastic regression approach to the index numbers for example see Maqsood and Burney [1] . Several authors have done their research regarding these matters, for example, many but to the few names Clements and Izan [2] [3] , Selvanathan [4] -[6] , Burney and Maqsood [7] discussed these issues. Laspeyre price index number is the most widely used measure to see the level of price stability within a country and represents a cost of living index number, which is calculated based on the fixed items of consumer basket. Many countries use Laspeyre index number as an economic indicator that represents a situation of the economy where the prices are continuously rising over a period of time. This paper deals with the problem of estimation of Laspeyre price index numbers when the errors are assumed to be generated from autoregressive process AR(2).
Several studies are available on the detection of leverages and influential observations in a simple linear regression and multiple linear regression when the errors are from first-order autoregressive process. For instance, initially, Prais and Winsten [8] , Kadiyala [9] , Girilches and Rao [10] , Maeshiro [11] , and Park and Mitchell [12] have observed the significant effect of the first observation on the parameter estimates of regression model.
The most common approach in determining the influence of ith observation is the case deletion diagnostics with ith case deleted. This approach has been used and studied by many authors, including Belsley et al. [13] , Cook [14] [15] , Cook and Weisberg [16] , Draper and John [17] , and Draper and Smith [18] . They examined the effect of individual observation or a set of observations on the estimation of model parameters. Puterman [19] observed the impact of first transformed observation in linear regression model on the parameter estimates. Some authors agreed that the effect of not including the first observation is not always magnificent as suggested by Cochrane and Orcutt [20] (see also Kadiyala [9] ). Stemann and Trenkler [21] extended the approach of Puterman [19] to the regression model with more than one regressor and showed that the effect of the presence of a constant term on a leverage point when the magnitude of error correlation was large. Pena [22] proposed a new statistic, called Pena’s statistic, used to measure the influence of an observation based on how this value is being influenced by the rest of data. Turkan and Toktamis [23] [24] formulated the Pena’s statistic to ridge, modified ridge, and semiparametric regression models and results are described using real and artificial data. Barry et al. [25] extended the study of influential observations to the regression model with AR(2) errors and developed the diagnostic techniques using a hat matrix. Burney and Maqsood [26] used the analytical tools of hat matrix and DFBETA measures to identify the influential observations in estimating the Divisia price index number model with AR(1) errors. The objective of this paper is to extend the study of influential observations to the simple Laspeyre price index number model with AR(2) errors.
The paper is organized as follows. Section 2 introduces the concept of influence diagnostics in autocorrelated error models. Simple Laspeyre price index number model with AR(2) errors and the role of the initial observation in estimation of model are discussed in Section 3. An illustration is presented with reference to Pakistan price data in Section 4 and lastly, Section 5 recapitulates the results.
2. Optimum Influence in Autocorrelated Error Models
To find an observation or a group of observations, disrupting the parameter estimates and the forecasted values, has recently been the area of study of much interest and attraction to the economist, researchers, and the statisticians. Such observations are called influential observations. Several diagnostic measures and plots have been developed to detect the influential observations in linear regression with one regressor as well as for more than one regressor. Hat matrix is one of the most common quantity that is widely employed in detecting the influential points when the OLS procedure for estimation of regression parameter is used. The matrix is obtained by the following expression
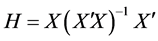 (1)
(1)
The diagonal entries of the hat matrix, denoted by  or
or![]() , are used as diagnostic technique for measuring the influence of a specific observation i on regression parameter estimates. The entries of matrix depend only on the values of design matrix X, and thus they serve as a measure of the distance of an observation from the centre of data. The large diagonal values indicate potentially large impact of the corresponding observation on regression estimates. Thus a point is considered to be an influential point if it satisfies the criteria that have the cut off value i.e.
, are used as diagnostic technique for measuring the influence of a specific observation i on regression parameter estimates. The entries of matrix depend only on the values of design matrix X, and thus they serve as a measure of the distance of an observation from the centre of data. The large diagonal values indicate potentially large impact of the corresponding observation on regression estimates. Thus a point is considered to be an influential point if it satisfies the criteria that have the cut off value i.e.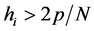 .
.
A number of considerable expressions are derived based on hat matrix in order to assess the effect of removing an observation on parameter estimates and predicted values. For instance, another significant measure of influence DFBETA given by Belsley et al. [13] , which describes the difference between the estimates of the vector ![]() with and without the ith observation i.e.;
with and without the ith observation i.e.;
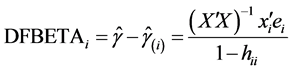 (2)
(2)
where ![]() is the estimate of
is the estimate of ![]() with ith observation excluded. If hii is large, then the denominator of DFBETAi will be small and thus deleting an ith observation would have a larger impact on estimation (see Barry et al. [25] ). An ith observation is considered to be an influential point if it exceeds the cut-off value
with ith observation excluded. If hii is large, then the denominator of DFBETAi will be small and thus deleting an ith observation would have a larger impact on estimation (see Barry et al. [25] ). An ith observation is considered to be an influential point if it exceeds the cut-off value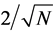 . This recommended criteria to judge the influence is only a guideline that could not be correct for all cases.
. This recommended criteria to judge the influence is only a guideline that could not be correct for all cases.
3. The Simple Laspeyre Price Model
The most commonly used simple Laspeyre price index number is given by Laspeyre in 1871. The stochastic model of Laspeyre index number is defined as follows.
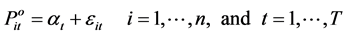 (3)
(3)
where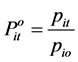 , ratio of current period price to the base period price for ith commodity,
, ratio of current period price to the base period price for ith commodity, ![]() common trend in the prices of all commodities at time t, and
common trend in the prices of all commodities at time t, and ![]() is the random component. This can be expressed more compactly in matrix form as follows
is the random component. This can be expressed more compactly in matrix form as follows
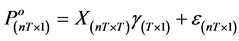 (4)
(4)
where X is an 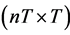 design matrix and
design matrix and ![]() is the vector of parameters. Po and
is the vector of parameters. Po and 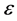 are, respectively
are, respectively 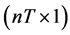 vectors of the observed Laspeyre index number and the errors with
vectors of the observed Laspeyre index number and the errors with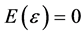 , and
, and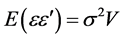 . Assuming V is known with symmetric and positive definite in nature, then the inverse of V can be decomposed using Choleski decomposition to get
. Assuming V is known with symmetric and positive definite in nature, then the inverse of V can be decomposed using Choleski decomposition to get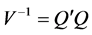 , where Q is a lower triangular matrix. It is well known that under the above assumption, the best linear unbiased estimator (BLUE) of
, where Q is a lower triangular matrix. It is well known that under the above assumption, the best linear unbiased estimator (BLUE) of ![]() in model (2) could be obtained by the generalized least square (GLS) approach as given below
in model (2) could be obtained by the generalized least square (GLS) approach as given below

The transformed model is obtained by multiplying both sides of Equation (4) by Q, and then we apply the simple ordinary least square (OLS) estimator to the transformed data to obtain estimated generalized least square (EGLS) and we have
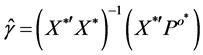 (5)
(5)
There are many processes that are used to formulate the error term and then determine the variance-covariance matrix V of random component. The computation for the simplest autoregressive process i.e. AR(1) is easy to carry out, we therefore leave this to the reader. However, the results of influential measurements, the hat values and DFBETA measures for simple Laspeyre price index number with AR(1) errors are similar to that derived by Burney and Maqsood [26] for Divisia index number with AR(1) errors. In this paper, we take the autoregressive process of order two to model the error term. In the first phase, we estimate the Laspeyre index number based on these assumption. The second phase will then be to compute the influential measures to find the impact of respective commodities on resulting estimates.
Assuming the errors to be generated from the second order autoregressive scheme, that is 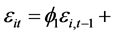
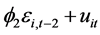 . For AR(2) process to be stationary, the roots of
. For AR(2) process to be stationary, the roots of 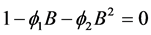 lie outside the unit circle. Here B denotes the backshift operator i.e.
lie outside the unit circle. Here B denotes the backshift operator i.e.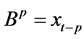 . We, therefore, have the stationary condition for AR(2) process that is the parameters
. We, therefore, have the stationary condition for AR(2) process that is the parameters 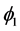 and
and  must take values such that
must take values such that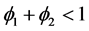 ,
,  , and
, and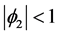 . Assuming
. Assuming
 , yields the error structure of model (4). The inverse of variance-covariance matrix V of AR(2) process is given by Wise [27]
, yields the error structure of model (4). The inverse of variance-covariance matrix V of AR(2) process is given by Wise [27]
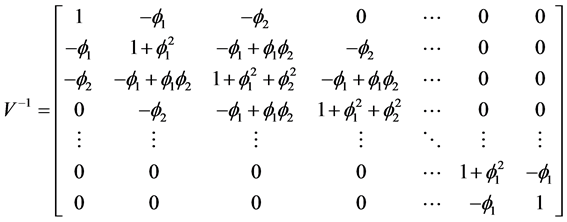 (6)
(6)
Barry et al. [25] obtain the transformation matrix Q for above variance-covariance matrix V. We obtain the matrix Q with our assumptions, given as
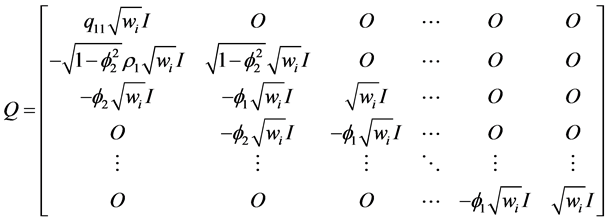 (7)
(7)
where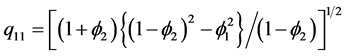 ,
, 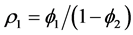 ,
, 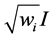 and O are the diagonal matrix with diagonal elements
and O are the diagonal matrix with diagonal elements 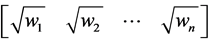 and matrix of zeros respectively. The transformed vector
and matrix of zeros respectively. The transformed vector  and the design matrix
and the design matrix 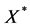 are given by
are given by
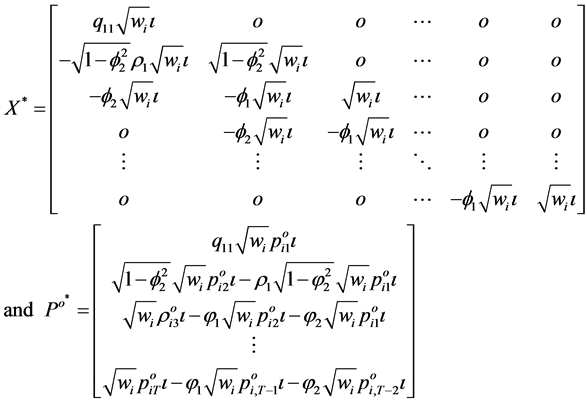 (8)
(8)
where , and o is the vector of zero i.e.
, and o is the vector of zero i.e.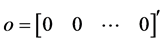 . Applying the ordinary least square (OLS) estimator in (5) to the transformed data to obtain the expression for usual Laspeyre index number.
. Applying the ordinary least square (OLS) estimator in (5) to the transformed data to obtain the expression for usual Laspeyre index number.
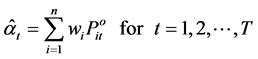 (9)
(9)
The next step is to have an idea about the presence of influential observation and its impact on Laspeyre regression model. For this purpose, we find the hat matrix for transformed data using Equation (1) and we get.
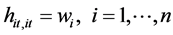 (10)
(10)
We use the subscript of hat values “it, it” due to a matrix of order nT × nT, where nT = N are the total number of observations. The diagonal elements of matrix i.e. 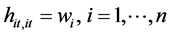 clearly show that the weights of commodities determine how much the important of particular commodity is in order to find the Laspeyre index number. The greater the value of weight, the more influential the commodity is, irrespective of the time period. They are not affected by the parameters of autoregressive process.
clearly show that the weights of commodities determine how much the important of particular commodity is in order to find the Laspeyre index number. The greater the value of weight, the more influential the commodity is, irrespective of the time period. They are not affected by the parameters of autoregressive process.
Next, we determine the vector DFBETA using Equation (2) for simple Laspeyre price index number and the result is given below
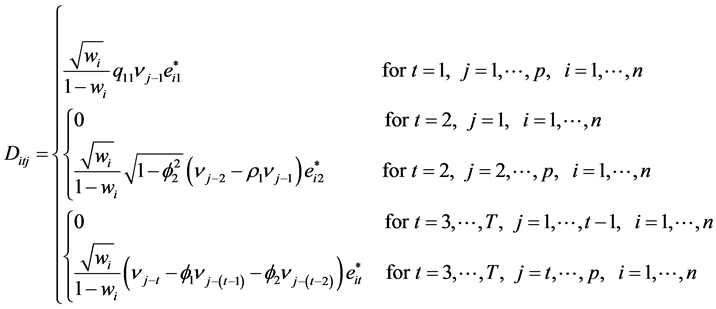 (11)
(11)
where p denotes the number of parameters in vector![]() . It is clearly seen that the DFBETA values are affected by the autoregressive coefficients of AR(2) process. We have different expressions for different time periods. These depend not only on the weights of items and the parameters of AR(2) process, but also the function of covariance terms. The
. It is clearly seen that the DFBETA values are affected by the autoregressive coefficients of AR(2) process. We have different expressions for different time periods. These depend not only on the weights of items and the parameters of AR(2) process, but also the function of covariance terms. The  values in DFBETA matrix decreases parallel to increasing number of covariance lags, this happen as we move towards finding the measure respective to
values in DFBETA matrix decreases parallel to increasing number of covariance lags, this happen as we move towards finding the measure respective to ![]() for higher value of t. Beside this all values depend on the constant factor of ith weight embodied by the first part of expression (11).
for higher value of t. Beside this all values depend on the constant factor of ith weight embodied by the first part of expression (11).
4. An Illustration
This section presents an application to the price data of Pakistan for the period from July 2001 to June 2011. The source of data is monthly bulletin of statistics, published by Pakistan bureau of statistics (PBS) [28] . The data consists of 374 consumer items that are further classified in ten groups by PBS. The groups are food and beverages, apparel textile and footwear, house rent, fuel and lighting, household furniture and equipment, transportation and communication, recreation and entertainment, education, cleaning laundry and personal appearance, and medicare. The first year (July 2001-June 2002) is taken as base year and the prices of subsequent months are compared with the corresponding month of base year through Laspeyre price index number.
Considering the case of simple Laspeyre price model described in Section 3, the first phase of computation involve the estimation of the parameter vector based on observed price data. We get the same values of estimates as Burney and Maqsood [7] obtained. The residuals versus observation numbers are plotted in Figure 1,
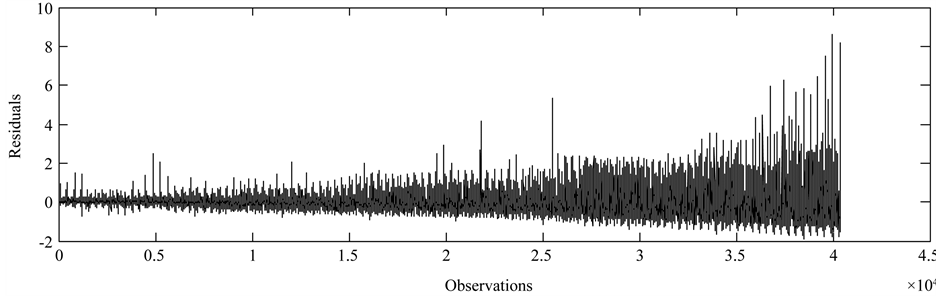
Figure 1. Plot of residual series from simple Laspeyre price model.
which shows the jumps along the constant central line. It has the longer ups and down as the time period increases proceeding far from the base period, however it exhibits the stationary situation. The value of Ljung-Box statistics is found to be 17,139, indicating the strong evidence towards second order serial correlation in series. We now estimate the autoregressive parameters of AR(2) process using Yule-walker method. Table 1 summarizes the results obtained in fitting AR(2) models. Akaike information criterion (AIC) of fitting AR(2) model is −1.7613, which is less than the AIC obtained in fitting AR(1) process. We have also checked for higher order of autoregressive processes but found no remarkable difference in values of AIC. Rather increasing the order of autoregressive process, it is recommended to choose a parsimonious model with comparatively less value of AIC.
The next phase certainly includes the extraction of influential observations using hat matrix and DFBETA measure. The diagonal hat values depend only on the weights of respective consumer items as shown in Equation (10). We, therefore, get the same results as we acquired in Divisia index numbers (see Burney and Maqsood [26] ). For the expediency of reader, the large quantities of hat entries that exceed the cut-off value 0.005348 are presented in Table 2. The highest hat value is parallel to house rent index, implying its importance in estimating the index numbers. Other leading items include milk fresh, wheat flour bag, and electric charges for the consumption of more than 1000 units.
We compute DFBETA measure using Equation (11) for AR(2) process. The items that have more than 50 significant DFBETAs exceeding threshold point 0.009951 are listed in Table 3. The large hat values are represented by the values with superscript *. Several items have significant DFBETA values implying its influence in estimating the simple Laspeyre price model. The reason behind this might be the comparison of current period prices to the fixed base period prices, and thus increasing the variation in prices as the difference between two periods rises. However, we may conclude here the first group food and beverages has the largest impact on estimation of parameter vector as 16 out of 28 items are from this group that influence more than 50 parameters in parameter vector. The curd and milk tetra pack with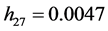 , and
, and 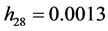 respectively, may have a large impact on estimating index numbers relating to 103 months. In other words, these affect the values of 103 alphas in parameter vector. Other major significant commodity groups include fuel and lighting, and transportation and communication.
respectively, may have a large impact on estimating index numbers relating to 103 months. In other words, these affect the values of 103 alphas in parameter vector. Other major significant commodity groups include fuel and lighting, and transportation and communication.
The house rent index with the highest 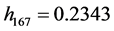 have an influence on only eight regression estimate of
have an influence on only eight regression estimate of![]() . It might indicate that the items with large diagonal entries of hat matrix have not necessarily an influence on the parameter estimates.
. It might indicate that the items with large diagonal entries of hat matrix have not necessarily an influence on the parameter estimates.
5. Conclusions
In this paper, we considered the simple Laspeyre price model when the errors are generated from autoregressive process of order AR(2). We got the estimate of ![]() as the standard Laspeyre price index number formula. Next, we used the general form of hat matrix and DFBETA measure to extract the influential commodities in estimating the Laspeyre price index number when the errors are serially correlated. The hat values are directly equal to the weights of respective items, implying that the greater the hat value, the more important commodity is, regardless of the values of autoregressive parameter. While, DFBETA measures are the functions of both hat values and parameter of autoregressive process.
as the standard Laspeyre price index number formula. Next, we used the general form of hat matrix and DFBETA measure to extract the influential commodities in estimating the Laspeyre price index number when the errors are serially correlated. The hat values are directly equal to the weights of respective items, implying that the greater the hat value, the more important commodity is, regardless of the values of autoregressive parameter. While, DFBETA measures are the functions of both hat values and parameter of autoregressive process.
Lastly, an example was presented with reference to price data of Pakistan, which numerically confirms the results. From the findings of both hat values and DFBETA measure, the first commodity group of food and beverages is the core group of items as the maximum number of items from this group has larger hat values and DFBETA measures. The wheat flour bag, milk fresh, meat with bones, electric consumption with more than 1000 units, and house rent index are the more crucial commodities that may have a larger impact on estimating the Laspeyre price index numbers.
Further motivation can be acquired on the techniques of influential cases of Laspeyre price index number
Table 1. Summary of fitting AR(2) process to the errors obtained in simple Laspeyre price model.
Table 2. Significant hat values corresponding to commodities with AR(1) and AR(2) processes for simple Laspeyre price model.
Table 3. Frequency of significant DFBETA for αt corresponding to items and their hat values for simple Laspeyre price model.
model by extending the approach with autoregressive processes of higher lags and then using the same methods described in Section 3 and Section 4. Moreover, it opens many opportunities to work with other index numbers, particularly for those, which are used to show the current consumption pattern of consumers instead of relying on fixed base approach.
Acknowledgements
The authors are thankful to Dept. of Computer Science and Dept. of Statistics University of Karachi for providing computing and research facilities.
References
- Maqsood, A. and Burney, S.M.A. (2008) Study of Inflation in Pakistan Using Statistical Approach. 4th International Statistical (ISSOS), University of Gujrat, Hafiz Hayat Campus, Pakistan.
- Clements, K.W. and Izan, H.Y. (1981) A Note on Estimating Divisia Index Numbers. International Economic Review, 22, 745-747. http://dx.doi.org/10.2307/2526174
- Clements, K.W. and Izan, H.Y. (1987) The Measurement of Inflation: A Stochastic Approach. Journal of Business and Economic Statistics, 5, 339-350.
- Selvanathan, E.A. (1991) Standard Errors for Laspeyers and Paasche Index Numbers. Economics Letters, 35, 35-38. http://dx.doi.org/10.1016/0165-1765(91)90101-P
- Selvanathan, E.A. (1993) More on the Laspeyers Price Index. Economics Letters, 43, 157-162. http://dx.doi.org/10.1016/0165-1765(93)90029-C
- Selvanathan, E.A. (2003) Extending the Stochastic Approach to Index Numbers: A Comment. Applied Economics Letters, 10, 213-215. http://dx.doi.org/10.1080/1350435022000043986
- Burney, S.M.A. and Maqsood, A. (2013) Extending the Stochastic Approach to Paasches Price Index Numbers. Pakistan Journal of Engineering Technology & Science, 3, 1-17.
- Prais, G.J. and Winsten, C.B. (1954) Trend Estimates and Serial Correlation. Cowles Commission Discussion Paper, Stat. No. 383, University of Chicago, Chicago.
- Kadiyala, K.R. (1968) A Transformation Used to Circumvent the Problem of Autocorrelation. Econometrica, 36, 93- 96. http://dx.doi.org/10.2307/1909605
- Griliches, Z. and Rao, P. (1969) Small-Sample Properties of Several Two-Stage Regression Methods in the Context of Autocorrelated Disturbances. Journal of American Statistical Association, 64, 253-272. http://dx.doi.org/10.1080/01621459.1969.10500968
- Maeshiro, A. (1979) On the Retention of the First Observation in Serial Correlation Adjustment of Regression Models. International Economic Review, 20, 259-265. http://dx.doi.org/10.2307/2526430
- Park, R.E. and Mitchell, B.M. (1980) Estimating the Autocorrelated Error Model with Trended Data. Journal of Econometrics, 13, 185-201. http://dx.doi.org/10.1016/0304-4076(80)90014-7
- Belsley, P.A., Kuh, E. and Welsch, R.E. (1980) Regression Diagnostics. John Wiley, New York. http://dx.doi.org/10.1002/0471725153
- Cook, R.D. (1977) Detection of Influential Observations in Linear Regression. Technometrics, 19, 15-18. http://dx.doi.org/10.2307/1268249
- Cook, R.D. (1979) Influential Observations in Linear Regression. Journal of American Statistical Association, 74, 169- 174. http://dx.doi.org/10.1080/01621459.1979.10481634
- Cook, R.D. and Weisberg, S. (1982) Residuals and Influence in Regression. Chapman and Hall, New York.
- Draper, N.R. and John, J.A. (1981) Influential Observations and Outliers in Regression. Technometrics, 23, 21-26. http://dx.doi.org/10.1080/00401706.1981.10486232
- Draper, N.R. and Smith, H. (1998) Applied Regression Analysis. 3rd Edition, John Wiley, New York.
- Puterman, M.L. (1988) Leverage and Influence in Autocorrelated Regression Model. Journal of the Royal Statistical Society, 37, 76-86.
- Cochrane, D. and Orcutt, G.H. (1949) Application of Least Squares Regression to Relationships Containing Auto-Correlated Error Terms. Journal of the American Statistical Association, 44, 32-61.
- Stemann, D. and Trenkler, G. (1993) Leverage and Cochrane-Orcutt Estimation in Linear Regression. Communications in Statistics-Theory and Methods, 22, 1315-1333. http://dx.doi.org/10.1080/03610929308831088
- Pena, D. (2005) A New Statistic for Influence in Linear Regression. Technometrics, 47, 1-12. http://dx.doi.org/10.1198/004017004000000662
- Turkan, S. and Toktamis, O. (2012) Detection of Influential Observations in Ridge Regression and Modified Ridge Regression. Model Assisted Statistics and Applications, 7, 91-97.
- Turkan, S. and Toktamis, O. (2013) Detection of Influential Observations in Semiparametric Regression Model. Revista Colombiana de Estadistica, 36, 91-97.
- Barry, A.M., Burney, S.M.A. and Bhatti, M.I. (1997) Optimum Influence of Initial Observations in Regression Models with AR(2) Errors. Applied Mathematics and Computation, 82, 57-65. http://dx.doi.org/10.1016/S0096-3003(96)00024-0
- Burney, S.M.A. and Maqsood, A. (2014) Influential Observations in Stochastic Model of Divisia Index Numbers with AR(1) Errors. Applied Mathematics, 5, 975-982. http://dx.doi.org/10.4236/am.2014.56093
- Wise, J. (1955) The Autocorrelation Function and the Spectral Density Function. Biometrika, 42, 151-159. http://dx.doi.org/10.2307/2333432
- Pakistan Bureau of Statistics. Monthly Bulletin of Statistics. http://www.pbs.gov.pk/sites/default/files/tables/Monthly%20Bulletin%20Of%20Statistics.pdf


