Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27373,8 pages DOI:10.4236/ojdm.2013.31006
Polynomial Generalizations and Combinatorial Interpretations for Sequences Including the Fibonacci and Pell Numbers
Universidade Estadual de Campinas, Campinas-SP, São Paulo, Brazil
Email: cissamat@gmail.com, josepli@ime.unicamp.br, elenvps@gmail.com, keycpsilva@gmail.com
Received September 12, 2012; revised October 12, 2012; accepted October 22, 2012
Keywords: Partitions; Fibonacci Numbers; Pell Numbers; Jacobsthal Numbers; q-Analog
ABSTRACT
In this paper we present combinatorial interpretations and polynomials generalizations for sequences including the Fibonacci numbers, the Pell numbers and the Jacobsthal numbers in terms of partitions. It is important to mention that results of this nature were given by Santos and Ivkovic in two papers published on the Fibonacci Quarterly, Polynomial generalizations of the Pell sequence and the Fibonacci sequence [1] and Fibonacci Numbers and Partitions [2] , and one, by Santos, on Discrete Mathematics, On the Combinatorics of Polynomial generalizations of Rogers-Ramanujan Type Identities [3]. By these results one can see that from the q-series identities important combinatorial information can be obtained by a careful study of the two variable function introduced by Andrews in Combinatorics and Ramanujan’s lost notebook [4].
1. Introduction
In this paper following some ideas introduced by Andrews [4] and results given by Santos [5] we give polynomial generalizations and combinatorial interpretations for sequences, including Fibonacci numbers, the Pell numbers and the Jacobsthal numbers in terms of partitions. To do this we use identities 12, 16, 20, 28, 44, 66, 67, 80 and 81, listed below, that are among the 130 q-series identities given by Slater in [6].
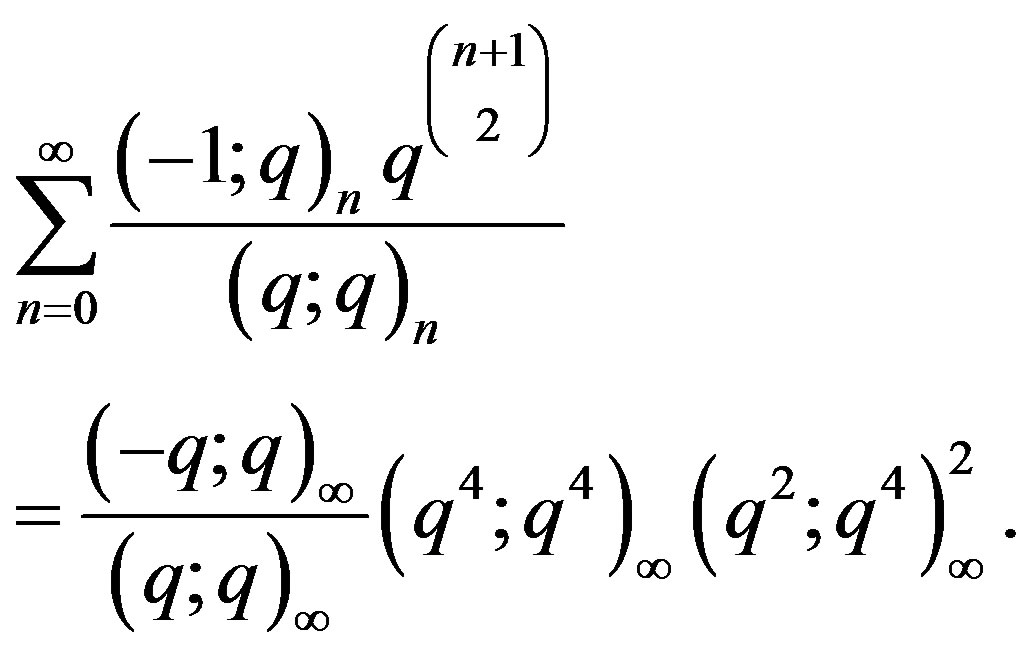 (1)
(1)
 (2)
(2)
 (3)
(3)
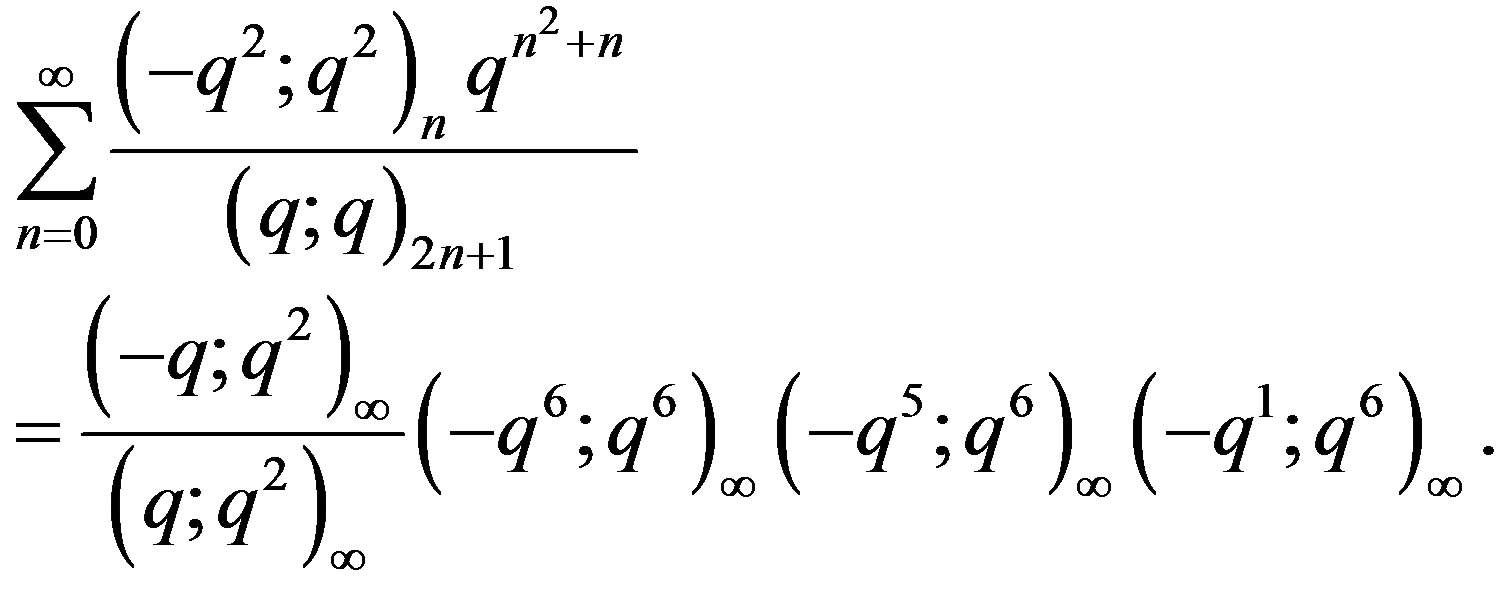 (4)
(4)
 (5)
(5)
 (6)
(6)
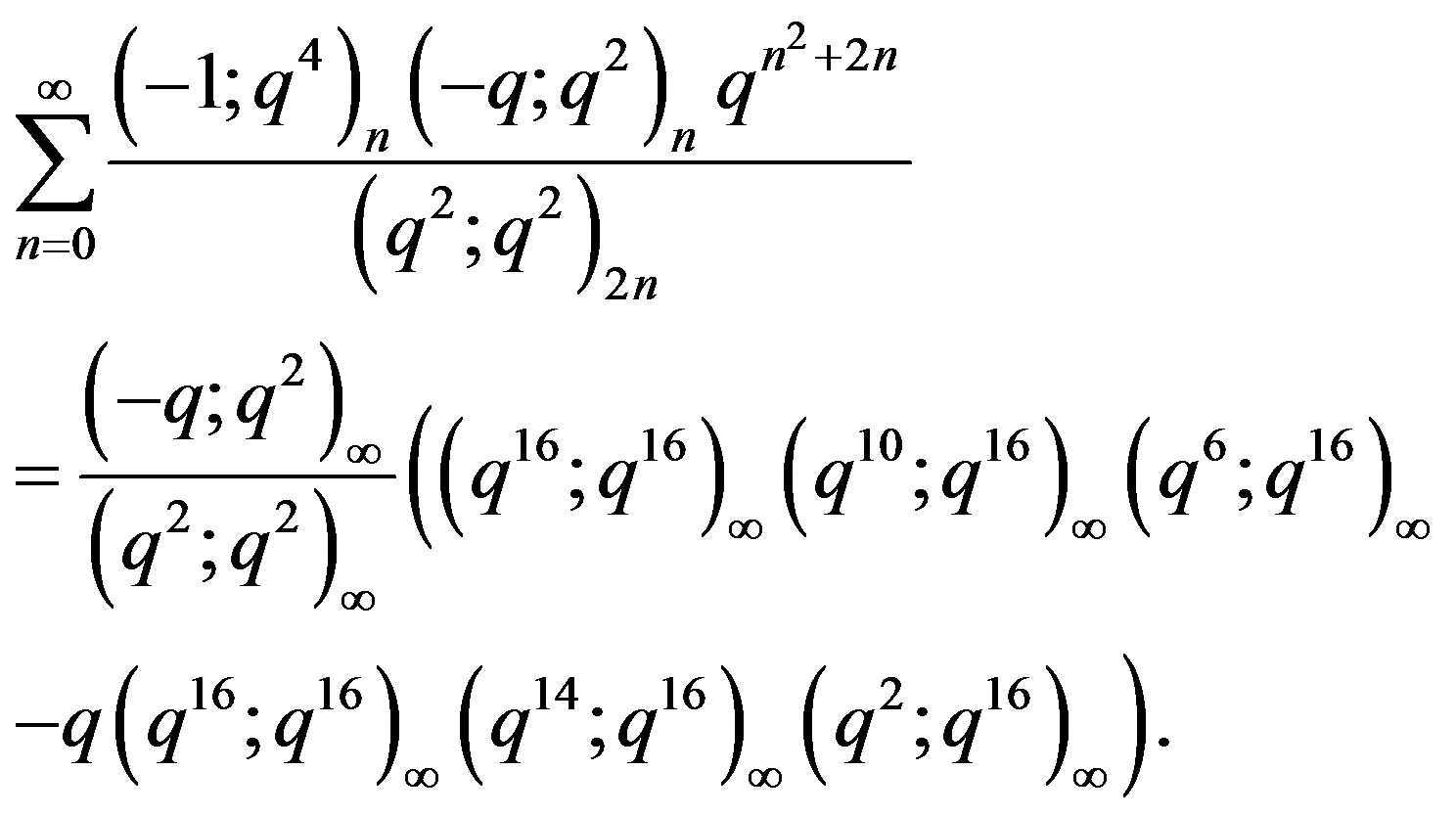 (7)
(7)
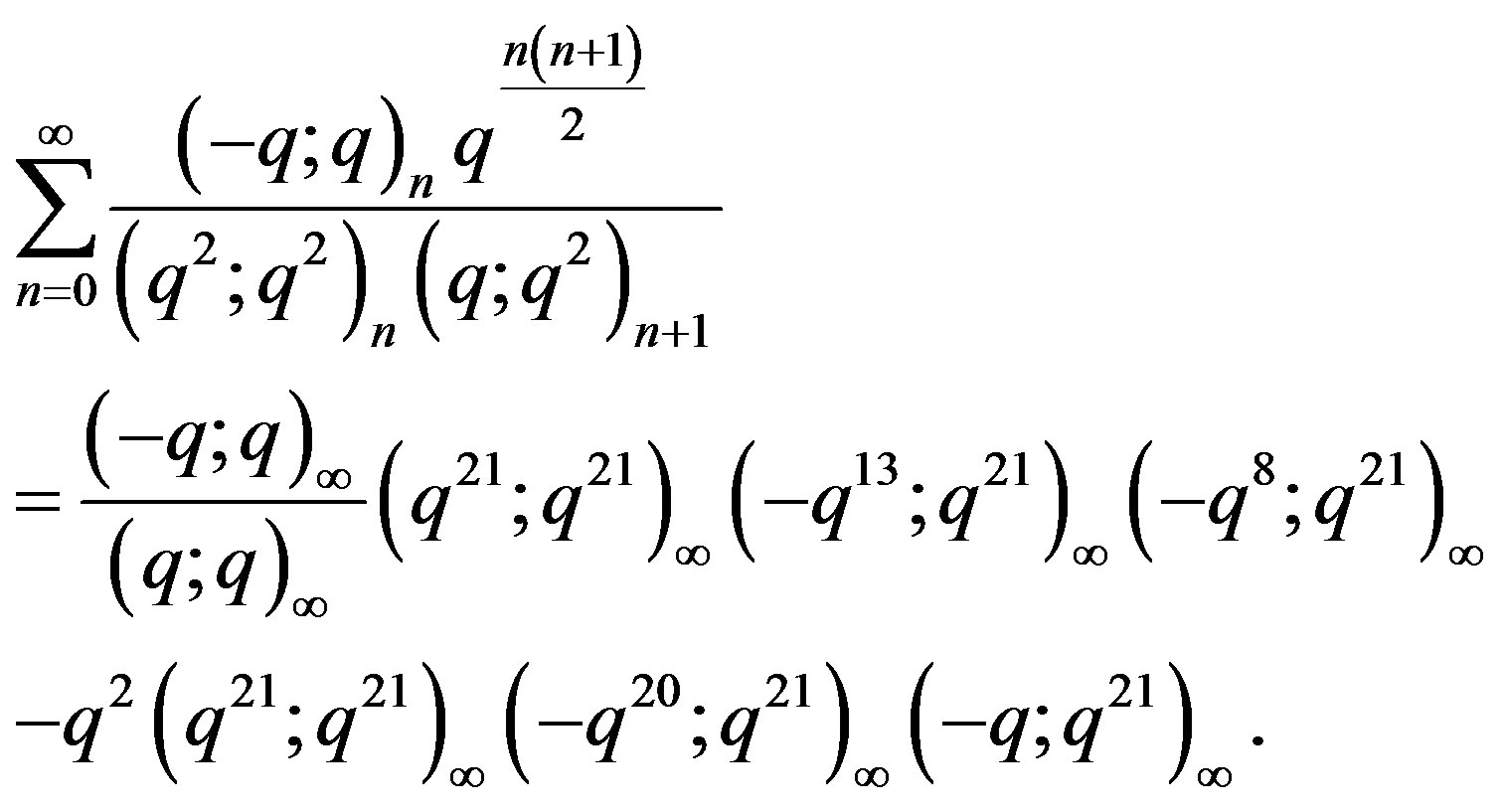 (8)
(8)
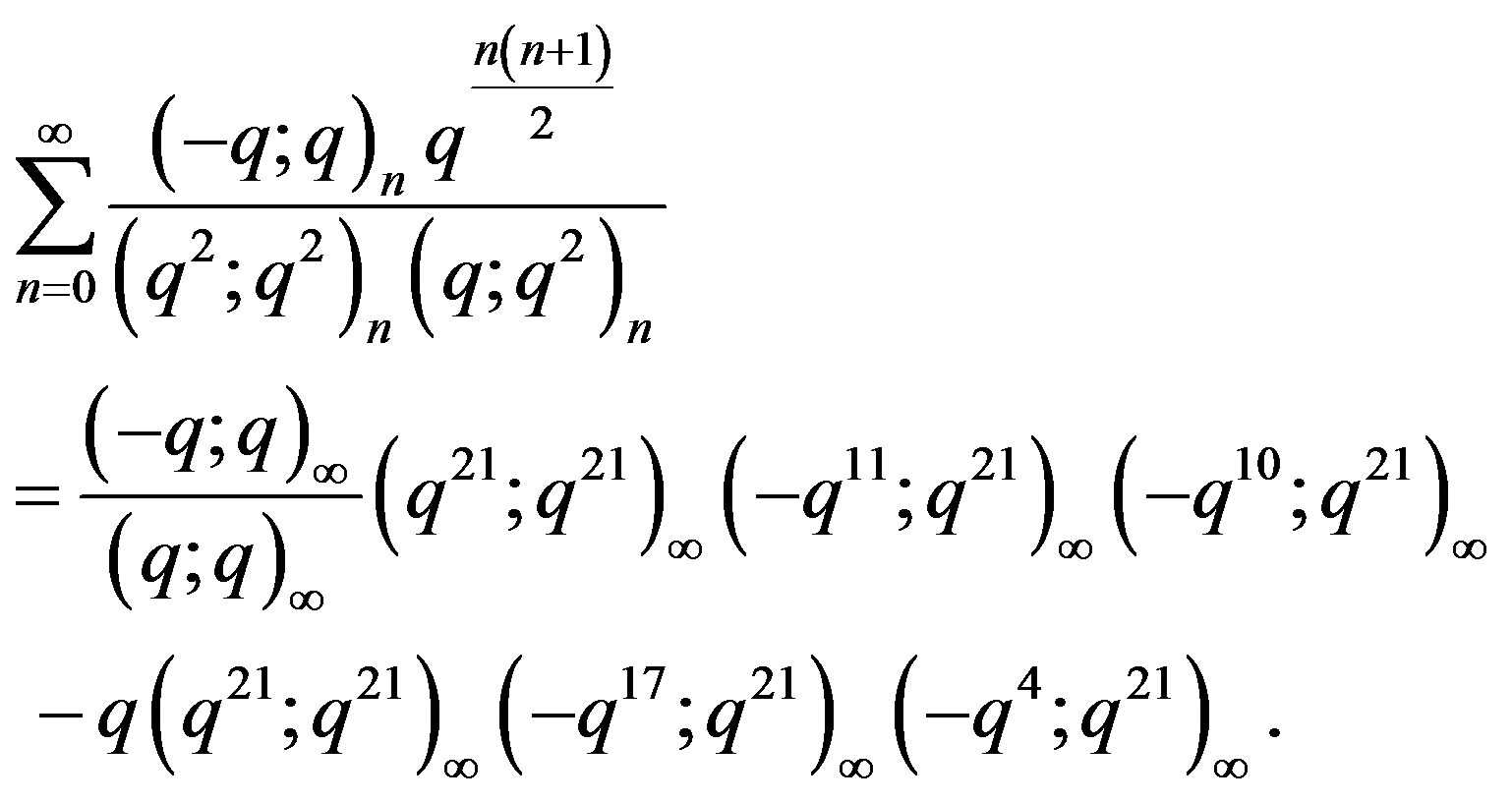 (9)
(9)
Here we are using the standard notation of q-series
 (10)
(10)
when n is a positive integer, and
 (11)
(11)
2. Background
Before explaining how to get the combinatorial interpretation for the sequences mentioned above we need a few definitions.
Definition 2.1 The Pell numbers 1, 2, 5, 12, 29, ···, defined by the recurrence relation 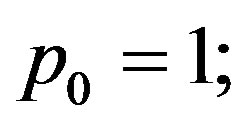

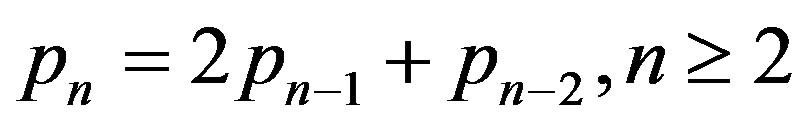 are the denominators of the sequence of rational numbers
are the denominators of the sequence of rational numbers

that are the continued fraction convergent to 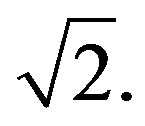
Definition 2.2 The Fibonacci numbers 0, 1, 1, 2, 3, 5, 8, 13, ···, are defined by
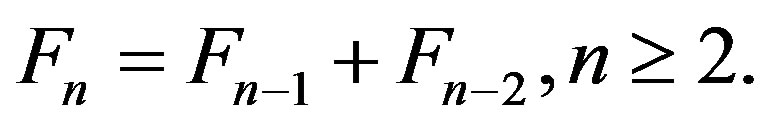
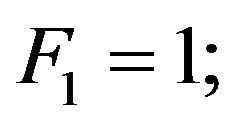

Definition 2.3 The Jacobsthal numbers 1, 1, 3, 5, 11, 21, 43, ··· are defined by

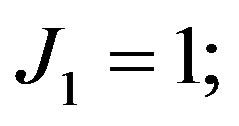
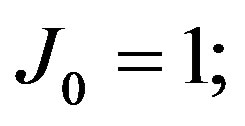 .
.
Definition 2.4 The Gaussian polynomials are defined as follows:
 (12)
(12)
Definition 2.5 The coefficients of 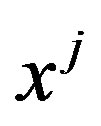 in the expanded form of
in the expanded form of  are given by:
are given by:
 (13)
(13)
We call these numbers trinomial coefficients.
The following two expressions are q-analog for the trinomial coefficients.
 (14)
(14)
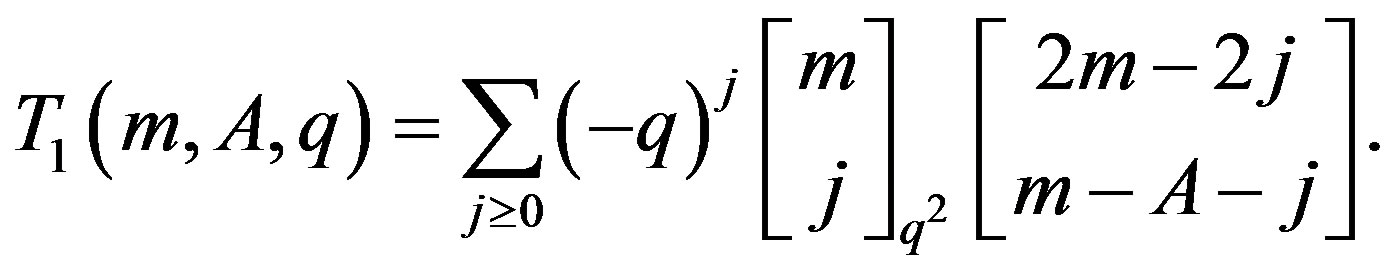 (15)
(15)
Finally we define:
Definition 2.6
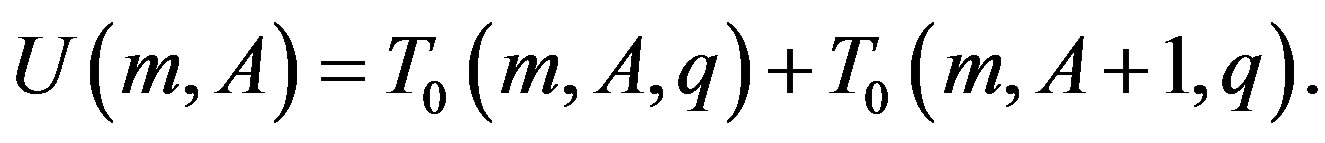 (16)
(16)
 (17)
(17)
3. The Results from Equations (12) and (16)
In [1-3] we have presented a number of results of the same nature as the ones given is this paper. For this reason we are not describing all the steps needed in the process but just a general description. In a series of two papers [6,7], Slater gave a list of 130 identities of the Rogers-Ramanujan type. In [4] Andrews introduced a two variable function in order to look for combinatorial interpretations for those identities. In [5] one of us, Santos, gave conjectures for explicit formulas for families of polynomials that can be obtained using Andrews’ method for more than 70 identities of Slater’s list. The conjectures listed there can be proved as we did in [3] for identity 20, by doing a lot of calculations, or with the help of packages given by Sills in [8].
Then, following Andrews [4] one can introduce a parameter  in the left hand side of (1) to get
in the left hand side of (1) to get
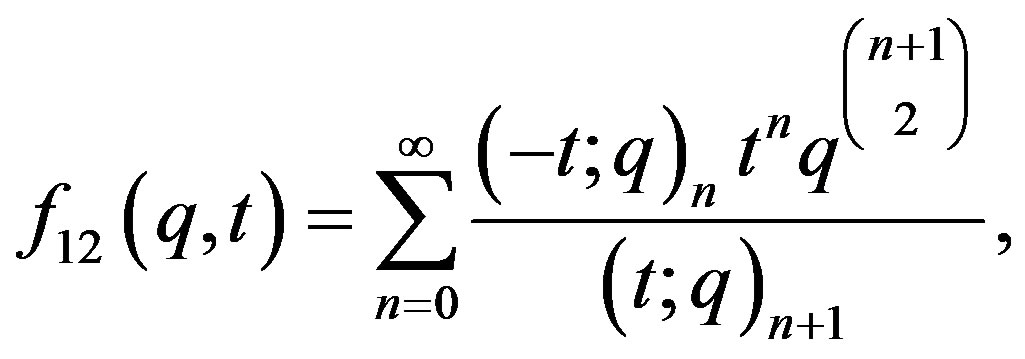 (18)
(18)
from which a functional equation can be obtained:

Knowing that the coefficient of 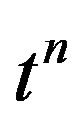 in the expansion of (18) is a polynomial in
in the expansion of (18) is a polynomial in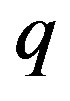 , i.e., that
, i.e., that

it is easy to see that
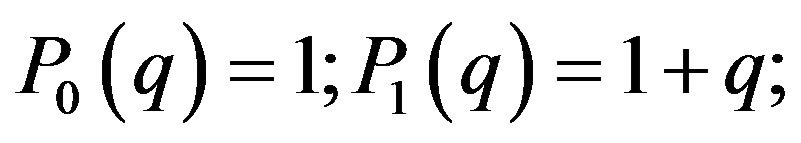
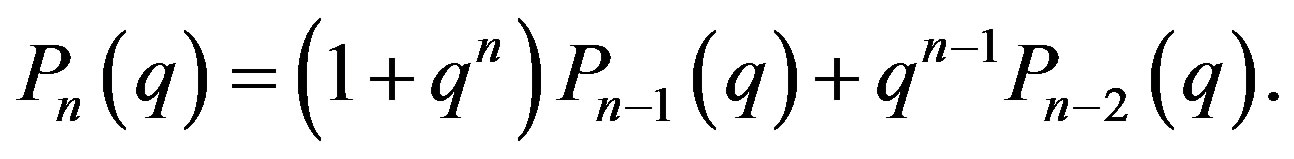 (19)
(19)
Santos gave in [5] the following conjecture for an explicity formula for this family of polynomials:
 (20)
(20)
where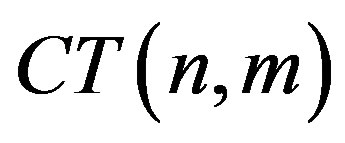 , defined by Equation (17), is a q-analog of the trinomial coefficient in the same way that the Gaussian polynomial is a q-analog of the binomial coefficient, that is, its limit, when q approaches 1, is equal to the trinomial coefficient given by (13).
, defined by Equation (17), is a q-analog of the trinomial coefficient in the same way that the Gaussian polynomial is a q-analog of the binomial coefficient, that is, its limit, when q approaches 1, is equal to the trinomial coefficient given by (13).
To explain how to get a combinatorial interpretation for (18) we write it in the following form:
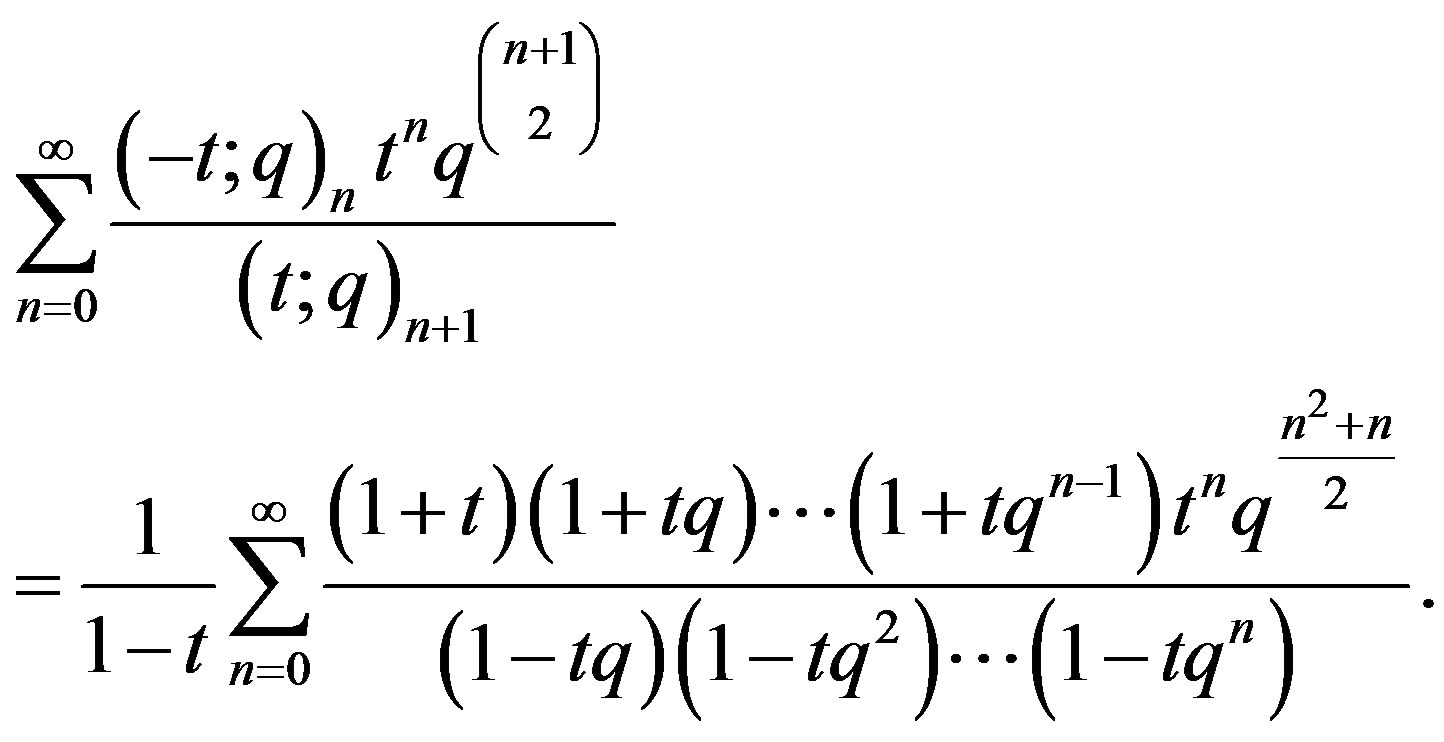 (21)
(21)
Considering that 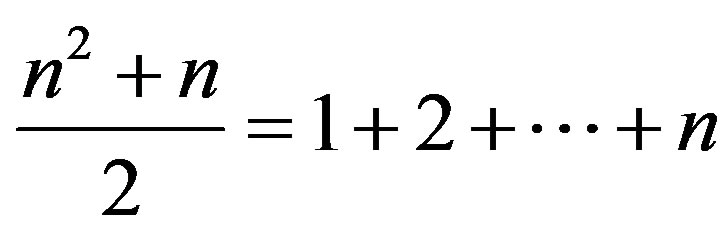 and looking just to the term inside the sum we can see that the coefficient of
and looking just to the term inside the sum we can see that the coefficient of  in that sum is the generating function for overpartitions where every (non-overlined) integer from one to the largest part appears at least once, the overlined parts are less than the largest non-overlined part and the number of parts is either
in that sum is the generating function for overpartitions where every (non-overlined) integer from one to the largest part appears at least once, the overlined parts are less than the largest non-overlined part and the number of parts is either 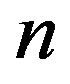 or
or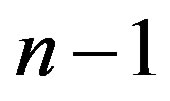 . We call those overpartitions of type
. We call those overpartitions of type .
.
Now, by making  in (19), one can see that we get the sequence of the Pell numbers which allows us, taking into consideration the factor
in (19), one can see that we get the sequence of the Pell numbers which allows us, taking into consideration the factor  outside the sum, to state the following theorem:
outside the sum, to state the following theorem:
Theorem 3.1 The total number of overpartitions of type 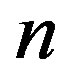 for all
for all  up to
up to  is equal to
is equal to .
.
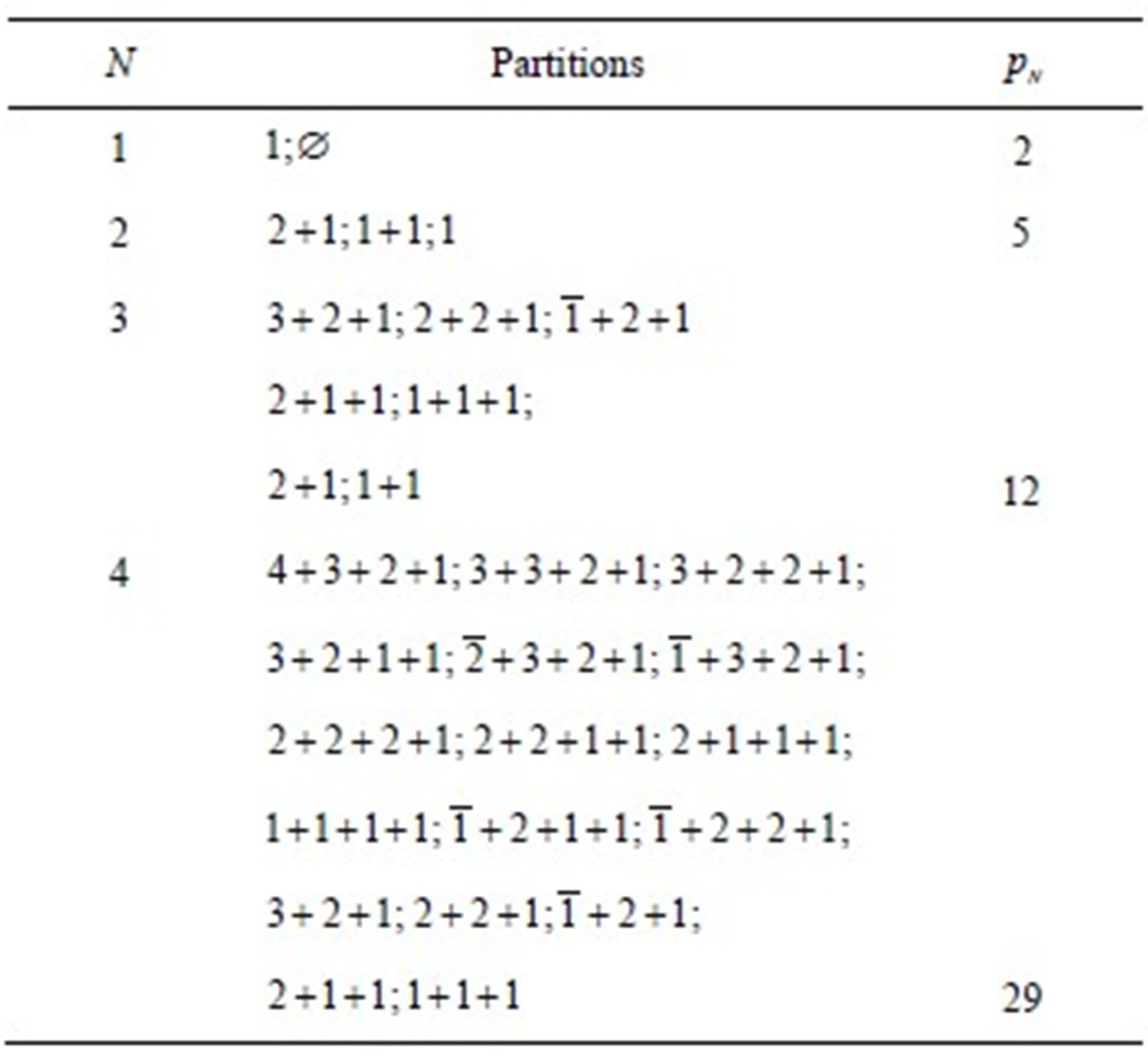
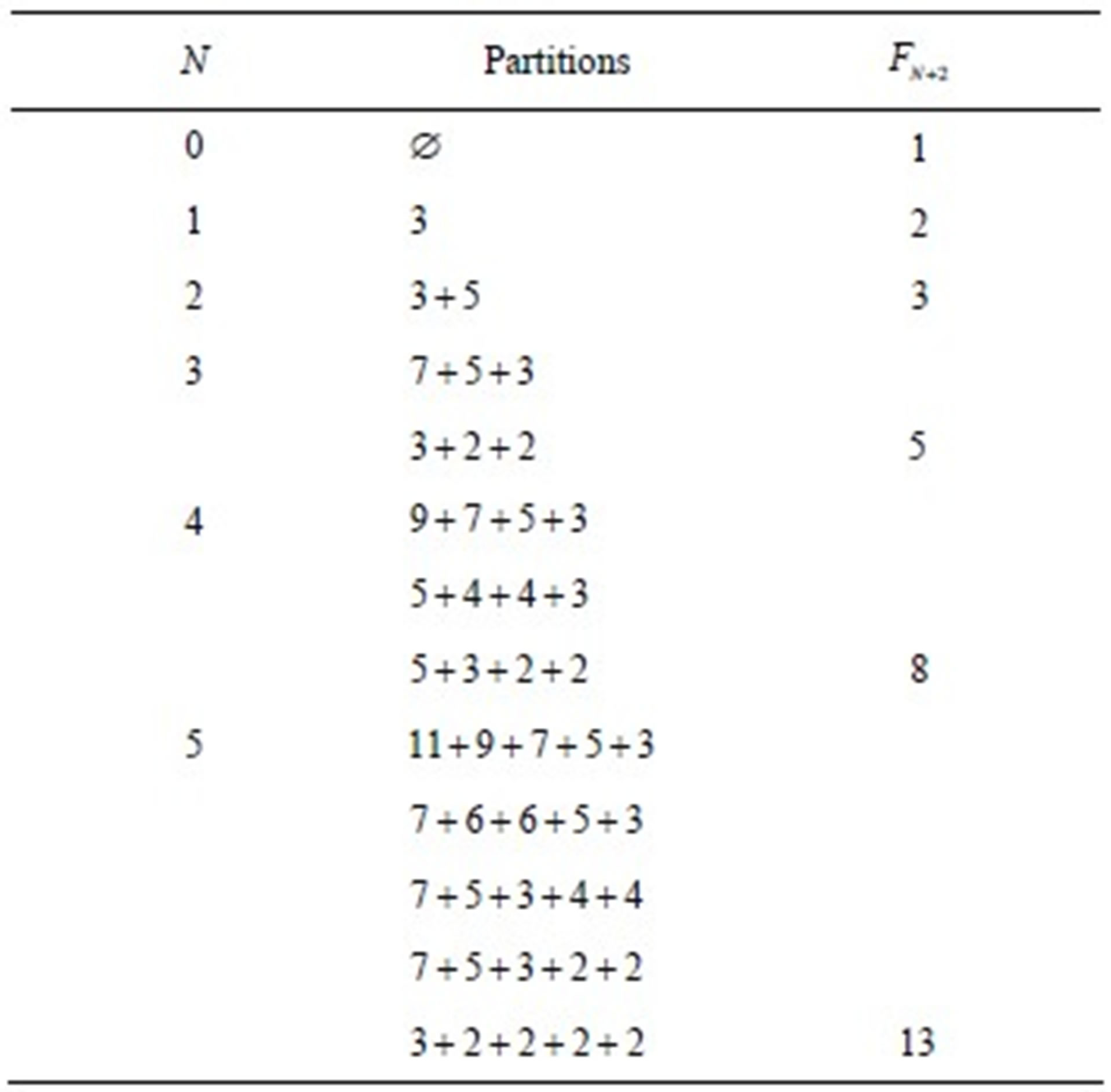
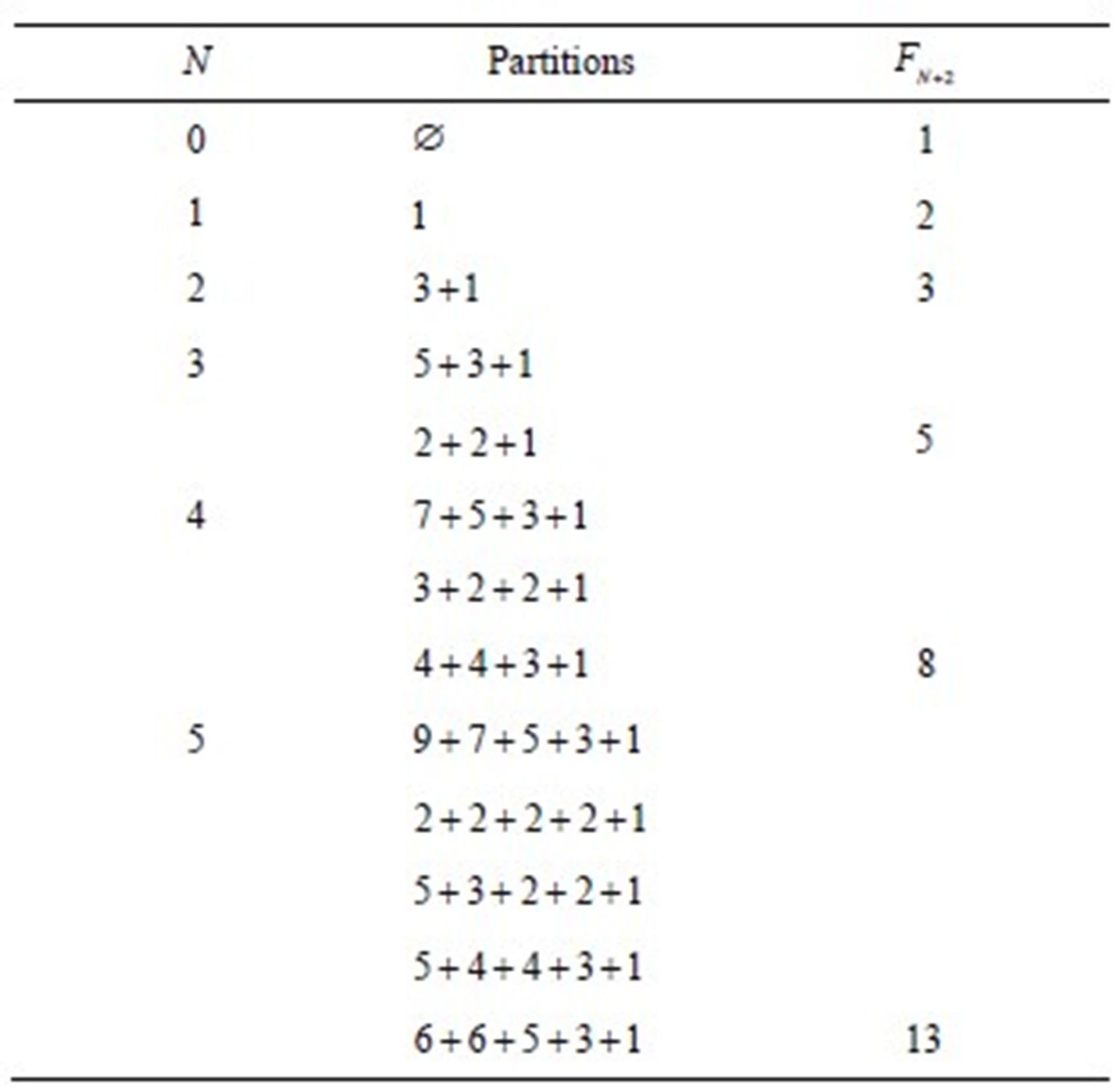
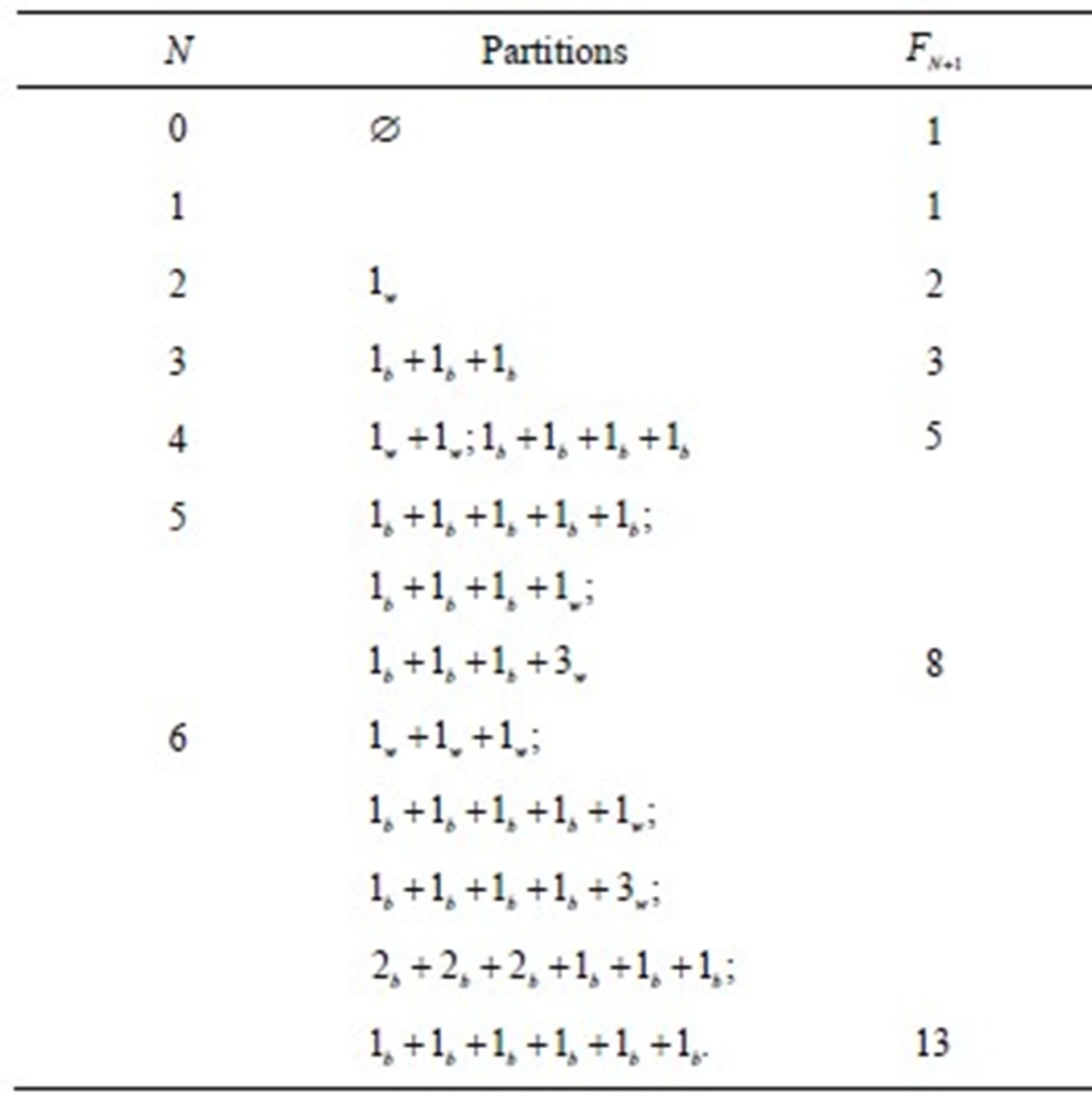
In Table 1 we present the overpartitons for a few values of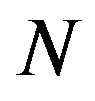 . For example, in the third line, second column we have all overpartitions of type 3, i.e., the ones with either 3 or 2 parts. 12 is the total up to that line.
. For example, in the third line, second column we have all overpartitions of type 3, i.e., the ones with either 3 or 2 parts. 12 is the total up to that line.
Table 1. Partitions as in Theorem 3.1.
For Equation (2) we have, with the parameter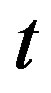 :
:
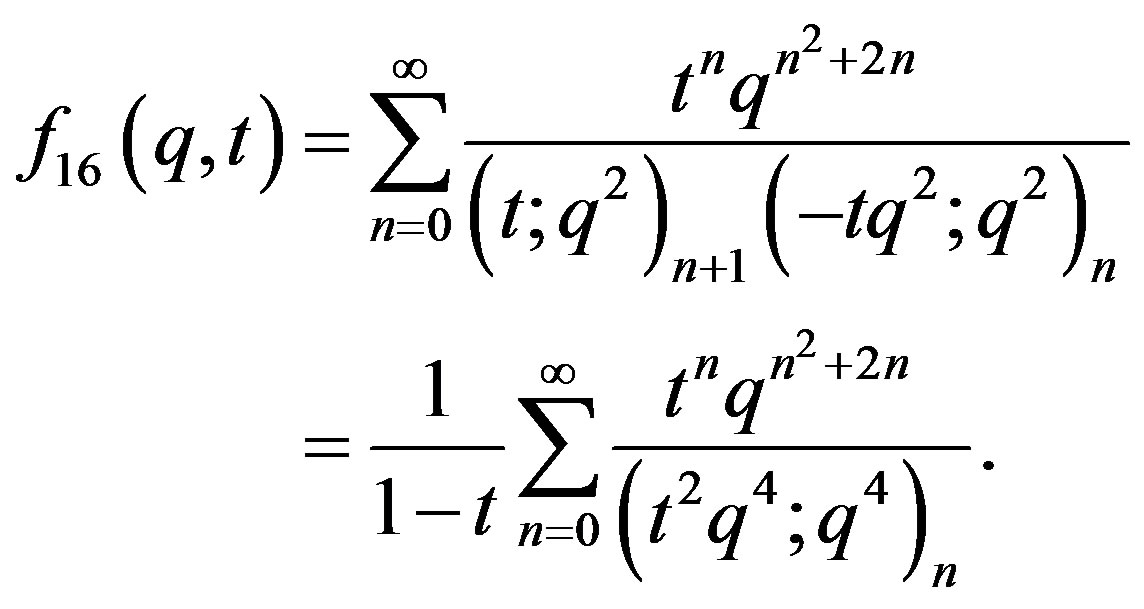 (22)
(22)
From this sum one can get

Knowing that the coefficient of 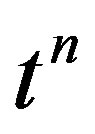 in the expansion of (22) is a polynomial in
in the expansion of (22) is a polynomial in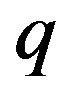 , i.e., that:
, i.e., that:
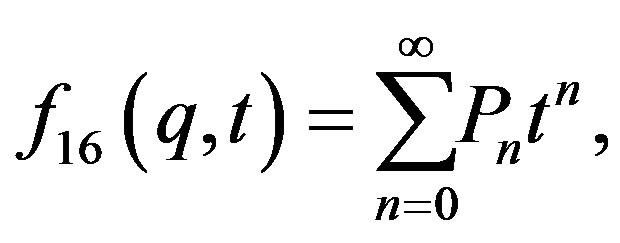
we get:
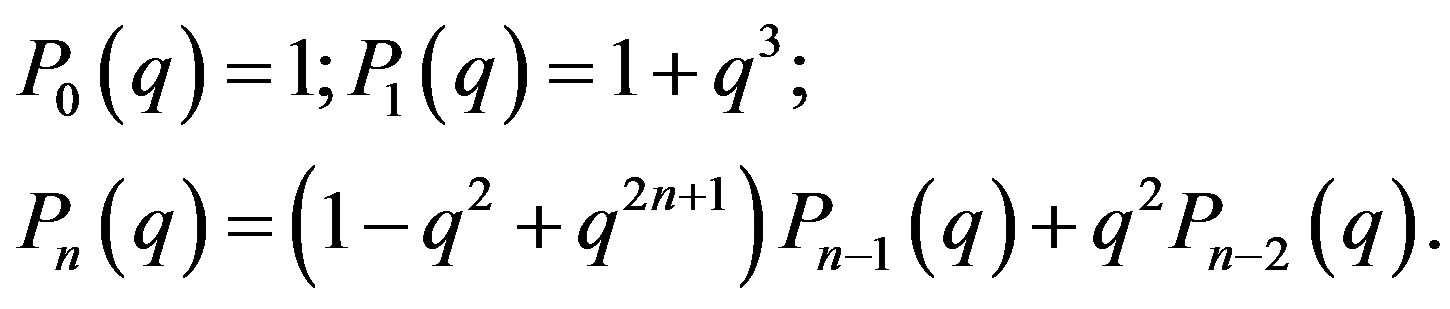 (23)
(23)
It is ease to see that at  the sequence above is the Fibonacci sequence.
the sequence above is the Fibonacci sequence.
An explicity formula for this sequence is given bellow:
 (24)
(24)
We explain now how to get a combinatorial interpretation for
 (25)
(25)
We consider the exponent 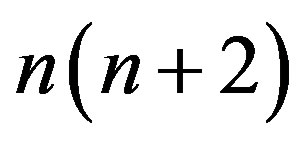 of
of 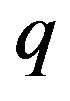 as the sum
as the sum  which means that the largest part is odd and every odd from 3 up to
which means that the largest part is odd and every odd from 3 up to  appears exactly once. In the denominator we will see a number of the form
appears exactly once. In the denominator we will see a number of the form  as
as 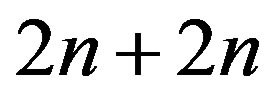 which implies that each even number appears an even number of times. With these observations and taking into consideration the factor
which implies that each even number appears an even number of times. With these observations and taking into consideration the factor 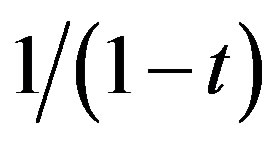 we can state the following theorem.
we can state the following theorem.
Theorem 3.2 The total number of partitions into at most  parts where the largest part is odd, every odd from 3 up to the largest part appears exactly once and each even part appears an even number of times is equal to
parts where the largest part is odd, every odd from 3 up to the largest part appears exactly once and each even part appears an even number of times is equal to .
.
Table 2 has, as an illustration, a few partitions as described in this theorem.
For identities 20, 28, 44, 66, 67, 80 and 81 we are going to list, for each one of them, the two variable function, the functional equation, the recurrence relation for the family of polynomials associated to it, the formula for this family and the corresponding theorem that it is possible to get with the combinatorial interpretation at 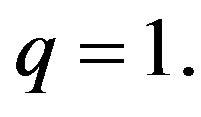 A table to illustrate the result for small values of
A table to illustrate the result for small values of 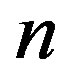 is also given.
is also given.
4. The Results from Equation (20)
The two variable function:
 (26)
(26)
Table 2. Partitions as in Theorem 3.2.
The functional equation:
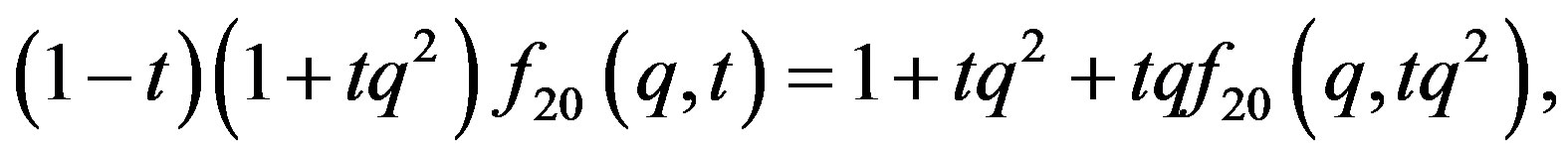

The recurrence relation:
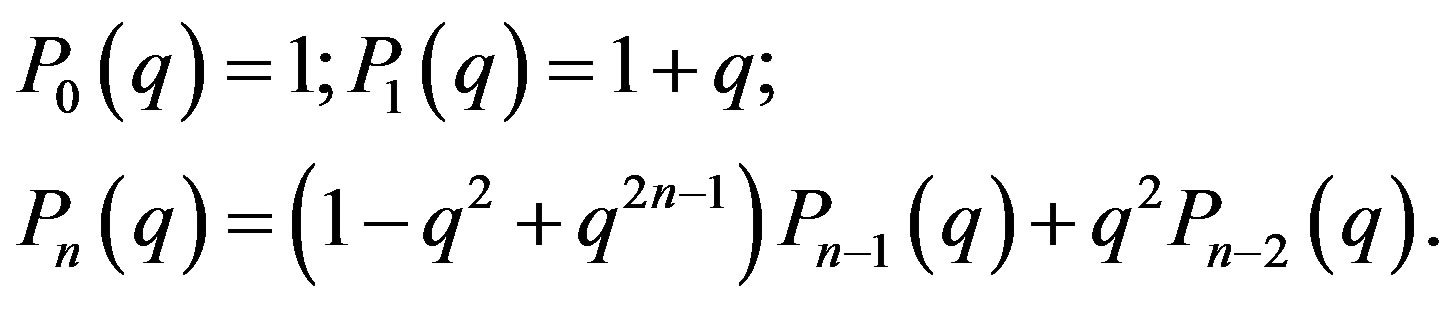 (27)
(27)
An explicit formula for this family:
 (28)
(28)
Here we will see a number of the form 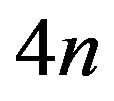 as
as  as we have done for Equation (2).
as we have done for Equation (2).
Theorem 4.1 The total number of partitions into at most 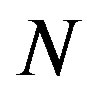 parts where every odd from one up to the largest appears exactly once, every even appears an even number of times and the largest even is at most one plus the largest odd is equal to
parts where every odd from one up to the largest appears exactly once, every even appears an even number of times and the largest even is at most one plus the largest odd is equal to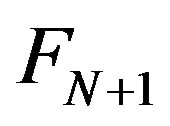 .
.
Table 3 has, as an illustration, a few partitions as described in this theorem.
5. The Results from Equation (28)
The two variable function:
 (29)
(29)
Table 3. Partitions as in Theorem 4.1.
The functional equation:
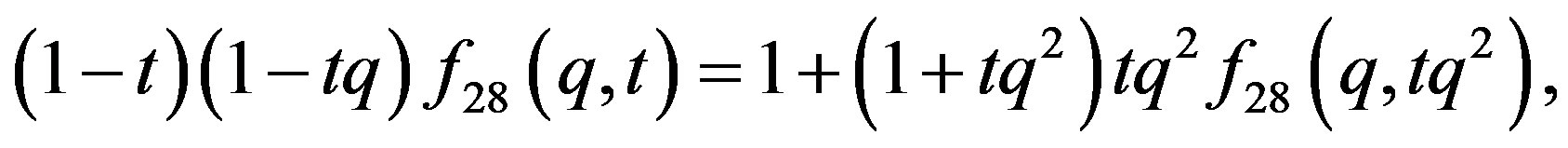
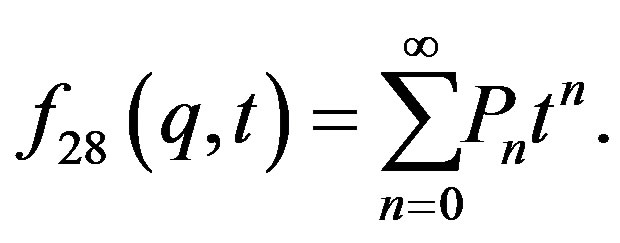
The recurrence relation:

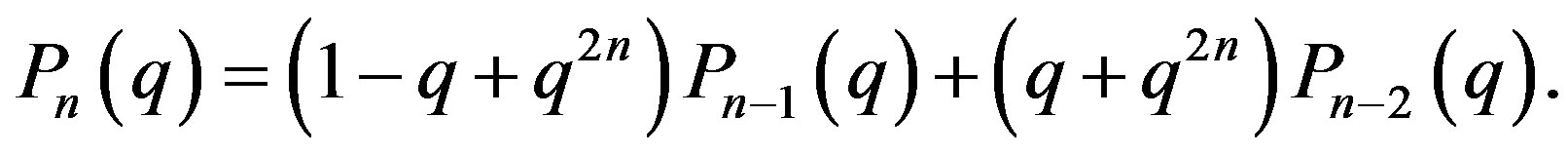 (30)
(30)
An explicit formula for this family:
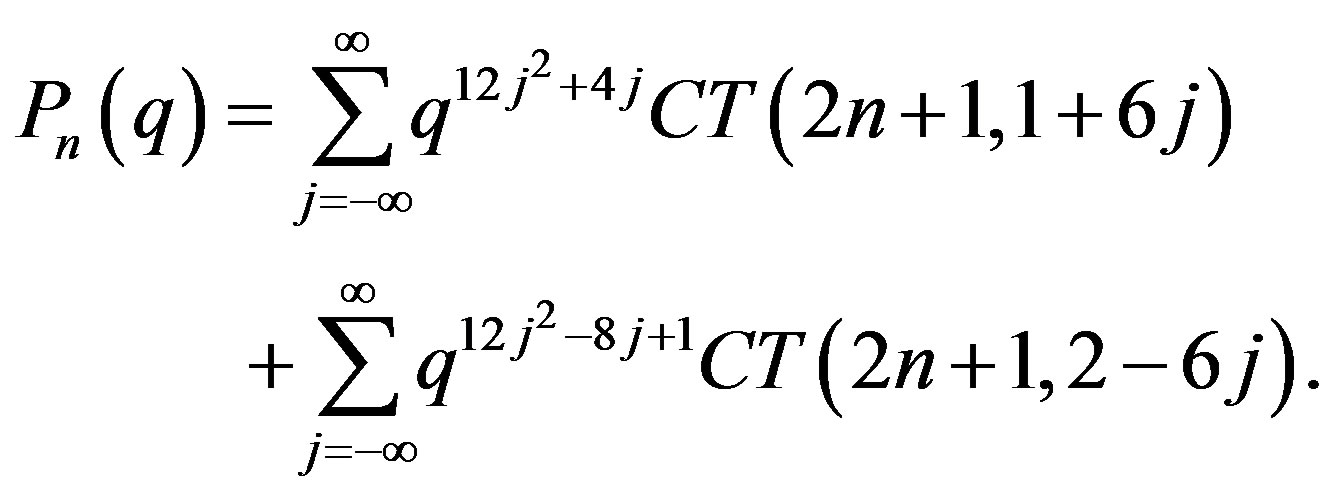 (31)
(31)
Before stating the corresponding theorem we need a definition.
We call a green-yellow partition as the one where the parts may be of two colors, green or yellow, where the green parts are even and appear at least once and at most twice. For the yellow parts the only restriction is that the largest part is at most one plus twice the largest green part.
Theorem 5.1 The total number of green-yellow partitions into at most  parts with an even number of odd parts minus the number of those having an odd number of odd parts is equal to
parts with an even number of odd parts minus the number of those having an odd number of odd parts is equal to .
.
Table 4 has, as an illustration, a few partitions as described in this theorem.
6. The Results from Equation (44)
The two variable function:
Table 4. Partitions as described in Theorem 5.1.

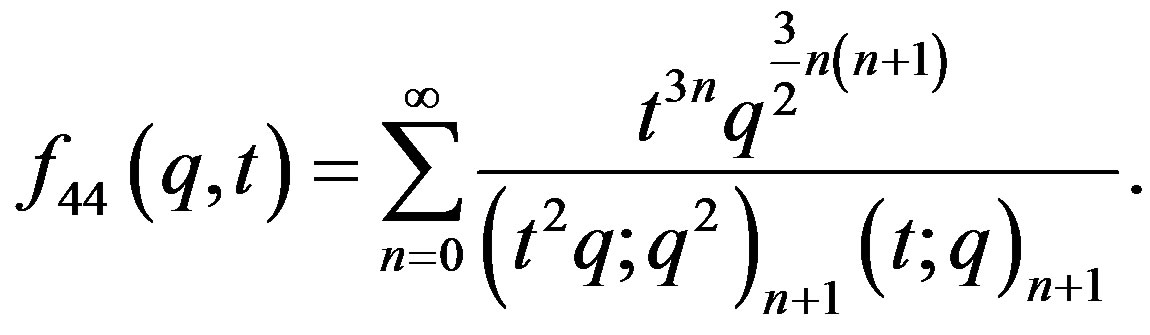 (32)
(32)
The functional equation:
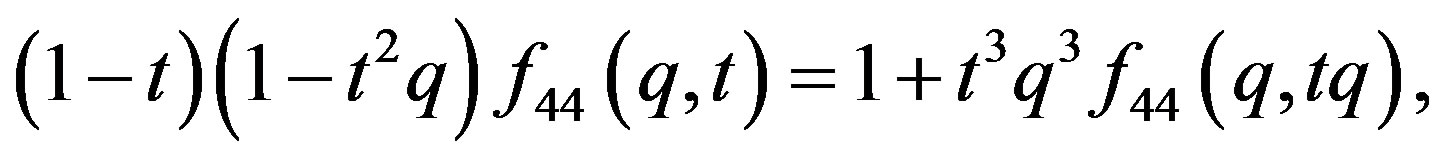
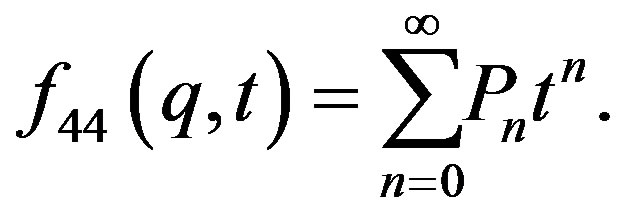
The recurrence relation:
 (33)
(33)
An explicit formula for this family:
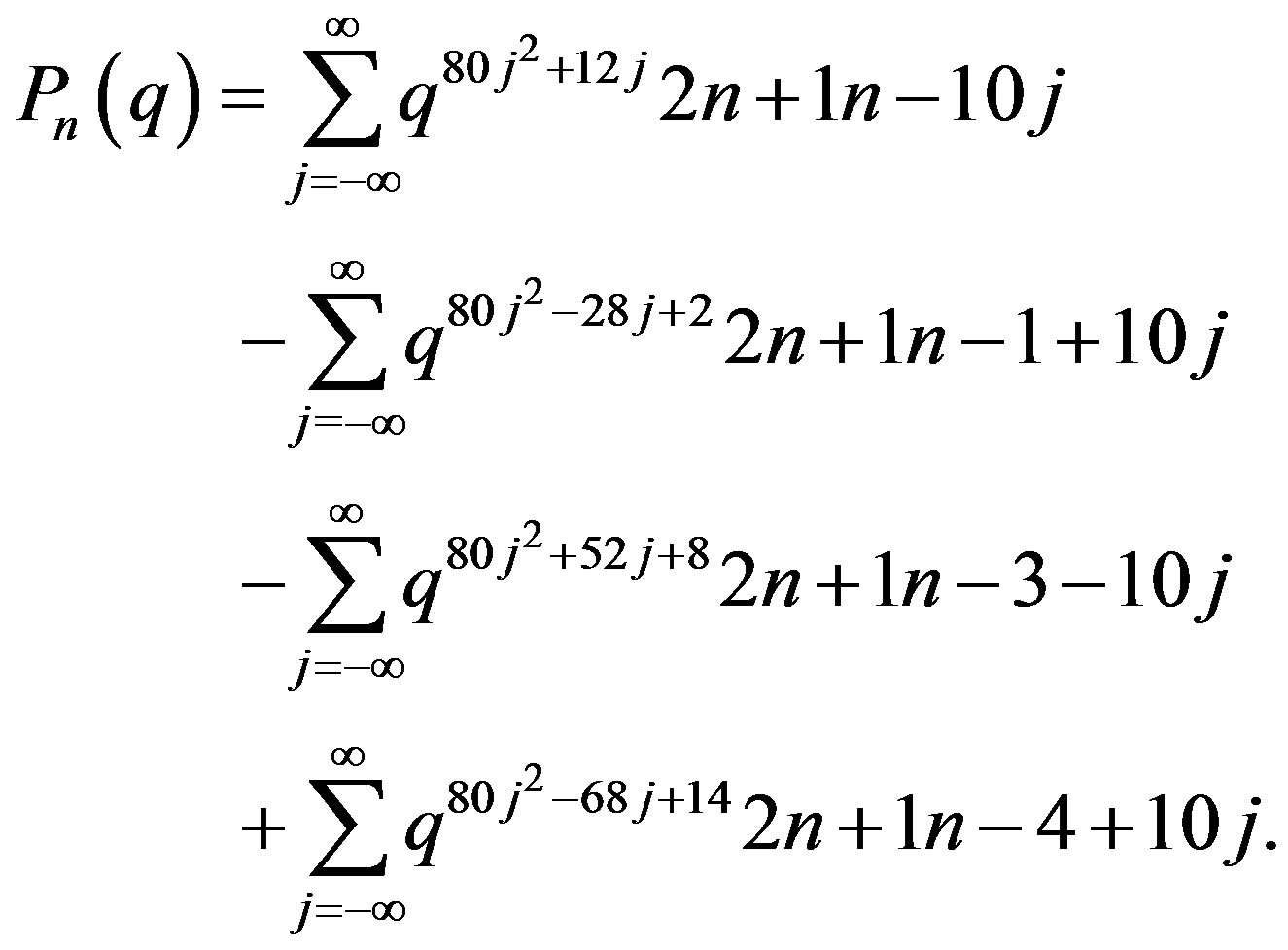 (34)
(34)
We need a definition before stating the next theorem.
We call a black-white partition as the one where the parts may be of two colors, black or white, each black part from one up to the largest part appears at least three times, each white part is odd and counted twice and the largest white part is at most one plus twice the largest black part.
Theorem 6.1 The total number of black-white partitions into at most  parts is equal to
parts is equal to .
.
Table 5 has, as an illustration, a few partitions as described in this theorem.
7. The Results from Equation (66)
The two variable function:
 (35)
(35)
The functional equation:
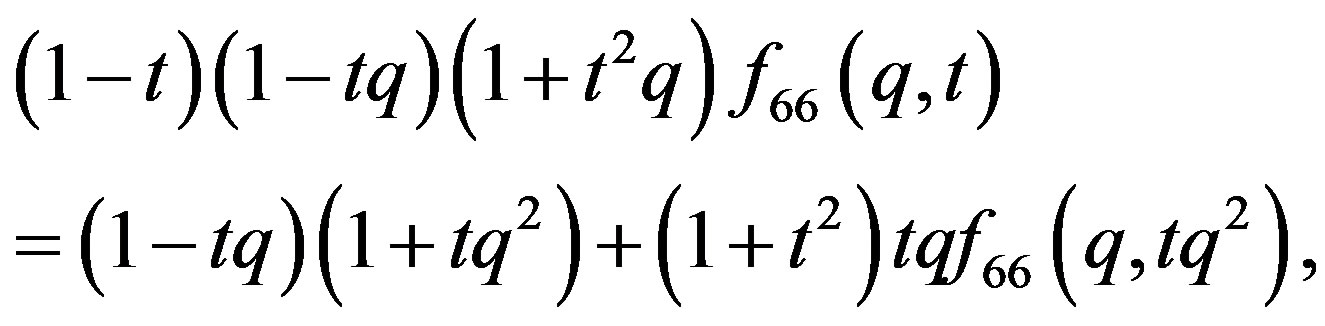 (36)
(36)

Table 5. Partitions as described in Theorem 6.1.
The recurrence relation:
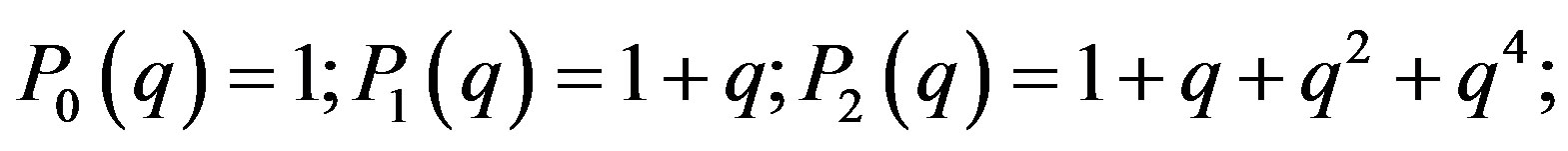
 (37)
(37)
An explicit formula for this family:
 (38)
(38)
We define a yellow-white partition as the one where the parts may be of two colors, yellow or white, where the white parts are odd and every odd from 1 up to the largest odd part 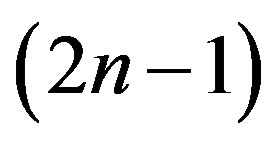 appears at least once, the yellow parts are even, appearing in pairs, with the largest one being one plus the largest odd
appears at least once, the yellow parts are even, appearing in pairs, with the largest one being one plus the largest odd  and for each pair of even up to the largest odd minus one there is a overlined part, i.e., for those parts (pairs of even from 2 up to
and for each pair of even up to the largest odd minus one there is a overlined part, i.e., for those parts (pairs of even from 2 up to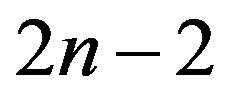 ) actually we do have an overpartition.
) actually we do have an overpartition.
Theorem 7.1 If we consider for each 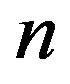 the yellowwhite partitions with
the yellowwhite partitions with  or
or 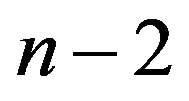 part then the total number of all such partitions with
part then the total number of all such partitions with 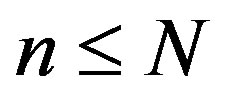 is equal to
is equal to , where
, where 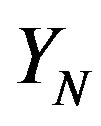 denote the general term for sequence A052542 from The On-Line Encyclopedia of Integer Sequences. This sequence, apart form the inicial 1, is simply twice the Pell numbers.
denote the general term for sequence A052542 from The On-Line Encyclopedia of Integer Sequences. This sequence, apart form the inicial 1, is simply twice the Pell numbers.
Table 6 has, as an illustration, a few partitions as described in this theorem.
8. The Results from Equation (67)
The two variable function:
 (39)
(39)
The functional equation:

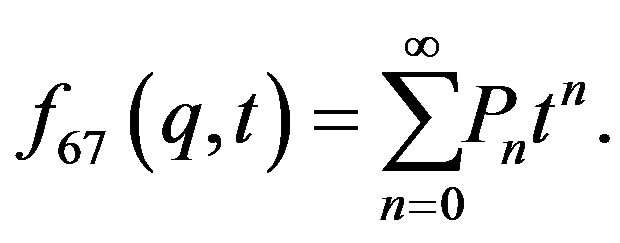
The recurrence relation:
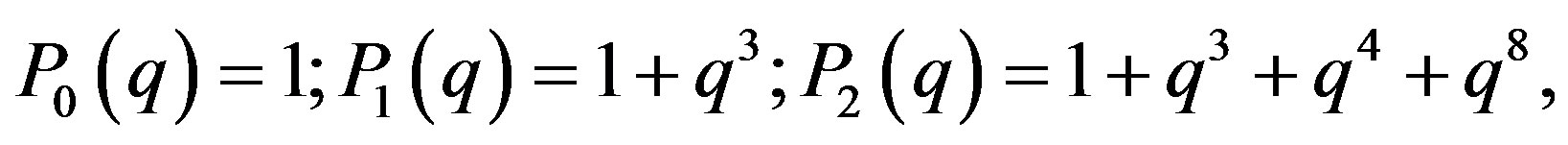
 (40)
(40)
An explicit formula for this family:
 (41)
(41)
Table 6. Partitions as described in Theorem 7.1.
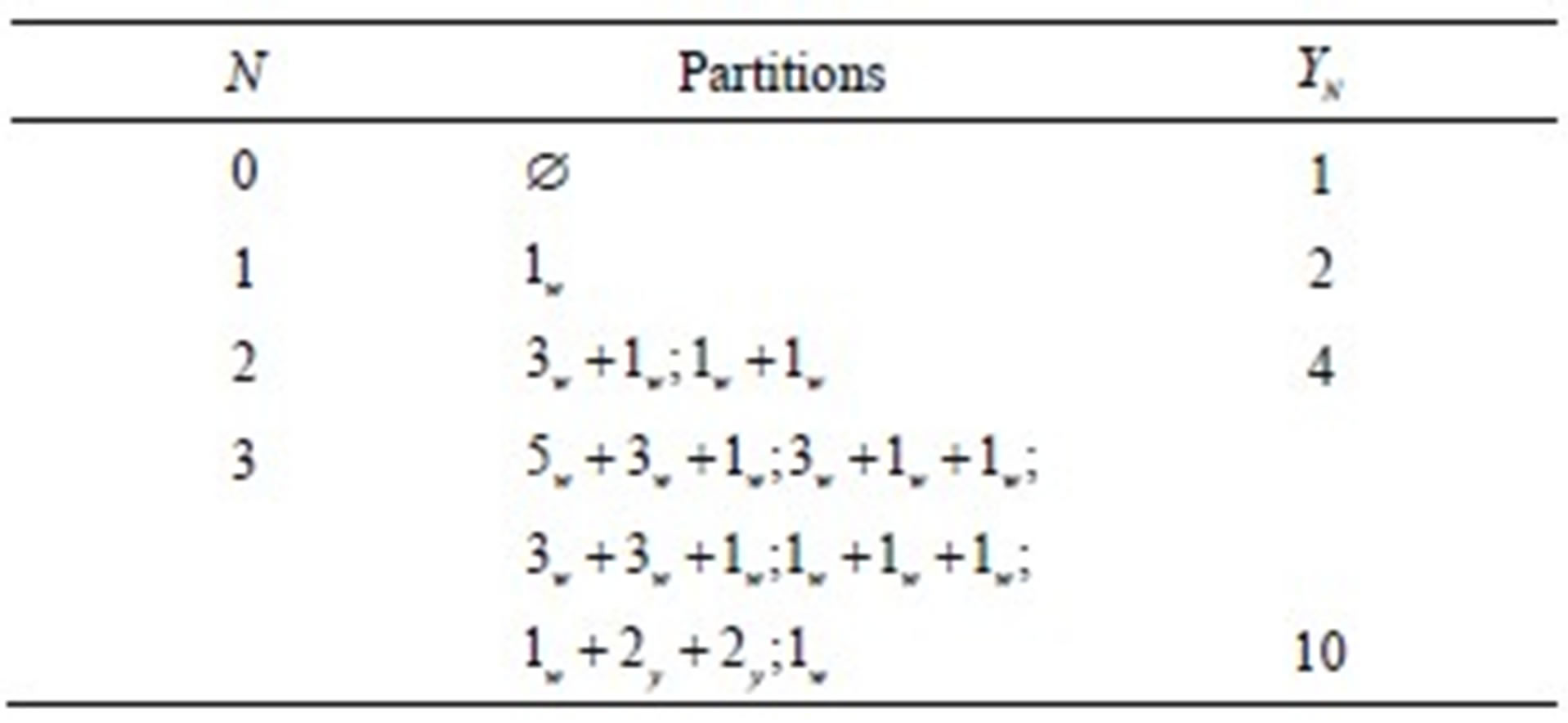
We define a blue-red partition as the one where the parts may be of two colors, blue or red, where the red parts are odd, the largest red part  appears only once and every odd from 3 up to the largest odd part
appears only once and every odd from 3 up to the largest odd part 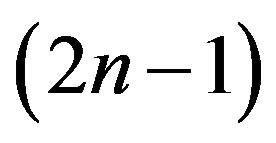 appears at least once, the blue parts are even, appearing in pairs, with the largest blue part
appears at least once, the blue parts are even, appearing in pairs, with the largest blue part 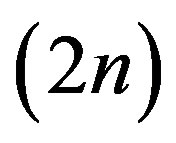 been one plus the largest odd and for each pair of even up to the largest odd minus one there is a overlined part, i.e., for those parts (pairs of even from 2 up to
been one plus the largest odd and for each pair of even up to the largest odd minus one there is a overlined part, i.e., for those parts (pairs of even from 2 up to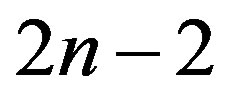 ) actually we do have an overpartition.
) actually we do have an overpartition.
Theorem 8.1 If we consider for each  the blue-red partitions with
the blue-red partitions with  or
or 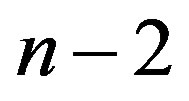 parts then the total number of all such partitions with
parts then the total number of all such partitions with  is equal to
is equal to , where
, where  denote the general term for sequence A052542 from The On-Line Encyclopedia if Integer Sequences.
denote the general term for sequence A052542 from The On-Line Encyclopedia if Integer Sequences.
Table 7 has, as an illustration, a few partitions as described in this theorem.
9. The Results from Equation (80)
The two variable function:
 (42)
(42)
The functional equation:
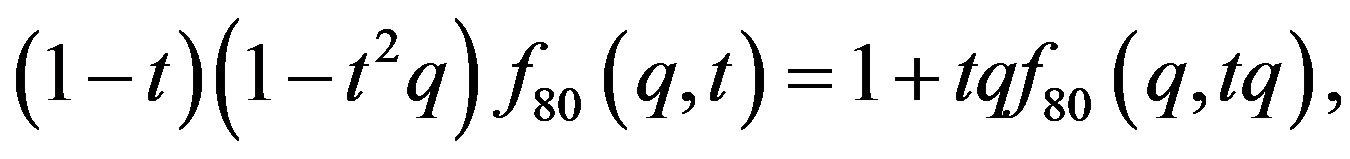

The recurrence relation:
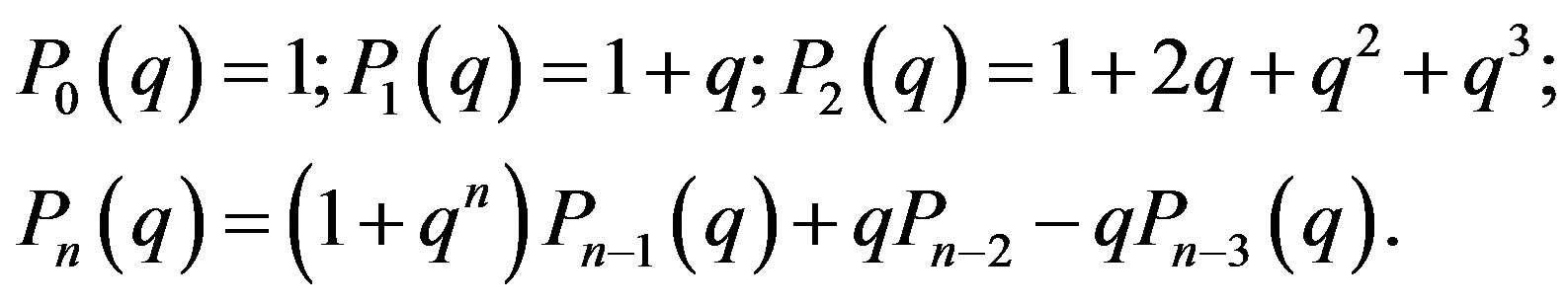 (43)
(43)
An explicit formula for this family:
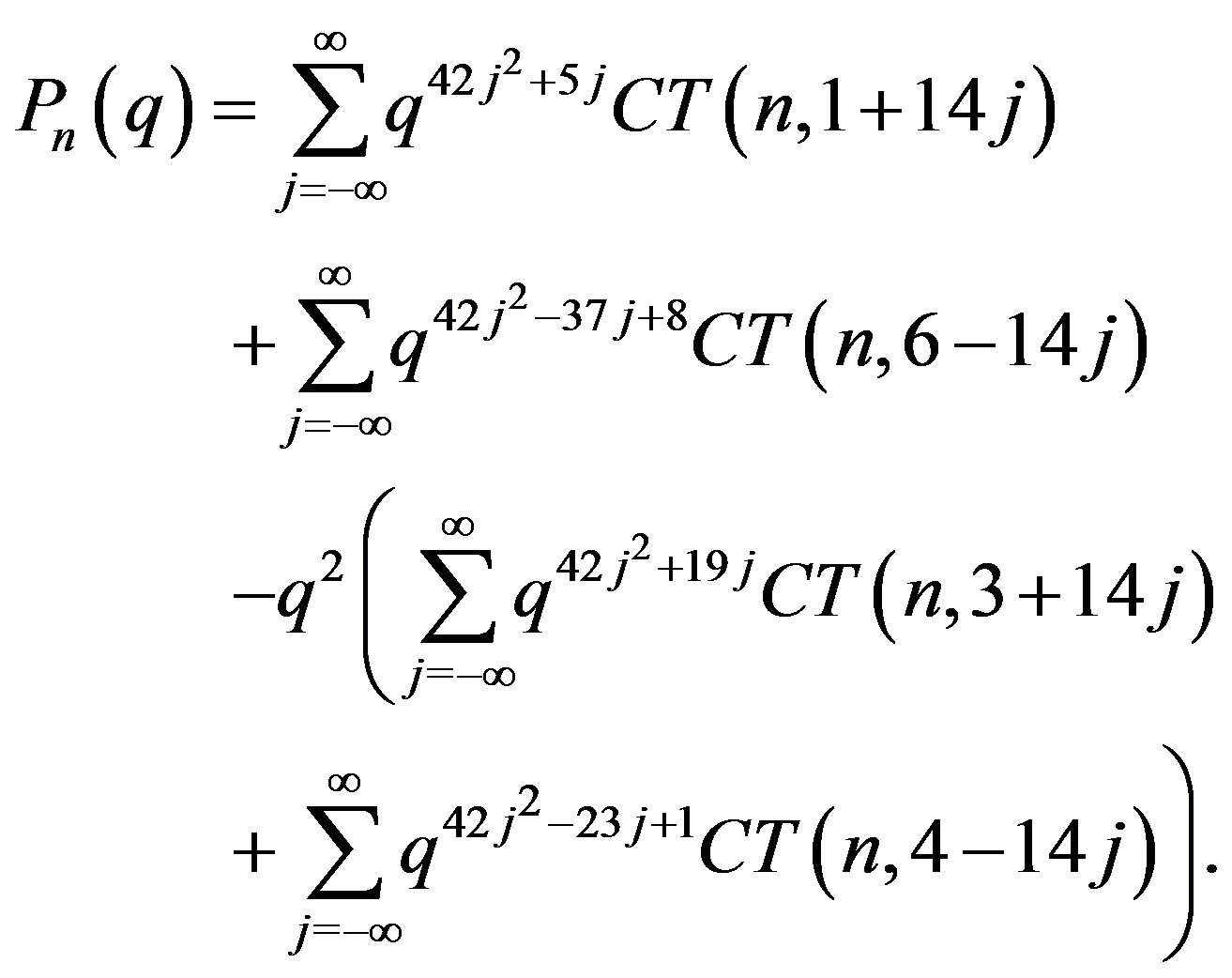 (44)
(44)
We need a definition before stating the next theorem.
We call a green-black partition as the one where the parts may be of two colors, green or black, each green part from one up to the largest part appears at least once and at most twice, each black part is counted twice and the largest black part is at most one plus twice the largest green part.
Theorem 9.1 The total number of green-black partitions into at most  parts is equal to
parts is equal to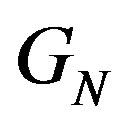 , where
, where 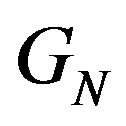 denote the general term for sequence A006054 from The On-Line Encyclopedia if Integer Sequences.
denote the general term for sequence A006054 from The On-Line Encyclopedia if Integer Sequences.
Table 8 has, as an illustration, a few partitions as described in this theorem.
10. The Results from Equation (81)
The two variable function:
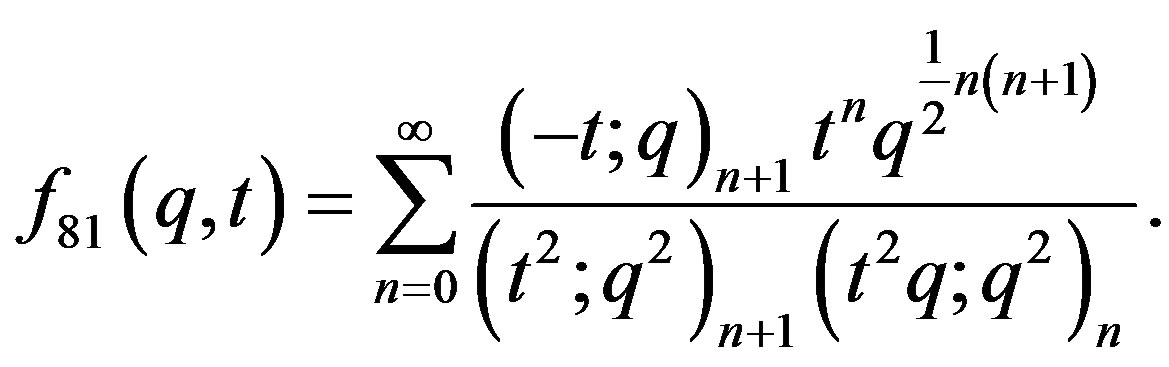 (45)
(45)
The functional equation:
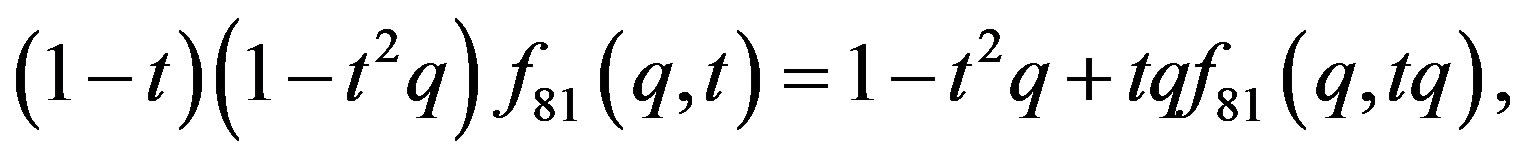
The recurrence relation:
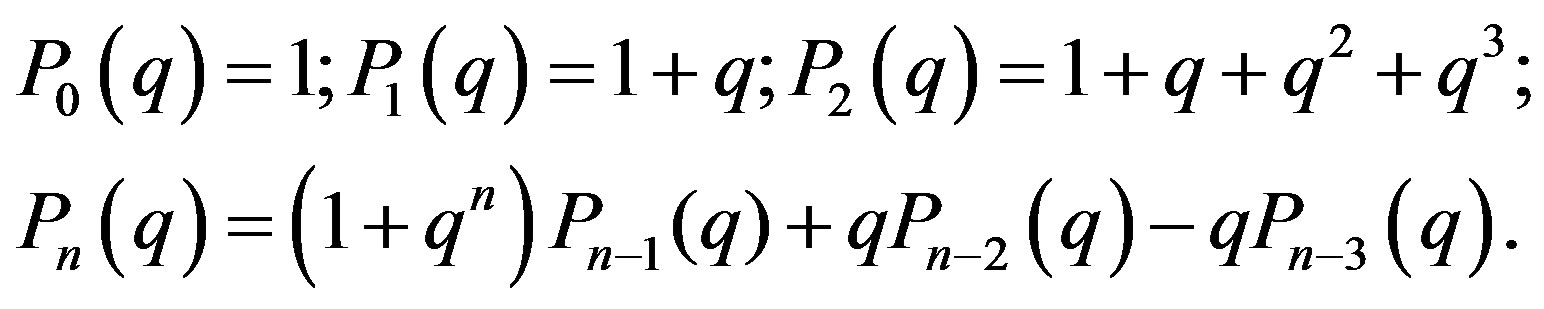 (46)
(46)
An explicit formula for this family:
Table 7. Partitions as described in Theorem 8.1.

Table 8. Partitions as described in Theorem 9.1.

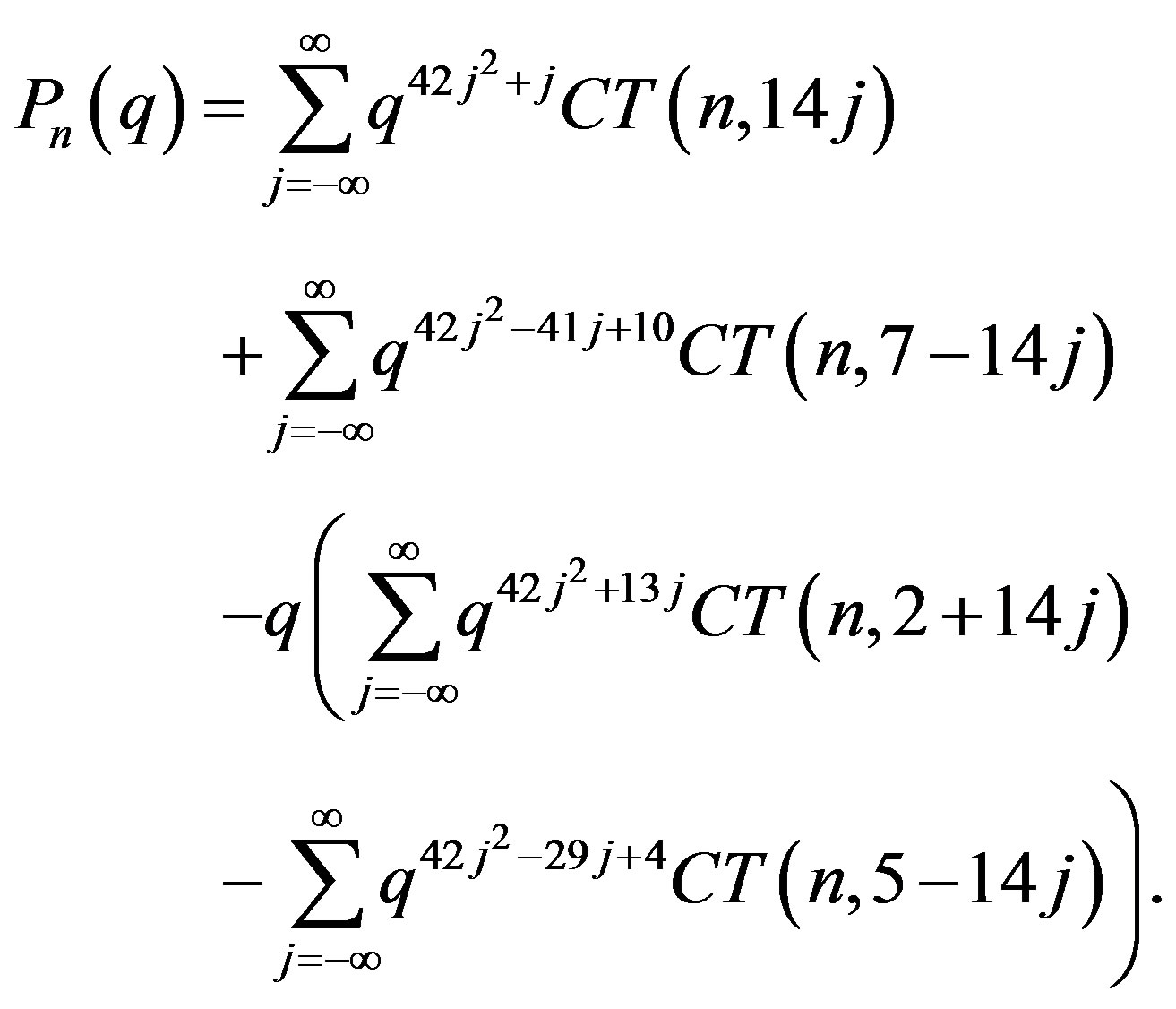 (47)
(47)
We need a definition before stating the next theorem.
We call a red-black partition as the one where the parts may be of two colors, red or black, each red part from one up to the largest part appears at least once and at most twice, each black part is counted twice and the largest black part is at most twice the largest red part.
Theorem 10.1 The total number of red-black partitions into at most  parts is equal to
parts is equal to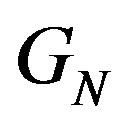 , where
, where 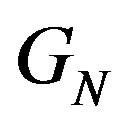 denote the general term for sequence A052534 from The On-Line Encyclopedia of Integer Sequences.
denote the general term for sequence A052534 from The On-Line Encyclopedia of Integer Sequences.
Table 9 has, as an illustration, a few partitions as described in this theorem.
Table 9. Partitions as described in Theorem 10.1.

11. Conclusion
It is our believe that more results of similar type may be obtained following the ideas used in this paper. The computer algebra packages available today are a powerful tool in the study of q-series identities of the RogersRamanujan type.
REFERENCES
- J. P. O. Santos and M. Ivkovic, “Polynomial Generalizations of the Pell Sequence and the Fibonacci Sequence,” The Fibonacci Quarterly, Vol. 43, No. 4, 2005, pp. 328- 338.
- J. P. O. Santos and M. Ivkovic, “Fibonacci Numbers and Partitions,” The Fibonacci Quarterly, Vol. 41, No. 3, 2003, pp. 263-278.
- J. P. O. Santos, “On the Combinatorics of Polynomial Generalizations of Rogers-Ramanujan-Type Identities,” Discrete Mathematics, Vol. 254, No. 1-3, 2002, pp. 497- 511. doi:10.1016/S0012-365X(01)00378-8
- G. E. Andrews, “Combinatorics and Ramanujan’s ‘Lost’ Notebook,” In: London Mathematical Society Lecture Note Series, No. 103, Cambridge University Press, London, 1985, pp. 1-23.
- J. P. O. Santos, “Computer Algebra and Identities of the Rogers-Ramanujan Type,” Ph.D. Thesis, Pennsylvania State University, University Park, 1991.
- L. J. Slater, “Further Identities of the Rogers-Ramanujan Type,” Proceedings London Mathematical Society, Vol. s2-54, No. 1, 1952, pp. 147-167. doi:10.1112/plms/s2-54.2.147
- L. J. Slater, “A New Proof of Roger’s Transformations of Infinite Series,” Proceedings London Mathematical Society, Vol. s2-53, No. 1, 1951, pp. 460-475. doi:10.1112/plms/s2-53.6.460
- A. V. Sills. “RRtools—A Maple Package for Aiding the Discovery and Proof of Finite Rogers-Ramanujan Type Identities,” Journal of Symbolic Computation, Vol. 37, No. 4, 2004, pp. 415-448. http://math.georgiasouthern.edu/asills/maple/RRtools1
NOTES
*Partially supported by FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo).

